An Object- and Shapelet-Based Method for Mapping Planted Forest Dynamics from Landsat Time Series
Abstract
1. Introduction
2. Materials and Methods
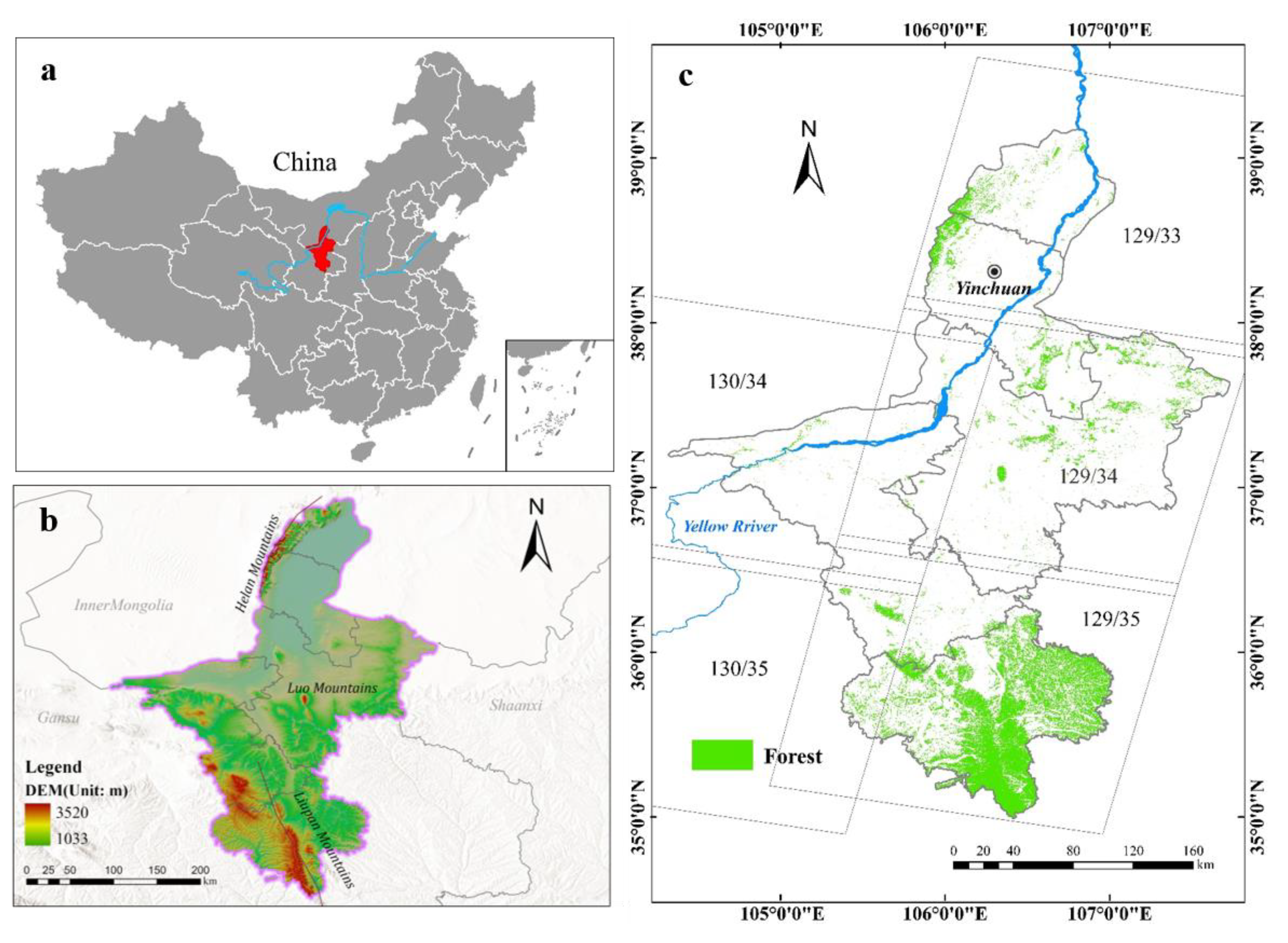
2.1. Study Area
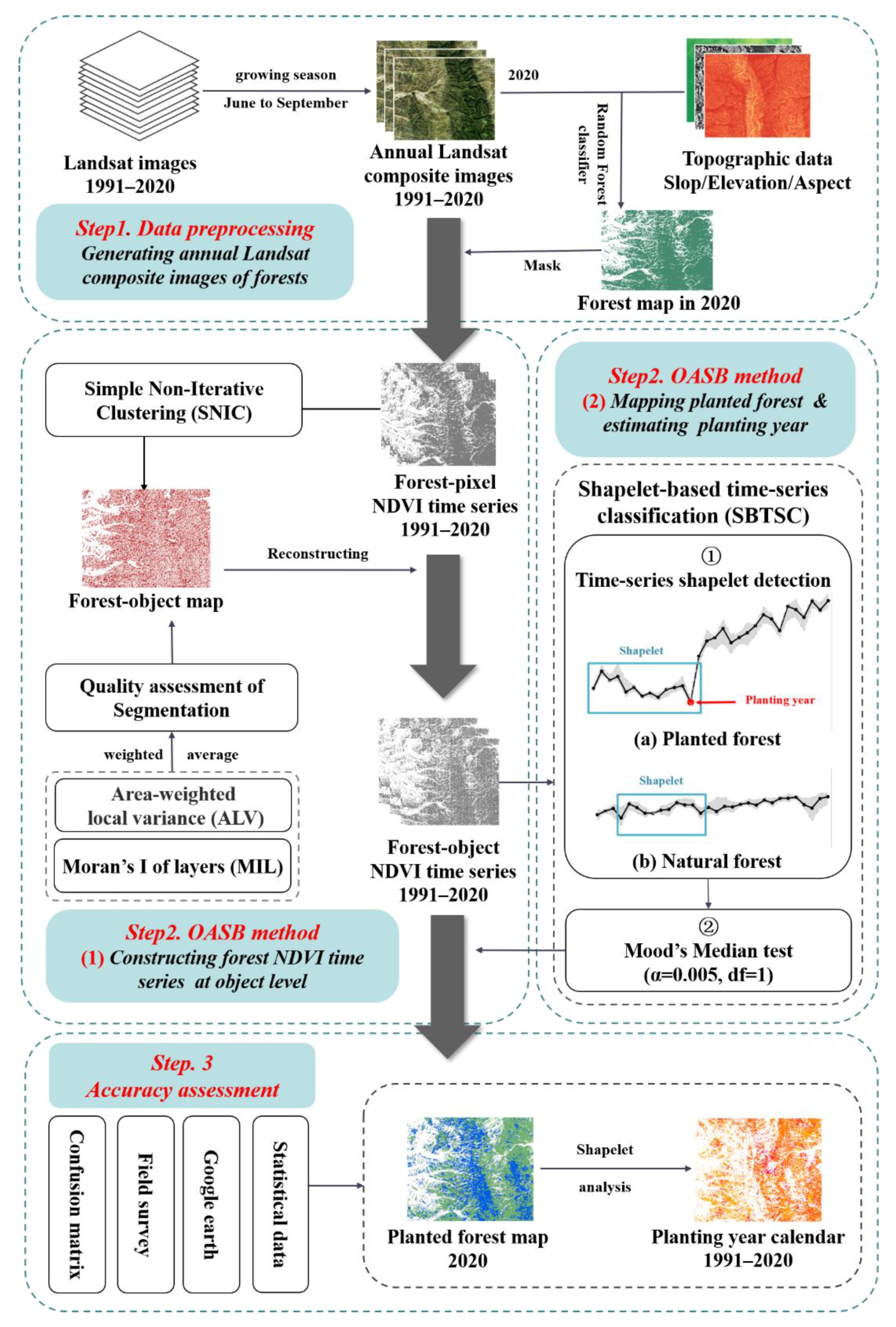
2.2. Methods
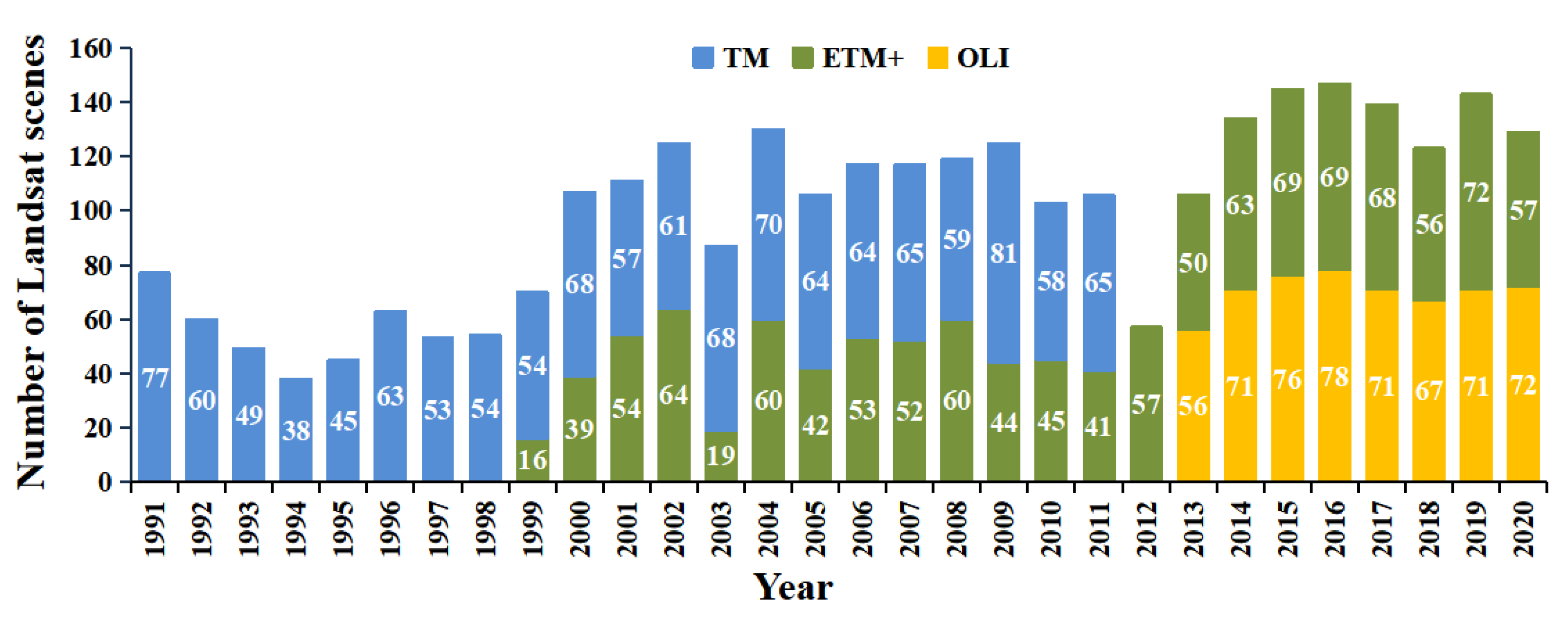
2.2.1. Data and Processing
| Category | Variables | Acronym | Equations or Descriptions | References | Importance |
|---|---|---|---|---|---|
| Topographic index | Slope | - | Slope/elevation calculated from digital elevation model (DEM) data | - | 1 |
| Elevation | - | 4 | |||
| Textural index | Variance (VAR) | VAR_64 | [40] | 2 | |
| Sum average (SAVG) | SAVG_64 | 7 | |||
| SAVG_8 | 8 | ||||
| SAVG_3 | 9 | ||||
| SAVG_16 | 12 | ||||
| SAVG_32 | 14 | ||||
| Correlation (CORR) | CORR_64 | 11 | |||
| Spectral band | Blue | B1 | - | - | 3 |
| Red | B3 | - | - | 6 | |
| Spectral index | Modified normalized difference water index | MNDWI | [41] | 5 | |
| Enhanced vegetation index | EVI | [42] | 10 | ||
| Normalized difference built-up index | NDBI | [43] | 13 | ||
| Land surface water index | LSWI | [44] | 15 |
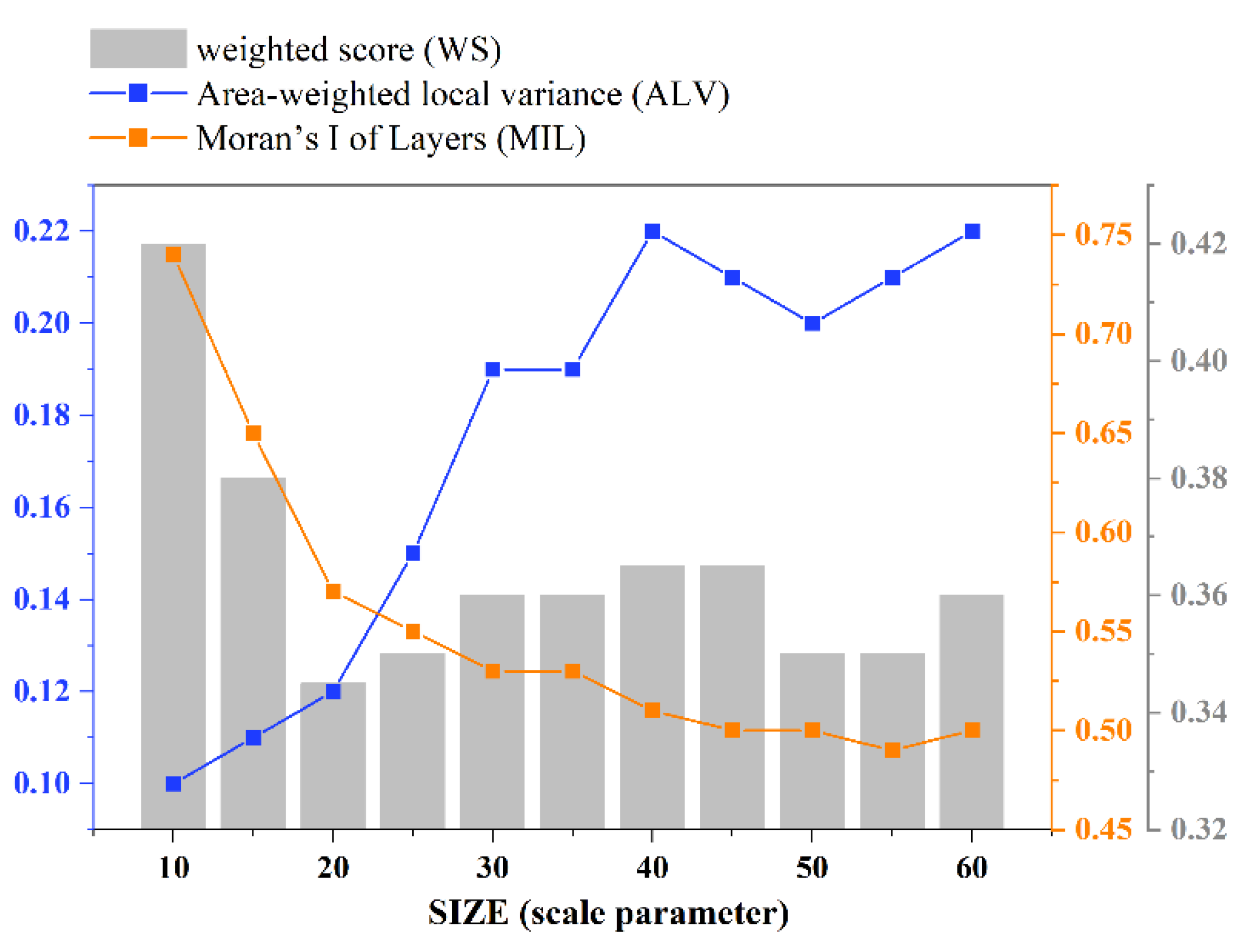
2.2.2. Forest Object Generation
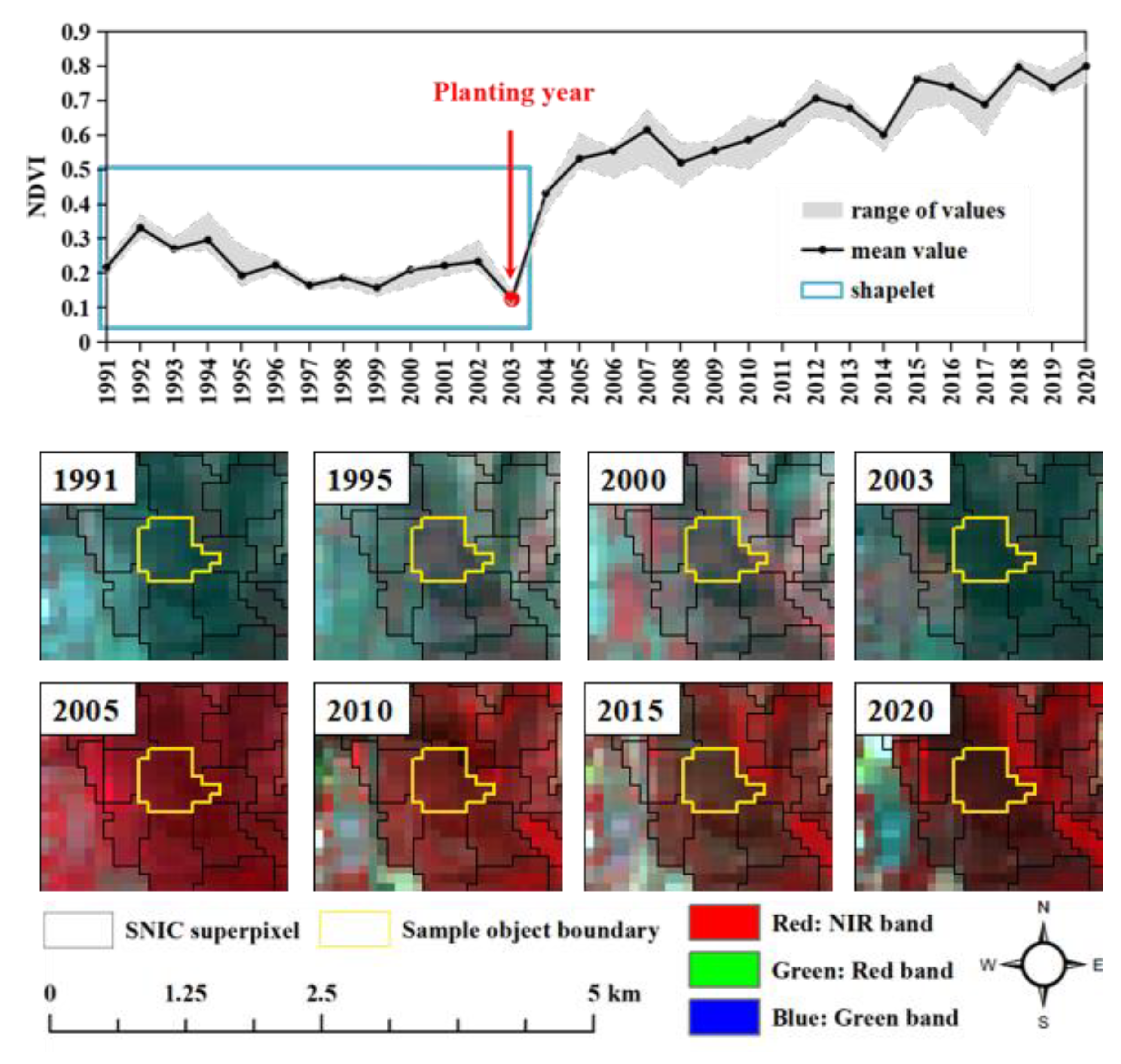
2.2.3. Time-Series Shapelet Detection
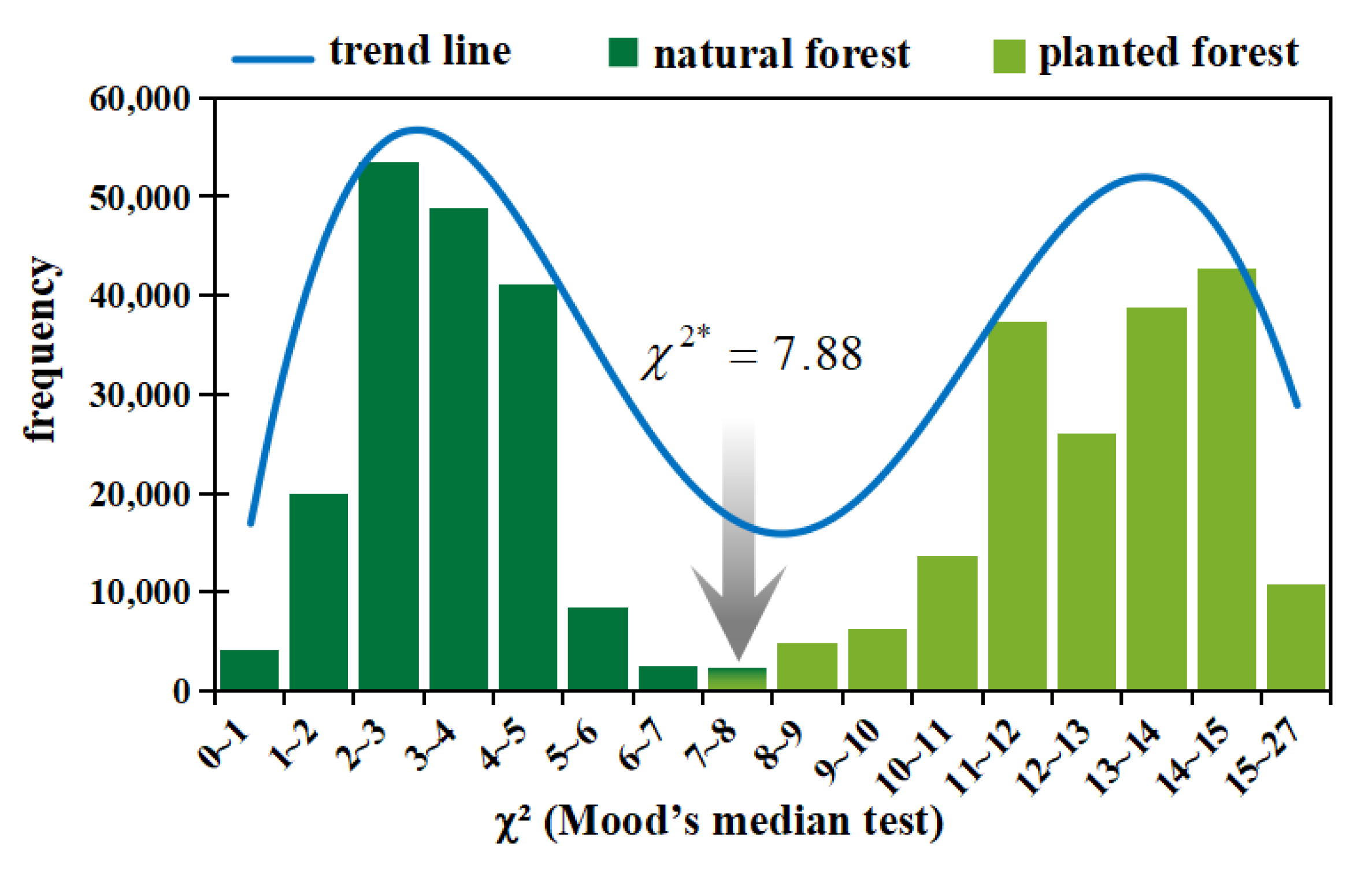
2.2.4. Mood Median Test
2.2.5. Planting Year Estimation
3. Results
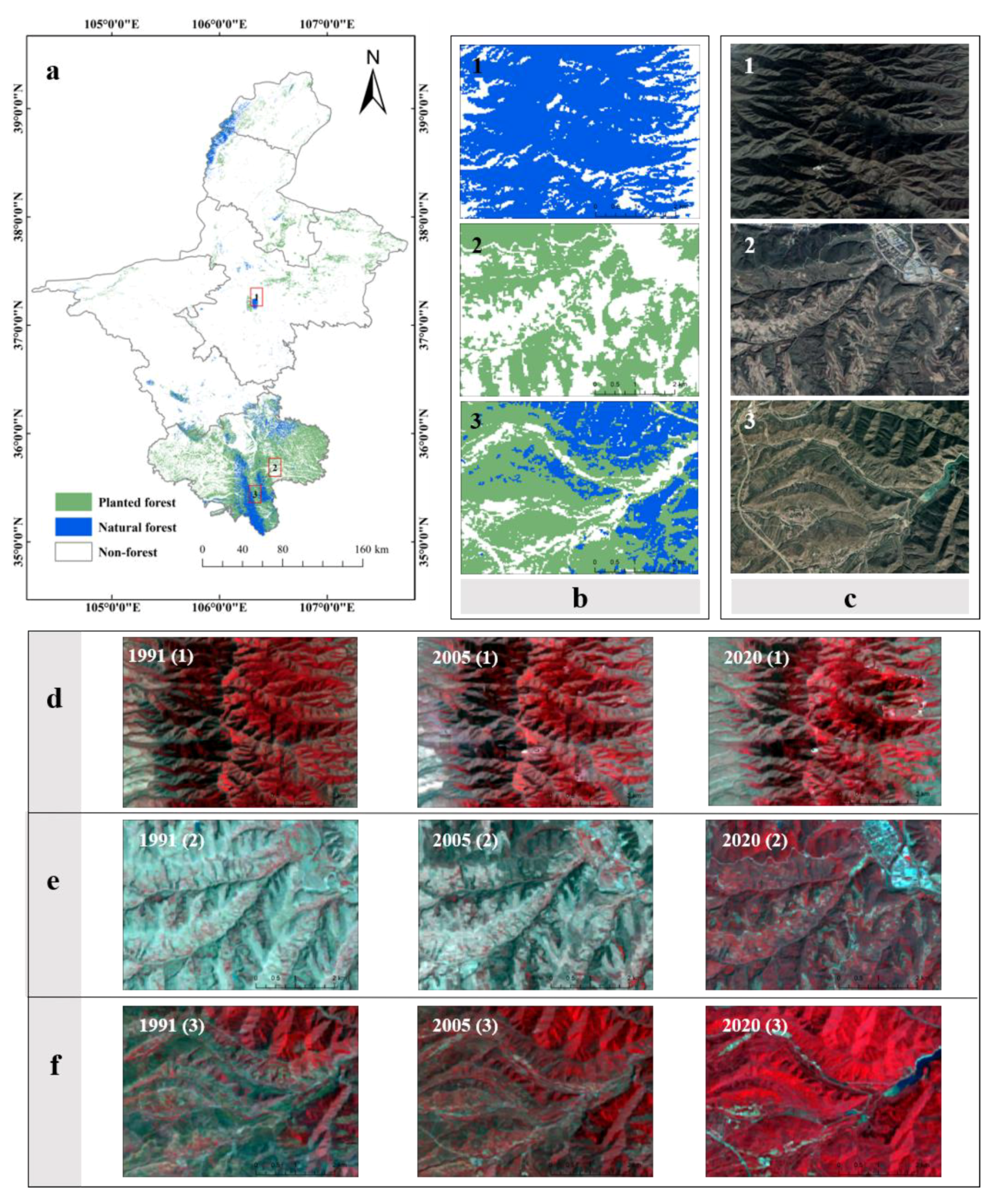
3.1. Superpixel Segmentation of Forested Areas
3.2. Planted and Natural Forest Mapping
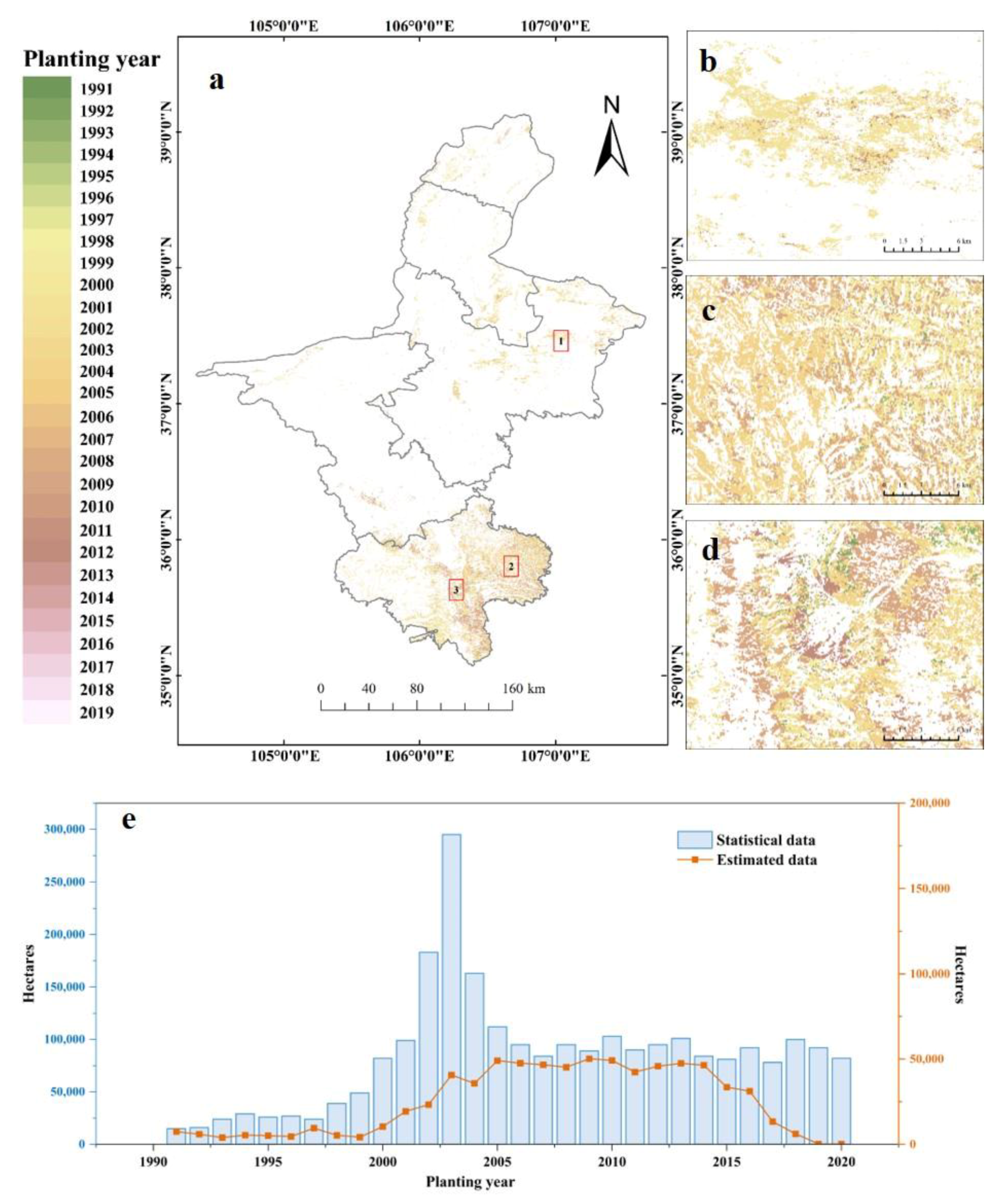
3.3. Planting Year Characterization
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, Z.; Zhao, H.; Liu, S.; Zhou, G.; Fang, J.; Yu, G.; Tang, X.; Wang, W.; Yan, J.; Wang, G.; et al. Mapping Forest Type and Age in China’s Plantations. Sci. Total Environ. 2020, 744, 140790. [Google Scholar] [CrossRef]
- FAO. Global Forest Resources Assessment 2020: Main Report; FAO: Rome, Italy, 2020. [Google Scholar] [CrossRef]
- Malagnoux, M.; Sène, E.H.; Atzmon, N. Forests, Trees and Water in Arid Lands: A Delicate Balance. Unasylva 2007, 58, 24–29. [Google Scholar]
- Lu, C.; Zhao, T.; Shi, X.; Cao, S. Ecological Restoration by Afforestation May Increase Groundwater Depth and Create Potentially Large Ecological and Water Opportunity Costs in Arid and Semiarid China. J. Clean. Prod. 2018, 176, 1213–1222. [Google Scholar] [CrossRef]
- Zhou, K.; Cao, L.; Liu, H.; Zhang, Z.; Wang, G.; Cao, F. Estimation of Volume Resources for Planted Forests Using an Advanced LiDAR and Hyperspectral Remote Sensing. Resour. Conserv. Recycl. 2022, 185, 106485. [Google Scholar] [CrossRef]
- Schiefer, F.; Kattenborn, T.; Frick, A.; Frey, J.; Schall, P.; Koch, B.; Schmidtlein, S. Mapping Forest Tree Species in High Resolution UAV-Based RGB-Imagery by Means of Convolutional Neural Networks. ISPRS J. Photogramm. Remote Sens. 2020, 170, 205–215. [Google Scholar] [CrossRef]
- Zhao, H.; Zhong, Y.; Wang, X.; Hu, X.; Luo, C.; Boitt, M.; Piiroinen, R.; Zhang, L.; Heiskanen, J.; Pellikka, P. Mapping the Distribution of Invasive Tree Species Using Deep One-Class Classification in the Tropical Montane Landscape of Kenya. ISPRS J. Photogramm. Remote Sens. 2022, 187, 328–344. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, W.; Yao, Y.; Wang, W. Individual Tree Segmentation and Tree Species Classification in Subtropical Broadleaf Forests Using UAV-Based LiDAR, Hyperspectral, and Ultrahigh-Resolution RGB Data. Remote Sens. Environ. 2022, 280, 113143. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, T.; Skidmore, A.K.; Holzwarth, S.; Heiden, U.; Heurich, M. Mapping Individual Silver Fir Trees Using Hyperspectral and LiDAR Data in a Central European Mixed Forest. Int. J. Appl. Earth Obs. Geoinf. 2021, 98, 102311. [Google Scholar] [CrossRef]
- Spadoni, G.L.; Cavalli, A.; Congedo, L.; Munafò, M. Analysis of Normalized Difference Vegetation Index (NDVI) Multi-Temporal Series for the Production of Forest Cartography. Remote Sens. Appl. 2020, 20, 100419. [Google Scholar] [CrossRef]
- Ahmad, B.; Wang, Y.; Hao, J.; Liu, Y.; Bohnett, E.; Zhang, K. Optimizing Stand Structure for Tradeoffs between Overstory and Understory Vegetation Biomass in a Larch Plantation of Liupan Mountains, Northwest China. For. Ecol. Manag. 2019, 443, 43–50. [Google Scholar] [CrossRef]
- Kou, W.; Dong, J.; Xiao, X.; Hernandez, A.J.; Qin, Y.; Zhang, G.; Chen, B.; Lu, N.; Doughty, R. Expansion Dynamics of Deciduous Rubber Plantations in Xishuangbanna, China during 2000–2010. Gisci. Remote Sens. 2018, 55, 905–925. [Google Scholar] [CrossRef]
- Deng, X.; Guo, S.; Sun, L.; Chen, J. Identification of Short-Rotation Eucalyptus Plantation at Large Scale Using Multi-Satellite Imageries and Cloud Computing Platform. Remote Sens. 2020, 12, 2153. [Google Scholar] [CrossRef]
- Xu, W.; Huang, S.; Wu, C.; Xiong, Y.; Wang, L.; Lu, N.; Kou, W. The Pruning Phenological Phase-Based Method for Extracting Tea Plantations by Field Hyperspectral Data and Landsat Time Series Imagery. Geocarto. Int. 2022, 37, 2116–2136. [Google Scholar] [CrossRef]
- FRAChina. Available online: https://www.fao.org/3/ca9980en/ca9980en.pdf (accessed on 26 June 2022).
- FAO. Global Forest Resources Assessment 2020—Key Findings; Rome, Italy. Available online: https://www.fao.org/3/CA8753EN/CA8753EN.pdf (accessed on 26 June 2022).
- Fagan, M.E.; Morton, D.C.; Cook, B.D.; Masek, J.; Zhao, F.; Nelson, R.F.; Huang, C. Mapping Pine Plantations in the Southeastern U.S. Using Structural, Spectral, and Temporal Remote Sensing Data. Remote Sens. Environ. 2018, 216, 415–426. [Google Scholar] [CrossRef]
- Bey, A.; Meyfroidt, P. Improved Land Monitoring to Assess Large-Scale Tree Plantation Expansion and Trajectories in Northern Mozambique. Environ. Res. Commun. 2021, 3, 115009. [Google Scholar] [CrossRef]
- Li, S.; Yang, S.; Liu, X.; Liu, Y.; Shi, M. NDVI-Based Analysis on the Influence of Climate Change and Human Activities on Vegetation Restoration in the Shaanxi-Gansu-Ningxia Region, Central China. Remote Sens. 2015, 7, 11163–11182. [Google Scholar] [CrossRef]
- Ye, S.; Rogan, J.; Sangermano, F. Monitoring Rubber Plantation Expansion Using Landsat Data Time Series and a Shapelet-Based Approach. ISPRS J. Photogramm. Remote Sens. 2018, 136, 134–143. [Google Scholar] [CrossRef]
- Ye, L.; Keogh, E. Time Series Shapelets: A New Primitive for Data Mining. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 947–955. [Google Scholar] [CrossRef]
- Yin, H.; Camacho, D.; Tino, P.; Tallón-Ballesteros, A.J.; Menezes, R.; Allmendinger, R. (Eds.) Intelligent Data Engineering and Automated Learning—IDEAL 2019; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 11871, ISBN 978-3-030-33606-6. [Google Scholar]
- Song, Y.; Zhai, J.; Zhang, J.; Qiao, L.; Wang, G.; Ma, L.; Xue, S. Forest Management Practices of Pinus Tabulaeformis Plantations Alter Soil Organic Carbon Stability by Adjusting Microbial Characteristics on the Loess Plateau of China. Sci. Total Environ. 2021, 766, 144209. [Google Scholar] [CrossRef]
- Li, Z.; Sun, X.; Huang, Z.; Zhang, X.; Wang, Z.; Li, S.; Zheng, W.; Zhai, B. Changes in Nutrient Balance, Environmental Effects, and Green Development after Returning Farmland to Forests: A Case Study in Ningxia, China. Sci. Total Environ. 2020, 735, 139370. [Google Scholar] [CrossRef]
- Zhu, J.; Song, L. A Review of Ecological Mechanisms for Management Practices of Protective Forests. J. For. Res. 2021, 32, 435–448. [Google Scholar] [CrossRef]
- Martini, F.; Sun, I.F.; Chen, Y.Y. Effects of Plant Diversity and Leaf Traits on Insect Herbivory in Plantation and Natural Forests. For. Ecol. Manag. 2022, 509, 120085. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of Studies on Tree Species Classification from Remotely Sensed Data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Chen, G.; Thill, J.C.; Anantsuksomsri, S.; Tontisirin, N.; Tao, R. Stand Age Estimation of Rubber (Hevea Brasiliensis) Plantations Using an Integrated Pixel- and Object-Based Tree Growth Model and Annual Landsat Time Series. ISPRS J. Photogramm. Remote Sens. 2018, 144, 94–104. [Google Scholar] [CrossRef]
- Wang, X.; Yang, B. Divergent Tree Radial Growth at Alpine Coniferous Forest Ecotone and Corresponding Responses to Climate Change in Northwestern China. Ecol. Indic. 2021, 121, 107052. [Google Scholar] [CrossRef]
- Zeng, X.; Wei, C.; Liu, X.; Zhang, L. Qinghai Spruce (Picea Crassifolia) and Chinese Pine (Pinus Tabuliformis) Show High Vulnerability and Similar Resilience to Early-Growing-Season Drought in the Helan Mountains, China. Ecol. Indic. 2020, 110, 105871. [Google Scholar] [CrossRef]
- Wang, B.; Chen, T.; Li, C.; Xu, G.; Wu, G.; Liu, G. Discrepancy in Growth Resilience to Drought among Different Stand-Aged Forests Declines Going from a Semi-Humid Region to an Arid Region. For. Ecol. Manage. 2022, 511, 120135. [Google Scholar] [CrossRef]
- Gao, Y.; He, Z.; Zhu, X.; Chen, L.; Du, J.; Lin, P.; Tian, Q.; Kong, J. Potential Distribution and Habitat Suitability of Picea Crassifolia with Climate Change Scenarios. Can. J. Forest Res. 2021, 51, 1903–1915. [Google Scholar] [CrossRef]
- Xiaoyan, B.; Suocheng, D.; Wenbao, M.; Fujia, L. Spatial-Temporal Change of Carbon Storage and Sink of Wetland Ecosystem in Arid Regions, Ningxia Plain. Atmos. Environ. 2019, 204, 89–101. [Google Scholar] [CrossRef]
- Tian, A.; Wang, Y.; Webb, A.A.; Liu, Z.; Ma, J.; Yu, P.; Wang, X. Water Yield Variation with Elevation, Tree Age and Density of Larch Plantation in the Liupan Mountains of the Loess Plateau and Its Forest Management Implications. Sci. Total Environ. 2021, 752, 141752. [Google Scholar] [CrossRef]
- Buchner, J.; Yin, H.; Frantz, D.; Kuemmerle, T.; Askerov, E.; Bakuradze, T.; Bleyhl, B.; Elizbarashvili, N.; Komarova, A.; Lewińska, K.E.; et al. Land-Cover Change in the Caucasus Mountains since 1987 Based on the Topographic Correction of Multi-Temporal Landsat Composites. Remote Sens. Environ. 2020, 248, 111967. [Google Scholar] [CrossRef]
- Zhu, Z. Change Detection Using Landsat Time Series: A Review of Frequencies, Preprocessing, Algorithms, and Applications. ISPRS J. Photogramm. Remote Sens. 2017, 130, 370–384. [Google Scholar] [CrossRef]
- Li, S.; Yan, J.; Liu, X.; Wan, J. Response of Vegetation Restoration to Climate Change and Human Activities in Shaanxi-Gansu-Ningxia Region. J. Geogr. Sci. 2013, 23, 98–112. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and Expansion of the Fmask Algorithm: Cloud, Cloud Shadow, and Snow Detection for Landsats 4–7, 8, and Sentinel 2 Images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Haralick, R.M.; Dinstein, I.; Shanmugam, K. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Haralick, R.M. Glossary and Index to Remotely Sensed Image Pattern Recognition Concepts. Pattern Recognit. 1973, 5, 391–403. [Google Scholar] [CrossRef]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Zheng, Y.; Tang, L.; Wang, H. An Improved Approach for Monitoring Urban Built-up Areas by Combining NPP-VIIRS Nighttime Light, NDVI, NDWI, and NDBI. J. Clean. Prod. 2021, 328, 129488. [Google Scholar] [CrossRef]
- Liu, W.; Dong, J.; Xiang, K.; Wang, S.; Han, W.; Yuan, W. A Sub-Pixel Method for Estimating Planting Fraction of Paddy Rice in Northeast China. Remote Sens. Environ. 2018, 205, 305–314. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A Review of Supervised Object-Based Land-Cover Image Classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Yang, F.; Sun, Q.; Jin, H.; Zhou, Z. Superpixel Segmentation with Fully Convolutional Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Yi, S.; Ma, H.; Wang, X.; Hu, T.; Li, X.; Wang, Y. Weakly-Supervised Semantic Segmentation with Superpixel Guided Local and Global Consistency. Pattern Recognit. 2022, 124, 108504. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2281. [Google Scholar] [CrossRef] [PubMed]
- Achanta, R.; Süsstrunk, S. Superpixels and Polygons Using Simple Non-Iterative Clustering. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 4895–4904. [Google Scholar]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17. [Google Scholar] [CrossRef]
- Yin, H.; Prishchepov, A.V.; Kuemmerle, T.; Bleyhl, B.; Buchner, J.; Radeloff, V.C. Mapping Agricultural Land Abandonment from Spatial and Temporal Segmentation of Landsat Time Series. Remote Sens. Environ. 2018, 210, 12–24. [Google Scholar] [CrossRef]
- Terms and Definitions FRA 2020. Available online: https://www.fao.org/3/I8661EN/i8661en.pdf (accessed on 26 June 2022).
- Hills, J.; Lines, J.; Baranauskas, E.; Mapp, J.; Bagnall, A. Classification of Time Series by Shapelet Transformation. Data Min. Knowl. Discov. 2014, 28, 851–881. [Google Scholar] [CrossRef]
- Zakaria, J.; Mueen, A.; Keogh, E. Clustering Time Series Using Unsupervised-Shapelets. In Proceedings of the IEEE International Conference on Data Mining, ICDM, Brussels, Belgium, 10–13 December 2012; pp. 785–794. [Google Scholar]
- Chen, Z. Extension of Mood’s Median Test for Survival Data. Stat. Probab. Lett. 2014, 95, 77–84. [Google Scholar] [CrossRef]
- Jensen, C.M.; Hines, E.; Holzman, B.A.; Moore, T.J.; Jahncke, J.; Redfern, J.V. Spatial and Temporal Variability in Shipping Traffic Off San Francisco, California. Coast. Manag. 2015, 43, 575–588. [Google Scholar] [CrossRef]
- Lines, J.; Bagnall, A. Alternative Quality Measures for Time Series Shapelets. In International Conference on Intelligent Data Engineering and Automated Learning, IDEAL; Springer: Berlin/Heidelberg, Germany, 2012; pp. 475–483. [Google Scholar] [CrossRef]
- Wei, J.; Cheng, J.; Li, W.; Liu, W. Comparing the Effect of Naturally Restored Forest and Grassland on Carbon Sequestration and Its Vertical Distribution in the Chinese Loess Plateau. PLoS ONE 2012, 7, e40123. [Google Scholar] [CrossRef]
- Lyu, R.; Zhang, J.; Xu, M.; Li, J. Impacts of Urbanization on Ecosystem Services and Their Temporal Relations: A Case Study in Northern Ningxia, China. Land Use Policy 2018, 77, 163–173. [Google Scholar] [CrossRef]
- Song, W.; Feng, Y.; Wang, Z. Ecological Restoration Programs Dominate Vegetation Greening in China. Sci. Total Environ. 2022, 848, 157729. [Google Scholar] [CrossRef]
- Zhai, J.; Wang, L.; Liu, Y.; Wang, C.; Mao, X. Assessing the Effects of China’s Three-North Shelter Forest Program over 40 Years. Sci. Total Environ. 2023, 857, 159354. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Ouyang, H.; Maclaren, V.; Yin, Y.; Shao, B.; Boland, A.; Tian, Y. Evaluation of the Economic and Environmental Impact of Converting Cropland to Forest: A Case Study in Dunhua County, China. J. Environ. Manag. 2007, 85, 746–756. [Google Scholar] [CrossRef] [PubMed]
- del Campo, A.D.; Segura-Orenga, G.; Bautista, I.; Ceacero, C.J.; González-Sanchis, M.; Molina, A.J.; Hermoso, J. Assessing Reforestation Failure at the Project Scale: The Margin for Technical Improvement under Harsh Conditions. A Case Study in a Mediterranean Dryland. Sci. Total Environ. 2021, 796, 148952. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Du, P.; Xia, J.; Tang, P.; Wang, X.; Meng, Y.; Wang, H. Spatiotemporal Changes of Glacier and Seasonal Snow Fluctuations over the Namcha Barwa–Gyala Peri Massif Using Object-Based Classification from Landsat Time Series. ISPRS J. Photogramm. Remote Sens. 2021, 177, 21–37. [Google Scholar] [CrossRef]
- Meng, Y.; Wei, C.; Guo, Y.; Tang, Z. A Planted Forest Mapping Method Based on Long-Term Change Trend Features Derived from Dense Landsat Time Series in an Ecological Restoration Region. Remote Sens. 2022, 14, 961. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting Trends in Forest Disturbance and Recovery Using Yearly Landsat Time Series: 1. LandTrendr—Temporal Segmentation Algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Shiravand, H.; Khaledi, S.; Behzadi, S.; Sanjabi, H.A. Monitoring and Assessing the Changes in the Coverage and Decline of Oak Forests in Lorestan Province Using Satellite Images and BFAST Model. J. Appl. Res. Geogr. Sci. 2020, 20, 265–280. [Google Scholar] [CrossRef]
- Bandara Senanayaka, J.; Thilanka Morawaliyadda, D.; Tharuka Senarath, S.; Indika Godaliyadda, R.; Parakrama Ekanayake, M. Adaptive Centroid Placement Based SNIC for Superpixel Segmentation. In Proceedings of the 2020 Moratuwa Engineering Research Conference, MERCon, Moratuwa, Sri Lanka, 28–30 July 2020; pp. 242–247. [Google Scholar] [CrossRef]
- Márquez-Neila, P.; Fua, P.; Süsstrunk, S.; Achanta, R. Scale-Adaptive Superpixels. Color Imaging Conf. 2018, 26, 1–6. [Google Scholar] [CrossRef][Green Version]
- Zou, X.; Zheng, X.; Ji, C.; Zhang, Y. An Improved Fast Shapelet Selection Algorithm and Its Application to Pervasive EEG. Pers. Ubiquitous Comput. 2022, 26, 941–953. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, X.; Ji, C. Fast Shapelet Discovery with Trend Feature Symbolization. In CCF Conference on Computer Supported Cooperative Work and Social Computing; Springer: Singapore, 2021; pp. 352–363. [Google Scholar] [CrossRef]
- Poortinga, A.; Tenneson, K.; Shapiro, A.; Nquyen, Q.; Aung, K.S.; Chishtie, F.; Saah, D. Mapping Plantations in Myanmar by Fusing Landsat-8, Sentinel-2 and Sentinel-1 Data along with Systematic Error Quantification. Remote Sens. 2019, 11, 831. [Google Scholar] [CrossRef]
- Rendenieks, Z.; Nita, M.D.; Nikodemus, O.; Radeloff, V.C. Half a Century of Forest Cover Change along the Latvian-Russian Border Captured by Object-Based Image Analysis of Corona and Landsat TM/OLI Data. Remote Sens. Environ. 2020, 249, 112010. [Google Scholar] [CrossRef]
- Dalponte, M.; Jucker, T.; Liu, S.; Frizzera, L.; Gianelle, D. Characterizing Forest Carbon Dynamics Using Multi-Temporal Lidar Data. Remote Sens. Environ. 2019, 224, 412–420. [Google Scholar] [CrossRef]
- Huertas, C.; Sabatier, D.; Derroire, G.; Ferry, B.; Jackson, T.D.; Pélissier, R.; Vincent, G. Mapping Tree Mortality Rate in a Tropical Moist Forest Using Multi-Temporal LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2022, 109, 102780. [Google Scholar] [CrossRef]
- Mueen, A.; Keogh, E.; Young, N. Logical-Shapelets: An Expressive Primitive for Time Series Classification. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, San Diego, CA, USA, 21–24 August 2011; pp. 1154–1162. [Google Scholar] [CrossRef]
- Ji, C.; Zhao, C.; Liu, S.; Yang, C.; Pan, L.; Wu, L.; Meng, X. A Fast Shapelet Selection Algorithm for Time Series Classification. Comput. Netw. 2019, 148, 231–240. [Google Scholar] [CrossRef]



| Land Cover | Classified Data | Total | Producer Accuracy (PA) | |||
|---|---|---|---|---|---|---|
| Natural Forest | Planted Forest | Non-Forest | ||||
| Referenced Data | Natural forest | 89 | 2 | 9 | 100 | 89.0% |
| Planted forest | 2 | 81 | 17 | 100 | 81.0% | |
| Non-forest | 3 | 5 | 92 | 100 | 92.0% | |
| Total | 94 | 88 | 118 | 300 | ||
| User Accuracy (UA) | 94.7% | 92.0% | 78.0% | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, X.; Wei, C.; Yang, Q.; Tian, L.; Zhu, L.; Meng, Y.; Liu, X. An Object- and Shapelet-Based Method for Mapping Planted Forest Dynamics from Landsat Time Series. Remote Sens. 2022, 14, 6188. https://doi.org/10.3390/rs14246188
Xue X, Wei C, Yang Q, Tian L, Zhu L, Meng Y, Liu X. An Object- and Shapelet-Based Method for Mapping Planted Forest Dynamics from Landsat Time Series. Remote Sensing. 2022; 14(24):6188. https://doi.org/10.3390/rs14246188
Chicago/Turabian StyleXue, Xiaojing, Caiyong Wei, Qin Yang, Lingwen Tian, Lihong Zhu, Yuanyuan Meng, and Xiangnan Liu. 2022. "An Object- and Shapelet-Based Method for Mapping Planted Forest Dynamics from Landsat Time Series" Remote Sensing 14, no. 24: 6188. https://doi.org/10.3390/rs14246188
APA StyleXue, X., Wei, C., Yang, Q., Tian, L., Zhu, L., Meng, Y., & Liu, X. (2022). An Object- and Shapelet-Based Method for Mapping Planted Forest Dynamics from Landsat Time Series. Remote Sensing, 14(24), 6188. https://doi.org/10.3390/rs14246188






