Transmit Beampattern Design for Distributed Satellite Constellation Based on Space–Time–Frequency DoFs

Abstract

For distributed satellite constellations, detection performance can be equivalently regarded as a single large satellite by the cooperative operation of multiple small satellites, which is a promising research topic of the Next-Generation Radar (NGR) system. However, dense grating lobes inevitably occur in the synthetic transmit pattern due to its distributed configuration, as a result of which the detection performance of dynamic coherent radar is seriously weakened. In this paper, a novel transmit beampattern optimization method for dynamic coherent radar based on a distributed satellite constellation is presented. Firstly, the effective coherent detection range interval is determined by several influence factors, i.e., coherent detection, far-field, and system link constraints. Then, we discuss the quantitative evaluation method for coherent integration in terms of synchronization error, beam pointing error, and high-speed motion characteristics and we allocate the corresponding terms in a reasonable way from the perspective of engineering. Finally, the space–time–frequency degrees of freedom (DOFs), which can be collected from satellite spacing, carrier frequencies, and platform motion characteristics, are utilized to realize a robust transmit beampattern with low sidelobe by invoking a genetic algorithm (GA). Simulation results validate the effectiveness of our theoretic analysis, and unambiguous coherent transmit beamforming with a satellite constellation of limited scale is accomplished.

1. Introduction

With the rapid development of the aerospace field, satellite platform technologies and their payloads are gradually transforming towards lightweight, standardized, and low-cost models, which lays a foundation for the rapid layout of LEO-based radar and the collaborative processing of satellite constellations [1,2,3]. However, space-based radar (SBR) is confronted with long detection distances and small radar cross-section (RCS) issues in the time-varying sensitive target detection process, hence resulting in low SNR echoes. The distributed satellite constellation is composed of several radar units, which can be rapidly deployed, and the corresponding target echoes can be added with an identical phase by employing a signal-level fusion strategy [4,5,6]. As a result, $N^3$ times of the signal-to-noise ratio gain [7] can be achieved ($N$ represents the satellite number), which provides an effective way to enhance the detection capability of a single large aperture radar.

Generally, distributed coherent radars are divided into closed-loop and open-loop systems. For the former, in order to achieve signal-level coherent integration, the multiple-input multiple-output (MIMO) mode is adopted to estimate the target parameters, serving to compensate for the time delay differences with regard to radar arrays. However, there exists a boost period for this mode, and coherent integration can be simply performed on the target unit under the condition that accurate parameters can be obtained [8,9,10]. The MIT Lincoln Laboratory and the Chinese Academy of Astronautics and Astronautics have carried out distributed coherent experiments of closed-loop systems [11,12]. For the latter, an open-loop system does not depend on the prior target information, which is more suitable for large-scale early-warning applications. The key point lies in the space–time–frequency synchronization strategy [13,14,15].

Space–time–frequency synchronization includes three aspects, i.e., space, frequency, time, and phase synchronization. Space synchronization means high-precision calibration for radar array configuration. In [16], the ranging accuracy could reach the milli-meter level by employing a sparse spectrum signal instead of a broadband signal, but there exists a time delay ambiguity problem. By combining a dual-frequency waveform and step frequency waveform, the ranging ambiguity issue can be solved [17]. Further, the relative positions among subarrays can be obtained by means of least square (LS) estimation methods [18,19,20]. As for frequency synchronization, it is accomplished by an auxiliary utilizing Global Positioning System (GPS) signals [21], but the estimation accuracy is somewhat low. In [22], a dual-frequency continuous wave (CW) signal was adopted to realize frequency synchronization, and its effectiveness was verified in a two-node system. For time and phase synchronization, time synchronization errors with regard to different signal waveforms are analyzed in [23] and signal phase differences before and after passing through the oscillator are measured by a phase detector to estimate initial phases in [13]. In [24], the identifiability analysis of the phase synchronization error was studied, and it proved that only their relative values are identifiable.

For dynamic coherent radar based on distributed satellite constellation, the signal envelope movement between radar nodes can be ignored because the detection range is larger than that of the radar-radar spacing. Meanwhile, the detection area needs to be quickly covered by the angle scanning mode, which is not suitable for the grid scanning mode starting from real-time processing requirements. Distributed dynamic coherent radar can be regarded as a special sparse array radar, and hence, spatial undersampling will result in an angle ambiguity problem for the synthetic transmit pattern. However, dense grating lobes inevitably occur in the pattern due to their distributed configurations, and thus the dynamic coherent radar detection performance deteriorated. In the literature [25], the spatial ambiguity resolution method is presented based on a multi-scale combination technique, but its disadvantage lies in the requirement of multiple antennas in each spaceborne radar. Staggered carrier frequency [26] and spacing [27] strategies can be applied to solve angle ambiguity resolution problems at the expense of consuming higher system resources. From the perspective of configuration optimization, a particle swarm optimization algorithm was employed in [28] to design a coherent and unambiguous transmit pattern, but this method only applies to radar node spacing optimization.

In this manuscript, a novel transmit beampattern optimization method for dynamic coherent radar based on a distributed satellite constellation is proposed. On one hand, the impacts of synchronization error, beam pointing error, and high-speed motion characteristics on coherent integration are quantitatively evaluated based on coherent detection constraints. On the other hand, due to the insufficient satellite number, robust low-sidelobe beamforming could be realized by a multi-dimensional optimization technique. In this way, the unambiguous spatial field can be extended for distributed coherent radar arrays. The remaining parts are outlined as follows. The transmit beampattern optimization method for dynamic coherent radar based on a distributed satellite constellation is given in Section 2, where the distributed coherent radar detection range, the coherent integration efficiency analysis, and the multi-dimensional low sidelobe beamforming technique are discussed comprehensively. In Section 3, numerical results are demonstrated to verify the effectiveness of the proposed method. The performance of our research scheme is discussed in detail in Section 4. We draw a brief conclusion in Section 5.

2. Materials and Methods

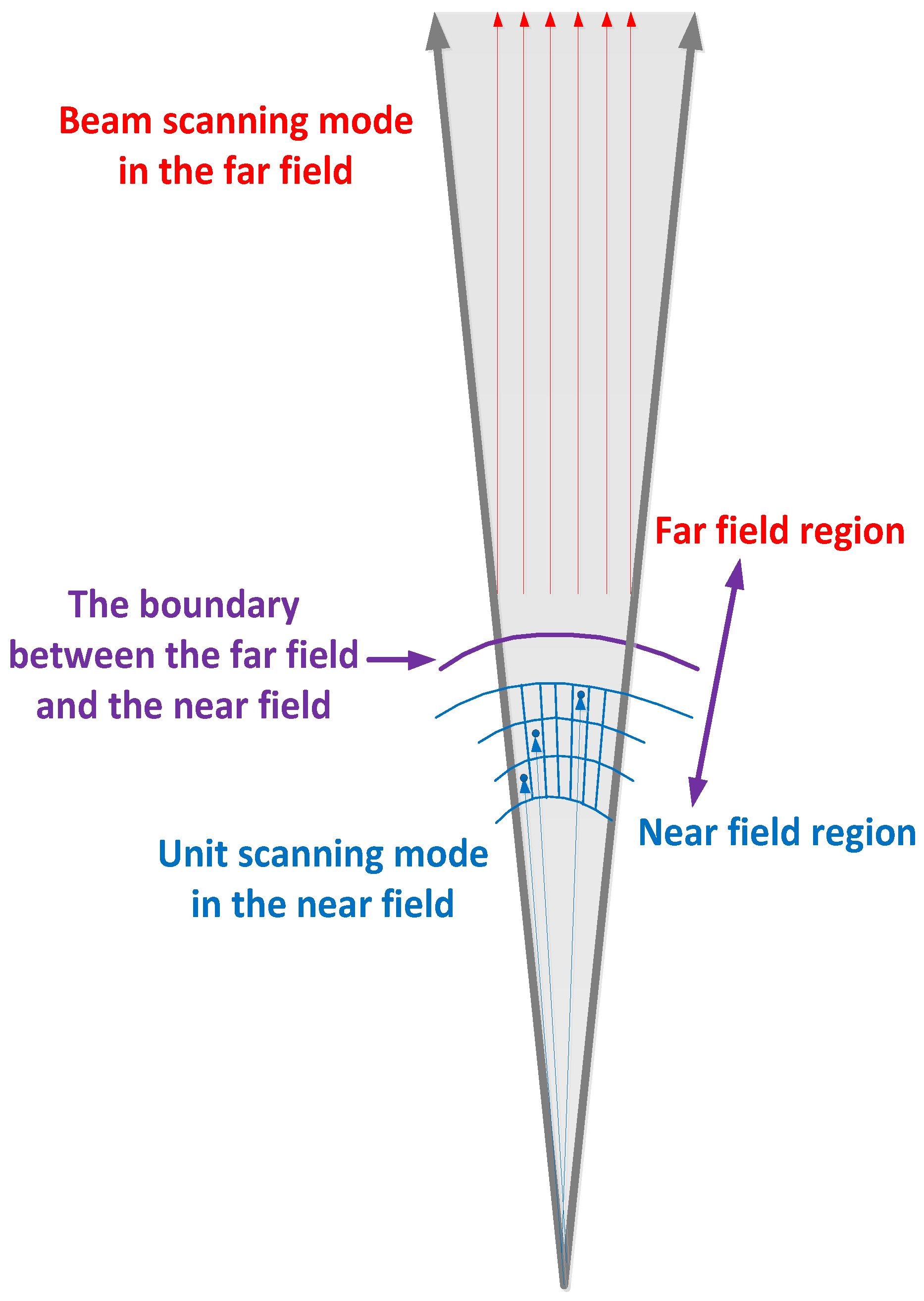
The dynamic coherent radar detection diagram is demonstrated in Figure 1, in which the satellites are modeled on a sphere. In order to demonstrate the satellite constellation configuration clearly, the Vehicle Velocity Local Horizontal (VVLH) coordinate system is employed, where the red plane is parallel to the orbital plane, the purple arrow represents the direction of platform motion, the white arrow points to the center of Earth, and the green arrow is perpendicular to the orbital plane. We assume that the distributed satellite constellation is composed of $N$ satellites and the subarray pattern for each radar is given by $F_{\mathrm{e}}\left(\theta ,\varphi \right)$. The mathematical expression of the distributed array pattern is defined as

$$F\left(\theta ,\varphi \right)={\displaystyle \sum _{n=0}^{N-1}{F}_{\mathrm{e}}\left({\theta }_n,{\varphi }_n\right){\mathrm{e}}^{\frac{\mathrm{j}2\mathsf{\pi }}{\lambda }\mathsf{\Delta }{R}_n}}$$

(1)

where ${\theta }_n$, ${\varphi }_n$$(n=1,2,\cdots ,N)$ denotes the azimuth angle and the elevation angle of the nth satellite and $\lambda$ is the signal wavelength. $\mathsf{\Delta }{R}_n$ represents the wave path difference among different satellites. The elevation and azimuth angles of these spaceborne radars can be approximately considered to be equivalent, that is, ${\theta }_n\approx \theta$, ${\varphi }_n\approx \varphi$. Therefore, Equation (1) can be changed to

$$F\left(\theta ,\varphi \right)=F_{\mathrm{e}}\left(\theta ,\varphi \right){\displaystyle \sum _{n=0}^{N-1}{\mathrm{e}}^{\frac{\mathrm{j}2\mathsf{\pi }}{\lambda }\mathsf{\Delta }{R}_n}}$$

(2)

For coherent radars [7], the whole field of the array manifold is given by

$$w={\left[1,{\mathrm{e}}^{\frac{\mathrm{j}2\mathsf{\pi }d\left(\sqrt{R^2+d^2-2Rd\cos \psi }-R\right)}{\lambda }},\cdots ,{\mathrm{e}}^{\frac{\mathrm{j}2\mathsf{\pi }{d}_n\left(\sqrt{R^2+d_n^2-2R{d}_n\cos \psi }-R\right)}{\lambda }}\right]}^{\mathrm{T}}$$

(3)

where $d_n$ stands for the array element spacing between the reference radar and the nth radar. $R$ represents the distance from the antenna phase center to the target and $\psi$ is the scanning angle. In particular, if the detection region belongs to the far-field, Equation (3) can be rewritten as

$$w={\left[1,{\mathrm{e}}^{\frac{\mathrm{j}2\mathsf{\pi }d\cos \psi }{\lambda }},\cdots ,{\mathrm{e}}^{\frac{\mathrm{j}2\mathsf{\pi }N{d}_n\cos \psi }{\lambda }}\right]}^{\mathrm{T}}$$

(4)

From Equations (2) and (3), the detection space is generally divided into two parts, i.e., the near field and the far-field, according to the range difference between the target and the satellite constellation. The distributed coherent radar is confronted with resource scheduling problems when it operates under the unit scanning mode in the near field. As a result, the combination strategy, including range scanning and angle scanning, should be conducted to solve the variant issue of spatial steering vectors for different range cells in a single beam, which would not meet the requirement of real-time detection. The spatial steering vectors of different range cells, with regard to a specific beam, are considered to be approximately constant in the far-field, and hence only the beam scanning strategy is applied here. Therefore, the latter operation mode is adopted in the wide-range scanning process based on a distributed satellite constellation. The target searching diagram of the coherent radar in the whole field is shown in Figure 2.

In this paper, a transmit beampattern optimization method for dynamic coherent radar based on a distributed satellite constellation is presented to deal with the moving target detection problem. Here, three main steps are given below.

Step 1 Detection range design for distributed coherent radar.

For the distributed satellite constellation, its detection performance can be equivalently regarded as a single large satellite by employing the cooperative operation mode for multiple small satellites. However, the coherent detection area is restricted due to its distributed configuration. Therefore, it is necessary to determine the effective detection range before designing the distributed coherent radar.

(1)

Coherent detection constraint.

Owing to the fact that a large distance exists between adjacent satellites, the coherent integration performance will be affected to some extent when the detecting target is within a certain size. In this section, the coherent integration efficiency is quantitatively analyzed based on the literature [29]. For extended targets with the size $\mathsf{\Delta }X\times \mathsf{\Delta }Y$ along the plane X–Y, the geometric center is located at $p={(p_x,p_y,p_z)}^{\mathrm{T}}$. After compensating for the time delay from the radar to the target geometric center, the echo signal corresponding to the transmitter k/receiver l pair $(k,l)$ can be expressed as

$${\tilde{r}}_{k,l}\left(t\right)={\rho }_{k,l}u\left(t\right)$$

(5)

where $u\left(t\right)$ stands for the baseband waveform, and the transmit signal energy is normalized, i.e., ${\displaystyle {\int }_{T_{\mathrm{p}}}|u(t){|}^2\mathrm{d}t=1}$, where $T_{\mathrm{p}}$ indicates the pulse duration. The gain of the pair $(k,l)$ is defined as

$${\rho }_{k,l}={\displaystyle {\int }_{-\frac{\mathsf{\Delta }X}{2}}^{\frac{\mathsf{\Delta }X}{2}}{\displaystyle {\int }_{-\frac{\mathsf{\Delta }Y}{2}}^{\frac{\mathsf{\Delta }Y}{2}}{\mathrm{e}}^{-\mathrm{j}2\mathsf{\pi }\left[\frac{\alpha \left(x_{\mathrm{u}k}-p_x\right)+\beta \left(y_{\mathrm{u}k}-p_y\right)}{\lambda {\Vert u_k-p\Vert }_2}+\frac{\alpha \left(x_{\mathrm{u}l}-p_x\right)+\beta \left(y_{\mathrm{u}l}-p_y\right)}{\lambda {\Vert u_l-p\Vert }_2}\right]}G\left(\alpha ,\beta \right)}}\mathrm{d}\alpha \mathrm{d}\beta$$

(6)

where $u_k={(x_{\mathrm{u}k},y_{\mathrm{u}k},z_{\mathrm{u}k})}^{\mathrm{T}}$ represents the 3-D coordinate of the kth satellite. $\lambda$ is the signal wavelength. $G(\alpha ,\beta )$ is the complex gain of the scattering point $(x+x_0,y+y_0,0)$, which is modeled as a complex Gaussian random variable with zero means, that is

$$E\left\{G\left({\alpha }_i,{\beta }_i\right)G^{*}\left({\alpha }_j,{\beta }_j\right)\right\}=\frac{1}{\mathsf{\Delta }X\mathsf{\Delta }Y}\delta \left({\alpha }_i-{\alpha }_j,{\beta }_i-{\beta }_j\right)$$

(7)

where $\delta (\alpha ,\beta )$ indicates the 2-D Dirac-delta function. As a result, the mean, variance, and cross-correlation of the random variable ${\rho }_{k,l}$ are given by [29]

$$E\left\{{\rho }_{k,l}\right\}=0$$

(8)

$$E\left\{{\left|{\rho }_{k,l}\right|}^2\right\}=1$$

(9)

$$E\left\{{\rho }_{k,l}{\rho }_{k^{\prime },l^{\prime }}^{\ast }\right\}=\sin \mathrm{c}\left(\frac{{\mu }_{k,l,k^{\prime },l^{\prime }}^{\mathrm{x}}}{\lambda }\mathsf{\Delta }X\right)\sin \mathrm{c}\left(\frac{{\mu }_{k,l,k^{\prime },l^{\prime }}^{\mathrm{y}}}{\lambda }\mathsf{\Delta }Y\right)$$

(10)

respectively, where

$${\mu }_{k,l,k^{\prime },l^{\prime }}^{\mathrm{x}}=\frac{x_{\mathrm{u}k}-p_x}{{\Vert u_k-p\Vert }_2}+\frac{x_{\mathrm{u}l}-p_x}{{\Vert u_l-p\Vert }_2}-\frac{x_{\mathrm{u}{k}^{\prime }}-p_x}{{\Vert u_{k^{\prime }}-p\Vert }_2}-\frac{x_{\mathrm{u}{l}^{\prime }}-p_x}{{\Vert u_{l^{\prime }}-p\Vert }_2}$$

(11)

$${\mu }_{k,l,k^{\prime },l^{\prime }}^{\mathrm{y}}=\frac{y_{\mathrm{u}k}-p_y}{{\Vert u_k-p\Vert }_2}+\frac{y_{\mathrm{u}l}-p_y}{{\Vert u_l-p\Vert }_2}-\frac{y_{\mathrm{u}{k}^{\prime }}-p_y}{{\Vert u_{k^{\prime }}-p\Vert }_2}-\frac{y_{\mathrm{u}{l}^{\prime }}-p_y}{{\Vert u_{l^{\prime }}-p\Vert }_2}$$

(12)

The integrated signal energy related to all subarrays can be written as

$$E=\left\{{\displaystyle {\int }_{T_{\mathrm{p}}}{\left|\tilde{r}\left(t\right)\right|}^2}\mathrm{d}t\right\}={\displaystyle \sum _{l=1}^K{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{l^{\prime }=1}^K{\displaystyle \sum _{k^{\prime }=1}^K{\tilde{r}}_{k,l}\left(t\right){\tilde{r}}_{k^{\prime },l^{\prime }}^{*}\left(t\right)}}}}$$

(13)

Thus, the coherent integration efficiency can be quantitatively described as

$${\eta }_{\mathrm{T}}=\frac{E}{\overline{E}}=\frac{1}{N^4}{\displaystyle \sum }_{l=1}^N{\displaystyle \sum }_{k=1}^N{\displaystyle \sum }_{l^{\prime }=1}^N{\displaystyle \sum }_{k^{\prime }=1}^N\sin \mathrm{c}\left(\frac{{\mu }_{k,l,k^{\prime },l^{\prime }}^{\mathrm{x}}}{\lambda }\mathsf{\Delta }X\right)\sin \mathrm{c}\left(\frac{{\mu }_{k,l,k^{\prime },l^{\prime }}^{\mathrm{y}}}{\lambda }\mathsf{\Delta }Y\right)$$

(14)

where $\overline{E}=N^4$ represents the optimal signal integration gain. In order to meet the coherent detection condition, the effective detection area under a certain topological structure is constrained by

$$S_C=\left\{p\in W|\frac{x_{\mathrm{u}k}-p_x}{{\Vert u_k-p\Vert }_2}+\frac{x_{\mathrm{u}l}-p_x}{{\Vert u_l-p\Vert }_2}=\frac{x_{\mathrm{u}{k}^{\prime }}-p_x}{{\Vert u_{k^{\prime }}-p\Vert }_2}+\frac{x_{\mathrm{u}{l}^{\prime }}-p_x}{{\Vert u_{l^{\prime }}-p\Vert }_2},\frac{y_{\mathrm{u}k}-p_y}{{\Vert u_k-p\Vert }_2}+\frac{y_{\mathrm{u}l}-p_y}{{\Vert u_l-p\Vert }_2}=\frac{y_{\mathrm{u}{k}^{\prime }}-p_y}{{\Vert u_{k^{\prime }}-p\Vert }_2}+\frac{y_{\mathrm{u}{l}^{\prime }}-p_y}{{\Vert u_{l^{\prime }}-p\Vert }_2}\right\}$$

(15)

where $W$ indicates the detection space.

(2)

Far-field constraint.

From Section 2, the detection range interval of the distributed satellite constellation should be limited to the far-field, and thus to meet the real-time detection requirements, that is ${\Vert u_k-p\Vert }_2\ge 2D^2/\lambda$, $k=1,2,\cdots ,K$, where $D$ represents the array aperture. Then the effective detection area under the far-field condition is constrained as

$$S_F=\left\{p\in W|\underset{k=1,2,\cdots ,N}{\min }\left\{{\Vert u_k-p\Vert }_2\right\}\ge \frac{2D^2}{\lambda },\right\}$$

(16)

(3)

System link constraint.

The lower bound of the detection range is determined by two factors, including the coherent detection constraint condition and the far-field constraint condition, whereas the upper bound is limited by the minimum detectable signal-to-noise ratio ${(S/N)}_0$. According to the radar equation, system link constraints of the coherent radar are given by

$$R_{\max }={\left(\frac{P_t{G}^2{\lambda }^2\sigma M}{{(4\pi )}^{3}k{T}_{0}F{B}_{}{(S/N)}_0{L}_s}\right)}^{\frac{1}{4}}$$

(17)

where $P_t$ stands for the transmit peak power, $G$ represents the antenna gain, $\sigma$ indicates the target RCS, and $k$ and $T_0$ indicate the Boltzmann constant and the equivalent noise temperature. $F$ is the noise coefficient, $B$ is the receiver bandwidth, and $L_s$ is the system loss, and hence the signal processing gain $M$ is given by

$$M=\tau B{N}_{chirp}\frac{{\left(\eta N\right)}^4}{N}$$

(18)

In Equation (18), $\tau$ stands for the signal bandwidth and $N_{chirp}$ is the integration pulse number within a coherent processing cycle. $\eta$ is the coherent integration efficiency. Combining the above constraints, the final detection range interval of the distributed coherent radar satisfies

$$S\left(p\right)\le R\le R_{\max }$$

(19)

where the set $S(p)$ is represented by

$$S\left(p\right)=\left\{R\left(p\right)|R\left(p\right)=\underset{\begin{array}{l}p\in S_F\cap S_C,\\ k=1,2,\cdots ,N\end{array}}{\min }\left\{{\Vert u_k-p\Vert }_2\right\}\right\}$$

(20)

In particular, if the distributed satellite constellation is limited to a certain size and all satellites operate with approximately the same viewing angle, Equation (19) can be simplified as

$$\frac{2D^2}{\lambda }\le R\le R_{\max }$$

(21)

Step 2 Coherent integration efficiency analysis of distributed coherent radar.

For a dynamic coherent radar, the coherent integration efficiency is mainly influenced by several factors, i.e., system synchronization error, beam pointing error, and high-speed motion characteristics. Here, a quantitative evaluation of these items is carried out.

(a) The impact of system synchronization error on coherent integration efficiency.

The considered system synchronization errors are composed of position, time, frequency, and phase synchronization errors. The transmit signal of the kth radar is established relative to the reference radar, that is,

$${\tilde{s}}_k\left(t\right)=u_1\left(t-\mathsf{\Delta }{t}_k+{\overline{\tau }}_k\right){\mathrm{e}}^{\mathrm{j}2\mathsf{\pi }\left(f_0+\mathsf{\Delta }{f}_k\right)\left(t+{\overline{\tau }}_k\right)}{e}^{\mathrm{j}\mathsf{\Delta }{\varphi }_k}$$

(22)

where $t\in [-T_p/2,T_p/2]$ represents the signal transmit time. Let radar 1 be the reference, $\mathsf{\Delta }{t}_k$ is the time synchronization error of the kth radar, ${\overline{\tau }}_k$ is the ideal signal propagation delay from the kth radar to the target, $\mathsf{\Delta }{f}_k$ is the frequency synchronization error of the kth radar, and $\mathsf{\Delta }{\varphi }_k$ is composed of the channel phase error, local oscillator initial phase error, and space-time synchronization error terms, i.e., $\mathsf{\Delta }{\varphi }_k=2\mathsf{\pi }(f_0+\mathsf{\Delta }{f}_k)\mathsf{\Delta }{t}_k+\mathsf{\Delta }{\overline{\varphi }}_k$, where $\mathsf{\Delta }{\overline{\varphi }}_k=\mathsf{\Delta }{\overline{\varphi }}_{k1}+\mathsf{\Delta }{\overline{\varphi }}_{k2}$.

After down conversion operation, the signal received by the lth radar is given by

$${\tilde{r}}_l\left(t\right)={\displaystyle \sum _{k=1}^N{u}_1\left(t-\mathsf{\Delta }{t}_{k,l}-\delta {\tau }_{k,l}\right){\mathrm{e}}^{\mathrm{j}2\mathsf{\pi }\left(f_0+\mathsf{\Delta }{f}_k\right)\left(t-\delta {\tau }_{k,l}\right)}{e}^{\mathrm{j}\mathsf{\Delta }{\varphi }_k}{\mathrm{e}}^{-\mathrm{j}2\mathsf{\pi }\left(f_0+\mathsf{\Delta }{f}_l\right)t}}{e}^{-\mathrm{j}\mathsf{\Delta }{\varphi }_l}$$

(23)

where $\mathsf{\Delta }{t}_{k,l}=\mathsf{\Delta }{t}_k-\mathsf{\Delta }{t}_l$, $\mathsf{\Delta }{\varphi }_l=2\mathsf{\pi }(f_0+\mathsf{\Delta }{f}_l)\mathsf{\Delta }{t}_l+\mathsf{\Delta }{\overline{\varphi }}_l$, with $\mathsf{\Delta }{\varphi }_l$, in analogy to $\mathsf{\Delta }{\varphi }_k$, involving the similar error terms. $\delta {\tau }_{k,l}=\delta {\tau }_k+\delta {\tau }_l$ describes the difference between the real-time delay ${\tau }_{k,l}={\tau }_k+{\tau }_l$ and the ideal time delay ${\overline{\tau }}_{k,l}={\overline{\tau }}_k+{\overline{\tau }}_l$, with ${\tau }_k=\left|\right|u_k+\mathsf{\Delta }{u}_k-p{\left|\right|}_2$ and ${\overline{\tau }}_k=\left|\right|u_k-p{\left|\right|}_2$.$\mathsf{\Delta }{u}_k$ is inevitable due to the limited measurement accuracy and uncontrollable orbit error, and we define it as the position error. Noting that the influence of the position error on the signal envelope and the synchronization error coupling term $\mathsf{\Delta }{f}_k\cdot \delta {\tau }_{k,l}$ are negligible, Equation (23) can be rewritten as

$$r_l\left(t\right)\approx {\displaystyle \sum _{k=1}^N\left[u_1\left(t-\mathsf{\Delta }{t}_{k,l}\right){\mathrm{e}}^{\mathrm{j}2\mathsf{\pi }\mathsf{\Delta }{f}_{k,l}t}\right]{\mathrm{e}}^{-\mathrm{j}2\mathsf{\pi }{f}_0\delta {\tau }_{k,l}}{\mathrm{e}}^{\mathrm{j}\mathsf{\Delta }{\varphi }_k}{\mathrm{e}}^{-\mathrm{j}\mathsf{\Delta }{\varphi }_l}}$$

(24)

where $\mathsf{\Delta }{f}_{k,l}=\mathsf{\Delta }{f}_k-\mathsf{\Delta }{f}_l$. By stacking all subarray-level signals, the integrated signal can be expressed as

$$r\left(t\right)\approx {\displaystyle \sum _{l=1}^N{\displaystyle \sum _{k=1}^N\left[u_1\left(t-\mathsf{\Delta }{t}_{k,l}\right){\mathrm{e}}^{\mathrm{j}2\mathsf{\pi }\mathsf{\Delta }{f}_{k,l}t}\right]{\mathrm{e}}^{-\mathrm{j}2\mathsf{\pi }{f}_0\delta {\tau }_{k,l}}{e}^{\mathrm{j}\mathsf{\Delta }{\varphi }_k}{e}^{-\mathrm{j}\mathsf{\Delta }{\varphi }_l}}}$$

(25)

The coherent integration efficiency, taking into account the system synchronization error, is represented by

$${\eta }_1=\frac{1}{N^4}E\left[{\displaystyle \sum _{l=1}^N{\displaystyle \sum _{k=1}^N{\displaystyle \sum _{l^{\prime }=1}^N{\displaystyle \sum _{k^{\prime }=1}^N{e}^{\mathrm{j}\left(\mathsf{\Delta }{\varphi }_k-\mathsf{\Delta }{\varphi }_{k^{\prime }}\right)}{e}^{\mathrm{j}\left(\mathsf{\Delta }{\varphi }_l-\mathsf{\Delta }{\varphi }_{l^{\prime }}\right)}{\mathrm{e}}^{-\mathrm{j}2\mathsf{\pi }{f}_0\left(\delta {\tau }_k-\delta {\tau }_{k^{\prime }}+\delta {\tau }_l-\delta {\tau }_{l^{\prime }}\right)}\chi \left(\mathsf{\Delta }{t}_{k,l}-\mathsf{\Delta }{t}_{k^{\prime },l^{\prime }},\mathsf{\Delta }{f}_{k,l}-\mathsf{\Delta }{f}_{k^{\prime },l^{\prime }}\right)}}}}\right]$$

(26)

where

$$\chi \left(\tau ,f\right)\triangleq {\displaystyle {\int }_{-\infty }^{\infty }{u}_1\left(t\right)u_1^{*}\left(t-\tau \right){\mathrm{e}}^{\mathrm{j}2\mathsf{\pi }ft}\mathrm{d}t}$$

(27)

is the ambiguity function of the baseband waveform. Applying the Cauchy–Schwarz (CS) inequality to Equation (26), we have

$${\eta }_1\ge {\eta }_{\mathrm{e}}{\eta }_{\mathrm{p}}$$

(28)

where

$${\eta }_{\mathrm{e}}=\frac{1}{N^4}E\left[{\displaystyle \sum _{l=1}^N{\displaystyle \sum _{k=1}^N{\displaystyle \sum _{l^{\prime }=1}^N{\displaystyle \sum _{k^{\prime }=1}^N\chi \left(\mathsf{\Delta }{t}_{k,l}-\mathsf{\Delta }{t}_{k^{\prime },l^{\prime }},0\right)}}}}\right]$$

(29)

and

$${\eta }_{\mathrm{p}}=\frac{1}{N^4}E\left[{\displaystyle \sum _{l=1}^N{\displaystyle \sum _{k=1}^N{\displaystyle \sum _{l^{\prime }=1}^N{\displaystyle \sum _{k^{\prime }=1}^N{e}^{\mathrm{j}\left(\mathsf{\Delta }{\varphi }_k-\mathsf{\Delta }{\varphi }_{k^{\prime }}\right)}{e}^{\mathrm{j}\left(\mathsf{\Delta }{\varphi }_l-\mathsf{\Delta }{\varphi }_{l^{\prime }}\right)}{\mathrm{e}}^{-\mathrm{j}2\mathsf{\pi }{f}_0\left(\delta {\tau }_k-\delta {\tau }_{k^{\prime }}+\delta {\tau }_l-\delta {\tau }_{l^{\prime }}\right)}}}}}\right]$$

(30)

are the envelope coherent integration efficiency and phase coherent integration efficiency, respectively.

Notice that the position error is negligible relative to the detection range. By utilizing the first-order Taylor approximation, the position error is obtained by

$$c\left(\delta {\tau }_k-\delta {\tau }_{k^{\prime }}\right)\approx s_k^{\mathrm{H}}\mathsf{\Delta }{u}_k$$

(31)

where

$$s_k=\frac{{\left(u_k-p\right)}^{\mathrm{T}}}{{\Vert u_k-p\Vert }_2}={\left(a_k,b_k,c_k\right)}^{\mathrm{T}}$$

(32)

represents the observation direction vector of the kth satellite with the target position $p={(p_x,p_y,p_z)}^{\mathrm{T}}$. We assume that the synchronization errors are uncorrelated from each other. The relative position errors are given by $\mathsf{\Delta }{x}_k\sim N(0,{\sigma }_x^2)$, $\mathsf{\Delta }{y}_k\sim N(0,{\sigma }_y^2)$, $\mathsf{\Delta }{z}_k\sim N(0,{\sigma }_z^2)$, and $k=1,2,\cdots ,N$, yielding

$$\left(\delta {\tau }_k-\delta {\tau }_{k^{\prime }}\right)\sim N\left(0,2{\sigma }_{\tau }^2\right)$$

(33)

where ${\sigma }_{\tau }^2\triangleq ({\sigma }_x^2{\alpha }^2+{\sigma }_y^2{\beta }^2+{\sigma }_z^2{\gamma }^2)/c^2$ is calculated with $a_k\approx a$, $b_k\approx b$, and $c_k\approx c$, $k=1,2,\cdots ,N$ implying almost the same observation direction among radars. When the relative time, frequency, and phase errors obey $\mathsf{\Delta }{f}_k\sim N(0,{\sigma }_f^2)$, $\mathsf{\Delta }{t}_k\sim N(0,{\sigma }_t^2)$, and $\mathsf{\Delta }{\overline{\varphi }}_k\sim N(0,{\sigma }_{\overline{\varphi }}^2)$, respectively, we obtain

$$\left(\mathsf{\Delta }{\varphi }_k-\mathsf{\Delta }{\varphi }_{k^{\prime }}\right)\sim N\left(0,2{\sigma }_{\varphi }^2\right)$$

(34)

where ${\sigma }_{\varphi }^2={\sigma }_{\overline{\varphi }}^2+4{\mathsf{\pi }}^2{f}_0^2{\sigma }_t^2+4{\mathsf{\pi }}^2{\sigma }_f^2{\sigma }_t^2/\left({\sigma }_f^2+{\sigma }_t^2\right)$.

Notice that if $x\sim N(0,{\sigma }^2)$, then $E{[\mathrm{e}}^{\mathrm{j}x}]={\mathrm{e}}^{-{\sigma }^2/2}$. By substituting Equations (33) and (34) into (30), ${\eta }_{\mathrm{p}}$ simplifies to

$${\eta }_{\mathrm{p}}=\frac{1}{N^4}{\left[\left(N-1\right)\left(N-2\right){\mathrm{e}}^{-{\sigma }_{\varphi }^2}{\mathrm{e}}^{-4{\mathsf{\pi }}^2{f}_0^2{\sigma }_{\tau }^2}+2(N-1){\mathrm{e}}^{-\frac{{\sigma }_{\varphi }^2}{2}}{\mathrm{e}}^{-2{\mathsf{\pi }}^2{f}_0^2{\sigma }_{\tau }^2}+N\right]}^2$$

(35)

Once the product of the envelope coherent integration efficiency ${\eta }_{\mathrm{e}}$ and phase coherent integration efficiency ${\eta }_{\mathrm{P}}$ satisfies the requirement of the indicator of arranged coherent integration efficiency, we can declare that the resulting coherent integration efficiency satisfies the arranged indicator also using Equation (28).

(b) The impact of other non-ideal factors on coherent integration efficiency.

① Beam pointing error.

Assume that the beam pointing error is $T$ times the mainlobe width ${\theta }_{3dB}$, then the corresponding coherent integration efficiency can be expressed as

$${\eta }_2=\left|\frac{\sin \left(\frac{\pi }{2}\left(N-1\right)\sin (\frac{2T}{N-1})\right)}{\frac{\pi }{2}\left(N-1\right)\sin (\frac{2T}{N-1})}\right|$$

(36)

② High-speed motion characteristic.

Assume that $CPI$ stands for the coherent processing interval, the tangential velocity of the target relative to the satellite is $V_{re}$, and $R_0$ denotes the radar detection range. Thus, for one $CPI$, the maximum viewing angle offset caused by the high-speed motion characteristic is given by

$$\mathsf{\Delta }\theta =\mathrm{atand}\left(\frac{CPI*V_{re}}{R_0}\right)$$

(37)

where $\mathrm{atand}$ denotes arctangent operation.

Let the normalized antenna pattern and the antenna beam directivity be $F(\theta )$ and ${\theta }_0$, and the corresponding coherent integration efficiency can be shown by

$${\eta }_3=\frac{F({\theta }_0+\mathsf{\Delta }\theta )}{F({\theta }_0)}$$

(38)

Based on the above-mentioned analysis, the final coherent integration efficiency of the distributed satellite constellation is given by

$$\eta =1-[(1-{\eta }_1)+(1-{\eta }_2)+(1-{\eta }_3)]$$

(39)

Step 3 Multi-dimensional low sidelobe beamforming for the distributed coherent radar.

For the multi-dimensional low sidelobe beamforming method, each satellite in the distributed constellation synchronously sends pulse signals with the same pulse repetition interval (PRI), where the frequency points within different $CPIs$ are changeable. We assume that $f_1,f_2,\cdots ,f_K$ denote the $K$ frequency points, and the corresponding beampatterns are $F_1\left(\theta \right),F_2\left(\theta \right),\cdots ,F_K\left(\theta \right)$. The multi-frequency pattern $\stackrel{⌢}{F}\left(\theta \right)$ can be obtained by multiplying the absolute value of these pattern functions related to different frequency points, i.e., $\stackrel{⌢}{F}\left(\theta \right)=\sqrt{{\displaystyle \prod _{j=1}^K\left|F_j\left(\theta \right)\right|}}$. Based on the high-speed motion characteristics of satellite constellation, the multi-frequency pattern corresponding to $L$ sets of different positions can be generated by repeating the above- mentioned steps. On the basis of multiplying the absolute value of the acquired multi-frequency pattern, the final synthetic beampattern can be written as $\overline{F}\left(\theta \right)=\sqrt{{\displaystyle \prod _{t=1}^L\left|{\stackrel{⌢}{F}}_t\left(\theta \right)\right|}}$. In this way, the multi-dimensional joint low sidelobe beamforming for distributed satellite constellation can be achieved.

Based on the above statement, a genetic algorithm (GA) [30] is adopted to design low sidelobe beamforming. Here, the satellite positions $\text{{}[x_i{y}_i]\text{}},1⩽i⩽N$, as well as the radar frequency points $\text{{}{f}_j\text{}},1⩽j⩽K$, are optimization variables to achieve the minimum peak-to-sidelobe ratio (PSLR) of the distributed satellite constellation, where these variables are regarded as individuals in GA. For each individual, in order to achieve high calculating accuracy and low computation complexity, genes are constructed by real floating point numbers, i.e., a real value encoding method. As a result, not only is better population diversity in GA mutation process maintained, but the shortcoming of the poor operating performance of binary coding can be relieved. Furthermore, the distance of adjacent satellites should be greater than the minimum safe distance $d_c$, and the optimized frequency points should be selected from the L-band (1 GHz~2 GHz). We assume $V_{re}$ is the radial velocity between the target and the satellite. The multi-dimensional low sidelobe beamforming problem can be formulated as

$$\begin{array}{l}\min \mathrm{PSLR}\left(\begin{array}{l}\left[x_1{y}_1\right],\left[x_2{y}_2\right],\cdots ,\left[x_N{y}_N\right],\\ f_1,f_2,\cdots ,f_K,{\stackrel{⌢}{F}}_1,{\stackrel{⌢}{F}}_2,\cdots ,{\stackrel{⌢}{F}}_L\end{array}\right)\\ \mathrm{s}.\mathrm{t}.d_c\le \sqrt{{(x_i-x_j)}^2+(y_i-y_j{)}^2},1⩽j<i⩽N\\ \left|x_i-x_j\right|\le D,\left|y_i-y_j\right|\le D,1⩽j<i⩽N\\ 1e^9<f_{ii}<2e^9,1⩽ii⩽K\\ L\le \frac{c}{4BK{V}_{ve}CPI}\end{array}$$

(40)

In order to evaluate each individual when one employs the GA method, the fitness function is constructed according to the maximum PSLR, shown by

$$fit\left(\begin{array}{l}\left[x_1{y}_1\right],\left[x_2{y}_2\right],\cdots ,\left[x_N{y}_N\right],\\ f_1,f_2,\cdots ,f_K,{\stackrel{⌢}{F}}_1,{\stackrel{⌢}{F}}_2,\cdots ,{\stackrel{⌢}{F}}_L\end{array}\right)=\max \left\{\left|\frac{\overline{F}(u)}{{\overline{F}}_{\max }}\right|\right\}$$

(41)

where ${\overline{F}}_{\max }$ stands for the peak value of the mainlobe pattern. u represents the sidelobe region. By searching two bilateral valleys closest to the mainlobe, the desired sidelobe region could be calculated from these valleys to the direction away from the mainlobe.

The optimization objective function can be described as

$$\begin{array}{l}\min \left\{fit\left(\begin{array}{l}\left[x_1{y}_1\right],\left[x_2{y}_2\right],\cdots ,\left[x_N{y}_N\right],\\ f_1,f_2,\cdots ,f_K,{\stackrel{⌢}{F}}_1,{\stackrel{⌢}{F}}_2,\cdots ,{\stackrel{⌢}{F}}_L\end{array}\right)\right\}\\ =\min \left\{\max \left\{\left|\frac{\overline{F}(u)}{{\overline{F}}_{\max }}\right|\right\}\right\}\end{array}$$

(42)

In order to demonstrate the optimization technique clearly, a pseudo code is presented in Algorithm 1.

Algorithm 1. The pseudo code with regard to multi-dimensional optimization technique.

$\left[{\left\{{\mathrm{PSLR}}_g\right\}}_{g=1}^{Generations}\right]=\mathrm{GA}\left[{\left\{\begin{array}{l}{\mathrm{PSLR}}_{g-1},\left[x_1{y}_1\right],\left[x_2{y}_2\right],\cdots ,\left[x_N{y}_N\right],\\ f_1,f_2,\cdots ,f_K,{\stackrel{⌢}{F}}_1,{\stackrel{⌢}{F}}_2,\cdots ,{\stackrel{⌢}{F}}_L\end{array}\right\}}_{g=1}^{Generations}\right]$· · Initialization Satellite positions $\text{{}[x_i{y}_i]\text{}},1⩽i⩽N$, radar frequency points $\text{{}{f}_j\text{}},1⩽j⩽K$, the initial ${\mathrm{PSLR}}_0$· ·  g = 1: Generations —      For $t=1:L$ —      For $j=1:K$ —     Constructing beampatterns $F_1\left(\theta \right),F_2\left(\theta \right),\cdots ,F_K\left(\theta \right)$ —      End For —     Constructing the multi-frequency pattern

${\stackrel{⌢}{F}}_t\left(\theta \right)=\sqrt{{\displaystyle \prod _{j=1}^K\left|F_j\left(\theta \right)\right|}}$

—      End For ·  Constructing synthetic beampattern corresponding to $L$ sets of different positions $\overline{F}\left(\theta \right)=\sqrt{{\displaystyle \prod _{t=1}^L\left|{\stackrel{⌢}{F}}_t\left(\theta \right)\right|}}$ · Constructing the fitness function $fit\left(\begin{array}{l}\left[x_1{y}_1\right],\left[x_2{y}_2\right],\cdots ,\left[x_N{y}_N\right],\\ f_1,f_2,\cdots ,f_K,{\stackrel{⌢}{F}}_1,{\stackrel{⌢}{F}}_2,\cdots ,{\stackrel{⌢}{F}}_L\end{array}\right)=\max \left\{\left|\frac{\overline{F}(u)}{{\overline{F}}_{\max }}\right|\right\}$ · Formulating the multi-dimensional low sidelobe beamforming problem $\begin{array}{l}\min {\mathrm{PSLR}}_g\\ \mathrm{s}.\mathrm{t}.d_c\le \sqrt{{(x_i-x_j)}^2+(y_i-y_j{)}^2},1⩽j<i⩽N\\ \left|x_i-x_j\right|\le D,\left|y_i-y_j\right|\le D,1⩽j<i⩽N\\ 1e^9<f_{ii}<2e^9,1⩽ii⩽K\\ L\le \frac{c}{4BK{V}_{ve}CPI}\end{array}$ ·  End For

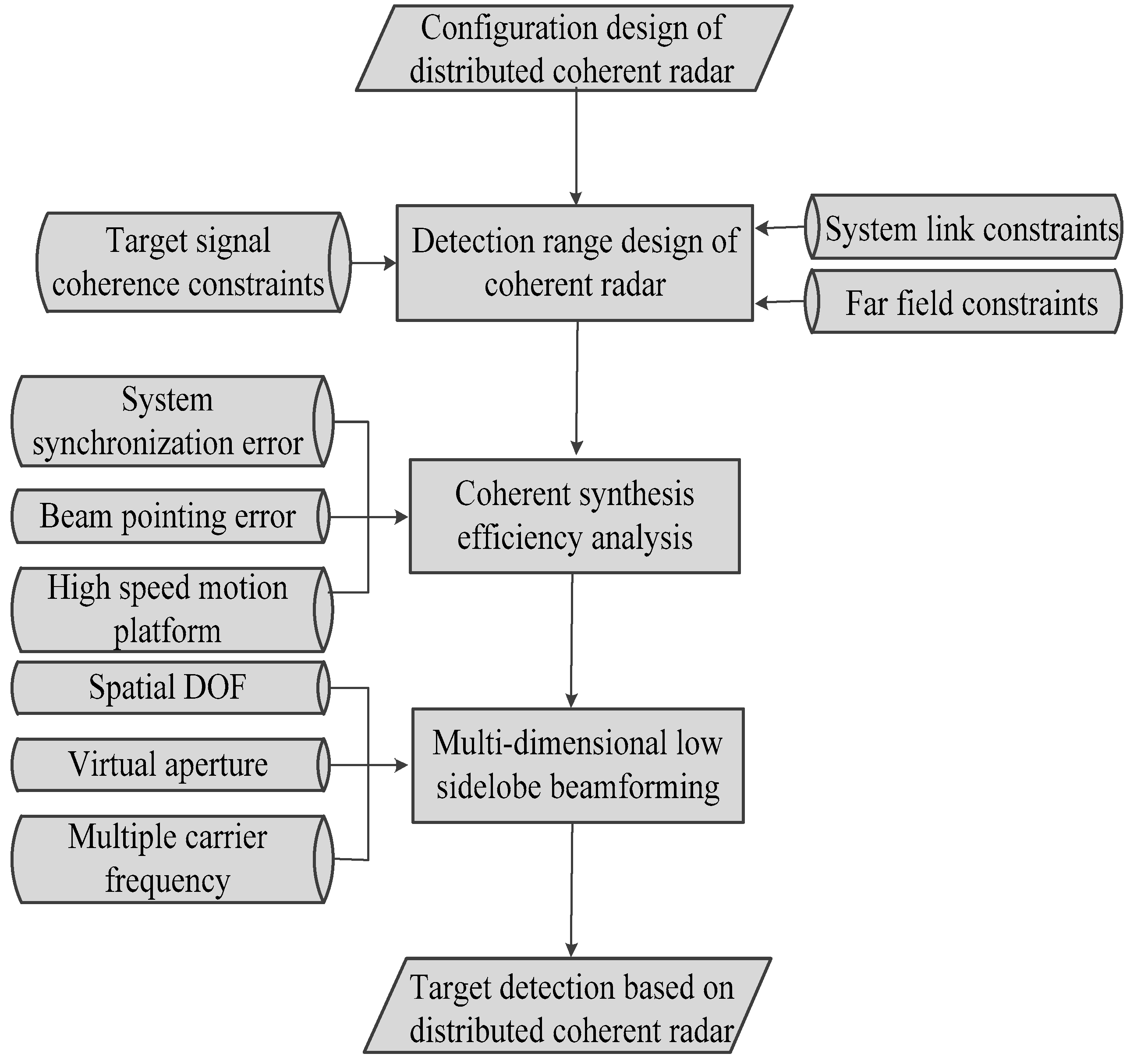
In summary, the proposed method provides a quantitative evaluation method for the impact of space–time–frequency synchronization error, beam pointing error, and high-speed motion characteristics on coherent integration efficiency. Figure 3 shows the flowchart of the dynamic coherent radar designing method.

3. Results

We assume the constellation configuration is a 6×6 square array with an anti-collision distance of 50 m, as shown in Figure 4. The beam pointing error is set to one percent of the mainlobe width. The considered simulation parameters are summarized in

Table 1. Simulation parameters.

Parameters	Platform Height	Signal Bandwidth	Coherent Processing Interval	RCS
Value	500 km	1 MHz	5 ms	0.03 m2
Parameters	Peaktransmission power	Antenna gain	Radar system loss	Noise coefficient
Value	5 kw	34 dB	8 dB	2 dB

. The constellation height is set to 500 km, and the reason is that low orbit is conductive to decreasing the radar detection range. However, if the satellite’s height is too low, it will suffer from atmospheric resistance, which will reduce the satellite’s lifetime. As a result, 500 km is a suitable value. The signal bandwidth, coherent processing interval, and target RCS are selected according to the target motion characteristics and its scattering characteristics. The peak transmission power and antenna gain are calculated based on the radar detection link. When the radar system loss and noise coefficient are selected on the basis of L-band radar system composition, the total radar signal processing gain is 86.9 dB.

In order to implement the proposed distributed satellite constellation system, a circular relative orbit configuration is used. As the circular orbit configuration diverges [31,32] slowly over time, the long-term stable configuration has been designed to maintain the fixed relative geometry based on the J2 perturbation correction strategy. Meanwhile, the distributed satellite configuration will also be affected by atmospheric drag, third-body gravitation, and other perturbation forces, so we employ the configuration maintenance method based on relative distance measurement and Gaussian perturbation equation to realize a highly stable orbit, in which the fuel consumption for correcting the same position accuracy can be reduced by adopting the appropriate control theory. 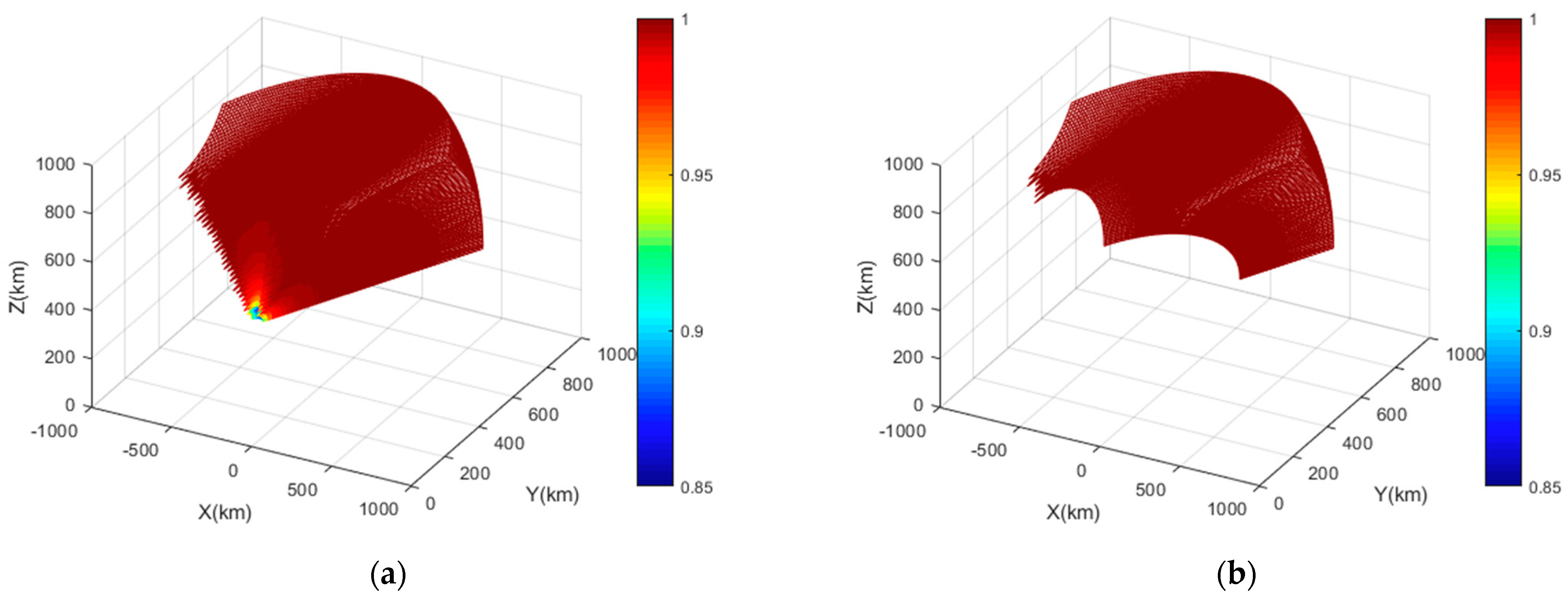For space-based radar detection, the coordinate transformation is generally adopted, that is $S_s\to S_g\to S_i\to S_e\to S_n$, where $S_s$, $S_g$, $S_i$, $S_e$, and $S_n$ stand for the Satellite Body-fixed Coordinate, Geocentric Orbit Coordinate, Geocentric Equatorial Inertial Coordinate, Geocentric Equatorial Rotating Coordinate, and East North Up Coordinate, respectively. In this section, target detection processes are performed in the ENU (East North Up) coordinate by employing the coordinate system transformation operation. The sub-satellite point is the coordinate origin, and thus the geometric center coordinate of the distributed coherent radar is given by [0 km, 0 km, 500 km]. In terms of the far-field boundary condition and the system link, the available detection range interval in regard to the above-mentioned distributed satellite constellation configuration is given by 600 km~1000 km. The coherent integration efficiency of the typical missile target is demonstrated in Figure 5, where its size is given by $20$ $\times$ $1.8$ m². From Figure 5a, the target coherent integration efficiency ${\eta }_{\mathrm{T}}$ tends to be 1 under ideal conditions as the detection range increases. In this case, extended target detection can be regarded as equivalent to point target detection, while the detectable coherent range interval in Figure 5b is restricted under coherent detection constraints, far-field constraints, and system link constraints. Evidently, the target coherent integration efficiency ${\eta }_{\mathrm{T}}$ also tends to be 1 in the far-field region, and the coherent range interval is only restrained by the geometric relationship between the distributed satellite constellation and the target.

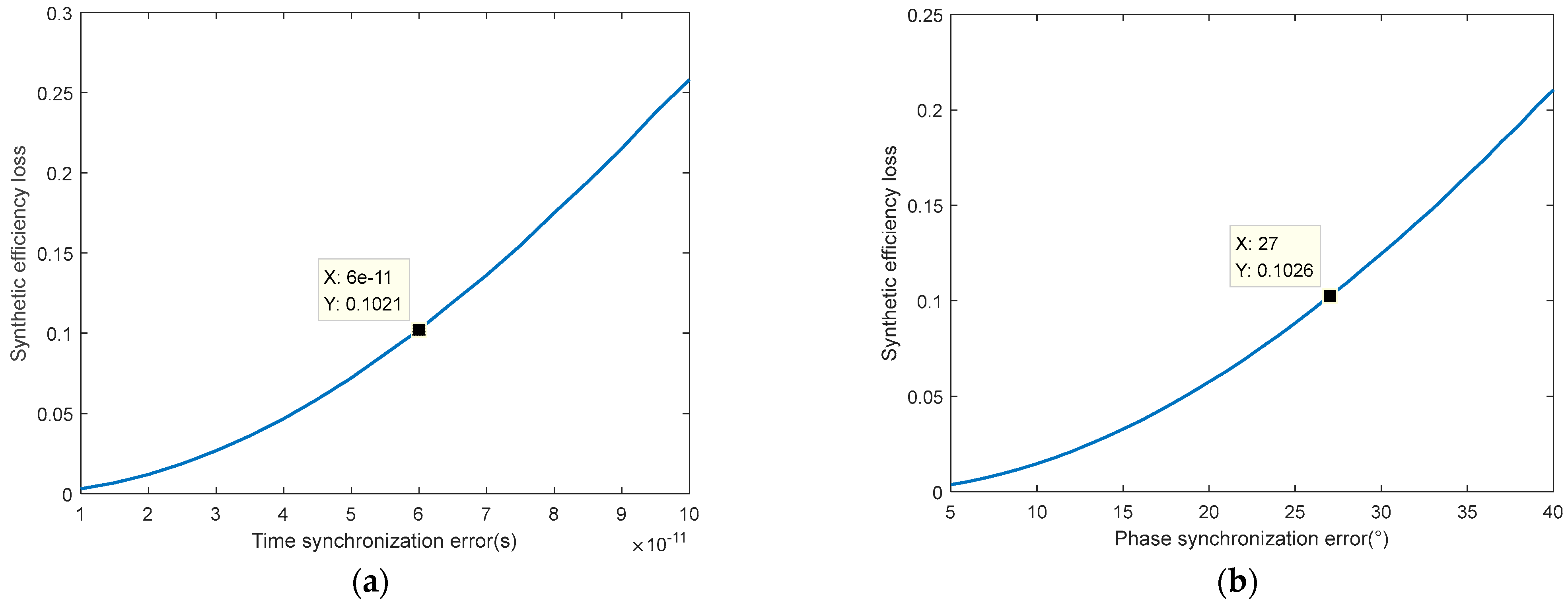
The coherent integration efficiency of the distributed satellite constellation system is 90%, and the boundary condition related to the time synchronization error, phase synchronization error, beam pointing error, and that caused by the high-speed motion platform is represented in Figure 6. Here, the time synchronization accuracy and the phase synchronization accuracy should be better than 60 ps and 27°. The ratio of the beam pointing error to the mainlobe width should be less than 0.25. Furthermore, the upper bound of the relative tangential velocity between the satellite and the target should not exceed 23,700 m/s. These boundary values provide an effective reference for designing system and synchronization terms.

According to the theoretical analysis presented in Section 2, the coherent integration efficiency can be measured quantitatively based on the system synchronization errors, among which the time synchronization error, the channel consistency error, the position error, and the relative frequency stability are set to 48 ps, 5°, 5 mm, and 10⁻¹² in turn, and the corresponding coherent integration efficiency losses caused by the above terms are given as 7.74%, 0.02%, and 1.69%, respectively. Hence, the total coherent integration efficiency is better than 90%.

Based on the above satellite constellation configuration, the virtual aperture can be formed by utilizing the rotation characteristics of these satellites in the temporal domain. In this way, the vacancies between adjacent satellites are compensated to further suppress the grid lobes as well as the sidelobes. Figure 7 shows the virtual array diagram of the distributed satellite constellation within three $CPIs$, including the real aperture related to the current $CPI$ and the virtual aperture related to the other two $CPI\mathrm{s}$.

For the proposed multi-dimensional low sidelobe beamforming method, based on the minimum sidelobe objective function and GA [30], the optimized frequencies $f_1,f_2,f_3,f_4,f_5,f_6,f_7,f_8,f_9,f_{10}$ are shown in

Table 2. Radar system carrier frequency optimization results.

Frequency Point	$f_1$	$f_2$	$f_3$	$f_4$	$f_5$
Value(Hz)	1.0000 GHz	1.0782 GHz	1.1233 GHz	1.1869 GHz	1.2500 GHz
Frequency Point	$f_6$	$f_7$	$f_8$	$f_9$	$f_{10}$
Value(Hz)	1.5853 GHz	1.6491 GHz	1.6787 GHz	1.7962 GHz	1.8176 GHz

, where the lower limit of the satellite safety distance and that of the target detection distance are set to 50 m and 600 km, respectively.

Figure 8 shows the beampattern under an elevation angle of 90 and an azimuth angle of 90. One can see that the first sidelobe is approximately 2 dB if only a single frequency is applied, which cannot meet the detection requirements. Both maximum sidelobes corresponding to the elevation and azimuth dimensions are better than −13.5 dB if the space–frequency–time joint optimization strategy is adopted, and it possesses a slight improvement compared to the space–frequency joint optimization algorithm. From the stochastic perspective, the target velocity is 5 km/s, and the time-sensitive target has a radial velocity relative to the satellite. Therefore, the clutters whose Doppler interval coincides with the target are generally located 5° away from the beam center, and the two-dimensional sidelobes within these regions are better than −30 dB, which meets the requirement for weak target detection.

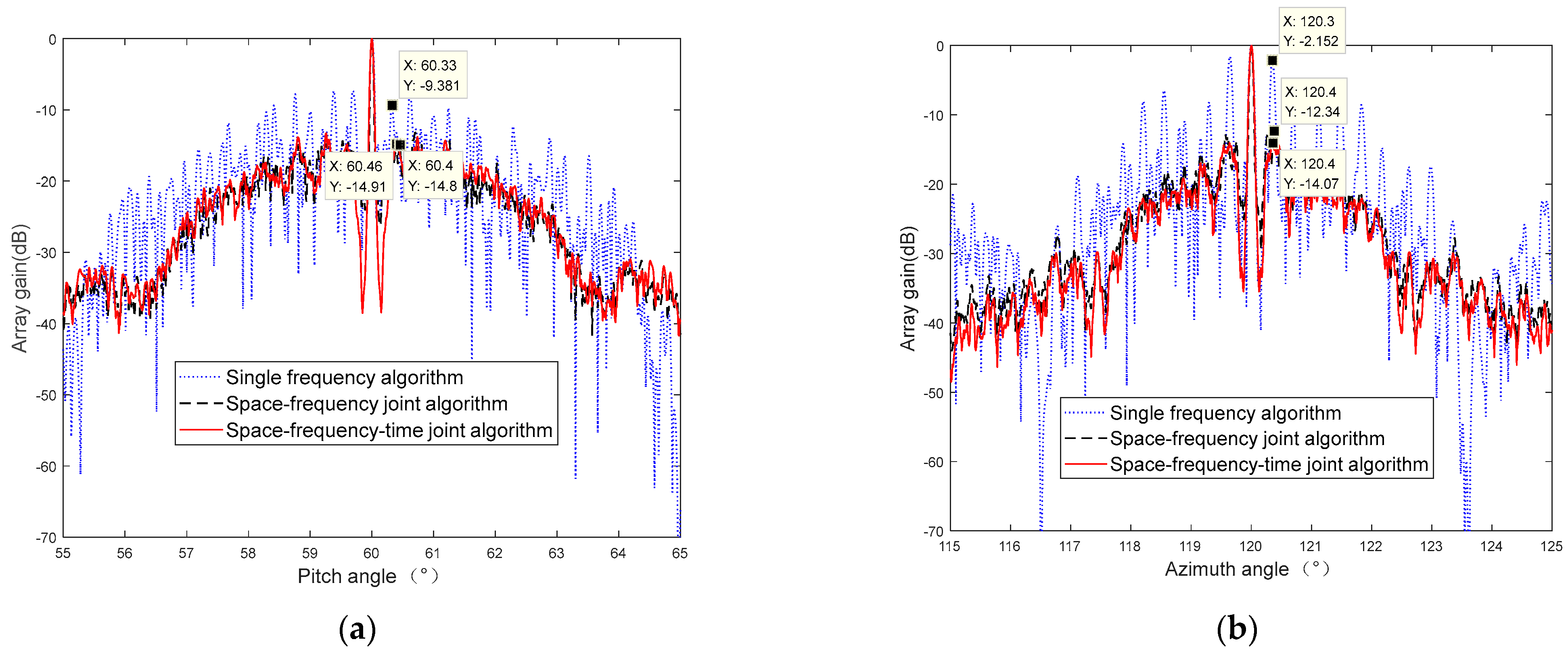
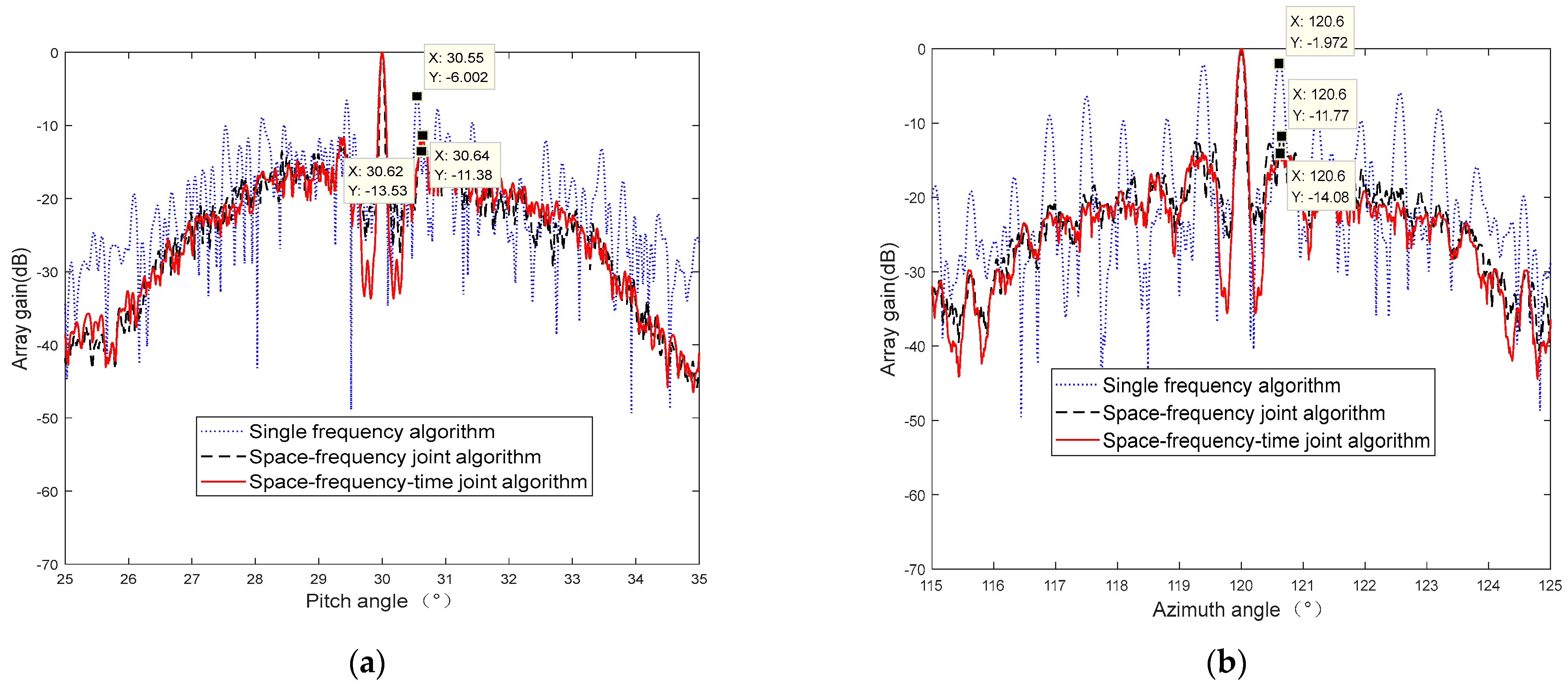
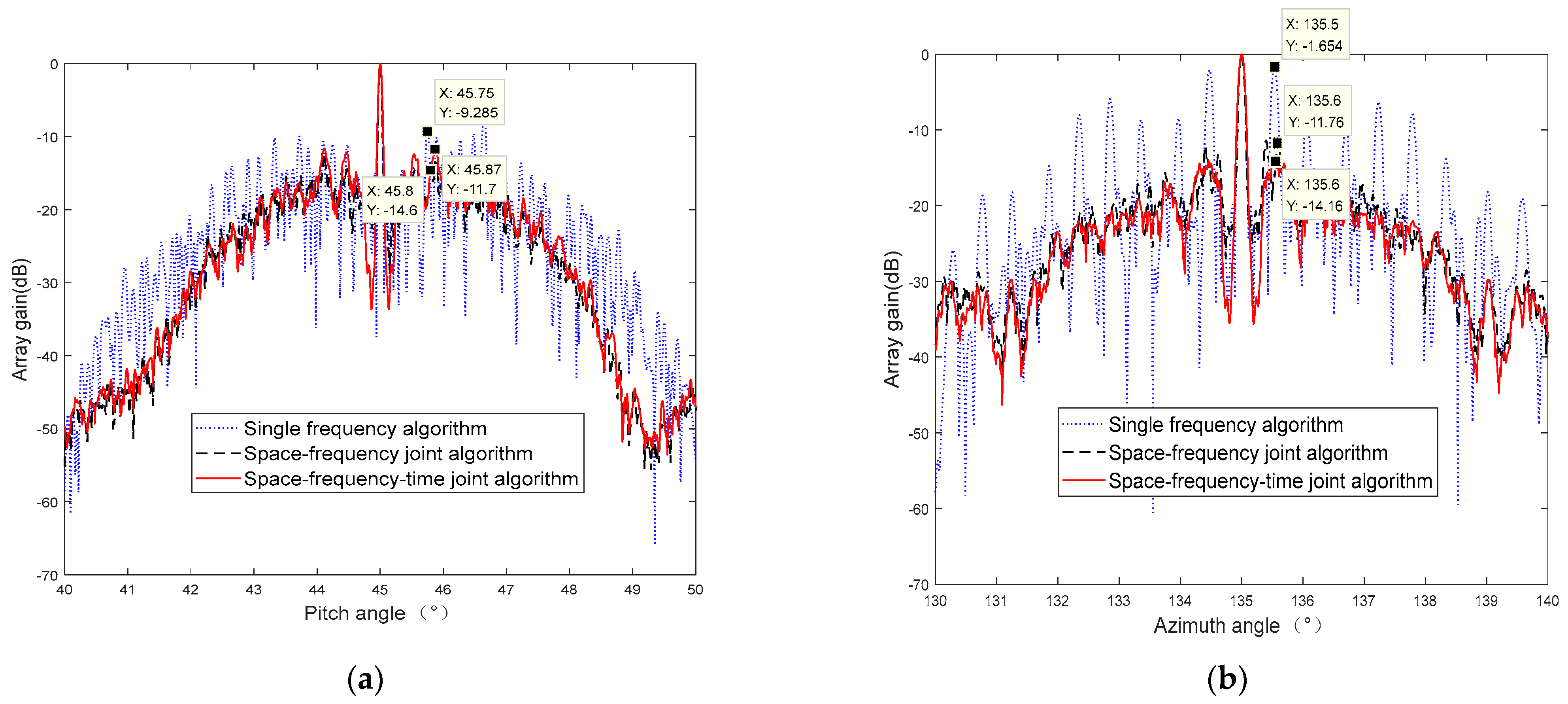
In order to further verify the performance of the robust low sidelobe beamforming algorithm, the maximum sidelobe of beam patterns with regard to different antenna-pointing angles are demonstrated in Figure 9, Figure 10 and Figure 11, which are under an elevation angle of 60 and an azimuth angle of 120, an elevation angle of 30 and an azimuth angle of 120, and an elevation angle of 45 and an azimuth angle of 135, respectively. One can see that the first sidelobes corresponding to different scanning angles are better than −14 dB by means of the space–frequency–time joint optimization strategy. Furthermore, the sidelobes beyond 5 degrees are better than −30 dB. Thus, the sidelobe level can be greatly reduced by utilizing the space–frequency joint optimization beamforming algorithm compared with the single-frequency beamforming algorithm and space–frequency joint beamforming algorithm. Different from the orthogonal mode, the equivalent antenna aperture becomes smaller when one conducts the beam scanning procedure, which could relieve the sparsity of the satellite constellation. The disadvantage is that the mainlobe of the beampattern is widened and the gain of the antenna array is decreased.

From Figure 8, Figure 9, Figure 10 and Figure 11, one can see that the proposed robust low-sidelobe beamforming method, with limited spatial degrees of freedom (DOFs), can be realized under the beam scanning mode and distributed array configuration, where the coherent integration efficiency can be optimized to more than 90%.

4. Discussion

In this paper, the impacts of synchronization error, beam pointing error, and high-speed motion characteristics on coherent integration have been systematically evaluated in our studies for a spaceborne satellite constellation. On this basis, the angle ambiguity problem is discussed in consideration of the distributed dynamic coherent radar configuration. From Section 2, the target should be in the far-field for a distributed satellite constellation when conducting a coherent detection process. As a result, the constellation scale is limited, and low sidelobe beamforming cannot be performed in the spatial domain with limited DOFs in a robust way. In order to enhance the unambiguous field, the multi-dimensional joint method, involving three spatial DOFs, multi-carrier-frequency, and temporal virtual array elements, is adopted to suppress the grating lobes and achieve robust low-sidelobe beamforming. The strategy for reducing grating lobes and sidelobes can be summarized as follows: Firstly, high-speed motion characteristics are employed to form virtual apertures within different $CPIs$, and hence increase the spatial domain DOFs. Moreover, multiple frequency points are introduced in the frequency domain to further improve the radar system DOFs. Finally, the non-uniform array optimization criterion is adopted to minimize the system’s grating lobes and sidelobes, where safe distances between satellites are guaranteed. This strategy has two advantages: On one hand, the integration time within one $CPI$ is at approximately the millisecond level, and consequently, temporal virtual array elements are obtained by utilizing high-speed motion characteristics of the satellite so that the blank space between adjacent platforms can be compensated. On the other hand, the multi-carrier-frequency method is introduced based on spatial and temporal beamforming, that is, the multi-frequency beampatterns are combined to obtain low sidelobe beamforming.

5. Conclusions

The distributed coherent radar array achieves wide applications in the space surveillance field. However, the dense grating lobe problem inevitably exists when one conducts radar array beamforming of a sparse satellite configuration. From the perspective of distributed radar coherent detection constraints and the robust low-sidelobe beamforming technique, a novel transmit beampattern optimization method for dynamic coherent radar based on a distributed satellite constellation is presented, which provides a feasible coherent detection scheme for the distributed satellite constellation. It should be noted that the mainlobe for the distributed array pattern is extremely narrow, which seriously contradicts the data rate. As a result, the trade-off between the dense grating lobes and data rate should be balanced.