Urban Traffic Imaging Using Millimeter-Wave Radar
Abstract
1. Introduction
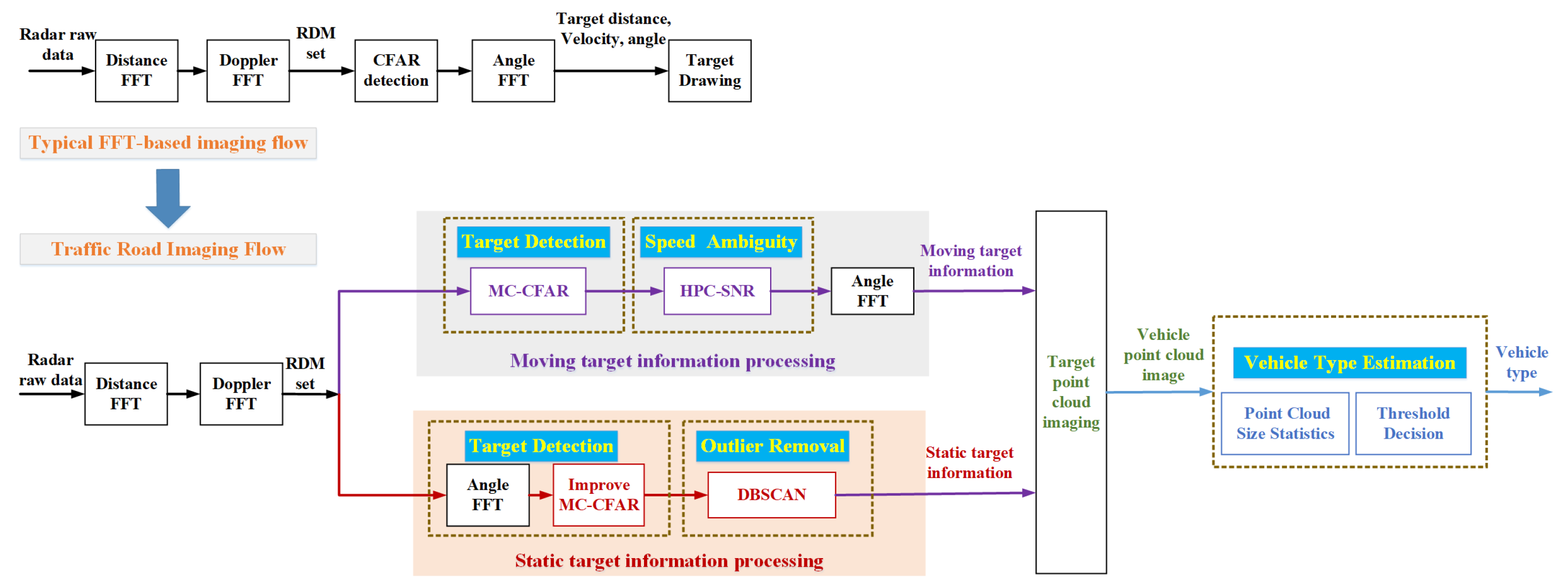
- An improved 3D-FFT imaging algorithm architecture is presented and discussed for urban traffic imaging using the millimeter-wave radar system. It enables the concurrence of dynamic and static target imaging within 50 m (speed up to 70 km/h) in the form of a 2D point cloud.
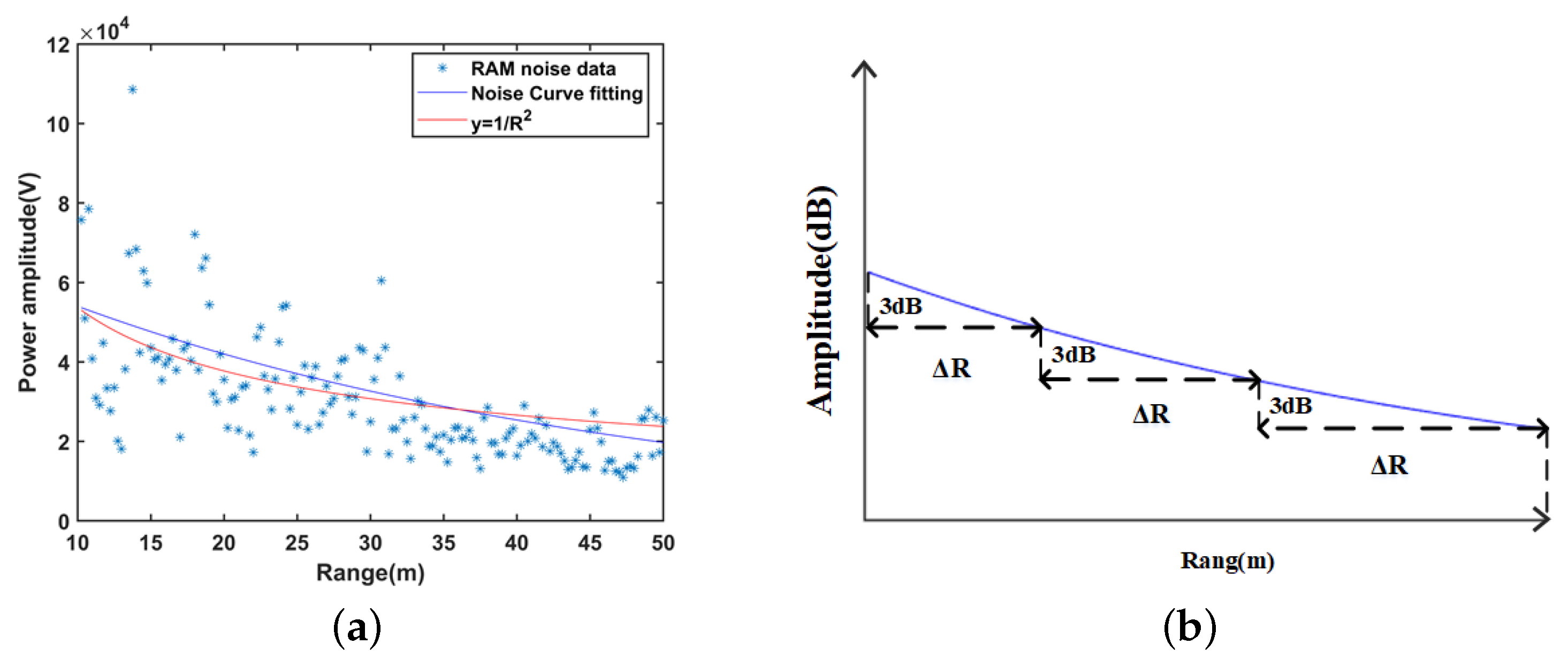
- In the proposed imaging algorithm framework, Monte-Carlo-based CFAR detection algorithm (the MC-CFAR) and improved MC-CFAR are applied and proposed, respectively, to detect moving vehicles and traffic static objects. The MC-CFAR algorithm estimates the background noise of the moving target by random sampling of the RDM, which avoids reference window design and sliding. Compared with the traditional CFAR algorithm, the MC-CFAR algorithm has higher detection efficiency and provides a more complete target output, which is more suitable for “plaque-like” target detection. The improved MC-CFAR uses RAM as the detection object. While maintaining the advantages of the MC-CFAR algorithm, it achieves static target extraction with non-uniform background noise and a larger “plaque-like” area by dividing the RAM area with a noise power drop gradient.
- In the proposed imaging algorithm framework, an improved HPC algorithm is proposed for velocity ambiguity solution with a large ambiguity cycle. We changed the evaluation method to estimate speed—that is, by choosing the hypothesis with the strongest SNR in the angular power spectrum instead of the peak value to obtain the real speed. Compared with the original HPC algorithm (which we call HPC-Peak), the effectiveness of the velocity disambiguation is guaranteed when there are multiple targets in the same range-Doppler cell.
- The DBSCAN algorithm is used to eliminate the isolated noise generated by the detection of false alarms to obtain a clean point cloud image. In addition, we performed a preliminary estimation experiment for the vehicle type based on the target point cloud image, which is not possible with traffic detection radar. Although the method is still crude in the type identification of the vehicle, it avoids errors caused by target distance, plane mapping relationship, and occlusion, etc. To a certain extent, it is able to provide accurate dimensions of ordinary small cars and buses in sparse vehicle scenarios.
2. Model and Scenario Analysis
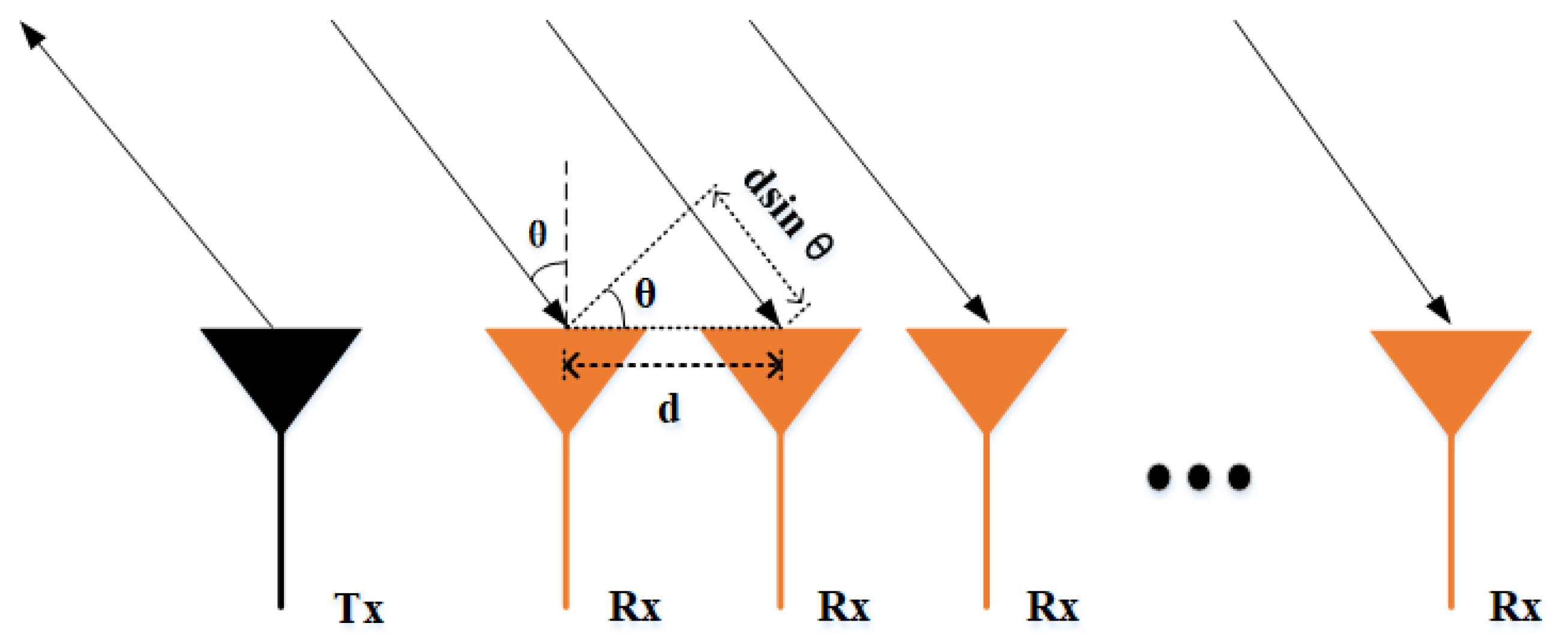
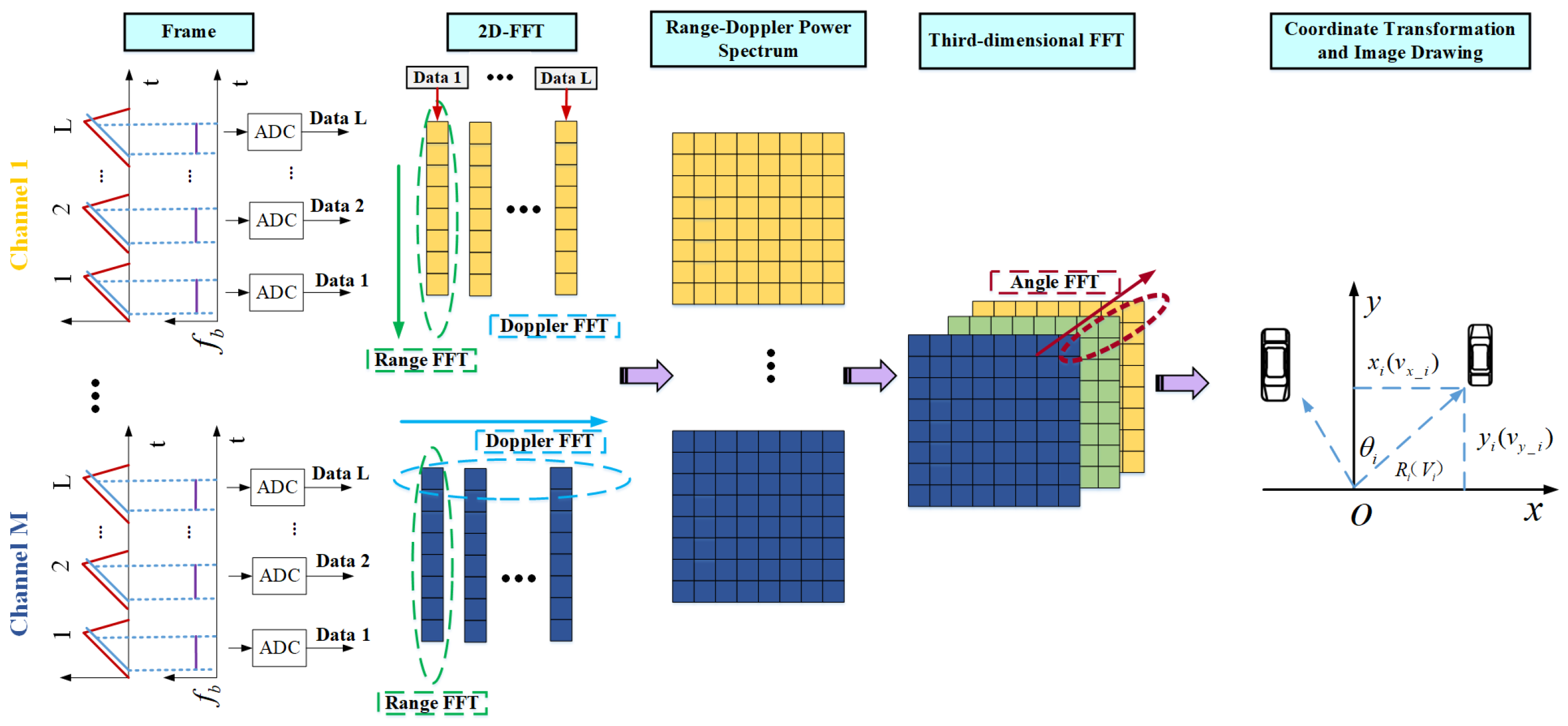
2.1. Radar Detection Principle and FFT-Based Processing Model
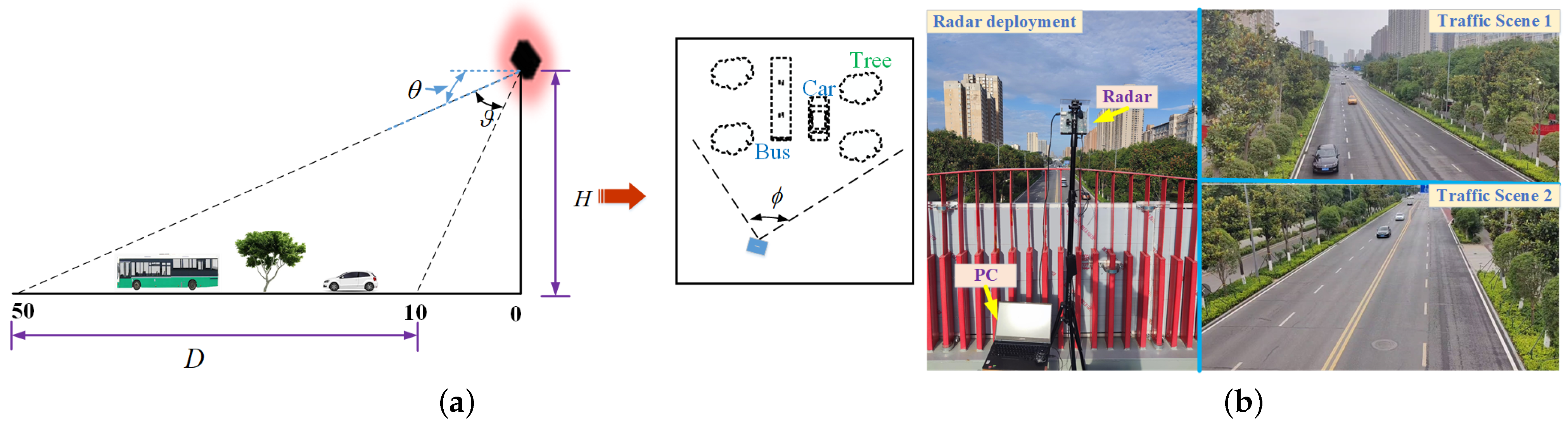
2.2. Traffic Scene Model and Radar System
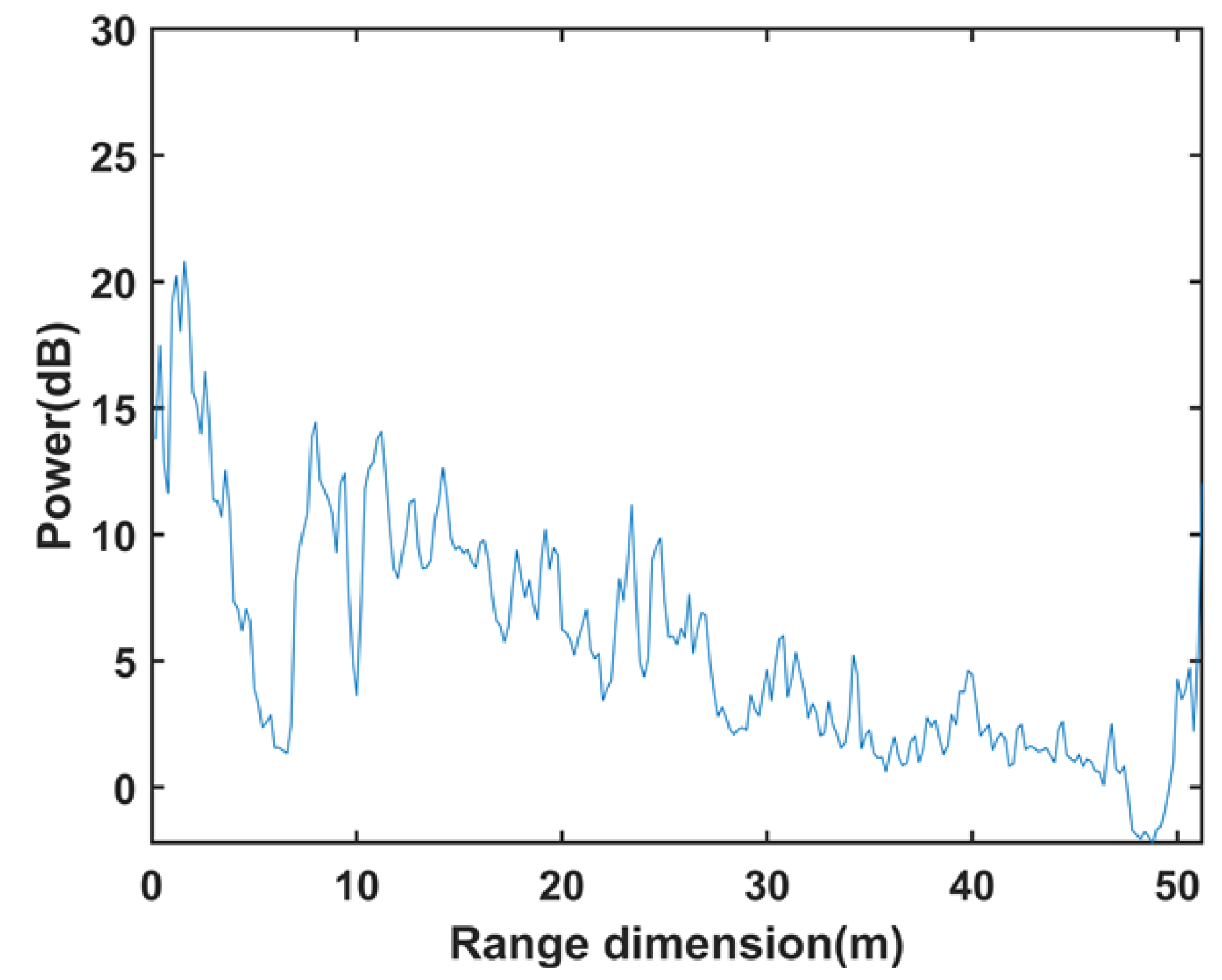
2.3. Scenario Analysis
3. The Proposed Imaging Architecture and Algorithms
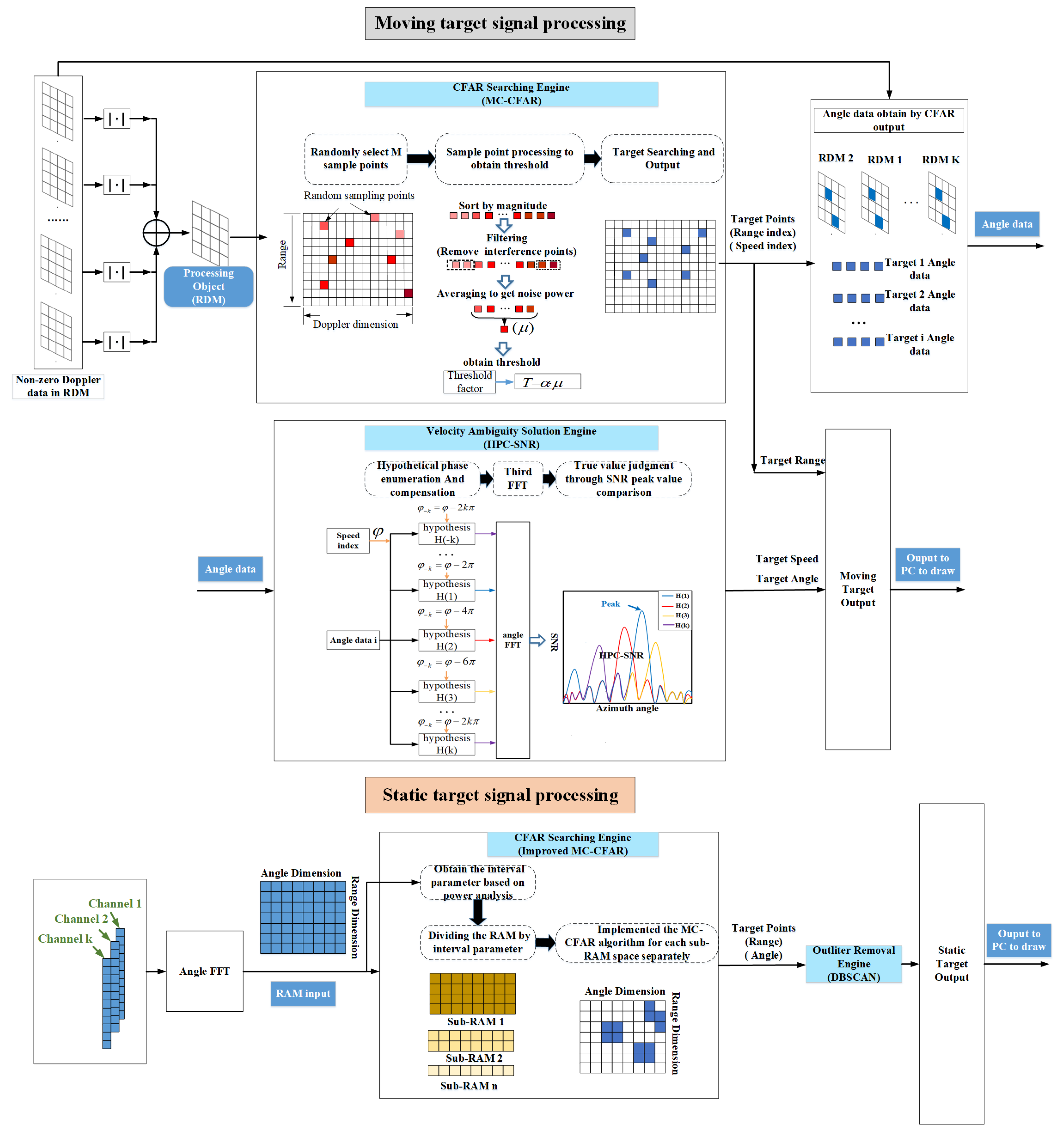
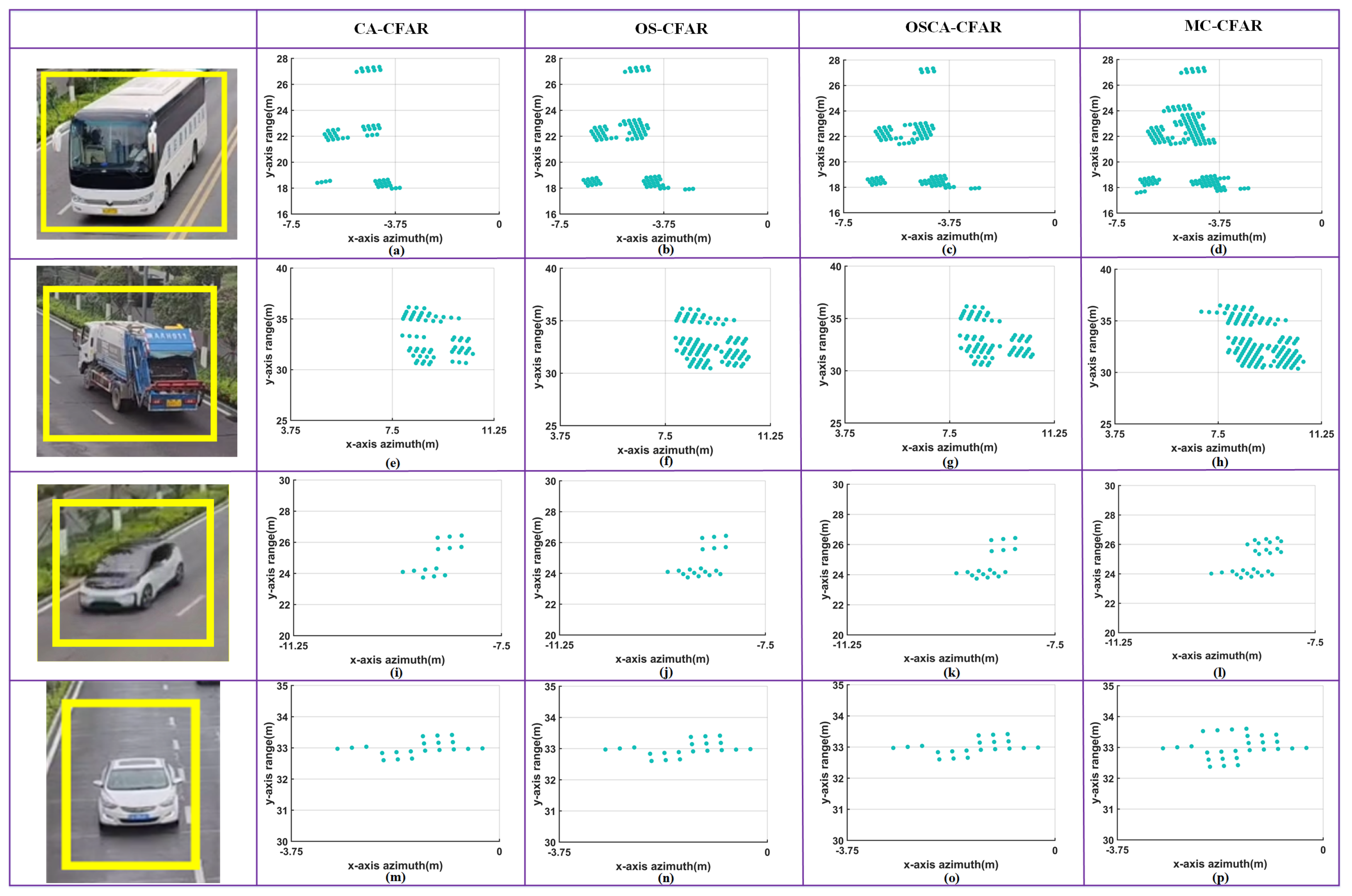
3.1. The MC-CFAR Algorithm and Improved MC-CFAR Algorithm for Target Detection
3.1.1. The MC-CFAR Algorithm for Moving Target Detection
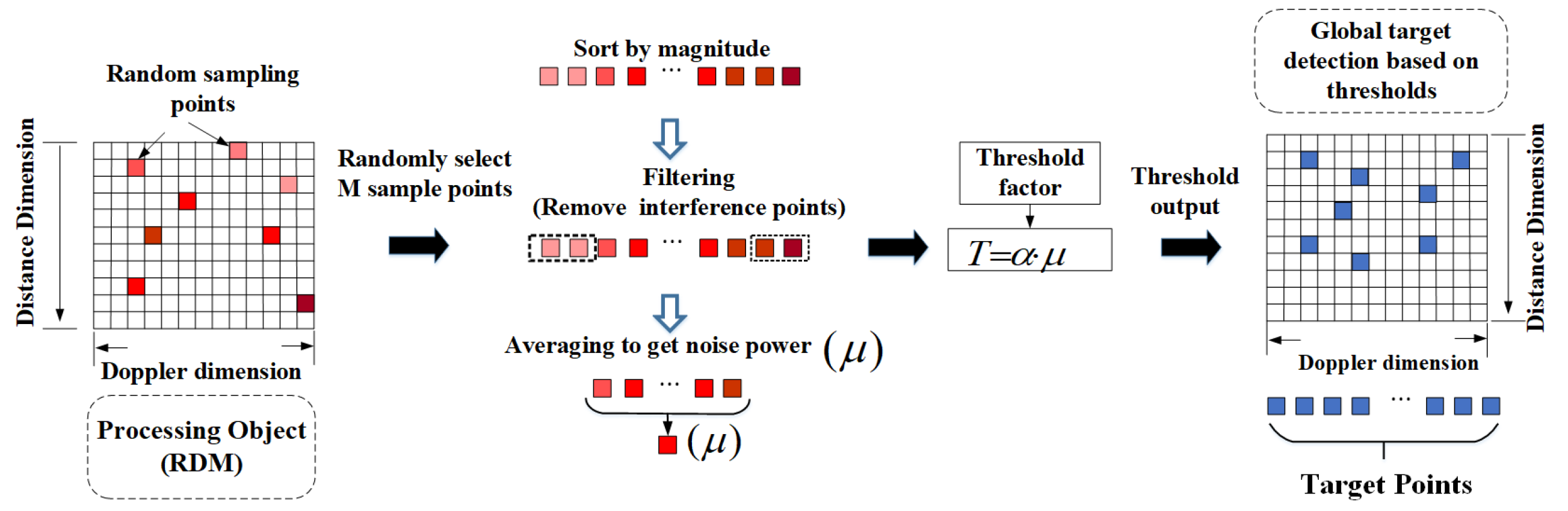
- Step 1: Use Monte Carlo experiments to obtain configuration parameters (sampling points M and the threshold factor ). When the detection environment and platform remain unchanged, this step only needs to be performed once.
- Step 2: Randomly draw M sample points (X) in the RDM non-zero-Doppler region. Sort the sample points according to the magnitude of the power magnitude:
- Step 3: k maximum points and q minimum points are removed, and it is considered that the remaining sample points only contain background noise power points.
- Step 4: Average the remaining sample points to obtain the estimated value of the current background average noise power in the RDM.
- Step 5: Each detection cell in the RDM is sequentially compared with the threshold value . If , the target exists; otherwise, the target does not exist.
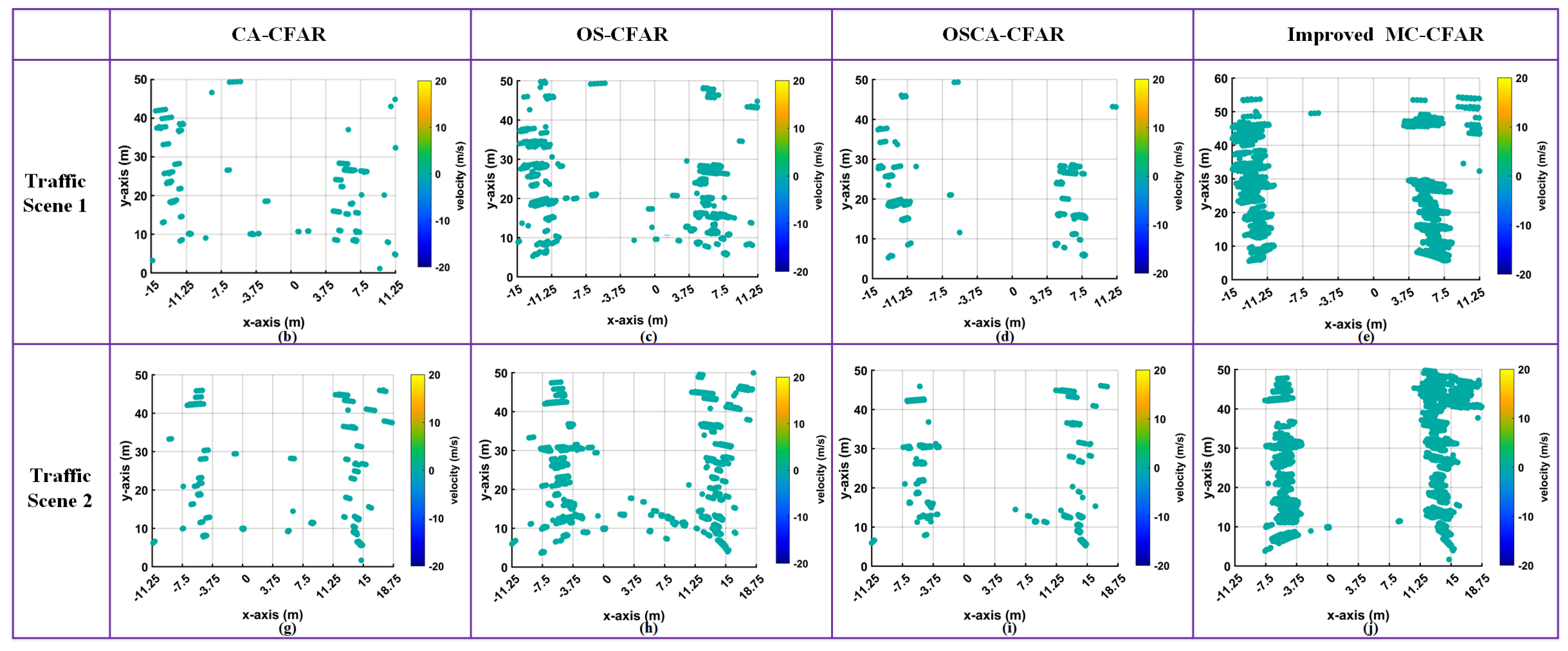
3.1.2. The Improved MC-CFAR Algorithm for Static Target Detection
- Step 1: Extract the zero-Doppler column of each RDM from different receiving channels and implement the angle dimension FFT on each range cell to obtain the RAM.
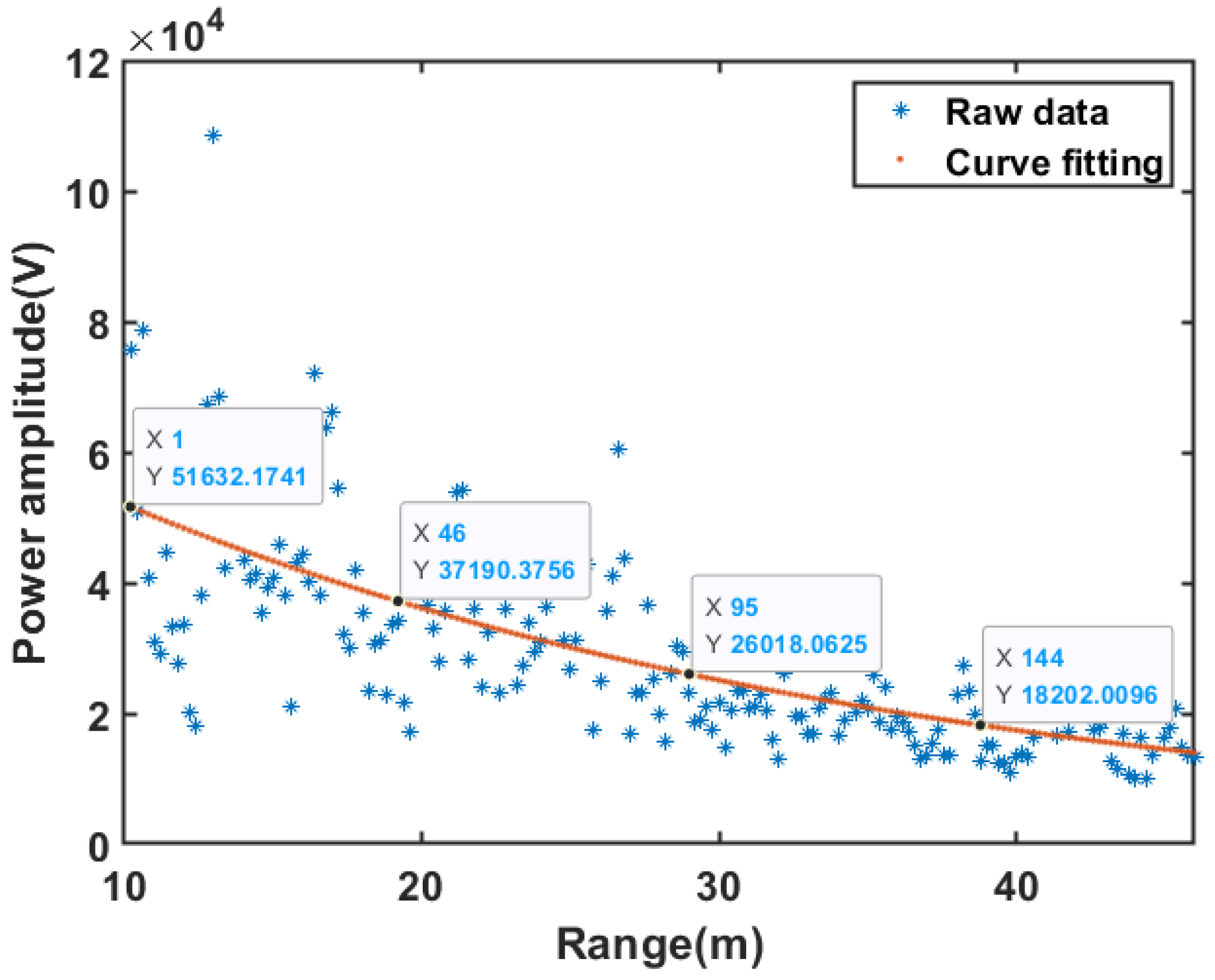
- Step 2: Obtain the interval parameter for dividing RAM. Firstly, the background noise samples in RAM are extracted, and the change curve between noise power and distance is fitted. Then, we obtain the interval parameters based on the scale of the 3 dB drop of the fitted curve. When the detection environment and platform remain unchanged, this step only needs to be performed once.
- Step 3: Divide the RAM to form multiple sub-RAM spaces along the distance dimension based on interval parameters.
- Step 4: Implement the MC-CFAR algorithm for each sub-RAM space separately to search and extract all static targets.
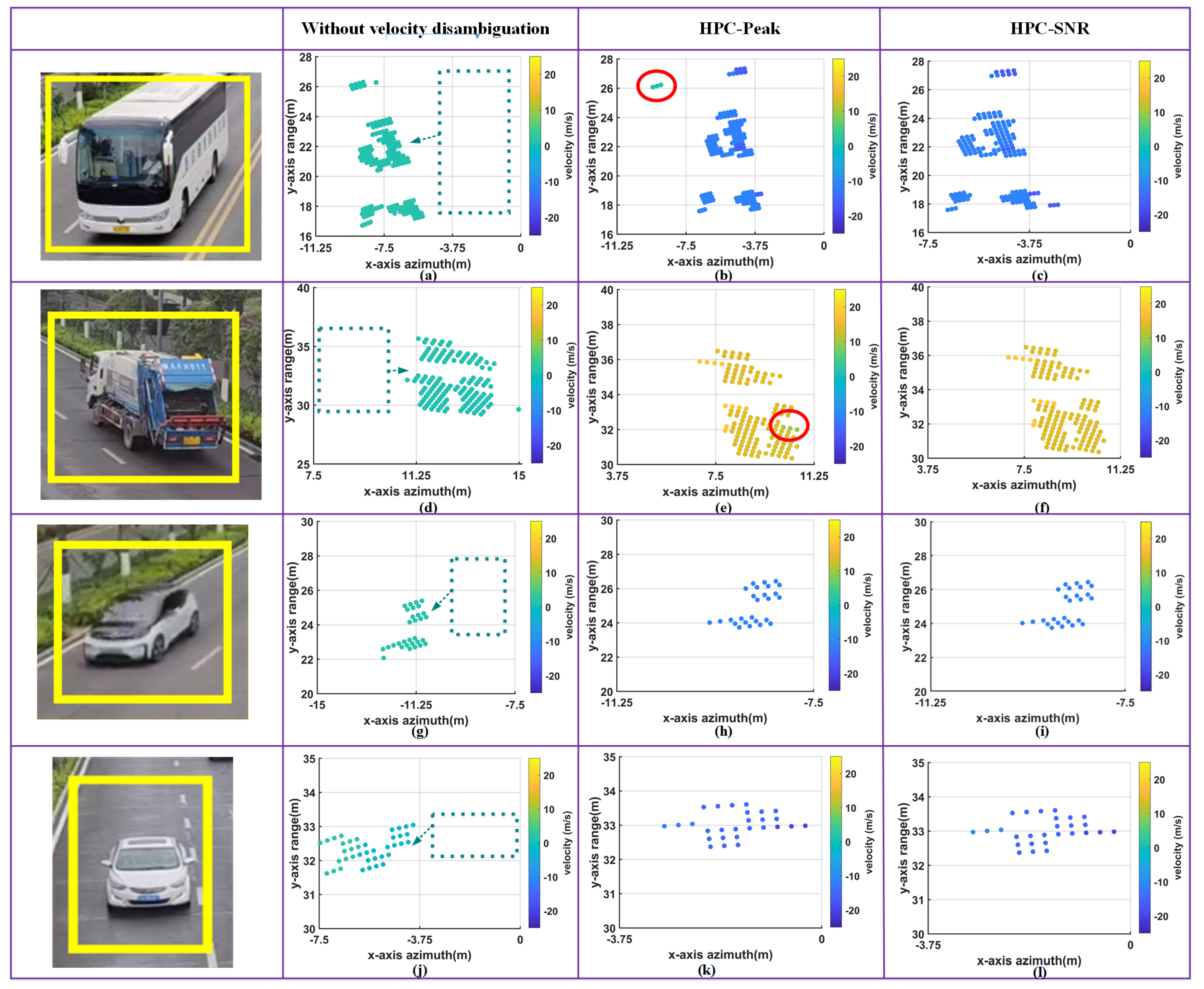
3.2. The HPC-SNR Algorithm for Speed Ambiguity
- Step 1: Based on the output phase of the CFAR detector (), enumerate all possible Doppler phases () that may need to be compensated:where indicates the speed estimation range.
- Step 2: Calibrate the radar data with each hypothetical phase sequentially:where is the echo signal data from the i-th transmitting antenna.
- Step 3: Perform FFT operation on the calibrated radar data to obtain the angular power spectrum under each hypothetical condition ().
- Step 4: According to the HPC-Peak algorithm, if the hypothesis with maximum peak point in the FFT power spectrum is accurate, then the velocity and the angle corresponding to this hypothesis are the true velocities and angle of the target. Unlike the HPC-Peak algorithm, HPC-SNR will extract the maximum value of SNR in each hypothesis and consider the hypothesis with the largest SNR value as true. Then, the speed and the angle corresponding to this hypothesis will be the actual speed and angle of the target.
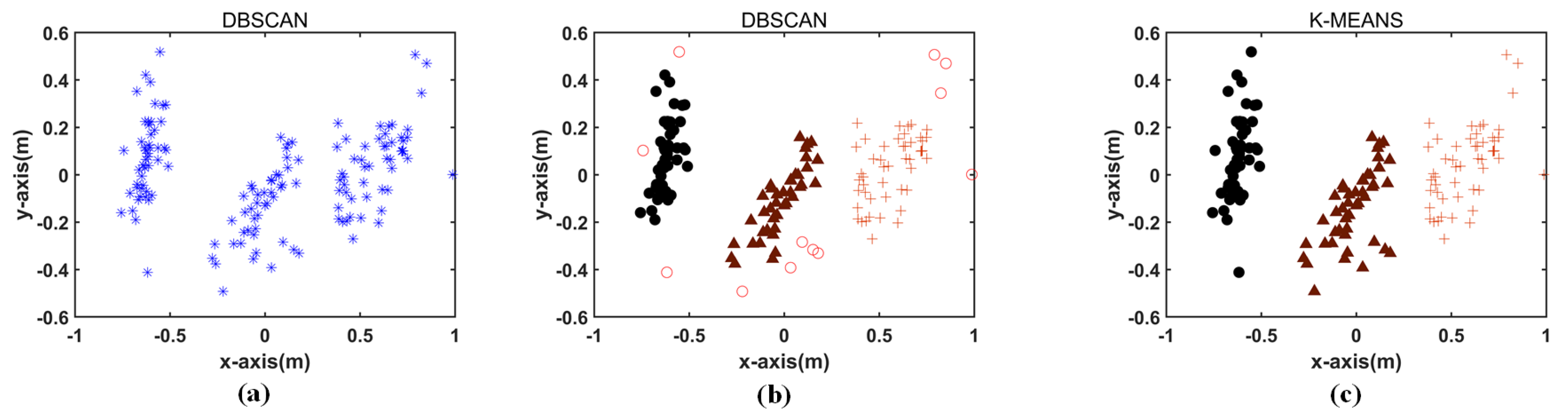
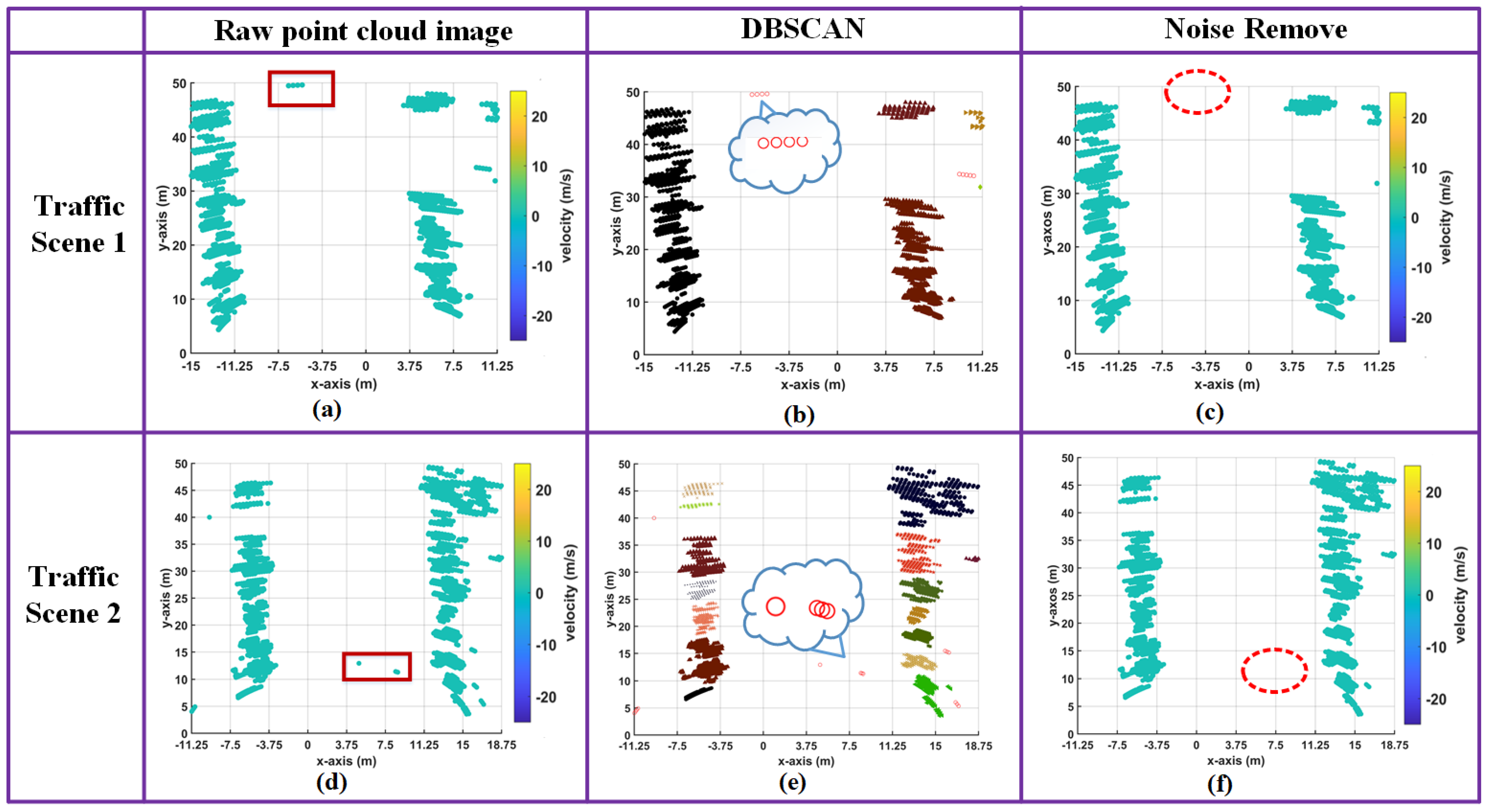
3.3. Noise Removal Based on DBSCAN Algorithm
- Step 1: Determine the parameters and . represents the maximum radius. If the distance between data points is less than or equal to the specified radius, they belong to the same neighborhood. stands for the minimum number of points. When the number of points in a domain is the minimum number, these points are considered a cluster.
- Step 2: Find core points to form temporary clusters. All sample points are scanned; if the number of sample points within the radius of a sample point is greater than , the sample point is considered to be a core point. With the core point as the center, the set of all points with direct density with the core point is regarded as a temporary cluster.
- Step 3: Start from any core point; merge the temporary clusters that satisfy the distance relationship (<) to obtain the final cluster.
- Step 4: Points that do not belong to any clusters are considered outliers and should be removed.
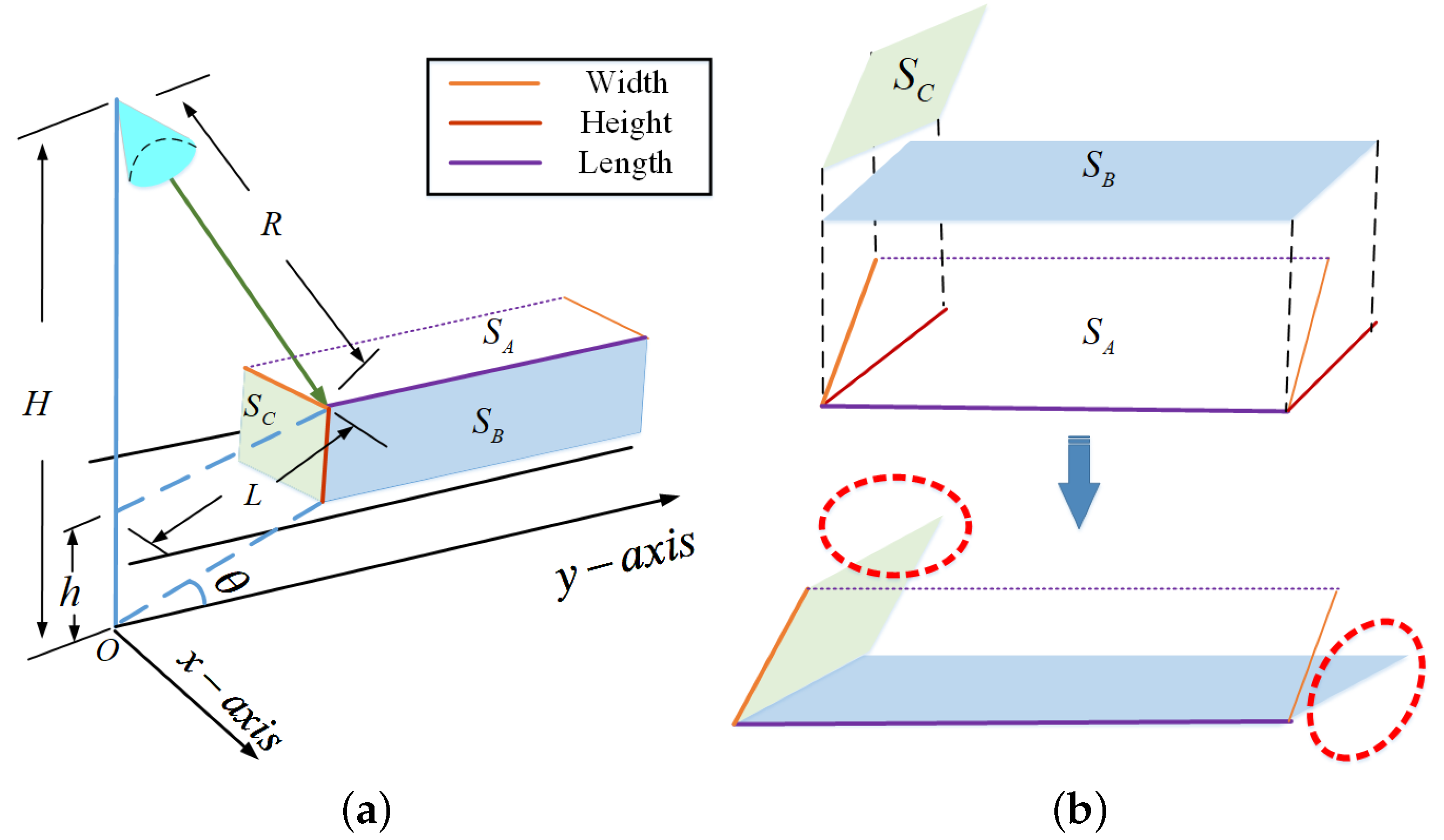
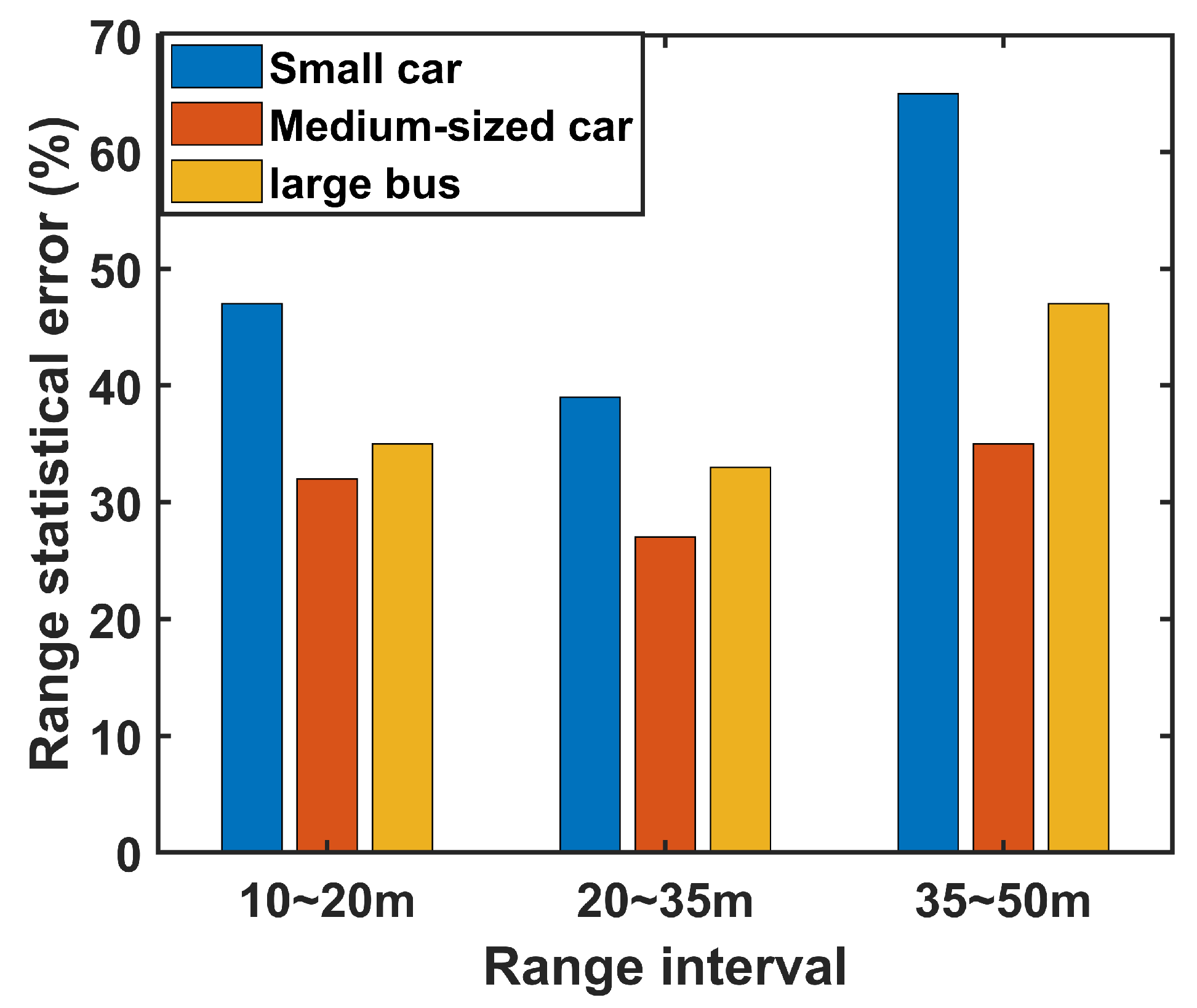
3.4. 2D Point Cloud Imaging and Vehicle Information Perception
- Step 1: By calculating the area of different targets in the radar image, we set the minimum area unit U.
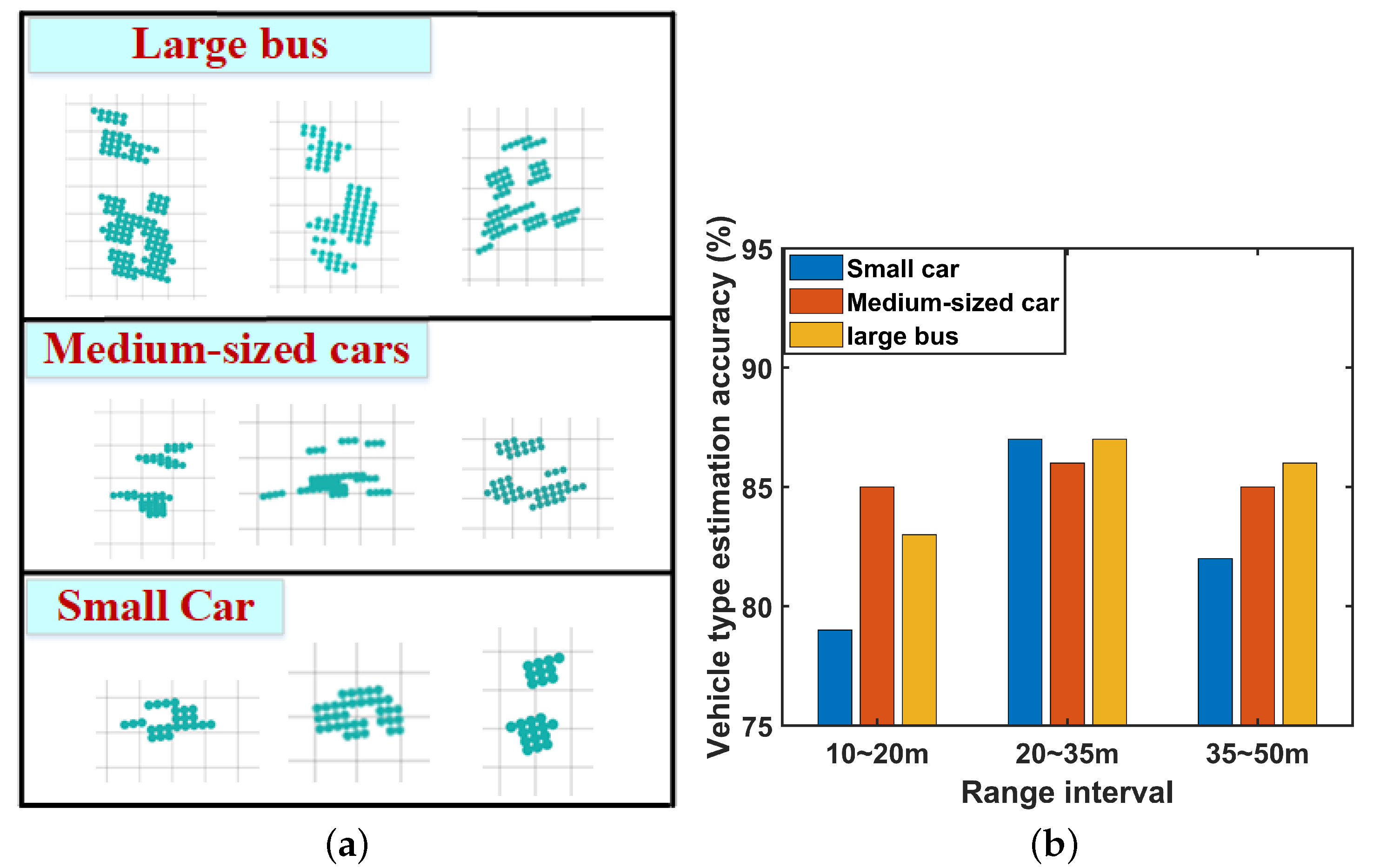
- Step 2: Divide the target into three categories based on the relationship between the point cloud area of the target (S) and the minimum unit: ordinary small cars (), medium-sized cars (), and large buses ().
- Step 3: The vehicle size is inferred in a reverse way according to the industry rules on vehicle types and sizes.
4. Numerical Simulations and Comparison
4.1. Target Detection Algorithm Performance Simulation and Comparison
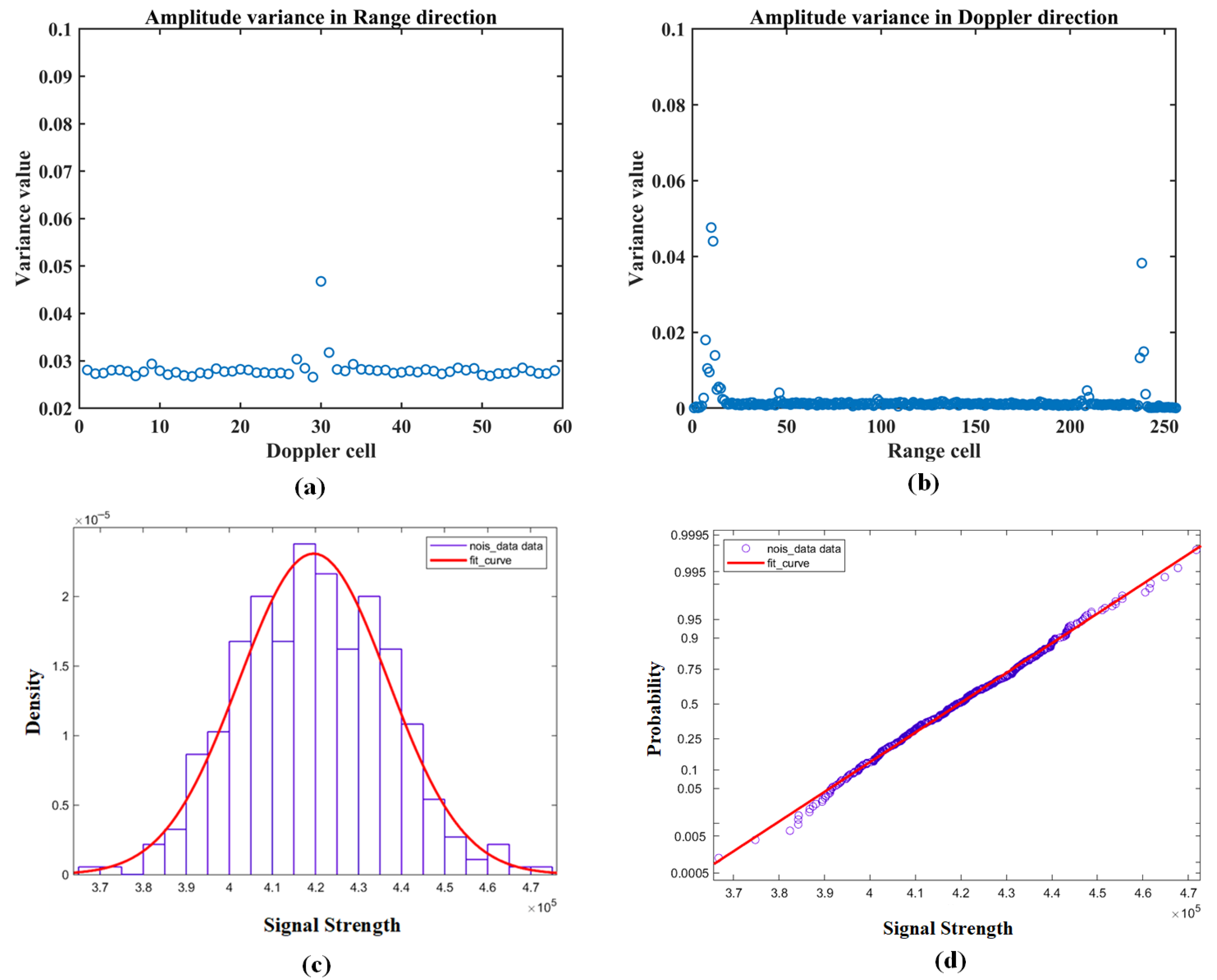
4.1.1. The MC-CFAR Algorithm Performance
4.1.2. The Improved MC-CFAR Algorithm Performance
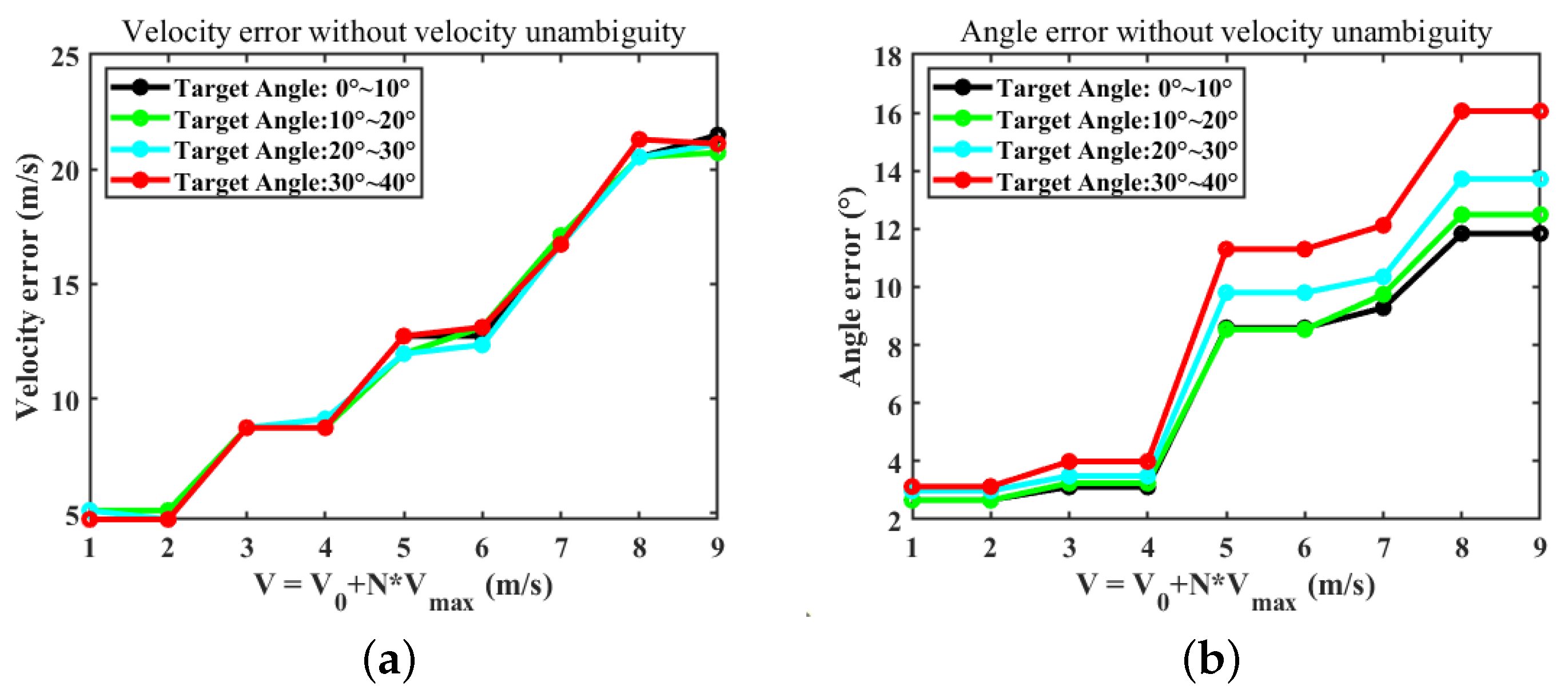
- When there are multiple targets in the same range-Doppler cell, the performance of the HPC-Peak algorithm is unstable. Once the algorithm fails, there is a large error between the estimated angle and the true value, and the number of targets is incorrectly estimated. However, the HPC-SNR algorithm maintains good performance in multi-object situations. Moreover, the angular power spectrum can correctly reflect the number of targets.
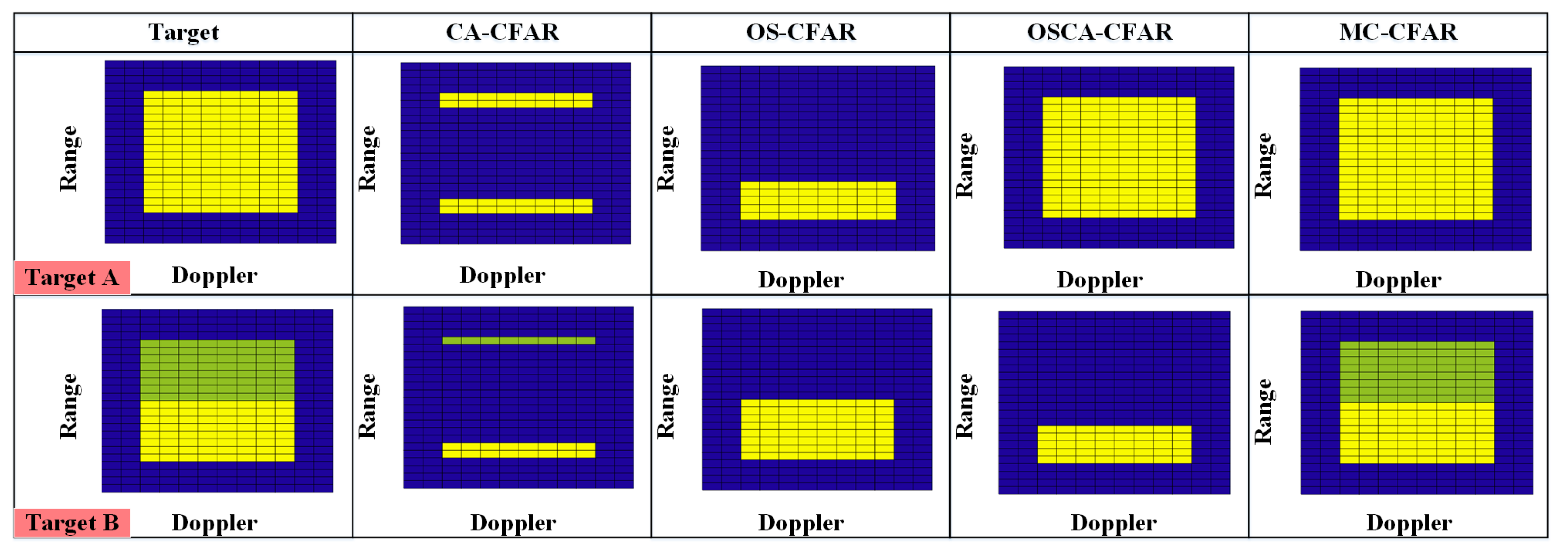
- The improved MC-CFAR algorithm maintains the advantages of the MC-CFAR algorithm and realizes target detection under a non-uniform noise background by fitting and dividing the noise curve, which makes up for the shortage of the MC-CFAR algorithm.
4.2. The HPC-SNR Algorithm Performance Simulation and Comparison
- When there are multiple targets in the same range-Doppler cell, the performance of the HPC-Peak algorithm is unstable. Once the algorithm fails, there is a large error between the estimated angle and the true value, and the number of targets is incorrectly estimated. However, the HPC-SNR algorithm maintains good performance in multi-object situations. Moreover, the angular power spectrum can correctly reflect the number of targets.
- In the case where both algorithms are valid, the HPC-SNR algorithm performs better, i.e., the error of angle estimation is smaller, especially in the case of multi-objective situations.
4.3. Noise Removal Algorithm Simulation
5. Experiment and Result Analysis
5.1. Moving Target Imaging Experiment and Analysis
5.1.1. Experiment on the Performance of MC-CFAR Algorithm and Comparison with Other Algorithm
5.1.2. Velocity Disambiguation for Accurate Imaging
- For the imaging of high-speed target, velocity ambiguity will affect the accuracy of the lateral position of the target. The faster the speed, the larger the error in the lateral position. Velocity disambiguation is one of the key techniques to ensure the imaging accuracy of moving targets.
- Compared with HPC-Peak, the HPC-SNR algorithm can obtain fewer abnormal points and more stable imaging results. When there are multiple targets in the same range-Doppler cell, the HPC-Peak algorithm may fail.
5.2. Static Target Imaging Experiments
5.2.1. Improved MC-CFAR Algorithm for Static Target Extraction
5.2.2. Noise Points Removal Based on the DBSCAN Algorithm
5.3. Urban Traffic Road Scenes 2D Imaging and Vehicle Information Perception
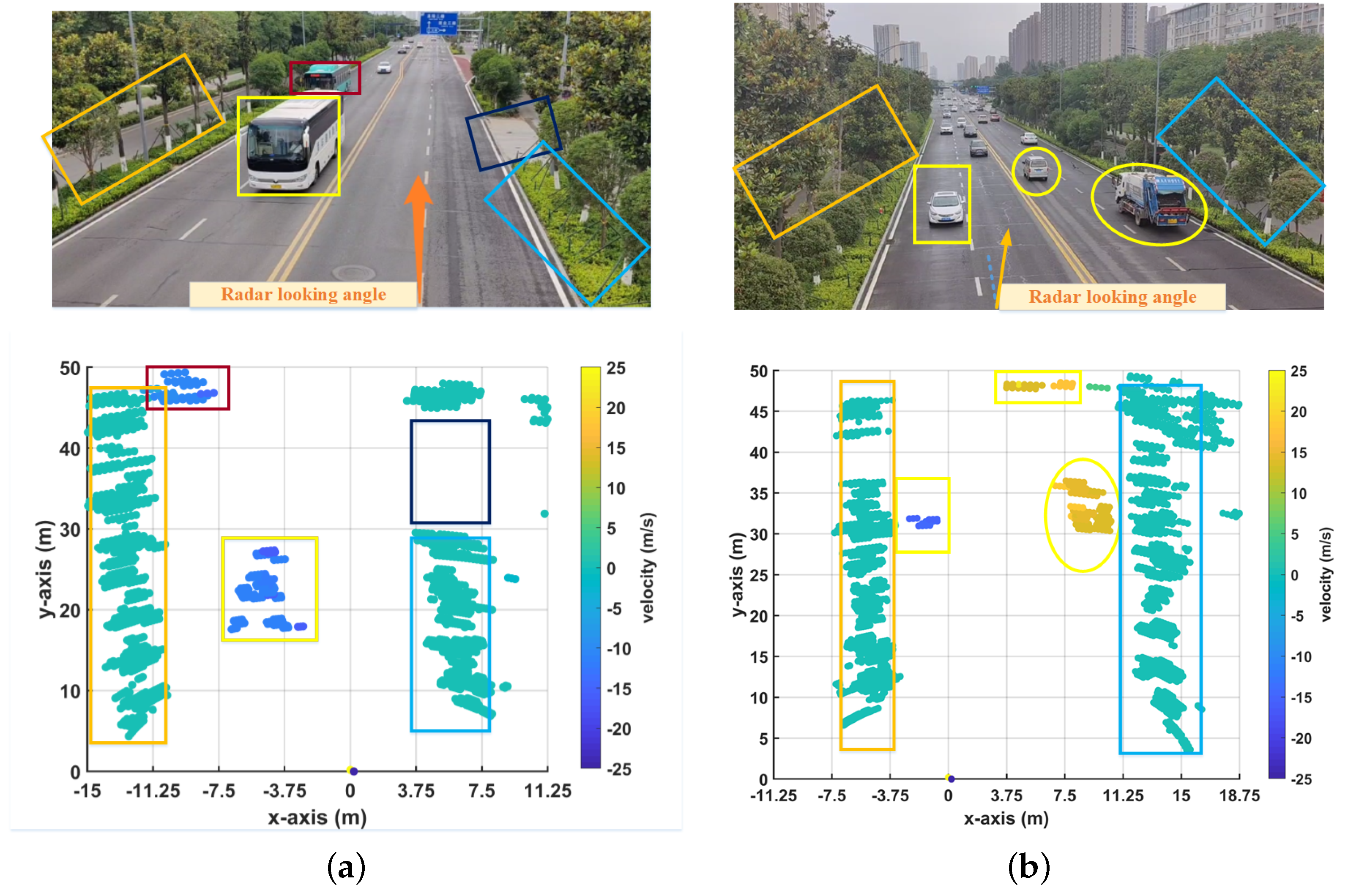
5.3.1. Dynamic and Static Target Imaging Integration
5.3.2. Vehicle Information Perception
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LFMCW | Linear Frequency Modulated Continuous Wave |
| MIMO | Multiple-input Multiple-output |
| 3D-FFT | The 3-dimensional Fast Fourier Transform |
| RMA | Range Migration algorithm |
| BPA | Backpropagation algorithm |
| CFAR | Constant False Alarm Rate |
| CA-CFAR | Cell Average CFAR |
| OS-CFAR | Ordered Statistical CFAR |
| OSCA-CFAR | Fusion CFAR algorithm combining CA and OS |
| MC-CFAR | CFAR algorithm based on the Monte Carlo principle |
| RDM | Range-Doppler power spectrum matrix |
| MPRF | Multiple pulse repetition frequency |
| HPC | Hypothetical Phase Compensation |
| HPC-SNR | Improved Hypothetical Phase Compensation |
| RAM | Range–angle power spectrum matrix |
| CRT | Chinese Remainder Theorem |
| IF | Intermediate frequency |
| TX | Transmitting antennas |
| RX | Receiving antennas |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
Appendix A
Appendix A.1

Appendix A.2
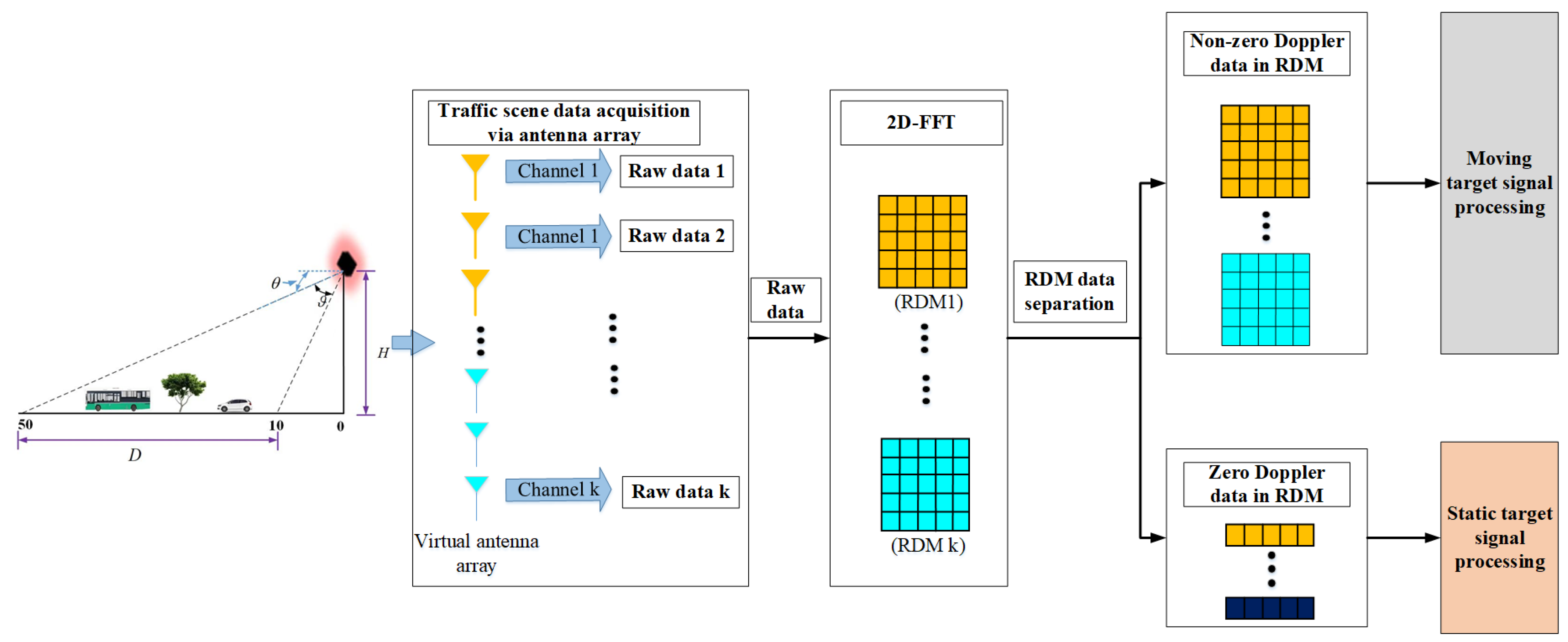
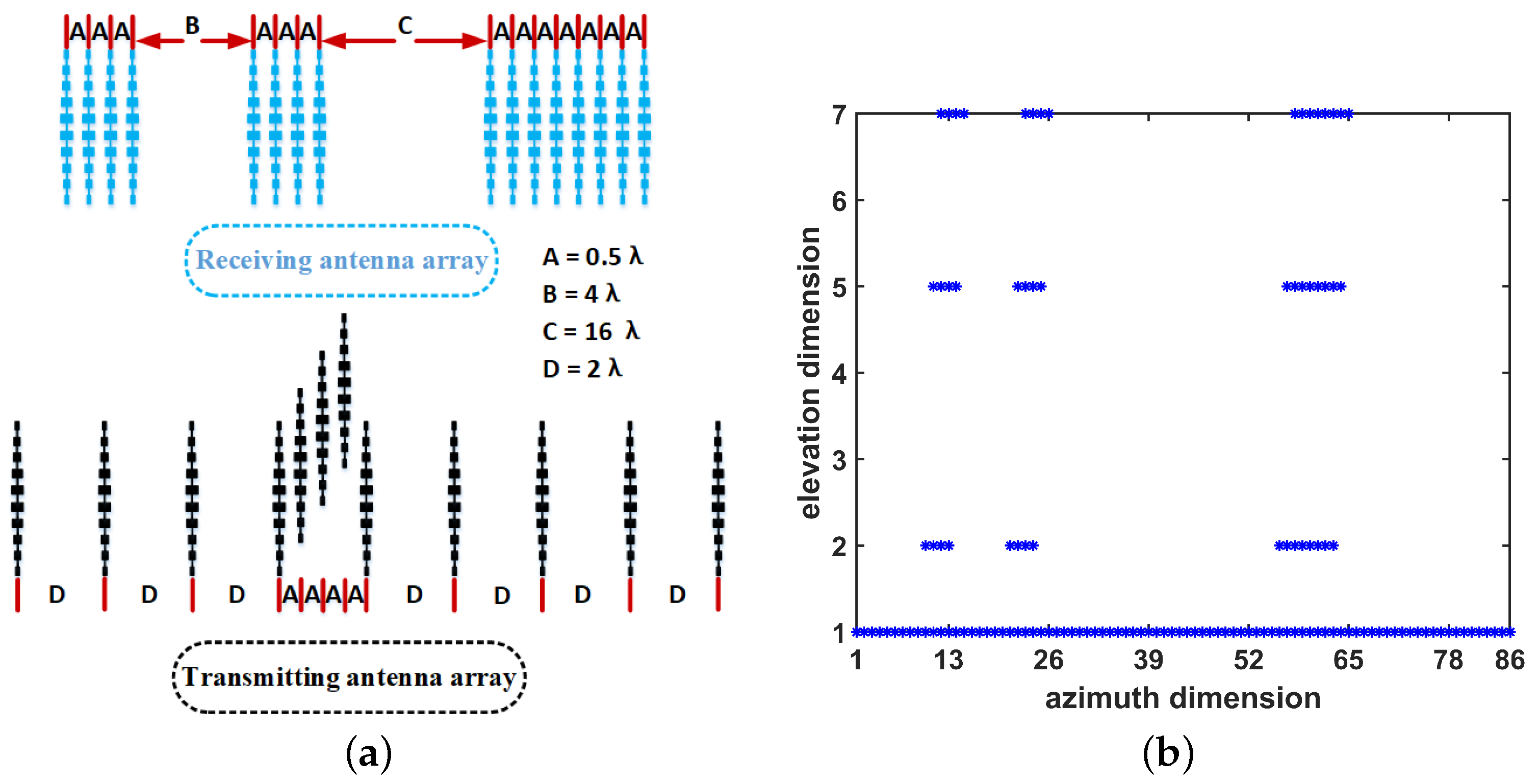
- First, the radar uses the antenna array to obtain the raw data of the traffic scene. In the working mode of TDM-MIMO, the radar can obtain raw data from azimuth antenna channels at one time.
- Then, the data of each azimuth antenna channel are subjected to a 2D-FFT operation to obtain k RDM matrices.
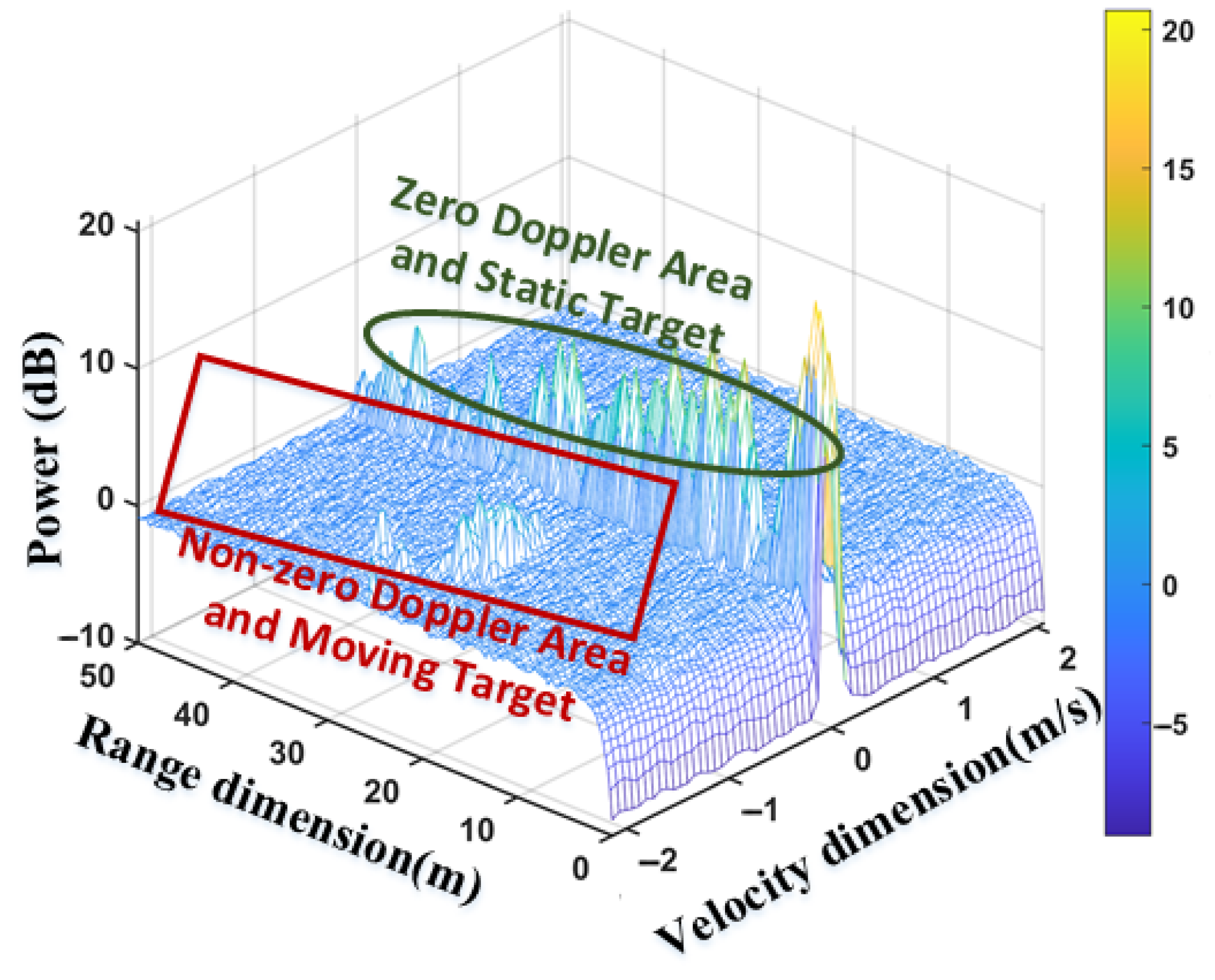
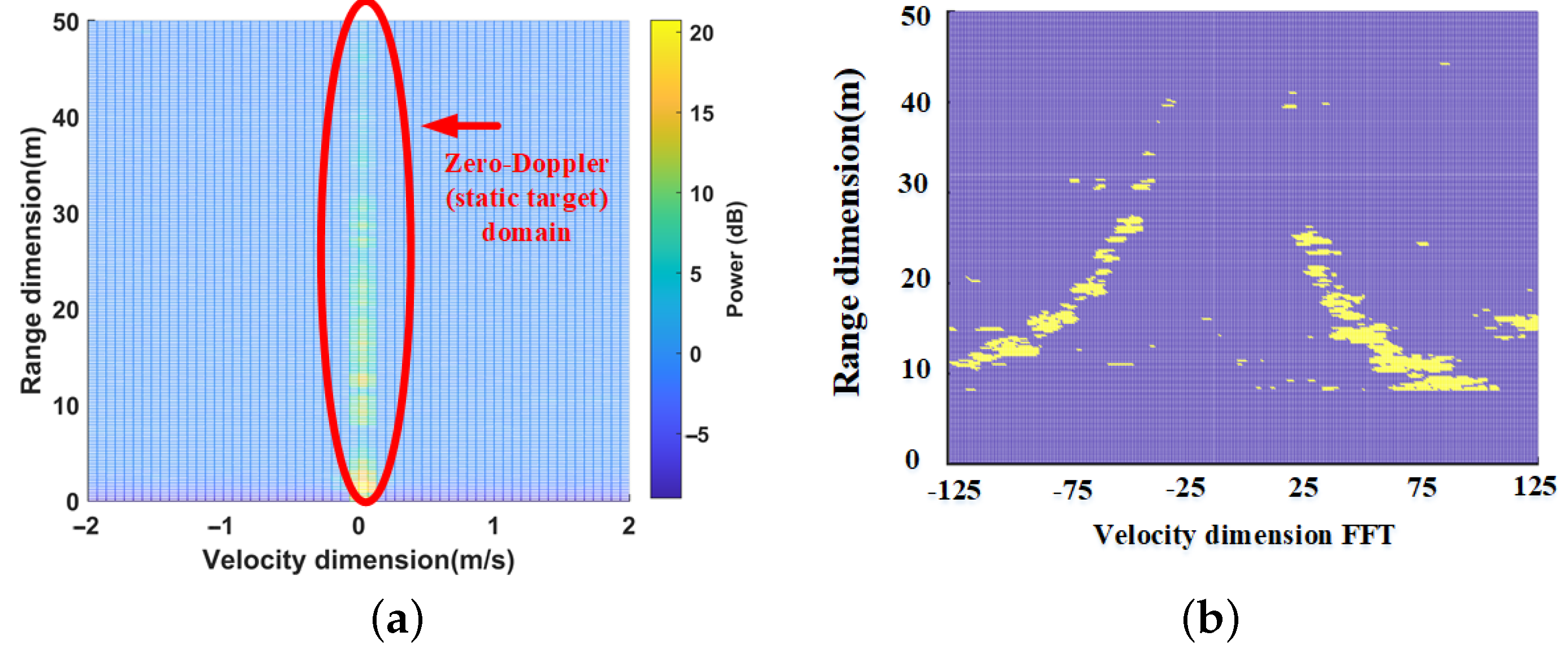
- Next, we divide RDM data into two categories: zero-Doppler data and non-zero-Doppler data.
- Finally, the non-zero-Doppler data and zero-Doppler data will be sent to the moving target signal processing unit and static target signal processing unit, respectively, in the post-processing of the radar signal to realize the detection and extraction of moving and static targets.
- A new RDM matrix is obtained by incoherent accumulation of all non-zero-Doppler data. The new RDM matrix will be processed by the moving target CFAR search engine.
- In the moving target CFAR search engine, the MC-CFAR algorithm is implemented to obtain the indices of target distance and velocity. In addition, the CA-CFAR, OS-CFAR, and OSCA-CFAR algorithms are implemented and compared to verify the performance of MC-CFAR algorithm.
- The raw data on the target angle are obtained from the RDM set according to the index information. The angle data of all targets are sent to the velocity disambiguation engine for processing.
- In the velocity disambiguation engine, the HPC-SNR algorithm is implemented to obtain the true velocity and azimuth of the target. Furthermore, the HPC-Peak algorithm is implemented and compared to verify the performance of HPC-SNR algorithm.
- Finally, the real distance, speed, and angle of the target obtained through the CFAR engine and the velocity disambiguation engine are output to the PC terminal and drawn by drawing tools such as MATLAB.
- The RDM zero-Doppler data in all channels are sent to the static target signal processing unit. The RAM matrix is obtained after FFT processing of the angle. The RAM matrix will be processed by the static target CFAR search engine.
- In the static target CFAR search engine, the improved MC-CFAR algorithm is implemented to obtain indices of the target distance and angle. In addition, the CA-CFAR, OS-CFAR, and OSCA-CFAR algorithms are implemented and compared to verify the performance of the improved MC-CFAR algorithm.
- All target points are input into the Outlier Removal Engine to eliminate interference points.
- Finally, the static target point, after being processed by the DBSCAN algorithm, is output to the PC terminal to be drawn by tools such as MATLAB.
Appendix B
References
- Prabhakara, A.; Jin, T.; Das, A.; Bhatt, G.; Kumari, L.; Soltanaghaei, E.; Bilmes, J.; Kumar, S.; Rowe, A. High Resolution Point Clouds from mmWave Radar. arXiv 2022, arXiv:2206.09273. [Google Scholar]
- Liu, H.; Li, N.; Guan, D.; Rai, L. Data feature analysis of non-scanning multi target millimeter-wave radar in traffic flow detection applications. Sensors 2018, 18, 2756. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.; Zhang, Y.; Zhang, F.; Zhao, X.; Huang, S.; Feng, Z.; Wei, Z. Spatial attention fusion for obstacle detection using mmwave radar and vision sensor. Sensors 2020, 20, 956. [Google Scholar] [CrossRef]
- Pegoraro, J.; Meneghello, F.; Rossi, M. Multiperson continuous tracking and identification from mm-wave micro-Doppler signatures. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2994–3009. [Google Scholar] [CrossRef]
- Dankert, H.; Horstmann, J.; Rosenthal, W. Wind-and wave-field measurements using marine X-band radar-image sequences. IEEE J. Ocean. Eng. 2005, 30, 534–542. [Google Scholar] [CrossRef]
- Nieto-Borge, J.; Hessner, K.; Jarabo-Amores, P.; De La Mata-Moya, D. Signal-to-noise ratio analysis to estimate ocean wave heights from X-band marine radar image time series. IET Radar Sonar Navig. 2008, 2, 35–41. [Google Scholar] [CrossRef]
- Wei, S.; Zhou, Z.; Wang, M.; Wei, J.; Liu, S.; Zhang, X.; Fan, F. 3DRIED: A high-resolution 3-D millimeter-wave radar dataset dedicated to imaging and evaluation. Remote Sens. 2021, 13, 3366. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, Q.; Tian, X.; Chang, T.; Cui, H.L. Near-field 3-D millimeter-wave imaging using MIMO RMA with range compensation. IEEE Trans. Microw. Theory Tech. 2018, 67, 1157–1166. [Google Scholar] [CrossRef]
- Zhao, Y.; Yarovoy, A.; Fioranelli, F. Angle-insensitive Human Motion and Posture Recognition Based on 4D imaging Radar and Deep Learning Classifiers. IEEE Sens. J. 2022, 22, 12173–12182. [Google Scholar] [CrossRef]
- Qian, K.; He, Z.; Zhang, X. 3D point cloud generation with millimeter-wave radar. Proc. Acm Interact. Mob. Wearable Ubiquitous Technol. 2020, 4, 148. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, Z.; Chang, T.; Cui, H.L. Millimeter-Wave 3-D Imaging Testbed with MIMO Array. IEEE Trans. Microw. Theory Tech. 2020, 68, 1164–1174. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, Y.D. 4D Automotive Radar Sensing for Autonomous Vehicles: A Sparsity-Oriented Approach. IEEE J. Sel. Top. Signal Process. 2021, 15, 879–891. [Google Scholar] [CrossRef]
- Gao, X.; Xing, G.; Roy, S.; Liu, H. Ramp-cnn: A novel neural network for enhanced automotive radar object recognition. IEEE Sens. J. 2020, 21, 5119–5132. [Google Scholar] [CrossRef]
- Li, G.; Sit, Y.L.; Manchala, S.; Kettner, T.; Ossowska, A.; Krupinski, K.; Sturm, C.; Goerner, S.; Lübbert, U. Pioneer study on near-range sensing with 4D MIMO-FMCW automotive radars. In Proceedings of the 2019 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019; pp. 1–10. [Google Scholar]
- Lee, T.Y.; Skvortsov, V.; Kim, M.S.; Han, S.H.; Ka, M.H. Application of W -Band FMCW Radar for Road Curvature Estimation in Poor Visibility Conditions. IEEE Sens. J. 2018, 18, 5300–5312. [Google Scholar] [CrossRef]
- Sabery, S.M.; Bystrov, A.; Gardner, P.; Stroescu, A.; Gashinova, M. Road Surface Classification Based on Radar Imaging Using Convolutional Neural Network. IEEE Sens. J. 2021, 21, 18725–18732. [Google Scholar] [CrossRef]
- Farina, A.; Studer, F.A. A review of CFAR detection techniques in radar systems. Microw. J. 1986, 29, 115. [Google Scholar]
- Gandhi, P.; Kassam, S. Analysis of CFAR processors in nonhomogeneous background. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 427–445. [Google Scholar] [CrossRef]
- Finn, H.M. Adaptive detection mode with threshold control as a function of spatially sampled-clutter-level estimates. RCA Rev. 1968, 29, 414–464. [Google Scholar]
- Yan, J.; Li, X.; Shao, Z. Intelligent and fast two-dimensional CFAR procedure. In Proceedings of the 2015 IEEE International Conference on Communication Problem-Solving (ICCP), Guilin, China, 16–18 October 2015; pp. 461–463. [Google Scholar] [CrossRef]
- Rohling, H. Resolution of Range and Doppler Ambiguities in Pulse Radar Systems. In Proceedings of the Digital Signal Processing, Florence, Italy, 7–10 September 1987; p. 58. [Google Scholar]
- Kronauge, M.; Schroeder, C.; Rohling, H. Radar target detection and Doppler ambiguity resolution. In Proceedings of the 11-th International Radar Symposium, Vilnius, Lithuania, 16–18 June 2010; pp. 1–4. [Google Scholar]
- Kellner, D.; Klappstein, J.; Dietmayer, K. Grid-based DBSCAN for clustering extended objects in radar data. In Proceedings of the IEEE Intelligent Vehicles Symposium, Madrid, Spain, 3–7 June 2012; pp. 365–370. [Google Scholar]
- Roos, F.; Bechter, J.; Appenrodt, N.; Dickmann, J.; Waldschmidt, C. Enhancement of Doppler unambiguity for chirp-sequence modulated TDM-MIMO radars. In Proceedings of the 2018 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Munich, Germany, 16–17 April 2018; pp. 1–4. [Google Scholar]
- Gonzalez, H.A.; Liu, C.; Vogginger, B.; Mayr, C.G. Doppler Ambiguity Resolution for Binary-Phase-Modulated MIMO FMCW Radars. In Proceedings of the 2019 International Radar Conference (RADAR), Toulon, France, 23–27 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Gonzalez, H.A.; Liu, C.; Vogginger, B.; Kumaraveeran, P.; Mayr, C.G. Doppler disambiguation in MIMO FMCW radars with binary phase modulation. IET Radar Sonar Navig. 2021, 15, 884–901. [Google Scholar] [CrossRef]
- Liu, C.; Gonzalez, H.A.; Vogginger, B.; Mayr, C.G. Phase-based doppler disambiguation in TDM and BPM MIMO FMCW radars. In Proceedings of the 2021 IEEE Radio and Wireless Symposium (RWS), San Diego, CA, USA, 17–22 January 2021; pp. 87–90. [Google Scholar]
- Stolz, M.; Wolf, M.; Meinl, F.; Kunert, M.; Menzel, W. A new antenna array and signal processing concept for an automotive 4D radar. In Proceedings of the 2018 15th European Radar Conference (EuRAD), Madrid, Spain, 26–28 September 2018; pp. 63–66. [Google Scholar]
- Phippen, D.; Daniel, L.; Hoare Sr, E.; Gishkori Sr, S.; Mulgrew, B.; Cherniakov, M.; Gashinova, M. Height estimation for 3-D automotive scene reconstruction using 300 GHz multireceiver radar. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2339–2351. [Google Scholar] [CrossRef]
- Laribi, A.; Hahn, M.; Dickmann, J.; Waldschmidt, C. A new height-estimation method using FMCW radar Doppler beam sharpening. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos Island, Greece, 28 August–2 September 2017; pp. 1932–1936. [Google Scholar]
- Laribi, A.; Hahn, M.; Dickmann, J.; Waldschmidt, C. A novel target-height estimation approach using radar-wave multipath propagation for automotive applications. Adv. Radio Sci. 2017, 15, 61–67. [Google Scholar] [CrossRef]
- Cui, H.; Wu, J.; Zhang, J.; Chowdhary, G.; Norris, W.R. 3D Detection and Tracking for On-road Vehicles with a Monovision Camera and Dual Low-cost 4D mmWave Radars. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19 September 2021; pp. 2931–2937. [Google Scholar]
- Jin, F.; Sengupta, A.; Cao, S.; Wu, Y.J. Mmwave radar point cloud segmentation using gmm in multimodal traffic monitoring. In Proceedings of the 2020 IEEE International Radar Conference (RADAR), Washington, DC, USA, 28–30 April 2020; pp. 732–737. [Google Scholar]
- Yang, B.; Zhang, H. A CFAR Algorithm Based on Monte Carlo Method for Millimeter-Wave Radar Road Traffic Target Detection. Remote Sens. 2022, 14, 1779. [Google Scholar] [CrossRef]






| Item | Parameters | Item | Parameters |
|---|---|---|---|
| Range FFT points | 512 | Chirp number | 64 |
| 50 m | 2.14 m/s | ||
| 0.098 m | 0.067 m/s | ||
| Operating mode | TDM-MIMO | ||
| Item | Imaging Radar | Detection Radar |
|---|---|---|
| Mission Focus | Traffic Perception | Moving target detection |
| Detection Object | Moving target and Static target | Moving target |
| Target Size | Not Negligible | Ideal point |
| Target Velocity | >(5∼8) | <2 |
| Output | Target point clouds | Target trajectory |
| Vehicle Type | Driving Direction | Lane (Relative to Radar) | X-Axis Range (m) |
|---|---|---|---|
| Vehicle 1 | close | Second lane on the left radar | [−7.5, −3.5] |
| Vehicle 2 | far away | Third lane on the right radar | [7.5, 11.5] |
| Vehicle 3 | close | First lane on the left radar | [−11.5, −7.5] |
| Vehicle 4 | close | Third lane on the left radar | [−3.5, 0] |
| Algorithm | Window Length/Samples Number | Threshold Factor |
|---|---|---|
| CA-CFAR | 16 | 3 |
| OS-CFAR | 16 | 3 |
| OSCA-CFAR | 16 | 4 |
| MC-CFAR | 768 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Zhang, H.; Chen, Y.; Zhou, Y.; Peng, Y. Urban Traffic Imaging Using Millimeter-Wave Radar. Remote Sens. 2022, 14, 5416. https://doi.org/10.3390/rs14215416
Yang B, Zhang H, Chen Y, Zhou Y, Peng Y. Urban Traffic Imaging Using Millimeter-Wave Radar. Remote Sensing. 2022; 14(21):5416. https://doi.org/10.3390/rs14215416
Chicago/Turabian StyleYang, Bo, Hua Zhang, Yurong Chen, Yongjun Zhou, and Yu Peng. 2022. "Urban Traffic Imaging Using Millimeter-Wave Radar" Remote Sensing 14, no. 21: 5416. https://doi.org/10.3390/rs14215416
APA StyleYang, B., Zhang, H., Chen, Y., Zhou, Y., & Peng, Y. (2022). Urban Traffic Imaging Using Millimeter-Wave Radar. Remote Sensing, 14(21), 5416. https://doi.org/10.3390/rs14215416







