Abstract
We examine a dome within the boundary between Fracastorius crater and Mare Nectaris. The dome has a noticeable vent structure and appears to be perpendicular to wrinkle ridges in the southern Mare Nectaris basin. The spectral signature of this dome, derived from Clementine UVVIS and Chandrayaan-1 M3 reflectance data, revealed that Fracastorius has low TiO2 content and primarily basaltic material. Using altimeter data, we measured the dome diameter to be 28.6 km, with a dome height of 241.5 m, and a flank slope of 1°. Based on rheological modeling of the dome and a viscoelastic model of the presumed feeder dike, we obtained a magma viscosity of 3.1 × 105 Pa s, an effusion rate of 5.9 m3 s−1, a duration of multiple effusion processes of 4.15 years, and a magma rise speed of 2.1 × 10−4 m s−1. From these measurements, we estimate the feeder dike geometry to have a horizontal dike length of 234 km and a width of 11.8 m. A comparison of the Fracastorius dome with other noted lunar domes with similar morphometric properties reveal similar magma viscosities to domes found near craters Mee, Milichius and Petavius.
1. Introduction
Mare Nectaris is a multi-ring mare basin located on the eastern lunar nearside (centered at −15.19°N, 34.60°E), with a diameter of 860 km and an approximate age of 3.8–3.9 Gyr [1,2]. During the Nectaris basin-forming impact, the lunar crust uplifted and overturned, creating the highland mountains, mostly situated in the eastern portion of the basin. Subsequently, the basaltic magma rose to the surface through fractures and shallow dikes, in-filling the basin floor. Previous compositional analysis using Clementine UVVIS (ultraviolet-visible) data of Mare Nectaris showed distinctive mare basalt units and pyroclastic deposits of volcanic origin, with the majority being compositionally low-Fe (<8.5 wt.%), low-Ti (<1 wt.%) basalt, typical of the early Imbrian unit (~2.01–3.57 Ga) [1,2,3,4]. From [1], SELENE gravity and topographic models show that Mare Nectaris has a relatively thin crust (thickness of 10–25 km).
The Fracastorius dome (−18.94°N, 33.02°E) is situated at the northern rim of Fracastorius crater (−21.36°N, 33.07°E), a 120.6 km diameter crater cutting into the south of the Mare Nectaris basin (Figure 1 and Figure 2). The dome is elongated, with a putative vent on its surface, with some asymmetry of its flanks. The average flank slope is ~1° near the vent, but the eastern flank is steepest (~2.7°). Figure 1 shows the positive relief of the putative dome in an oblique solar illumination. The dome is situated within the Im2 unit (upper Imbrian mare unit mainly consisting of basaltic lava flows), bounded by Ip (Imbrian plains unit, likely from Orientale or other major impact ejecta) to the south and It (Imbrian terra unit of basin ejecta debris and mega-regolith material) to the east [5] (Figure 3).

Figure 1.
CCD image of the Fracastorius crater and oblique solar illuminated angle of the dome (highlighted with white arrows). Image courtesy of P. Lazzarotti using a Gladius XLI Cassegrain with an aperture of 400 mm f/16.

Figure 2.
(A) LROC image of southern Mare Nectaris and Fracastorius crater. Scale bar 50 km. (B) Subset image of the Fracastorius dome. Scale bar 10 km. White arrows indicate the northern flanks of the dome. Red arrow marks the irregular vent structure.
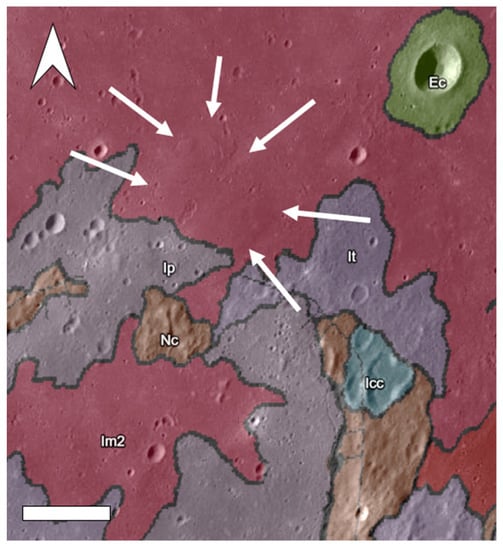
Figure 3.
Fracastorius dome area (as outlined by the white arrows) and surrounding region overlain with the unified global lunar geologic map from the USGS Astrogeology Science Center, accessed using LROC Quick Map. The units displayed are: Ip (Imbrian plains unit); Im2 (Upper mare unit); It (Terra unit); Nc, Icc, Ec (crater units). Scale bar 20 km.
In this study, we use the morphologic and morphometric characteristics of the dome as a basis for estimation of its yield strength, viscosity, eruption rate, eruption duration, and make assumptions on the feeder dike geometry (e.g., dike length and width). We then compare these values to other known effusive lunar domes from [6] and [7].
2. An Overview about Lunar Mare Domes
Mare domes are typically smooth, low-sloped convex profiles [6] and can be circular to elliptical in shape. Lunar domes are formed either by: (i) outpouring of magma from a central vent; (ii) subsurface accumulation of magma that causes an up-welling of the bedrock, creating a positive relief [8,9]. Such volcanic domes usually have some central vent, pit chains, or vents [3], which can be associated with pyroclastic deposits or proximal lava plains with known volcanic origins [10]. Domes found in lunar mare are typically interpreted to be shield-like volcanoes or laccoliths [10,11,12,13].
Lunar domes in mare probably formed during the latter phase of a volcanic eruption [6]. Initially, such lavas would be fluid in their high temperature, but would lower with decreased flow rates and crystallization increased. This would accumulate around a central vent or fissure and form a dome [14,15]. Typically, steeper domes would represent cooler, more viscous lavas [16]. Alongside the viscosity and temperature of the lavas, other factors relating to the morphological construction of dome edifices are also the lava composition, duration and rate of the eruption, and the number of eruptions. The viscosity of the lava would naturally depend on the temperature [17,18], and the eruption rate and duration would depend on crystalline material (and the material’s phase temperatures) [8].
The source of this lunar magma is presumed to be from feeder dikes from source regions at the crustal base or deeper in the mantle [6,19]. Therefore, the surface material emplaced from dikes below the surface is dependent on the dike geometry and depth. From [20], a dike must propagate at a shallow depth to gain surface access and subsequent fractures and lava effusion will occur. After the high effusion rates that formed the extensive mare units, this mass flux decreased as crystallization increased (and temperatures decreased). Lower-sloped mare domes were formed by low-viscous lavas and higher eruption rates, while steep sloped domes favored lower temperatures, higher crystallinity, and higher viscosities of the lunar lava [7,15,16].
3. Methods and Materials
Lunar image data from the Lunar Reconnaissance Orbiter (LRO) Wide-angle camera (WAC; 100 m/px) and Narrow-angle camera (NAC; ~32 m/px) were used to map the parameters of the Fracastorius dome. The Lunar Orbiter Laser Altimeter (LOLA) data was then used (using 64 ppd maps) to create digital elevation models (DEMs) to determine the diameter and height of the dome, along with the vent morphology.
Clementine UVVIS spectral data has been calibrated and normalized, as provided by [21]. The TiO2 content derived by the abundance maps were created from topographically correct mineral reflectance maps acquired by the JAXA Selene/Kaguya. Chandrayann-1’s Moon Mineralogy Mapper (M3) imaging reflectance spectrometer can detect 85 channels (460–3000 nm) with a spatial resolution of 140 m and 280 m/pixel [22]. M3 data were calibrated and photometrically corrected and converted to apparent reflectance. The spectral continuum is the line connecting the reflectance values at 750 nm and 1500 nm, by which the reflectance spectrum is divided to obtain the continuum-removed spectrum [23].
4. Dome Composition
The 750 nm wavelength is an indicator for soil composition variations, maturity, and particle size [24]. The R415/R750 color ratio is a measure for the TiO2 content of basaltic soils, where high ratios correspond to high TiO2 content and vice versa [25]. The R950/R750 color ratio is related to the strength of the mafic absorption band (mainly FeO content of the soil) and is sensitive to the optical maturity of mare and highland materials [26]. The Fracastorius dome is revealed to have a 750 nm reflectance of R750 = 0.1273, a low value for the UVVIS color ratio of R415/R750 = 0.6010 and a R950/R750 = 1.0647, indicating low TiO2 content. This TiO2 content is measured to be ~2 wt.%, while the FeO content varies 12–14 wt.%.
The M3 spectrum of Fracastorius dome (Figure 4) displays a trough ~1000 nm with a minimum wavelength at 980 nm and an absorption band ~2200 nm. This corresponds to a typical high-Ca pyroxene signature [27], indicating a basaltic composition. The highland material to the north of the dome displays a spectrum of a more feldspathic composition, which also lacks any observable mafic absorption feature in the range between 1000–2400 nm. Thus, the Fracastorius dome consists of basaltic material.
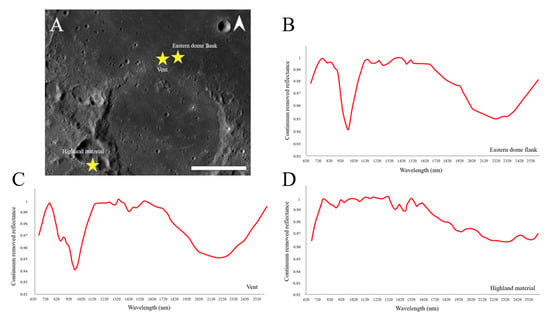
Figure 4.
Mineralogical characteristics of the Fracastorius dome from Chandrayaan-1’s Moon Mineralogy Mapper (M3). (A) Sites at the Fracastorius dome and nearby highlands in which reflectance spectra have been obtained; (B) Spectrum of the eastern flank of the dome; (C) Spectrum of the vent; (D) Spectrum of the nearby highlands.
5. Morphologic and Morphometric Dome Properties
As observed in Figure 2 and Figure 5, the surface of the dome appears to be smooth and elliptical. The southwestern edge of the dome is bordered by higher-elevation remnants of the Fracastorius crater and Mare Nectaris basin material. Figure 5 shows the cross-sections of the Fracastorius dome in SW-NE (A–A′) and NW-SE (B–B′) orientations to provide morphometric information on the dome shape and vent structure. We find that the dome radius is 14.3 km and a height of ~241.5 m. The vent of the Fracastorius dome (Figure 6) is angled to the northeast inward to the Nectaris basin. Every lunar dome, sinuous rille, and many other depressions are vents or source regions for volcanic eruptions. These vents are elongated and typically a few km wide, 3–10 km long. The depression is 5.8 km long and 110 m depth, based on the measurements. The morphology is observed to be an irregular depression, with a fairly smooth center and steeper slopes to the eastern portion of the vent, as seen in NAC (with slope) maps (Figure 6). The location of this elongated depression on a typical dome relief (Figure 2) is suggestive of its volcanic origin, even if it might also be, as an alternative explanation, a degraded impact or secondary crater.
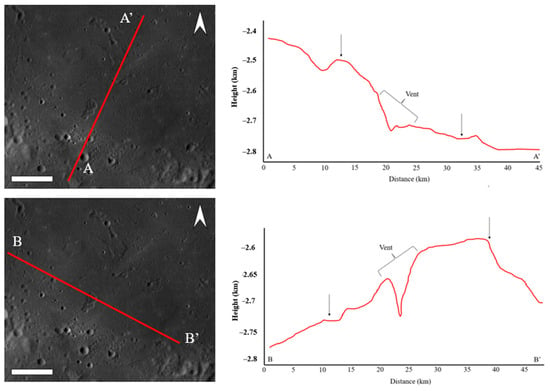
Figure 5.
Digital elevation profiles of the Fracastorius dome on the semi-major and semi-minor axes across the dome. Transects are shown, with the vent labeled. Black arrows indicate the approximate dome edges. Scale bar shown is 25 km.

Figure 6.
Images of the irregularly shaped vent at Fracastorius dome. (A) WAC image with scale bar of 5 km; (B) NAC image with scale bar 1000 m (with large inclination of 55–80° and resolution of 0.5 m/px) overlain on the WAC Global Morphological basemap; (C) High-resolution lunar topography (SLDEM2015)—Slope image with scale bar 1000 m from the 512 ppd SLDEM2015+LOLA product, obtained using LROC Quick Map. Slopes from [28].
6. Modeling of Rheological Properties and Dike Geometries
We presume that magma erupting from a dome-forming structure would spread outward onto a flat plane in all directions, as proposed by [7]. Such a model regarding the properties of the dome and magma behavior would estimate the yield strength τ, i.e., the pressure that must be exceeded for the lava to flow, the fluidity of the erupted lava with plastic viscosity η, and the effusion rate E (i.e., lava volume erupted per second) [6]. From this rheological model by [7], the flow is treated as a Bingham plastic (expressed in Pa) as
where is the lava density, which we use a value of 2000 kg/m3 as used in several previous studies [6,7,29,30], g = 1.63 m s−2, h the height of the dome, and D the dome diameter, where h and D are measured from the elevation profiles as obtained in Section 5. Plastic viscosity η is then estimated by
where η is expressed in Pa s. From the equations above, we obtained values for τ = 4.28 × 103 Pa and η = 3.12 × 105 Pa s. From h and D, we estimate the volume of the dome to be V = 77.4 km3.
The front of a lava flow unit is limited by cooling until some critical depth of penetration of the cooled boundary layer into the flow is finally reached [7]. The relation for the lava effusion rate E is based on the effective flow thickness of the dome. From previous studies [6,15,30], a cf2 = 0.72 is realistic due to flattened cross-sectional dome shapes, and comparable to a cf value of 0.7 used by [7] for the Gruithuisen and Mairan highland domes. The rheologic model developed by [7] depends on D, h, V, and , and the effective flow thickness (cf · h). This is approximated by the elevation of the dome profile obtained through DEMs halfway between the dome summit and the rim. However, it should be noted that this assumption is not straightforward to determine as it is unknown if the ad hoc assumption of measuring cf halfway between the dome summit and rim appropriately reflects the effective flow thickness [30]. As the effusion rate, E, depends on the square of cf, we assume that the values for the lava effusion rate may be off by factors of up to 2. Therefore, these values reflect an order of magnitude of E, but should not be taken to be accurate.
The relation for the effusion rate is then
where κ = 10−6 m2 s−1 as the thermal diffusivity of the lava [7,24]. From Equation (3), we obtained E to be 5.91 × 102 m3 s−1.
The duration of the lava effusion process (T) corresponds to
with V as the volume, as mentioned earlier. While the values for τ, η, and E computed from Equations (1)–(3) are mostly for single-flow, monogenetic volcanoes, these should be taken as upper limits otherwise. We calculated that the duration of the lava effusion, probably from multiple eruption events at the Fracastorius dome, is T ~4.15 years.
Dike Geometry
We assume that in the case of dome formation the melt reached the surface from a source region at least at the base of the lunar anorthositic crust [7]. These inferred rheological properties can be used to model the geometry of the subsurface dike through which the magma ascended, and the magma rise speed U, given dike length L and width W, as described in more detail in [7,29]. Of note is that the horizontal length L and width W of the dike are not independent, due to their ratio being a function of the plastic (and elastic) properties of the crustal rocks and magma viscosity. From determining E from Equation (3) above, the dike width W can be determined (recursively) by
Using the rheological properties τ and η determined earlier, together with the eruption rate of 5.91 × 102 m3 s−1, we find that the dike width W = 11.8 m. We can then determine the magma rise speed by balancing the driving pressure gradient against the wall friction and allowing for overcoming the yield strength by [7,31]:
The magma rise speed is calculated to be 2.1 × 10−4 m/s.
Assuming a mean crustal density c = 2800 kg/m3 and the magma density of = 2000 kg/m3, the effusion rate E are related to the dike geometry L and W and magma ascension speed U by
thus making dike length L = 234 km, again assuming that the magma density = 2000 kg/m3. From Table 1, the width of the dike for this dome is relatively smaller than other studied lunar domes, but the dike length is comparatively larger than the domes found at Petavius (Pe1) and Milichius (M2) craters (see [24]).

Table 1.
Values of the Fracastorius dome for dike width (W) and length (L) compared to other lunar mare domes.
We have repeated the solution of Equations (5) and (6) with a range of magma densities. Increasing the magma density makes U smaller and W and L larger. Table 2 shows the results using magma densities of = 1600, 2000, 2400, and 3000 kg/m3 (from [7]) to give a possible range of dike geometries at Fracastorius dome.

Table 2.
Values of the magma rise speed (U), dike width (W), and dike length (L) at Fracastorius dome as a function of varying magma densities from Equations (5) and (6).
7. Discussion
It has been observed that the Fracastorius dome is perpendicular to local wrinkle ridges in the southern Mare Nectaris basin (Figure 7). This perpendicular alignment may be due to dome-forming lavas guided by internal stress fields induced by major basin-forming impact events, which are also caused by crustal fractures and faulting [3,29,32]. This alignment may also perpetuate the hypothesis that the stress fields caused by impact events can facilitate the ascent of dike material through the subsurface from the lunar mantle to the crust [6,33]. From [34], fractures are closed at depths of ~20 km, so we assume that the stress field favors the formation and ascension of dikes.

Figure 7.
Map of local wrinkle ridges (red lines) around the Fracastorius dome (as indicated by white arrows). Wrinkle ridges mapping have been obtained from LROC Quick Map. See also [35].
There have been seven classes of lunar domes identified based on their dome morphometry and slopes [7] (Figure 8). Based on the slope and shape, the Fracastorius dome is a Class 7 (or Class D as defined in [30,36]). Class 7 describes complex and irregularly shaped domes and topography and are similar to many of the domes observed in the Marius Hills region [30]. With a slope of 1° and a comparatively large volume and eruption rate, the Fracastorius dome probably consisted of lower-viscous lavas, favoring a low shield to develop, and thus a lower degree of crystallization during magma ascent, leading to a duration of formation to 4.15 years. Domes belonging to this same classification also share similar compositional characteristics, especially with the reflectance at 750 nm wavelength and the R415/R750 and R950/R750 color ratios [37]. Furthermore, this dome displays a complex texture and vent structure with irregular elevations in the northeastern portion of the dome construct, likely due to several effusive activities, which are also typical of this Class of dome structure. With the observed asymmetry of the dome profile, it may be inferred that this dome is a non-monogenetic structure likely formed during several stages of effusion, like the Marius Hills [37].
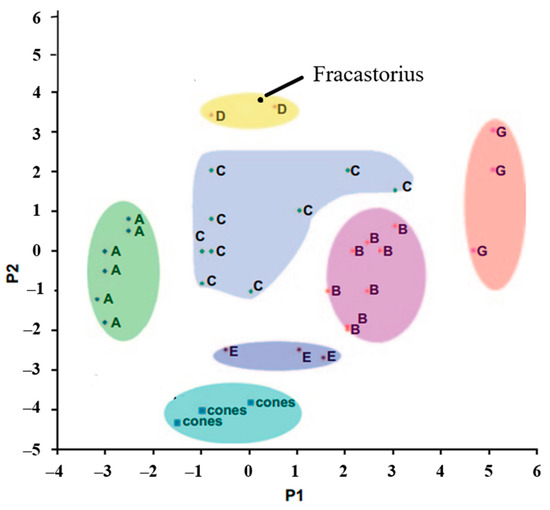
Figure 8.
Classification scheme of effusive lunar mare domes introduced in reference [27,37]. In this subspace lunar domes form several clusters, which can be identified based on the correspondingly transformed dome coordinates, where the main groups appear in the coordinate system spanned by the first two principal components P1 and P2. The examined Fracastorius dome belonging to class D is marked.
From [29], there are three rheologic groups of effusive lunar mare domes, each differing by lava viscosities and associated dike geometry: (i) R1-types have lava viscosities of 104–106 Pa s, magma rise speeds of 10−5–10−3 m s−1, dike widths ~10–30 m, and dike lengths of 10s to 100s km; (ii) R2-types have lower lava viscosities between 102–104 Pa s, fast magma ascent up to 4 × 10−3 m s−1, narrow dike widths <10 m, and shorter dike lengths 7–20 km; (iii) R3-types are highly viscous at 106–108 Pa s, with ascension at very low speeds 10−6–10−5 m s−1, broad dikes of several 10 s to 100 s m width and 100–200 km length. From the determined morphometric and rheologic measurements at the Fracastorius dome, this dome is predominantly an R1-type.
For viscosity comparisons (Table 3), the Fracastorius dome is similar to lunar domes observed at Mee H (Mee 1 dome), Milichius (M2), and Petavius (Pe1) craters (see [24]). The eruption rate at Fracastorius is also like these domes as well. The volume of Fracastorius, however, is on a similar scale (and similar slopes) to the Mairan domes, being slightly larger in volume. In terms of the effusion process duration, the Fracastorius dome is comparative to the M2 dome at Milichius crater, and much shorter durations than those domes at Gruithuisen and Mairan.

Table 3.
Values for the rheologic properties of the Fracastorius dome compared to other lunar mare domes, such as viscosity volume eruption rate (E), dome volume (V), and duration of formation as time.
8. Conclusions
In this study we have examined the lunar dome in Mare Nectaris and Fracastorius crater in terms of the spectral and morphometric properties and the eruption conditions. The dome has a diameter of 28.6 km, height of 241.5 m, and has a volume of 77.4 km3. This dome also has a slope of 1°, typical of class 7 (or class D) lunar domes and inferred to be a non-monogenetic dome likely formed from several stages of effusion. The dome has also been observed to have a basaltic composition using Clementine and Chandrayaan-1 M3 spectral data. The Fracastorius dome formed from lavas with viscosities around 3.12 Pa s, with an effusion rate ~ 5.91 × 102 m3 s−1 over a time period of ~4.2 years, probably from multiple effusive eruption events. With this slope degree and comparatively large volume, the Fracastorius dome probably consisted of a lower lava temperature and thus an increased degree of crystallization during magma ascent.
The perpendicular alignment of the dome in accordance with the local wrinkle ridges suggest their formation by a radially-oriented feeder dike, indicating that the impact-induced stress field may have guided the ascent of dikes from the lunar mantle to the crust. The rheological properties inferred that the feeder dike has a geometry of 11.8 m width and 234 km length. Future work includes an extension to similar Class D lunar mare domes, especially in regions where wrinkle ridges are prevalent. Such studies may help to gain more insight into regional geological processes and mare basin dome evolution.
Author Contributions
Conceptualization, C.A.; resources, C.A. and R.L.; writing and draft preparation, C.A.; review and editing, C.A. and R.L. All authors have read and agreed to the published version of the manuscript.
Funding
C.A. is supported by an appointment to the NASA Postdoctoral Program at the NASA Goddard Space Flight Center administered by Oak Ridge Associated Universities under contract 80HQTR21CA005 with NASA.
Acknowledgments
The authors would like to thank Paolo Lazzarotti for the submitted CCD image of Fracastorius (Figure 1). The authors would also like to thank the three anonymous reviewers for their time for their constructive feedback.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaur, P.; Chauhan, P.; Rajawat, A.S.; Kumar, A.K. Study of olivine-rich dark halo crater–Beaumont L in Mare Nectaris using high resolution remote sensing data. Planet. Space Sci. 2015, 109, 92–105. [Google Scholar] [CrossRef]
- Kramer, G.Y.; Jolliff, B.L.; Neal, C.R. Distinguishing high-alumina mare basalts using Clementine UVVIS and Lunar Prospector GRS data: Mare Moscoviense and Mare Nectaris. J. Geophys. Res. Planets 2008, 113, 1–18. [Google Scholar] [CrossRef]
- Wilhelms, D. The Geologic History of the Moon; USGS Prof. Paper 1348; USGS: Reston, VA, USA, 1987. [Google Scholar]
- Morgan, G.A.; Campbell, B.A.; Campbell, D.B.; Hawke, B.R. Investigating the stratigraphy of Mare Imbrium flow emplacement with Earth-based radar. J. Geophys. Res. Planets 2016, 121, 1498–1513. [Google Scholar] [CrossRef]
- Fortezzo, C.M.; Spudis, P.D.; Harrel, S.L. Release of the Digital Unified Global Geologic Map of the Moon At 1:5,000,000- Scale. In Proceedings of the 51st Lunar and Planetary Science Conference, Houston, TX, USA, 16–20 March 2020; Lunar and Planetary Institute: Houston, TX, USA, 2020. Abstract #2760. [Google Scholar]
- Lena, R.; Wöhler, C.; Bregante, M.T.; Lazzarotti, P.; Lammel, S. Lunar domes in Mare Undarum: Spectral and morphometric properties, eruption conditions, and mode of emplacement. Planet. Space Sci. 2008, 56, 553–569. [Google Scholar] [CrossRef]
- Wilson, L.; Head, J.W. Lunar Gruithuisen and Mairan domes: Rheology and mode of emplacement. J. Geophys. Res. Planets 2003, 108, 1–7. [Google Scholar] [CrossRef]
- Wood, J.A. Petrology of the lunar soil and geophysical implications. J. Geophys. Res. 1970, 75, 6497–6513. [Google Scholar] [CrossRef]
- Spudis, P.D.; McGovern, P.J.; Kiefer, W.S. Large shield volcanoes on the Moon. J. Geophys. Res. Planets 2013, 118, 1063–1081. [Google Scholar] [CrossRef]
- Head, J.W.; Gifford, A. Lunar mare domes: Classification and modes of origin. Moon Planets 1980, 22, 235–258. [Google Scholar] [CrossRef]
- Baldwin, R. The Measure of the Moon; Univ. Chicago Press: Chicago, IL, USA, 1963; pp. 390–394. [Google Scholar]
- Wilhelms, D.E.; McCauley, J.F. Geologic Map of the Near Side of the Moon; US Geological Survey: Washington, DC, USA, 1971. [Google Scholar]
- Guest, J.E.; Murray, J.B. Volcanic features of the nearside equatorial lunar maria. J. Geol. Soc. 1976, 132, 251–258. [Google Scholar] [CrossRef]
- Mursky, G. Introduction to Planetary Volcanism; Prentice-Hall: Bergen, Norway, 1996. [Google Scholar]
- Wöhler, C.; Lena, R.; Lazzarotti, P.; Phillips, J.; Wirths, M.; Pujic, Z.; Group, G.L.R.G. A combined spectrophotometric and morphometric study of the lunar mare dome fields near Cauchy, Arago, Hortensius, and Milichius. Icarus 2006, 183, 237–264. [Google Scholar] [CrossRef]
- Weitz, C.M.; Head, J.W., III. Spectral properties of the Marius Hills volcanic complex and implications for the formation of lunar domes and cones. J. Geophys. Res. Planets 1999, 104, 18933–18956. [Google Scholar] [CrossRef]
- Griffiths, R.W. The dynamics of lava flows. Annu. Rev. Fluid Mech. 2000, 32, 477–518. [Google Scholar] [CrossRef]
- Diniega, S.; Smrekar, S.E.; Anderson, S.; Stofan, E.R. The influence of temperature-dependent viscosity on lava flow dynamics. J. Geophys. Res. Earth Surf. 2013, 118, 1516–1532. [Google Scholar] [CrossRef]
- Wilson, L.; Head, J.W. Lunar linear rilles as surface manifestations of dikes: Theoretical considerations. In Proceedings of the Lunar and Planetary Science Conference; Houston, TX, USA, 18–22 March 1996; Volume 27. [Google Scholar]
- Jackson, P.A.; Wilson, L.; Head, J.W. The use of magnetic signatures in identifying shallow intrusions on the moon. In Proceedings of the Lunar and Planetary Science Conference, Houston, TX, USA, 17–21 March 1997; Volume 28, p. 649. [Google Scholar]
- Eliason, E.; Isbell, C.; Lee, E.; Becker, T.; Gaddis, L.; McEwen, A.; Robinson, M. The Clementine UVVIS Global Lunar Mosaic; PDS volumes USA NASA PDS CL 4001 4078; Lunar and Planetary Institute: Houston, TX, USA, 1999. [Google Scholar]
- Pieters, C.M.; Boardman, J.; Buratti, B.; Chatterjee, A.; Clark, R.; Glavich, T.; White, M.; Varanasi, P.; Tompkins, S.; Taylor, L.; et al. The Moon mineralogy mapper (M³) on chandrayaan-1. Curr. Sci. 2009, 96, 500–505. [Google Scholar]
- Lena, R.; Wöhler, C.; Phillips, J.; Chiocchetta, M.T. Determination of Spectral Properties. In Lunar Domes; Springer: Milano, Italy, 2013; pp. 39–48. [Google Scholar]
- Lena, R.; Wöhler, C.; Phillips, J.; Sellini, M.; Zompatori, D.; Group, G.L.R.G. A lunar cryptomare dome near Mee H and Drebbel F. Planet. Space Sci. 2009, 57, 267–275. [Google Scholar] [CrossRef]
- Charette, M.P.; McCord, T.B.; Pieters, C.; Adams, J.B. Application of remote spectral reflectance measurements to lunar geology classification and determination of titanium content of lunar soils. J. Geophys. Res. 1974, 79, 1605–1613. [Google Scholar] [CrossRef]
- Lucey, P.G.; Blewett, D.T.; Hawke, B.R. Mapping the FeO and TiO2 content of the lunar surface with multispectral imagery. J. Geophys. Res. Planets 1998, 103, 3679–3699. [Google Scholar] [CrossRef]
- Besse, S.; Sunshine, J.M.; Gaddis, L.R. Volcanic glass signatures in spectroscopic survey of newly proposed lunar pyroclastic deposits. J. Geophys. Res. Planets 2014, 119, 355–372. [Google Scholar] [CrossRef]
- Barker, M.K.; Mazarico, E.; Neumann, G.A.; Zuber, M.T.; Haruyama, J.; Smith, D.E. A new lunar digital elevation model from the Lunar Orbiter Laser Altimeter and SELENE Terrain Camera. Icarus 2016, 273, 346–355. [Google Scholar] [CrossRef]
- Wöhler, C.; Lena, R.; Phillips, J. Formation of lunar mare domes along crustal fractures: Rheologic conditions, dimensions of feeder dikes, and the role of magma evolution. Icarus 2007, 189, 279–307. [Google Scholar] [CrossRef]
- Lena, R.; Wöhler, C.; Phillips, J.; Wirths, M.; Bregante, M.T. Lunar domes in the Doppelmayer region: Spectrophotometry, morphometry, rheology, and eruption conditions. Planet. Space Sci. 2007, 55, 1201–1217. [Google Scholar] [CrossRef]
- Wilson, L.; Head, J.W., III. Ascent and eruption of basaltic magma on the Earth and Moon. J. Geophys. Res. Solid Earth 1981, 86, 2971–3001. [Google Scholar] [CrossRef]
- Spudis, P.D.; Hawke, B.R.; Lucey, P. Composition of Orientale basin deposits and implications for the lunar basin-forming process. J. Geophys. Res. Solid Earth 1984, 89, C197–C210. [Google Scholar] [CrossRef]
- Rubin, A.M. Dikes vs. diapirs in viscoelastic rock. Earth Planet. Sci. Lett. 1993, 117, 653–670. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Zuber, M.T.; Phillips, R.J. The role of magma buoyancy on the eruption of lunar basalts. Earth Planet. Sci. Lett. 2001, 185, 71–83. [Google Scholar] [CrossRef]
- Thompson, T.J.; Robinson, M.S.; Watters, T.R.; Johnson, M.B. Global lunar wrinkle ridge identification and analysis. In Proceedings of the 48th Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 20–24 March 2017; No. 1964. p. 2665. [Google Scholar]
- Pike, R.J. Volcanoes on the inner planets-Some preliminary comparisons of gross topography. In Lunar and Planetary Science Conference Proceedings; Lunar and Planetary Science Institute: Houston, TX, USA, 1978; Volume 9, pp. 3239–3273. [Google Scholar]
- Lena, R.; Wöhler, C.; Phillips, J.; Chiocchetta, M.T. Lunar Domes Classification Scheme. In Lunar Domes; Springer: Milano, Italy, 2013; pp. 59–65. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).