DiTBN: Detail Injection-Based Two-Branch Network for Pansharpening of Remote Sensing Images
Abstract
1. Introduction
2. Background and Related Work
2.1. The CS and MRA Methods
2.2. The CNN Methods for Pansharpening
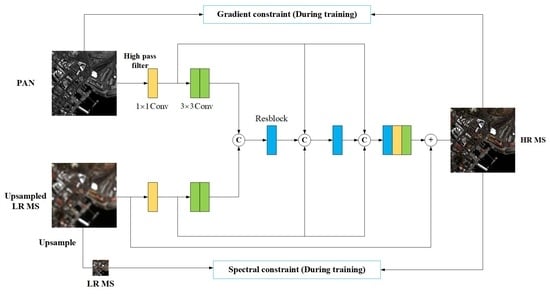
3. Detail Injection-Based Two-Branch Network
3.1. Motivation
3.2. The Network Architecture
3.3. The Loss Function
4. Experiments
4.1. Experimental Datasets
4.2. Implement Details
4.3. The Evaluation Indicators and Comparison Algorithms
4.4. The Ablation Study of Different Network Structures
4.5. The Ablation Studies of the Proposed Loss Function and Kernel Size
4.6. Performance Evaluation at Reduced-Resolution Scale
4.7. Performance Evaluation at Full-Resolution Scale
4.8. Parameters and Complexity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, X.; Feng, J.; Shang, R.; Zhang, X.; Jiao, L. CMNet: Classification-oriented multi-task network for hyperspectral pansharpening. Knowl.-Based Syst. 2022, 256, 109878. [Google Scholar] [CrossRef]
- Wu, X.; Feng, J.; Shang, R.; Zhang, X.; Jiao, L. Multiobjective Guided Divide-and-Conquer Network for Hyperspectral Pansharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5525317. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, W.; Yang, N.; Hu, H.; Huang, X.; Cao, Y.; Cai, W. Unsupervised self-correlated learning smoothy enhanced locality preserving graph convolution embedding clustering for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5536716. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, Y.; Li, S.; Deng, B.; Cai, W. Self-supervised locality preserving low-pass graph convolutional embedding for large-scale hyperspectral image clustering. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5536016. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Li, W.; Cai, W.; Zhan, Y. AF2GNN: Graph convolution with adaptive filters and aggregator fusion for hyperspectral image classification. Inf. Sci. 2022, 602, 201–219. [Google Scholar] [CrossRef]
- Tu, T.M.; Su, S.C.; Shyu, H.C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2001, 2, 177–186. [Google Scholar] [CrossRef]
- Kwarteng, P.; Chavez, A. Extracting spectral contrast in Landsat Thematic Mapper image data using selective principal component analysis. Photogramm. Eng. Remote Sens. 1989, 55, 339–348. [Google Scholar]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 4 January 2000. [Google Scholar]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Chavez, P.; Sides, S.C.; Anderson, J.A. Comparison of three different methods to merge multiresolution and multispectral data- Landsat TM and SPOT panchromatic. Photogramm. Eng. Remote Sens. 1991, 57, 295–303. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Scarpa, G.; Vitale, S.; Cozzolino, D. Target-adaptive CNN-based pansharpening. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5443–5457. [Google Scholar] [CrossRef]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5449–5457. [Google Scholar]
- Liu, X.; Liu, Q.; Wang, Y. Remote sensing image fusion based on two-stream fusion network. Inf. Fusion 2020, 55, 1–15. [Google Scholar] [CrossRef]
- He, L.; Rao, Y.; Li, J.; Chanussot, J.; Plaza, A.; Zhu, J.; Li, B. Pansharpening via detail injection based convolutional neural networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1188–1204. [Google Scholar] [CrossRef]
- Deng, L.J.; Vivone, G.; Jin, C.; Chanussot, J. Detail injection-based deep convolutional neural networks for pansharpening. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6995–7010. [Google Scholar] [CrossRef]
- Yang, Y.; Tu, W.; Huang, S.; Lu, H. PCDRN: Progressive cascade deep residual network for pansharpening. Remote Sens. 2020, 12, 676. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, Z.; Liu, H.; Xie, G. MSDRN: Pansharpening of multispectral images via multi-scale deep residual network. Remote Sens. 2021, 13, 1200. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, A.; Zhang, F.; Diao, W.; Sun, J.; Bruzzone, L. Spatial and spectral extraction network with adaptive feature fusion for pansharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5410814. [Google Scholar] [CrossRef]
- Lei, D.; Chen, P.; Zhang, L.; Li, W. MCANet: A Multidimensional Channel Attention Residual Neural Network for Pansharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5411916. [Google Scholar] [CrossRef]
- Tu, W.; Yang, Y.; Huang, S.; Wan, W.; Gan, L.; Lu, H. MMDN: Multi-Scale and Multi-Distillation Dilated Network for Pansharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5410514. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, H.; Xu, Q.; Liu, X.; Wang, Y. PSGAN: A generative adversarial network for remote sensing image pan-sharpening. IEEE Trans. Geosci. Remote Sens. 2020, 59, 10227–10242. [Google Scholar] [CrossRef]
- Ma, J.; Yu, W.; Chen, C.; Liang, P.; Guo, X.; Jiang, J. Pan-GAN: An unsupervised pan-sharpening method for remote sensing image fusion. Inf. Fusion 2020, 62, 110–120. [Google Scholar] [CrossRef]
- Benzenati, T.; Kessentini, Y.; Kallel, A. Pansharpening approach via two-stream detail injection based on relativistic generative adversarial networks. Expert Syst. Appl. 2022, 188, 115996. [Google Scholar] [CrossRef]
- Wang, W.; Liu, H. An Efficient Detail Extraction Algorithm for Improving Haze-Corrected CS Pansharpening. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5000505. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef]
- Nah, S.; Hyun Kim, T.; Mu Lee, K. Deep multi-scale convolutional neural network for dynamic scene deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3883–3891. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef]
- Zhong, J.; Yang, B.; Huang, G.; Zhong, F.; Chen, Z. Remote sensing image fusion with convolutional neural network. Sens. Imaging 2016, 17, 10. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Wei, Y.; Yuan, Q.; Shen, H.; Zhang, L. Boosting the accuracy of multispectral image pansharpening by learning a deep residual network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1795–1799. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J. Remote sensing image fusion with deep convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1656–1669. [Google Scholar] [CrossRef]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Choi, J.S.; Kim, Y.; Kim, M. S3: A spectral-spatial structure loss for pan-sharpening networks. IEEE Geosci. Remote Sens. Lett. 2019, 17, 829–833. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Liu, W.; Huang, J. Image fusion with local spectral consistency and dynamic gradient sparsity. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2760–2765. [Google Scholar]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O.; Benediktsson, J.A. Quantitative quality evaluation of pansharpened imagery: Consistency versus synthesis. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1247–1259. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Context-driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2300–2312. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. In Summaries of the Third Annual JPL Airborne Geoscience Workshop. Volume 1: AVIRIS Workshop; JPL and NAS; Colorado University: Boulder, CO, USA, 1992. Available online: https://ntrs.nasa.gov/citations/19940012238 (accessed on 1 April 2022).
- Wald, L. Data Fusion: Definitions and Architectures: Fusion of Images of Different Spatial Resolutions. Presses des MINES. 2002. Available online: https://hal-mines-paristech.archives-ouvertes.fr/hal-00464703 (accessed on 1 April 2022).
- Choi, M. A new intensity–hue–saturation fusion approach to image fusion with a trade-off parameter. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1672–1682. [Google Scholar] [CrossRef]
- Zhou, J.; Civco, D.L.; Silander, J. A wavelet transform method to merge Landsat TM and SPOT panchromatic data. Int. J. Remote Sens. 1998, 19, 743–757. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef]
- Vivone, G. Robust band-dependent spatial-detail approaches for panchromatic sharpening. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6421–6433. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Garzelli, A.; Lolli, S. Fast reproducible pansharpening based on instrument and acquisition modeling: AWLP revisited. Remote Sens. 2019, 11, 2315. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2565–2586. [Google Scholar] [CrossRef]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated Residual Transformations for Deep Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]










| Satellites | Spectral Range/nm | Spatial Resolution/m | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Coastal | Blue | Green | Yellow | Red | Red Edge | Nir | Nir2 | PAN | PAN | MS | |
| Ikonos | - | 450–530 | 520–610 | - | 640–720 | - | 760–860 | - | 450–900 | 1 | 4 |
| GeoEye-1 | - | 450–510 | 510–580 | - | 655–690 | - | 780–920 | - | 450–900 | 0.5 | 2 |
| WorldView-3 | 400–450 | 450–510 | 510–580 | 585–625 | 630–690 | 705–745 | 770–895 | 860–1040 | 450–800 | 0.31 | 1.24 |
| Satellites | Number of Source Images/Group | Data Type | Number of Groups | Patch Number |
|---|---|---|---|---|
| Ikonos | 240 × (200 × 200, 800 × 800) | Train | 192 | 12,288 × (8 × 8, 32 × 32) |
| Valid | 24 | 1536 × (8 × 8, 32 × 32) | ||
| Test | 24 | 24 × (50 × 50, 200 × 200) | ||
| GeoEye-1 | 250 × (200 × 200, 800 × 800) | Train | 200 | 12,800 × (8 × 8, 32 × 32) |
| Valid | 25 | 1600 × (8 × 8, 32 × 32) | ||
| Test | 25 | 25 × (50 × 50, 200 × 200) | ||
| WorldView-3 | 250 × (200 × 200, 800 × 800) | Train | 200 | 12,800 × (8 × 8, 32 × 32) |
| Valid | 25 | 1600 × (8 × 8, 32 × 32) | ||
| Test set | 25 | 25 × (50 × 50, 200 × 200) |
| SAM↓ | ERGAS↓ | RASE↓ | SCC↑ | Q↑ | SSIM↑ | |
|---|---|---|---|---|---|---|
| HPF2, reuse2 | 2.6461 | 1.8537 | 7.5817 | 0.9472 | 0.8691 | 0.9543 |
| HPF1, reuse2 | 2.5097 | 1.7846 | 7.2815 | 0.9530 | 0.8737 | 0.9578 |
| HPF1, no reuse | 2.5196 | 1.7861 | 7.2836 | 0.9531 | 0.8739 | 0.9577 |
| HPF1, reuse1 | 2.5298 | 1.7929 | 7.3119 | 0.9530 | 0.8747 | 0.9577 |
| Loss | SAM↓ | ERGAS↓ | RASE↓ | SCC↑ | Q↑ | SSIM↑ |
|---|---|---|---|---|---|---|
| The MSE loss function | 2.5445 | 1.8060 | 7.3646 | 0.9518 | 0.8718 | 0.9569 |
| The loss function without | 2.5191 | 1.7962 | 7.3250 | 0.9526 | 0.8733 | 0.9575 |
| The loss function without | 2.5263 | 1.7993 | 7.3456 | 0.9525 | 0.8738 | 0.9571 |
| The proposed loss function | 2.5097 | 1.7846 | 7.2815 | 0.9530 | 0.8737 | 0.9578 |
| Kernel Size | SAM↓ | ERGAS↓ | RASE↓ | SCC↑ | Q↑ | SSIM↑ |
|---|---|---|---|---|---|---|
| 1 × 1 | 2.5097 | 1.7846 | 7.2815 | 0.9530 | 0.8737 | 0.9578 |
| 3 × 3 | 2.5103 | 1.7870 | 7.2904 | 0.9531 | 0.8743 | 0.9577 |
| Methods | SAM↓ | ERGAS↓ | RASE↓ | SCC↑ | Q↑ | SSIM↑ | |
|---|---|---|---|---|---|---|---|
| The indicator values in Figure 2 | GS2-GLP | 3.3848 | 3.3752 | 13.0279 | 0.9331 | 0.9350 | 0.9191 |
| BDSD-PC | 3.5979 | 3.5113 | 13.5917 | 0.9300 | 0.9308 | 0.9171 | |
| AWLP-H | 3.1770 | 3.4612 | 13.3689 | 0.9326 | 0.9337 | 0.9248 | |
| MTF-GLP | 3.5667 | 3.8054 | 14.6481 | 0.9301 | 0.9207 | 0.9057 | |
| PanNet | 2.6250 | 2.2085 | 8.5422 | 0.9783 | 0.9618 | 0.9581 | |
| DiCNN1 | 2.5199 | 2.1116 | 8.1636 | 0.9811 | 0.9621 | 0.9612 | |
| FusionNet | 2.4568 | 2.0755 | 8.0386 | 0.9815 | 0.9633 | 0.9628 | |
| TFNet | 2.7608 | 2.6473 | 10.2455 | 0.9699 | 0.9509 | 0.9468 | |
| Proposed | 2.3822 | 2.0604 | 7.9741 | 0.9817 | 0.9644 | 0.9636 | |
| The average indicator values | GS2-GLP | 3.8824 | 2.6749 | 10.7669 | 0.8818 | 0.7867 | 0.9070 |
| BDSD-PC | 3.8636 | 2.6820 | 10.7902 | 0.8885 | 0.7965 | 0.9117 | |
| AWLP-H | 3.5207 | 2.6405 | 10.6203 | 0.8931 | 0.8098 | 0.9201 | |
| MTF-GLP | 4.0959 | 2.7863 | 11.7074 | 0.8716 | 0.7747 | 0.8959 | |
| PanNet | 2.6712 | 1.8804 | 7.6997 | 0.9444 | 0.8673 | 0.9527 | |
| DiCNN1 | 2.6529 | 1.8696 | 7.6126 | 0.9466 | 0.8671 | 0.9535 | |
| FusionNet | 2.5791 | 1.8169 | 7.4268 | 0.9500 | 0.8687 | 0.9562 | |
| TFNet | 3.0225 | 2.2030 | 8.9109 | 0.9298 | 0.8392 | 0.9401 | |
| Proposed | 2.5097 | 1.7846 | 7.2815 | 0.9530 | 0.8737 | 0.9578 |
| Methods | SAM↓ | ERGAS↓ | RASE↓ | SCC↑ | Q↑ | SSIM↑ | |
|---|---|---|---|---|---|---|---|
| The indicator values in Figure 4 | GS2-GLP | 3.8439 | 4.1591 | 20.3177 | 0.7741 | 0.8599 | 0.9256 |
| BDSD-PC | 5.3266 | 3.6951 | 17.9216 | 0.8355 | 0.8640 | 0.9230 | |
| AWLP-H | 3.6043 | 3.8770 | 18.0543 | 0.8226 | 0.8759 | 0.9313 | |
| MTF-GLP | 3.8435 | 4.1684 | 20.2097 | 0.7749 | 0.8594 | 0.9251 | |
| PanNet | 2.0523 | 1.9989 | 9.1007 | 0.9469 | 0.9063 | 0.9727 | |
| DiCNN1 | 1.8240 | 1.9016 | 8.7054 | 0.9535 | 0.9190 | 0.9761 | |
| FusionNet | 1.8441 | 1.8955 | 8.5859 | 0.9535 | 0.9110 | 0.9767 | |
| TFNet | 2.1218 | 2.2806 | 10.3625 | 0.9315 | 0.8752 | 0.9675 | |
| Proposed | 1.6372 | 1.7813 | 8.1048 | 0.9581 | 0.9216 | 0.9793 | |
| The average indicator values | GS2-GLP | 3.2744 | 2.8539 | 13.3318 | 0.8168 | 0.8206 | 0.8929 |
| BDSD-PC | 3.0881 | 2.5465 | 11.8565 | 0.8794 | 0.8601 | 0.9222 | |
| AWLP-H | 2.4347 | 2.3470 | 10.8151 | 0.9124 | 0.8789 | 0.9427 | |
| MTF-GLP | 2.9326 | 2.7003 | 12.2147 | 0.8766 | 0.8431 | 0.9186 | |
| PanNet | 1.5137 | 1.4808 | 6.7133 | 0.9609 | 0.9320 | 0.9691 | |
| DiCNN1 | 1.4790 | 1.4567 | 6.7126 | 0.9617 | 0.9326 | 0.9704 | |
| FusionNet | 1.4653 | 1.4657 | 6.5833 | 0.9631 | 0.9294 | 0.9708 | |
| TFNet | 1.6539 | 1.6889 | 7.6106 | 0.9499 | 0.9137 | 0.9633 | |
| Proposed | 1.3642 | 1.3772 | 6.2741 | 0.9663 | 0.9380 | 0.9734 |
| Methods | SAM↓ | ERGAS↓ | RASE↓ | SCC↑ | Q↑ | SSIM↑ | |
|---|---|---|---|---|---|---|---|
| The indicator values in Figure 6 | GS2-GLP | 5.2773 | 3.6583 | 10.9792 | 0.9000 | 0.9411 | 0.9060 |
| BDSD-PC | 5.5379 | 3.9007 | 11.9896 | 0.8981 | 0.9402 | 0.9034 | |
| AWLP-H | 5.4564 | 3.9955 | 11.3766 | 0.8769 | 0.9401 | 0.9099 | |
| MTF-GLP | 5.1129 | 3.6498 | 11.0362 | 0.8957 | 0.9421 | 0.9090 | |
| PanNet | 3.4405 | 2.2765 | 6.8848 | 0.9594 | 0.9785 | 0.9598 | |
| DiCNN1 | 3.2887 | 2.1864 | 6.6807 | 0.9643 | 0.9803 | 0.9634 | |
| FusionNet | 3.2403 | 2.1687 | 6.6682 | 0.9652 | 0.9803 | 0.9642 | |
| Proposed | 3.0829 | 2.0869 | 6.2865 | 0.9665 | 0.9824 | 0.9668 | |
| The average indicator values | GS2-GLP | 5.2773 | 4.4745 | 10.0756 | 0.8602 | 0.8972 | 0.9125 |
| BDSD-PC | 6.3906 | 4.6631 | 10.5381 | 0.8659 | 0.8937 | 0.9064 | |
| AWLP-H | 4.9514 | 4.5022 | 10.2020 | 0.8651 | 0.9094 | 0.9263 | |
| MTF-GLP | 5.1142 | 4.4390 | 9.9565 | 0.8587 | 0.8998 | 0.9184 | |
| PanNet | 3.3803 | 2.5651 | 6.1025 | 0.9590 | 0.9503 | 0.9681 | |
| DiCNN1 | 3.2656 | 2.4916 | 5.9104 | 0.9628 | 0.9520 | 0.9700 | |
| FusionNet | 3.1362 | 2.4790 | 5.9783 | 0.9642 | 0.9518 | 0.9709 | |
| Proposed | 2.9323 | 2.3374 | 5.6141 | 0.9674 | 0.9556 | 0.9737 |
| Methods | SAM↓ | QNR↑ | ↓ | ↓ | |
|---|---|---|---|---|---|
| The indicator values in Figure 8 | GS2-GLP | 1.7843 | 0.7440 | 0.1313 | 0.1436 |
| BDSD-PC | 2.3185 | 0.8121 | 0.0694 | 0.1274 | |
| AWLP-H | 1.7375 | 0.7812 | 0.1114 | 0.1208 | |
| MTF-GLP | 1.7896 | 0.7469 | 0.1320 | 0.1395 | |
| PanNet | 1.8068 | 0.8655 | 0.0653 | 0.0740 | |
| DiCNN1 | 1.9846 | 0.8282 | 0.0597 | 0.1193 | |
| FusionNet | 1.3841 | 0.8875 | 0.0283 | 0.0867 | |
| TFNet | 1.6332 | 0.9012 | 0.0626 | 0.0385 | |
| Proposed | 1.2243 | 0.9114 | 0.0256 | 0.0647 | |
| The average indicator values | GS2-GLP | 1.5272 | 0.7301 | 0.1407 | 0.1663 |
| BDSD-PC | 2.0043 | 0.8021 | 0.0823 | 0.1389 | |
| AWLP-H | 1.4829 | 0.7583 | 0.1332 | 0.1410 | |
| MTF-GLP | 1.5746 | 0.7186 | 0.1510 | 0.1680 | |
| PanNet | 1.5322 | 0.8443 | 0.0705 | 0.0999 | |
| DiCNN1 | 1.6077 | 0.8337 | 0.0647 | 0.1203 | |
| FusionNet | 1.1487 | 0.8436 | 0.0569 | 0.1146 | |
| TFNet | 1.2775 | 0.7940 | 0.1057 | 0.1162 | |
| Proposed | 1.0702 | 0.8499 | 0.0484 | 0.1144 |
| Methods | SAM↓ | QNR↑ | ↓ | ↓ | |
|---|---|---|---|---|---|
| The indicator values in Figure 9 | GS2-GLP | 1.4054 | 0.8336 | 0.0548 | 0.1181 |
| BDSD-PC | 2.4208 | 0.9694 | 0.0172 | 0.0137 | |
| AWLP-H | 1.2412 | 0.8825 | 0.0417 | 0.0791 | |
| MTF-GLP | 1.3570 | 0.8188 | 0.0664 | 0.1229 | |
| PanNet | 1.3215 | 0.9465 | 0.0168 | 0.0374 | |
| DiCNN1 | 1.2947 | 0.9567 | 0.0034 | 0.0400 | |
| FusionNet | 0.7754 | 0.9289 | 0.0310 | 0.0414 | |
| TFNet | 0.6595 | 0.9441 | 0.0243 | 0.0322 | |
| Proposed | 0.6559 | 0.9679 | 0.0059 | 0.0264 | |
| The average indicator values | GS2-GLP | 0.8168 | 0.8373 | 0.0532 | 0.1170 |
| BDSD-PC | 1.2219 | 0.9036 | 0.0287 | 0.0702 | |
| AWLP-H | 0.7132 | 0.8837 | 0.0437 | 0.0764 | |
| MTF-GLP | 0.7895 | 0.8056 | 0.0701 | 0.1348 | |
| PanNet | 0.7997 | 0.9155 | 0.0289 | 0.0575 | |
| DiCNN1 | 0.7984 | 0.9210 | 0.0226 | 0.0582 | |
| FusionNet | 0.5210 | 0.9235 | 0.0215 | 0.0564 | |
| TFNet | 0.5324 | 0.9199 | 0.0262 | 0.0553 | |
| Proposed | 0.4390 | 0.9319 | 0.0239 | 0.0459 |
| Methods | SAM↓ | QNR↑ | ↓ | ↓ | |
|---|---|---|---|---|---|
| The indicator values in Figure 10 | GS2-GLP | 1.5944 | 0.8970 | 0.0379 | 0.0677 |
| BDSD-PC | 1.8056 | 0.9322 | 0.0151 | 0.0536 | |
| AWLP-H | 1.6647 | 0.9034 | 0.0412 | 0.0578 | |
| MTF-GLP | 1.5049 | 0.8812 | 0.0491 | 0.0733 | |
| PanNet | 1.6182 | 0.9632 | 0.0106 | 0.0264 | |
| DiCNN1 | 1.6209 | 0.9470 | 0.0120 | 0.0416 | |
| FusionNet | 1.3064 | 0.9647 | 0.0102 | 0.0254 | |
| Proposed | 1.1929 | 0.9548 | 0.0055 | 0.0400 | |
| The average indicator values | GS2-GLP | 1.3276 | 0.8405 | 0.0645 | 0.1027 |
| BDSD-PC | 1.9317 | 0.8708 | 0.0483 | 0.0867 | |
| AWLP-H | 1.3235 | 0.8404 | 0.0729 | 0.0959 | |
| MTF-GLP | 1.3326 | 0.8240 | 0.0763 | 0.1090 | |
| PanNet | 1.4054 | 0.8925 | 0.0452 | 0.0673 | |
| DiCNN1 | 1.5031 | 0.8784 | 0.0444 | 0.0834 | |
| FusionNet | 1.1291 | 0.9173 | 0.0256 | 0.0599 | |
| Proposed | 1.0475 | 0.9072 | 0.0284 | 0.0677 |
| PanNet | DiCNN1 | FusionNet | TFNet | Proposed | |
|---|---|---|---|---|---|
| Parameters | 0.083 M | 0.047 M | 0.079 M | 2.363 M | 0.403 M |
| FLOPs | 20.72 B | 6.12 B | 20.58 B | 18.77 B | 52.76 B |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhou, Z.; Zhang, X.; Lv, T.; Liu, H.; Liang, L. DiTBN: Detail Injection-Based Two-Branch Network for Pansharpening of Remote Sensing Images. Remote Sens. 2022, 14, 6120. https://doi.org/10.3390/rs14236120
Wang W, Zhou Z, Zhang X, Lv T, Liu H, Liang L. DiTBN: Detail Injection-Based Two-Branch Network for Pansharpening of Remote Sensing Images. Remote Sensing. 2022; 14(23):6120. https://doi.org/10.3390/rs14236120
Chicago/Turabian StyleWang, Wenqing, Zhiqiang Zhou, Xiaoqiao Zhang, Tu Lv, Han Liu, and Lili Liang. 2022. "DiTBN: Detail Injection-Based Two-Branch Network for Pansharpening of Remote Sensing Images" Remote Sensing 14, no. 23: 6120. https://doi.org/10.3390/rs14236120
APA StyleWang, W., Zhou, Z., Zhang, X., Lv, T., Liu, H., & Liang, L. (2022). DiTBN: Detail Injection-Based Two-Branch Network for Pansharpening of Remote Sensing Images. Remote Sensing, 14(23), 6120. https://doi.org/10.3390/rs14236120