A Hybrid Method for Vibration-Based Bridge Damage Detection
Abstract
1. Introduction
2. Damage-Sensitive Features
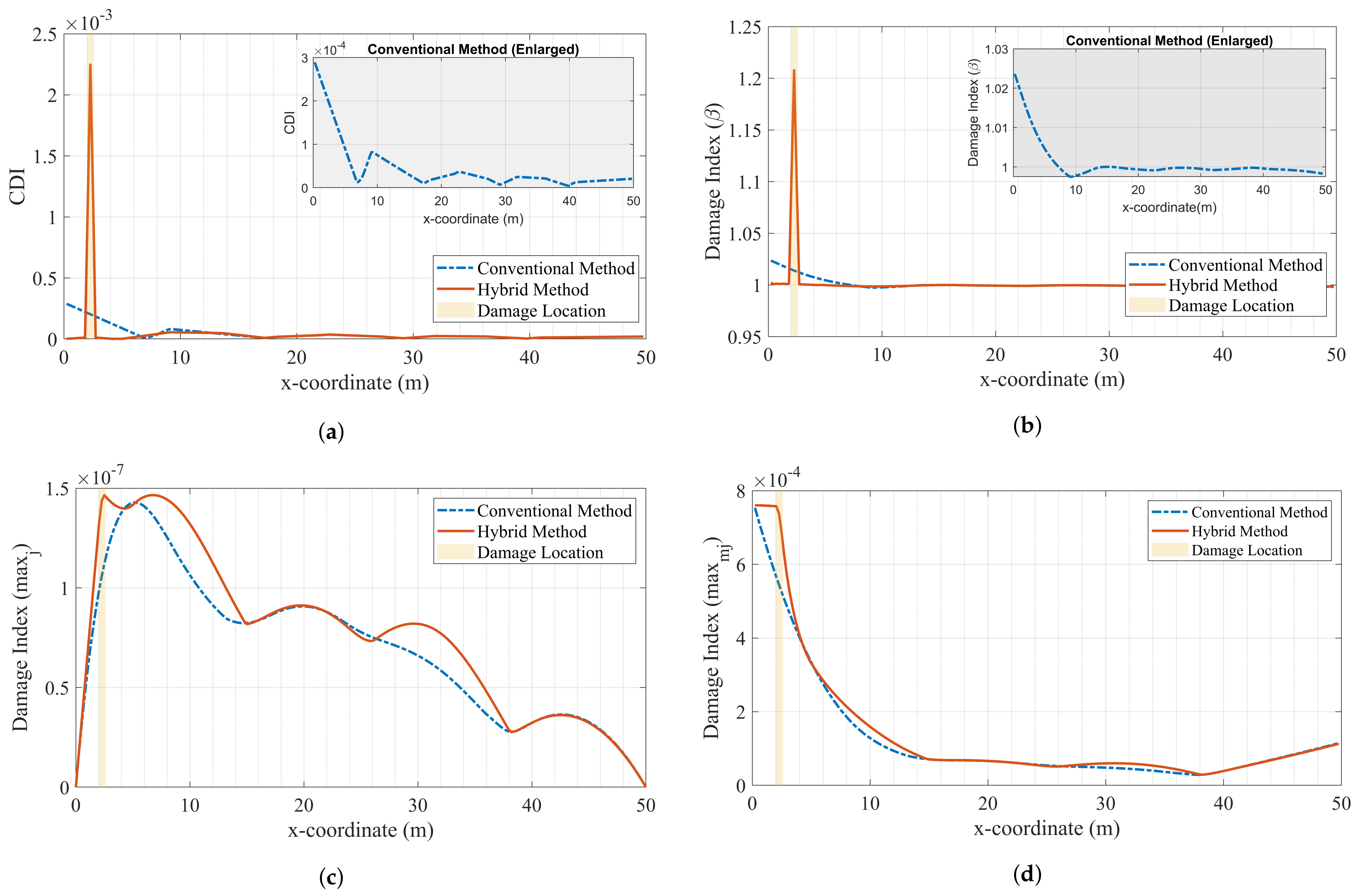
2.1. Mode Shape Curvature
2.2. Modal Strain Energy
2.3. Modal Flexibility
2.4. Modified Modal Flexibility
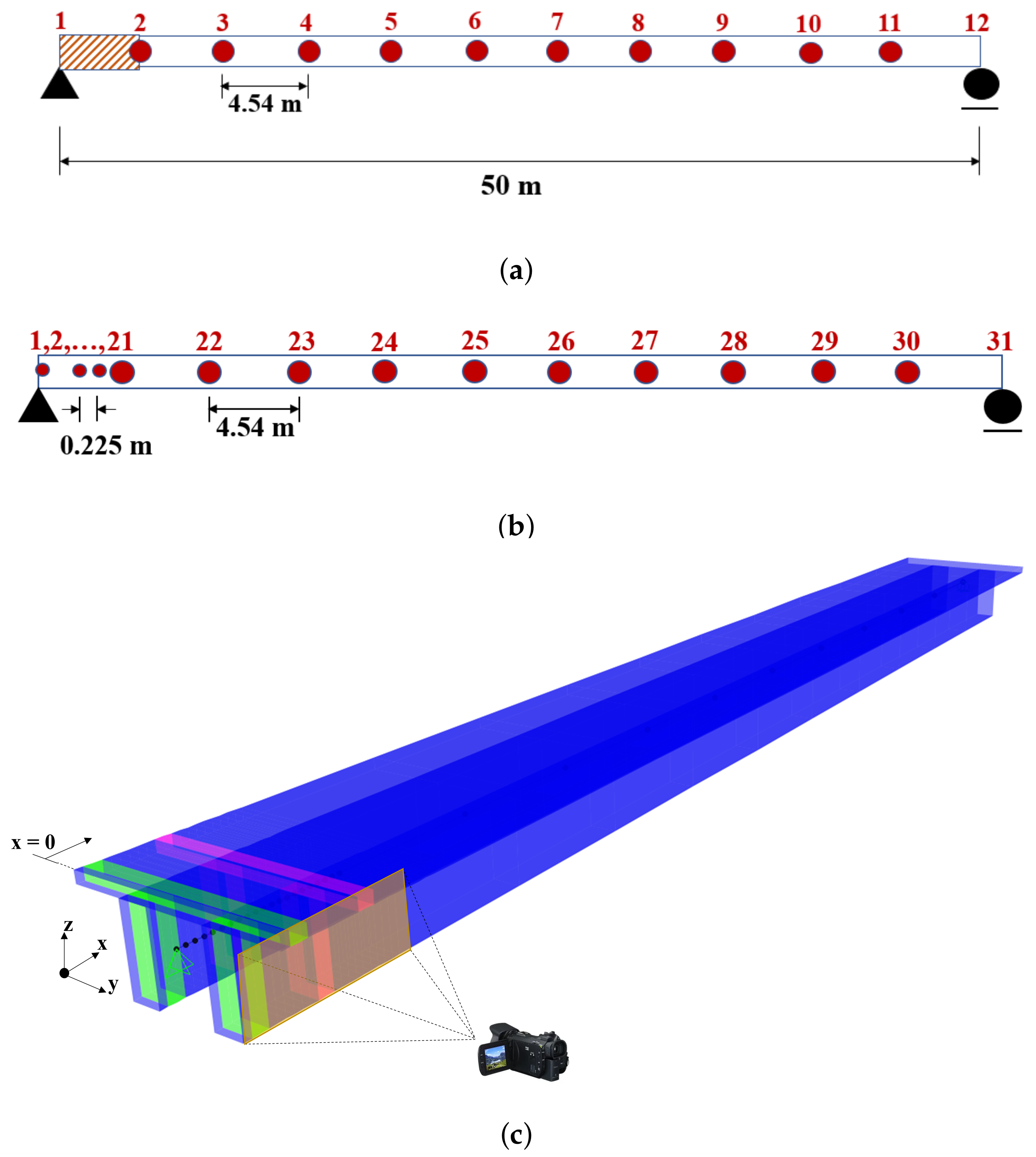
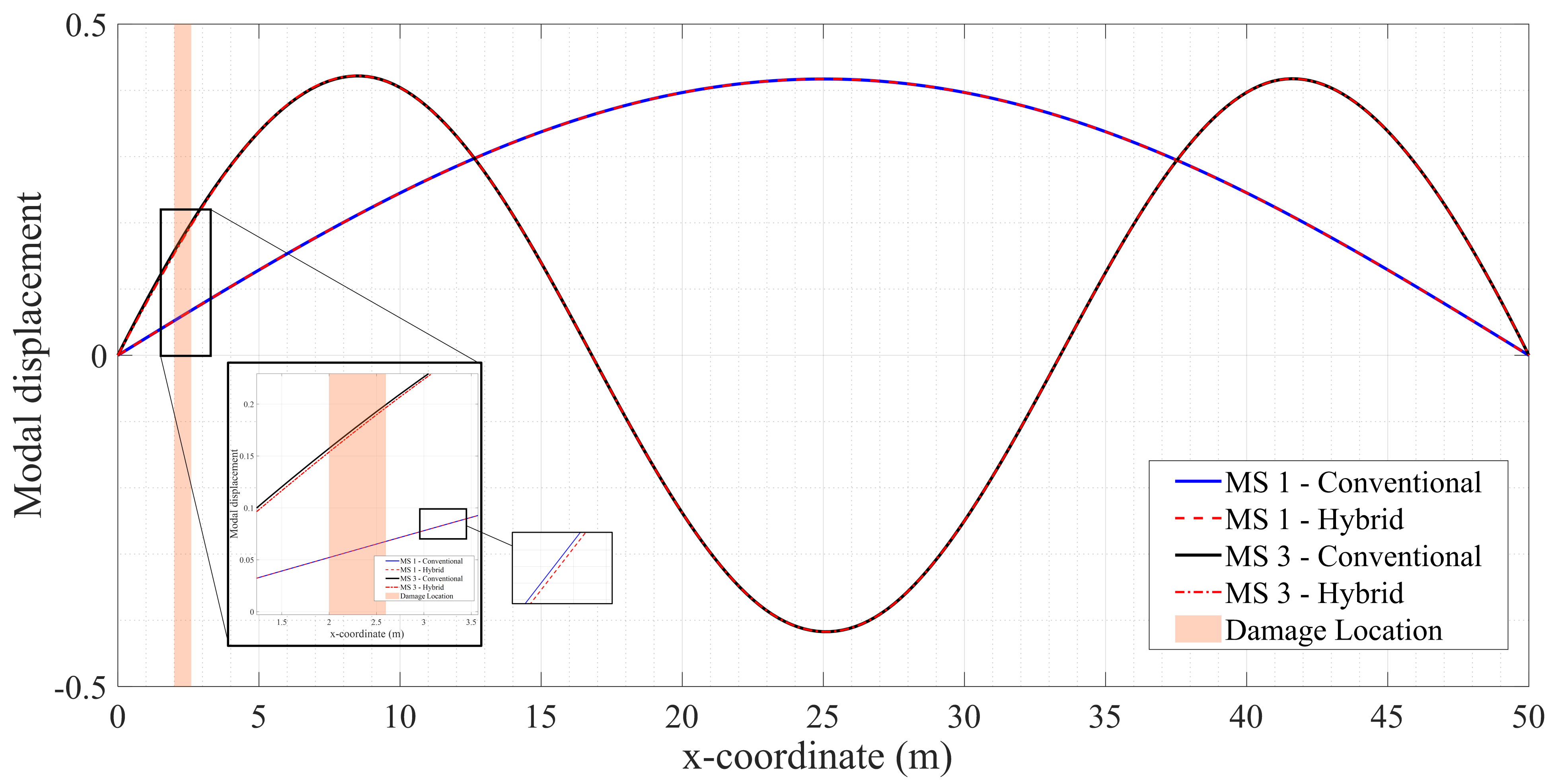
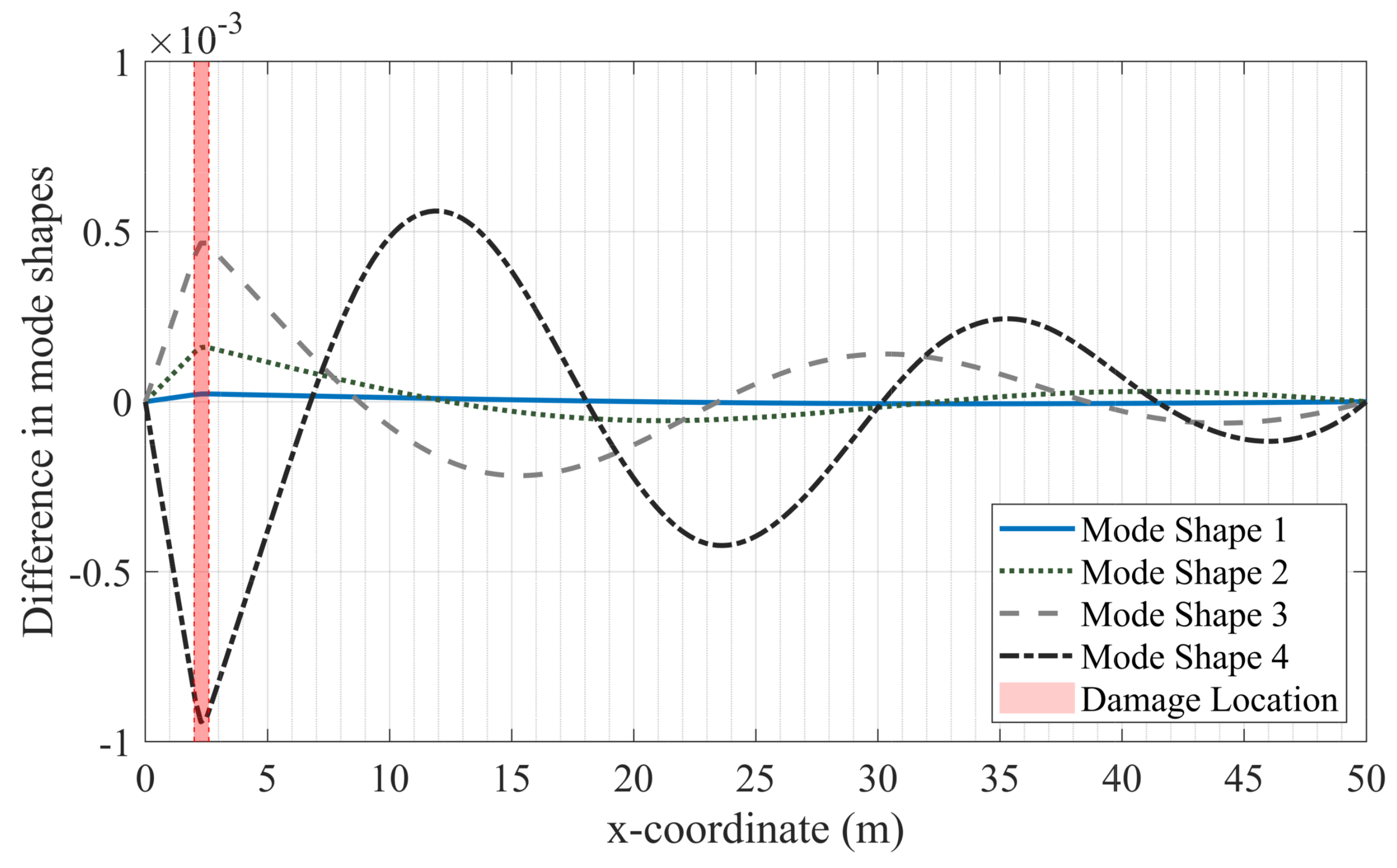
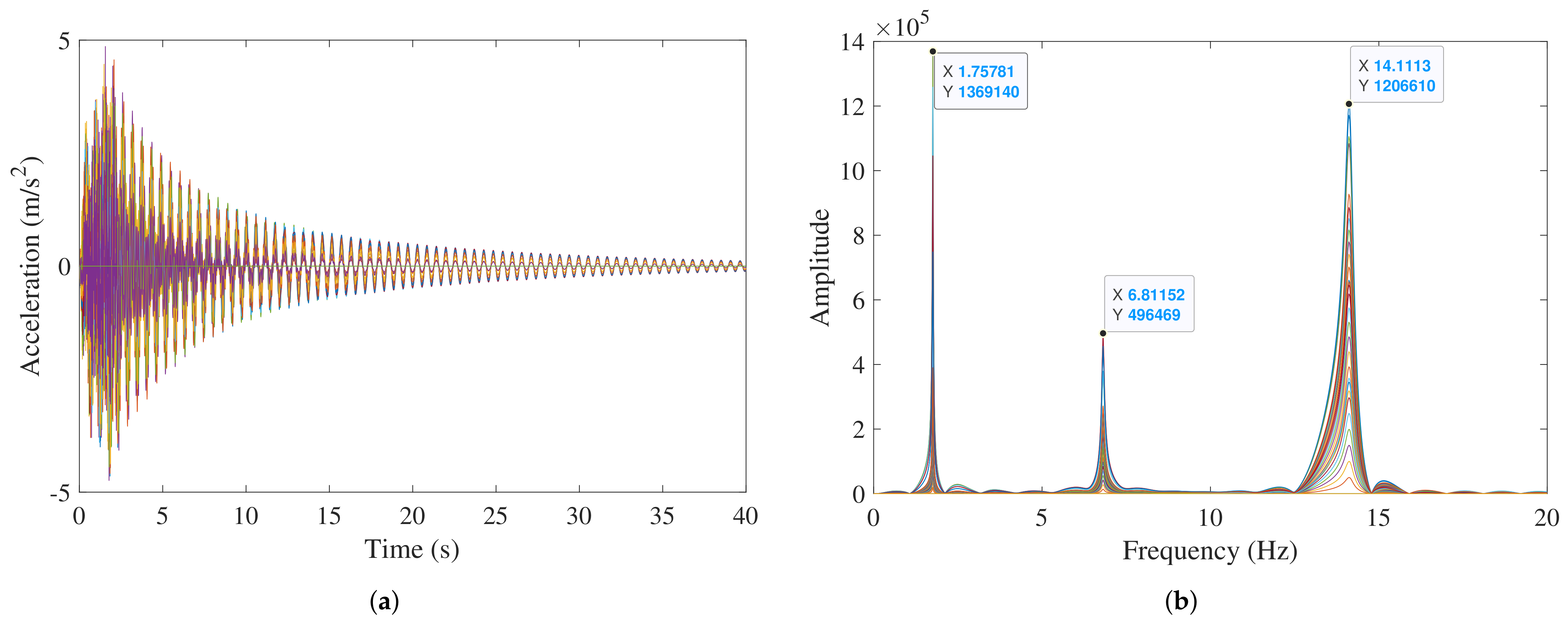
3. Verification Study: Case I
4. Case Studies
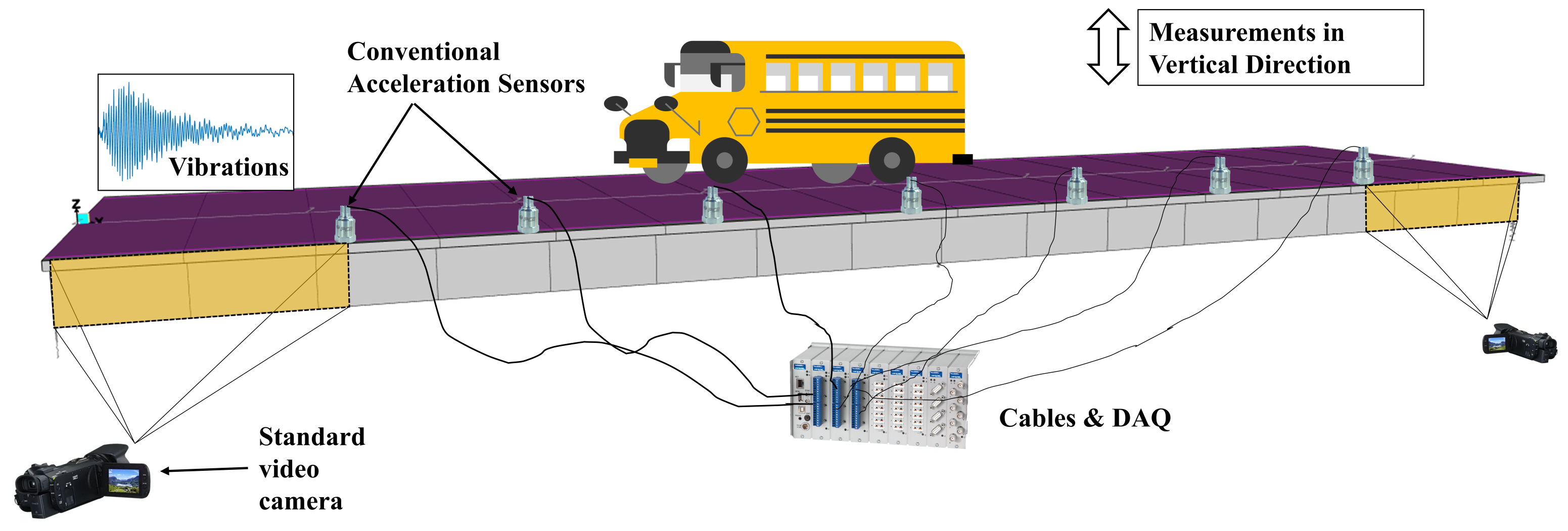
4.1. Train Crossings
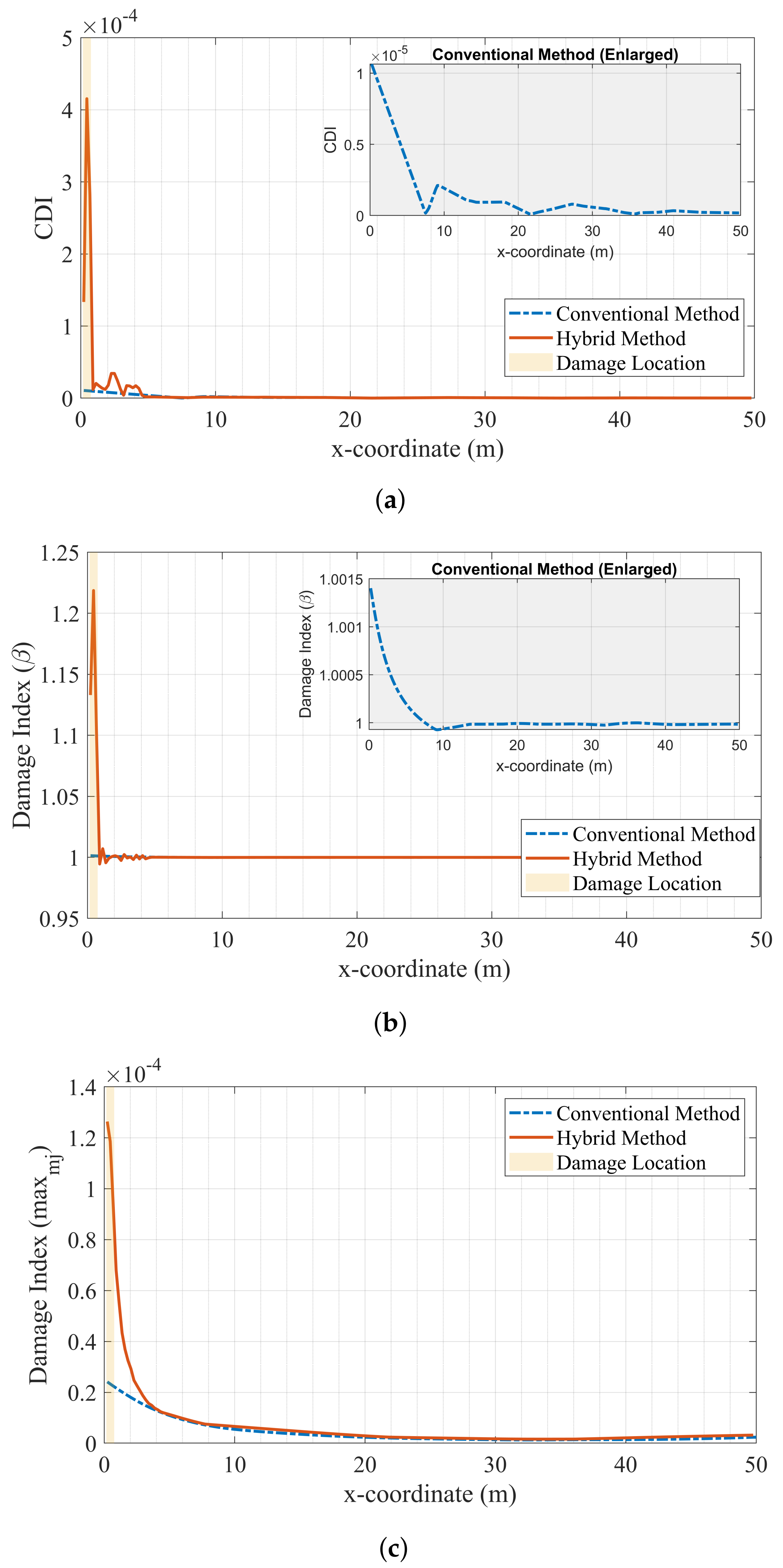
4.1.1. Damage Next to the Support: Case II
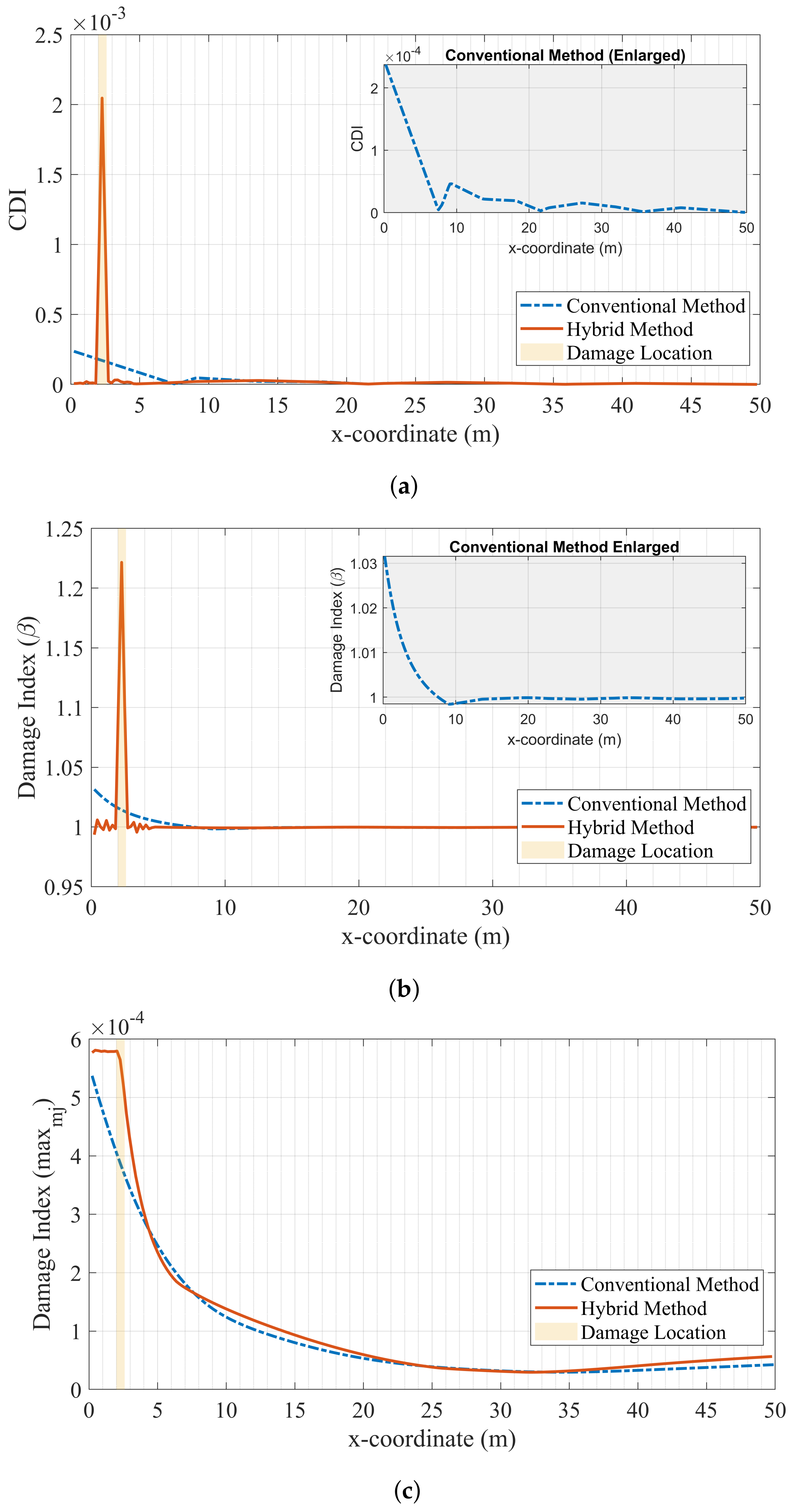
4.1.2. Damage near the Support: Case III
4.2. Ambient Vibration
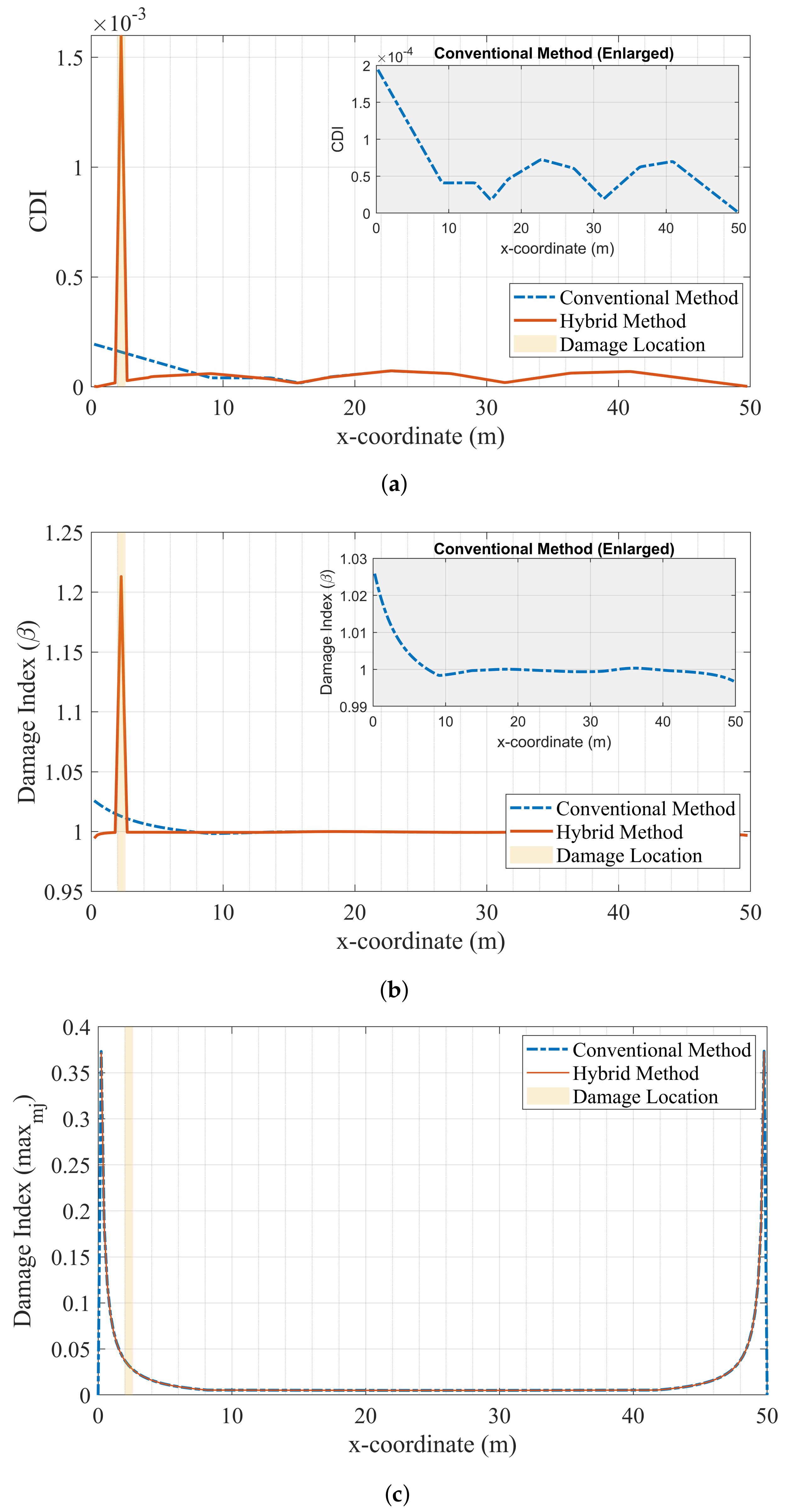
4.2.1. Low Noise: Case IV
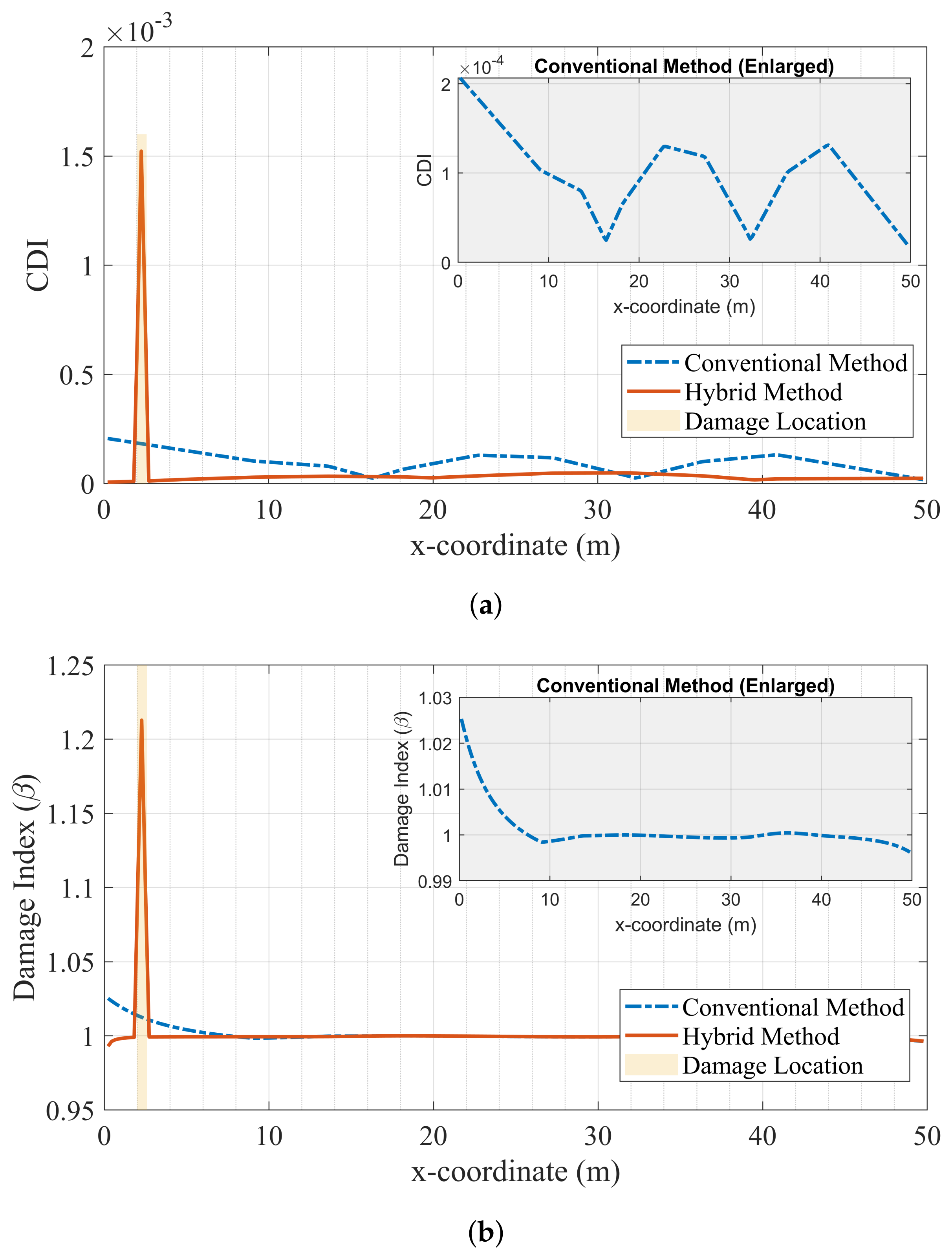
4.2.2. Moderate Noise: Case V
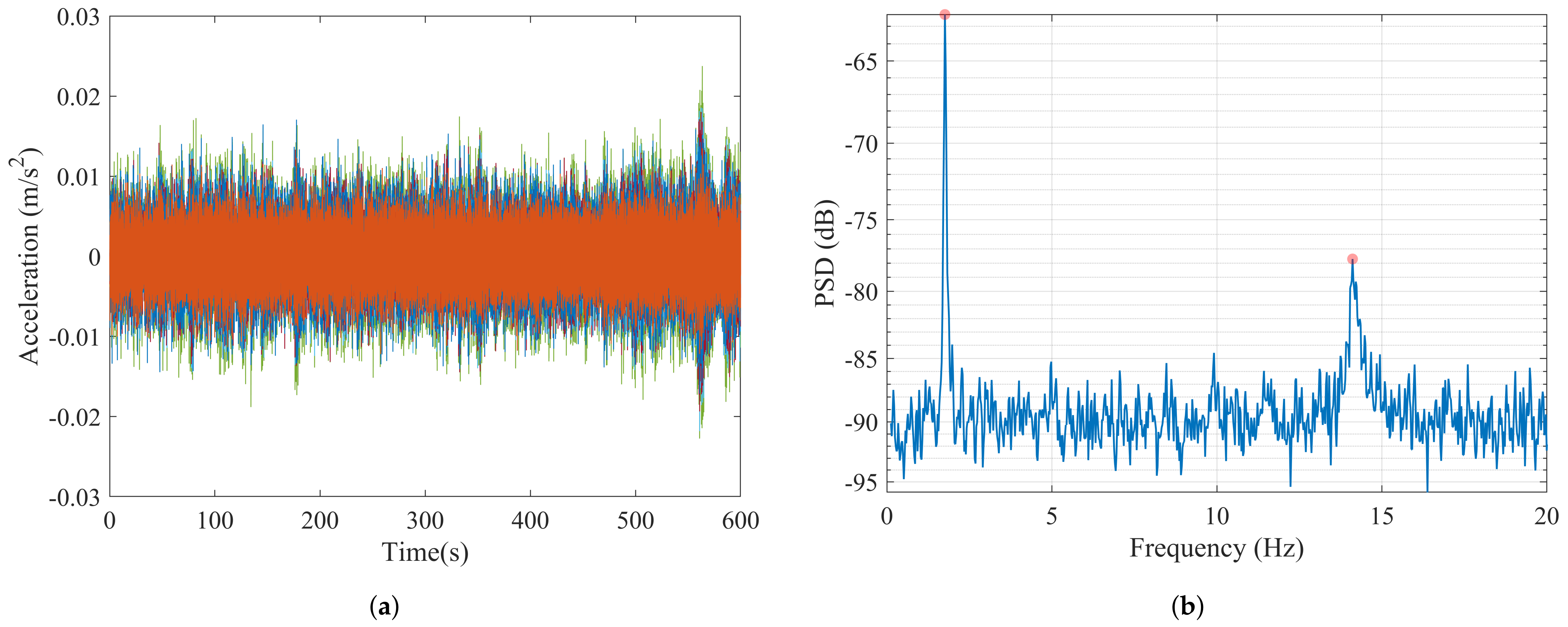
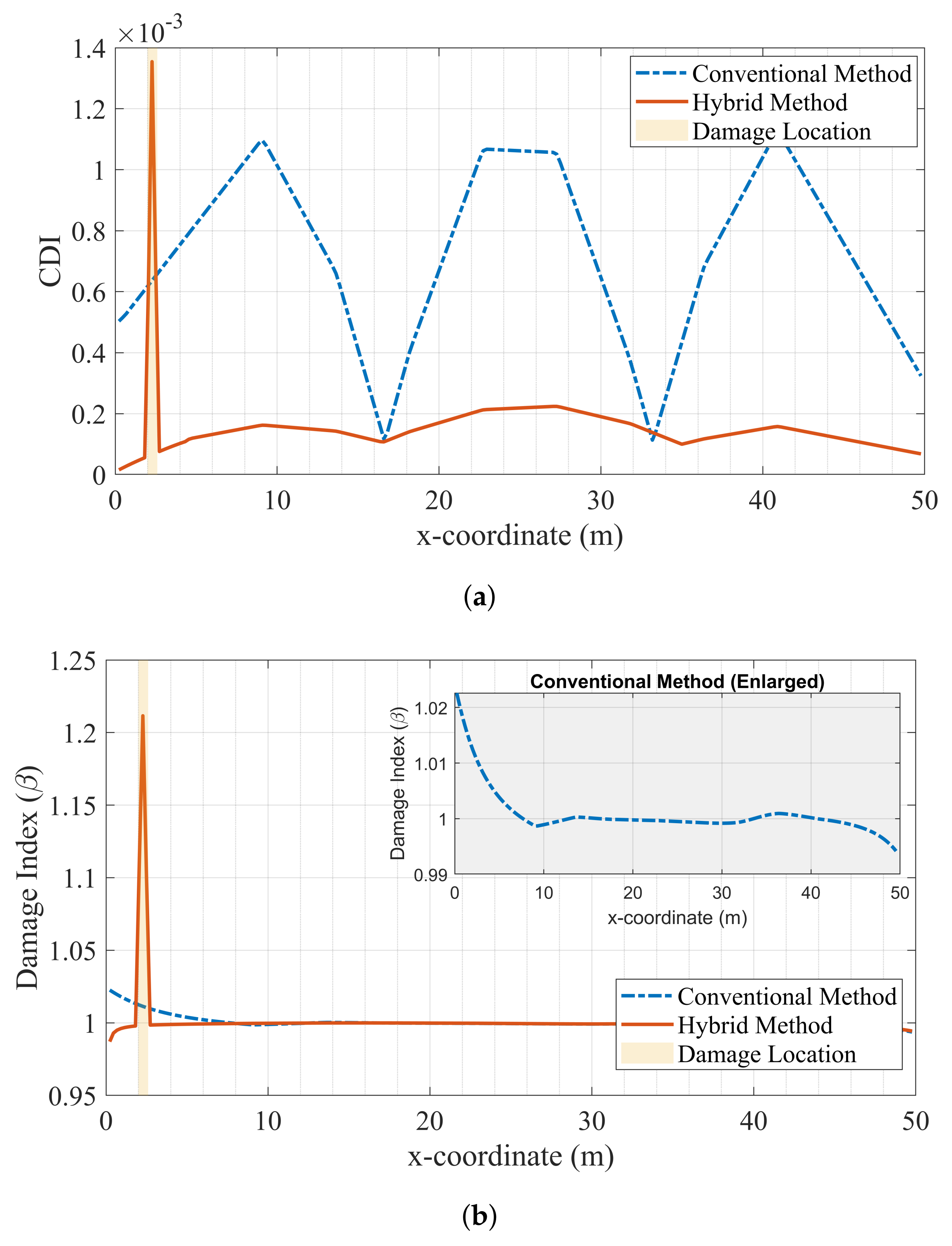
4.2.3. High Noise: Case VI
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Casas, J.R.; Moughty, J.J. Bridge damage detection based on vibration data: Past and new developments. Front. Built Environ. 2017, 3, 4. [Google Scholar] [CrossRef]
- ASCE. Report Card for America’s Infrastructure; Technical Report; American Society of Civil Engineers, ASCE: Reston, VA, USA, 2021. [Google Scholar]
- Statistical Pocketbook 2021—EU Transport in Figures; Technical Report; European Commission: Luxembourg, 2021. [CrossRef]
- Toksoy, T.; Aktan, A.E. Bridge condition assessment by flexibility. Exp. Mech. 1994, 34, 271–278. [Google Scholar] [CrossRef]
- Figueiredo, E.; Park, G.; Figueriras, J.; Farrar, C.; Worden, K. Structural Health Monitoring Algorithm Comparisons Using Standard Data Sets; Technical Report Report: LA-14393; Los Alamos National Laboratory: Los Alamos, NM, USA, 2009.
- Farrar, C.; Jauregui, D. Comparative study of damage identification algorithms to a bridge: I. Experiment. Smart Mater. Struct. 1998, 7, 704–719. [Google Scholar] [CrossRef]
- Cruz, P.J.S.; Salgado, R. Performance of vibration-based damage detection methods in bridges. Comput. Aided Civ. Infrastruct. Eng. 2009, 24, 62–79. [Google Scholar] [CrossRef]
- Maek, J.; Peeters, B.; Roeck, G.D. Damage identification on the Z24 bridge using vibration monitoring. Smart Mater. Struct. 2001, 10, 512–517. [Google Scholar] [CrossRef]
- Farrar, C.R.; Doebling, S.W.; Nix, D.A. Vibration-based structural damage identification. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2001, 359, 131–149. [Google Scholar] [CrossRef]
- Carden, E.; Fanning, P. Vibration Based Condition Monitoring: A Review. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Salawu, O. Detection of structural damage through changes in frequency: A review. Eng. Struct. 1998, 19, 718–723. [Google Scholar] [CrossRef]
- Dawari, V.; Vesmawala, G. Structural damage identification using modal curvature differences. IOSR J. Mech. Civ. Eng. 2013, 4, 33–38. [Google Scholar]
- Altunışık, A.C.; Okur, F.Y.; Karaca, S.; Kahya, V. Vibration-based damage detection in beam structures with multiple cracks: Modal curvature vs. modal flexibility methods. Nondestruct. Test. Eval. 2019, 34, 33–53. [Google Scholar] [CrossRef]
- Ni, Y.; Zhou, H.; Chan, K.; Ko, J. Modal flexibility analysis of cable-stayed Ting Kau Bridge for damage identification. Comput.-Aided Civ. Infrastruct. Eng. 2008, 23, 223–236. [Google Scholar] [CrossRef]
- Aktan, A.; Lee, K.; Chuntavan, C.; Aksel, T. Modal testing for structural identification and condition assessment of constructed facilities. In Proceedings–SPIE the International Society for Optical Engineering; The International Society for Optics and Photonics: Bellingham, WA, USA, 1994; p. 462. [Google Scholar]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A summary review of vibration-based damage identification methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- An, Y.; Chatzi, E.; Sim, S.H.; Laflamme, S.; Blachowski, B.; Ou, J. Recent progress and future trends on damage identification methods for bridge structures. Struct. Control. Health Monit. 2019, 26, 1–30. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Gönen, S.; Soyöz, S. Seismic analysis of a masonry arch bridge using multiple methodologies. Eng. Struct. 2021, 226, 111354. [Google Scholar] [CrossRef]
- Soyoz, S.; Feng, M.Q.; Shinozuka, M. Structural Reliability Estimation with Vibration-Based Identified Parameters. J. Eng. Mech. 2010, 136, 100–106. [Google Scholar] [CrossRef]
- Özer, E.; Soyöz, S. Vibration-based damage detection and seismic performance assessment of bridges. Earthq. Spectra 2015, 31, 137–157. [Google Scholar] [CrossRef]
- Huseynov, F.; Kim, C.; OBrien, E.J.; Brownjohn, J.M.; Hester, D.; Chang, K.C. Bridge damage detection using rotation measurements – Experimental validation. Mech. Syst. Signal Process. 2020, 135, 106380. [Google Scholar] [CrossRef]
- Flint, M.M.; Fringer, O.; Billington, S.L.; Freyberg, D.; Diffenbaugh, N.S. Historical Analysis of Hydraulic Bridge Collapses in the Continental United States. J. Infrastruct. Syst. 2017, 23, 04017005. [Google Scholar] [CrossRef]
- Fenerci, A.; Kvåle, K.A.; Wiig Petersen, Ø.; Rønnquist, A.; Øiseth, O. Data Set from Long-Term Wind and Acceleration Monitoring of the Hardanger Bridge. J. Struct. Eng. 2021, 147, 04721003. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, M.; Wang, L.; Zhang, J. Recent Highway Bridge Collapses in China: Review and Discussion. J. Perform. Constr. Facil. 2016, 30, 04016030. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, F.; Han, Y. Assessment of wind-induced nonlinear post-critical performance of bridge decks. J. Wind. Eng. Ind. Aerodyn. 2020, 203, 104251. [Google Scholar] [CrossRef]
- Dilena, M.; Morassi, A. Dynamic testing of a damaged bridge. Mech. Syst. Signal Process. 2011, 25, 1485–1507. [Google Scholar] [CrossRef]
- Grande, E.; Imbimbo, M. A multi-stage approach for damage detection in structural systems based on flexibility. Mech. Syst. Signal Process. 2016, 76–77, 455–475. [Google Scholar] [CrossRef]
- Limongelli, M.P.; Giordano, P.F. Vibration-based damage indicators: A comparison based on information entropy. J. Civ. Struct. Health Monit. 2020, 10, 251–266. [Google Scholar] [CrossRef]
- Giordano, P.F.; Limongelli, M.P. Response-based time-invariant methods for damage localization on a concrete bridge. Struct. Concr. 2020, 21, 1254–1271. [Google Scholar] [CrossRef]
- Erduran, E.; Ulla, F.K.; Næss, L. A framework for long-term vibration-based monitoring of bridges. Sensors 2021, 21, 4739. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective, 2nd ed.; John Wiley & Sons: West Sussex, UK, 2013. [Google Scholar]
- Feng, D.; Feng, M.Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detectio—A review. Eng. Struct. 2018, 156, 105–117. [Google Scholar] [CrossRef]
- Dong, C.Z.; Catbas, F.N. A review of computer vision–based structural health monitoring at local and global levels. Struct. Health Monit. 2020, 20, 692–743. [Google Scholar] [CrossRef]
- Baqersad, J.; Poozesh, P.; Niezrecki, C.; Avitabile, P. Photogrammetry and optical methods in structural dynamics—A review. Mech. Syst. Signal Process. 2017, 86, 17–34. [Google Scholar] [CrossRef]
- Yoon, H.; Elanwar, H.; Choi, H.; Golparvar-Fard, M.; Spencer, B.F. Target-free approach for vision-based structural system identification using consumer-grade cameras. Struct. Control. Health Monit. 2016, 23, 1405–1416. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Mancini, T.; Talken, Z.; Kenyon, G.; Farrar, C.; Mascareñas, D. Blind identification of full-field vibration modes from video measurements with phase-based video motion magnification. Mech. Syst. Signal Process. 2017, 85, 567–590. [Google Scholar] [CrossRef]
- Liu, G.; Li, M.Z.; Mao, Z.; Yang, Q.S. Structural motion estimation via Hilbert transform enhanced phase-based video processing. Mech. Syst. Signal Process. 2022, 166, 108418. [Google Scholar] [CrossRef]
- Bregar, T.; Zaletelj, K.; Čepon, G.; Slavič, J.; Boltežar, M. Full-field FRF estimation from noisy high-speed-camera data using a dynamic substructuring approach. Mech. Syst. Signal Process. 2021, 150, 107263. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Vision-based multipoint displacement measurement for structural health monitoring. Struct. Control. Health Monit. 2016, 23, 876–890. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Experimental validation of cost-effective vision-based structural health monitoring. Mech. Syst. Signal Process. 2017, 88, 199–211. [Google Scholar] [CrossRef]
- Chen, J.G.; Adams, T.M.; Sun, H.; Bell, E.S.; Büyüköztürk, O. Camera-Based Vibration Measurement of the World War I Memorial Bridge in Portsmouth, New Hampshire. J. Struct. Eng. 2018, 144, 1–19. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.M.; Huseynov, F. Accurate Deformation Monitoring on Bridge Structures Using a Cost-Effective Sensing System Combined with a Camera and Accelerometers: Case Study. J. Bridge Eng. 2019, 24, 05018014. [Google Scholar] [CrossRef]
- Hu, H.; Wang, J.; Dong, C.z.; Chen, J.; Wang, T. A hybrid method for damage detection and condition assessment of hinge joints in hollow slab bridges using physical models and vision-based measurements. Mech. Syst. Signal Process. 2023, 183, 109631. [Google Scholar] [CrossRef]
- Dong, C.Z.; Celik, O.; Catbas, F.N. Marker-free monitoring of the grandstand structures and modal identification using computer vision methods. Struct. Health Monit. 2019, 18, 1491–1509. [Google Scholar] [CrossRef]
- Bolognini, M.; Izzo, G.; Marchisotti, D.; Fagiano, L.; Limongelli, M.P.; Zappa, E. Vision-based modal analysis of built environment structures with multiple drones. Autom. Constr. 2022, 143, 104550. [Google Scholar] [CrossRef]
- Fioriti, V.; Roselli, I.; Tatì, A.; Romano, R.; De Canio, G. Motion Magnification Analysis for structural monitoring of ancient constructions. Meas. J. Int. Meas. Confed. 2018, 129, 375–380. [Google Scholar] [CrossRef]
- Gonen, S.; Erduran, E. A Hybrid Method for Damage Detection Using Acceleration Response of Bridges. Lect. Notes Civ. Eng. 2023, 254, 865–875. [Google Scholar] [CrossRef]
- Pandey, A.; Biswas, M.; Samman, M. Damage detection from changes in curvature mode shapes. J. Sound Vib. 1991, 145, 321–332. [Google Scholar] [CrossRef]
- Stubbs, N.; Kim, J.T.; Topole, K. An efficient and robust algorithm for damage localization in offshore structures. In Proceedings of the 10th ASCE Structures Conference, San Antonio, TX, USA, 13–15 April 1992; American Society of Civil Engineers: Reston, VA, USA, 1992; pp. 543–546. [Google Scholar]
- Limongelli, M.P.; Manoach, E.; Quqa, S.; Giordano, P.F.; Bhowmik, B.; Pakrashi, V.; Cigada, A. Vibration Response-Based Damage Detection. In Structural Health Monitoring Damage Detection Systems for Aerospace; Springer Aerospace Technology; Sause, M., Jasiūnienė, E., Eds.; Springer Science and Business Media Deutschland GmbH: Berlin, Germany, 2021; pp. 133–173. [Google Scholar] [CrossRef]
- Yao, R.; Pakzad, S.N. Autoregressive statistical pattern recognition algorithms for damage detection in civil structures. Mech. Syst. Signal Process. 2012, 31, 355–368. [Google Scholar] [CrossRef]
- Meixedo, A.; Santos, J.; Ribeiro, D.; Calçada, R.; Todd, M. Damage detection in railway bridges using traffic-induced dynamic responses. Eng. Struct. 2021, 238, 112189. [Google Scholar] [CrossRef]
- Corbally, R.; Malekjafarian, A. A data-driven approach for drive-by damage detection in bridges considering the influence of temperature change. Eng. Struct. 2022, 253, 113783. [Google Scholar] [CrossRef]
- Duvant, G.; Lions, J.L. Structural Health Monitoring of Large Civil Engineering Structures; Wiley-Blackwell: West Sussex, UK, 2018. [Google Scholar]
- Yang, X.M.; Yi, T.H.; Qu, C.X.; Li, H.N.; Liu, H. Performance Assessment of a High-Speed Railway Bridge through Operational Modal Analysis. J. Perform. Constr. Facil. 2021, 35, 1–11. [Google Scholar] [CrossRef]
- Gonen, S.; Soyoz, S. Dynamic identification of masonry arch bridges using multiple methodologies. In Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Gonen, S.; Demirlioglu, K.; Erduran, E. Modal Identification of a Railway Bridge Under Train Crossings: A Comparative Study. Dyn. Civ. Struct. 2023, 2, 33–40. [Google Scholar] [CrossRef]
- Erduran, E.; Gonen, S.; Alkanany, A. Parametric analysis of the dynamic response of railway bridges due to vibrations induced by heavy-haul trains. Struct. Infrastruct. Eng. 2022, 1–14. [Google Scholar] [CrossRef]
- Erduran, E.; Nordli, C.; Gonen, S. Effect of Elastomeric Bearing Stiffness on the Dynamic Response of Railway Bridges Considering Vehicle—Bridge Interaction. Appl. Sci. 2022, 12, 11952. [Google Scholar] [CrossRef]
- Glatz, B.; Fink, J. A redesigned approach to the additional damping method in the dynamic analysis of simply supported railway bridges. Eng. Struct. 2021, 241, 112415. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef]
- Wei, X.; Liu, J.C.; Bi, S. Uncertainty quantification and propagation of crowd behaviour effects on pedestrian-induced vibrations of footbridges. Mech. Syst. Signal Process. 2022, 167, 108557. [Google Scholar] [CrossRef]
- Gönen, S.; Soyöz, S. Reliability-based seismic performance of masonry arch bridges. Struct. Infrastruct. Eng. 2021, 18, 1658–1673. [Google Scholar] [CrossRef]
- Srivastava, V.; Baqersad, J. An optical-based technique to obtain operating deflection shapes of structures with complex geometries. Mech. Syst. Signal Process. 2019, 128, 69–81. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonen, S.; Erduran, E. A Hybrid Method for Vibration-Based Bridge Damage Detection. Remote Sens. 2022, 14, 6054. https://doi.org/10.3390/rs14236054
Gonen S, Erduran E. A Hybrid Method for Vibration-Based Bridge Damage Detection. Remote Sensing. 2022; 14(23):6054. https://doi.org/10.3390/rs14236054
Chicago/Turabian StyleGonen, Semih, and Emrah Erduran. 2022. "A Hybrid Method for Vibration-Based Bridge Damage Detection" Remote Sensing 14, no. 23: 6054. https://doi.org/10.3390/rs14236054
APA StyleGonen, S., & Erduran, E. (2022). A Hybrid Method for Vibration-Based Bridge Damage Detection. Remote Sensing, 14(23), 6054. https://doi.org/10.3390/rs14236054









