Ellipse Crater Recognition for Lost-in-Space Scenario

Abstract

In the field of deep space exploration, a crater recognition algorithm is key to landing navigation based on craters. When there is only visual information, determining how to identify the crater and provide the initial pose of the lander for a lost-in-space (LIS) scenario is a difficulty in terrain relative navigation (TRN). In this paper, a fast and robust crater recognition method for absolute pose estimation based on projective invariants is proposed, which can provide an accurate initial pose for tracking navigation. First, the method selects navigation craters to establish a small-capacity and high-efficiency crater database, and crater pair serial numbers and projective invariants are stored. Second, our method uses a dynamic threshold to solve the problem that the projective invariants are sensitive to noise. Then, an iterative pyramid algorithm is proposed to quickly filter redundancies. Using a dynamic threshold, the matching rate was increased by at least 10%, and the average processing speed was increased by 40%. When the detection errors of the major and minor axes of the ellipse reached 5%, the detection error of the center point reached 1 pixel, and the tilt angle error reached 5°; the matching rate was still >80%. Finally, the pose was estimated by solving the perspective-n-point (PNP) problem based on the recognized craters. The initial pose error in the simulation environment was less than 2°, and the position error was less than 44 m.

1. Introduction

Soft landing technology on planetary surfaces has become an important part of deep space exploration [1]. At present, precise landing is required [2,3] for the landing and navigation missions on Mars, the Moon, and asteroids [4]. The inertial navigation method has a large cumulative error, which can cause distance errors of several kilometers from the precise landing target [5]. TRN is an optical-based autonomous navigation approach [6,7] that enhances navigation capabilities by providing measurement information about the position or orientation relative to a known celestial surface [8].

NASA’s Perseverance rover adopted the TRN method based on image features to estimate the pose, to avoid dangerous obstacles during the Mars landing test, and finally to determine its position relative to the ground, with high accuracy [9]. In addition to the local area and image features used by Perseverance, the landmarks in TRN can also be distinct natural features, such as craters [10,11], rocks, or artificial landmarks. The Near-Earth Asteroid Rendezvous (NEAR) mission of NASA in 2003 [12] was the first use of a crater-based navigation method, which proved that craters are a powerful form of orbit determination data. Craters have since become the landmarks of choice.

To increase the value of planetary scientific research, landing in the complex terrain of many craters has become an inevitable trend. Navigation methods based on traditional descriptors such as scale-invariant feature transform (SIFT [13]) for image matching are not suitable for terrain where the shadows of craters change with light. Crater recognition and estimation of the landing pose will be the focus of research in the field of planetary landing for a long time in the future [8]. The crater-based navigation method has the following advantages:

• Extraterrestrial objects have a large number of rich craters of various sizes and shapes, and also have a large number of annotated crater datasets [14,15,16,17,18,19,20,21,22,23,24,25];
• The method is able to estimate absolute pose without initial pose information;
• Compared with template-matching and feature-matching methods, the crater-based navigation method does not require a three-dimensional model or a complete digital elevation model (DEM), which can reduce the memory and computing power.

According to the crater images returned by the probe in the landing segment, most of the craters are ellipses [7,26]. In particular, when the descending camera observes the craters in a non-vertical state, the tilt of the crater is relatively large. Therefore, methods that describe craters directly with circular approximations are often inaccurate. Crater recognition is the process of matching the detected craters with the craters in the database through descriptors. When the descriptors are similar in terms of a certain distance metric, the recognition is considered correct [27]. According to the navigation application, the crater recognition methods can be divided into orbital segment recognition [28,29] and landing segment recognition [30]. Due to the crater projection’s deformation and scale, the latter is more difficult than the former. Whether it is orbiting segment or landing segment navigation, these methods can be divided into lost-in-space (LIS) recognition and tracking recognition. LIS recognition has no initial pose, while tracking recognition is provided with an initial pose.

During the navigation of an orbital segment, the camera shoots vertically downward, and its line of sight (LOS) is small. Christian et al. [31] studied the LIS recognition method, designed two crater-projective transformation invariants and their descriptors, including coplanar and non-coplanar invariants, and designed a new elliptical distance metric function that satisfied the four characteristics of the distance. Doppenberg [32] used both crater invariants and crater triangle invariants for LIS recognition in the orbital segment. They considered the order invariance of triangular craters in the matching process and established a feature descriptor to match the craters. Hanak [28,29] proposed a crater matching method for the situation of “Lost in Low Orbit” and used the voting method to obtain the maximum matching probability. It was mainly used in the circumstance of a low-orbit encircling segment and lacking of prior attitude.

During the tracking navigation of an orbital segment, the crater scale changes are very small between sequence images, and the crater pattern is generally used for direct matching (DM). Lena et al. [5] used the nearest-neighbor algorithm to directly match the craters or construct multiple craters into a descriptor for matching. Wei Shao et al. [33] proposed a crater matching method using a feature descriptor, extracting crater arc features through a Gaussian pyramid algorithm and edge line segment detector (ELSD) algorithm. They also proposed a descriptor of arc zone and finally used distance constraints to match the craters.

The LIS recognition of a landing segment is performed without any initial information at all, which means that craters from the catalog must be projected into the image. The LIS matching conditions of the landing segment are the most severe, and the matching accuracy is always very low. LIS recognition is similar to the star pattern recognition method. Mortari et al. [34] proposed a pyramid algorithm in the field of star pattern recognition which can identify and discard many false stars. The navigation of a landing segment has larger attitude changes, and the projective invariants can greatly be disturbed by noise. Park et al. [30] addressed this issue by adding constraints, using 30 projective invariants of the crater triangle. In their method, the triangular arrangement sequence was used to establish a database, and the Euclidean distance was used for matching to improve the LIS matching rate of the crater. However, adding invariants will make the database larger, which will increase the redundancy in the process of crater triangle searching and limit the further improvement of the LIS matching rate.

The tracking recognition of the landing segment provides the initial pose through other sensors and performs matching between sequence images. The traditional template-matching method is suitable for the case where the crater deformations are small [35,36]. Cheng et al. [2] used the initial estimated pose to filter out impossible matches and then corrected the inertial navigation with elliptical invariants. Chen [37] matched the sequence images with the crater database when the initial pose was provided and used the Kuhn-Munkres (KM) algorithm to match the sequence images. Maass et al. [38] combined LIS recognition and tracking recognition to form an absolute navigation system, that is, the algorithm was initialized in an LIS scenario to provide pose estimations, and then image sequence tracking and recognition were performed, which could continuously estimate the motion state of the entire aircraft.

The LIS recognition of craters for landing navigation has the following difficulties:

• The projective invariants of the ellipse are greatly disturbed by noise, that is, the recognition rate is very sensitive to the detection errors of elliptical craters;
• The matching library is huge, resulting in slow search and low efficiency. More redundant matching will lead to a lower recognition rate;
• An unstable lander state during landing often has a larger tilt, resulting in larger deformation of the actual crater projected onto the image plane and increasing the difficulty of recognition.

Some methods [28,29,30] have tried to solve the aforementioned difficulties. They took the idea of increasing the number of invariants or assuming that the lander shoots vertically downward to recognize craters. But these ideas still have some shortcomings. On the one hand, it will increase the database capacity. On the other hand, the landing process itself is extremely unstable.

The main contributions of this research are summarized as follows. A crater recognition algorithm in the navigation of a landing segment is proposed which provides an accurate and fast attitude estimation for an LIS scenario. To address the aforementioned difficulties, first we established a small-capacity and high-efficiency crater pair database of invariants based on elliptical craters for LIS recognition. Second, an iterative pyramid algorithm was proposed, which can achieve robust crater recognition even in the case of large projection deformation. Moreover, a dynamic threshold was designed to quickly reduce redundancy to solve the problem that the projective invariants are greatly disturbed by noise. Combined with a dynamic threshold, the matching rate can reach over 80%, and the average processing speed is improved by 40% compared with a fixed threshold.

The rest of the paper is organized as follows. In Section 2, the crater recognition method and pose estimation algorithm are introduced in detail. In Section 3, the experimental results are described, and the efficiency of the algorithm is evaluated. In Section 4, the results are discussed. Conclusions and future research work are presented in Section 5.

2. Materials and Methods

The crater recognition method is divided into three parts: establishment of a crater pair database, LIS recognition, and re-projection verification, as shown in Figure 1. First, the navigation craters are selected from the craters on the map to establish a database, and the crater pair’s serial numbers and projective invariants are stored. Second, the craters detected in the sequence images are matched with the craters in the database, and the iterative pyramid algorithm is used to identify four craters, one of which will have multiple solutions for the recognition of craters, as shown in set $\left\{l\right\}$ in Figure 1. Finally, the PNP problem is composed of four pairs of three-dimensional (3D)–two-dimensional (2D) points. For the case where there are multiple solutions for the fourth crater, all possible craters are traversed. The estimated pose is obtained, and re-projection verification is performed iteratively for all navigation craters. If the current image and the re-projection image are the same, the pose is considered to be correct, and then the fourth crater is recognized.

Considering the unstable landing state, the camera will not strictly shoot vertically downward, and any increase in the lander’s tilt angle will often lead to an increase in the tilt of the crater in the image plane. Therefore, elliptical features are used to recognize craters. The ellipse equation is as follows:

$$A{x}^2+Bxy+C{y}^2+Dx+Fy+G=0,$$

(1)

$$\begin{gathered} A=a^2{\sin }^2\theta +b^2{\cos }^2\theta , \\ B=2\left(b^2-a^2\right)\cos \theta \sin \theta , \\ C=a^2{\cos }^2\theta +b^2{\sin }^2\theta , \\ D=-2A{X}_c-B{Y}_c, \\ F=-B{X}_c-2C{Y}_c, \\ G=A{X}_c^2+B{X}_c{Y}_c+C{Y}_c^2-a^2{b}^2, \end{gathered}$$

(2)

where the center coordinates are $X_c$ and $Y_c$, the major and minor semi-axes are a and b, respectively, and the inclination angle is $\theta$.

The key to crater recognition is determining how to find the invariant relationship of craters in the projective transformation, and the invariant theory proves the existence of crater projection invariants [31]. Because the spacecraft in the landing state is close to the planetary surface, it can be assumed that all craters are locally coplanar, and the elliptical crater pair can form quadratic curve invariants $I_{ij}$ and $I_{ji}$ [39,40], defined as follows:

$$I_{ij}=Tr\left[H_i^{-1}{H}_j\right], I_{ji}=Tr\left[H_j^{-1}{H}_i\right].$$

(3)

where Tr represents the matrix trace. $H_i$ and $H_j$ are normalized ellipse equations, defined as follows:

$$\begin{gathered} M_i=\left[\begin{array}{ccc}{A}_i& \frac{B_i}{2}& \frac{D_i}{2}\\ \frac{B_i}{2}& C_i& \frac{F_i}{2}\\ \frac{D_i}{2}& \frac{F_i}{2}& G_i\end{array}\right], H_i=\frac{M_i}{\left|M_i\right|}, \\ {M}_j=\left[\begin{array}{ccc}{A}_j& \frac{B_j}{2}& \frac{D_j}{2}\\ \frac{B_j}{2}& C_j& \frac{F_j}{2}\\ \frac{D_j}{2}& \frac{F_j}{2}& G_j\end{array}\right], H_j=\frac{M_j}{\left|M_j\right|}. \end{gathered}$$

(4)

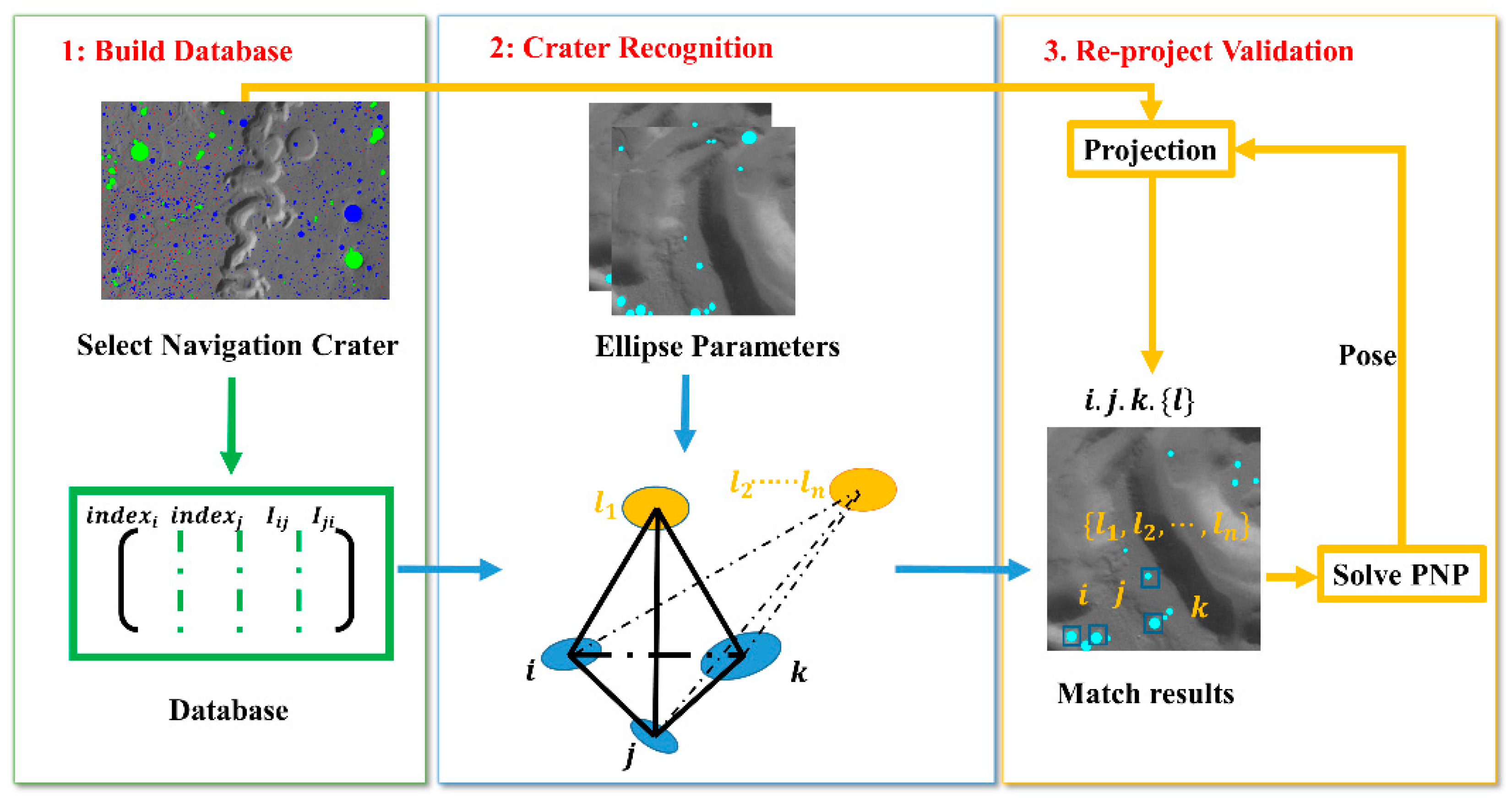
2.1. Database Establishment

An appropriate number of navigation craters are selected to build a database. Too many navigation craters will make the database large, which will increase the redundancy of craters for filtering and increase the computational burden. When there are too few navigation craters, the probability of selecting non-navigation craters in the recognition process will increase, and the matching rate will decrease. A suitable selection principle is designed, similar to the first step of data preprocessing in the LIS recognition. First, considering the principle of prioritizing large craters, it is necessary to eliminate small craters and retain large craters as navigation craters. Secondly, considering the possible detection errors caused by overlapping craters in the sequence images, it is necessary to remove the overlapping craters. Finally, the navigation crater table will be selected, as shown in

Table 1. Comparison of matching rates calculated by different methods.

Methods	$\mathit{a},\mathit{b} (\%)$	x, y	$\mathit{\theta }$	Matching Rate (%)
Park’s method [30]	N(0,1)	N(0,0.5)	N(0,5)	41.70
Iterative pyramid approach (factor = 0.3)	N(0,1)	N(0,0.5)	N(0,5)	89.67
	N(0,2)	N(0,1)	N(0,10)	86.29
Iterative pyramid approach (factor = 0.4)	N(0,1)	N(0,0.5)	N(0,5)	89.67
	N(0,2)	N(0,1)	N(0,10)	78.16
Doppenberg’s method [32]	N(0,1)	N(0,1)	u(−10,10)	14.00
Iterative pyramid approach (factor = 0.3)	N(0,1)	N(0,1)	u(−10,10)	86.99
	N(0,2)	N(0,2)	u(−20,20)	79.93
Iterative pyramid approach (factor = 0.4)	N(0,1)	N(0,1)	u(−10,10)	78.82
	N(0,2)	N(0,2)	u(−20,20)	72.25

in Figure 2. Table 1 is conducive to the design of a state table in the recognition process and speeds up the algorithm efficiency, as discussed in Section 2.2.3. Table 1 stores the index, true number, coordinates, and radius of navigation craters, respectively. The records in Table 1 are arranged according to the index. The table is stored as a two-dimensional matrix, and the row index of each matrix is the real serial number of the navigation crater.

The diameter of the maximum FOV at the highest landing height is recorded as d, and the invariants $I_{ij}$ and $I_{ji}$ are calculated according to formula (5) for all the navigation craters $H_i$ and $H_j$ within distance d. The constructed database is shown in “Database” in Figure 2. In the program, Database is stored as a two-dimensional matrix, and each one-dimensional row vector consists of the serial numbers of crater pair and the related invariants. At the same time, the database records are arranged according to the invariants $I_{ij}$ from small to large. The database can subsequently be searched by binary search method. The database in this paper has various advantages, including a small capacity, fast search, and suitability for iterative recognition algorithms. Rather than storing at least seven projective invariants formed by crater triangles, the database only stores two invariants formed by crater pairs. Whether it is the number of stored records or the number of invariants in a single record, the database capacity is greatly reduced, thereby increasing the search speed.

2.2. LIS Recognition

The flow of the LIS recognition algorithm is shown in Figure 3, and it includes data preprocessing, crater pair filtering based on dynamic thresholds, crater tuple construction, and iterative pyramid matching. The image preprocessing principle corresponds to the navigation crater selection principle, which is to remove overlapping craters and recognize large craters first (Section 2.2.1). After preprocessing, three craters i, j, and k are selected in pairs, the invariants and dynamic thresholds of the three crater pairs are calculated, and the database is searched to obtain three sets of crater pairs ij, ik, and jk (Section 2.2.2). Through the collection of three crater pairs ij, ik, and jk, all tuple combinations that are connected end to end are obtained to form a tuple set ijk (Section 2.2.3). Finally, the fourth crater l is added to form a pyramid with i, j, and k, and the database is searched in the same way to obtain the sets il, jl, and kl. Combined with the ijk tuple set, a part of the tuple redundancy can be removed. Each additional l removes some of the redundancy of ijk. When only one tuple is left, the recognition finishes, and the recognition set of the last l is retained (Section 2.2.4). The recognized craters in this paper are ellipses that have been detected by the image processing method, and the craters in each frame of images are represented by the ellipse parameters.

2.2.1. Data Preprocessing

The detected craters’ data in the image need to be preprocessed before applying the crater recognition algorithm. The preprocessing principles include removing overlapping craters and prioritizing large craters. First, because the detection error of overlapping craters is large, all overlapping craters in the image are removed first. As shown in Figure 4, when elliptical craters overlap, it is generally easier to detect only large craters, as shown in Figure 4a. When elliptical craters are close enough or even overlap, it is generally easy to be mistakenly detected as red ellipses in Figure 4b,c. Second, because the large craters are less sensitive to detection noise, they are preferred to be selected for recognition, as shown in Figure 5d.

Knowing all the detected elliptical crater parameters in the image, including the center coordinates x, y and the major and minor semi-axes a, b of each ellipse, the method calculates the distance between the centers of any two ellipses and the average radius $\frac{a+b}{2}$ of each ellipse. Two craters are considered to be overlapping if the distance is less than the radius. The use of the average radius fully takes the false detections of various ellipse crater into account, as shown in Figure 4b,c. The semi-axes of ellipse craters in most landing sequence images are approximately equal. The calculation procedure is detailed in Algorithm 1.

Algorithm 1. Remove overlapping craters

Input: Set1, craters detected in the sequence image

Output: craters without overlapping

Initialization: the center coordinate of crater is x, y, the major and minor half axis is a, b

1:    for crater m in Set1 do:

2:        for another crater n in Set1 do:

3:              dis = $\sqrt{{\left(x_m-x_n\right)}^2+{\left(y_m-y_n\right)}^2}$;

4:              sum_r = $\left(a_m+b_m+a_n+b_n\right)/2$

5:              if dis < sum_r then:

6:                  delete m, n in Set1

7:              end if

8:        end for

9:    end for

2.2.2. Crater Pair Filtering Based on Dynamic Thresholds

The crater pair filtering method needs to calculate the invariant of the crater pair to be recognized, and the database is searched within a threshold range to obtain a set of possible crater pairs. Although projective invariants can help to recognize craters in the image coordinates with the database, the invariants are greatly disturbed by detection noise, which will affect the final matching rate [32].

In the application of crater matching, the invariant $I_{ij}$ is the function value determined by the center coordinates $X_c$ and $Y_c$, the major and minor semi-axes a and b, and the tilt angle $\theta$. If the ellipse parameters deviate greatly, the invariants will also deviate greatly from the true values. A correlation experiment proved that the relationship is nonlinear, that is, when the parameters are closer to the true values, the errors of the invariants are not necessarily smaller. The error is defined as $\Delta I_{ij}=\left|I_{noise}-I_{true}\right|$. $I_{noise}$ represents the invariant calculated from the detected noise parameters, and $I_{true}$ represents the true invariant obtained from the ellipse parameters without noise. If using the fixed $\Delta I_{ij}$ to filter all possible redundant crater pairs, there are the following issues:

(1)

The magnitudes of the invariants calculated by different craters are different;

(2)

Small thresholds filter out less redundancy, but the probability of not being able to filter out the true craters is high;

(3)

The crater sets filtered by a large threshold have a high probability of including the true crater, but the redundancy of the sets is also large.

The aforementioned problems show that the uncertainty caused by the fixed threshold is large, so the dynamic threshold is used instead. The dynamic threshold factor is defined as the ratio of the invariant change to the true value of the invariant, denoted as $factor=\frac{\Delta I_{ij}}{\left|I_{ij}\right|}$. Thus, the dynamic $\Delta I_{ij}$ for each pair of craters is calculated by $\Delta I_{ij}=factor\times \left|I_{ij}\right|$.

The experiment in Figure 5 proves that with certain noise conditions, the dynamic threshold calculated by factor is smaller than the fixed threshold. According to Figure 5b, if the maximum fixed threshold is set to 1200, there will be considerable redundancy, especially when $I_{ij}\in \left(-2000, 0\right)$. If using the dynamic threshold, as shown in Figure 5c, the factor is set to 0.3, and the maximum threshold calculated by the invariant in $I_{ij}\in \left(-2000, 0\right)$ is 600 < 1200. The smaller the value of $\left|I_{ij}\right|$, the smaller the value of $\Delta I_{ij}$, and the fewer the possible crater pairs in the filtered set. In addition, it can be seen from Figure 5d that if the crater is larger, the calculated $\left|I_{ij}\right|$ will be smaller, the obtained search range will also be smaller, and the possible craters will be fewer. In summary, the smaller the absolute value of the invariant, the less suitable it is to use a fixed threshold to filter crater pairs, and it is more suitable to use a dynamic threshold. Therefore, in the recognition experiment, an invariant with a smaller absolute value (large craters) should be selected as much as possible.

A dynamic threshold can not only reduce a considerable amount of redundancy and improve the efficiency of the algorithm, but it can also select the true crater with a large probability to improve the matching rate. According to the aforementioned three problems caused by the fixed threshold, the dynamic threshold effectively solves the first problem, and the second and third problems are comprehensively considered to obtain a suitable dynamic threshold factor. Experiments of dynamic threshold are discussed in Section 3.2.

Based on the invariants $I_{ij}$ and $I_{ji}$ calculated for each pair of craters and the search range calculated by the dynamic threshold factor, the lower and upper search limits of the two groups of invariants, denoted as $mi{n}_{ij}$,$mi{n}_{ji}$ and $ma{x}_{ij}$, $ma{x}_{ji}$, respectively, are calculated as follows:

$$\begin{gathered} mi{n}_{ij}=I_{ij}-\Delta I_{ij}, ma{x}_{ij}=I_{ij}+\Delta I_{ij}, \\ mi{n}_{ji}=I_{ji}-\Delta I_{ji}, ma{x}_{ji}=I_{ji}+\Delta I_{ji}. \end{gathered}$$

(5)

A binary search of all possible crater pairs that satisfy $mi{n}_{ij}\le I_{ij}\le ma{x}_{ij}$ and $mi{n}_{ji}\le I_{ji}\le ma{x}_{ji}$ is performed.

2.2.3. Crater Tuple Construction

There are many crater pairs that meet the search conditions, and all possible crater pairs are filtered based on the pyramid structure. All redundant sets of base tuples of the pyramid need to be found, as shown in Figure 6. The set of crater pairs that have been searched are ij, ik, and jk, and the number of crater pairs contained therein is n(ij), n(jk), and n(ik), respectively. The first step of recognition needs to find three crater pairs $p_1\in ij$, $p_2\in jk$, and $p_3\in ik$, and the condition of the end-to-end connection needs to be satisfied, that is, these crater pairs only have one common navigation crater. If ($p_1$, $p_2$, $p_3$) satisfies the conditions, it can constitute a base tuple of the pyramid, whose set is denoted as ijk.

In general, it takes $n\left(ij\right)\times n\left(jk\right)\times n\left(ik\right)$ comparison operations to search by a traversal combination method in the three sets of ij, ik, and jk, which is time-consuming. To avoid this situation, a simple and fast searching method based on the state table can be used with the table of navigation crater pairs (Table 1 in Figure 3). It searches for qualified ($p_1$, $p_2$, $p_3$) values by setting and judging the state of the navigation crater, as shown in Figure 6. The calculation procedure is detailed in Algorithm 2, and the sequential steps are as follows.

(1)

Set a status flag for each navigation crater in the navigation table and initialize it to ‘0’ before recognition;

(2)

Traverse the set of ij. Set the status of the navigation crater in ij to ‘1’ and record the serial number j of the other crater that forms the crater pair with i;

(3)

Traverse the set of ik. If the status of the corresponding navigation crater is not ‘0’, set the status of the crater to ‘2’ and record the serial number k of the other crater that forms the crater pair with i;

(4)

Traverse the state table. If the status of navigation crater is ‘2’, then judge whether the recorded (j, k) is in set jk, and if so, store it in the tuple set ijk.

Algorithm 2. Tuple searching

Input: three sets of ij, ik, and jk

Output: tuple set ijk 1:    Initialization: initialize the stateTable to 1160 rows and three columns of 2D         vectors, representing state = ‘0’, j, and k. Initialize ijk to an empty list. 2:    for m in ij do: 3:        change the state of m [0] to  ‘1’ 4:        stateTable[m [0]][1] = m [1] 5:        change the state of m [1] to ‘1’ 6:        stateTable[m [1]][1] = m [0]

7:    end for 8:    for n in ik do: 9:          if stateTable[n [0]][0] is not ‘0’ then: 10:            stateTable[n [0]][0] = ‘2’ 11:            stateTable[n [0]][2] = n [1]  12:        end if 13:        if stateTable[n [1]][0] is not ‘0’ then: 14:            stateTable[n [1]][0] = ‘2’ 15:            stateTable[n [1]][2] = n [0]  16:        end if 17:    end for 18:    for crater ‘i’ in stateTable do: 19:        if the state of crater ‘i’ is ‘2’ then: 20:            if all combinations of set j and set k are in jk, then append current tuple to ijk 21:            end if 22:        end if 23:    end for

The efficiency of this algorithm is O(n(ij) + n(ik) + len(navigation craters)), which is proportional to the length of the crater pair set. It also proves that the crater pairs with less redundancy are preferred in the preprocessing step. The ijk set obtained by the tuple recognition algorithm needs to be further filtered by the iterative pyramid algorithm.

2.2.4. Iterative Pyramid Matching

The purpose of the pyramid algorithm is to find the correct recognition in the set of tuples ijk, and this process needs to provide filtering conditions to remove redundant tuples in the set. The pyramid algorithm adds another crater to the base tuple to form a pyramid, which can add three more crater pairs to filter the redundancy, as shown in Figure 7.

The fourth crater can form three crater pairs with the base tuple. The invariants and thresholds are calculated with the same method, and the database is searched to obtain the set of crater pairs il, jl, and kl, as shown in Figure 7. We know that the correct craters i, j, and k must be in the sets il, jl, and kl, respectively, which can be a filtering condition to remove redundant tuples in the set ijk. A pyramid often cannot obtain a unique filtering result, so multiple iterations are needed to select multiple craters l to form a pyramid. The recognition result of crater l can be obtained when filtering the tuple set, but there are often multiple solutions. Thus, when the solution is reduced to only one tuple, the unique tuple and the recognized set of the last crater l are returned. The flow diagram of the iterative pyramid-matching algorithm is shown in Figure 8.

Generally, only running the iterative pyramid algorithm for a set of tuples is likely to filter the redundancy to 0 due to non-navigation craters. Another likely situation is that all possible craters l are traversed, and the algorithm fails to obtain a unique recognition result, so it is necessary to traverse other base tuples ijk and implement the iterative pyramid algorithm to find a unique recognition. Combined with the crater pair filtering algorithm and the iterative pyramid algorithm, the calculation procedure is detailed in Algorithm 3, and the main steps for a sequence image matching are as follows.

(1)

Input the current sequence image and preprocess the crater data. Generate a sorted tuple set to be matched according to the number of redundancies, from small to large;

(2)

Traverse the tuple set. If the redundancy of the current tuple is greater than the limit (set as 20,000), then the image fails to match. If not, a binary search method will be used to form three sets of crater pairs ij, ik, jk;

(3)

Get tuple ijk by the crater tuple construction method;

(4)

Traverse the remaining craters l and get the sets of il, jl, kl by the binary search method. Then, input them to the pyramid algorithm to get the set ijkl. If the tuple set is filtered to only 1, the pyramid algorithm will return the recognized results and the last {l}, and the algorithm ends;

(5)

If the number of ijkl is 0, go back to step (2);

(6)

If the crater l is the last crater in the current image, go back to step (2);

(7)

If the number of matched tuples reaches to the limit (set as 10), the algorithm ends.

Algorithm 3. LIS Recognition

Input: craters in a sequence image, navigation crater database

Output: identified craters 1:    Initialization: all overlapping craters in the image are eliminated, and the matching          crater tuples are sorted by the length of crater pair sets from smallest to largest; the          sorted set is sortTuples   2:    selectedCrater is an empty list to store the selected crater in the image 3:    flag is used to break from the operation and is initialized to 0 4:    num is used for recording the number of tuples and is initialized to 0   5:    max_tuple is the maximum number of matching tuples 6:    for i, j, k in sortTuples do: 7:          num = num + 1

8:          selectedCrater append the i, j, k 9:          binary search ij, ik, and jk in database 10:        search tuple ijk by Algorithm 1 11:        for l in remaining craters do: 12:                if l not in selectedCrater then: 13:                    selectedCrater append the l 14:                    binary search il, jl, and kl in database 15:                    filter ijk by iterative pyramid algorithm to ijkl 16:                    if len(ijkl) == 1 then: 17:                        flag = 1 18:                        break 19:                    end if 20:                    if len(ijkl) == 0 then: 21:                        break 22:                    end if 23:                end if 24:        end for 25:        if flag == 1 then break 26:        end if 27:        if num == max_tuple then break 28:        end if 29:    end for

2.3. Reprojection Validation

As shown in Figure 9, the world coordinate system is ${\mathrm{O}}_{\mathit{xyz}}^w$, and the center of the map is the origin of the world coordinate system. The coordinate system of the lander body is ${\mathrm{O}}_{\mathit{xyz}}^m$, and the camera is fixed on the lander to shoot vertically downward. The camera coordinate system is ${\mathrm{O}}_{\mathit{xyz}}^c$, which can be transformed to the image plane ${\mathrm{O}}_{\mathit{xy}}^{image}$ by a perspective transformation. According to the perspective projection model of the camera, the image coordinates converted from the world coordinate of the crater are denoted as

$$\mathrm{s}\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{\alpha }_x& 0& u_0\\ 0& {\alpha }_y& v_0\\ 0& 0& 1\end{array} \begin{array}{c}0\\ 0\\ 0\end{array}\right]\left[\begin{array}{cc}R& t\\ o^T& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ \begin{array}{c}{Y}_w\\ \begin{array}{c}{Z}_w\\ 1\end{array}\end{array}\end{array}\right]=K\left[R|t\right]P_w,$$

(6)

where K is the camera-internal parameter matrix, R the rotation matrix, t the translation vector, $P_w$ the world coordinate, and (u, v) are the pixel coordinates on the image plane. R and t constitute the pose T.

The crater recognition can estimate the correspondence between the craters observed on the image plane and the craters in the world coordinate system. The LIS recognition algorithm outputs the recognized results of the three craters i, j, and k and the crater l that constitute the last pyramid, as shown in Figure 9. With the 3D coordinates of the four crater centers in the world coordinate system, the 2D coordinates in the image coordinate system, and the camera-internal matrix known, the problem of estimating the transformation matrix from the world coordinate system to the camera coordinate system can be converted into a PNP problem. Because the crater l has multiple solutions, it is necessary to traverse the set l to obtain the pose. At present, the research on solving the PNP problem is very mature. This paper uses the non-linear Levenberg–Marquardt iterative method [41,42] to solve the PNP problem, which has been integrated into the opencv [43] library.

For each possible crater l, it is determined whether it is likely to be in the same field of view with the recognized craters i, j, and k. If possible, then the rotation matrix and translation vector are solved, and all navigation craters are converted to the image coordinate system according to formula (6) to obtain the re-projected image. The crater distances in the re-projected image and the real frame image are compared. If they are close enough, the current pose is correct, that is, the current crater l is correctly recognized. In this paper, the Gaussian angle [31] is used to measure the ellipse distance d, as shown in Equation (7), and the Euclidean distance is not suitable for an ellipse.

$$d\left(p,q\right)=arccos\left\{\frac{4\sqrt{\left|Y_p\right|\left|Y_q\right|}}{\left|Y_p+Y_q\right|}\exp \left[-\frac{1}{2}{\left(y_p-y_q\right)}^T{Y}_p{\left(Y_p+Y_q\right)}^{-1}{Y}_q\left(y_p-y_q\right)\right]\right\}$$

(7)

where p, q represent two ellipses, and $Y_p=\left[\begin{array}{cc}\cos {\theta }_p& -\sin {\theta }_p\\ \sin {\theta }_p& \cos {\theta }_p\end{array}\right]\left[\begin{array}{cc}1/a_p^2& 0\\ 0& 1/b_p^2\end{array}\right]\left[\begin{array}{cc}\cos {\theta }_p& \sin {\theta }_p\\ -\sin {\theta }_p& \cos {\theta }_p\end{array}\right]$, $y_p^T=\left[X_p,Y_p\right]$ is the center coordinate of the ellipse.

The initial inputs of the re-projection validation method are the recognized craters i, j, k and the recognized set {l}. Finally, the algorithm returns the lander pose. The sequential steps of the method are as follows:

(1)

Traverse the set {l}. Obtain the 3D center coordinate set of the craters i, j, k, l in the world coordinate system and the 2D center coordinate set in the image coordinate system. These two point sets are in one-to-one correspondence;

(2)

For each possible crater l, it is determined whether it is likely to be in the same field of view with the recognized craters i, j, and k. If not, go back to step (1);

(3)

Use the non-linear Levenberg–Marquardt iterative method to solve the PNP problem and get the pose T;

(4)

Project all navigation craters to the image plane by formula (6) to get the projected image;

(5)

Calculate the Gaussian angular distance between the projected and the real craters by formula (8) and record it as a 2D matrix dis. The number of rows is the number of real craters, and the number of columns is the number of projected craters;

(6)

If each column in dis has only one value less than or equal to a distance threshold (set to arccos(0.001)), it is considered that the currently recognized I, j, k, l and the calculated pose are correct. If not, go back to step (1).

3. Results

The experiment was conducted using a constructed landing environment, and sequence images and the corresponding pose were collected. Then, an appropriate dynamic threshold factor was selected to search for the set of crater pairs, and finally the crater matching rates at different heights and different sequences were evaluated. Finally, the results were compared with those of other methods under the same conditions. Section 3.1 introduces the construction of the used dataset and simulation environment, while Section 3.2 and Section 3.3 evaluate the crater matching rate and pose error. The processor used in the experiment was an Intel Core i7-10750H, and the amount of RAM was 16 GB.

3.1. Dataset

3.1.1. Select Navigation Craters

At present, many researchers have studied various crater detection methods and established crater datasets of planets such as Mars under the guidance of geographic experts [19,20,21,22]. In this paper, the landing navigation research was carried out based on the Bandeira Mars dataset [22], as shown in Figure A1. This dataset has been used in many studies [37,44], and its map was captured by a high-precision stereo camera on Mars Express. The Bandeira database included a 40 km × 59 km region, covering an area of 2360${ \mathrm{km}}^2$, located between Mars −47.66′E/−48.68′E and North latitude 7.28′N/7.95′N. This area contained a huge number of craters. There are a total of 3050 craters in the database, with radii between 20 and 5000 m. The number and sizes of the craters in the dataset were analyzed, as shown in Figure 10. Most of the craters had small radii. There were only 20 large craters with radii greater than 40 pixels, and 947 craters had radii of less than 6 pixels.

An appropriate number of navigation craters in the Bandeira database were selected. Large craters were prioritized. Thus, it was necessary to eliminate small craters as much as possible and retain large craters as navigation craters. In the Bandeira dataset, small craters (the red craters in Figure 11) were proposed, and there were 1263 remaining craters. Then, according to the “non-overlapping” principle, the overlapping craters (the green craters in Figure 11) were removed, and finally 1160 craters remained (the blue craters in Figure 11). Our database contained 111,133 crater pairs that were generated in the FOV.

3.1.2. Collecting Landing Data

In this paper, a simulation platform was used to collect the landing and descent sequence data, including a total of 12,160 sequence images and the pose corresponding to each frame image. The simulation platform was based on a Linux system and included three components: A Gazebo physical simulation platform, a Robotic Operating System (ROS), and PX4 aircraft firmware in the ROS system. The control program interacted with the Gazebo world through the Mavlink protocol. The aircraft was equipped with a monocular camera, which could obtain the pose information of the aircraft and output images in real time.

Based on the landing parameters of Perseverance [45], the height of the TRN was 2–4.2 km, the camera FOV was set to 90°, and the image size was set to 1024 × 1024 pixels. Because different numbers of navigation craters in the descent area affected the matching rate, we collected different sequences in different areas from sparse to dense. The craters in the descending area of sequence 1 were the sparsest, and the craters in the descending area of sequence 5 were the densest.

The transformation matrix from the body coordinate system ${\mathrm{O}}_{xyz}^m$ to the camera coordinate system ${\mathrm{O}}_{xyz}^c$ in the simulation environment is denoted as $T_{cm}$, and the camera-internal parameter is K. These are defined as follows:

$$T_{\mathit{cm}}=\left[\begin{array}{c}0\\ \begin{array}{c}-1\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array} \begin{array}{c}-1\\ \begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array} \begin{array}{c}0\\ \begin{array}{c}0\\ \begin{array}{c}-1\\ 0\end{array}\end{array}\end{array} \begin{array}{c}0\\ \begin{array}{c}0\\ \begin{array}{c}0\\ -1\end{array}\end{array}\end{array}\right],K=\left[\begin{array}{ccc}512.4& 0& 512\\ 0& 512.4& 512\\ 0& 0& 1\end{array}\right].$$

(8)

We used the ROS system to send flight instructions, and then the aircraft flew after receiving the message and output the captured image. At the same time, it accepted the real attitude $T_{mw}$ of the aircraft sent by Gazebo and collected the descending sequence images. The true ellipse value of the crater in each image was obtained as follows:

$$\left[\begin{array}{c}{u}_{img}\\ v_{img}\end{array}\right]=K\cdot T_{cm}\cdot T_{mw}\cdot \left[\begin{array}{c}{X}_w\\ \begin{array}{c}{Y}_w\\ \begin{array}{c}{Z}_w\\ 1\end{array}\end{array}\end{array}\right].$$

(9)

Several points were selected on the crater edge in the world coordinate system, converted to the image coordinate system through formula (9), and an ellipse was fit. Solving for the pose was just the inverse of the aforementioned process, which required the image coordinates of the crater and the actual world coordinates.

3.2. Dynamic Threshold Experiment

According to Section 2.2.2, an appropriate dynamic threshold factor needed to be selected. If the selected threshold factor were too large, the number of redundant crater pairs would increase, and the matching rate and recognition efficiency would be reduced.

Different Gaussian noise was added to the major and minor semi-axes a and b, the inclination angle $\theta$, and the coordinates of the center point x and y [46]. Crater pairs were randomly selected, and $\frac{\Delta I_{ij}}{I_{ij}}$ was calculated, as shown in Figure 12, Figure 13 and Figure 14. The a and b axes of different craters were quite different, so the added noise of the axes could not be fixed. On the one hand, considering the ellipse detection algorithm, the radius of the elliptical crater detected by the traditional method was much less than 5% of the true value [47]. The a and b axes of the ellipse detected by a deep learning method were 10.3% of the true value [48]. Other studies generally added 5% Gaussian noise or less to the axes of the ellipse [30]. On the other hand, other crater-based recognition methods [32] usually add N(0,1) Gaussian noise to x and y and add a mean noise below 10° to $\theta$. Thus, a reasonable but strict condition of the noise was set in this study: ${\sigma }_{a,b}\le 10$% and ${\sigma }_{\theta }\le 10°,{ \sigma }_{x,y}\le 2$.

Figure 12, Figure 13 and Figure 14 show the distributions of $\frac{{\mathsf{\Delta }I}_{\mathrm{ij}}}{I_{ij}}$ for different ${\sigma }_{a,b}$, ${\sigma }_{\theta }$, and ${\sigma }_{x,y}$ values, respectively. It can be seen that the noise of the major and minor axes of the ellipse had a greater impact on the invariant than the other ellipse parameters.

In this paper, the factor of 0.3 was selected. As shown by the red lines in Figure 15, 0.3 could capture most of the points. For all the sequence images, the matching rate was the proportion of images whose poses were solved correctly in all sequence images. However, beyond a certain limit, a larger factor will not have a larger matching rate, as shown in Figure 15. The larger the dynamic threshold, the more redundant the matching. In this case, the number of non-navigation craters increased, the matching rate decreased, and the processing time also greatly increased. Considering the matching rate and efficiency comprehensively, the dynamic threshold factor was reasonably chosen as 0.3.

The experiment compared the crater recognition results of a dynamic threshold and a fixed threshold. As shown in Figure 16, fixed thresholds of 40, 50, 60, and 70 were selected to compare the matching rates under different noise conditions (Figure 16a,c,e) and the average processing time per frame (Figure 16b,d,f). It can be seen that the smaller the fixed threshold, the lower the matching rate, and the larger the fixed threshold, the slower the speed. Compared with the fixed threshold, the dynamic threshold improved the matching rate by at least 10%, and the average processing speed was increased by 40%. This again demonstrated the effectiveness of the dynamic threshold.

3.3. Matching Results

Under different noise conditions, the matching rates of different sequences were calculated, as shown in Figure 17. The matching rate of sequence 1 was always the smallest, while the matching rate of sequence 5 was the highest. The main reason was the density of the navigation craters. The navigation craters in the descending area of sequence 1 were sparse, while the navigation craters in the descending area of sequence 5 were dense.

In addition, the noise of $\theta$ had less impact on the matching rate, and the noise of a and b had a greater impact on the matching rate. The indirect reason was that a and b had a greater impact on $\frac{\mathsf{\Delta }{I}_{ij}}{I_{\mathit{ij}}}$. Except for sequence 1, other sequences still had a matching rate of more than 80% under different noise conditions of $\theta$, $x$, and $y$ when ${\sigma }_{a,b}\le 5\%$. The matching rate in our method had a strong robustness to noise.

For the actual situation of landing navigation, LIS recognition is used for the initialization process of pose estimation. In the subsequent process, when the initial pose is known, tracking recognition is used for relative navigation. Once the tracking is lost, initialization is performed again to obtain the estimated value of the attitude. Therefore, the matching rates of all the sequences with different heights under different noise conditions were analyzed, as shown in Figure 18.

When fewer than three craters were observed, the matching method failed, so when the altitude range was [2–2.5] km, the matching rate decreased. When ${\sigma }_{a,b}\le 5\%$, the matching rates of other height ranges were maintained at 80% and above, which proved that after observing at least three craters, the probability of normally initializing and obtaining the pose at each height was >80%.

Compared with the matching rates obtained by other LIS recognition methods, our method had outstanding advantages, as shown in Table 1. N(0,1) means that the parameter followed a Gaussian distribution with mean value of 0 and variance of 1. u(−10, 10) means that the parameter followed a uniform distribution from −10 to 10. Under the same noise, the matching rate of the iterative pyramid algorithm was greatly improved compared with Park’s method [30] and Doppenberg’s method [32]. With the noise of a, b~N(0,1), x, y~N(0, 0.5), and $\theta$~N(0,5), the iterative pyramid algorithm with a threshold factor of 0.3 could achieve a matching rate of 89.67% >> 41.70%. When the noise was set to two times the original, the matching rate obtained by the iterative pyramid algorithm decreased, but it still reached 86.29%.

Under the noise of a, b~N(0,1), x, y~N(0,1), and $\theta$~u(−10,10), the iterative pyramid algorithm with a threshold factor of 0.3 reached a matching rate of 86.99%. When the noise was set to two times the original, the matching rate obtained by our method was 79.93%, which was much higher than that obtained by Doppenberg’s method. At the same time, the matching rate of the iterative pyramid algorithm with a threshold factor of 0.4 was tested with the same noise conditions. Compared with the matching rate for a threshold factor of 0.3, the matching rate with a factor of 0.4 was lower, but it was still higher than that of the first two methods, even with stricter noise conditions, which further confirmed the effectiveness and robustness of the dynamic threshold and iterative pyramid algorithm.

Based on the recognized craters, the pose was obtained by solving the PNP problem and using the ellipse center coordinates. Figure 19 shows the influence of different ${\sigma }_{\theta }$, ${\sigma }_{a,b}$, and ${\sigma }_{x,y}$ on the error of the pose. Overall, the accuracy of the estimated pose was high, and the angle errors were less than about 2°.

${\left[t_1,t_2,t_3\right]}^T$ represents the position coordinates of the lander in the world coordinate system, and Figure 20 shows the influence of ${\sigma }_{\theta }$, ${\sigma }_{a,b}$, and ${\sigma }_{x,y}$ on the position error. The distance $\sqrt{t_1^2+t_2^2+t_3^2}$ was calculated with different amounts of noise, which showed that the maximum distance error was 44 m, and the minimum error was 20 m.

In 2020, the Tianwen-1 lander used image matching for landing [49]. Under the guidance of the initial pose, the final attitude error of the lander was 2°, and the position error was estimated to be about 100 m. In the same year, NASA used an inertial measurement unit (IMU) and vision-aided technology for track navigation in the Mars 2020 lander vision system field test, whose landing error was 40 m [9]. In this paper, with more severe navigation conditions, that is, only relying on visual information and without any initial attitude, the measured attitude error was 2° and the position error was 44 m, which provides a robust and accurate initial position for subsequent tracking and navigation. This further proved the robustness of the crater recognition method in this paper.

For each sequence image, the time complexity of the program mainly comes from two parts. The first is the algorithm to find the crater tuples to be matched, including the pair-searching algorithm and the tuple-searching algorithm. The time complexity of searching the database by binary method is O(log(n)), and the time complexity of obtaining the tuple set by the tuple-searching algorithm is O(n(ij) + n(ik) + length(naviCraters)), which is proportional to the length of the crater pair set. The second is the pyramid algorithm to filter tuple redundancy, and the time complexity is O(n(ijk)), which is proportional to the length of the tuple. So, the total time complexity is O(log(n)) + O(n(ij) + n(ik) + length(naviCraters)) + O(n(ijk)). The average LIS recognition time per frame is 2.555 s from the experiment.

4. Discussion

In the field of deep space exploration, crater-based landing navigation algorithms are required to provide an accurate and fast initial attitude estimation result for an LIS scenario. Pose estimation is related to the recognition algorithm, so the recognition algorithm and the pose estimation algorithm must be considered a whole, and the recognition result needs to be verified by estimating the pose using a re-projection method. When the detection error of the major and minor axes of the ellipse reached 5%, the detection error of the center point reached 1 pixel, and the tilt angle error reached 5°. Figure 17 and Figure 18 show that the LIS matching rate on the iterative pyramid algorithm could still reach >80% after re-projection verification. The estimated attitude error in the simulation environment was less than 2°, and the position error was less than 44 m, which showed that the method was robust and accurate.

The dynamic threshold was designed to solve the problem that the projective invariants were greatly disturbed by noise. Figure 16 shows that compared with the fixed threshold, the dynamic threshold could improve the matching rate by at least 10%, and the average processing speed was increased by 40%, which proved the effectiveness of the dynamic threshold. In addition, this paper mainly solves the problem of the initial pose estimation for LIS scenarios. Determining how to use the obtained initial pose for tracking navigation and how to use fuse other sensors to improve the navigation accuracy and design a long-term, stable, and real-time pose estimation algorithm deserves further attention.

5. Conclusions

This paper introduces the known crater recognition methods and proposes a crater LIS recognition method based on an iterative pyramid algorithm for absolute pose estimation. It is mainly divided into three parts. First, navigation craters are selected from the craters in the selected map to establish a small-capacity and high-efficiency crater database, and the serial numbers and projective invariants of the crater pair are stored. Second, based on the iterative pyramid algorithm, the detected craters are matched with the craters in the database, and four craters are recognized. Finally, four pairs of 3D–2D points can constitute the PNP problem. For the case of the fourth crater with multiple solutions, the estimated pose is obtained by iteratively traversing all possible craters, and then all navigation craters are re-projected for verification. The pose is considered correct if the craters in the current image and the re-projected image are very close.

Through experimental analysis, this paper effectively solved the problem that the projective invariant is sensitive to noise, and a matching rate of >80% was achieved based on a dynamic threshold and the iterative pyramid algorithm. The estimated attitude error in the simulation environment was less than 2°, and the position error was less than 44 m. Compared with the fixed threshold, the dynamic threshold could improve the matching rate by at least 10% and the average processing speed by 40%, providing a fast, accurate, and robust initial pose for subsequent tracking navigation.