Snowfall Microphysics Characterized by PARSIVEL Disdrometer Observations in Beijing from 2020 to 2022
Abstract
1. Introduction
2. Data and Methods
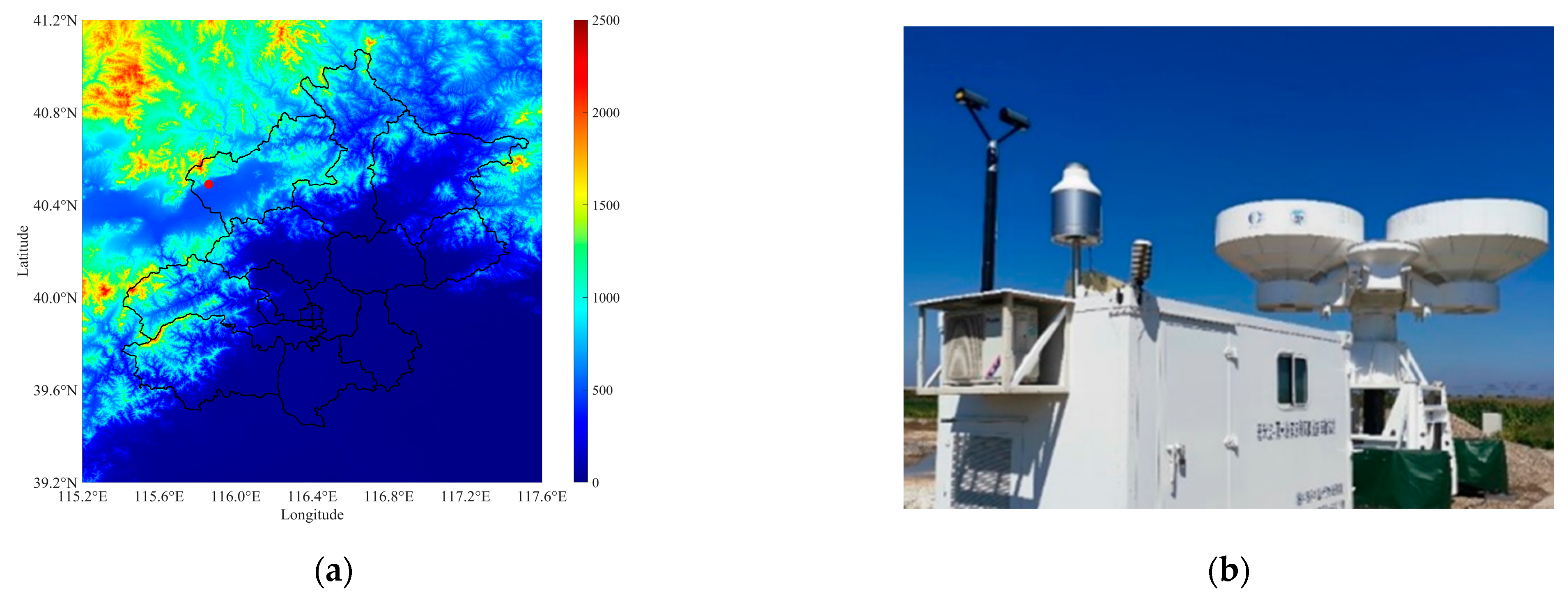
2.1. Observation Experiment and Instrumentation
2.2. Data Set
2.3. Calculation of Microphysical Properties of Snowfall Particles
2.3.1. Snow PSD
2.3.2. Snow Density and Intensity
2.3.3. Quantitative Estimation of Snow
3. Results
3.1. Characteristics of Snow PSD
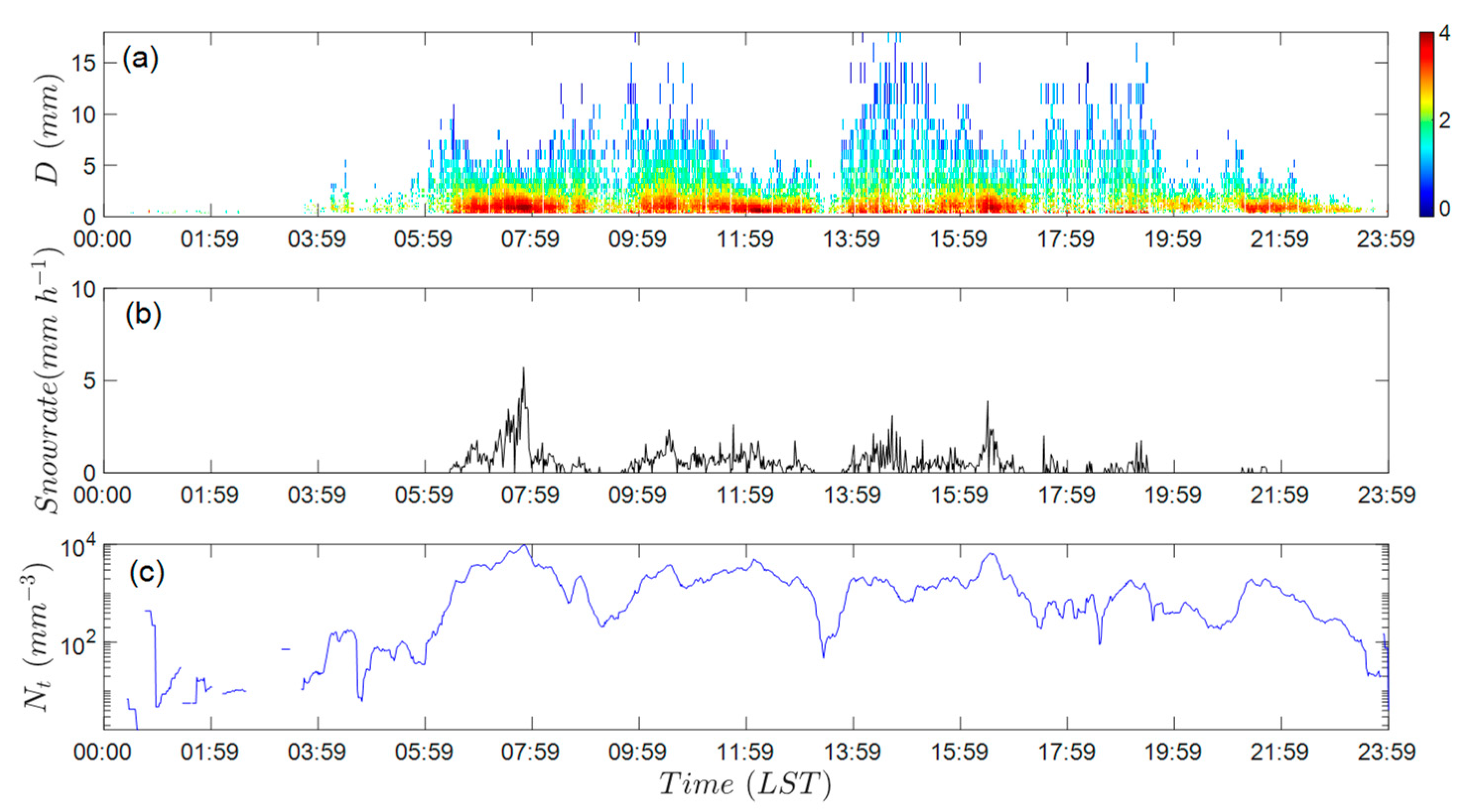
3.2. Time Series Characteristics of Snow PSD
3.3. Relationship between and of Different
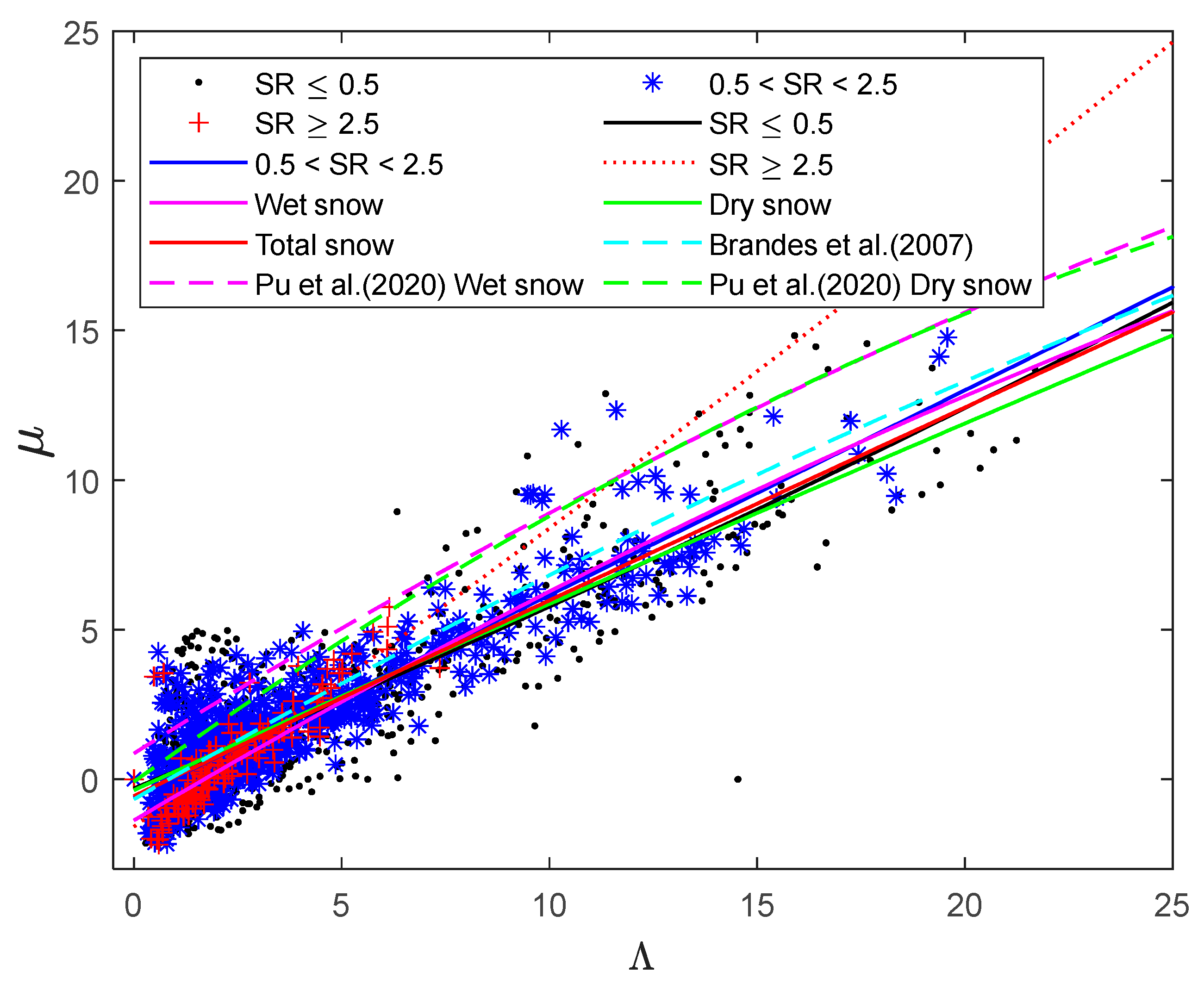
3.4. μ−Λ Relationship of Different
3.5. Snowfall and Snow Density
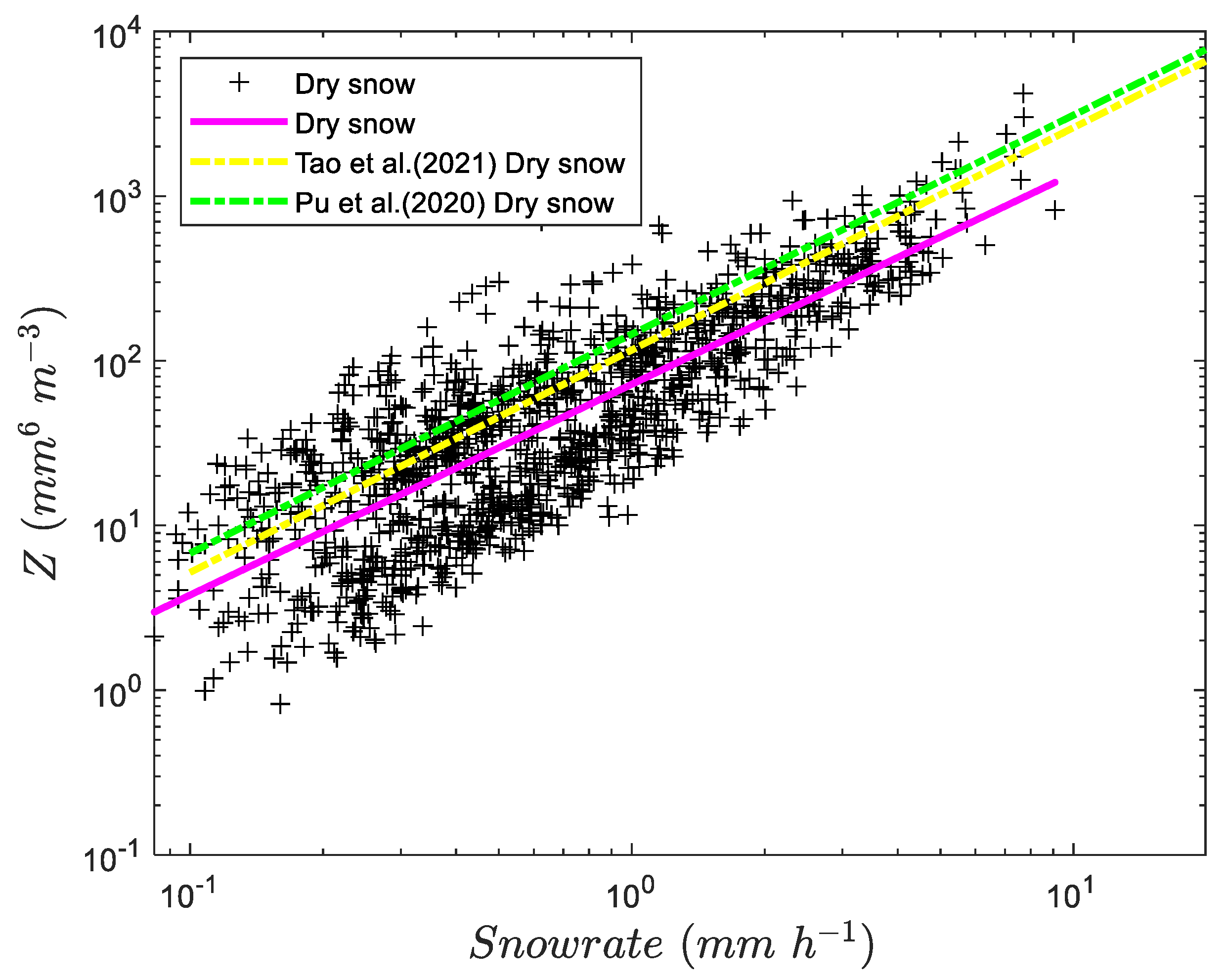
3.6. Ze−SR Relationship
3.7. Terminal Velocity for Different
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, Z.; Deng, G.; Hu, G.; Zhang, H.; Pan, H.; Sang, G. Satellite Observed Spatiotemporal Variability of Snow Cover and Snow Phenology over High Mountain Asia from 2002 to 2021. J. Hydrol. 2022, 613, 128438. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, X.; Deng, G.; Wang, X.; Jiang, Z.; Sang, G. Spatiotemporal Variation of Snowline Altitude at the End of Melting Season across High Mountain Asia, Using MODIS Snow Cover Product. Adv. Sp. Res. 2020, 66, 2629–2645. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Hudak, D.; Petersen, W.; Nesbitt, S.W.; Chandrasekar, V.; Durden, S.; Gleicher, K.J.; Huang, G.J.; Joe, P.; Kollias, P.; et al. Global Precipitation Measurement Cold Season Precipitation Experiment (GCPEX): For Measurement’s Sake, Let It Snow. Bull. Am. Meteorol. Soc. 2015, 96, 1719–1741. [Google Scholar] [CrossRef]
- Kulie, M.S.; Pettersen, C.; Merrelli, A.J.; Wagner, T.J.; Wood, N.B.; Dutter, M.; Beachler, D.; Kluber, T.; Turner, R.; Mateling, M.; et al. Snowfall in the Northern Great Lakes: Lessons Learned from a Multisensor Observatory. Bull. Am. Meteorol. Soc. 2021, 102, E1317–E1339. [Google Scholar] [CrossRef]
- Schirle, C.E.; Cooper, S.J.; Wolff, M.A.; Pettersen, C.; Wood, N.B.; L’ecuyer, T.S.; Ilmo, T.; Nygård, K. Estimation of Snowfall Properties at a Mountainous Site in Norway Using Combined Radar and in Situ Microphysical Observations. J. Appl. Meteorol. Climatol. 2019, 58, 1337–1352. [Google Scholar] [CrossRef]
- Bracci, A.; Baldini, L.; Roberto, N.; Adirosi, E.; Montopoli, M.; Scarchilli, C.; Grigioni, P.; Ciardini, V.; Levizzani, V.; Porcù, F. Quantitative Precipitation Estimation over Antarctica Using Different Ze-Sr Relationships Based on Snowfall Classification Combining Ground Observations. Remote Sens. 2022, 14, 82. [Google Scholar] [CrossRef]
- Lubin, D.; Zhang, D.; Silber, I.; Scott, R.C.; Kalogeras, P.; Battaglia, A.; Bromwich, D.H.; Cadeddu, M.; Eloranta, E.; Fridlind, A.; et al. The Atmospheric Radiation Measurement (ARM) West Antarctic Radiation Experiment. Bull. Am. Meteorol. Soc. 2020, 101, E1069–E1091. [Google Scholar] [CrossRef]
- Houze, R.A.; McMurdie, L.A.; Petersen, W.A.; Schwall Er, M.R.; Baccus, W.; Lundquist, J.D.; Mass, C.F.; Nijssen, B.; Rutledge, S.A.; Hudak, D.R.; et al. The Olympic Mountains Experiment (Olympex). Bull. Am. Meteorol. Soc. 2017, 98, 2167–2188. [Google Scholar] [CrossRef]
- Petäjä, T.; O’Connor, E.J.; Moisseev, D.; Sinclair, V.A.; Manninen, A.J.; Väänänen, R.; Von Lerber, A.; Thornton, J.A.; Nicoll, K.; Petersen, W.; et al. A Field Campaign to Elucidate the Impact of Biogenic Aerosols on Clouds and Climate. Bull. Am. Meteorol. Soc. 2016, 97, 1909–1928. [Google Scholar] [CrossRef]
- Löhnert, U.; Kneifel, S.; Battaglia, A.; Hagen, M.; Hirsch, L.; Crewell, S. A Multisensor Approach toward a Better Understanding of Snowfall Microphysics the Tosca Project. Bull. Am. Meteorol. Soc. 2011, 92, 613–628. [Google Scholar] [CrossRef]
- Li, H.; Moisseev, D.; von Lerber, A. How Does Riming Affect Dual-Polarization Radar Observations and Snowflake Shape? J. Geophys. Res. Atmos. 2018, 123, 6070–6081. [Google Scholar] [CrossRef]
- Li, H.; Korolev, A.; Moisseev, D. Supercooled Liquid Water and Secondary Ice Production in Kelvin-Helmholtz Instability as Revealed by Radar Doppler Spectra Observations. Atmos. Chem. Phys. 2021, 21, 13593–13608. [Google Scholar] [CrossRef]
- Li, H.; Möhler, O.; Petäjä, T.; Moisseev, D. Two-Year Statistics of Columnar-Ice Production in Stratiform Clouds over Hyytiälä, Finland: Environmental Conditions and the Relevance to Secondary Ice Production. Atmos. Chem. Phys. 2021, 21, 14671–14686. [Google Scholar] [CrossRef]
- Li, H.; Moisseev, D. Melting Layer Attenuation at Ka- and W-Bands as Derived From Multifrequency Radar Doppler Spectra Observations. J. Geophys. Res. Atmos. 2019, 124, 9520–9533. [Google Scholar] [CrossRef]
- Li, H.; Moisseev, D. Two Layers of Melting Ice Particles Within a Single Radar Bright Band: Interpretation and Implications. Geophys. Res. Lett. 2020, 47, 1–10. [Google Scholar] [CrossRef]
- Li, H.; Tiira, J.; Von Lerber, A.; Moisseev, D. Towards the Connection between Snow Microphysics and Melting Layer: Insights from Multifrequency and Dual-Polarization Radar Observations during BAECC. Atmos. Chem. Phys. 2020, 20, 9547–9562. [Google Scholar] [CrossRef]
- Mason, S.L.; Chiu, C.J.; Hogan, R.J.; Moisseev, D.; Kneifel, S. Retrievals of Riming and Snow Density From Vertically Pointing Doppler Radars. J. Geophys. Res. Atmos. 2018, 123, 13807–13834. [Google Scholar] [CrossRef]
- Mason, S.; Hogan, R.; Westbrook, C.; Kneifel, S.; Moisseev, D. The Importance of Particle Size Distribution Shape for Triple-Frequency Radar Retrievals of the Morphology of Snow. Atmos. Meas. Tech. 2019, 12, 4993–5018. [Google Scholar] [CrossRef]
- Kneifel, S.; Von Lerber, A.; Tiira, J.; Moisseev, D.; Kollias, P.; Leinonen, J. Observed Relations between Snowfall Microphysics and Triple-Frequency Radar Measurements. J. Geophys. Res. 2015, 120, 6034–6055. [Google Scholar] [CrossRef]
- Leinonen, J.; Moisseev, D. What Do Triple-Frequency Radar Signatures Reveal about Aggregate Snowflakes? J. Geophys. Res. 2015, 120, 229–239. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Engdahl, B.J.K.; Nygaard, B.E.K.; Losnedal, V.; Thompson, G.; Bengtsson, L. Effects of the ICE-T Microphysics Scheme in HARMONIE-AROME on Estimated Ice Loads on Transmission Lines. Cold Reg. Sci. Technol. 2020, 179, 103139. [Google Scholar] [CrossRef]
- Lin, Y.-L.; Farley, R.D.; Orville, H.D. Bulk Parameterization of the Snow Field in a Cloud Model. J. Appl. Meteorol. Climatol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Morrison, H.; Thompson, G.; Tatarskii, V. Impact of Cloud Microphysics on the Development of Trailing Stratiform Precipitation in a Simulated Squall Line: Comparison of One- and Two-Moment Schemes. Mon. Weather Rev. 2009, 137, 991–1007. [Google Scholar] [CrossRef]
- Liu, C.; Ikeda, K.; Thompson, G.; Rasmussen, R.; Dudhia, J. High-Resolution Simulations of Wintertime Precipitation in the Colorado Headwaters Region: Sensitivity to Physics Parameterizations. Mon. Weather Rev. 2011, 139, 3533–3553. [Google Scholar] [CrossRef]
- Adirosi, E.; Baldini, L.; Roberto, N.; Gatlin, P.; Tokay, A. Improvement of Vertical Profiles of Raindrop Size Distribution from Micro Rain Radar Using 2D Video Disdrometer Measurements. Atmos. Res. 2016, 169, 404–415. [Google Scholar] [CrossRef]
- Brawn, D.; Upton, G. Estimation of an Atmospheric Gamma Drop Size Distribution Using Disdrometer Data. Atmos. Res. 2008, 87, 66–79. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, L.; Yang, D.; Xiao, Y.; Zhang, L.; Qiao, Y. Analysis of Raindrop Size Distribution Characteristics in Permafrost Regions of the Qinghai-Tibet Plateau Based on New Quality Control Scheme. Water 2019, 11, 2265. [Google Scholar] [CrossRef]
- Marzano, F.S.; Cimini, D.; Montopoli, M. Investigating Precipitation Microphysics Using Ground-Based Microwave Remote Sensors and Disdrometer Data. Atmos. Res. 2010, 97, 583–600. [Google Scholar] [CrossRef]
- Park, S.G.; Kim, H.L.; Ham, Y.W.; Jung, S.H. Comparative Evaluation of the OTT PARSIVEL2 Using a Collocated Two-Dimensional Video Disdrometer. J. Atmos. Ocean. Technol. 2017, 34, 2059–2082. [Google Scholar] [CrossRef]
- Raupach, T.H.; Berne, A. Correction of Raindrop Size Distributions Measured by Parsivel Disdrometers, Using a Two-Dimensional Video Disdrometer as a Reference. Atmos. Meas. Tech. 2015, 8, 343–365. [Google Scholar] [CrossRef]
- Thurai, M.; Petersen, W.A.; Tokay, A.; Schultz, C.; Gatlin, P. Drop Size Distribution Comparisons between Parsivel and 2-D Video Disdrometers. Adv. Geosci. 2011, 30, 3–9. [Google Scholar] [CrossRef]
- Tokay, A.; Petersen, W.A.; Gatlin, P.; Wingo, M. Comparison of Raindrop Size Distribution Measurements by Collocated Disdrometers. J. Atmos. Ocean. Technol. 2013, 30, 1672–1690. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural Variations in the Analytical Form of the Raindrop Size Distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Zhang, G.; Sun, J.; Brandes, E.A. Improving Parameterization of Rain Microphysics with Disdrometer and Radar Observations. J. Atmos. Sci. 2006, 63, 1273–1290. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop Size Distribution in Different Climatic Regimes from Disdrometer and Dual-Polarized Radar Analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Cao, Q.; Zhang, G. Errors in Estimating Raindrop Size Distribution Parameters Employing Disdrometer and Simulated Raindrop Spectra. J. Appl. Meteorol. Climatol. 2009, 48, 406–425. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, K.; Wen, L.; Wang, M.; Huang, H.; Wang, M.; Yang, Z.; Zhang, G.; Zhang, P.; Lee, W.C. Microphysical Characteristics of Three Convective Events with Intense Rainfall Observed by Polarimetric Radar and Disdrometer in Eastern China. Remote Sens. 2019, 11, 2004. [Google Scholar] [CrossRef]
- Ji, L.; Chen, H.; Li, L.; Chen, B.; Xiao, X.; Chen, M.; Zhang, G. Raindrop Size Distributions and Rain Characteristics Observed by a PARSIVEL Disdrometer in Beijing, Northern China. Remote Sens. 2019, 11, 1479. [Google Scholar] [CrossRef]
- Kim, H.-J.; Jung, W.; Suh, S.-H.; Lee, D.-I.; You, C.-H. The Characteristics of Raindrop Size Distribution at Windward and Leeward Side over Mountain Area. Remote Sens. 2022, 14, 2419. [Google Scholar] [CrossRef]
- Loh, J.L.; Lee, D.I.; Kang, M.Y.; You, C.H. Classification of Rainfall Types Using Parsivel Disdrometer and S-Band Polarimetric Radar in Central Korea. Remote Sens. 2020, 12, 642. [Google Scholar] [CrossRef]
- Luo, L.; Guo, J.; Chen, H.; Yang, M.; Chen, M.; Xiao, H.; Ma, J.; Li, S. Microphysical Characteristics of Rainfall Observed by a 2dvd Disdrometer during Different Seasons in Beijing, China. Remote Sens. 2021, 13, 2303. [Google Scholar] [CrossRef]
- Luo, L.; Xiao, H.; Yang, H.; Chen, H.; Guo, J.; Sun, Y.; Feng, L. Raindrop Size Distribution and Microphysical Characteristics of a Great Rainstorm in 2016 in Beijing, China. Atmos. Res. 2020, 239, 104895. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; Beguería, S.; Latorre, B.; Fernández-Raga, M. Comparison of Precipitation Measurements by OTT Parsivel2 and Thies LPM Optical Disdrometers. Hydrol. Earth Syst. Sci. 2018, 22, 2811–2837. [Google Scholar] [CrossRef]
- Kruger, A.; Krajewski, W.F. Two-Dimensional Video Disdrometer: A Description. J. Atmos. Ocean. Technol. 2002, 19, 602–617. [Google Scholar] [CrossRef]
- Brandes, E.A.; Ikeda, K.; Zhang, G.; Schönhuber, M.; Rasmussen, R.M. A Statistical and Physical Description of Hydrometeor Distributions in Colorado Snowstorms Using a Video Disdrometer. J. Appl. Meteorol. Climatol. 2007, 46, 634–650. [Google Scholar] [CrossRef]
- Battaglia, A.; Rustemeier, E.; Tokay, A.; Blahak, U.; Simmer, C. PARSIVEL Snow Observations: A Critical Assessment. J. Atmos. Ocean. Technol. 2010, 27, 333–344. [Google Scholar] [CrossRef]
- Zhang, G.; Luchs, S.; Ryzhkov, A.; Xue, M.; Ryzhkova, L.; Cao, Q. Winter Precipitation Microphysics Characterized by Polarimetric Radar and Video Disdrometer Observations in Central Oklahoma. J. Appl. Meteorol. Climatol. 2011, 50, 1558–1570. [Google Scholar] [CrossRef]
- Huang, G.J.; Bringi, V.N.; Moisseev, D.; Petersen, W.A.; Bliven, L.; Hudak, D. Use of 2D-Video Disdrometer to Derive Mean Density-Size and Ze-SR Relations: Four Snow Cases from the Light Precipitation Validation Experiment. Atmos. Res. 2015, 153, 34–48. [Google Scholar] [CrossRef]
- Lee, J.E.; Jung, S.H.; Park, H.M.; Kwon, S.; Lin, P.L.; Lee, G.W. Classification of Precipitation Types Using Fall Velocity-Diameter Relationships from 2D-Video Distrometer Measurements. Adv. Atmos. Sci. 2015, 32, 1277–1290. [Google Scholar] [CrossRef]
- Wen, G.; Xiao, H.; Yang, H.; Bi, Y.; Xu, W. Characteristics of Summer and Winter Precipitation over Northern China. Atmos. Res. 2017, 197, 390–406. [Google Scholar] [CrossRef]
- Jia, X.; Liu, Y.; Ding, D.; Ma, X.; Chen, Y.; Bi, K.; Tian, P.; Lu, C.; Quan, J. Combining Disdrometer, Microscopic Photography, and Cloud Radar to Study Distributions of Hydrometeor Types, Size and Fall Velocity. Atmos. Res. 2019, 228, 176–185. [Google Scholar] [CrossRef]
- Yu, T.; Chandrasekar, V.; Xiao, H.; Joshil, S.S. Characteristics of Snow Particle Size Distribution in the Pyeongchang Region of South Korea. Atmosphere 2020, 11, 1093. [Google Scholar] [CrossRef]
- Pu, K.; Liu, X.; He, H.; Sun, Y.; Hu, S.; Wu, Y. Microphysical Characteristics of Winter Precipitation in Eastern China from 2014 to 2019. Water 2020, 12, 920. [Google Scholar] [CrossRef]
- Tao, R.; Zhao, K.; Huang, H.; Wen, L.; Zhang, G.; Zhou, A.; Chen, H. Snow Particle Size Distribution from a 2-D Video Disdrometer and Radar Snowfall Estimation in East China. IEEE Trans. Geosci. Remote Sens. 2021, 59, 196–207. [Google Scholar] [CrossRef]
- OTT Hydromet GmbH. Operating Instructions Present Weather Sensor OTT Parsivel2. 2016, 52. Available online: https://www.ott.com/download/operating-instructions-present-weather-sensor-ott-parsivel2-with-screen-heating-1/ (accessed on 20 November 2022).
- Löffler-Mang, M.; Blahak, U. Estimation of the Equivalent Radar Reflectivity Factor from Measured Snow Size Spectra. J. Appl. Meteorol. 2001, 40, 843–849. [Google Scholar] [CrossRef]
- Sekhon, R.S.; Srivastava, R.C. Snow Size Spectra and Radar Reflectivity. J. Atmos. Sci. 1970, 27, 299–307. [Google Scholar] [CrossRef]
- Marshall, J.S.; Gunn, K.L.S. Measurement Of Snow Parameters By Radar. J. Atmos. Sci. 1952, 9, 322–327. [Google Scholar] [CrossRef]
- Fujiyoshi, Y.; Endoh, T.; Yamada, T.; Tsuboki, K.; Tachibana, Y.; Wakahama, G. Determination of a Z-R Relationship for Snowfall Using a Radar and High Sensitivity Snow Gauges. J. Appl. Meteorol. 1990, 29, 147–152. [Google Scholar] [CrossRef]
- Matrosov, S.Y. Assessment of Radar Signal Attenuation Caused by the Melting Hydrometeor Layer. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1039–1047. [Google Scholar] [CrossRef]
- Locatelli, J.D.; Hobbs, P.V. Fall Speeds and Masses of Solid Precipitation Particles. J. Geophys. Res. 1974, 79, 2185–2197. [Google Scholar] [CrossRef]
- Yuter, S.E.; Kingsmill, D.E.; Nance, L.B.; Löffler-Mang, M. Observations of Precipitation Size and Fall Speed Characteristics within Coexisting Rain and Wet Snow. J. Appl. Meteorol. Climatol. 2006, 45, 1450–1464. [Google Scholar] [CrossRef]
- Gunn, R.; Kinzer, G.D. The Terminal Velocity of Fall for Water Droplets in Stagnant Air. J. Meteorol. 1949, 6, 243–248. [Google Scholar] [CrossRef]
- Mitchell, D.L. Use of Mass-and Area-Dimensional Power Laws for Determining Precipitation Particle Terminal Velocities. J. Atmos. Sci. 1996, 53, 1710–1723. [Google Scholar] [CrossRef]
- Fehlmann, M.; Rohrer, M.; Von Lerber, A.; Stoffel, M. Automated Precipitation Monitoring with the Thies Disdrometer: Biases and Ways for Improvement. Atmos. Meas. Tech. 2020, 13, 4683–4698. [Google Scholar] [CrossRef]
- Magono, C.; Nakamura, T. Aerodynamic Studies of Falling Snowflakes. J. Meteorol. Soc. Japan. Ser. II 1965, 43, 139–147. [Google Scholar] [CrossRef]

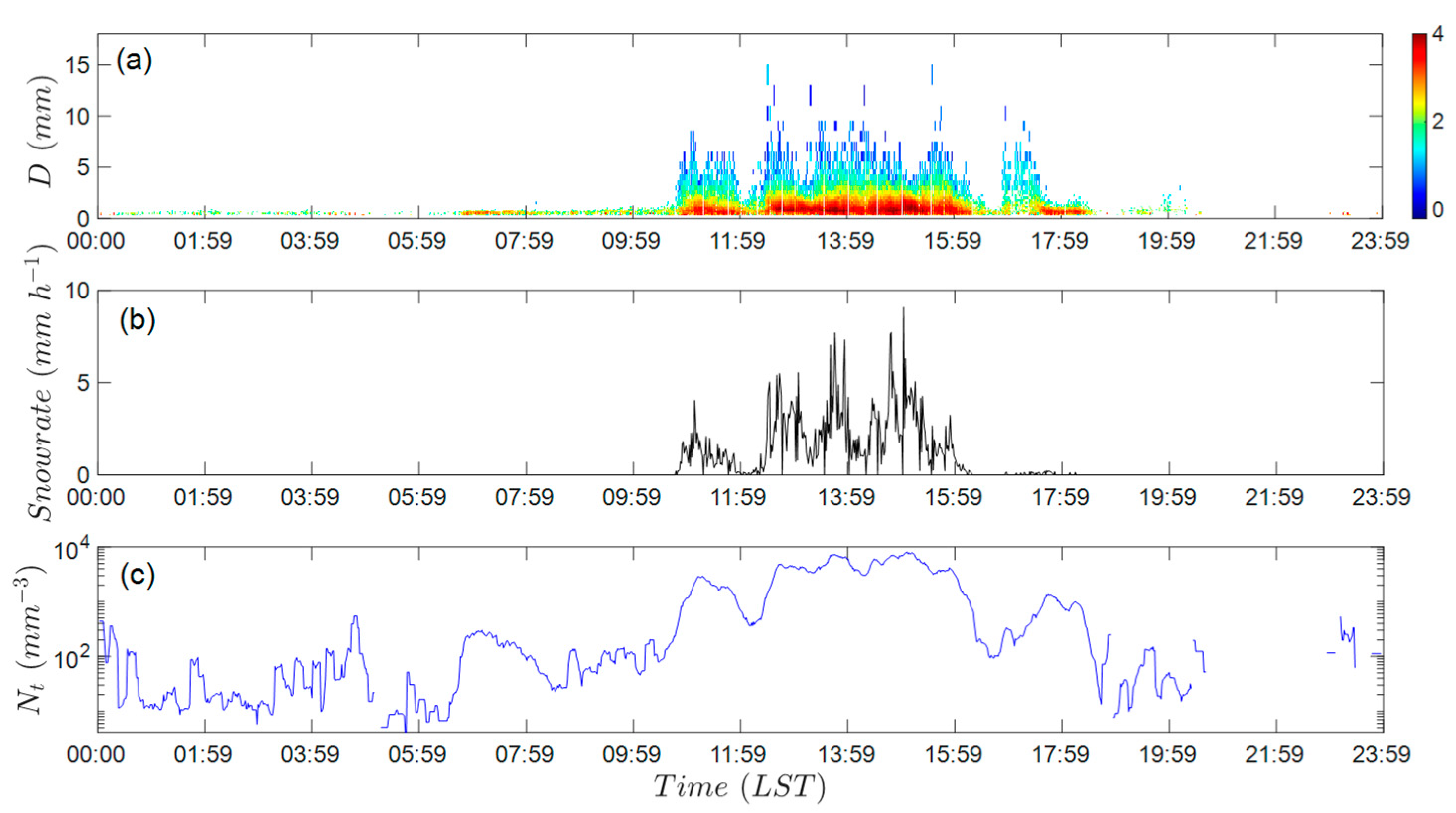

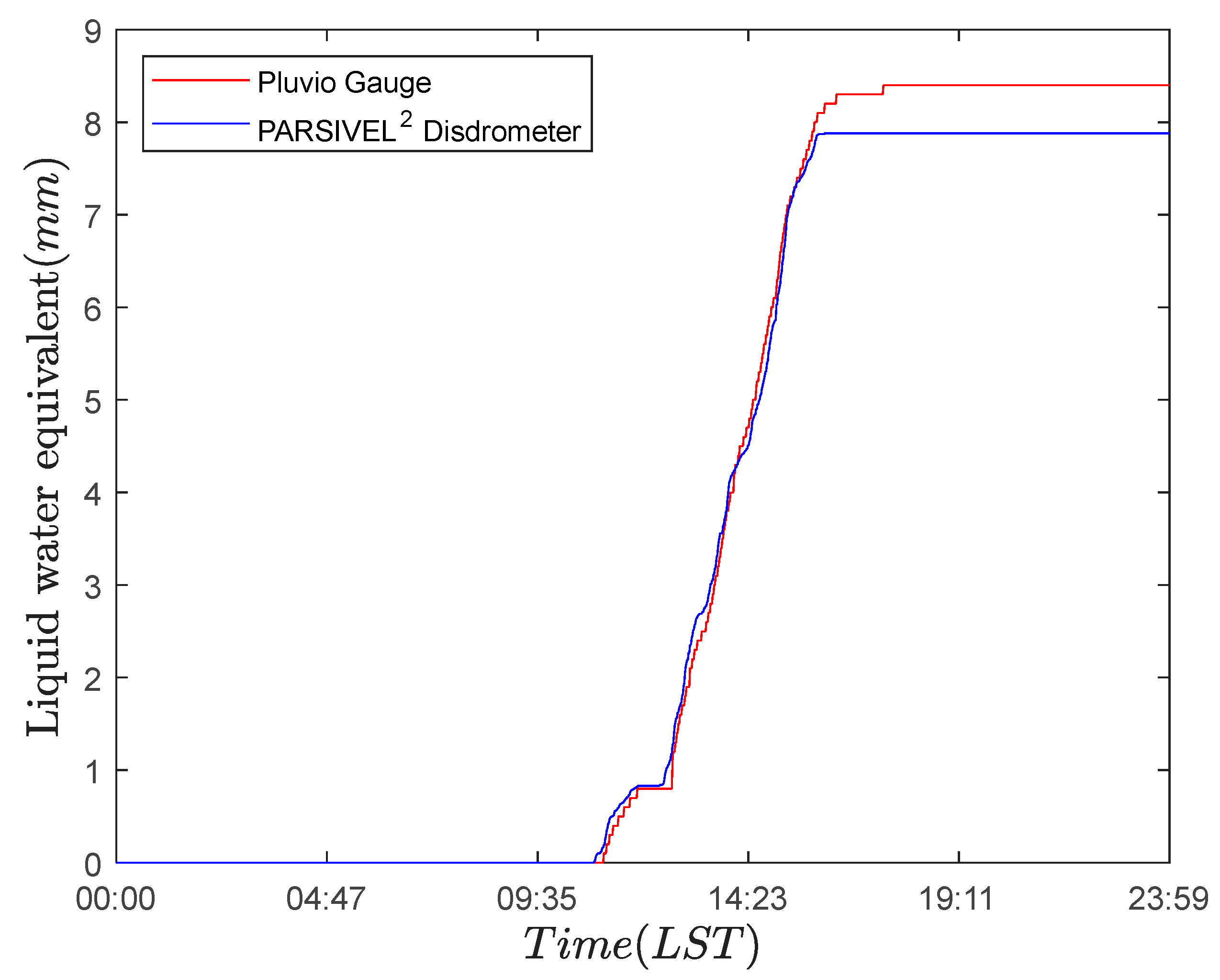
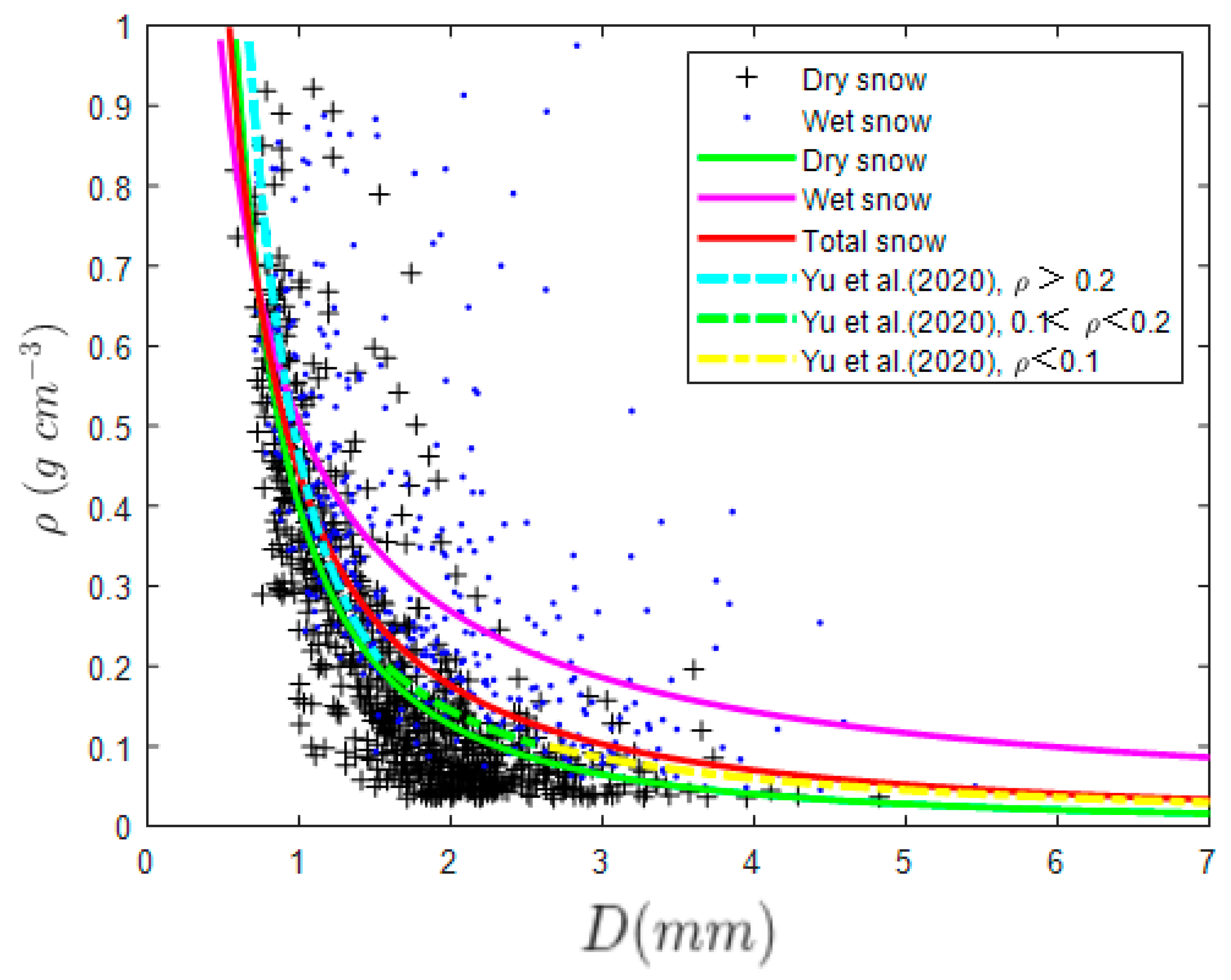

| Case No. | Date | Weather System | DZ | RADZ | RA | RASN | −SN | SN | +SN | GS |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2021.02.15 | Upper trough | 11 | - | - | - | 52 | 3 | - | - |
| 2 | 2021.02.23 | Return flow and upper trough | 17 | - | - | - | 97 | 107 | 5 | - |
| 3 | 2021.02.28 | Return flow and low vortex | 9 | 46 | 189 | 4 | 93 | 219 | 3 | 63 |
| 4 | 2021.03.18 | Upper trough | 24 | 86 | 113 | 18 | 31 | 1 | 12 | 63 |
| 5 | 2021.03.19 | Upper trough | - | 12 | 193 | 5 | 17 | 69 | 10 | 50 |
| 6 | 2022.01.21 | Return flow and upper trough | 4 | 1 | - | - | 118 | 30 | - | - |
| 7 | 2022.02.13 | Return flow and low vortex | - | - | - | - | 213 | 277 | 19 | - |
| 8 | 2022.03.18 | Low vortex | 2 | 2 | - | - | 65 | 145 | 88 | - |
| Snow Types | ||||
|---|---|---|---|---|
| ME | SD | ME | SD | |
| SR ≤ 0.5 | 3.55 | 0.76 | 2.53 | 1.90 |
| 0.5 < SR < 2.5 | 3.81 | 0.70 | 2.73 | 2.15 |
| SR ≥ 2.5 | 4.20 | 0.67 | 2.49 | 1.75 |
| Wet snow | 3.75 | 0.71 | 1.80 | 0.82 |
| Dry snow | 3.73 | 0.75 | 2.94 | 2.23 |
| Pu et al. (2020) [54] Wet snow | 2.95 | 0.49 | 3.17 | 1.78 |
| Pu et al. (2020) [54] Dry snow | 2.99 | 0.63 | 3.49 | 2.00 |
| Snow Types | Location | |
|---|---|---|
| SR ≤ 0.5 | Beijing, China | |
| 0.5 < SR < 2.5 | Beijing, China | |
| SR ≥ 2.5 | Beijing, China | |
| Wet snow | Beijing, China | |
| Dry snow | Beijing, China | |
| Total snow | Beijing, China | |
| Brandes et al. [46] | Colorado, USA | |
| Pu et al. [54] Wet snow | Nanjing, China | |
| Pu et al. [54] Dry snow | Nanjing, China |
| Snow Types | Location | |
|---|---|---|
| Wet snow | Beijing, China | |
| Dry snow | Beijing, China | |
| Total snow | Beijing, China | |
| Yu et al. [53] | Pyeongchang, Republic of Korean |
| Snow Type | Location | |
|---|---|---|
| Dry snow | Beijing, China | |
| Tao, et al. [55] Dry snow | Nanjing, China | |
| Pu et al. [54] Dry snow | Nanjing, China |
| Precipitation Types | |
|---|---|
| Rain | |
| Melting | |
| Graupel | |
| Snow |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Chen, Y.; Bi, Y.; Lyu, D.; Chen, H.; Duan, S. Snowfall Microphysics Characterized by PARSIVEL Disdrometer Observations in Beijing from 2020 to 2022. Remote Sens. 2022, 14, 6025. https://doi.org/10.3390/rs14236025
Shen Y, Chen Y, Bi Y, Lyu D, Chen H, Duan S. Snowfall Microphysics Characterized by PARSIVEL Disdrometer Observations in Beijing from 2020 to 2022. Remote Sensing. 2022; 14(23):6025. https://doi.org/10.3390/rs14236025
Chicago/Turabian StyleShen, Yonghai, Yichen Chen, Yongheng Bi, Daren Lyu, Hongbin Chen, and Shu Duan. 2022. "Snowfall Microphysics Characterized by PARSIVEL Disdrometer Observations in Beijing from 2020 to 2022" Remote Sensing 14, no. 23: 6025. https://doi.org/10.3390/rs14236025
APA StyleShen, Y., Chen, Y., Bi, Y., Lyu, D., Chen, H., & Duan, S. (2022). Snowfall Microphysics Characterized by PARSIVEL Disdrometer Observations in Beijing from 2020 to 2022. Remote Sensing, 14(23), 6025. https://doi.org/10.3390/rs14236025