Abstract
Automatically detecting the wet/dry shoreline from remote sensing imagery has many benefits for beach management in coastal areas by enabling managers to take measures to protect wildlife during high water events. This paper proposes the use of a modified HED (Holistically-Nested Edge Detection) architecture to create a model for automatic feature identification of the wet/dry shoreline and to compute its elevation from the associated DSM (Digital Surface Model). The model is generalizable to several beaches in Texas and Florida. The data from the multiple beaches was collected using UAS (Uncrewed Aircraft Systems). UAS allow for the collection of high-resolution imagery and the creation of the DSMs that are essential for computing the elevations of the wet/dry shorelines. Another advantage of using UAS is the flexibility to choose locations and metocean conditions, allowing to collect a varied dataset necessary to calibrate a general model. To evaluate the performance and the generalization of the AI model, we trained the model on data from eight flights over four locations, tested it on the data from a ninth flight, and repeated it for all possible combinations. The AP and F1-Scores obtained show the success of the model’s prediction for the majority of cases, but the limitations of a pure computer vision assessment are discussed in the context of this coastal application. The method was also assessed more directly, where the average elevations of the labeled and AI predicted wet/dry shorelines were compared. The absolute differences between the two elevations were, on average, 2.1 cm, while the absolute difference of the elevations’ standard deviations for each wet/dry shoreline was 2.2 cm. The proposed method results in a generalizable model able to delineate the wet/dry shoreline in beach imagery for multiple flights at several locations in Texas and Florida and for a range of metocean conditions.
Keywords:
wet/dry shoreline; UAS; feature extraction; deep learning; HED; coastal inundation; edge detection 1. Introduction
The wet/dry shoreline, also called the high-water line, is defined as the maximum runup limit on a rising tide where the part of the beach is still wet, but beyond this line, the sand is dry [1]. This shoreline is affected by the wind, wave, runup, setup, currents, and tidal conditions of the present moment. Detecting and predicting changes in the position of the wet/dry shoreline on the time scale of a hours or less is essential for beach risk management, and coastal researchers [2,3,4,5].
The wet/dry shoreline was selected as the best indicator of beach inundation among forty-five other shoreline indicators [6]. This indicator is well suited for research based on imagery and requires a stable and repeatable inundation metric. McCurdy [7], and McBeth [8] studied the wet/dry shoreline and concluded that there was an insignificant difference between the water line of the previous high tide and the wet/dry shoreline on the studied imagery. Stafford [9] further confirmed, stating that this was the result of the stable nature of the wet/dry shoreline over a tidal cycle. Furthermore, Dolan [10] stated that the wet/dry shoreline is a stable shoreline indicator and is less sensitive to the tidal stage than the instantaneous runup limit. Thus, the wet/dry shoreline is a shoreline definition that is well suited to accomplish the goal of measuring and predicting coastal inundation.
Relative to elevation proxies or tidal datums, such as Mean High Water (MHW), as an indicator of shoreline position, previous literature [1] has mentioned that the wet/dry shoreline is generally not a stable indicator for measuring shoreline change due to its dependence on the tide, water level, runup, and subjectivity in the delineation. Despite that, that is not a concern for this paper since we are not trying to monitor the wet/dry shoreline change or erosion over a lengthy time period, i.e., days or longer. Instead, this paper uses the wet/dry shoreline to calibrate and train an AI model for the creation of a time series of the position of the wet/dry shoreline that, in future research, will be used in an AI model to predict coastal inundation at a time scale of hours or less.
Additionally, using the wet/dry shoreline is critical for the operational application of this research. We interviewed multiple beach managers, and they are most interested in the short-term predictions represented by the position of the wet/dry shoreline. From an operational point of view, they are not looking for a long-term model, they want to know how far the runup will reach on the beach in the next couple of hours to couple of days. They are interested in the short-term model because they need short-term predictions to determine if beach access roads should be closed, and if the lifeguards’ stand should stay on the beach during the next inundation event. Having a prediction of the wet/dry shoreline rather than the average water level at a tide gauge will be most helpful for beach managers to be able to make such decisions. These are important decisions on beach access to protect ecological, biological, and economic resources [11,12,13]. Thus, using the wet/dry shoreline is the best indicator to satisfy the needs of beach managers since it captures the current metocean conditions.
Given the significant benefits of detecting the wet/dry shoreline, there is a need for an automated method to detect it from remote sensing imagery [14]. Traditional approaches consist of using semi-automatic software applied on satellite imagery [15,16,17,18]. These methods are capable of identifying the wet/dry shoreline, but they are not as accurate as newer machine learning, and deep learning approaches [11]. Many recent studies do combine the use of machine learning or deep learning with satellite imagery [19,20,21,22]. These approaches do obtain more accurate shoreline predictions, but their main limitation is in the use of satellite imagery. Satellite imagery has many benefits, primarily the ability to collect multi-band imagery [23,24,25]. The disadvantage of satellite imagery is that data is only available at a location when the satellite goes over that specific area, and there is no cloud cover at that time. Then, it is possible that the area of interest is not covered by any open-source satellite.
A great option to overcome these challenges and have fast and timely access to the study area is to use UAS for the data collection [26,27,28]. UAS provide fast and timely data acquisition of the wet/dry shoreline conditions. Additionally, UAS allow the collection of very high-resolution imagery, given their proximity to the ground, focused on the region of interest [29]. Imagery collected at lower altitudes results in higher ground sample distance (GSD), and any error in predicted features within the image will be significantly lower than the error from satellite imagery, on the order of as low as a few centimeters for UAS imagery. This assures a more accurate wet/dry shoreline feature location, essential if the imagery is used to compare the location’s evolution over time and calibrate predictive models. Similarly to satellite and aerial imagery, all UAS data can be georeferenced [30,31,32]. This can thus provide the precise coordinates for the shoreline, including its vertical datum referenced to a terrestrial datum.
Another challenge with detecting the wet/dry shoreline is consistent labeling. When using raw UAS imagery data, it is challenging to consistently label the wet/dry shoreline since only a small portion of the beach is visible in each image. We found that if the images are labeled first and georeferenced after, we often have inconsistent labeling and a discontinuous wet/dry shoreline. To solve this inconsistency problem, we used orthomosaic data. In this way, we assure consistent labeling of the wet/dry shoreline along the beach, thus improving the deep learning model performance [33,34,35]. This is discussed in greater detail in the data processing and data preparation Section 2.2.
Detecting the wet/dry shoreline is an edge detection problem. HED (Holistically-Nested Edge Detection) [36], VGG (Visual Geometry Group) [37], Dexined [38], and Deep Hybrid Net [39] architectures have shown excellent results in similar applications. This paper proposes using a modified HED architecture to create a generalizable model for several locations. The method includes using CLAHE (Contrasted Limited Adaptive Histogram Equalization) as a pre-processing step to adjust and normalize the images’ contrast. The new method allows the detection of the wet/dry shoreline in a wide range of lighting conditions and beach characteristics. Based on our results with wet/dry shoreline detection from nine UAS flights in different locations in Texas and Florida, we believe this model can be generalized to a wide variety of beach conditions.
This paper proposes two major contributions: (1) creating a generalizable wet/dry shoreline detection model that performs well in several locations that were not part of the model training, and (2) computing the elevation of the predicted wet/dry shoreline. Creating a generalized model is only possible because of the use of CLAHE (Contrasted Limited Adaptive Histogram Equalization) as a pre-processing step, using UAS high-resolution imagery from multiple locations along the Texas and Florida coast, and training with imagery with a large variety of different atmospheric conditions. Computing the wet/dry shoreline elevations is only possible because we are using orthomosaic and DSM (Digital Surface Model) data that was created using the raw UAS imagery for each of the UAS flights. This allowed us to use high-resolution georeferenced data to train the neural network. Then, once the wet/dry shoreline was predicted, we were able to georeference this data back using ArcGIS Pro. This allowed us to use the AI predicted imagery in combination with the DSM to compute the elevation of the wet/dry shoreline. This paper is the first to propose this additional step to compute the elevation of the wet/dry shoreline. This method, combined with the collection of imagery over a broad range of metocean conditions, allows the creation of a time series of wet/dry shoreline elevations and enables the analysis and prediction of total water level and inundation for that location in addition to average water levels.
2. Study Area and Dataset
The research goal of this article is to create a generalizable wet/dry shoreline detection model that performs well under various atmospheric and geological conditions at different locations. For this reason, it was necessary to have multiple study areas. We gathered UAS imagery from four study areas: Packery Channel, Mustang Island SP (State Park), Fish Pass, and Little Saint George Island. The first three locations are in Texas, while the last is a State Reserve in Florida. Figure 1 shows the locations of the different study areas along the Gulf of Mexico. Nine UAS flights collected data at the different study areas, flown in 2017, 2018, 2019, and 2020. Even if there are multiple flights in the same area, the flights collected are in different regions in the areas, and they had different study area lengths. UAS data were collected under different lighting conditions, different wind and weather conditions, and over different beach geomorphology and sediment type across the study areas. The data used in this study were collected and processed by the Measurement Analytics Lab (MANTIS) at the Conrad Blucher Institute for Surveying and Science (CBI). Locations in Texas are the northernmost part of North Padre Island and two locations along Mustang Island. The sand composition of all three sites is very similar consisting of well sorted fine sediments with uniform properties all along the length of Mustang Island [40], 26 km, and continuing for the northernmost part of North Padre Island. The sediments are 86.9% quartz, 9.4% feldspar and 3.7% rock fragments [41]. All locations in Florida are along the 15 km of gulf facing beach of Little Saint George Island composed of medium-fine sediments composed of over 99% quartz sand [42]. The composition differences result in lighter color for the Florida sands than the Texas sands as can be seen in Figure 2 and Figure 3. Another difference between the Florida and the Texas study sites is that cars are allowed to drive on the Texas beaches resulting in tire marks while driving is not allowed on the Florida study site. This makes detecting the wet/dry shoreline more challenging since car tires create edges and lines on the sand. Furthermore, access to Little Saint George Island is very limited, only by boat, while the Texas beaches are continuously visited resulting in people, and other related objects, in the Texas images but not the Florida images. For all study sites, the morphology of the beaches is modified by events such as high-water events, high wave heights and long wave periods, and high winds, all potentially contributing to a changing wet/dry shoreline. When the above forcings subside, the water does not reach as far, creating a new wet/dry shoreline closer to the water. This challenges the detection of the wet/dry shoreline since there may be multiple shorelines visible within the same image. In Figure 2, it can be observed that half of the sand area of the beach contains evidence of past wet/dry shorelines. Using images significantly different from each other, different locations and recent metocean conditions, enables the training of a more general model if successful.

Figure 1.
Study Area. Blue pin: Packery Channel; purple pin: Fish Pass; orange pin: Mustang Island SP; red pin: Little Saint George Island.

Figure 2.
Texas Beach (Image Source: Google Maps).

Figure 3.
Florida Beach (Image Source: Google Maps).
2.1. Data Collection
UAS was the method selected to collect imagery data because of its flexibility in deciding the collection date, time, and location. Compared to satellite imagery, this flexibility was important since we were looking for various oceanographic conditions. We could evaluate the model’s generalization with a greater diversity of data. Additionally, UAS have the ability to collect georeferenced high-resolution RGB imagery at a relatively small scale. Accurately georeferenced imagery allows comparing the difference between the labeled and the predicted wet/dry shorelines with a metric more directly relevant to the study of beach dynamics and inundation. Figure 4 shows a sample of the beach imagery diversity from Texas and Florida.

Figure 4.
Imagery Challenges in a Sample Dataset from Multiple Beaches.
Analyzing the images in Figure 4, one will notice significant differences in the imagery saturation, luminosity, and overall beach conditions. In Figure 4d, car tire marks can be observed. This adds complexity to training the deep learning edge detection model since the tire marks add more edges to the images that do not represent the wet/dry shoreline and must be ignored by the detection algorithm.
By looking in detail at Figure 4e, two candidates’ wet/dry shorelines can be identified. The first one is at the bottom part of the image, and the second one is at the top. In the case of this work, the correct wet/dry shoreline is close to the bottom because it is the most recent shoreline. Similarly, in Figure 4a, the image has two edges to distinguish from. Another challenge on the dataset is that sometimes there is both a wet/dry shoreline and a waterline, as shown in Figure 4b,e. The waterline is another challenge that could confuse the neural network as it has a clear edge.
Figure 4c is characterized by very different light conditions than the rest of the dataset. Additionally, it contains plant debris that has washed ashore on the sand. This all adds to the complexity of identifying the shoreline. Figure 4d,e show another common challenge, where there are objects on the beach close to the shoreline. In the case of Figure 4d, a surveying target can be observed. In the case of Figure 4e, there is a car close to the shoreline. Thus, it is necessary to develop a robust model to predict the wet/dry shoreline that can ignore objects on the beach.
2.1.1. UAS and Camera Used
The imagery used in this research was collected using five UAS with five RGB single-frame cameras to further increase the model’s generalization. Table 1 describes the UAS and cameras used. The table shows that this research combines quadcopters and fixed-wing UAS. We used the diversity of UAS and cameras to increase the model’s generalization.

Table 1.
UAS and Camera Used.
Table 2 describes the properties of the cameras used. The table shows a combination of fixed-focal and auto-focal lenses with a range of 8.8 to 35 mm. The MP (Megapixels) from the cameras ranges from 20 to 42. Finally, the maximum resolution ranges from 4000 × 4000 to 7952 × 5304. The resulting imagery used as input for the neural network was taken by significantly different cameras with different properties. This will allow the determination of whether the proposed model works well, independent of the cameras’ photogrammetric properties.

Table 2.
Camera’s Properties.
2.1.2. Atmospheric and Oceanic Conditions during Data Collection
Figure 5, and Table 3 document the range of metocean conditions for our UAS flights. This study used imagery from nine UAS flights, but the figures only include data for six of the flights because there was no station collecting atmospheric condition data near Little Saint George Island in Florida. Figure 5 is a wind rose representing the wind direction and speed for the UAS flights in Texas. The wind direction is indicated by the vector direction, while the wind speed is the length of the vector. The Texas beaches are along the Coastal Bend, and their orientations with respect to north/south are similar and displayed in the background image behind the wind rose graphic. Both wind direction and speed impact the reach of the water on a beach. The wind speeds ranged between 6 m/s and 8 m/s, with wind directions onshore for all but one case (flight 5).

Figure 5.
Wind Direction and Speed (Data Source: NOAA [43]).

Table 3.
Oceanic Conditions.
The second force that is important to the wet/dry shoreline’s location is the water level’s height, as recorded by a nearby tide gauge. NOAA (National Oceanic and Atmospheric Administration) collects 181 continuous measurements at a 1 Hz frequency prior to processing and averaging the data to compute an average [44]. The higher the average water level during a flight, the further the wet/dry shoreline will reach up on the beach. Table 3 represents the average water level relative to the NAVD88 datum during each UAS flight. During our flights, the water level in meters varied from 0.191 m for Flight 6 to 0.484 m for Flight 1.
The third important condition is the significant wave height because the vertical height reached by the runup is similar to the significant breaking wave height [44]. During events with larger significant wave heights, the wet/dry shoreline will be located further up the beach. Table 3 represents the significant wave height for the different UAS flights. Note that for flight 6, the significant wave height information was unavailable for the location and time of the UAS flight. Moreover, there was no relevant wave information for the two Florida locations as the closest National Data Buoy Center buoy was located too far from the study beaches. As shared in Table 3, the significant wave height was smaller for flights 3, 4, and 5, measuring 0.23 m for flight 5 and 0.79 m for flights 3 and 4, as compared to the significant wave heights of 1.06 m for flight 6 and 1.37 m for flight 2.
Table 4 summarizes the specific information for the different UAS flights, the flight’s location, date, and flight time. Table 5 summarizes the study area length, number of images for each flight, flight height, and the GSD for all flights. The study area length varies from 118 m to 17.5 km. The flight heights range from 10 m to 120 m. The GSD depends on the flight height and the camera. The smallest GSD of 0.25 cm is associated with the lowest altitude flight. The largest GSD of 1.91 cm is for flight number 6, flying at an altitude of 85 m.

Table 4.
UAS Flight Location and Time Information.

Table 5.
UAS Flight Information.
2.2. Data Processing and Data Preparation
Each UAS flight captured a set of overlapping images, which were then processed using structure-from-motion (SfM) photogrammetry with Agisoft Metashape software to create point clouds, elevation models, and orthomosaics. To create the SfM products, most of the water from the products was removed to obtain a higher degree of accuracy for the SfM products. In the places where the water was removed, null values were given.
All the UAS flights had GCPs (Ground Control Points). The number of the GCPs depended on the length of the study area (Table 5). The GCPs were surveyed using RTK (Real-Time Kinematics) GNSS (Global Navigation Satellite Systems) tied into the Texas DOT Real-Time Network and the Florida DOT Real-Time Network (RTN), respectively. The mean RMSE in Table 6 represents the overall RMSE (average of each 3D component’s RMSE) based on the positional differences between the X, Y, and Z coordinates of the GCPs and the reconstructed/estimated X, Y, and Z coordinate from the SfM photogrammetry solution for each respective GCP.

Table 6.
UAS SfM Solution.
For this research, using orthomosaic data is important since this provides consistent georeferenced and accurately rectified imagery. Manually labeling images individually would create inconsistencies in the location of the wet/dry shoreline and difficulties in the learning process for the deep learning model, so it is better to combine the images into an orthomosaic. ArcGIS Pro was then used to label the orthomosaic images from a single flight all at once.
The initial step was to load the orthomosaic raster and manually draw a vector at the wet/dry shoreline location. The second step consisted of augmenting the wet/dry shoreline vector width to 30 cm using a buffer. The third step was to create a new raster for the labeled imagery using the extract-by-mask tool. The input raster was the original orthomosaic, and the feature mask data were the buffer. This new raster had the same orthomosaic data as the original imagery, with the difference being that now there was a black wet/dry shoreline marking on it. The fourth step was creating a polygon feature class to select the wet/dry shoreline area from the orthomosaic. The polygon was used to mark where to split the orthomosaic into unscaled 512 × 256 pixel sub-images without any overlap, as these are the selected input dimensions for the neural network. The fifth step was to use the split raster geoprocessing tool to split both the original orthomosaic and the labeled raster equally. The original orthomosaic raster was first divided using the dimensions of the previously created polygon, then repeated with the labeled raster, followed by splitting the orthomosaic images into individual images. All images were then exported from ArcGIS Pro. Since the orthomosaics had some null values, some of the output images had null values as well, represented with black pixels. Images with null values were removed from the dataset as the transition to black pixels in the images creates an artificial edge, which would result in unphysical difficulties for training an edge detection algorithm. For our study, we were able to output datasets without images containing null values for most of the flights. All images without null values were used for the study. Finally, the sixth step consisted of writing and running a Python script to rotate the imagery to a consistent orientation. At this point, the wet/dry shoreline was represented with a black shade, while the rest of the image was white.
3. Methodology
The methodology consists mainly of two steps: (1) predicting the wet/dry shoreline and (2) computing the elevation of the predicted wet/dry shoreline.
3.1. Deep Learning Architecture
Deep learning was selected as the approach to detect the wet/dry shoreline because computer vision deep learning models have shown excellent results on edge detection problems [36,37,38]. Deep learning models can adapt to multiple beach morphologies and perform better with a larger number of images, thus allowing one model to be generalized for more than one location. One architecture that has obtained excellent results in similar problems is HED (Holistically-Nested Edge Detection). For this reason, this paper proposes using a HED architecture with some modifications to improve performance.
3.1.1. HED
The HED architecture was developed to improve edge detection predictions developed by Xie et al., 2015 [36]. HED is characterized by making image-to-image predictions by using fully convolutional neural networks. In addition, it is characterized by training and making predictions based on the entire image by having a multi-scale and multi-level learning process that allows extracting different levels of representation from each convolutional level [36]. HED architecture is composed of five blocks of convolutions with a max-pooling layer and a side output at the end of the last convolution of each block. The side outputs are then fused together, resulting in the final output for the model. Using a max-pooling layer in each block creates a multi-scale and multi-layer feature. The first two blocks consist of two 2-D convolutions and one max-pooling layer. The third and fourth blocks consist of three 2-D convolutions and one max-pooling layer. The final block consists of three 2-D convolution layers with no max-pooling.
HED uses an unbalanced loss function, which is necessary for edge detection in our case study since the number of pixels where there is the wet/dry shoreline is very small compared with the total number of pixels. HED uses cross-entropy-balanced functions, as defined by:
where = and and denote the edge and non-edge ground truth label sets, respectively.
The resulting neural network loss function, shown in Equation (3), is the cumulative sum for the side outputs and the loss for the function:
W is the collection of all standard network layer parameters; w is the weight for each side output; h is the fusion weight.
3.1.2. Proposed Architecture: Modified HED
HED was designed for natural image edge detection, not for environmental UAS or satellite imagery with different light conditions, angles of the camera, etc. Despite the success of HED in natural image edge detection problems, it had some difficulties performing well in our application. Since one of the main goals of our work is to develop a generalized model for different locations with different environmental conditions, we adjusted the HED model by adding the following modifications. (1) To generalize better, first, we added the use of CLAHE [47] as a pre-processing step through the training process. Using CLAHE, we were able to equalize the dataset while simultaneously increasing the contrast of the edges on the dataset, allowing for better wet/dry shoreline detection. This histogram equalization step resulted in significant improvements in the model’s performance. (2) The second modification was the implementation of L2 regularization. L2 adds a penalty to the model parameters, so the model is able to generalize better [48]. This was essential because it allowed us to prevent the initial overfitting problem because of the datasets’ diversity. (3) The last modification was adding a dilation rate. Dilation rate allowed for extracting different features in a different view of the receptive field of the convolution layer. By making these three modifications to the HED architecture, we were able to generalize the model successfully. Figure 6, describes the new modified HED architecture. The reader is invited to examine the code implementation in GitHub (https://github.com/conrad-blucher-institute/wetDryShoreline/) (accessed on 19 October 2022).
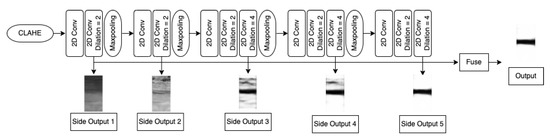
Figure 6.
Proposed Architecture.
3.1.3. Hyperparameter Tuning
This study used all of the available imagery obtained after the data processing and data preparation steps. 2128 images from 9 UAS flights in 4 locations with two unique geomorphologies (see Table 5) were used. The model calibration was done in two steps. In the first step the model architecture is determined while using the full datasets, all flights, and all locations, and splitting the data 65% training, 15% validation, and 20% testing randomly. These results were also used to compare the performance of HED with the modified HED in Table 7. Using the best architecture from the previous step, the modified HED architecture, we proceed with testing the model for different flights. We repeatedly train the model on the data from eight flights and test the model performance on the ninth flight that the model has not seen yet. We repeated this process for all combinations. For this latter step, we split the data from each UAS flight 70% for training and 30% for validation before combining the data from the eight flights. Then, we took the remaining flight data not yet seen by the model and used 100% of the data of this independent test.

Table 7.
HED vs. Modified HED Architecture.
To optimize the model, the Adam optimizer was used [49]. The model’s optimal hyperparameters include a batch size of 16, an L2 regularization of , a learning rate of , and a clip limit value of . To control the overfitting problem, in training, we used the early stopping technique [50] with a patience value of 25. Figure 7a shows the loss function for the HED architecture, where one can notice some overfitting problems. On the other hand, in Figure 7b, we see that the overfitting problem was reduced significantly with our modified architecture. Additionally, the new model could train for almost double the number of epochs.
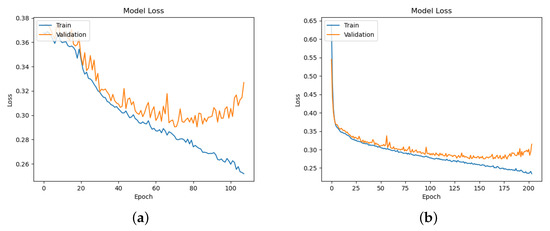
Figure 7.
Learning curve of the loss function: (a) Original HED architecture; (b) Modified HED architecture.
3.2. Geo-Referencing the Wet/Dry Shoreline and Computing Its Elevation
Only predicting the wet/dry shoreline on an image does not provide enough information for coastal management. To be of practical use, it is necessary to georeference the predicted images and compute the elevation of the predicted shoreline in order to model inundation. Identifying the wet/dry shoreline elevation is necessary for forecasting the water run-up on the beach. ArcGIS Pro was used to georeference the predicted wet/dry shoreline images from the neural network by storing the coordinate information for each output image. Then, using this information, we were able to georeference the images back to their initial position accurately.
Once all the images for the location were georeferenced, one could compute the elevation for the predicted wet/dry shoreline by using the image pixels coordinates for each cell in the image that are classified as wet/dry shoreline and correlating them with the DSM for each flight location. To compute the elevation, it is essential to have a specific DSM for each flight. In our case, this model was created together with the orthomosaic model. The first step to compute the predicted wet/dry shoreline elevation is to create a buffer that includes all of the predicted wet/dry shoreline points, then convert the wet/dry shoreline polygon into a raster using the “Polygon to Raster” geoprocessing conversion tool, then using the “Raster Calculator” spatial analyst tool in ArcGIS Pro to compute the elevation for each point on the wet/dry shoreline. The final step computes the mean elevations, standard deviation, and other statistics from the labeled and predicted wet/dry shoreline points, where they could then be compared.
4. Results and Discussion
Results and analysis of the models developed in this study will be presented and discussed. First, the performances and outputs of the HED and the modified HED architectures are compared. The ability of the trained models to predict the location of the wet/dry shoreline at new locations is then tested using cross-validation, training on 8 of the study areas to predict the ninth. The georeferenced imagery allows for a comparison between the predicted wet/dry shoreline with the labeled shoreline. The agreement between predicted and labeled wet/dry shorelines is quantified using computer vision statistics, but the elevation of the wet/dry shoreline, a more relevant metric for this method to be applied, is discussed at the end of the section.
4.1. HED vs. Modified HED
The metrics used to evaluate the predicted imagery are F1-Score (Equation (4)) and AP (Average Precision) (Equation (5)). Since we use binary labels to predict the location of the wet/dry shoreline and there is no threshold value, one cannot use metrics such as ODS (Optimal Dataset Scale) and OIS (Optimal Image Scale).
Table 7 shows the performances of the two deep learning architectures using the same dataset. The model was trained, validated, and tested with the full dataset in both cases. Comparing the results, we can see that the AP performance of the modified HED is 6.4% better, and the performance on the F1-Score is 8.5% better. These results support the use of the modified architecture that can better account for the diversity of the dataset and is better suited for this coastal imagery problem.
4.2. Model Generalization and Performance
To evaluate the modified HED model’s generalization performance, the model was successively trained using data from all but one of the UAS flights, with the data from the last UAS flight kept for independent testing. All possible combinations were made so that the data from each flight was used once only as an independent testing dataset. Figure 8 shows some of the predicted images by the neural network. For each example, the image on the left represents the original image used as an input for the neural network, the middle image represents the labeled imagery, and the right image represents the deep learning predicted wet/dry shoreline. We can observe the challenges encountered by the model for these three cases. Figure 8a is characterized by car tire marks on the back of the wet/dry shoreline, which could have confused the model since it adds edges to the image. Figure 8b is characterized by having a second edge a little above the real wet/dry shoreline. The model ignores the false lines for these two instances and accurately predicts the real wet/dry shoreline. Figure 8c is characterized by having a car on the beach and shells around the car and between the car and the wet/dry shoreline. The model mostly ignores both and accurately predicts the wet/dry shoreline except for a few false positive artifacts resulting from the presence of the shells. Orthomosaics from this study’s nine flights were captured at different times of the day and under different lighting conditions. The three examples in Figure 8 show a gradient from a darker scene (a) to a brighter scene (c) without a noticeable impact on the performance of the model, while lighting conditions were a problem at the start of this work, applying the CLAHE algorithm [47] in the modified HED model resolved the problem, and lighting conditions did not appear to affect performance for any of this study’s orthomosaics.

Figure 8.
Neural Network Predicted Wet/Dry Shoreline Results. The left column images are the original image, the middle column images are ground-truth, and the right column images are the modified HED model prediction. (a–c) are samples of the AI outputs.
To further study the model’s performance on the independent locations the frequently used for computer vision problems, AP and F-1 Score metrics were computed (Table 8) for each individual UAS flight. In some locations, the performance is significantly better than at other locations. For flights 1, 2, and 3 in Texas and 8 in Florida, the model’s performance based on AP and F-1 is very good, 75% or better. Such good performance is desirable but not strongly correlated with the more important metric based on the vertical height of the wet/dry shoreline, as discussed in the next section. However, the model’s performance based on AP and F-1 is not very good, lower than 50% for flights 4, 6, and 7 in Texas and flight 9 in Florida and deemed acceptable for an edge detection problem for Flight 5, with AP = 65% and F-1 = 70%.

Table 8.
Metrics on the Independent Testing Locations.
Figure 9 helps to understand the reasons for the low AP and F-1 scores for the above four flights. For flight 9, Figure 9d, the AI predicted wet/dry shoreline width is thin, with a standard deviation of 0.074 m, and mostly not collocated with the labeled data, which has a thin width as well with a standard deviation of 0.113 m. This mismatch results in very few true positives and hence a low AP and a low F-1 score. For this orthomosaic, the challenge for the AI, as well as for the human labeling, is the absence of a clear wet/dry shoreline. Interestingly, the AI model correctly ignored the wide line of different colors and varying thicknesses located just inland from the true wet/dry shoreline. The scores are poor, AP = 17% and F-1 Score = 22%, but as we will see in the next section, and in Table 9, the mean vertical elevations of the labeled and AI predicted wet/dry shoreline differ by only 1.2 cm. This case highlights the fact that while the AP and F-1 scores are useful indicators, by themselves they are not sufficient to determine the performance and the applicability of a wet/dry shoreline prediction. In some cases, it is possible to have an accurate mean vertical elevation without having good AP and F1-Scores.
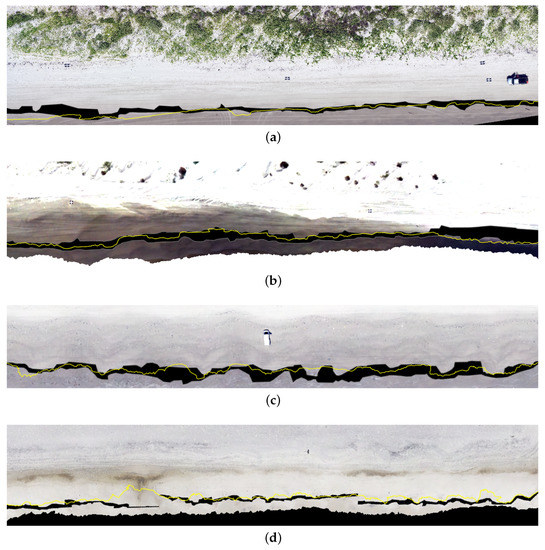
Figure 9.
(a) Flight 4, (b) Flight 6, (c) Flight 7, (d) Flight 9. The yellow line is the labeled wet/dry shoreline, while the black area is the predicted AI wet/dry shoreline.

Table 9.
Metrics on the Independent Testing Locations.
For Figure 9b,c, the AI predictions for the wet/dry shoreline are wider than the labeled wet/dry shoreline. This results in a substantial number of false positives, which lower the average precision and the F-1 score. However, the predicted and labeled shoreline agreement is generally quite good. As we will see in the next section, the AI predictions’ mean vertical height and the label differ by 4.2 cm for flight 6 (b) and 2.3 cm for flight 7. These are good results that are relatively close to the precision of the measurements. These cases, with a relatively wide AI predicted wet/dry shoreline, show that poor AP and F-1 scores are not always good indicators of the performance for the ultimate goal of computing the vertical height of the wet/dry shoreline. The case of Figure 9a is a combination of a smaller mismatch between the two wet/dry shorelines as compared to Figure 9d but a wider AI prediction wet/dry shoreline.
The AP and F-1 scores are appropriate for many computer vision problems, these metrics are easy to implement and frequently used. They are, however, not used as frequently for environmental problems. Other studies have found that computer vision scores do not necessarily identify the best algorithms. In such cases, using other metrics or even subjective ranking may lead to a better selection. These include the cases described by Ledig et al. [51] and Wang et al. [52], where usual metrics do not appropriately quantify the algorithm performance.
In this study, we need to identify a metric that allows one to gauge the accuracy of the wet/dry shoreline prediction location with the goal of eventually creating a total water level elevation time series. The most important output is computing the vertical location of the wet/dry shoreline. From a computer vision point of view, one can focus on the location of the pixels. However, the corresponding error of the average vertical coordinates of the pixels will depend on the slope of the beach, the width of the predicted wet/dry shoreline, and other factors. If we look at Figure 9, we can see that the model is able to accurately compute the wet/dry shoreline elevation for the flights despite some low F1-Scores and AP metrics. For example, if we examine flight 4, we obtain an F1-Score of 47.9% and an AP of 44.7%. However, if we look at Figure 9a, we can see that the AI accurately predicts the wet/dry shoreline. The difference is that predicting it has many false positive values by predicting a thicker wet/dry shoreline, resulting in lower AP and F1-Scores. Similarly, the same problem happens with flight 6 (Figure 9b), 7 (Figure 9c), and 9 (Figure 9d). Even when the AI is able to predict the wet/dry shoreline, the AP and F-1 scores are not the most appropriate metrics to apply to environmental problems.
4.3. Wet/Dry Shoreline Elevation
As discussed above, the traditional image processing metrics are not the most important. For this project, the elevation of the predicted wet/dry shoreline is the most important metric because a good prediction of the mean vertical height will allow for a temporal inundation prediction. 3D metrics of the wet/dry shoreline position, including their horizontal location on the beach, are problematic when predicting the position of the wet/dry shoreline as the morphology of a beach will change over time and during energetic events. The height of the wet/dry shoreline, however, is a more stable indicator since the extent of the runup depends mostly on the significant breaking wave height [53]. Thus, Table 9 shows the model’s performance in computing the vertical height. For all of the flights, the difference between the vertical height for the labeled and the AI predicted wet/dry shoreline is very close, with just a few centimeters difference. Additionally, the standard deviation is very similar for the labeled, and the AI predicted wet/dry shoreline (see Table 10). Another important metric in this research is understanding the vertical range of the beach within the image. It is important in order to be able to show that the beaches are not flat. These metrics were calculated using all of the elevation points on the original image beach area. Then, the top and bottom five percent elevation points were removed to remove the outliers on the datasets, such as cars and targets. Then, ten percent of the remaining points were used to compute the vertical range and average of the top and bottom. In this way, it is possible to make a more accurate computation of the wet/dry shoreline vertical range. When we analyze the flights’ results, we see that the DSM elevation range constrained to the georeferenced imagery for most flight locations is at least 30 cm. Another important metric to further show that the beaches were not flat was to compute the beach slope and the slope within the imagery area. To compute the beach slope, we took multiple elevation points close to the toe of the dune and averaged them (average dune toe elevation). Similarly, we took the same number of points near the water and averaged them (average elevation near water). We then took the distance between each of the dune toes with its corresponding water points to compute the distance. We did that for all the points and averaged the distance (average distance). Then, we applied Equation (6) to compute the slope.

Table 10.
Metrics on the Independent Testing Locations.
Similarly, we computed the slope within the imagery area, i.e., the slope for the area covered by the imagery using a DSM. In Table 10, we see that the slopes for the beaches range from 1.6 to 10.4 degrees, while the slope within the imagery area ranges from 1.6 to 3.0 degrees (Table 10). These values suggest that the studied beaches are not characterized as flat beaches. As shown in Table 9, the model does an excellent job at computing the vertical height of the wet/dry shoreline, which is the most important metric for this project. With this, we can say that the model is able to generalize to several locations in Texas and Florida by predicting an accurate height for the wet/dry shoreline there.
Figure 10 shows an example of the georeferenced labeling and predictions over the orthomosaic data. Figure 10a shows how the images predicted by the neural network are georeferenced back to ArcGIS Pro and added to the top of the orthomosaic of the beach. The yellow line represented the labeled wet/dry shoreline. In contrast, the black pixels on the image represent the predicted AI wet/dry shoreline. Figure 10b removes the images from the orthomosaic and only displays the predicted AI wet/dry shoreline. In both cases, we can see that the AI model accurately predicts the wet/dry shoreline.

Figure 10.
Georeferencing Neural Network Predicted Results (Flight 3). (a) shows the AI georeferenced images overlaid over the orthomosaic, (b) compares the AI predicted (black) with the labeled wet/dry shoreline (yellow).
5. Conclusions
This research shows how to create a model to predict the wet/dry shoreline and compute its elevation using UAS imagery. This model is able to generalize to several locations in Texas and Florida. To test the model’s generalization performance, nine UAS flights were performed at four locations along the Gulf of Mexico in Texas and Florida during a period of four years. The flights were performed in various conditions on beaches characterized by different morphologies. Despite the challenges of the diversity of the conditions, the proposed model was able to generalize and perform well at all of the locations based on the accuracy of the computed elevations of the wet/dry shorelines. To further evaluate the model’s generalization performance, it was successively trained for eight of the locations while testing the model on the ninth (unseen) location. Considering all the combinations, the absolute mean total elevation differences between labeled and AI predicted wet/dry shorelines was 2.1 cm, while the absolute mean standard deviation was 2.2 cm. These results show the model’s success in computing the wet/dry elevation in unseen locations. The next step for this research, and the ultimate goal, is to create an accurate time series of total water levels to complement tide gauge measurements and help better predict, prepare for, and manage coastal inundation events.
Future work on this project is to include more locations. This would increase the beach diversity and further improve the model’s generalization performance. Additionally, the proposed method will be tested on satellite and stationary camera data. Although stationary cameras will not contribute to the variety of locations, they allow us to measure wet/dry shoreline elevations for a broad range of metocean conditions. These additions would increase the model’s robustness. Further, we would like to explore what factors impact the sensitivity of the shoreline delineation horizontal error.
Author Contributions
M.V.-M. was the principal researcher on the project, F.A.M. was the supervisor, P.E.T. was the physics advisor, H.K. the deep learning advisor, M.J.S. was the remote sensing and photogrammetry advisor, and K.C. created the definition of the wet/dry shoreline. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based in part upon work supported by the National Science Foundation under award 2019758. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Data Availability Statement
Not applicable.
Acknowledgments
The data used in this study was acquired by the MANTIS Lab (Measurement Analytics Lab) at the Conrad Blucher Institute, Texas A&M University-Corpus Christi, and was provided to us for research purposes.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- Baok, E.; Turner, I. Shoreline definition and detection: A review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef]
- Young, R.; Pikey, O.; Bush, D.; Thieler, E. A discussion of the generalized model for simulating shoreline change (GENESIS). J. Coast. Res. 1995, 10, 875–886. [Google Scholar]
- Toure, S.; Diop, O.; Kpalma, K.; Maiga, A. Shoreline detection using optical remote sensing: A review. ISPRS Int. J.-Geo-Inf. 2019, 8, 75. [Google Scholar] [CrossRef]
- Cenci, L.; Persichillo, M.; Disperati, L.; Oliveira, E.; Alves, F.; Pulvirenti, L. Remote sensing for coastal risk reduction purposes: Optical and microwave data fusion for shoreline evolution monitoring and modelling. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1417–1420. [Google Scholar]
- Douglas, B.; Crowell, M. Long-term shoreline position prediction and error propagation. J. Coast. Res. 2000, 16, 145–152. [Google Scholar]
- Dolan, R.; Hayden, B.; May, P.; May, S. The reliability of shoreline change measurements from aerial photographs. Shore Beach 1980, 48, 22–29. [Google Scholar]
- McCurdy, P. Coastal delineation from aerial photographs. Photogram. Eng. 1950, 16, 550–555. [Google Scholar]
- McBeth, F. A method of shoreline delineation. Photogram. Eng. 1956, 400–405. [Google Scholar]
- Stafford, D. Development and evaluation of a procedure for using aerial photographs to conduct a survey of coastal erosion. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA. unpublished work.
- Dolan, R.; Hayden, B.; Heywood, J. A new photogrammetric method for determining shoreline erosion. Coast. Eng. 1978, 2, 21–39. [Google Scholar] [CrossRef]
- Calkoen, F.; Luijendijk, A.; Rivero, C.; Kras, E.; Baart, F. Traditional vs. machine-learning methods for forecasting sandy shoreline evolution using historic satellite-derived shorelines. Remote. Sens. 2021, 13, 934. [Google Scholar] [CrossRef]
- Cabezas-Rabadan, C.; Pardo-Pascual, J.; Palomar-Vazquez, J. Characterizing the relationship between the sediment grain size and the shoreline variability defined from Sentinel-2 derived shorelines. Remote. Sens. 2021, 13, 2829. [Google Scholar] [CrossRef]
- Leatherman, S. Social and economic costs of sea level rise. Int. Geophys. 2001, 75, 181–223. [Google Scholar]
- Vicens-Miquel, M.; Medrano, F.A.; Tissot, P.; Kamangir, H.; Starek, M. Deep Learning Automatic Detection of the Wet/Dry Shoreline at Fish Pass, Texas. In Proceedings of the 2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia , 7–22 July 2022; pp. 1876–1879. [Google Scholar]
- Kannan, R.; Kanungo, A.; Murthy, M. Detection of shoreline changes Visakhapatnam coast, Andhra Pradesh from multi-temporal satellite images. J. Remote Sens. GIS 2016, 5, 157. [Google Scholar]
- Kermani, S.; Boutiba, M.; Guendouz, M.; Guettouch, M.; Khelfani, D. Detection and analysis of shoreline changes using geospatial tools and automatic computation: Case of Jijelian sandy coast (East Algeria). Ocean. Coast. Manag. 2016, 132, 46–58. [Google Scholar] [CrossRef]
- Gens, R. Remote sensing of coastlines: Detection, extraction and monitoring. Int. J. Remote. Sens. 2010, 31, 1819–1836. [Google Scholar] [CrossRef]
- Foody, G.; Muslim, A.; Atkinson, P. Super-resolution mapping of the shoreline through soft classification analyses. IEEE Int. Geosci. Remote. Sens. Symp. 2003, 6, 3429–3431. [Google Scholar]
- Tajima, Y.; Wu, L.; Watanabe, K. Development of a shoreline detection method using an artificial neural network based on satellite SAR imagery. Remote. Sens. 2021, 13, 2254. [Google Scholar] [CrossRef]
- Aryal, B.; Escarzaga, S.; Zesati, S.; Velez-Reyes, M.; Fuentes, O.; Tweedie, C. Semi-automated semantic segmentation of arctic shorelines using very high-resolution airborne imagery, spectral indices and weakly supervised machine learning approaches. Remote. Sens. 2021, 13, 4572. [Google Scholar] [CrossRef]
- McAllister, E.; Payo, A.; Novellino, A.; Dolphin, T.; Medina-Lopez, E. Multispectral satellite imagery and machine learning for the extraction of shoreline indicators. Coast. Eng. 2022, 174, 104102. [Google Scholar] [CrossRef]
- Choung, Y.; Jo, M. Comparison between a machine-learning-based method and a water-index-based method for shoreline mapping using a high-resolution satellite image acquired in Hwado island, South Korea. J. Sens. 2017, 8245204. [Google Scholar] [CrossRef]
- Abdelhady, H.; Troy, C.; Habib, A.; Manish, R. A simple, fully automated shoreline detection algorithm for high-resolution multi-spectral imagery. Remote. Sens. 2022, 14, 557. [Google Scholar] [CrossRef]
- Kaiser, S.; Grosse, G.; Boike, J.; Langer, M. Monitoring the transformation of arctic landscapes: Automated shoreline change detection of lakes using very high resolution imagery. Remote. Sens. 2021, 13, 2802. [Google Scholar] [CrossRef]
- Gairin, E.; Collin, A.; James, D.; Maueau, T.; Roncin, Y.; Lefort, L.; Lecchini, D. Spatiotemporal trends of Bora Bora’s shoreline classification and movement using high-resolution imagery from 1955 to 2019. Remote. Sens. 2021, 13, 4692. [Google Scholar] [CrossRef]
- Smith, K.; Terrano, J.; Pitchford, J.; Archer, M. Coastal wetland shoreline change monitoring: A comparison of shorelines from high-resolution worldView satellite imagery, aerial imagery, and field surveys. Remote. Sens. 2021, 13, 3030. [Google Scholar] [CrossRef]
- Rahnemoonfar, M.; Murphy, R.; Miquel, M.; Dobbs, D.; Adams, A. Flooded area detection from UAV images based on densely connected recurrent neural networks. IEEE Int. Geosci. Remote. Sens. Symp. 2018, 10, 1788–1791. [Google Scholar]
- Gonçalves, J.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote. Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Chen, X.; Chen, J.; Cheng, X.; Zhu, L.; Li, B.; Li, X. Retreating shorelines as an emerging threat to adélie penguins on Inexpressible island. Remote. Sens. 2021, 13, 4718. [Google Scholar] [CrossRef]
- Padro, J.; Muñoz, F.; Planas, J.; Pons, X. Comparison of four UAV georeferencing methods for environmental monitoring purposes focusing on the combined use with airborne and satellite remote sensing platforms. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 130–140. [Google Scholar] [CrossRef]
- Forlani, G.; Diotri, F.; Cella, U.; Roncella, R. Indirect UAV strip georeferencing by on-board GNSS data under poor satellite coverage. Remote. Sens. 2019, 11, 1765. [Google Scholar] [CrossRef]
- Xiang, H.; Tian, L. Method for automatic georeferencing aerial remote sensing (RS) images from an unmanned aerial vehicle (UAV) platform. Biosyst. Eng. 2011, 108, 104–113. [Google Scholar] [CrossRef]
- Liba, N.; Berg-Jurgens, J. Accuracy of orthomosaic generated by different methods in example of UAV platform MUST Q. IOP Conf. Ser. Mater. Sci. Eng. 2015, 96, 012041. [Google Scholar] [CrossRef]
- Vieira, G.; Mora, C.; Pina, P.; Ramalho, R.; Fernandes, R. UAV-based very high resolution point cloud, digital surface model and orthomosaic of the Chã Das Caldeiras Lava fields (Fogo, Cabo Verde). Earth Syst. Sci. Data 2021, 7, 3179–3201. [Google Scholar] [CrossRef]
- Lowe, M.; Adnan, F.; Hamulton, S.; Carvalho, R.; Woodroffe, C. Assessing reef-island shoreline change using UAV-derived Orthomosaics and digital surface models. Drones 2019, 3, 44. [Google Scholar] [CrossRef]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]
- Symonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Poma, X.; Riba, E.; Sappa, A. Dense extreme inception network: Towards a robust CNN model for edge detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 4–8 January 2020; pp. 1923–1932. [Google Scholar]
- Kamangir, H.; Rahnemoonfar, M.; Dobbs, D.; Paden, J.; Fox, G. Deep hybrid wavelet network for ice boundary detection in radra imagery. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2001; pp. 3449–3452. [Google Scholar]
- Mason, C.; Folk, R. Differentiation of beach, dune, and aeolian flat environments by size analysis, Mustang Island, Texas. J. Sediment. Res. 1958, 28, 211–226. [Google Scholar]
- McBride, E.; Abel-Wahab, A.; McGilvery, T. Loss of sand-size feldspar and rock fragments along the South Texas Barrier Island, USA. Sediment. Geol. 1996, 107, 37–44. [Google Scholar] [CrossRef]
- Priestas, A.M.; Fagherazzi, S. Morphological barrier island changes and recovery of dunes after Hurricane Dennis, St. George Island, Florida. Geomorphology 2010, 114, 614–626. [Google Scholar] [CrossRef]
- NOAA. Available online: https://www.noaa.gov/ (accessed on 8 March 2022).
- Park, J.; Heitsenrether, R.; Sweet, W. Water level and wave height estimates at NOAA tide stations from acoustic and microwave sensors. J. Atmos. Ocean. Technol. 2014, 31, 2294–2308. [Google Scholar] [CrossRef]
- NOAA Water Level. Available online: https://tidesandcurrents.noaa.gov/waterlevels.html?id=8775792 (accessed on 2 July 2022).
- NOAA Significant Wave Height. Available online: https://www.ndbc.noaa.gov/ (accessed on 4 May 2022).
- Reza, A. Realization of the contrast limited adaptive histogram equalization (CLAHE) for real-time image enhancement. J. VLSI Signal Process. Syst. Signal Image Video Technol. 2004, 38, 35–44. [Google Scholar] [CrossRef]
- Schreiber-Gregory, D. Ridge Regression and multicollinearity: An in-depth review. Model Assist. Stat. Appl. 2018, 13, 359–365. [Google Scholar] [CrossRef]
- Bae, K.; Rye, H.; Shin, H. Does adam optimizer keep close to the optimal point? arXiv 2019, arXiv:1911.00289. [Google Scholar]
- Prechelt, L. Early stopping-but when? In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 1998; pp. 55–69. [Google Scholar]
- Ledig, C. Photo-realistic single image super-resolution using a generative adversarial networke. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Wang, X. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Roberts, T.M.; Wang, P.; Kraus, N.C. Limits of wave runup and corresponding beach-profile change from large-scale laboratory data. J. Coast. Res. 2010, 26, 184–198. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).