Comparison of the WRF-FDDA-Based Radar Reflectivity and Lightning Data Assimilation for Short-Term Precipitation and Lightning Forecasts of Severe Convection
Abstract
1. Introduction
2. Methodology and Model Setups
2.1. Data for Assimilation and Verification
2.2. Radar Reflectivity Data Assimilation Scheme
2.3. Lightning Data Assimilation Scheme
2.4. Lightning Forecast Scheme
2.5. Model Configuration and Case Description
3. Results
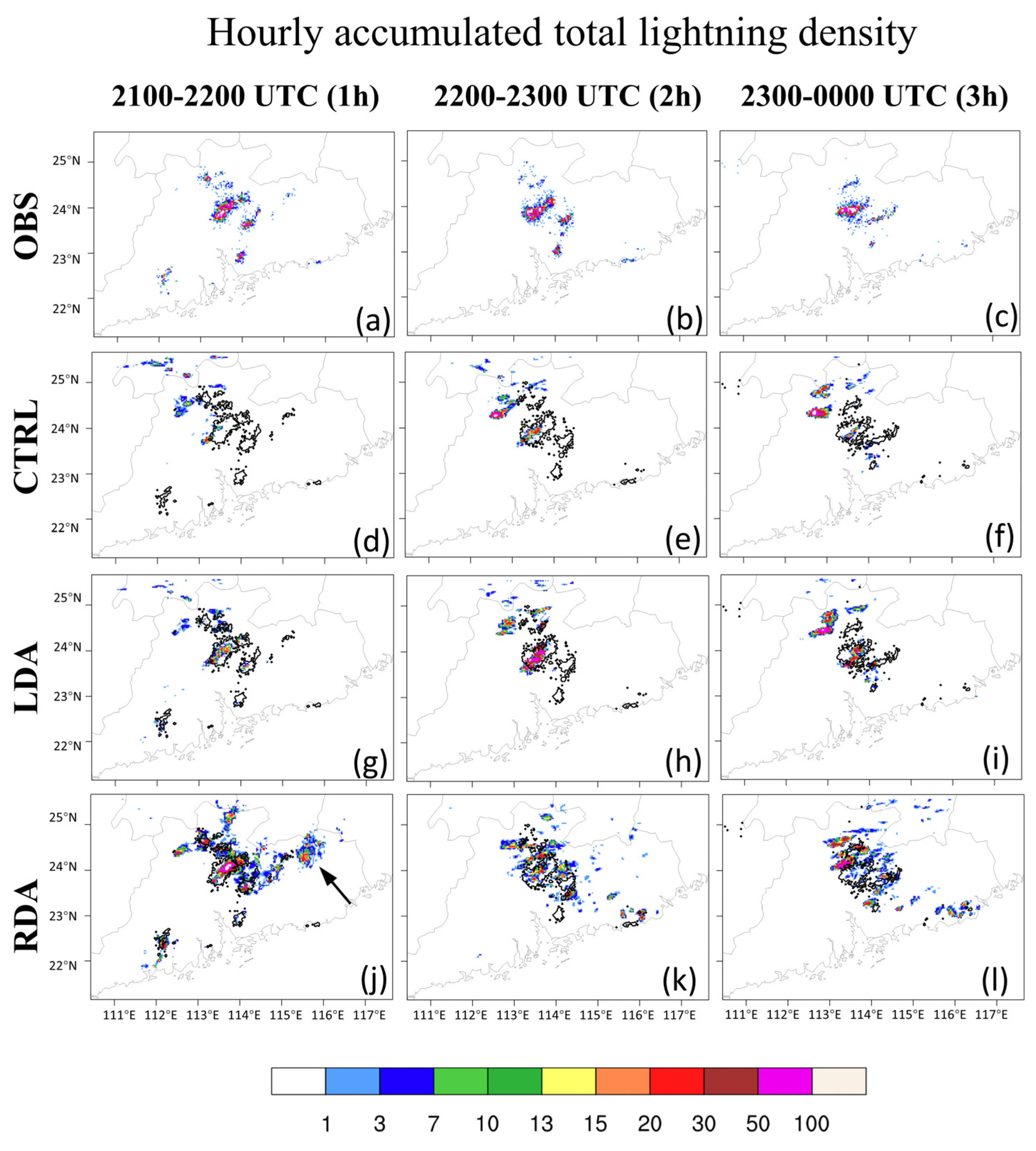
3.1. Case Study of 8 June 2020
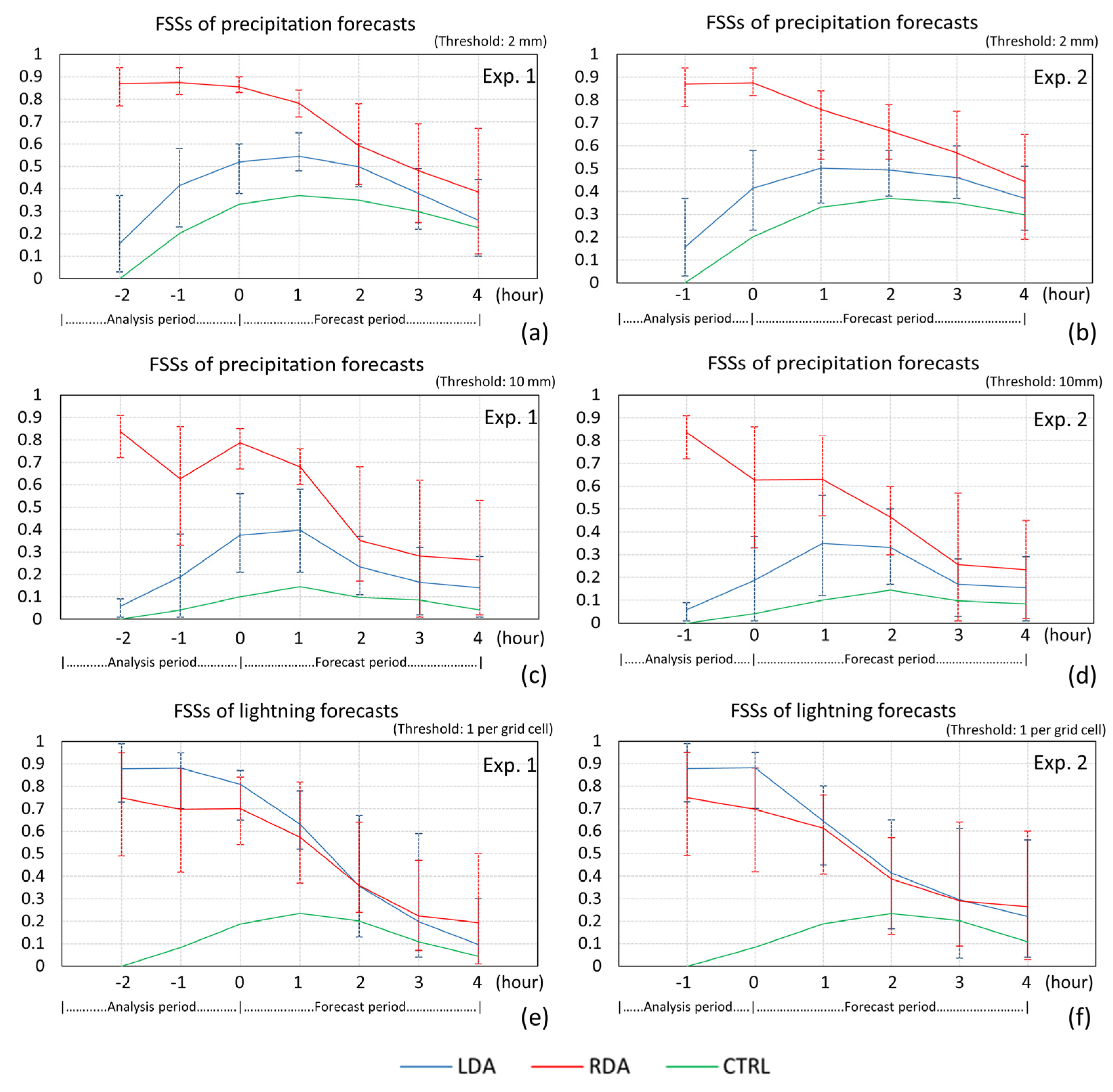
3.2. Statistical Evaluation Results
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Clark, A.J.; Gallus, W.A.; Xue, M.; Kong, F.Y. A Comparison of Precipitation Forecast Skill between Small Convection-Allowing and Large Convection-Parameterizing Ensembles. Weather Forecast. 2009, 24, 1121–1140. [Google Scholar] [CrossRef]
- Fierro, A.O.; Mansell, E.R.; MacGorman, D.R.; Ziegler, C.L. The Implementation of an Explicit Charging and Discharge Lightning Scheme within the WRF-ARW Model: Benchmark Simulations of a Continental Squall Line, a Tropical Cyclone, and a Winter Storm. Mon. Weather Rev. 2013, 141, 2390–2415. [Google Scholar] [CrossRef]
- Fierro, A.O.; Clark, A.J.; Mansell, E.R.; MacGorman, D.R.; Dembek, S.R.; Ziegler, C.L. Impact of Storm-Scale Lightning Data Assimilation on WRF-ARW Precipitation Forecasts during the 2013 Warm Season over the Contiguous United States. Mon. Weather Rev. 2015, 143, 757–777. [Google Scholar] [CrossRef]
- Lynn, B.H. The Usefulness and Economic Value of Total Lightning Forecasts Made with a Dynamic Lightning Scheme Coupled with Lightning Data Assimilation. Weather Forecast. 2017, 32, 645–663. [Google Scholar] [CrossRef]
- Wang, H.L.; Liu, Y.B.; Cheng, W.Y.Y.; Zhao, T.L.; Xu, M.; Liu, Y.W.; Shen, S.; Calhoun, K.M.; Fierro, A.O. Improving Lightning and Precipitation Prediction of Severe Convection Using Lightning Data Assimilation With NCAR WRF-RTFDDA. J. Geophys. Res.-Atmos. 2017, 122, 12296–12316. [Google Scholar] [CrossRef]
- Chen, Y.D.; Yu, Z.; Han, W.; He, J.; Chen, M. Case Study of a Retrieval Method of 3D Proxy Reflectivity from FY-4A Lightning Data and Its Impact on the Assimilation and Forecasting for Severe Rainfall Storms. Remote Sens. 2020, 12, 1165. [Google Scholar] [CrossRef]
- Feng, J.; Wang, X.G. Impact of increasing horizontal and vertical resolution during the HWRF hybrid EnVar data assimilation on the analysis and prediction of Hurricane Patricia. Mon. Weather Rev. 2021, 149, 419–441. [Google Scholar] [CrossRef]
- Zhang, F.Q.; Snyder, C.; Rotunno, R. Effects of Moist Convection on Mesoscale Predictability. J. Atmos. Sci. 2003, 60, 1173–1185. [Google Scholar] [CrossRef]
- Xue, M.; Wang, D.H.; Gao, J.D.; Brewster, K.; Droegemeier, K.K. The Advanced Regional Prediction System (ARPS), storm-scale numerical weather prediction and data assimilation. Meteorol. Atmos. Phys. 2003, 82, 139–170. [Google Scholar] [CrossRef]
- Dawson, D.T.; Xue, M. Numerical Forecasts of the 15–16 June 2002 Southern Plains Mesoscale Convective System: Impact of Mesoscale Data and Cloud Analysis. Mon. Weather Rev. 2006, 134, 1607–1629. [Google Scholar] [CrossRef]
- Hu, M.; Xue, M.; Keith, B. 3DVAR and cloud analysis with WSR-88D level-II data for the prediction of the Fort Worth, Texas, tornadic thunderstorms. Part I: Cloud analysis and its impact. Mon. Weather Rev. 2006, 134, 675–698. [Google Scholar] [CrossRef]
- Huang, Y.J.; Liu, Y.B.; Xu, M.; Liu, Y.W.; Pan, L.L.; Wang, H.L.; Cheng, W.Y.Y.; Jiang, Y.; Lan, H.P.; Yang, H.L.; et al. Forecasting severe convective storms with WRF-based RTFDDA radar data assimilation in Guangdong, China. Atmos. Res. 2018, 209, 131–143. [Google Scholar] [CrossRef]
- Gao, J.D.; Stensrud, D.J. Assimilation of Reflectivity Data in a Convective-Scale, Cycled 3DVAR Framework with Hydrometeor Classification. J. Atmos. Sci. 2012, 69, 1054–1065. [Google Scholar] [CrossRef]
- Liu, C.S.; Xue, M.; Kong, R. Direct Assimilation of Radar Reflectivity Data using 3DVAR: Treatment of Hydrometeor Background Errors and OSSE Tests. Mon. Weather Rev. 2019, 147, 17–29. [Google Scholar] [CrossRef]
- Xiao, Q.N.; Kuo, Y.H.; Sun, J.Z.; Lee, W.C.; Barker, D.M.; Lim, E. An Approach of Radar Reflectivity Data Assimilation and Its Assessment with the Inland QPF of Typhoon Rusa (2002) at Landfall. J. Appl. Meteorol. Clim. 2007, 46, 14–22. [Google Scholar] [CrossRef]
- Sun, J.Z.; Crook, N.A. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. Part I: Model development and simulated data experiments. J. Atmos. Sci. 1997, 54, 1642–1661. [Google Scholar] [CrossRef]
- Wang, H.L.; Sun, J.Z.; Zhang, X.; Huang, Y.X.; Thomas, A. Radar data assimilation with WRF 4D-Var. Part I: System development and preliminary testing. Mon. Weather Rev. 2013, 141, 2224–2244. [Google Scholar] [CrossRef]
- Aksoy, A.; David, C.D.; Chris, S. A multicase comparative assessment of the ensemble Kalman filter for assimilation of radar observations. Part I: Storm-scale analyses. Mon. Weather Rev. 2009, 137, 1805–1824. [Google Scholar] [CrossRef]
- Aksoy, A.; David, C.D.; Chris, S. A multicase comparative assessment of the ensemble Kalman filter for assimilation of radar observations. Part II: Short-range ensemble forecasts. Mon. Weather Rev. 2010, 138, 1273–1292. [Google Scholar] [CrossRef]
- Calhoun, K.; Edward, R.M.; Donald, R.M.; David, C.D. Numerical simulations of lightning and storm charge of the 29–30 May 2004 Geary, Oklahoma, supercell thunderstorm using EnKF mobile radar data assimilation. Mon. Weather Rev. 2014, 142, 3977–3997. [Google Scholar] [CrossRef]
- Dowell, D.C.; Wicker, L.J.; Snyder, C. Ensemble Kalman filter assimilation of radar observations of the 8 May 2003 Oklahoma City supercell: Influences of reflectivity observations on storm-scale analyses. Mon. Weather Rev. 2011, 139, 272–294. [Google Scholar] [CrossRef]
- Snyder, C.; Zhang, F.Q. Assimilation of Simulated Doppler Radar Observations with an Ensemble Kalman Filter. Mon. Weather Rev. 2003, 131, 1663–1677. [Google Scholar] [CrossRef]
- Tong, M.J.; Xue, M. Ensemble Kalman Filter Assimilation of Doppler Radar Data with a Compressible Nonhydrostatic Model: OSS Experiments. Mon. Weather Rev. 2005, 133, 1789–1807. [Google Scholar] [CrossRef]
- Wang, H.L.; Liu, Y.B.; Duan, J.; Shi, Y.Q.; Lou, X.F.; Li, J.M. Assimilation of Radar Reflectivity Using a Time-Lagged Ensemble Based Ensemble Kalman Filter With the “Cloud-Dependent” Background Error Covariances. J. Geophys. Res.-Atmos. 2022, 127. [Google Scholar] [CrossRef]
- Gao, J.D.; Fu, C.H.; Stensrud, D.J.; Kain, J.S. OSSEs for an Ensemble 3DVAR Data Assimilation System with Radar Observations of Convective Storms. J. Atmos. Sci. 2016, 73, 2403–2426. [Google Scholar] [CrossRef]
- Kong, R.; Xue, M.; Liu, C.S.; Jung, Y.S. Comparisons of Hybrid En3DVar with 3DVar and EnKF for Radar Data Assimilation: Tests with the 10 May 2010 Oklahoma Tornado Outbreak. Mon. Weather Rev. 2021, 149, 21–40. [Google Scholar] [CrossRef]
- Tong, C.C.; Jung, Y.S.; Xue, M.; Liu, C.S. Direct Assimilation of Radar Data with Ensemble Kalman Filter and Hybrid Ensemble-Variational Method in the National Weather Service Operational Data Assimilation System GSI for the Stand-Alone Regional FV3 Model at a Convection-Allowing Resolution. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Wang, Y.M.; Wang, X.G. Development of convective-scale static background error covariance within GSI-based hybrid EnVar system for direct radar reflectivity data assimilation. Mon. Weather Rev. 2021, 149, 2713–2736. [Google Scholar] [CrossRef]
- Carey, L.D.; Rutledge, S.A. A multiparameter radar case study of the microphysical and kinematic evolution of a lightning producing storm. Meteorol. Atmos. Phys. 1996, 59, 33–64. [Google Scholar] [CrossRef]
- Deierling, W.; Petersen, W.A.; Latham, J.; Ellis, S.; Christian, H.J. The relationship between lightning activity and ice fluxes in thunderstorms. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Deierling, W.; Petersen, W.A. Total lightning activity as an indicator of updraft characteristics. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Petersen, W.A.; Christian, H.J.; Rutledge, S.A. TRMM observations of the global relationship between ice water content and lightning. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Wiens, K.; Rutledge, S.; Tessendorf, S. The 29 June 2000 Supercell Observed during STEPS. Part II: Lightning and Charge Structure. J. Atmos. Sci. 2005, 62, 4151–4177. [Google Scholar] [CrossRef]
- Fierro, A.O.; Mansell, E.R.; Ziegler, C.L.; MacGorman, D.R. Application of a Lightning Data Assimilation Technique in the WRF-ARW Model at Cloud-Resolving Scales for the Tornado Outbreak of 24 May 2011. Mon. Weather Rev. 2012, 140, 2609–2627. [Google Scholar] [CrossRef]
- Marchand, M.R.; Fuelberg, H.E. Assimilation of Lightning Data Using a Nudging Method Involving Low-Level Warming. Mon. Weather Rev. 2014, 142, 4850–4871. [Google Scholar] [CrossRef]
- Qie, X.S.; Zhu, R.P.; Yuan, T.; Wu, X.K.; Li, W.; Liu, D.X. Application of total-lightning data assimilation in a mesoscale convective system based on the WRF model. Atmos. Res. 2014, 145–146, 255–266. [Google Scholar] [CrossRef]
- Sun, H.; Wang, H.L.; Yang, J.; Zeng, Y.T.; Zhang, Q.L.; Liu, Y.B.; Gu, J.Y.; Huang, S.Y. Improving Forecast of Severe Oceanic Mesoscale Convective Systems Using FY-4A Lightning Data Assimilation with WRF-FDDA. Remote Sens. 2022, 14, 1965. [Google Scholar] [CrossRef]
- Fierro, A.O.; Gao, J.D.; Ziegler, C.L.; Mansell, E.R.; MacGorman, D.R.; Dembek, S.R. Evaluation of a cloud-scale lightning data assimilation technique and a 3DVAR method for the analysis and short-term forecast of the 29 June 2012 derecho event. Mon. Weather Rev. 2014, 142, 183–202. [Google Scholar] [CrossRef]
- Mansell, E.R. Storm-Scale Ensemble Kalman Filter Assimilation of Total Lightning Flash-Extent Data. Mon. Weather Rev. 2014, 142, 3683–3695. [Google Scholar] [CrossRef]
- Allen, B.J.; Mansell, E.R.; Dowell, D.C.; Deierling, W. Assimilation of Pseudo-GLM Data Using the Ensemble Kalman Filter. Mon. Weather Rev. 2016, 144, 3465–3486. [Google Scholar] [CrossRef]
- Kong, R.; Xue, M.; Fierro, A.O.; Jung, Y.; Liu, C.; Mansell, E.R.; MacGorman, D.R. Assimilation of GOES-R Geostationary Lightning Mapper Flash Extent Density Data in GSI EnKF for the Analysis and Short-Term Forecast of a Mesoscale Convective System. Mon. Weather Rev. 2020, 148, 2111–2133. [Google Scholar] [CrossRef]
- Wang, H.L.; Liu, Y.B.; Zhao, T.L.; Liu, Y.W.; Xu, M.; Shen, S.; Jiang, Y.; Yang, H.L.; Feng, S.L. Continuous assimilation of lightning data using time-lagged ensembles for a convection-allowing numerical weather prediction model. J. Geophys. Res.-Atmos. 2018, 17, 9652–9673. [Google Scholar] [CrossRef]
- Carey, L.D.; Rutledge, S.A. The relationship between precipitation and lightning in tropical island convection: A C-band polarimetric radar study. Mon. Weather Rev. 2000, 128, 2687–2710. [Google Scholar] [CrossRef]
- Takahashi, T. Precipitation mechanisms in east Asian monsoon: Videosonde study. J. Geophys. Res.-Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Hazra, A.; Chaudhari, H.S.; Saha, S.K.; Pokhrel, S. Effect of cloud microphysics on Indian summer monsoon precipitating clouds: A coupled climate modeling study. J. Geophys. Res.-Atmos. 2017, 122, 3786–3805. [Google Scholar] [CrossRef]
- Heiblum, R.H.; Koren, I.; Altaratz, O. Analyzing coastal precipitation using TRMM observations. Atmos. Chem. Phys. 2011, 11, 13201–13217. [Google Scholar] [CrossRef]
- Takahashi, T.; Soichiro, S.; Tetsuya, K.; Kenji, S. Riming electrification in Hokuriku winter clouds and comparison with laboratory observations. J. Atmos. Sci. 2017, 74, 431–447. [Google Scholar] [CrossRef]
- MacGorman, D.R.; Rust, W.D.; Schuur, T.J.; Biggerstaff, M.I.; Straka, J.M.; Ziegler, C.L.; Mansell, E.R.; Bruning, E.C.; Kuhlman, K.M.; Lund, N.R.; et al. TELEX the thunderstorm electrification and lightning experiment. Bull. Am. Meteorol. Soc. 2008, 89, 997–1014. [Google Scholar] [CrossRef]
- Saunders, C.P.R.; Norman, H.B.; Emersic, C.; Avila, E.E.; Castellano, N.E. Laboratory studies of the effect of cloud conditions on graupel/crystal charge transfer in thunderstorm electrification. Q. J. R. Meteor. Soc. 2010, 132, 2653–2673. [Google Scholar] [CrossRef]
- Lund, N.R.; MacGorman, D.R.; Schuur, T.J.; Biggerstaff, M.I.; Rust, W.D. Relationships between lightning location and polarimetric radar signatures in a small mesoscale convective system. Mon. Weather Rev. 2009, 137, 4151–4170. [Google Scholar] [CrossRef]
- Liu, Y.B.; Chen, F.; Warner, T.; Basara, J. Verification of a Mesoscale Data-Assimilation and Forecasting System for the Oklahoma City Area during the Joint Urban 2003 Field Project. J. Appl. Meteorol. Clim. 2006, 45, 912–929. [Google Scholar] [CrossRef]
- Liu, Y.B.; Warner, T.T.; Astling, E.G.; Bowers, J.F.; Davis, C.A.; Halvorson, S.F.; Rife, D.L.; Sheu, R.S.; Swerdlin, S.P.; Xu, M. The Operational Mesogamma-Scale Analysis and Forecast System of the U.S. Army Test and Evaluation Command. Part II: Interrange Comparison of the Accuracy of Model Analyses and Forecasts. J. Appl. Meteorol. Clim. 2008, 47, 1093–1104. [Google Scholar] [CrossRef][Green Version]
- Roux, G.; Liu, Y.B.; Monache, L.D.; Sheu, R.S.; Warner, T.T. Verification of high resolution WRF-RTFDDA surface forecasts over mountains and plains. In Proceedings of the 10th WRF Users’ Workshop, Boulder, CO, USA, 23–26 June 2009; pp. 20–23. [Google Scholar]
- Xu, M.; Sun, J.; Liu, Y.; Tessendorf, S. Radar data assimilation for the prediction of front range convection. In Proceedings of the 36th Conference on Radar Meteorology/Use of Radar Data for NWP Models: Radar Data Assimilation for NWP Model Initialization, Breckenridge, CO, USA, 16–20 September 2013; American Meteorological Society: Boston, MA, USA, 2013. [Google Scholar]
- Zhang, Y.J.; Lü, W.T.; Chen, S.D.; Zheng, D.; Zhang, Y.; Yan, X.; Chen, L.W.; Dong, W.S.; Dan, J.R.; Pan, H.B. A review of advances in lightning observations during the past decade in Guangdong, China. J. Meteorol. Res. 2016, 30, 800–819. [Google Scholar] [CrossRef]
- Pang, Z.H.; Shi, C.X.; Gu, J.X.; Pan, Y.; Xu, B. Assessment of a Gauge-Radar-Satellite Merged Hourly Precipitation Product for Accurately Monitoring the Characteristics of the Super-Strong Meiyu Precipitation over the Yangtze River Basin in 2020. Remote Sens. 2021, 13, 3850. [Google Scholar] [CrossRef]
- Lerach, D.G.; Rutledge, S.A.; Williams, C.R.; Cifelli, R. Vertical structure of convective systems during NAME 2004. Mon. Weather Rev. 2010, 138, 1695–1714. [Google Scholar] [CrossRef]
- Pan, Y.; Xue, M.; Ge, G. Incorporating diagnosed intercept parameters and the graupel category within the ARPS cloud analysis system for the initialization of double-moment microphysics: Testing with a squall line over south China. Mon. Weather Rev. 2016, 144, 371–392. [Google Scholar] [CrossRef]
- Smith, P.L.; Myers, C.G.; Orville, H.D. Radar reflectivity factor calculations in numerical cloud models using bulk parameterization of precipitation. J. Appl. Meteorol. Clim. 1975, 14, 1156–1165. [Google Scholar] [CrossRef]
- Carey, L.D.; Bain, A.L.; Retha, M. Kinematic and microphysical control of lightning in multicell convection over Alabama during DC3. In Proceedings of the 23rd International Lightning Detection Conference, Tucson, AZ, USA, 18–19 March 2014; Vaisala: Vantaa, Finland, 2014; pp. 20–21. [Google Scholar]
- Cressman, G.P. An operational objective analysis system. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Fierro, A.O.; Wang, Y.; Gao, J.; Mansell, E.R. Variational assimilation of radar data and GLM lightning-derived water vapor for the short-term forecasts of high-impact convective events. Mon. Weather Rev. 2019, 147, 4045–4069. [Google Scholar] [CrossRef]
- Qian, X.Y.; Wang, H.L. Evaluation of different storm parameters as the proxies for gridded total lightning flash rates: A convection-allowing model study. Atmosphere 2020, 12, 95. [Google Scholar] [CrossRef]
- Skamarock, C.; Klemp, B.; Dudhia, J.; Gill, O.; Liu, Z.Q.; Berner, J.; Wang, W.; Powers, G.; Duda, G.; Barker, D.; et al. A Description of the Advanced Research WRF Model Version 4; NCAR/TN-556+STR; NCAR: Boulder, CO, USA, 2019. [Google Scholar] [CrossRef]
- Janjić, Z.I. The Step-Mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: Implementation of a new snow parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface–hydrology model with the Penn State–NCAR MM5 modeling system, part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Grell, G.A.; Freitas, S.R. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. 2013, 13, 23845–23893. [Google Scholar] [CrossRef]
- Roberts, N.M.; Lean, H.W. Scale-Selective Verification of Rainfall Accumulations from High-Resolution Forecasts of Convective Events. Mon. Weather Rev. 2008, 136, 78–97. [Google Scholar] [CrossRef]
- Parker, M.D.; Johnson, R.H. Organizational Modes of Midlatitude Mesoscale Convective Systems. Mon. Weather Rev. 2000, 128, 3413–3436. [Google Scholar] [CrossRef]
- Houze, R.A. Mesoscale convective systems. Rev. Geophys. 2004, 42. [Google Scholar] [CrossRef]
- Houze, R.A. 100 Years of Research on Mesoscale Convective Systems. Meteorol. Monogr. 2018, 58, 1–17. [Google Scholar] [CrossRef]
- Carey, L.D.; Murphy, L.J.; McCormick, T.L.; Demetriades, N.W.S. Lightning location relative to storm structure in a leading-line, trailing-stratiform mesoscale convective system. J. Geophys. Res. 2005, 110, D03105. [Google Scholar] [CrossRef]
- Cazenave, F.; Gosset, M.; Kacou, M.; Alcoba, M.; Fontaine, E.; Duroure, C.; Dolan, B. Characterization of Hydrometeors in Sahelian Convective Systems with an X-Band Radar and Comparison with In Situ Measurements. Part I: Sensitivity of Polarimetric Radar Particle Identification Retrieval and Case Study Evaluation. J. Appl. Meteorol. Clim. 2016, 55, 231–249. [Google Scholar] [CrossRef]
- Gao, S.B.; Min, J.Z.; Liu, L.M.; Ren, C.Y. The development of a hybrid EnSRF-En3DVar system for convective-scale data assimilation. Atmos. Res. 2019, 229, 208–223. [Google Scholar] [CrossRef]
- Peters, J.M.; Schumacher, R.S. Objective Categorization of Heavy-Rain-Producing MCS Synoptic Types by Rotated Principal Component Analysis. Mon. Weather Rev. 2014, 142, 1716–1737. [Google Scholar] [CrossRef]
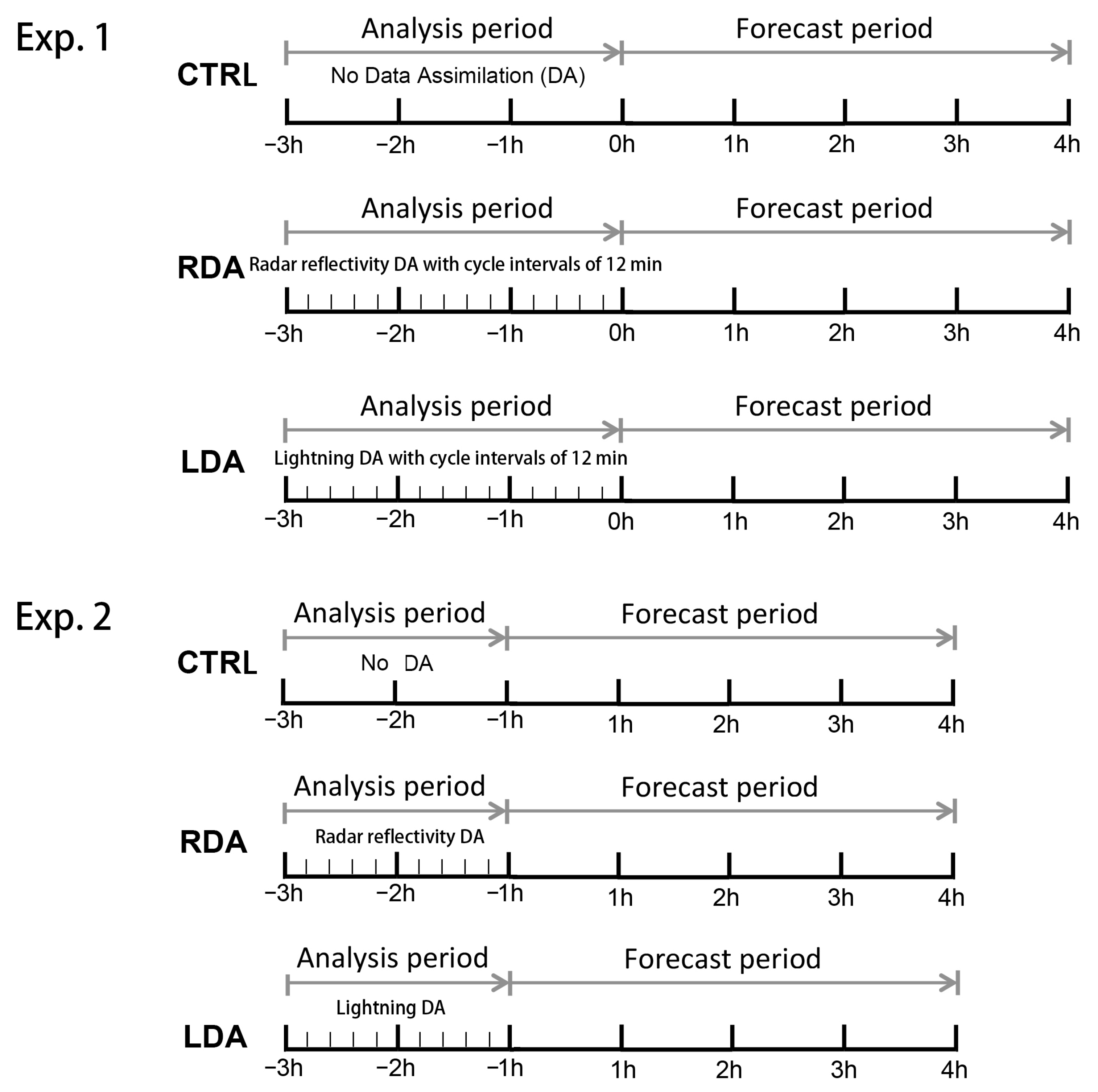
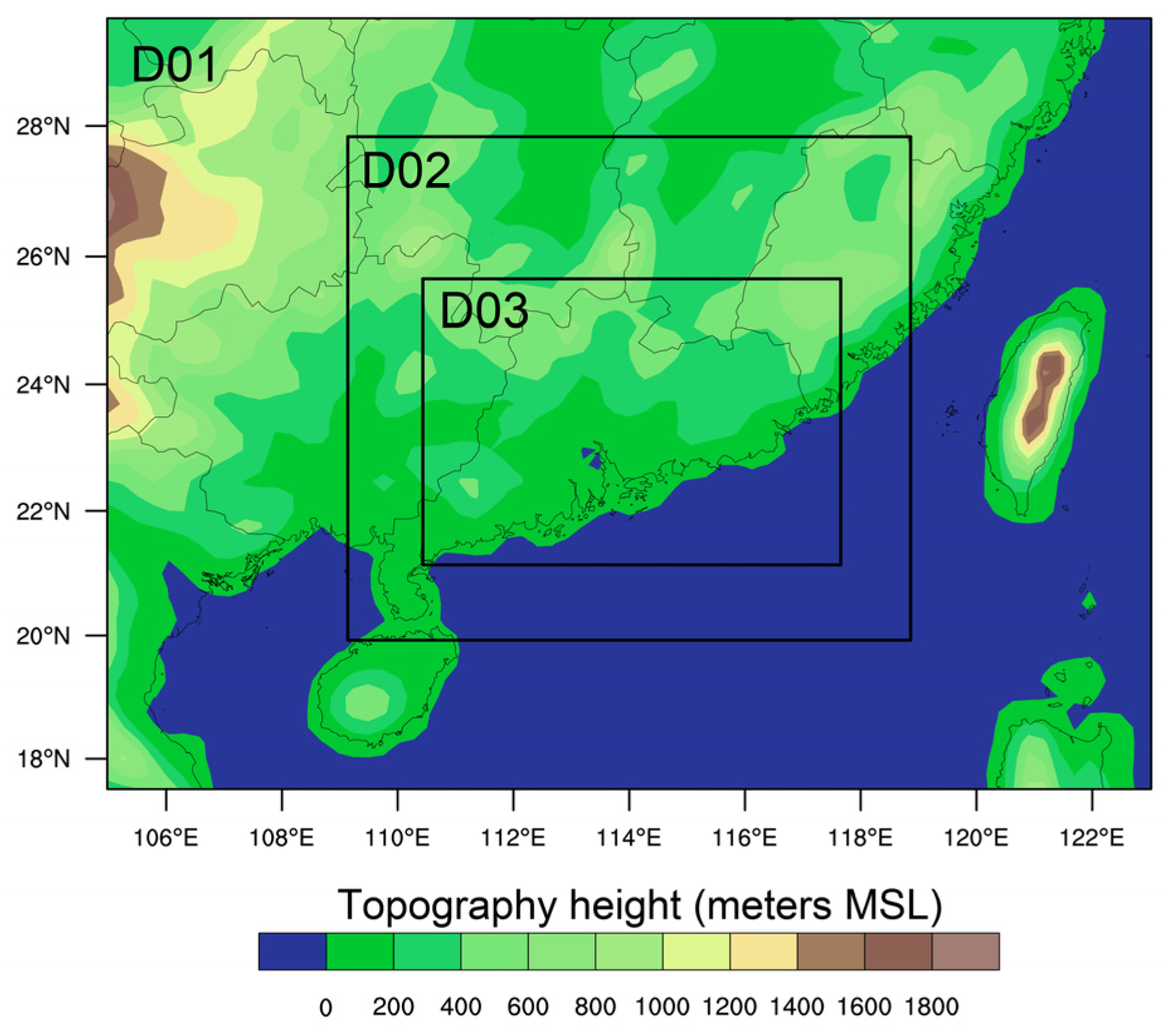

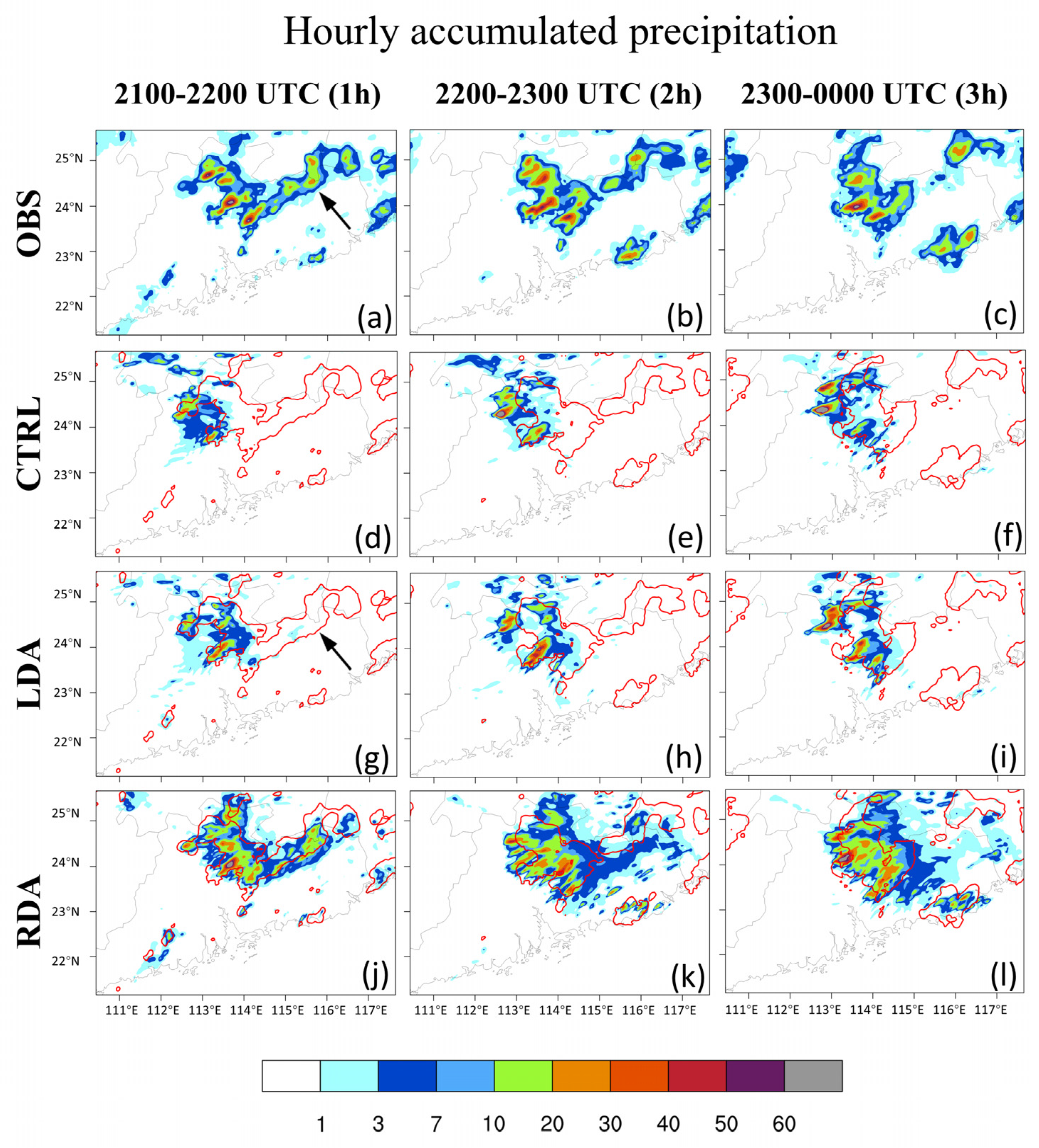
| Events | Simulation Time Periods (UTC) |
|---|---|
| CASE 1 | 2020-06-03_06:00–06-03_13:00 (06-03_12:00) |
| CASE 2 | 2020-06-05_06:00–06-05_13:00 (06-05_12:00) |
| CASE 3 | 2020-06-06_06:00–06-06_13:00 (06-06_12:00) |
| CASE 4 | 2020-06-08_18:00–06-09_01:00 (06-09_00:00) |
| CASE 5 | 2020-06-13_06:00–06-13_13:00 (06-13_12:00) |
| CASE 6 | 2020-06-25_06:00–06-25_13:00 (06-25_12:00) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Yuan, S.; Liu, Y.; Li, Y. Comparison of the WRF-FDDA-Based Radar Reflectivity and Lightning Data Assimilation for Short-Term Precipitation and Lightning Forecasts of Severe Convection. Remote Sens. 2022, 14, 5980. https://doi.org/10.3390/rs14235980
Wang H, Yuan S, Liu Y, Li Y. Comparison of the WRF-FDDA-Based Radar Reflectivity and Lightning Data Assimilation for Short-Term Precipitation and Lightning Forecasts of Severe Convection. Remote Sensing. 2022; 14(23):5980. https://doi.org/10.3390/rs14235980
Chicago/Turabian StyleWang, Haoliang, Shuangqi Yuan, Yubao Liu, and Yang Li. 2022. "Comparison of the WRF-FDDA-Based Radar Reflectivity and Lightning Data Assimilation for Short-Term Precipitation and Lightning Forecasts of Severe Convection" Remote Sensing 14, no. 23: 5980. https://doi.org/10.3390/rs14235980
APA StyleWang, H., Yuan, S., Liu, Y., & Li, Y. (2022). Comparison of the WRF-FDDA-Based Radar Reflectivity and Lightning Data Assimilation for Short-Term Precipitation and Lightning Forecasts of Severe Convection. Remote Sensing, 14(23), 5980. https://doi.org/10.3390/rs14235980







