Abstract
This paper aims to perform imaging and detect moving targets in a 3D scene for space-borne air moving target indication (AMTI). Specifically, we propose a feasible framework for distributed LEO space-borne SAR air moving target 3D imaging via spectral estimation. This framework contains four subsystems: the distributed LEO satellite and radar modeling, moving target information processing, baseline design framework, and spectrum estimation 3D imaging. Firstly in our method, we develop a relative motion model between the satellite platform and the 3D moving target for satellite and radar modeling. In a very short time, the relative motion between the platform and the target is approximated as a uniform motion. We then establish the space-borne distributed SAR moving target 3D imaging model based on the motion model. After that, we analyze the influencing factors, including the Doppler parameters, the three-dimensional velocity, acceleration, and baseline intervals, and further investigate the performance of the 3D imaging of the moving target. The moving target spectrum estimation 3D imaging finally obtains the 3D imaging results of the target, which preliminarily solves the imaging and resolution problems of slow air moving targets. Simulations are conducted to verify the effectiveness of the proposed distributed LEO space-borne SAR moving target 3D imaging framework.
1. Introduction
Synthetic Aperture Radar (SAR) provides two-dimensional images with higher resolutions. In addition, SAR has advantages often offered by non-optical sensors, such as working in all weather conditions and having a high penetrability [1]. The increasing demand for 3D information in various application fields, such as terrain mapping and target recognition, motivates research on 2D high-resolution SAR. However, the moving target introduces azimuth offset, range migration, and defocusing issues. Additionally, the single-channel system cannot obtain 3D information on a moving target and thus cannot perform 3D high-resolution imaging of the moving target [2]. On the other hand, distributed SAR offers various viewing angles and multiple baselines to obtain multi-dimensional scattering information of the target. A typical distributed SAR system with multiple vertical baselines acquires 3D information and the resolution capability in the height direction. Thus, we can provide a new solution for AMTI if the three-dimensional imaging of air-moving targets can be achieved. Moreover, moving target 3D imaging is of great significance for detecting and identifying air military targets and creates significant social and economic impacts on the traffic control of the air targets. Overall, 3D imaging of moving targets lays a good foundation for subsequent object detection and recognition.
Currently, most research activities focus on imaging and detecting two-dimensional ground-moving targets [3]. For instance, Zhang et al. [4] proposed an effective clutter suppression and 2D moving target imaging approach for the geosynchronous-low earth orbit (GEO-LEO) bistatic multichannel SAR system. The authors also performed experiments on fast-moving targets to verify the SAR ground moving target indication (GMTI) capabilities. By combining the geometric modeling of the turning motion and the imaging geometry of space-borne SAR, Wen et al. [5] also proved the accuracy of the analysis of the turning motion imaging signatures. Furthermore, the authors demonstrated the accuracy and validity of their velocity estimation method. Zhang et al. [6] developed an azimuth spectrum reconstruction and imaging method for 2D moving targets in Geosynchronous space-borne–airborne bistatic multichannel SAR, and confirmed a significant performance gain for SAR-GMTI. Moreover, Duan et al. [7] developed a CNN STAP method to improve clutter suppression performance and computation efficiency. Their approach employs a deep learning scheme to predict the high-resolution angle-Doppler profile of the clutter in the GMTI task. Zhan et al. [8] analyzed spaceborne early warning radar performance for AMTI.
The traditional GMTI or AMTI along-track baseline is inappropriate for imaging and detecting weak or slow targets [9]. Therefore, researchers have proposed a distributed vertical baseline architecture, which can distinguish ground and air targets in the height direction. Our method’s distributed vertical multi-baseline space-borne SAR takes full advantage of the discriminative ability along the height direction and overcomes the problem of poor detection of weak or slow targets. Therefore, this paper provides a new solution using the vertical multi-baseline distributed SAR to solve the weak and slow air-moving targets’ 3D imaging and resolution problems.
This paper focuses on 3D imaging of air moving targets for distributed LEO spaceborne SAR. At present, SAR 3D imaging is mainly applied to stationary targets [10] and very limited research has been conducted on the 3D imaging of moving targets. For example, TomoSAR [11] is applied to reconstruct urban buildings, and Fabrizio [12] proposed the new differential tomography framework with the deformation velocity, which provided the differential interferometry tomography concepts, allowing for joint elevation-velocity resolution capability. Budillon et al. [13] provided reliable estimates of the temporal and thermal deformations of the detected scatterers (5D tomography). Although current methods employ different times for the static target, for moving targets, if there are different time observations, the imaging process would bring a large offset of the same pixel in different sequences of images, resulting in the inability to register sequential images. In practice, however, detecting moving targets is required in many applications, e.g., future air traffic control systems. Nevertheless, few studies exist on the 3D imaging of moving targets. For instance, considering geometric invariance, Ferrara et al. [14] proposed two moving target imaging algorithms to solve the problem of reconstructing a 3D target image. The algorithms include a greedy algorithm and a version of basis pursuit denoising. However, in practice, the real target location is unknown. To reduce the system’s complexity and cost, Sakamoto et al. [15] suggested a UWB radar imaging algorithm that estimates unknown two-dimensional target shapes and motions using only three antennas. Their algorithm’s performance depends on the target’s shape characteristics and is not used in distributed SAR systems. Wang et al. [16] proposed the Fractional Fourier Transform (FrFT) algorithm to achieve 3D velocity estimation for moving targets via geosynchronous bistatic SAR. Gui et al. [17] introduced a two-dimensional imaging response algorithm for a three-dimensional moving target for a single SAR using a back-projection imaging algorithm. However, this method is not suitable for distributed SAR. Liu et al. [18] proposed a distributed SAR moving target 3D imaging method to solve the nonuniform 3D configuration clutter suppression problem. Nevertheless, in this method, the baseline distribution is not in the vertical baseline, and there is no discussion of the factors affecting imaging performance.
As was explained above, traditional SAR moving target imaging focuses on two-dimensional ground scenes, and thus current research on 3D moving targets is unable to detect the weak and slow air-moving targets for AMTI. Meanwhile, there are also the following difficulties, such as the azimuth offset caused by motion and the extra signal phase received by each array element, resulting in image defocus. Hence, a framework for the 3D imaging of moving targets is urgently required. Therefore, we propose a feasible framework for distributed LEO space-borne SAR moving target 3D imaging via spectral estimation, which preliminarily solves the imaging and resolution problems of weak and slow air-moving targets. Specifically, this paper proposes a three-dimensional imaging model for moving targets, and further proposes the spatial spectrum estimation method for joint motion in distributed LEO SAR imaging. Then, we analyze the effects of various factors such as azimuth offset, residual video phase (RVP), and different baseline intervals under various velocities. Experimental verification highlights the effectiveness of the proposed distributed LEO space-borne SAR moving target 3D imaging framework.
The main contributions of this paper are as follows:
(1) We propose a feasible framework for air-moving target 3D imaging in distributed LEO space-borne SAR. This framework comprises a distributed LEO satellite and radar modeling, target information processing structure, moving target imaging baseline design, and moving target spectrum estimation for 3D imaging.
(2) We develop a 3D imaging model of moving targets for the space-borne distributed LEO SAR and investigate the influencing factors, including the Doppler parameters, three-dimensional velocity and acceleration, RVP phase, and baseline interval on the performance of 3D imaging of moving targets.
(3) We obtain the 3D imaging result of the moving target using spatial spectrum estimation and compare them against the results of static scenes, different velocities and baseline intervals. The problem of imaging and resolution for slow air-moving targets is preliminarily solved.
The remainder of this paper is as follows. Part 2 presents the preliminaries and methods, establishes the SAR moving target 3D imaging model, and proposes the framework for distributed LEO space-borne SAR moving target 3D imaging. Additionally, this section provides the method design, and based on the SAR moving target 3D imaging model, we design the spatial spectrum estimation for the distributed SAR scene. Part 3 presents the simulation results, and Part 4 discusses the findings. Finally, Part 5 summarizes and concludes this work.
2. Preliminaries and Methods
2.1. Coordinate System
Figure 1 illustrates the frames, with their definitions provided below.
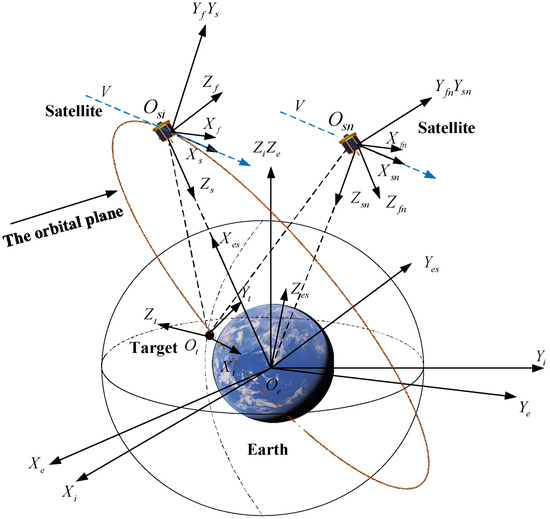
Figure 1.
Coordinate systems.
Earth-centered inertial frame : is the Earth’s center, the axis points to the vernal equinox of the J2000.0, the axis points to the Earth’s north pole along the Earth’s rotation axis, and the axis is obtained according to the right-hand rule.
Earth-centered Earth-Fixed frame : is the center of the Earth, the axis points to the intersection of the prime meridian and the equator, the axis points to the Earth’s north pole along the Earth’s rotation axis, and the axis is obtained according to the right-hand rule.
Earth-centered orbit frame : is the center of the Earth, the axis coincides with the geocentric vector of the reference spacecraft, pointing from the geocentric to the spacecraft, the axis is perpendicular to the axis in the orbital plane of the reference spacecraft pointing to the motion direction, and axis is obtained according to the right-hand rule.
Local vertical local horizontal frame : is the center of mass of the spacecraft, the axis points to the center of the Earth, the axis is along the velocity direction of spacecraft in the orbital plane, and the right-hand rule determines the axis .
Body-centered frame : The body-centered frame is fixed to the spacecraft, which is the reference coordinate system for defining the attitude angle including the yaw angle, pitch angle, and roll angle. is the center of mass of the spacecraft, the axis , axis , and axis aligns with the orthogonal inertial principal axes of the spacecraft. When the yaw angle, pitch angle, and roll angle are all zero, the axis points to the speed direction, the axis is the negative normal of the orbital plane, and the right-hand rule determines the axis .
The Scene frame is the scene center, the axis points from the center of the Earth, the axis is in the plane defined by the beam footprint velocity direction and is perpendicular to the , and the axis is obtained according to the right-hand rule. This coordinate system is attached to the surface of the Earth and rotates with the Earth’s rotation.
The conversion relationship between the coordinate systems is as follows:
The point target and the antenna position vector are converted to the scene coordinate system, where , , , , and are the rotation matrices between the coordinate systems.
Suppose that the position vector of the antenna in the body-centered frame is , is the coordinate of the scene coordinate system origin in the fixed Earth coordinate system, is the Earth’s radius, is the orbit height, , and is the distance from the satellite’s center of mass to the Earth’s center. We can then write:
Let the scene coordinate system coordinates of a point target be . The distance between the antenna phase center and the target is [19]:
In a very short observation synthetic aperture time , the motion of the satellite platform can be decomposed into a uniform acceleration linear motion along each coordinate axis [20]. For further details, see Appendix A.
2.2. Model of 3D SAR Moving Target Imaging
The SAR transmits a linear frequency modulation (LFM) signal and demodulates the received echo signal. The received signal is:
where represents the range time, denotes the azimuth time, is a complex constant, and represents the range envelope. Furthermore, represents the azimuth envelope, is the beam center deviation time, is the wavelength corresponding to the radar center frequency , is the speed of light, represents the chirp signal frequency modulation in the range direction, and is the instantaneous slant range.
Using the Born approximation, the complex value of the pixel indexed in the azimuth-range direction after a target’s two-dimensional imaging is [21]:
where is the span of the target’s height in the normal slant range (NSR) direction, is the three-dimensional distribution function of the complex scattering coefficient of the scene.
To align the two-dimensional image pixel sequence corresponding to the features of the same name, complex image registration is first required. The first image is selected as the main image, and the other images are registered based on the main image as a reference. The complex value can be expressed as [22]:
Figure 2 illustrates a schematic diagram of the SAR 3D moving target imaging model.
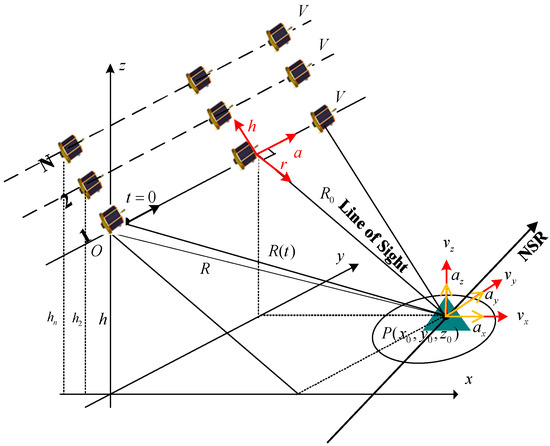
Figure 2.
Model for the SAR moving target 3D imaging.
Assuming that the same target is observed from different spatial positions, a SAR image can be obtained. Since all single-look complex image data of the target area are obtained independently, there are certain differences in the radar spatial position and angle of view.
From the moving target’s initial position and the geometric relationship, we have the following:
For the three-dimensional velocity , we have
For the three-dimensional acceleration , we have
where:
and , , .
We use the third-order Taylor expansion to investigate the impact of the moving target on the SAR image . For details, please refer to Appendix B.
There is no requirement to preserve the image’s phase Thus, the quadratic phase term can be ignored. Hence, the above formula can be rewritten as
where is the spatial frequency corresponding to height in the NSR direction and denotes the baseline interval. Note that the complex value of the resolution unit with the same name in the image sequence is a discrete sampling of the spectrum of the target’s characteristic scattering function in the NSR direction and considering a resolution unit.
The scattering characteristic function is [23]:
2.3. SAR Moving Target 3D Imaging Performance Analysis
In this paper, the performance of SAR 3D imaging contains Doppler and azimuth offset.
2.3.1. Doppler Performance with Velocity and Acceleration
By analyzing the Doppler performance of 3D moving targets, the relationship between 3D velocity and acceleration can be established. The acquisition is also significant for predicting target position, 3D focusing and matching, and laying the foundation for distributed LEO SAR 3D imaging of moving targets. For three-dimensional velocity, where is the Doppler centroid frequency and is the Doppler frequency rate, we write
and for three-dimensional acceleration, is the Doppler centroid frequency and is the Doppler frequency rate.
2.3.2. Azimuth Offset
The azimuth offset, , is [3]:
where is the range cell migration.
2.3.3. RVP Phase
The residual video phase (RVP) is [24]:
Suppose that the RVP phase of satellite 1 is , and the RVP phase of satellite k is . If the baseline direction is perpendicular to the line of sight, and . Hence, the difference between the two Doppler centers is mainly due to the slight difference in the direction of sight.
Assuming that the target’s speed to satellite 1 is at the line of sight, the velocity projected on satellite k is , where is the opening angle from the target to satellite 1 and satellite k and . Then, we calculate the difference between the two RVP terms as follows:

Table 1.
Initial elements from the nominal spacecraft.

Table 2.
Radar parameters.

Table 3.
Signal and antenna parameters.
In the moving target 3D imaging, the phase difference is very small and thus it can be ignored.
2.3.4. Azimuth Defocus and Range Contamination
Using the parameters in Table 1, Table 2 and Table 3, the constraint on the target not to be defocused is [19]:
Therefore, the constraint for preventing range contamination is:
where is the Chirp bandwidth.
2.3.5. Baseline Interval
Suppose is the baseline length of the distributed SAR. The resolution in the height direction is [25,26]:
where is the shortest interval, is the number of baselines, and denotes the baseline interval. The maximum allowable height of the target scene is:
2.4. Distributed LEO Spaceborne SAR Moving Target 3D Imaging Framework
The processing flow of the Distributed LEO space-borne SAR moving target 3D imaging framework is illustrated in Figure 3.
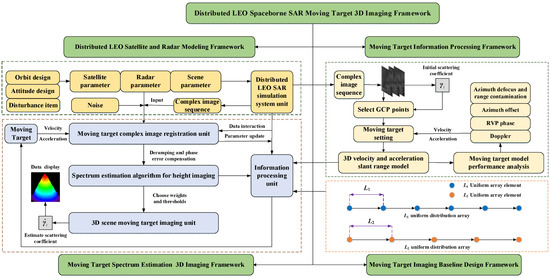
Figure 3.
Distributed LEO space-borne SAR moving target 3D imaging framework.
The processing flow includes four main parts: distributed LEO satellite and radar modeling, moving target information processing, moving target imaging baseline design, and moving target spectrum estimation 3D imaging. The distributed LEO satellite and radar modeling framework includes the satellite, radar, and scene parameters. It also includes the distributed LEO SAR simulation system unit, where the output is the complex image sequence. Furthermore, the proposed framework established the relative motion model and distributed SAR moving target 3D imaging model. The moving target information processing framework contains the ground control point (GCP), 3D velocity, and acceleration setting, and the moving target setting comprises the Doppler parameters, RVP phase, azimuth offset, azimuth defocus and range contamination. The moving target imaging baseline design framework performs the configuration and optimization of different baselines. Finally, all results are input into the information processing unit. The moving target spectrum estimation 3D imaging framework includes the moving target complex image registration unit where deramping and phase error compensation are carried out [27,28]. Furthermore, the spectrum estimation algorithm for height imaging and 3D scene moving target imaging are performed followed by data display [29].
2.5. Method of the Distributed LEO Spaceborne SAR Moving Target 3D Imaging
For the general spatial spectrum estimation, we have the following:
where denotes the weight vector, is the measurement signal, is the input signal, and is the signal power.
For the 3D moving target signal, we have the following:
where is a matrix, and is the scattering coefficient vector. If the velocity is zero, the matrix for the elevation direction is:
For a velocity of , we have [30]:
where is the radial velocity of the scattering point at position in the scattering point dictionary model. Additionally, is the scatter point dictionary model and is the number of speed samples in the speed dictionary.
where is the signal beam direction angle.
2.5.1. Beamforming for 3D Moving Target
Beamforming, also referred to as spatial filtering, is one of the hallmarks of array signal processing. Its essence is to perform spatial filtering by weighting each array element to enhance the desired signal and suppress interference. The weighting factor of each array element can also be adaptively changed according to the change in the signal environment. For , we have
where is the signal power and is the covariance matrix of moving target echo data.
2.5.2. Capon for 3D Moving Target
The weight vector is adaptively formed according to the input and output signals of the array. Different weight vectors can also direct the formed beam in different directions, and the direction of obtaining the maximum output power for the desired signal is the signal incident direction. Thus:
where is the signal power and is the covariance matrix of moving target echo data.
2.5.3. MUSIC for 3D Moving Target
The specific steps include (i) performing eigenvalue decomposition on the covariance matrix of the received data array to obtain the mutually orthogonal signal subspace and noise subspace and then (ii) using the orthogonal characteristics to estimate the signal parameters [31,32]:
where is the signal power, and is the covariance matrix of moving target echo data.
3. Simulation Results
This section generates the simulated SAR data using the Spaceborne Radar Advanced Simulator (SBRAS) system [33,34].
3.1. Simulation Parameters
3.1.1. Satellite Parameters
For SC1, SC2, SC3…SC20, the simulation conditions are as follows. Table 1 reports the spacecraft’s orbit parameters, where a is the semi-major axis, e is the eccentricity, i is the inclination, Ω is the right ascension of ascending node, ω is the argument of perigee, and f is the true anomaly.
For SC1, SC2, SC3…SC20, the tracks are as follows (See Figure 4).

Figure 4.
Tracks for SC1 to SC20 in the Satellite Tool Kit.
3.1.2. Radar Parameters
3.2. Simulation Results
3.2.1. SAR Moving Target 3D Imaging Performance Analysis
- Case 1: Doppler Performance with velocity and acceleration
For , , , the radial velocity is . The corresponding results are illustrated in the following figures.
Based on the given velocity, the Doppler centroid of the 1st and 20th images of the moving target continuously increases as the radial velocity and vertical velocity increase in Figure 5. The deviation of the two images is small in Figure 6, indicating that the Doppler centroid error under different heights is rather small. By increasing the radial and vertical velocities, the Doppler frequency rate of the 1st and 20th images becomes a quadratic function. Figure 5 highlights that for , there is a maximum value, and the impact of is small. Figure 6 also reveals that the Doppler frequency rate deviation of the two images is very small.
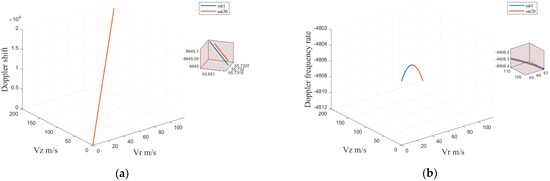
Figure 5.
(a) Doppler centroid with the velocity of the 1st and 20th image; (b) Doppler frequency rate with the velocity of the 1st and 20th image.
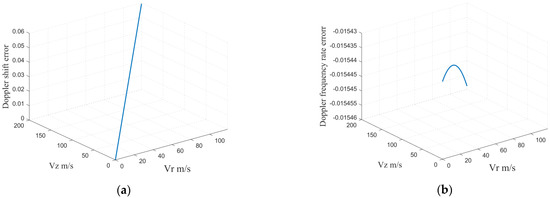
Figure 6.
(a) Deviation of the Doppler centroid with the velocity between the 1st and 20th images; (b) deviation of the Doppler frequency rate with the velocity between the 1st and 20th images.
For , , , the radial velocity is . We set , and the corresponding results are presented in the following figures.
Based on the given acceleration, the Doppler centroid of the 1st and 20th images of the moving target increases as the increasing radial and vertical velocities increase, regardless of the acceleration. Figure 7 highlights that the Doppler frequency rate of the 1st and 20th images also increases with the increasing radial velocity and the normal velocity . Additionally, the impact of is very small, which is directly related to and . We can also see that acceleration mainly affects the Doppler frequency rate instead of the Doppler centroid. Figure 8b also suggests that the Doppler frequency rate deviation of the two images is very small, inferring that acceleration estimation requires at least three Doppler frequency rate equations.
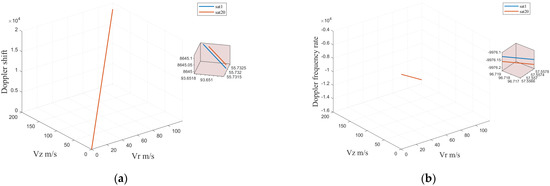
Figure 7.
(a) Doppler centroid with the velocity of the 1st and 20th image under the acceleration; (b) Doppler frequency rate with the velocity of the 1st and 20th image under the acceleration.
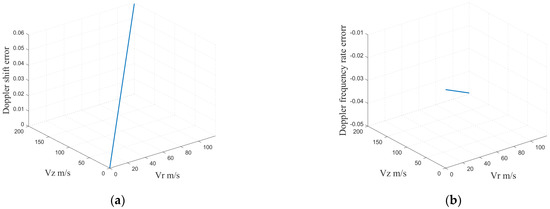
Figure 8.
(a) Deviation of the Doppler centroid with the velocity between the 1st and 20th images; (b) deviation of the Doppler frequency rate with the velocity between the 1st and 20th images.
- Case 2: Azimuth Offset
The azimuth and range offset due to the 1st and 20th satellites are illustrated in Figure 9 and Figure 10.
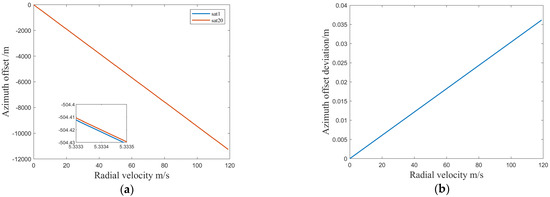
Figure 9.
(a) Azimuth offset with the radial velocity between the 1st and 20th images; (b) azimuth offset deviation with the radial velocity between the 1st and 20th images.
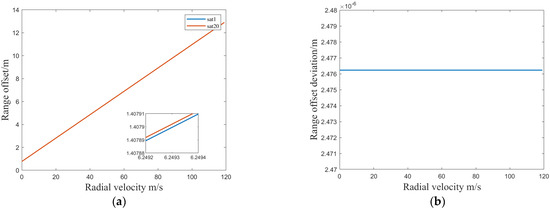
Figure 10.
(a) Range offset with the radial velocity between the 1st and 20th images; (b) range offset deviation with the radial velocity between the 1st and 20th images.
The azimuth direction of all 20 satellites is linearly related to the radial velocity, and the greater the velocity, the greater the offset. For a range velocity of 200 m/s, the difference between the moving point and azimuth offsets of the 1st and 20th satellites is 0.035–0.04 m. The offset difference is about 0.04 m, and the resolution is at the meter level. After registering the complete image, the moving target does not need additional registration.
- Case 3: Baseline Interval
For different baseline intervals, the results are presented in Figure 11.
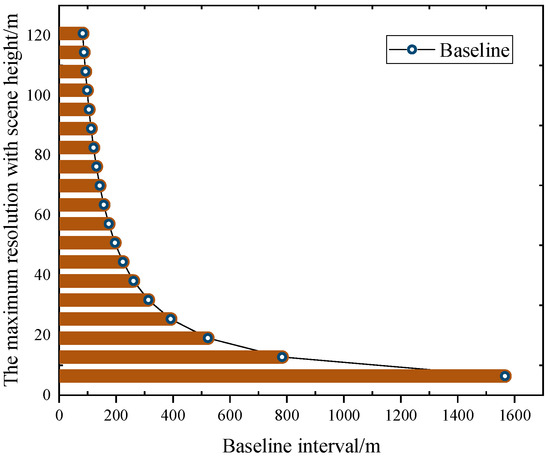
Figure 11.
Effect of baseline interval on scene height.
We set the baseline interval and obtained the maximum allowable height of the target scene. For L = 1566 m, we set the height resolution to 6.35 m for 20 satellites.
3.2.2. Static Target by Spectral Estimation
Through the distributed SAR simulation imaging system, 20 sequence images are obtained. The first trajectory image is used as the reference image, and the other images are registered with the first image. The interference phase is then calculated to find the image’s ground control point (GCP) (this paper sets 100 GCP points). We then find the reference slant distance, divide the grid using the spectral estimation method, focus the entire image, and finally achieve height-directional imaging. Figure 12 shows the 20 SAR images of the cone scene by GCP points.

Figure 12.
Schematic diagram of 20 images of the cone scene.
The results presented in the following figures are based on the spectral estimation method. Figure 13 illustrates the ground truth of the 3D scatter model, Figure 14a,b is the 3D imaging result under 20 and 10 tracks, respectively. Compared with the points corresponding to the ground truth, we observe that the 3D imaging result based on 100 GCP points presents a certain error relationship between them. Figure 15 presents the imaging results of the 1st and 55th points for 20 tracks, and Figure 16 shows the imaging results of the 1st and 55th points for 10 tracks. Both figures highlight that the NSR direction is offset by a certain distance, corresponding to a height of 8.4961 m for Target S1 and 8.2695 m for Target S2. The imaging error of this point is also smaller. Overall, the results reveal that when the total baseline length remains unchanged, the larger the baseline interval, the higher the height resolution.
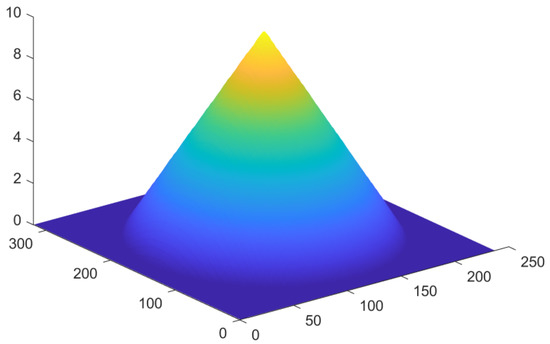
Figure 13.
The 3D scatter model (Ground truth).
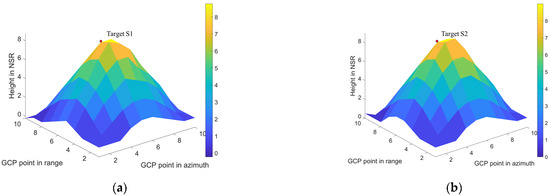
Figure 14.
The 3D imaging results in cone scene: (a) baseline number 20; (b) baseline number 10.
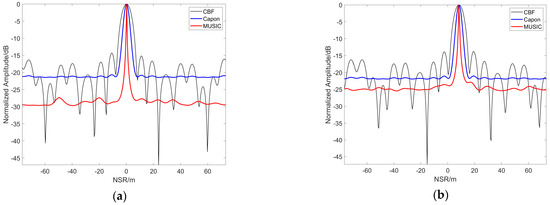
Figure 15.
GCP point results with baseline number 20: (a) 1st point; (b) 55th point.
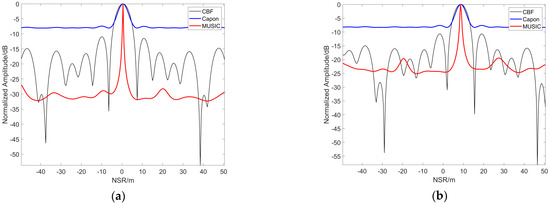
Figure 16.
GCP point results with baseline number 10: (a) 1st point; (b) 55th point.
3.2.3. A Moving Target by Spectral Estimation
Case 1: We set the point in the 5th row and the 6th column (the 55th point) as the moving target point (the red arrow), where for the moving target, its range velocity is vx = 0.1 m/s (preventing range contamination). The corresponding results are presented in Figure 17, Figure 18, Figure 19 and Figure 20. Specifically, Figure 17 shows the 1st, 2nd, and 3rd in 20 SAR images. Figure 18a is the 3D imaging result for 20 tracks, and Figure 18b is for 10 tracks. Figure 19 illustrates the imaging results of the 1st and 55th points for 20 tracks, and Figure 20 shows the imaging results of the 1st and 55th points for 10 tracks.
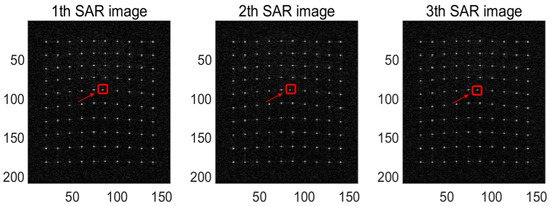
Figure 17.
Schematic diagram of the 1st, 2nd, and 3rd in 20 SAR images (vx = 0.1 m/s).
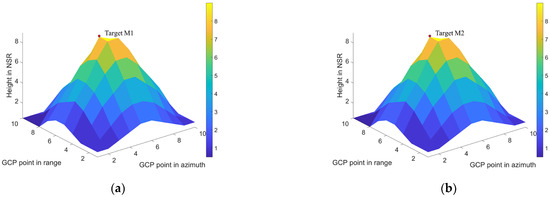
Figure 18.
3D imaging results (vx = 0.1 m/s) in cone scene: (a) baseline number 20; (b) baseline number 10.
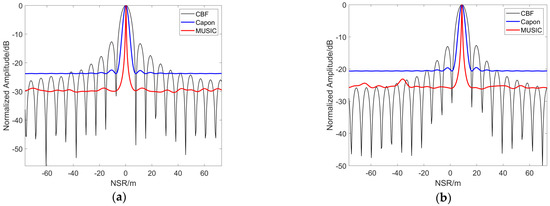
Figure 19.
Moving point result (vx = 0.1 m/s) with baseline number 20: (a) 1st point; (b) 55th point.
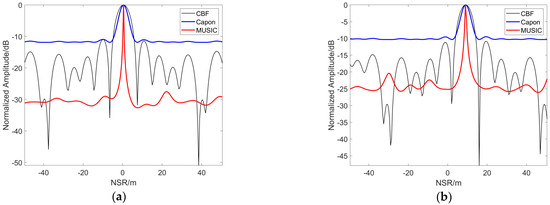
Figure 20.
Moving point result (vx = 0.1 m/s) with baseline number 10: (a) 1st point; (b) 55th point.
The above figures highlight that the 3D imaging result based on 100 GCP points has a certain offset error between them that is relative to the corresponding points in the static state. In the NSR direction, the result corresponds to a height of 8.9961 m for Target M1, and 8.7695 m for Target M2.
Case 2: Similarly, we set the point in row 5 and column 6 as the moving target point (the red arrow), where for the moving target, the range velocity is vx = 2 m/s. The corresponding results are illustrated in Figure 21, Figure 22, Figure 23 and Figure 24. Specifically, Figure 21 presents the 1st, 2nd, and 3rd in 20 SAR images. Figure 22a is the 3D imaging result for 20 tracks, and Figure 22b is for 10 tracks. Figure 23 shows the imaging results of the 1st and 55th points for 20 tracks, and Figure 24 also shows the imaging results of the 1st and 55th points for 10 tracks. The above figures infer that the 3D imaging result based on 100 GCP points has a certain offset error between them relative to the corresponding points in the static state. In the NSR direction, the result corresponds to a height of 16.2695 m for Target M3, and 16.4961 m for Target M4.
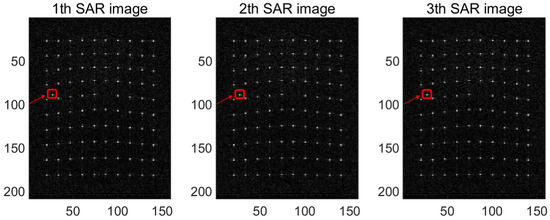
Figure 21.
Schematic diagram of the 1st, 2nd, and 3rd in 20 SAR images (vx = 2 m/s).
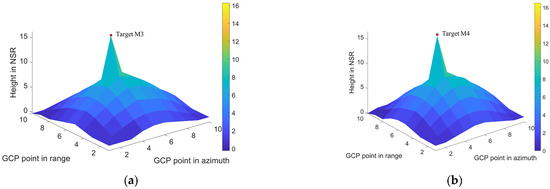
Figure 22.
3D imaging results (vx = 2 m/s) in cone scene: (a) baseline number 20; (b) baseline number 10.
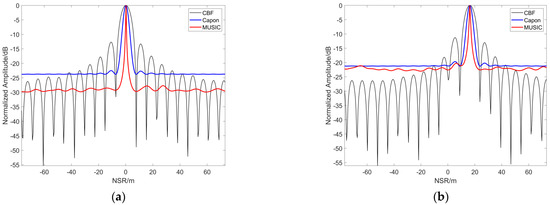
Figure 23.
Moving point result (vx = 2 m/s) with baseline number 20: (a) 1st point; (b) 55th point.
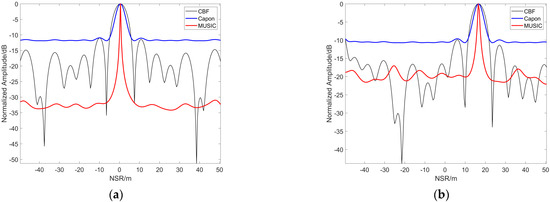
Figure 24.
Moving point result (vx = 2 m/s) with baseline number 10: (a) 1st point; (b) 55th point.
3.3. Simulation Evaluation
We set 100 GCP points 3D imaging time and employed the root means square error (RMSE) as the evaluation condition (performance shown in the Table 4):

Table 4.
Performance of the results.
4. Discussion
In this paper, we propose a framework for distributed LEO SAR air slow moving target 3D imaging via spectral estimation. Specifically, we design adequate simulations to verify the intermediate links’ effectiveness and the method’s final results, highlighting the influencing factors. The simulations demonstrate that we achieve air slow moving target 3D imaging at a speed of 0.1 m/s and 2 m/s. Instead of traditional AMTI methods, our method can distinguish slow-moving targets in the height direction. Compared with the static scene, we found that the moving targets at different speeds result in different effects. The greater the speed, the greater the offset of the moving target. Furthermore, the results suggest that the higher the number of baselines, the better the imaging quality. We also compared the above simulation evaluation results. Additionally, the speed of the moving target is higher, the time consumption is shorter, and the root mean square error is larger. These indicate that the moving target 3D image’s quality is inferior to that of at a low speed. When using different spectral estimation methods, the method’s times are similar. However, CBF requires the longest time, with Capon requiring the second longest time and MUSIC the shortest. Furthermore, regardless of the spectral estimation method, for different baseline numbers, the larger the baseline number, the longer the time and the smaller the root mean square error. It should be noted that the results are consistent with the performance analysis of 3D imaging of moving targets. Furthermore, the above simulation results confirm that the proposed distributed LEO SAR moving target 3D imaging framework meets the requirements and is suitable for AMTI.
5. Conclusions
This paper designs a feasible framework for distributed LEO space-borne SAR moving target 3D imaging space-borne for AMTI in the height of slow air moving targets. Our framework contains four subsystems: distributed LEO satellite and radar modeling, moving target information processing, baseline design framework, and spectrum estimation 3D imaging. Specifically, we first establish the relative motion model of the satellite platform and the 3D imaging of the distributed LEO SAR moving target. Based on the proposed model, a cone scene is designed, and the echo data of the moving target obtained by the distributed SAR simulation system-SBRAS are used to generate two-dimensional sequence images. Considering the key influencing factors, such as the three-dimensional velocity and acceleration, we then discuss the effects of velocities and different baseline intervals on the moving targets’ imaging performance. Moreover, spatial spectrum estimation is used to perform 3D moving target imaging in the NSR direction. The simulations and analysis for different speeds of the moving target are also presented, confirming the proposed method’s efficiency. Future work will improve the entire framework for the distributed LEO SAR moving target 3D imaging for the cases where the image is defocused due to the target’s high speed.
Author Contributions
Conceptualization, Y.H., T.L. and H.H.; methodology, Y.H. and R.J.; validation, Y.H.; formal analysis, Y.H. and T.L., investigation, Y.H., R.J., H.H., Q.W. and T.L.; resources, Y.H., T.L. and H.H.; data curation, Y.H.; writing—original draft preparation, Y.H.; writing—review and editing, Y.H., T.L., Q.W. and H.H.; visualization, Y.H.; supervision, T.L. and H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China (grant no. 62071499), Key Areas of R&D Projects in Guangdong Province (grant no. 2019B111101001), the introduced innovative R&D team project of “The Pearl River Talent Recruitment Program” (grant no. 2019ZT08X751), Guangdong Natural Science Foundation (grant no. 2019A1515011622), and Shenzhen Science technology planning project (grant no. JCYJ20190807153416984).
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the editors and anonymous reviewers for their constructive comments and efforts spent on this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Under the two-body model is the rotation matrix, and we have the following:
where is the orbital inclination, is a time function of the angle between the axis and the axis , , is the initial angle, and is the rotational angular velocity of the Earth. is the argument of latitude, which is the sum of the argument of perigee and the true anomaly, , is the initial argument of latitude, and , is the gravitational parameter of the Earth.
The coordinates of the satellite platform can be expressed as in Local vertical local horizontal frame and is the satellite platform position. Thus, we have:
We use the second-order Taylor expansion of the position . Therefore:
Hence, we have the following:
where is the initial satellite platform position, is the satellite platform speed, and is the satellite platform acceleration. Therefore, in a very short observation time , the motion of the satellite platform can be decomposed into a uniform acceleration linear motion along each coordinate axis.
Appendix B
For three-dimensional acceleration, we have
Since the terms including have no significant contribution, they can be ignored. Similarly, the and terms can be discarded. Hence the equation for the moving target simplifies to
References
- Pi, Y.M.; Yang, J.Y.; Fu, Y.S.; Yang, X.B. Synthetic Aperture Radar Imaging Principle; University of Electronic Science and Technology Press: Chengdu, China, 2007; pp. 50–60. [Google Scholar]
- Candes, E.J.; Tao, T. Near optimal signal recovery from random projections: Universal encoding strategies. IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Baumgartner, S.V.; Krieger, G. Multi-Channel SAR for Ground Moving Target Indication. In Academic Press Library in Signal Processing: Communications and Radar Signal Processing; Elsevier Science Publishers: Amsterdam, The Netherlands, 2014; pp. 911–986. [Google Scholar] [CrossRef]
- Zhang, S.X.; Gao, Y.X.; Xing, M.D.; Guo, R.; Chen, J.L.; Liu, Y.Y. Ground moving target indication for the geosynchronous-low Earth orbit bistatic multichannel SAR system. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 5072–5090. [Google Scholar] [CrossRef]
- Wen, X.J.; Qiu, X.L. Research on turning motion targets and velocity estimation in high resolution spaceborne SAR. Sensors 2020, 20, 2201. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xiong, W.; Dong, X.; Hu, C. A novel azimuth spectrum reconstruction and imaging method for moving targets in geosynchronous spaceborne–airborne bistatic multichannel SAR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5976–5991. [Google Scholar] [CrossRef]
- Duan, K.Q.; Chen, H.; Xie, W.C.; Wang, Y.L. Deep learning for high-resolution estimation of clutter angle-Doppler spectrum in STAP. IET Radar Sonar Navig. 2022, 16, 193–207. [Google Scholar] [CrossRef]
- Zhan, M.Y.; Huang, P.H.; Liu, X.Z.; Chen, J.L.; Gao, Y.S.; Liu, Z.L. Performance analysis of space-borne early warning radar for AMTI. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Li, X.; Deng, B.; Qin, Y.L.; Wang, H.Q.; Li, Y.P. The influence of target micromotion on SAR and GMTI. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2738–2751. [Google Scholar] [CrossRef]
- Zheng, L.F.; Zhang, S.S.; Zhang, X.Q. A novel strategy of 3D imaging on GEO SAR based on multi-baseline system. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1724–1727. [Google Scholar] [CrossRef]
- Knaell, K.K.; Cardillo, G.P. Radar tomography for the generation of three-dimensional images. IEE Eng. Radar Sonar Navig. 1995, 142, 54–60. [Google Scholar] [CrossRef]
- Fabrizio, L. Differential tomography: A new framework for SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 37–44. [Google Scholar] [CrossRef]
- Budillon, A.; Johnsy, A.C.; Schirinzi, G. Extension of a Fast GLRT Algorithm to 5D SAR Tomography of Urban Areas. Remote Sens. 2017, 9, 844. [Google Scholar] [CrossRef]
- Ferrara, M.; Jackson, J.; Stuff, M. Three-dimensional sparse-aperture moving-target imaging. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XV, Orlando, FL, USA, 16–20 March 2008; pp. 49–59. [Google Scholar] [CrossRef]
- Sakamoto, T.; Matsuki, Y.; Sato, T. Method for the three-dimensional imaging of a moving target using an ultra-wideband radar with a small number of antennas. IEICE Trans. Commun. 2012, 95, 972–979. [Google Scholar] [CrossRef]
- Wang, P.F.; Liu, M.; Wang, S.W.; Li, Y.J.; Tang, K. 3D Velocity Estimation for Moving Targets via Geosynchronous Bistatic SAR. In Proceedings of the 2018 China International SAR Symposium (CISS), Shanghai, China, 10–12 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Gui, S.L.; Li, J.; Zuo, F. Synthetic Aperture Radar Imaging Response of Three-dimensional Moving Target. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Lui, M.; Zhang, L.; Li, C.L. Nonuniform three-dimensional configuration distributed SAR signal reconstruction clutter suppression. Chin. J. Aeronaut. 2012, 25, 423–429. [Google Scholar] [CrossRef][Green Version]
- Yang, F.F. Spaceborne Radar GMTI System and Signal Processing Research. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2007. [Google Scholar]
- Zhou, L.; Yuan, J.Q.; Chen, A.L.; Hu, Z.M. Modeling and analysis of air target echo for space-based early warning radar. J. Air Force Early Warn. Acad. 2018, 32, 84–89. (In Chinese) [Google Scholar] [CrossRef]
- Fornaro, G.; Serafino, F.; Soldovieri, F. Three-dimensional focusing with multipass SAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 507–517. [Google Scholar] [CrossRef]
- Sun, X.L. Research on SAR Tomography and Differential SAR Tomography Imaging Technology. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2012. [Google Scholar]
- Zhu, X.X.; Bamler, R. Very high resolution spaceborne SAR tomography in urban environment. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4296–4308. [Google Scholar] [CrossRef]
- Lai, T. Study on HRWS Imaging Methods of Multi-channel Spaceborne SAR. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2010. [Google Scholar]
- Zhao, J.C.; Yu, A.X.; Zhang, Y.S.; Zhu, X.X.; Dong, Z. Spatial baseline optimization for spaceborne multistatic SAR tomography systems. Sensors 2019, 19, 2106. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.H.; Feng, Q.Y.; Liu, S.J.; Bignami, C.; Tolomei, C.; Zhao, D. Minimum redundancy array—A baseline optimization strategy for urban SAR tomography. Remote Sens. 2020, 12, 3100. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Liang, D.N.; Dong, Z. Analysis of time and frequency synchronization errors in spaceborne parasitic InSAR system. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 3047–3050. [Google Scholar] [CrossRef]
- Wang, Q.S.; Huang, H.H.; Yu, A.X.; Dong, Z. An efficient and adaptive approach for noise filtering of SAR interferometric phase images. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1140–1144. [Google Scholar] [CrossRef]
- Wang, Q.S.; Huang, H.H.; Dong, Z.; Yu, A.X.; Liang, D.N. High-precision, fast DEM reconstruction method for spaceborne InSAR. Sci. China-Inf. Sci. 2011, 54, 2400–2410. [Google Scholar] [CrossRef][Green Version]
- Pan, J.; Wang, S.; Li, D.J.; Lu, X.C. High-resolution Wide-swath SAR moving target imaging technology based on distributed compressed sensing. J. Radars 2020, 9, 166–173. (In Chinese) [Google Scholar] [CrossRef]
- Ren, X.Z.; Qin, Y.; Tian, L.J. Three-dimensional imaging algorithm for tomography SAR based on multiple signal classification. In Proceedings of the 2014 IEEE International Conference on Signal Processing, Communications and Computing, Guilin, China, 5–8 August 2014; pp. 120–123. [Google Scholar] [CrossRef]
- Li, H.; Yin, J.; Jin, S.; Zhu, D.Y.; Hong, W.; Bi, H. Synthetic Aperture Radar Tomography in Urban Area Based on Compressive MUSIC. J. Phys. Conf. Ser. 2021, 2005, 012055. [Google Scholar] [CrossRef]
- Chen, Q.; Yu, A.X.; Sun, Z.Y.; Huang, H.H. A multi-mode space-borne SAR simulator based on SBRAS. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 4567–4570. [Google Scholar] [CrossRef]
- Wang, M.; Liang, D.N.; Huang, H.H.; Dong, Z. SBRAS—An advanced simulator of spaceborne radar. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 4942–4944. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).