Numerical and Experimental Studies on the Micro-Doppler Signatures of Freely Flying Insects at W-Band

Abstract

Remote sensing techniques in the microwave frequency range have been successfully used in the context of bird, bat and insect measurements. This article breaks new ground in the analysis of freely flying insects by using a continuous-wave (CW) radar system in W-band, i.e., higher mm-wave frequencies, by measuring and analyzing the micro-Doppler signature of their wing beat motion. In addition to numerical and experimental methods, the investigation also includes the development of a new signal processing method using a cepstrogram approach in order to automatically determine the wing beat frequency. In this study, mosquitoes (culex pipiens) and bees (apis mellifera) are considered as model insects throughout the measurement campaign. It was found that 50 independent micro-Doppler measurements of mosquitoes and bees can be clearly distinguished from each other. Moreover, the proposed radar signal model accurately matches the experimental measurements for both species.

1. Introduction

Over the last two decades, the energy produced by wind turbines has increased significantly [1]. However, the growing presence of wind turbines in nature is problematic for flying animals, since they are in danger of colliding with the rotor blades of wind turbines. Recent studies indicate that collisions of birds and bats with wind turbines result in a significant decrease in biodiversity [2,3]. In Germany, the operators of wind turbines are forced to implement shutdown algorithms to reduce the number of bird and bat fatalities [4]. These algorithms need accurate information on the bird and bat activity in the surroundings in order to determine the time intervals in which the wind turbines need to be shut down. Recent studies have analyzed the detection of birds and bats near wind turbines by using radar systems [5,6]. Birds and bats feed on various insect species and might therefore be attracted by them. A recent study carried out in Southern Sweden found a positive correlation between insect abundance and the activity of bats in the vicinity of wind turbines [7]. Hence, monitoring insect activity in the vicinity of wind turbines could give useful information on the probability of approaching birds and bats. The insect activity can be tracked by various measurement systems, such as radar, lidar, and camera. Among these systems, radar is the most promising [8].

To date, radar technology has been used in many different ways to identify and characterize insects. For instance, the body mass of insects can be estimated by measuring their radar cross-section (RCS) [9,10]. Furthermore, radar polarimetry is commonly used to get information on the body length and width [11,12]. Another approach is to characterize insects based on their micro-Doppler signatures, which are generated by their wing motion. Recently, the micro-Doppler signatures of various radar targets, including birds, drones, and helicopters, have been studied [13,14]. On the other hand, there has been only one study on the micro-Doppler signatures of insects so far [15]. In that study, however, the movement of the insects was restricted, as their backs were adhered on a polystyrene foam. On the other hand, the micro-Doppler signatures of freely flying insects have not been studied so far and are explored for the first time in this paper.

The main goal of this study is to evaluate the feasibility of differentiating mosquitoes of the species culex pipiens and honeybees of the species apis mellifera from each other based on their micro-Doppler signatures. In the context of insect measurements at wind turbines, it is desired to differentiate these insect species autonomously without requiring a human operator. This can be achieved by extracting features, e.g., wingbeat frequency, automatically from the radar signal. The wingbeat frequency of an insect is equivalent to the repetition frequency of other targets, such as the spin frequency of a UAV’s rotor blade. Recent studies have analyzed the extraction of the spin frequency of UAVs by using transformations of the radar signal, such as CVD and cepstrogram [16,17,18]. This paper proposes a novel cepstrogram-based algorithm to extract the wingbeat frequency of the insects. The analysis in this paper is divided into a simulation study and an experimental study, which are both performed with a CW radar operating at $94.3\mathrm{GHz}$. That type of radar has the advantage of requiring a smaller bandwidth, having a simpler structure, and being cheaper compared to other types, such as the FMCW radar [19].

Radar measurements of insects can be challenging, since insects have a particularly small RCS compared to other radar targets, e.g., UAVs. Hence, the radar system should have a small noise level in order to recognize the micro-Doppler signatures of the insects. Among various noise types, flicker noise poses a major disturbance to the radar signal that affects mainly the low-frequency range. Moreover, for CW radars using an in-phase and a quadrature channel, the phase and amplitude imbalance between these channels results in a reduction of the signal quality. As described in recent studies, flicker noise and the imbalance between the in-phase and quadrature channel can be mitigated by using a digital intermediate frequency (IF) architecture for the radar system [20,21]. That architecture is also used in this study in order to increase the quality of the measured micro-Doppler signatures.

2. Materials and Methods

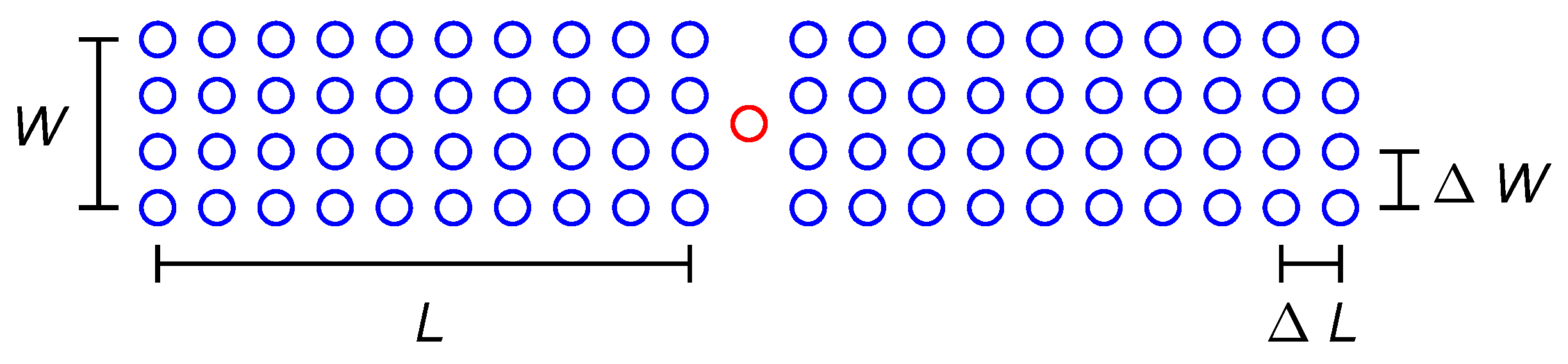
2.1. Radar Signal Modeling of Insects

This section describes the model of the radar signals and of the insects in the simulation. The signal transmitted from the antenna is implemented as a sinusoidal function with a frequency $f_t$:

$$s_t\left(t\right)=cos\left(2\pi f_{t}t\right)$$

(1)

The value of $f_t$ is set to be equal to the transmitted frequency of the radar used in the experimental study, which is $94.3\mathrm{GHz}$. The signal received from a target at a distance R from the radar is a time-delayed and attenuated version of the transmitted signal:

$$\begin{array}{c}{s}_r\left(t\right)=B·cos\left(2\pi f_t(t-\tau \left(t\right))\right)=B·cos\left(2\pi f_t(t-2R\left(t\right)/c)\right)\end{array}$$

(2)

Here, the factor B describes the attenuation of the received signal relative to the transmitted signal, whereas $\tau$ represents the round-trip time of the electromagnetic waves. The third expression in Equation (2) is obtained by plugging in the relation between the round-trip time and the distance, i.e., $\tau =2R/c$, with c being the speed of light. The amplitude of the backscattered signal B in Equation (2) is proportional to the square root of the radar cross-section and inversely proportional to the second power of the distance [22]. It is therefore implemented as $B=\sqrt{\sigma }/R^2$.

In the next step, the received signal is down-converted to the baseband signals $s_I$ and $s_Q$, which represent the in-phase and the quadrature signal, respectively. The in-phase signal is obtained by multiplying the transmitted signal with the received signal, whereas the quadrature signal is given by the product of a ${90}^{\circ }$-delayed version of the transmitted signal with the received one. These multiplications result in a low-frequency component and a high-frequency component, which is eliminated by applying a low-pass filter on the results of the multiplications. Accordingly, the two baseband signals are calculated in the simulation as follows:

$$s_I\left(t\right)=LPF\{s_t\left(t\right)·s_r\left(t\right)\}$$

(3)

$$s_Q\left(t\right)=LPF\{s_{t;{90}^{\circ }}\left(t\right)·s_r\left(t\right)\}$$

(4)

Here, $LPF\{·\}$ represents the applied low-pass filter. The two baseband signals are summarized as real and imaginary parts of a complex signal $s_C$:

$$s_C\left(t\right)=s_I\left(t\right)+i·s_Q\left(t\right)$$

(5)

That signal is then further processed as will be described in Section 2.6.

In recent studies, radar targets have been commonly modeled as a set of point-scatterers [23]. That model is also used in this study to simulate the radar signal of the insects. The received signal obtained from each point-scatterer is calculated according to the above expressions. Figure 1 shows the implemented insect model. The red point-scatterer represents the body, whereas the blue point-scatterers form rectangular arrays that represent the wings of the insect. For each insect, the wing length L and wing width W are implemented according to the corresponding literature values, which are summarized in Table 1 along with the corresponding reference. In that table, A describes the total area of both wings, which is given by $A=2LW$. In recent studies analyzing the simulation of radar targets, the distance between adjacent scatterers is commonly chosen to be a third of the radar wavelength, i.e., $\lambda /3$ [24]. The simulated radar operates at a frequency of $94.3\mathrm{GHz}$, which corresponds to a wavelength of ≈3.18 mm. Accordingly, the distances between adjacent point-scatterers, i.e., $\Delta L$ and $\Delta W$, are chosen to be $\lambda /3=1.06\mathrm{mm}$.

Insects have typically a RCS of the order of ${10}^{-5}{\mathrm{m}}^2$ [25]. However, the specific RCS values of the simulated insect species are not given in the literature. Hence, the aforementioned value of ${10}^{-5}{\mathrm{m}}^2$ is assumed to be the total RCS of both simulated insects. The distribution of the RCS between the body and the wings of insects has not been studied so far. However, the body has a much higher mass in general, i.e., the RCS of the body can be assumed to be significantly higher than that of the wings. In this study, the body of each simulated insect species is assumed to carry $90\%$ of the total RCS. The remaining $10\%$ of the RCS are equally distributed across the point-scatterers that represent the wings.

Table 1. Wing dimensions of the simulated insects.

Insect Species	L [mm]	W [mm]	A [mm${}^2$]	Reference
mosquito (culex pipiens)	3.94	0.79	6.22	[26]
bee (apis mellifera)	9.19	2.87	52.7	[27]

Table 1. Wing dimensions of the simulated insects.

Insect Species	L [mm]	W [mm]	A [mm${}^2$]	Reference
mosquito (culex pipiens)	3.94	0.79	6.22	[26]
bee (apis mellifera)	9.19	2.87	52.7	[27]

The micro-Doppler signatures of the insects are obtained by implementing a periodic wing motion for the model shown in Figure 1. As described in recent studies on the flight dynamics of insects, their wings move along a so-called stroke plane [28]. The position of the wings in that plane can be described by the three Euler angles, as explained in [29]: The angle $\varphi$ describes the position of the wings on the stroke plane, whereas $\psi$ represents the angle of attack of the wings. The third Euler angle, $\theta$, describes minor deviations of the wings from the stroke plain. That angle has only a small effect on the overall wing motion [30] and is therefore assumed to be zero in this study. The variation of the angles $\varphi$ and $\psi$ over time can be modeled as a cosine and a sine, respectively, [30]. Furthermore, the angle $\psi$ can be assumed to oscillate around a mean value of ${90}^{\circ }$ [31], which leads to the following expressions for the implemented wing motion:

$$\varphi \left(t\right)={\varphi }_{mean}+\frac{{\varphi }_{pp}}{2}cos\left(2\pi f_{w}t\right)$$

(6)

$$\psi \left(t\right)={90}^{\circ }-\frac{{\psi }_{pp}}{2}sin\left(2\pi f_{w}t\right)$$

(7)

In these equations, $f_w$ represents the wingbeat frequency, which is $408\mathrm{Hz}$ for culex pipiens [32] and $227\mathrm{Hz}$ for apis mellifera. Furthermore, the parameters ${\varphi }_{mean}$, ${\varphi }_{pp}$ and ${\psi }_{pp}$ describe the mean value and the peak-to-peak value of $\varphi \left(t\right)$ and $\psi \left(t\right)$, respectively. The values of these parameters are shown in

Table 2. Implemented parameters of the wing motion.

Insect Species	${\mathit{\varphi }}_{\mathit{mean}}$	${\mathit{\varphi }}_{\mathit{pp}}$	${\mathit{\psi }}_{\mathit{pp}}$	Reference
mosquitoes (culex pipiens)	${2.1}^{\circ }$	${48}^{\circ }$	${144}^{\circ }$	[31]
bees (apis mellifera)	${36.4}^{\circ }$	${86.7}^{\circ }$	${129}^{\circ }$	[33]

along with the corresponding reference.

In order to make the simulation more realistic, the signal received from the insects is superimposed with thermal noise. The probability distribution for the amplitude of thermal noise amplitude follows a Gaussian distribution. In the simulation, the thermal noise is implemented by generating a random value according to that probability distribution at each sampling point of the baseband signals. Thereby, the thermal noise values for $s_I$ and $s_Q$ are generated independently of each other. The SNR in the simulation is chosen as high as $40\mathrm{dB}$ in order to ensure that the micro-Doppler signatures are not shadowed by the thermal noise.

2.2. Radar System

Compared to other radar targets, such as birds and drones, insects have a relatively small RCS, which makes their measurement particularly challenging. Hence, a high radar sensitivity is critical for performing successful insect measurements.

Table 3. Parameters of the radar system.

Frequency range	75–110 GHz
Optimal frequency	$94.2996\mathrm{GHz}$
Output power	<$0\mathrm{dBm}$
Noise figure	$30\mathrm{dB}$
Dynamic range	$60\mathrm{dB}$
Antenna gain	$16\mathrm{dBi}$

summarizes the parameters of the radar system used in this study. The transmitted frequency of the system can range from $75\mathrm{GHz}$ to $110\mathrm{GHz}$. For this study, the radar is operated at the frequency featuring the highest SNR, which is $94.2996\mathrm{GHz}$. The radar has a heterodyne architecture, i.e., the backscattered signal is first down-converted to an intermediate frequency (IF) before being converted to the baseband. Usually, the IF signal is converted to the baseband by using electric mixers. However, the resulting baseband signal contains flicker noise, which mostly affects the lower frequencies range [34]. Furthermore, the amplitude and the phase of the in-phase and quadrature baseband signals can have a significant imbalance relative to each other. These problems can be mitigated significantly by performing the down-conversion of the IF signals in the digital domain [21,34]. In order to achieve a sufficiently high sensitivity for the insect measurements in this study, the IF signal is down-converted in the digital domain, as will be explained hereafter.

Figure 2 shows a schematic of the radar system used in the experimental study. The radar signals originate from the synthesizer, which has two outputs with frequencies of $15.7150\mathrm{GHz}$ and $15.7166\mathrm{GHz}$, respectively. Before reaching the radar components, the power of these output signals is attenuated by 16 dB, since their initial power is too high for being directly passed to the components of the radar. The $15.7166\mathrm{GHz}$ signal of the synthesizer is passed to the source where its frequency is multiplied by a factor of six, resulting in a signal with a frequency of $94.2996\mathrm{GHz}$. Subsequently, that signal is amplified and passed to the waveguide coupler, where it is split into two parts. The first one is passed to the antenna, where it generates the outgoing electromagnetic wave. The signal backscattered from the target is received by the same antenna. A part of the signal is passed to the receiver via the waveguide coupler. The frequency of that signal is shifted by the Doppler frequency of the moving target and can hence be written as $94.2996\mathrm{GHz}+f_D$. In the receiver, that signal is mixed with the sixfold frequency of the second output of the synthesizer, which is $6·15.7150\mathrm{GHz}=94.29\mathrm{GHz}$. Accordingly, the mixer down-converts the frequency of the received signal to an intermediate frequency (IF) of $(94.2996\mathrm{GHz}+f_D)-94.29\mathrm{GHz}=9.6\mathrm{MHz}+f_D$. As mentioned before, one part of the signal coming from the source is passed to the antenna through the waveguide coupler. The other part of that signal is passed to the reference receiver. The mixer inside the reference receiver outputs an IF signal, whose frequency is given by the difference of the frequencies of its two input signals, i.e., $(94.2996-94.29)\mathrm{GHz}=9.6\mathrm{MHz}$. As shown in Figure 2, the two IF signals are passed to an analog-digital converter (ADC), which is a Handyscope HS5 (TiePie Engineering). Due to the relatively small RCS of insects, their radar signal is prone to noise, e.g., thermal noise. The thermal noise power is inversely proportional to the sampling frequency, as explained in [35]. The sampling frequency of the ADC is chosen as high as $50\mathrm{MHz}$ in order to ensure a low thermal noise level.

Upon digitization, the IF signals are passed to a PC where they are down-converted with the help of a MATLAB script as follows: The first IF-signal, having a frequency of $9.6\mathrm{MHz}+f_D$, is multiplied with the second IF signal ($9.6\mathrm{MHz}$) and its ${90}^{\circ }$-shifted version. Applying a low-pass filter on the results of these multiplications leads to the in-phase and quadrature baseband signals. These signals are then further processed as described in Section 2.6.

2.3. Experimental Setup for Bee Measurements

Figure 3a shows a side view of the experimental setup used to measure the micro-Doppler signatures of bees. The bee flies inside the flight tunnel, which is a rectangular aluminum box that has a length of $37.5\mathrm{cm}$ and a height and width of $11.3\mathrm{cm}$. As shown in Figure 3a, an iris diaphragm is mounted into the side wall of the flight tunnel. The aperture of the diaphragm can be enlarged, such that the bee can enter or leave the flight tunnel. During the experiments, the aperture is closed down in order to prevent the bee from flying out of the tunnel. Figure 3b shows a front view of the experimental setup. The frontage of the flight tunnel is covered by a stretched cling film, which is barely visible in that figure due to its high light transparency. The radar beam enters the flight tunnel via that cling film. Aside from the frontage, all inner walls of the flight tunnel are covered by a layer of black absorbing material. The purpose of these absorbers is to prevent reflections of the radar waves from the inner walls of the flight tunnel, which might disturb the signal received from the bees. The absorbers on the side walls of the flight tunnel are coated by a thin layer of white paper, whereas the absorber on the rear wall is coated with a Rohacell block, resulting in a white and RF-transparent background inside the flight tunnel, which ensures a good contrast for the Raspberry Pi camera.

The setup described so far was used only for the bee measurements. Compared to bees, mosquitoes have a significantly smaller RCS. Preliminary measurements with mosquitoes inside that setup showed that their radar signal is too weak to be measured. Therefore, a different setup was used for the mosquito measurements, as will be explained in the following section.

2.4. Experimental Setup for Mosquito Measurements

Figure 4a shows the experimental setup used for mosquito measurements. The mosquito flies inside the glass tube shown in that figure. The glass tube is held by the arm of the tripod, which reaches the interior of the flight tunnel through the aperture in the side wall. In order to prevent reflections from the metallic arm of the tripod, an absorber is placed in front of it. Figure 4b shows a close-up of the glass tube. The frontage of the glass tube is covered by a stretched cling film that prevents the mosquito from flying out. The orientation of the glass tube is parallel to the radar beam, such that the mosquito always flies close to the center of the radar main lobe, resulting in a strong backscattered signal. With this setup, the micro-Doppler signatures of mosquitoes were found to be measurable in spite of their particularly small RCS.

2.5. Measurements Analyzed in the Experimental Results Section

During the experiments, the measurements of the mosquitoes and bees were triggered manually as soon as an insect was seen flying in the video of the Raspberry Pi camera. Most performed measurements were not successful because the insects flew outside the main lobe or too far away from the radar, such that their micro-Doppler signatures were not detectable. In total, fifty successful mosquito and bee measurements were recorded. These measurements are analyzed in Section 3.2.

2.6. Automatic Extraction of the Wingbeat Frequency

Insects can be identified based on the features contained in their radar signal, such as wingbeat frequency, bandwidth, and bulk Doppler frequency. This study proposes a novel cepstrogram-based algorithm (Figure 5) to extract the wingbeat frequency of the insects, as will be explained hereafter. In the first step of that algorithm, the time-domain signal is transformed into a time-frequency representation. Recent studies analyzing the micro-Doppler signatures of radar targets used a variety of transformations to obtain a time-frequency representation, including the short time Fourier transform (STFT) [36,37], the wavelet transform [38] and the Wigner Ville distribution [39]. Since this is the first study exploring the micro-Doppler signatures of freely flying insects, it focuses on the most traditional of the aforementioned representations, which is considered to be the STFT. In the future, this study can be extended by using other representations in addition to the STFT.

The STFT is obtained by first dividing the time domain signal into M subsequent time intervals of equal size. Each of these time intervals contains N sampling points. To obtain the frequency content, a Fourier transform is applied to each of these intervals. The STFT of the discrete time domain signal $x\left[n\right]$ can be expressed mathematically as [40]:

$$STFT[m,k]=\sum _{n=-\infty }^{\infty }w[n-Hm]x\left[n\right]e^{\frac{-2\pi ikn}{N}}$$

(8)

Here, the indices m and k represent the discrete time and frequency values, respectively. The spectrogram is obtained by taking the absolute value of the STFT. In recent studies analyzing the micro-Doppler signatures of radar targets, the spectrogram is widely used to reveal the time dependency of the Doppler frequencies. However, it is difficult to accurately extract features, e.g., wingbeat frequency or bandwidth, directly from the spectrogram [40]. Recent studies have used a representation called cepstrogram in order to extract features from the micro-Doppler signatures of radar targets [18]. Mostly, cepstrograms have been used to extract the rotation frequencies of UAV rotor blades [41,42,43]. In this study, that representation is used to extract the wingbeat frequencies of insects. The cepstrogram is obtained by inversely Fourier transforming the logarithm of the spectrogram along its Doppler axis [44]:

$$C[m,q]=IF{T}_D\left\{log\right(\left|STFT[m,k]\right|\left)\right\}=IF{T}_D\left\{log\left(S[m,k]\right)\right\}$$

(9)

Here, $IF{T}_D$ refers to an inverse Fourier transform along the Doppler axis. The index m in Equation (9) represents the time axis of the cepstrogram, whereas q represents the so-called quefrency. The cepstrogram features a maximum at the quefrency corresponding to the inverse repetition frequency of the micro-Doppler signature, i.e., the wingbeat frequency of the insect. To determine the quefrency featuring the maximum value, the cepstrogram is projected onto its quefrency-axis. The projected cepstrogram is described mathematically by the following expression:

$$C_p\left[q\right]=\sum _{m=1}^M{\left|C[m,q]\right|}^2$$

(10)

As with the cepstrogram, the maximum quefrency of the projected ceptrogram corresponds to the inverse wingbeat frequency of the insect. Hence, the wingbeat frequency $f_w$ can be obtained by taking the inverse value of the maximum quefrency $q_{max}$, as shown in the last step of Figure 5. That figure summarizes the steps used to automatically extract the wingbeat frequency of the insects in this study.

3. Results

3.1. Numerical Simulations

The length of a simulation interval was chosen to match the duration of an experimental measurement, which is $0.67\mathrm{s}$. Furthermore, the simulated insects were assumed to fly on a straight trajectory towards the radar. In order to make the simulation and experimental study comparable with each other, the initial distance between the radar and the insect in the simulation was chosen such that it agrees with typical values within the experimental setup, which are of the order of $10\mathrm{cm}$. The insects hover at the same position throughout the measurement, i.e., their flight velocity was assumed to be $0\mathrm{m}/\mathrm{s}$.

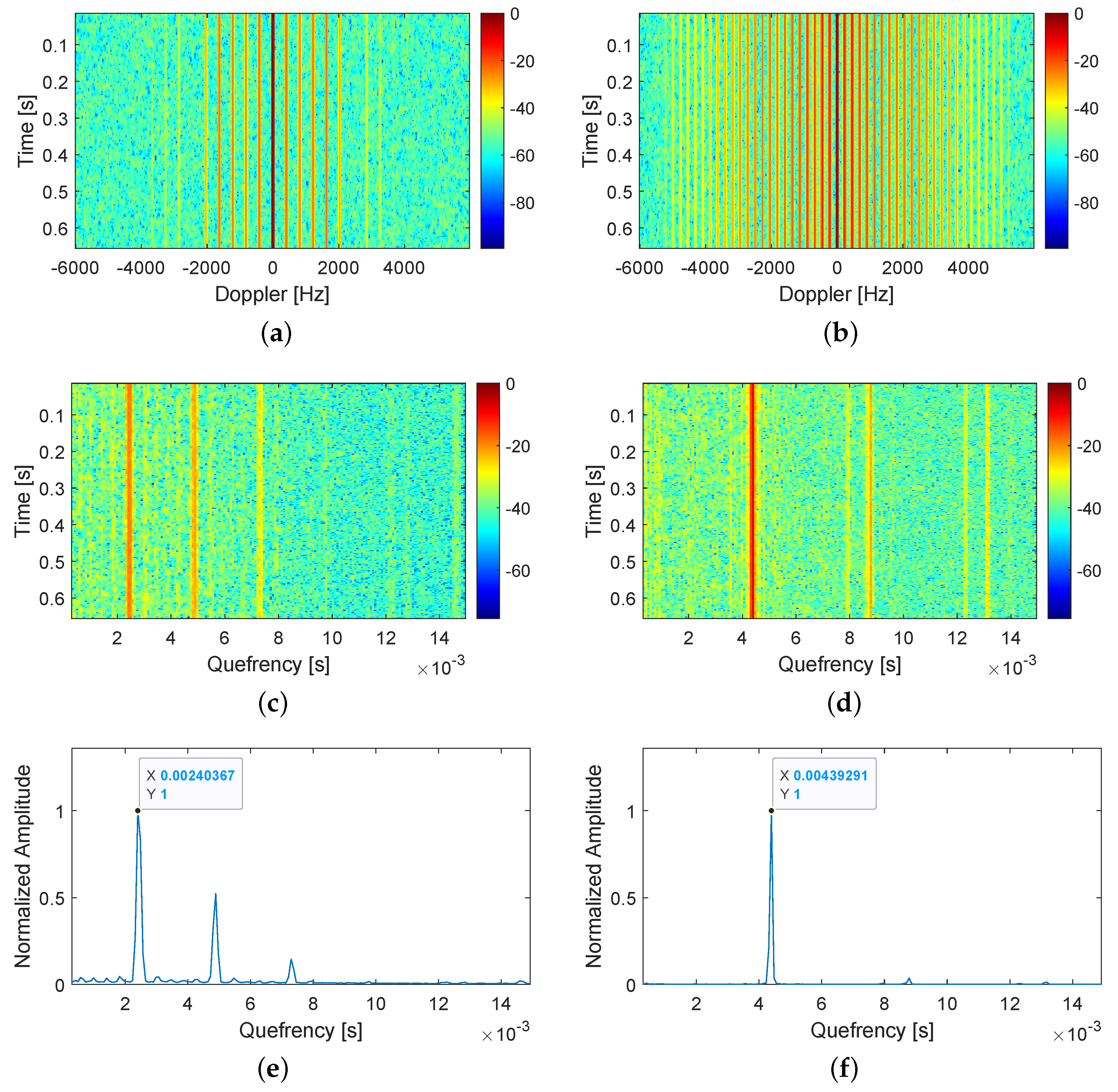
3.1.1. Simulation Results of a Mosquito

As shown in Figure 5, the starting point of the analysis is the spectrogram of the simulated insect. Figure 6a shows the spectrogram obtained from a mosquito simulation. As seen in that figure, the signal of the flying mosquito appears as a pattern of maxima that are equally distant along the Doppler axis. The maximum at $0\mathrm{Hz}$ has by far the highest amplitude. As mentioned before, the insects were assumed to fly with a velocity of $0\mathrm{m}/\mathrm{s}$, i.e., their body remains at the same position throughout the simulation. Accordingly, the maximum at $0\mathrm{Hz}$ in Figure 6a can be identified as the contribution of the mosquito’s body. On the other hand, the maxima at frequencies other than $0\mathrm{Hz}$ are generated by the periodic wing motion and hence represent the micro-Doppler signatures of the mosquito. The distance between these maxima matches the wingbeat frequency of the simulated mosquito, which is $408\mathrm{Hz}$.

As discussed in Section 2.6, the spectrogram is transformed into a cepstrogram in order to obtain the wing beat frequency. The cepstrogram, shown in Figure 6c, features a maximum at a quefrency of about ≈$2.5\times {10}^{-3}\mathrm{s}$. In addition, that cepstrogram contains weaker maxima at multiples of that quefrency. In order to determine the position of the strongest maximum more precisely, the cepstrogram was projected onto its quefrency-axis. Figure 6e shows the projection of the spectrogram. As seen in that figure, the strongest peak is located at a quefrency of $2.404\times {10}^{-3}\mathrm{s}$. As explained in Section 2.6, that value corresponds to the inverse wingbeat frequency. Accordingly, the extracted wingbeat frequency is given by $1/(2.404\times {10}^{-3}\mathrm{s})=416\mathrm{Hz}$. The relative error between the simulated and extracted wingbeat frequency is $1.96\%$, as shown in

Table 4. Error analysis between simulated and extracted frequency.

Insect Species	Simulated Frequency	Extracted Frequency	Relative Error
mosquito (culex pipiens)	408 Hz	416 Hz	1.96%
bee (apis mellifera)	227 Hz	227.6 Hz	0.26%

.

3.1.2. Simulation Results of a Bee

As shown in Figure 6b, the spectrogram obtained from the bee simulation features a pattern of equally distant maxima. The strongest maximum, located at $0\mathrm{Hz}$, can be identified as the contribution of the insect’s body, as explained in Section 3.1.1 for the mosquito simulation. As in the mosquito simulation, the distance between these maxima corresponds to the wingbeat frequency of the insect, which is $227\mathrm{Hz}$ for the simulated bee. Compared to Figure 6a, the micro-Doppler signature generated by the bee features a significantly higher Doppler bandwidth, which indicates that the wings of the bee reach higher velocities.

To extract the wingbeat frequency of the simulated bee, the spectrogram was transformed into a cepstrogram, shown in Figure 6d. That cepstrogram exhibits a strong maximum at a quefrency slightly above $4\times {10}^{-3}\mathrm{s}$. To obtain the exact position of that maximum, the cepstrogram was projected along its time axis. As shown in Figure 6f, the maximum quefrency has a value of $4.393\times {10}^{-3}\mathrm{s}$. Accordingly, the extracted wingbeat frequency is $1/(4.393\times {10}^{-3}\mathrm{s})=227.6\mathrm{Hz}$. Table 4 summarizes the simulated and extracted wingbeat frequencies along with the corresponding relative errors. For both insects, the wingbeat frequency extracted with the algorithm in Figure 5 has a relative error below $2\%$.

3.2. Experimental Results

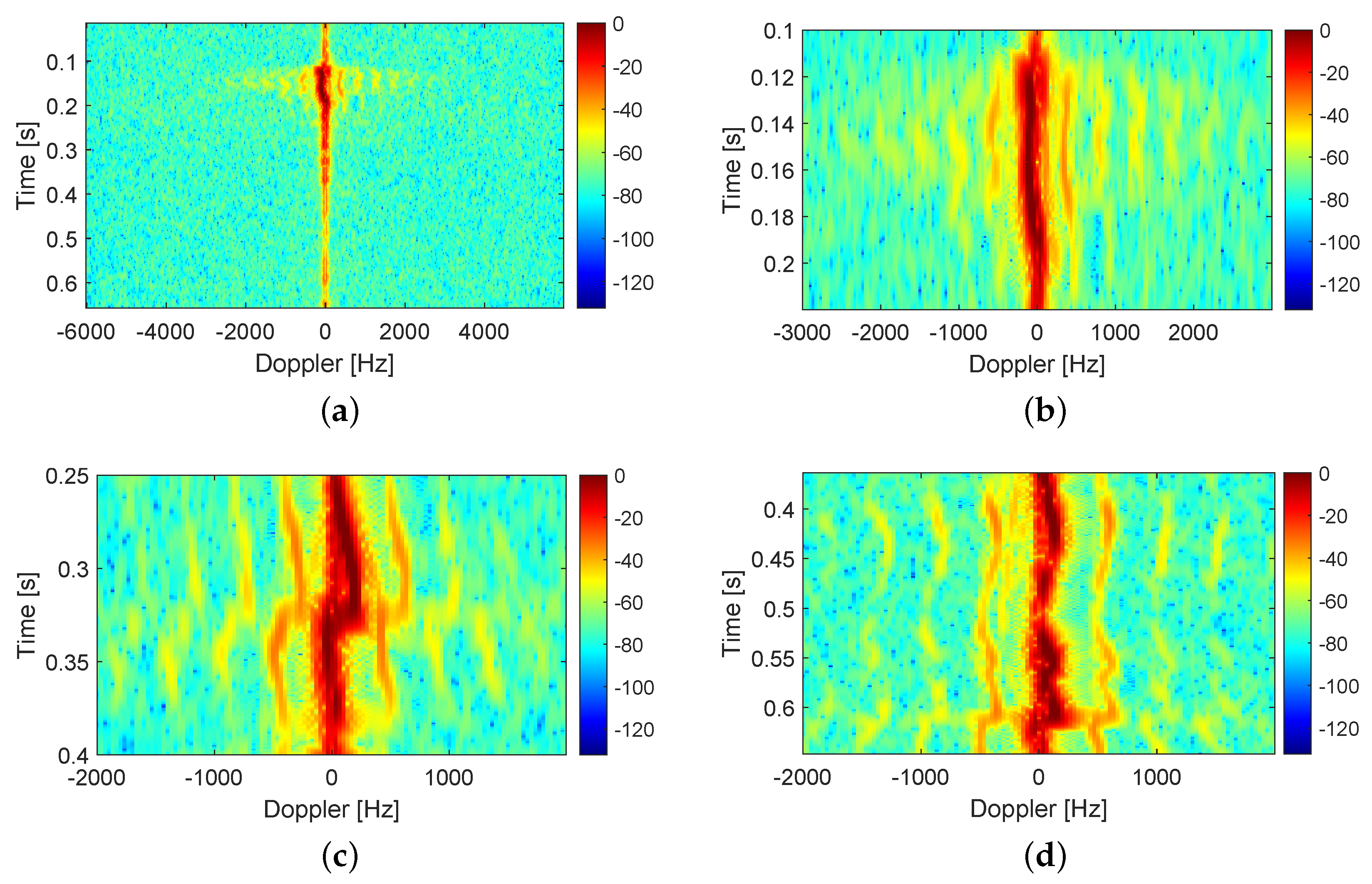
3.2.1. Results of the Mosquito Measurements

Figure 7a shows the spectrogram obtained from one of the mosquito measurements. It exhibits a signal close to $0\mathrm{Hz}$ over the whole measurement interval, i.e., the mosquito generates a detectable signal during that time. The spectrogram features frequencies other than $0\mathrm{Hz}$ during a short time interval ranging from $t\approx 0.12\mathrm{s}$ to $t\approx 0.2\mathrm{s}$. Figure 7a shows an excerpt of Figure 7b containing that time interval. In order to understand the occurrence of these frequencies in the aforementioned time interval, the corresponding video frames, shown in Figure 8, are evaluated hereafter. In these frames, the black arrow points at the position of the mosquito. In Figure 8a,b, the mosquito is sitting on the bottom of the glass tube without performing any significant motion. Thereafter, in Figure 8c,e, i.e., from $t=0.117\mathrm{s}$ to $t\approx 0.197\mathrm{s}$, the mosquito flies a short distance from the bottom to the top of the glass tube. The spectrogram (Figure 7b) features Doppler frequencies deviating from the DC value in precisely that time interval. Hence, the observed Doppler frequencies can be attributed to the wing motion of the flying mosquito. In the aforementioned time interval, i.e., from $t=0.117\mathrm{s}$ to $t\approx 0.197\mathrm{s}$, the spectrogram features a pattern of equidistant maxima, which matches the micro-Doppler signatures obtained in the simulation of a flying mosquito (Figure 6a) in many aspects: First, the distance between adjacent maxima approximately matches the average wingbeat frequency of the analyzed mosquito species culex pipiens, which is $408\mathrm{Hz}$ on average [32]. Moreover, the micro-Doppler signatures of the mosquito reach up to frequencies of $\pm 2000\mathrm{Hz}$ in the experiment as well as in the simulation. As seen in Figure 7b, the maximum near $0\mathrm{Hz}$ is significantly stronger than the maxima of higher order. As explained for the simulation results, that maximum can be identified as the contribution of the body motion.

Figure 7c,d show the spectrograms obtained from two other mosquito measurements. As in the mosquito measurement discussed before, these spectrograms feature a pattern of equidistant maxima that are separated by the wingbeat frequency of the mosquito. The spectrogram of each measurement in Figure 7 features a different curve shape of the bulk-Doppler maximum and of the higher-order maxima. These differences in the curve shapes can be attributed to the flight trajectory of the mosquito, which varies from measurement to measurement.

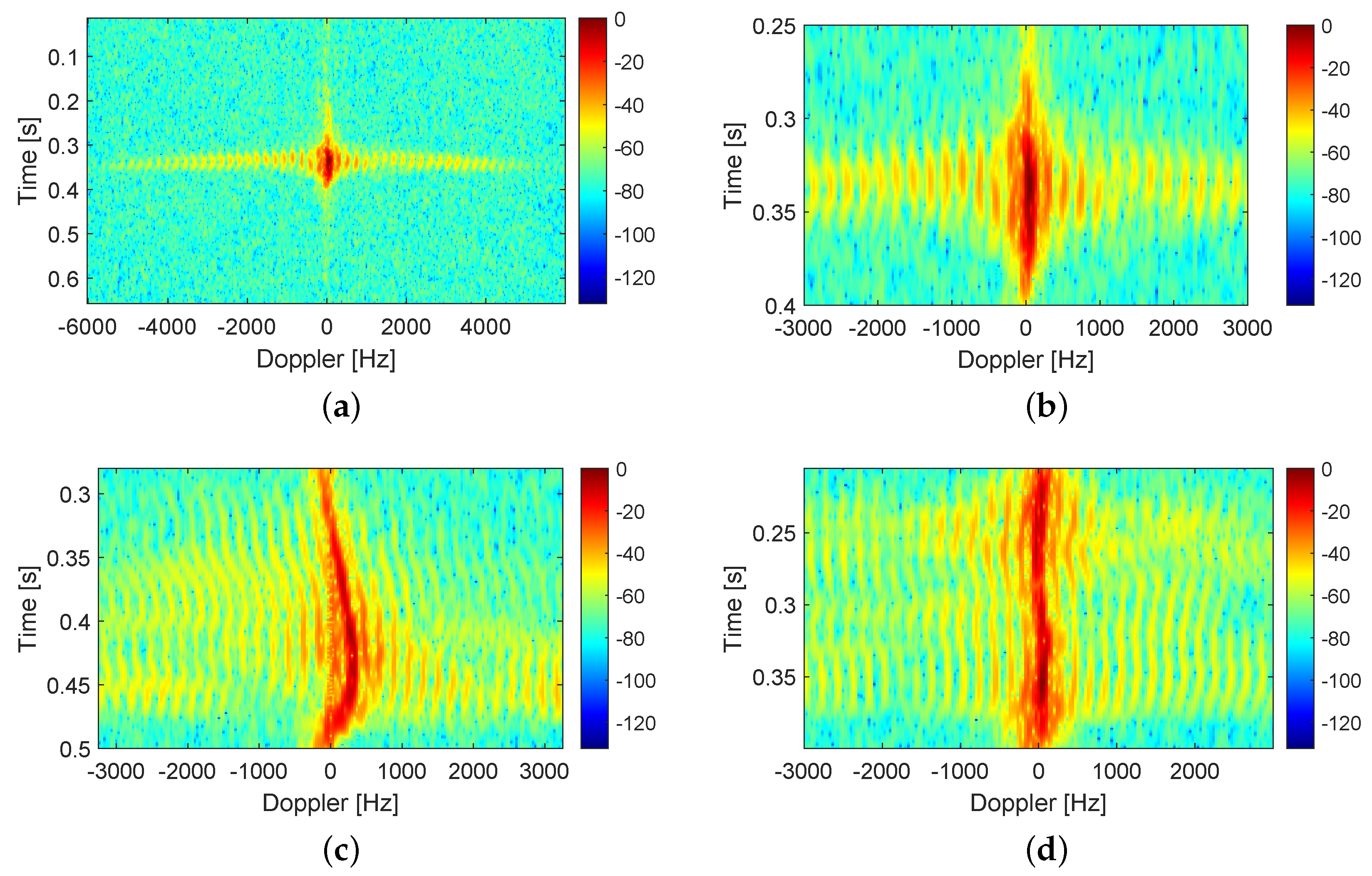
3.2.2. Results of the Bee Measurements

Figure 9a shows the spectrogram of a bee measurement. In a short time interval ranging from $t\approx 0.32\mathrm{s}$ to $t\approx 0.35\mathrm{s}$, the signal has a significantly higher amplitude and bandwidth compared to the rest of the measurement interval. The video frames of that measurement, shown in Figure 10, include the aforementioned time interval. The radar antenna is visible in the bottom center of these images. In Figure 10a, the bee is sitting on the cling film at the frontage of the flight tunnel. In the following frames, the bee flies upwards towards the upper right corner of the video image. In Figure 10e,f, taken at $t\approx 0.318\mathrm{s}$ and $t\approx 0.352\mathrm{s}$, the bee can be seen directly in front of the radar antenna. This agrees with the fact that the signal in the corresponding spectrogram (Figure 9b) exhibits a significantly increased amplitude and bandwidth in the aforementioned time interval. As in the bee simulation, that time interval features a pattern of equally distant maxima that are separated by approximately the average wingbeat frequency of the measured bee species, which is $227\mathrm{Hz}$ [33]. Moreover, the signal covers Doppler frequencies reaching up to values of about $\pm 5000\mathrm{Hz}$, which agrees with the bandwidth of the micro-Doppler signatures in the bee simulation.

Figure 9c,d show the spectrograms obtained from two other bee measurements. As in the first measurements, these spectrograms feature a pattern of equidistant maxima, which can be identified as the micro-Doppler signatures of the flying bee. Moreover, these spectrograms demonstrate the variability in the appearance of the micro-Doppler signatures. As discussed previously for the mosquito measurements, these differences can be attributed to the variability of the flight trajectory.

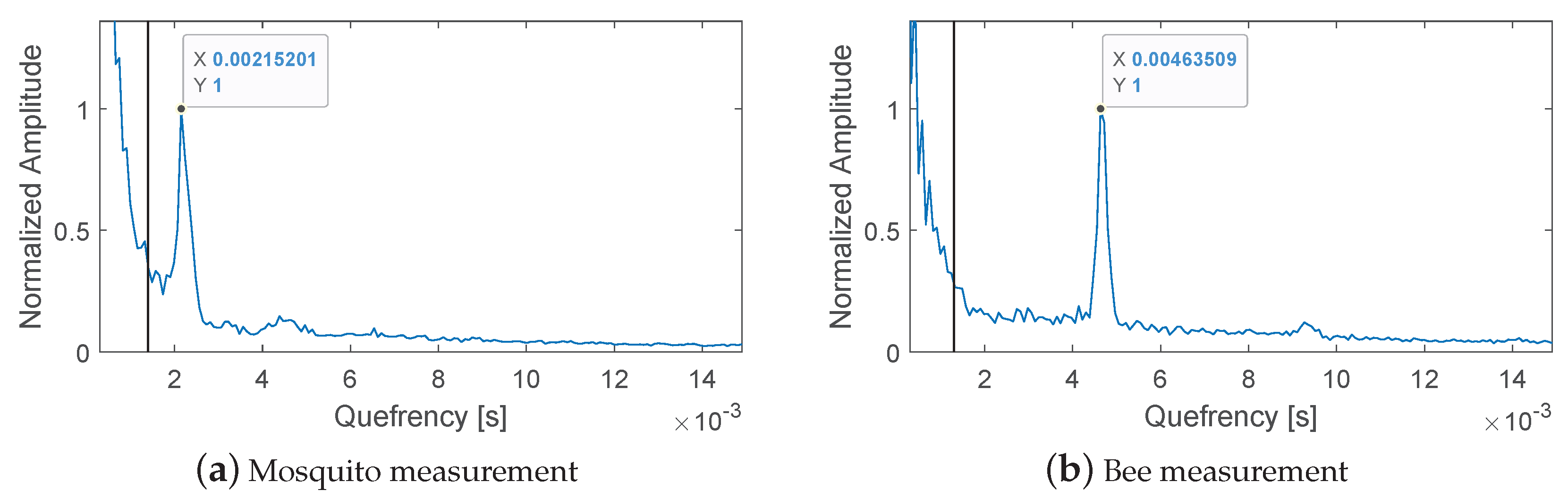
3.2.3. Automatic Extraction of the Wing Beat Frequency for Mosquitoes and Bees

The previous analysis of the simulation results shows that the wingbeat frequencies of the simulated insects can be extracted with high accuracy by using the algorithm illustrated in Figure 5. This section analyzes the feasibility of extracting the insects’ wingbeat frequencies with that algorithm from the experimental measurements. Figure 11a shows the projected spectrogram obtained from the spectrogram of the mosquito measurement in Figure 7c, whereas Figure 11b shows the projected cepstrogram of the bee measurement in Figure 9c. These projected cepstrograms exhibit significant peaks at quefrencies of $2.152\times {10}^{-3}\mathrm{s}$ and $4.635\times {10}^{-3}\mathrm{s}$. These values correspond to wingbeat frequencies of $1/(2.152\times {10}^{-3}\mathrm{s})=464.7\mathrm{Hz}$ and $1/(4.635\times {10}^{-3}\mathrm{s})=215.7\mathrm{Hz}$, respectively.

The algorithm in Figure 5 determines the maximum quefrency, $q_{max}$, based on the global maximum of the projected cepstrogram. However, the peaks in Figure 11 are local, but not global maxima, since the amplitudes are higher at the lower end of the quefrency range. To solve that problem, a lower limit $q_l$ was introduced for the analyzed quefrency interval. In Figure 11a,b, $q_l$ was marked by the black vertical lines that are located at a quefrency of $1.4\times {10}^{-3}\mathrm{s}$.

The aforementioned algorithm was applied to all of the performed measurements in order to extract the wingbeat frequencies of the measured insects. The count of the extracted wingbeat frequencies for 50 measurements of different individuals is visualized in the histogram in Figure 12. In that figure, the blue and orange bars represent the number of wingbeat frequencies extracted from mosquito and bee measurements, respectively. For both insects, the distribution of extracted frequencies can be characterized as a bell curve. The wingbeat frequencies extracted from the mosquito measurements have a mean value of $441.8\mathrm{Hz}$ and a standard deviation of $28.8\mathrm{Hz}$. On the other hand, the wingbeat frequencies extracted from the bee measurements have a mean value of $208.6\mathrm{Hz}$ and a standard deviation of $16.3\mathrm{Hz}$.

4. Discussion

As mentioned in the introduction, this study assesses the feasibility of a radar-based insect identification in the vicinity of wind turbines. Therefore, the micro-Doppler signatures of two prevalent insect species, i.e., culex pipiens and apis mellifera, are analyzed in a simulation and experimental study. The micro-Doppler signatures obtained from these two studies are found to agree with each other in many aspects: First, the micro-Doppler signatures of the two analyzed insect species appear as a set of equally distant maxima in the simulation as well as in the experiments. Moreover, the distance between adjacent maxima is found to match the wingbeat frequency of the respective insect, i.e., the maxima obtained from mosquito measurements are separated by a larger Doppler frequency compared to those of mosquitoes. Furthermore, the results of both studies show that the micro-Doppler signatures of bees have a significantly higher bandwidth (≈$5000\mathrm{Hz}$) than those of the mosquitoes (≈$2000\mathrm{Hz}$). Hence, the micro-Doppler signatures of mosquitoes are distinguishable from those of bees based on bandwidth and wingbeat frequency. The main difference between the results of the simulation study to those of the experimental study is that the maxima obtained from the experimental measurements can take arbitrary curve shapes, depending upon the flight trajectory of the insect. On the other hand, the maxima obtained in the simulation appear as straight lines parallel to the time axis of the spectrogram, since the insects are assumed to remain at the same position throughout the simulation.

In the context of insect identification near wind turbines, the features of the micro-Doppler signatures, e.g., wingbeat frequency, need to be extracted automatically from the radar signal in order to perform an autonomous classification that does not require a human operator. To extract the wingbeat frequency, this paper proposes a novel cepstrogram-based algorithm which is summarized in Figure 5. In the simulation study, the wingbeat frequencies extracted with that algorithm are found to have a relative error below $2\%$. The wingbeat frequencies extracted from the experimental measurements are $(441.8\pm 28.8)\mathrm{Hz}$ for the mosquito species culex pipiens and $(208.6\pm 16.3)\mathrm{Hz}$ for the bee species apis mellifera. The literature values for the average wingbeat frequencies of these insect species are $408.39\mathrm{Hz}$ and $226.8\mathrm{Hz}$, respectively [32,33]. The deviation of the wingbeat beat frequencies found in this study compared to those in the aforementioned studies can be explained based on differences in environmental conditions, such as temperature and humidity, which affect the wingbeat frequency of insects [45,46].

5. Conclusions

This article successfully demonstrated the results of a numerical and experimental study exploiting continuous-wave (CW) radar technology at W-band for the detection and classification of freely flying insects based on their unique micro-Doppler signatures generated by their wing beat motion. It was shown here that the radar signal model is able to predict the experimentally measured micro-Doppler characteristics. On top of that, a data analysis method has been proposed based on Cepstrum analysis that automatically extracts the wing beat frequencies. A histogram analysis showed that mosquitoes (culex pipiens) and bees (apis mellifera) can be discriminated from each other.

The results of this work can be helpful in the understanding of bat and bird mortality at wind turbine installations in order to identify the insect abundance. Further research is required that takes a larger number of different insect variants into account.