Rainfall Consistency, Variability, and Concentration over the UAE: Satellite Precipitation Products vs. Rain Gauge Observations
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. In Situ Data
2.3. GPM-IMERG
2.4. CMORPH
2.5. PERSIANN-CDR
2.6. CHIRPS
2.7. Methodology
2.8. Data Acquisition
2.9. Selection of the Grid Coordinates
2.10. Interpolation Technique
2.11. Performance Measures
2.12. Precipitation Extreme Indices
2.13. Precipitation Concentration Index (PCI)
2.14. Precipitation Variability
3. Results
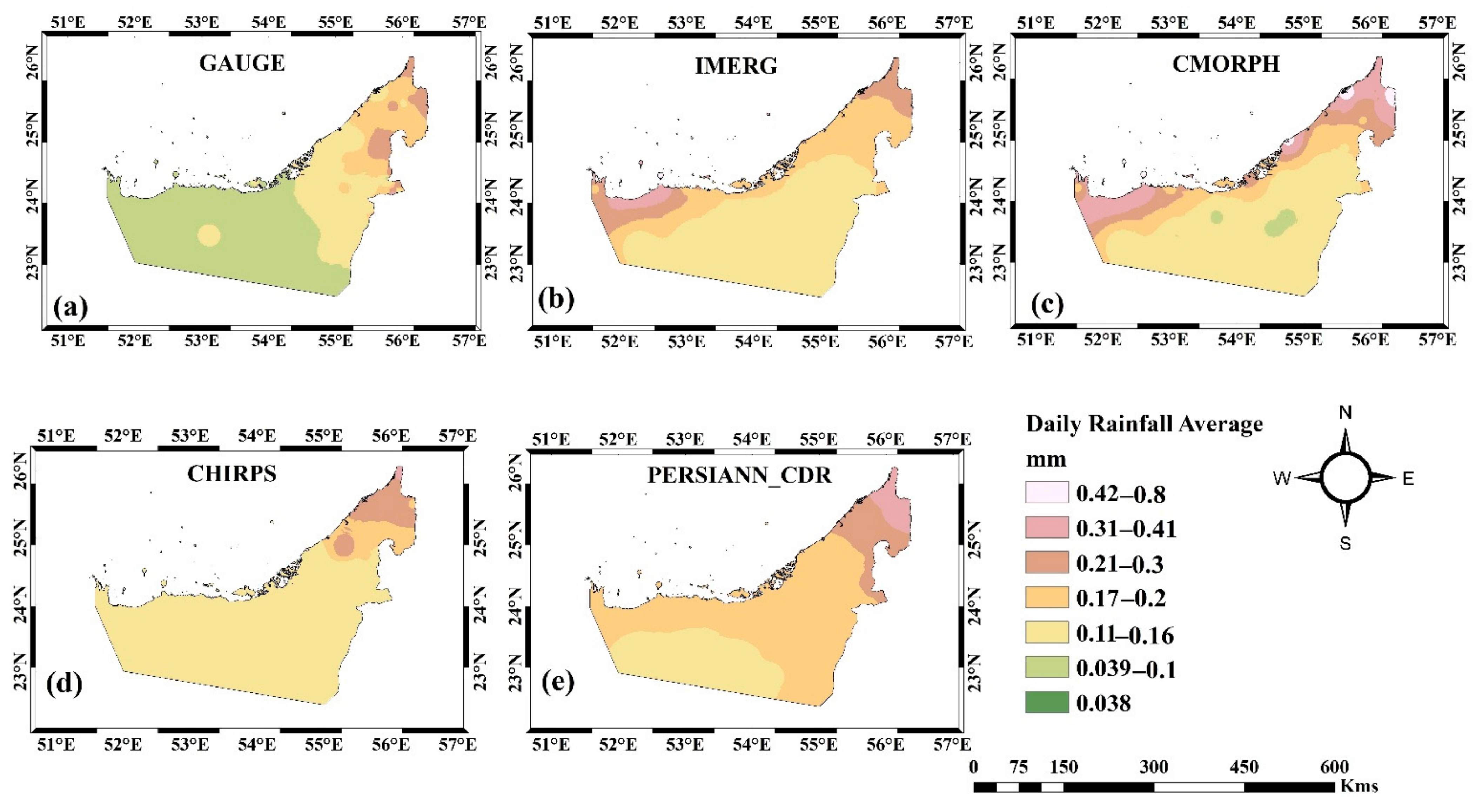
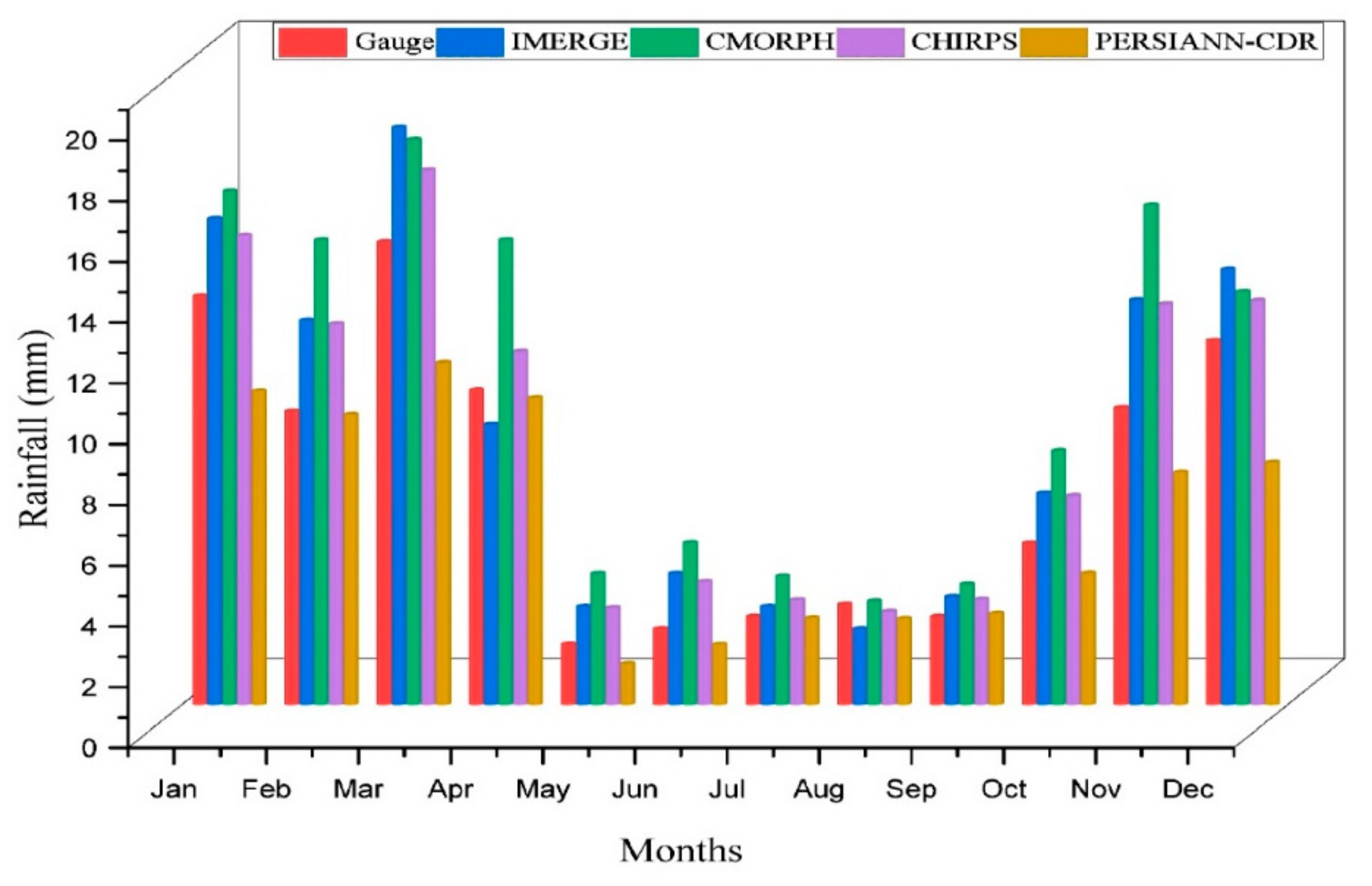
3.1. Spatial and Temporal Precipitation Distribution
3.2. Comparative Analysis of the Products
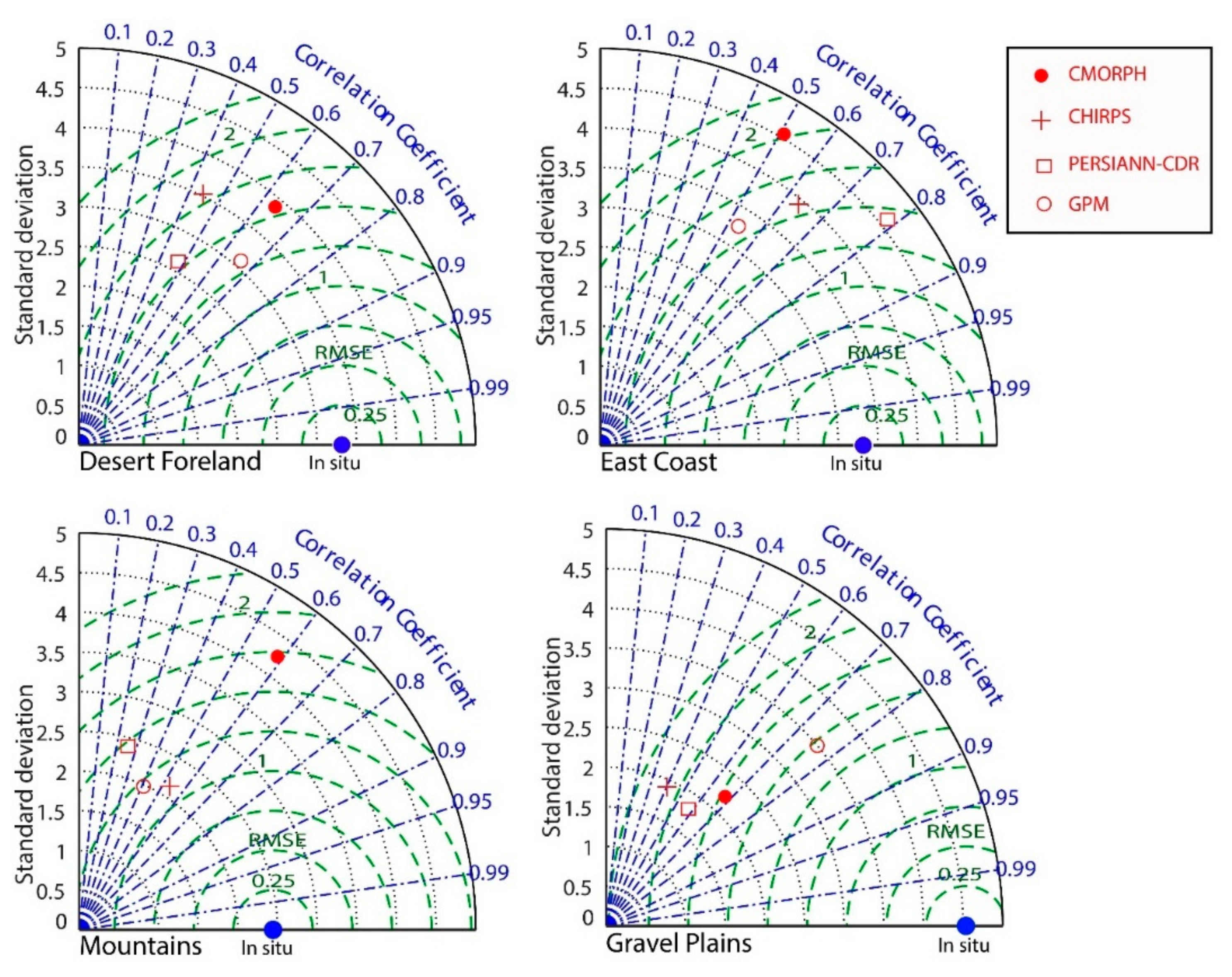
3.2.1. Statistical Performance
3.2.2. Detection Accuracy
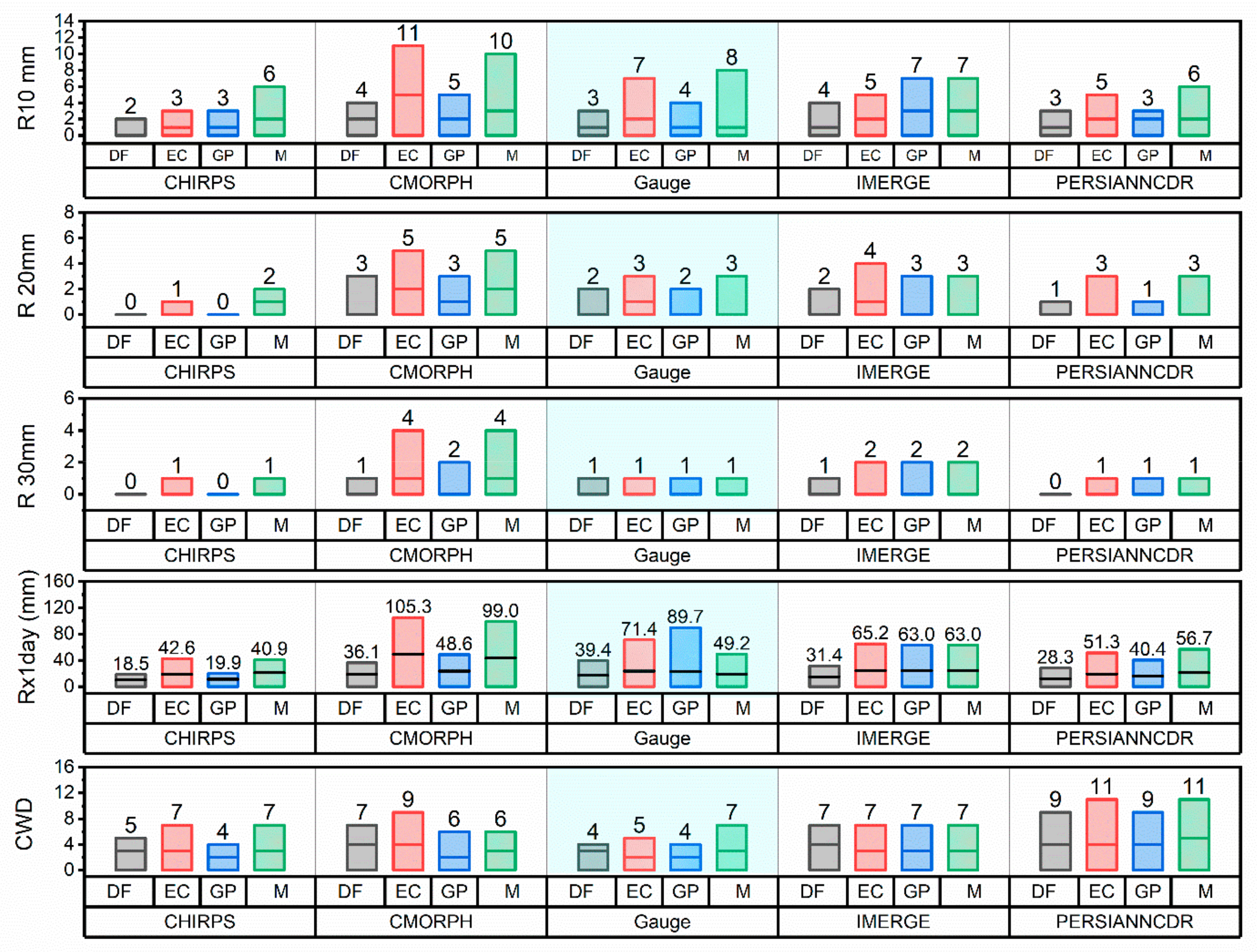
3.3. Rainfall Analysis Based on Climate Indices
3.4. Precipitation Variability
3.5. Precipitation Concentration Index (PCI)
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Stations | Mean | SE Mean | StDev | Var | CoefVar | Min | Q1 | Median | Q3 | Max | Range | IQR | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Abu Al Abyad | 48.2 | 18.4 | 63.7 | 4061.7 | 132.13 | 0.0 | 0.0 | 20.6 | 89.6 | 194.6 | 194.6 | 89.6 | 1.33 | 1.09 |
| Abu Al Bukhoosh | 52.9 | 20.1 | 69.6 | 4838.6 | 131.37 | 0.0 | 0.0 | 12.8 | 127.7 | 187.0 | 187.0 | 127.7 | 1.00 | −0.59 |
| Abu Dhabi | 56.9 | 22.5 | 77.9 | 6064.5 | 136.79 | 0.0 | 0.0 | 19.5 | 121.9 | 216.8 | 216.8 | 121.9 | 1.23 | 0.13 |
| Al Ain | 62.5 | 24.2 | 83.7 | 7012.0 | 133.89 | 1.8 | 16.1 | 22.4 | 91.5 | 255.4 | 253.6 | 75.4 | 1.75 | 1.88 |
| Al Aryam | 27.8 | 12.1 | 42.0 | 1761.6 | 150.84 | 0.0 | 0.0 | 7.9 | 48.4 | 126.8 | 126.8 | 48.4 | 1.63 | 1.83 |
| Al Faqa | 140.4 | 33.7 | 116.8 | 13,631.3 | 83.14 | 25.0 | 41.0 | 101.9 | 237.0 | 354.0 | 329.0 | 196.1 | 0.92 | −0.47 |
| Al Jazeera B.G | 30.7 | 11.1 | 38.4 | 1473.1 | 125.15 | 0.0 | 7.5 | 18.8 | 31.6 | 133.8 | 133.8 | 24.1 | 2.14 | 4.69 |
| Al Malaiha | 86.0 | 24.7 | 85.5 | 7304.7 | 99.33 | 8.8 | 25.4 | 52.9 | 140.4 | 283.3 | 274.5 | 115.1 | 1.37 | 1.22 |
| Al Qattara | 36.0 | 12.4 | 43.0 | 1846.3 | 119.25 | 1.8 | 8.8 | 23.8 | 34.4 | 143.5 | 141.7 | 25.5 | 1.95 | 3.22 |
| Al Shiweb | 125.3 | 49.4 | 171.0 | 29,254.2 | 136.55 | 5.1 | 17.8 | 42.0 | 179.6 | 569.2 | 564.1 | 161.8 | 1.94 | 3.62 |
| Alarad | 89.6 | 30.0 | 104.0 | 10,808.2 | 115.99 | 8.6 | 17.6 | 57.0 | 97.4 | 305.0 | 296.4 | 79.8 | 1.66 | 1.65 |
| Alfoah | 115.6 | 45.1 | 156.1 | 24,355.3 | 135.01 | 0.0 | 12.2 | 57.2 | 163.8 | 491.3 | 491.3 | 151.6 | 1.78 | 2.37 |
| Al Gheweifat | 57.7 | 16.4 | 56.9 | 3232.8 | 98.53 | 0.0 | 0.0 | 62.0 | 105.9 | 161.7 | 161.7 | 105.9 | 0.35 | −1.14 |
| Al Khazna | 80.1 | 35.5 | 122.8 | 15,091.9 | 153.31 | 0.0 | 1.1 | 29.9 | 137.2 | 410.8 | 410.8 | 136.1 | 2.06 | 4.53 |
| Alqlaa | 51.1 | 16.1 | 55.9 | 3126.6 | 109.37 | 3.8 | 12.5 | 16.1 | 110.3 | 165.1 | 161.3 | 97.8 | 1.05 | −0.33 |
| Alquaa | 71.0 | 21.6 | 75.0 | 5619.8 | 105.56 | 5.4 | 13.5 | 25.8 | 133.0 | 210.8 | 205.4 | 119.5 | 0.86 | −0.83 |
| Al Wathbah | 60.5 | 23.4 | 81.2 | 6588.9 | 134.15 | 0.0 | 0.0 | 30.9 | 93.8 | 253.4 | 253.4 | 93.8 | 1.60 | 1.94 |
| Al Tawiyen | 39.2 | 15.7 | 54.4 | 2958.7 | 138.79 | 0.0 | 3.5 | 18.9 | 45.5 | 162.6 | 162.6 | 42.1 | 1.77 | 2.05 |
| Bu Hamrah | 56.9 | 21.8 | 75.4 | 5682.7 | 132.58 | 0.0 | 0.0 | 23.5 | 121.5 | 226.4 | 226.4 | 121.5 | 1.27 | 0.78 |
| Das Island | 53.7 | 26.3 | 91.2 | 8321.7 | 169.82 | 0.0 | 2.6 | 20.0 | 34.3 | 253.0 | 253.0 | 31.7 | 1.97 | 2.44 |
| Damsa | 38.4 | 16.8 | 58.3 | 3399.5 | 151.67 | 0.0 | 0.0 | 14.2 | 50.8 | 166.9 | 166.9 | 50.8 | 1.66 | 1.66 |
| Dhudna | 135.3 | 48.5 | 168.0 | 28,233.6 | 124.18 | 0.0 | 0.4 | 59.7 | 294.7 | 495.1 | 495.1 | 294.3 | 1.24 | 0.35 |
| Falaj Al Moalla | 117.6 | 39.0 | 135.3 | 18,293.0 | 114.98 | 0.0 | 1.7 | 93.4 | 180.1 | 394.8 | 394.8 | 178.4 | 1.20 | 0.51 |
| Hamim | 52.2 | 16.9 | 58.5 | 3426.1 | 112.17 | 0.0 | 1.0 | 27.1 | 96.5 | 173.0 | 173.0 | 95.6 | 0.98 | −0.11 |
| Hatta | 92.0 | 27.8 | 96.2 | 9263.5 | 104.58 | 1.1 | 8.2 | 49.3 | 175.3 | 293.2 | 292.1 | 167.0 | 0.88 | −0.25 |
| Jabal Hafeet | 85.5 | 21.1 | 73.2 | 5354.6 | 85.62 | 2.1 | 27.4 | 63.2 | 137.2 | 248.1 | 246.0 | 109.9 | 1.03 | 0.62 |
| Jabal Jais | 153.7 | 52.5 | 182.0 | 33,105.9 | 118.40 | 0.0 | 0.9 | 112.8 | 228.3 | 526.4 | 526.4 | 227.4 | 0.98 | 0.02 |
| Jabal Mebreh | 84.9 | 35.0 | 121.2 | 14,683.4 | 142.67 | 0.0 | 1.2 | 24.2 | 165.2 | 376.5 | 376.5 | 164.0 | 1.52 | 1.80 |
| Khatam Al Shaklah | 149.3 | 47.9 | 166.0 | 27,564.8 | 111.18 | 0.0 | 24.1 | 94.9 | 225.1 | 551.0 | 551.0 | 201.0 | 1.52 | 2.08 |
| Madinat Zayed | 46.3 | 17.0 | 58.9 | 3467.6 | 127.19 | 0.0 | 1.6 | 27.0 | 76.8 | 191.2 | 191.2 | 75.1 | 1.58 | 2.34 |
| Manama | 44.0 | 14.5 | 50.1 | 2512.2 | 113.87 | 0.0 | 0.0 | 26.1 | 90.0 | 123.1 | 123.1 | 90.0 | 0.55 | −1.42 |
| Makassib | 72.7 | 21.5 | 74.3 | 5525.2 | 102.30 | 8.5 | 21.6 | 41.8 | 130.5 | 248.9 | 240.4 | 108.9 | 1.49 | 1.61 |
| Masafi | 97.4 | 31.1 | 107.7 | 11,603.8 | 110.57 | 1.5 | 15.6 | 39.8 | 206.9 | 295.0 | 293.5 | 191.3 | 1.00 | −0.67 |
| Mezaira | 54.5 | 13.1 | 45.4 | 2061.9 | 83.36 | 0.6 | 15.8 | 49.2 | 70.6 | 157.1 | 156.5 | 54.8 | 1.01 | 1.20 |
| Mezyed | 107.3 | 23.3 | 80.6 | 6494.7 | 75.10 | 13.6 | 47.2 | 95.9 | 135.1 | 301.2 | 287.6 | 87.9 | 1.28 | 1.98 |
| Mukhariz | 75.3 | 20.3 | 70.5 | 4965.9 | 93.56 | 19.8 | 26.1 | 43.4 | 91.7 | 262.5 | 242.7 | 65.6 | 1.98 | 4.21 |
| Owtaid | 62.2 | 18.7 | 64.7 | 4181.5 | 103.93 | 0.1 | 10.4 | 54.4 | 88.6 | 237.1 | 237.0 | 78.2 | 1.89 | 4.80 |
| Qarnen | 41.5 | 15.7 | 54.3 | 2948.6 | 130.82 | 0.0 | 0.0 | 16.8 | 80.0 | 153.6 | 153.6 | 80.0 | 1.16 | 0.16 |
| Raknah | 91.4 | 32.5 | 112.6 | 12,673.4 | 123.22 | 1.5 | 9.4 | 46.3 | 200.6 | 315.5 | 314.0 | 191.3 | 1.24 | −0.06 |
| Ras Ghanadah | 58.3 | 21.7 | 75.1 | 5635.9 | 128.75 | 0.0 | 0.0 | 19.3 | 102.2 | 213.2 | 213.2 | 102.2 | 1.11 | 0.12 |
| Ras Musherib | 25.19 | 8.95 | 31.02 | 962.07 | 123.13 | 0.00 | 0.00 | 8.85 | 47.90 | 96.30 | 96.30 | 47.90 | 1.22 | 0.92 |
| Rowdah | 72.6 | 29.8 | 103.3 | 10,663.2 | 142.17 | 6.4 | 17.6 | 30.0 | 74.2 | 327.2 | 320.8 | 56.7 | 2.02 | 3.11 |
| Saih Al Salem | 66.1 | 24.8 | 85.9 | 7379.2 | 130.04 | 0.0 | 2.3 | 42.7 | 93.9 | 286.4 | 286.4 | 91.6 | 1.80 | 3.33 |
| Sir Bani Yas | 46.4 | 14.9 | 51.7 | 2674.6 | 111.36 | 0.0 | 0.1 | 22.3 | 108.3 | 116.8 | 116.8 | 108.2 | 0.42 | −1.93 |
| Sir Bu Nair | 45.3 | 16.7 | 58.0 | 3366.4 | 128.01 | 0.0 | 0.0 | 7.0 | 104.4 | 143.5 | 143.5 | 104.4 | 0.79 | −1.21 |
| Swiehan | 92.1 | 32.7 | 113.2 | 12,823.3 | 123.01 | 1.0 | 13.0 | 29.4 | 131.5 | 345.4 | 344.4 | 118.6 | 1.51 | 1.35 |
| Um Azimul | 38.4 | 11.1 | 38.5 | 1483.8 | 100.40 | 0.0 | 0.5 | 33.7 | 69.5 | 112.2 | 112.2 | 69.0 | 0.69 | −0.63 |
| Um Ghafa | 57.3 | 17.6 | 60.9 | 3711.3 | 106.38 | 1.7 | 8.4 | 33.3 | 104.8 | 168.1 | 166.4 | 96.4 | 1.01 | −0.37 |
| Umm Al Quwain | 65.9 | 23.3 | 80.8 | 6522.8 | 122.49 | 0.0 | 2.3 | 22.7 | 140.6 | 231.4 | 231.4 | 138.3 | 0.99 | −0.32 |
| Yasat | 37.8 | 13.8 | 47.7 | 2271.7 | 126.23 | 0.0 | 0.0 | 19.1 | 73.7 | 134.9 | 134.9 | 73.7 | 1.04 | −0.07 |
Appendix B
| Stations | Mean | StDev | Var | CoefVar | Min | Q1 | Med | Q3 | Max | Range | IQR | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Abu Al Abyad | 34.04 | 37.28 | 1389.91 | 109.54 | 0.00 | 2.80 | 19.40 | 64.75 | 126.40 | 126.40 | 61.95 | 1.08 | 0.56 |
| Abu Al Bukhoosh | 37.3 | 42.4 | 1794.2 | 113.44 | 0.0 | 3.2 | 13.6 | 71.4 | 146.2 | 146.2 | 68.2 | 1.24 | 1.10 |
| Abu Dhabi | 39.9 | 44.6 | 1985.0 | 111.70 | 0.0 | 6.0 | 21.0 | 69.9 | 157.6 | 157.6 | 63.9 | 1.46 | 1.68 |
| Al Ain | 44.1 | 54.4 | 2960.9 | 123.31 | 0.0 | 1.7 | 30.2 | 62.5 | 194.6 | 194.6 | 60.8 | 1.84 | 3.25 |
| Al Aryam | 19.58 | 24.77 | 613.47 | 126.52 | 0.00 | 0.30 | 7.80 | 42.60 | 65.80 | 65.80 | 42.30 | 1.01 | −0.63 |
| Al Faqa | 98.5 | 69.7 | 4863.6 | 70.81 | 0.4 | 41.3 | 96.7 | 169.0 | 222.6 | 222.2 | 127.7 | 0.51 | −1.04 |
| Al Jazeera B.G | 21.64 | 23.73 | 563.18 | 109.66 | 0.00 | 0.00 | 12.60 | 41.05 | 77.80 | 77.80 | 41.05 | 0.94 | 0.13 |
| Al Malaiha | 60.2 | 56.0 | 3137.9 | 93.09 | 0.0 | 16.5 | 42.8 | 103.9 | 203.8 | 203.8 | 87.4 | 1.27 | 1.20 |
| Al Qattara | 24.84 | 37.78 | 1426.96 | 152.07 | 0.00 | 0.30 | 6.60 | 38.40 | 136.40 | 136.40 | 38.10 | 2.02 | 4.13 |
| Al Shiweb | 88.0 | 85.1 | 7236.0 | 96.61 | 0.2 | 25.9 | 60.8 | 134.3 | 327.2 | 327.0 | 108.4 | 1.47 | 2.63 |
| Alarad | 62.6 | 61.7 | 3807.6 | 98.54 | 0.0 | 15.9 | 44.6 | 86.1 | 208.9 | 208.9 | 70.2 | 1.55 | 2.00 |
| Alfoah | 81.2 | 76.8 | 5891.0 | 94.52 | 0.2 | 18.0 | 75.8 | 106.8 | 286.8 | 286.6 | 88.8 | 1.39 | 2.09 |
| Al Gheweifat | 40.7 | 41.4 | 1715.3 | 101.67 | 0.0 | 5.0 | 25.4 | 78.3 | 128.9 | 128.9 | 73.3 | 0.87 | −0.47 |
| Al Khazna | 56.12 | 38.92 | 1514.91 | 69.35 | 0.00 | 22.50 | 50.60 | 88.90 | 134.60 | 134.60 | 66.40 | 0.38 | −0.67 |
| Alqlaa | 35.9 | 52.6 | 2766.9 | 146.59 | 0.2 | 2.2 | 13.4 | 50.1 | 166.2 | 166.0 | 47.9 | 1.88 | 2.73 |
| Alquaa | 49.9 | 68.0 | 4628.7 | 136.28 | 0.0 | 2.8 | 22.4 | 67.5 | 223.2 | 223.2 | 64.7 | 1.65 | 1.72 |
| Al Wathbah | 42.7 | 42.2 | 1781.7 | 98.84 | 0.0 | 3.2 | 24.6 | 79.6 | 121.9 | 121.9 | 76.4 | 0.75 | −0.85 |
| Al Tawiyen | 26.55 | 35.65 | 1270.70 | 134.25 | 0.00 | 1.90 | 17.80 | 39.20 | 139.80 | 139.80 | 37.30 | 2.25 | 5.99 |
| Bu Hamrah | 40.1 | 54.6 | 2977.0 | 135.95 | 0.4 | 6.8 | 16.2 | 64.2 | 219.8 | 219.4 | 57.4 | 2.47 | 7.26 |
| Das Island | 37.8 | 63.6 | 4041.3 | 168.02 | 0.0 | 0.0 | 9.6 | 54.9 | 238.2 | 238.2 | 54.9 | 2.35 | 5.85 |
| Damsa | 27.11 | 36.45 | 1328.84 | 134.48 | 0.00 | 0.00 | 5.40 | 63.30 | 101.00 | 101.00 | 63.30 | 1.08 | −0.42 |
| Dhudna | 91.9 | 94.6 | 8941.6 | 102.93 | 2.0 | 16.1 | 59.8 | 157.5 | 285.3 | 283.3 | 141.4 | 1.06 | −0.03 |
| Falaj Al Moalla | 82.5 | 86.1 | 7419.9 | 104.43 | 0.6 | 25.5 | 58.0 | 112.0 | 303.0 | 302.4 | 86.5 | 1.77 | 2.68 |
| Hamim | 35.5 | 43.3 | 1876.4 | 121.88 | 0.0 | 6.2 | 14.6 | 55.5 | 158.0 | 158.0 | 49.3 | 1.75 | 2.92 |
| Hatta | 61.2 | 62.2 | 3874.1 | 101.66 | 0.0 | 10.1 | 43.2 | 105.0 | 208.9 | 208.9 | 94.9 | 1.08 | 0.40 |
| Jabal Hafeet | 59.0 | 61.4 | 3764.5 | 104.00 | 0.0 | 14.3 | 50.4 | 85.1 | 246.0 | 246.0 | 70.8 | 1.95 | 4.70 |
| Jabal Jais | 108.4 | 128.5 | 1614.7 | 118.51 | 0.0 | 17.0 | 58.0 | 174.8 | 461.6 | 461.6 | 157.8 | 1.67 | 2.39 |
| Jabal Mebreh | 58.8 | 86.5 | 7490.6 | 147.29 | 0.0 | 0.2 | 15.2 | 83.1 | 252.2 | 252.2 | 82.9 | 1.53 | 1.06 |
| Khatam Al Shaklah | 103.7 | 91.5 | 8380.6 | 88.25 | 0.0 | 18.3 | 81.8 | 168.8 | 305.7 | 305.7 | 150.5 | 0.71 | −0.28 |
| Madinat Zayed | 31.58 | 29.05 | 843.80 | 91.98 | 0.00 | 8.30 | 24.00 | 50.90 | 109.40 | 109.40 | 42.60 | 1.28 | 1.82 |
| Manama | 30.89 | 39.22 | 1538.44 | 126.96 | 0.00 | 3.45 | 13.00 | 56.45 | 143.80 | 143.80 | 53.00 | 1.77 | 3.16 |
| Makassib | 48.8 | 57.1 | 3264.9 | 117.19 | 0.4 | 10.8 | 21.0 | 89.9 | 206.9 | 206.5 | 79.1 | 1.56 | 2.31 |
| Masafi | 68.71 | 38.95 | 1516.83 | 56.69 | 0.00 | 40.20 | 61.60 | 104.90 | 124.80 | 124.80 | 64.70 | −0.45 | −0.92 |
| Mezaira | 35.1 | 59.4 | 3530.8 | 169.12 | 0.0 | 5.4 | 15.4 | 26.6 | 200.8 | 200.8 | 21.2 | 2.42 | 4.88 |
| Mezyed | 74.14 | 36.91 | 1362.05 | 49.78 | 28.00 | 39.96 | 61.80 | 113.26 | 127.58 | 99.59 | 73.30 | 0.27 | −1.62 |
| Mukhariz | 51.0 | 95.6 | 9140.6 | 187.62 | 0.0 | 5.6 | 18.6 | 36.4 | 347.0 | 347.0 | 30.8 | 2.63 | 6.33 |
| Owtaid | 42.22 | 38.15 | 1455.34 | 90.35 | 0.00 | 13.35 | 28.60 | 54.10 | 131.00 | 131.00 | 40.75 | 1.35 | 1.37 |
| Qarnen | 29.28 | 27.37 | 748.95 | 93.48 | 0.00 | 5.50 | 17.00 | 55.15 | 79.10 | 79.10 | 49.65 | 0.69 | −0.98 |
| Raknah | 64.1 | 59.2 | 3509.7 | 92.47 | 0.0 | 20.8 | 56.4 | 81.3 | 232.2 | 232.2 | 60.5 | 1.51 | 3.08 |
| Ras Ghanadah | 41.0 | 53.9 | 2905.1 | 131.44 | 0.0 | 3.7 | 19.0 | 63.3 | 185.5 | 185.5 | 59.6 | 1.75 | 2.42 |
| Ras Musherib | 17.30 | 20.25 | 409.95 | 117.04 | 0.00 | 1.95 | 4.60 | 34.45 | 63.10 | 63.10 | 32.50 | 1.04 | −0.15 |
| Rowdah | 51.2 | 61.7 | 3809.1 | 120.51 | 0.0 | 2.2 | 29.2 | 68.6 | 230.0 | 230.0 | 66.4 | 1.79 | 3.48 |
| Saih Al Salem | 46.4 | 61.9 | 3831.0 | 133.51 | 2.2 | 8.8 | 20.8 | 68.4 | 242.9 | 240.7 | 59.6 | 2.33 | 6.02 |
| Sir Bani Yas | 32.32 | 41.08 | 1687.58 | 127.09 | 0.00 | 2.35 | 16.60 | 51.50 | 132.80 | 132.80 | 49.15 | 1.47 | 1.24 |
| Sir Bu Nair | 31.88 | 32.83 | 1078.00 | 102.98 | 0.00 | 5.60 | 17.80 | 67.95 | 92.20 | 92.20 | 62.35 | 0.79 | −0.95 |
| Swiehan | 64.7 | 55.7 | 3105.0 | 86.06 | 0.0 | 10.9 | 55.8 | 101.2 | 192.1 | 192.1 | 90.3 | 0.76 | 0.01 |
| Um Azimul | 26.38 | 28.92 | 836.36 | 109.62 | 0.00 | 4.50 | 14.60 | 57.70 | 84.70 | 84.70 | 53.20 | 1.00 | −0.61 |
| Um Ghafa | 37.9 | 50.5 | 2551.6 | 133.18 | 0.0 | 0.7 | 21.0 | 58.3 | 165.5 | 165.5 | 57.6 | 1.64 | 1.94 |
| Umm Al Quwain | 46.5 | 49.2 | 2424.0 | 105.97 | 0.0 | 10.0 | 32.6 | 58.8 | 177.4 | 177.4 | 48.8 | 1.63 | 2.47 |
| Yasat | 26.64 | 34.97 | 1223.16 | 131.31 | 0.00 | 3.90 | 6.40 | 44.15 | 108.00 | 108.00 | 40.25 | 1.48 | 1.16 |
References
- Haile, A.T.; Yan, F.; Habib, E. Accuracy of the CMORPH Satellite-Rainfall Product over Lake Tana Basin in Eastern Africa. Atmos. Res. 2015, 163, 177–187. [Google Scholar] [CrossRef]
- Kim, J.; Han, H. Evaluation of the CMORPH High-Resolution Precipitation Product for Hydrological Applications over South Korea. Atmos. Res. 2021, 258, 105650. [Google Scholar] [CrossRef]
- Eini, M.R.; Rahmati, A.; Piniewski, M. Hydrological Application and Accuracy Evaluation of PERSIANN Satellite-Based Precipitation Estimates over a Humid Continental Climate Catchment. J. Hydrol. Reg. Stud. 2022, 41, 101109. [Google Scholar] [CrossRef]
- Prakash, S. Performance Assessment of CHIRPS, MSWEP, SM2RAIN-CCI, and TMPA Precipitation Products across India. J. Hydrol. 2019, 571, 50–59. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Stagl, J.; Mayr, E.; Koch, H.; Hattermann, F.F.; Huang, S. Effects of Climate Change on the Hydrological Cycle in Central and Eastern Europe. In Managing Protected Areas in Central and Eastern Europe Under Climate Change; Rannow, S., Neubert, M., Eds.; Advances in Global Change Research; Springer: Dordrecht, The Netherlands, 2014; pp. 31–43. ISBN 978-94-007-7960-0. [Google Scholar]
- Cavalcante, R.B.L.; da Silva Ferreira, D.B.; Pontes, P.R.M.; Tedeschi, R.G.; da Costa, C.P.W.; de Souza, E.B. Evaluation of Extreme Rainfall Indices from CHIRPS Precipitation Estimates over the Brazilian Amazonia. Atmos. Res. 2020, 238, 104879. [Google Scholar] [CrossRef]
- López-Bermeo, C.; Montoya, R.D.; Caro-Lopera, F.J.; Díaz-García, J.A. Validation of the Accuracy of the CHIRPS Precipitation Dataset at Representing Climate Variability in a Tropical Mountainous Region of South America. Phys. Chem. Earth A/B/C 2022, 127, 103184. [Google Scholar] [CrossRef]
- Nawaz, M.; Iqbal, M.F.; Mahmood, I. Validation of CHIRPS Satellite-Based Precipitation Dataset over Pakistan. Atmos. Res. 2021, 248, 105289. [Google Scholar] [CrossRef]
- Gragnani, G.L.; Colli, M.; Tavanti, E.; Caviglia, D.D. Advanced Real-Time Monitoring of Rainfall Using Commercial Satellite Broadcasting Service: A Case Study. Sensors 2021, 21, 691. [Google Scholar] [CrossRef]
- Han, L.; Zhang, J.; Chen, H.; Zhang, W.; Yao, S. Towards the Predictability of a Radar-Based Nowcasting System for Different Precipitation Systems. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1005705. [Google Scholar] [CrossRef]
- Huang, H.; Zhao, K.; Fu, P.; Chen, H.; Chen, G.; Zhang, Y. Validation of Precipitation Measurements from the Dual-Frequency Precipitation Radar Onboard the GPM Core Observatory Using a Polarimetric Radar in South China. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4104216. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.-P.; Willems, P.; Onof, C. A Review of Radar-Rain Gauge Data Merging Methods and Their Potential for Urban Hydrological Applications. Water Resour. Res. 2019, 55, 6356–6391. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Chen, H. A Machine Learning Approach to Derive Precipitation Estimates at Global Scale Using Space Radar and Ground-Based Observations. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium 2020, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 5376–5379. [Google Scholar]
- Han, L.; Zhao, Y.; Chen, H.; Chandrasekar, V. Advancing Radar Nowcasting through Deep Transfer Learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4100609. [Google Scholar] [CrossRef]
- Ji, L.; Xu, W.; Chen, H.; Chen, H. Identification of Convective Precipitation Feature Observed by Trmm/Gpm Pr Using a Revised Unsupervised Clustering Proposal. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 370–371. [Google Scholar]
- Zhang, J.; Chen, H.; Han, L. An investigation of a probabilistic nowcast system for dual-polarization radar applications. In Proceedings of the IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 5294–5297. [Google Scholar] [CrossRef]
- Prigent, C. Precipitation Retrieval from Space: An Overview. Comptes Rendus Geosci. 2010, 342, 380–389. [Google Scholar] [CrossRef]
- Jiang, S.; Zhou, M.; Ren, L.; Cheng, X.; Zhang, P. Evaluation of Latest TMPA and CMORPH Satellite Precipitation Products over Yellow River Basin. Water Sci. Eng. 2016, 9, 87–96. [Google Scholar] [CrossRef]
- Wang, Q.; Xia, J.; She, D.; Zhang, X.; Liu, J.; Zhang, Y. Assessment of Four Latest Long-Term Satellite-Based Precipitation Products in Capturing the Extreme Precipitation and Streamflow across a Humid Region of Southern China. Atmos. Res. 2021, 257, 105554. [Google Scholar] [CrossRef]
- Wehbe, Y.; Ghebreyesus, D.; Temimi, M.; Milewski, A.; Al Mandous, A. Assessment of the Consistency among Global Precipitation Products over the United Arab Emirates. J. Hydrol. Reg. Stud. 2017, 12, 122–135. [Google Scholar] [CrossRef]
- Ji, H.; Peng, D.; Gu, Y.; Liang, Y.; Luo, X. Evaluation of multiple satellite precipitation products and their potential utilities in the Yarlung Zangbo River Basin. Sci. Rep. 2022, 12, 1–15. [Google Scholar] [CrossRef]
- Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.-L.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-SatellitE Retrievals for GPM (IMERG); Global Precipitatoin Measurement; NASA: Washington, DC, USA, 2018; pp. 1–29. [Google Scholar]
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Thorstensen, A.R. The PERSIANN Family of Global Satellite Precipitation Data: A Review and Evaluation of Products. Hydrol. Earth Syst. Sci. 2018, 22, 5801–5816. [Google Scholar] [CrossRef]
- Tan, J.; Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. IMERG V06: Changes to the Morphing Algorithm. J. Atmos. Ocean. Technol. 2019, 36, 2471–2482. [Google Scholar] [CrossRef]
- Chen, Y.; Duan, J.; An, J.; Liu, H.; Görsdorf, U.; Berger, F.H. Satellite Estimates and Subpixel Variability of Rainfall in a Semi-Arid Grassland. Atmos. Ocean. Sci. Lett. 2021, 14, 100055. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Al-Zahrani, M.A.; Sharif, H.O. Assessment of Global Precipitation Measurement Satellite Products over Saudi Arabia. J. Hydrol. 2018, 559, 1–12. [Google Scholar] [CrossRef]
- Rincón-Avalos, P.; Khouakhi, A.; Mendoza-Cano, O.; la Cruz, J.L.-D.; Paredes-Bonilla, K.M. Evaluation of Satellite Precipitation Products over Mexico Using Google Earth Engine. J. Hydroinform. 2022, 24, jh2022122. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–84. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Aryastana, P.; Liu, G.-R.; Huang, W.-R. Assessment of Satellite Precipitation Product Estimates over Bali Island. Atmos. Res. 2020, 244, 105032. [Google Scholar] [CrossRef]
- Wang, H.; Zang, F.; Zhao, C.; Liu, C. A GWR Downscaling Method to Reconstruct High-Resolution Precipitation Dataset Based on GSMaP-Gauge Data: A Case Study in the Qilian Mountains, Northwest China. Sci. Total Environ. 2022, 810, 152066. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of High-Resolution Satellite Precipitation Products over China. J. Geophys. Res. Atmos. 2010, 115, D2. [Google Scholar] [CrossRef]
- Vernimmen, R.R.E.; Hooijer, A.; Mamenun; Aldrian, E.; van Dijk, A.I.J.M. Evaluation and Bias Correction of Satellite Rainfall Data for Drought Monitoring in Indonesia. Hydrol. Earth Syst. Sci. 2012, 16, 133–146. [Google Scholar] [CrossRef]
- Ghajarnia, N.; Liaghat, A.; Arasteh, P.D. Comparison and Evaluation of High Resolution Precipitation Estimation Products in Urmia Basin-Iran. Atmos. Res. 2015, 158–159, 50–65. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, J.; Bai, L.; Wang, B. Reliability of Gridded Precipitation Products in the Yellow River Basin, China. Remote Sens. 2020, 12, 374. [Google Scholar] [CrossRef]
- Duan, Z.; Liu, J.; Tuo, Y.; Chiogna, G.; Disse, M. Evaluation of Eight High Spatial Resolution Gridded Precipitation Products in Adige Basin (Italy) at Multiple Temporal and Spatial Scales. Sci. Total Environ. 2016, 573, 1536–1553. [Google Scholar] [CrossRef] [PubMed]
- Kidd, C.; Ferraro, R.; Turk, J.; Bauer, P.; Levizzani, V.; Ebert, E.; Janowiak, J.; Gruber, A. The International Precipitation Working Group; EUMETSAT: Amsterdam, The Netherlands, 2007; Available online: https://www-cdn.eumetsat.int/files/2020-04/pdf_conf_p50_s1_03_kidd_v.pdf (accessed on 29 October 2022).
- Dinku, T.; Ceccato, P.; Grover-Kopec, E.; Lemma, M.; Connor, S.J.; Ropelewski, C.F. Validation of Satellite Rainfall Products over East Africa’s Complex Topography. Int. J. Remote Sens. 2007, 28, 1503–1526. [Google Scholar] [CrossRef]
- Yin, Z.-Y.; Zhang, X.; Liu, X.; Colella, M.; Chen, X. An Assessment of the Biases of Satellite Rainfall Estimates over the Tibetan Plateau and Correction Methods Based on Topographic Analysis. J. Hydrometeorol. 2008, 9, 301–326. [Google Scholar] [CrossRef]
- Faiz, M.A.; Liu, D.; Tahir, A.A.; Li, H.; Fu, Q.; Adnan, M.; Zhang, L.; Naz, F. Comprehensive Evaluation of 0.25° Precipitation Datasets Combined with MOD10A2 Snow Cover Data in the Ice-Dominated River Basins of Pakistan. Atmos. Res. 2020, 231, 104653. [Google Scholar] [CrossRef]
- Peña-Arancibia, J.L.; van Dijk, A.I.J.M.; Renzullo, L.J.; Mulligan, M. Evaluation of Precipitation Estimation Accuracy in Reanalyses, Satellite Products, and an Ensemble Method for Regions in Australia and South and East Asia. J. Hydrometeorol. 2013, 14, 1323–1333. [Google Scholar] [CrossRef]
- Stampoulis, D.; Anagnostou, E.N. Evaluation of Global Satellite Rainfall Products over Continental Europe. J. Hydrometeorol. 2012, 13, 588–603. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Choudhury, B.J.; Garcia, M. Multitemporal Analysis of TRMM-Based Satellite Precipitation Products for Land Data Assimilation Applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]
- Elgamal, A.; Reggiani, P.; Jonoski, A. Impact Analysis of Satellite Rainfall Products on Flow Simulations in the Magdalena River Basin, Colombia. J. Hydrol. Reg. Stud. 2017, 9, 85–103. [Google Scholar] [CrossRef]
- Boluwade, A. Spatial-temporal assessment of satellite-based rainfall estimates in different precipitation regimes in water-scarce and data-sparse regions. Atmosphere 2020, 11, 901. [Google Scholar] [CrossRef]
- Safa, G.; Najiba, C.; El Houda, B.N.; Monji, H.; Soumaya, A.; Kamel, Z. Assessment of Urban Groundwater Vulnerability in Arid Areas: Case of Sidi Bouzid Aquifer (Central Tunisia). J. Afr. Earth Sci. 2020, 168, 103849. [Google Scholar] [CrossRef]
- Venkata Rao, G.; Venkata Reddy, K.; Srinivasan, R.; Sridhar, V.; Umamahesh, N.V.; Pratap, D. Spatio-Temporal Analysis of Rainfall Extremes in the Flood-Prone Nagavali and Vamsadhara Basins in Eastern India. Weather Clim. Extrem. 2020, 29, 100265. [Google Scholar] [CrossRef]
- Men, B.; Wu, Z.; Liu, H.; Tian, W.; Zhao, Y. Spatio-Temporal Analysis of Precipitation and Temperature: A Case Study Over the Beijing–Tianjin–Hebei Region, China. Pure Appl. Geophys. 2020, 177, 3527–3541. [Google Scholar] [CrossRef]
- Eris, E.; Cavus, Y.; Aksoy, H.; Burgan, H.I.; Aksu, H.; Boyacioglu, H. Spatiotemporal Analysis of Meteorological Drought over Kucuk Menderes River Basin in the Aegean Region of Turkey. Appl Clim. 2020, 142, 1515–1530. [Google Scholar] [CrossRef]
- Aydin, O.; Raja, N.B. Spatial-Temporal Analysis of Precipitation Characteristics in Artvin, Turkey. Appl Clim. 2020, 142, 729–741. [Google Scholar] [CrossRef]
- Tan, M.L.; Zhang, F.; Juinn, C.; Derek, C.; Yu, K.H.; Shaharudin, S.M.; Chan, N.W.; Asyirah, A.R. Spatio-Temporal Analysis of Precipitation, Temperature and Drought from 1985 to 2020 in Penang, Malaysia. Water Supply 2022, 22, 4757–4768. [Google Scholar] [CrossRef]
- Aksu, H.; Cetin, M.; Aksoy, H.; Yaldiz, S.G.; Yildirim, I.; Keklik, G. Spatial and Temporal Characterization of Standard Duration-Maximum Precipitation over Black Sea Region in Turkey. Nat. Hazards 2022, 111, 2379–2405. [Google Scholar] [CrossRef]
- Aksu, H.; Cavus, Y.; Aksoy, H.; Akgul, M.A.; Turker, S.; Eris, E. Spatiotemporal Analysis of Drought by CHIRPS Precipitation Estimates. Appl Clim. 2022, 148, 517–529. [Google Scholar] [CrossRef]
- Sherif, M.; Almulla, M.; Shetty, A.; Chowdhury, R.K. Analysis of Rainfall, PMP and Drought in the United Arab Emirates. Int. J. Climatol. 2014, 34, 1318–1328. [Google Scholar] [CrossRef]
- Adeyewa, Z.D.; Nakamura, K. Validation of TRMM Radar Rainfall Data over Major Climatic Regions in Africa. J. Appl. Meteorol. Climatol. 2003, 42, 331–347. [Google Scholar] [CrossRef]
- Sultana, R.; Nasrollahi, N. Evaluation of Remote Sensing Precipitation Estimates over Saudi Arabia. J. Arid Environ. 2018, 151, 90–103. [Google Scholar] [CrossRef]
- Anjum, M.N.; Irfan, M.; Waseem, M.; Leta, M.K.; Niazi, U.M.; ur Rahman, S.; Ghanim, A.; Mukhtar, M.A.; Nadeem, M.U. Assessment of PERSIANN-CCS, PERSIANN-CDR, SM2RAIN-ASCAT, and CHIRPS-2.0 Rainfall Products over a Semi-Arid Subtropical Climatic Region. Water 2022, 14, 147. [Google Scholar] [CrossRef]
- Hussein, K.A.; Alsumaiti, T.S.; Ghebreyesus, D.T.; Sharif, H.O.; Abdalati, W. High-Resolution Spatiotemporal Trend Analysis of Precipitation Using Satellite-Based Products over the United Arab Emirates. Water 2021, 13, 2376. [Google Scholar] [CrossRef]
- Murad, A.A. An Overview of Conventional and Non-Conventional Water Resources in Arid Region: Assessment and Constrains of the United Arab Emirates (UAE). J. Water Resour. Prot. 2010, 2, 181–190. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Charron, C.; Niranjan Kumar, K.; Marpu, P.R.; Ghedira, H.; Molini, A.; Khayal, I. Evolution of the Rainfall Regime in the United Arab Emirates. J. Hydrol. 2014, 514, 258–270. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Harrison, L.; Landsfeld, M.; Husak, G.; Davenport, F.; Shukla, S.; Turner, W.; Peterson, P.; Funk, C. Advancing Early Warning Capabilities with CHIRPS-Compatible NCEP GEFS Precipitation Forecasts. Sci. Data 2022, 9, 375. [Google Scholar] [CrossRef]
- NCM.AE. Available online: https://www.ncm.ae/?lang=ar (accessed on 29 October 2022).
- Ryu, S.; Song, J.J.; Kim, Y.; Jung, S.-H.; Do, Y.; Lee, G. Spatial Interpolation of Gauge Measured Rainfall Using Compressed Sensing. Asia Pac. J. Atmos. Sci. 2021, 57, 331–345. [Google Scholar] [CrossRef]
- Chen, F.-W.; Liu, C.-W. Estimation of the Spatial Rainfall Distribution Using Inverse Distance Weighting (IDW) in the Middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Yang, X.; Xie, X.; Liu, D.L.; Ji, F.; Wang, L. Spatial Interpolation of Daily Rainfall Data for Local Climate Impact Assessment over Greater Sydney Region. Adv. Meteorol. 2015, 2015, e563629. [Google Scholar] [CrossRef]
- Abd Elhamid, A.M.I.; Eltahan, A.M.H.; Mohamed, L.M.E.; Hamouda, I.A. Assessment of the Two Satellite-Based Precipitation Products TRMM and RFE Rainfall Records Using Ground Based Measurements. Alex. Eng. J. 2020, 59, 1049–1058. [Google Scholar] [CrossRef]
- Alsumaiti, T.S.; Hussein, K.; Ghebreyesus, D.T.; Sharif, H.O. Performance of the CMORPH and GPM IMERG Products over the United Arab Emirates. Remote Sens. 2020, 12, 1426. [Google Scholar] [CrossRef]
- Faiz, M.A.; Liu, D.; Fu, Q.; Sun, Q.; Li, M.; Baig, F.; Li, T.; Cui, S. How Accurate Are the Performances of Gridded Precipitation Data Products over Northeast China? Atmos. Res. 2018, 211, 12–20. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Hamouda, M.A.; Mohamed, M.M. Spatiotemporal Evaluation of the GPM Satellite Precipitation Products over the United Arab Emirates. Atmos. Res. 2019, 219, 200–212. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Cohen, I., Huang, Y., Chen, J., Benesty, J., Eds.; Springer Topics in Signal Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. ISBN 978-3-642-00296-0. [Google Scholar]
- Alexander, L.V.; Fowler, H.J.; Bador, M.; Behrangi, A.; Donat, M.G.; Dunn, R.; Funk, C.; Goldie, J.; Lewis, E.; Rogé, M.; et al. On the Use of Indices to Study Extreme Precipitation on Sub-Daily and Daily Timescales. Environ. Res. Lett. 2019, 14, 125008. [Google Scholar] [CrossRef]
- De Luis, M.; Gonzalez-Hidalgo, J.C.; Raventos, J.; Sanchez, J.R.; Cortina, J. Distribución Espacial de La Concentración y Agresividad de La Lluvia En El Territorio de La Comunidad Valenciana. Cuatern. Geomorfol. 1997, 11, 33–44. [Google Scholar]
- Oliver, J.E. Monthly Precipitation Distribution: A Comparative Index. Prof. Geogr. 1980, 32, 300–309. [Google Scholar] [CrossRef]
- Faiz, M.A.; Liu, D.; Fu, Q.; Wrzesiński, D.; Muneer, S.; Khan, M.I.; Li, T.; Cui, S. Assessment of Precipitation Variability and Uncertainty of Stream Flow in the Hindu Kush Himalayan and Karakoram River Basins of Pakistan. Meteorol. Atmos. Phys. 2019, 131, 127–136. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Bronikowski, A.; Webb, C. Appendix: A Critical Examination of Rainfall Variability Measures Used in Behavioral Ecology Studies. Behav. Ecol. Sociobiol. 1996, 39, 27–30. [Google Scholar] [CrossRef]
- Chapungu, L.; Nhamo, L.; Gatti, R.C.; Chitakira, M. Quantifying Changes in Plant Species Diversity in a Savanna Ecosystem Through Observed and Remotely Sensed Data. Sustainability 2020, 12, 2345. [Google Scholar] [CrossRef]
- Joseph, S.; Anitha, K.; Srivastava, V.K.; Reddy, C.S.; Thomas, A.P.; Murthy, M.S.R. Rainfall and Elevation Influence the Local-Scale Distribution of Tree Community in the Southern Region of Western Ghats Biodiversity Hotspot (India). Int. J. For. Res. 2012, 2012, e576502. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Li, C.; Zhang, H.; Singh, V.P.; Fan, J.; Wei, X.; Yang, J.; Wei, X. Investigating Variations of Precipitation Concentration in the Transitional Zone between Qinling Mountains and Loess Plateau in China: Implications for Regional Impacts of AO and WPSH. PLoS ONE 2020, 15, e0238709. [Google Scholar] [CrossRef] [PubMed]
- Michiels, P.; Gabriels, D.; Hartmann, R. Using the Seasonal and Temporal Precipitation Concentration Index for Characterizing the Monthly Rainfall Distribution in Spain. CATENA 1992, 19, 43–58. [Google Scholar] [CrossRef]
- Zhang, K.; Yao, Y.; Qian, X.; Wang, J. Various Characteristics of Precipitation Concentration Index and Its Cause Analysis in China between 1960 and 2016. Int. J. Climatol. 2019, 39, 4648–4658. [Google Scholar] [CrossRef]
- Da Motta Paca, V.H.; Espinoza-Dávalos, G.E.; Moreira, D.M.; Comair, G. Variability of Trends in Precipitation across the Amazon River Basin Determined from the CHIRPS Precipitation Product and from Station Records. Water 2020, 12, 1244. [Google Scholar] [CrossRef]
- Pereira Filho, A.J.; Vemado, F.; Vemado, G.; Gomes Vieira Reis, F.A.; do Carmo Giordano, L.; Cerri, R.I.; dos Santos, C.C.; Sampaio Lopes, E.S.; Gramani, M.F.; Ogura, A.T.; et al. A Step towards Integrating CMORPH Precipitation Estimation with Rain Gauge Measurements. Adv. Meteorol. 2018, 2018, e2095304. [Google Scholar] [CrossRef]
- De Almeida, C.T.; Delgado, R.C.; de Oliveira Junior, J.F.; Gois, G.; Cavalcanti, A.S. Avaliação das Estimativas de Precipitação do Produto 3B43-TRMM do Estado do Amazonas. Floresta Ambiente 2015, 22, 279–286. [Google Scholar] [CrossRef]
- De Moraes Cordeiro, A.L.; Blanco, C.J.C. Assessment of Satellite Products for Filling Rainfall Data Gaps in the Amazon Region. Nat. Resour. Model. 2021, 34, e12298. [Google Scholar] [CrossRef]






| GPM-IMERG | CMORPH | CHIRPS | PERSIANN-CDR | |
|---|---|---|---|---|
| Source | NASA | NOAA | CHC, UCB | CHRS, UCI |
| Spatial Distribution | 10 × 10 km | 8 × 8 km | 5 × 5 km | 25 × 25 km |
| Temporal Distribution | Daily | Half-Hourly | Daily | Daily |
| Data Availability | 2000-Present | 1998-Present | 1981-Present | 2000-Present |
| Span | 60°S–60°N | 60°S–60°N | 50°S–50°N | 60°S–60°N |
| Ground Observations | Satellite Estimates | ||
| Yes | No | ||
| Yes | A = Hits (Accurate forecasts) | B = Miss (Missed/unwarned events) | |
| No | C = False Alarm (Wolf Cry) | D = Correct No (Usually, we ignore this as rare event) | |
| Indices | Symbology | Units |
|---|---|---|
| Rx1 day | Maximum 1-day precipitation over a given period | mm |
| R10 mm | Yearly days count when | days |
| Rainfall ≥ 10 mm | ||
| R20 mm | Yearly days count when | days |
| Rainfall ≥ 20 mm | ||
| R30 mm | Yearly days count when | days |
| Rainfall ≥ 30 mm | ||
| CWD | The maximum length of the wet spell. | days |
| Max number of continuous days when Rainfall ≥ 1 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baig, F.; Abrar, M.; Chen, H.; Sherif, M. Rainfall Consistency, Variability, and Concentration over the UAE: Satellite Precipitation Products vs. Rain Gauge Observations. Remote Sens. 2022, 14, 5827. https://doi.org/10.3390/rs14225827
Baig F, Abrar M, Chen H, Sherif M. Rainfall Consistency, Variability, and Concentration over the UAE: Satellite Precipitation Products vs. Rain Gauge Observations. Remote Sensing. 2022; 14(22):5827. https://doi.org/10.3390/rs14225827
Chicago/Turabian StyleBaig, Faisal, Muhammad Abrar, Haonan Chen, and Mohsen Sherif. 2022. "Rainfall Consistency, Variability, and Concentration over the UAE: Satellite Precipitation Products vs. Rain Gauge Observations" Remote Sensing 14, no. 22: 5827. https://doi.org/10.3390/rs14225827
APA StyleBaig, F., Abrar, M., Chen, H., & Sherif, M. (2022). Rainfall Consistency, Variability, and Concentration over the UAE: Satellite Precipitation Products vs. Rain Gauge Observations. Remote Sensing, 14(22), 5827. https://doi.org/10.3390/rs14225827








