Marine Heatwaves in the South China Sea: Tempo-Spatial Pattern and Its Association with Large-Scale Circulation
Abstract
1. Introduction
2. Data and Methods
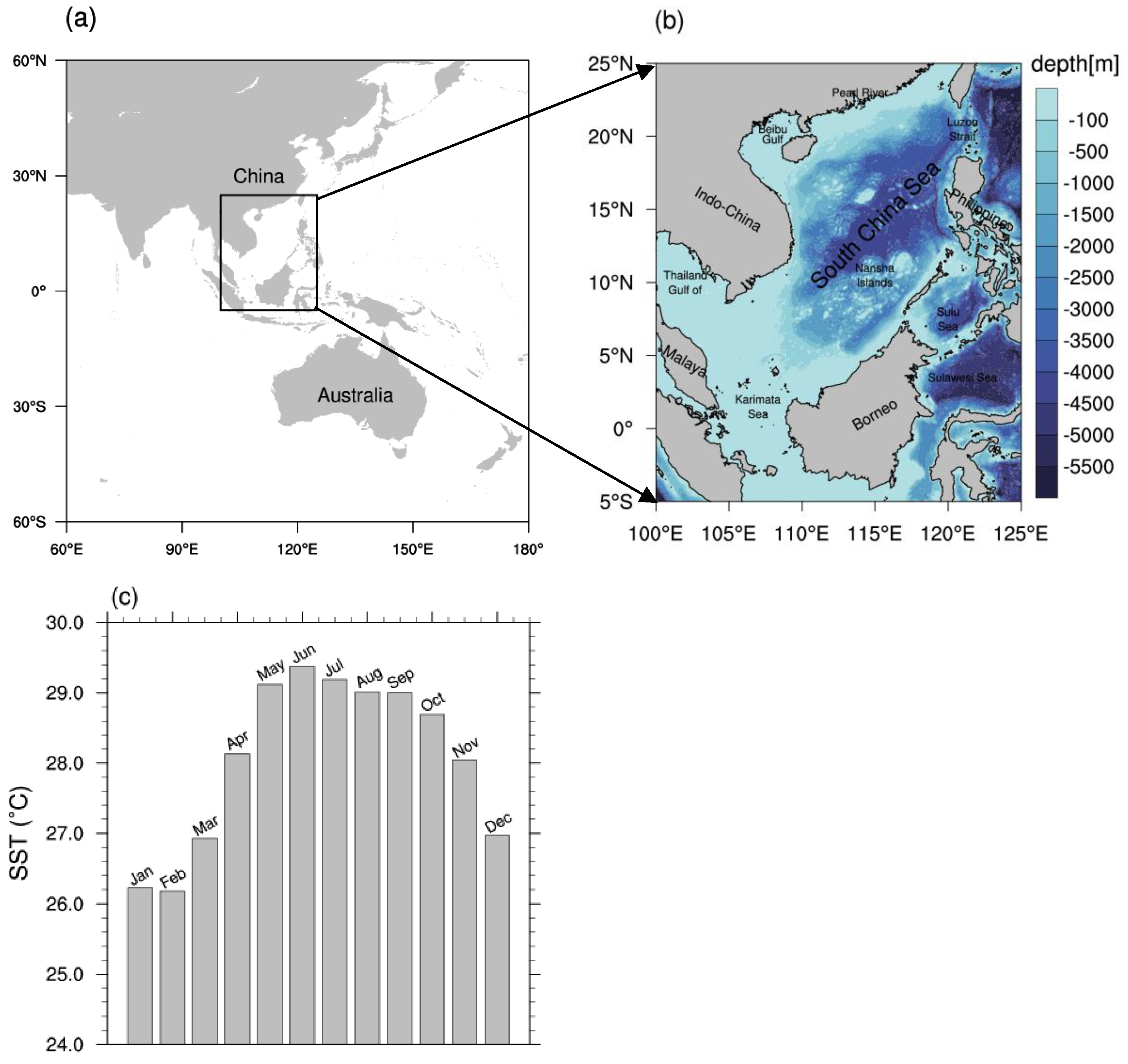
2.1. Study Region
2.2. Data Description
2.3. Identification of Marine Heatwaves (MHWs) and Indices
2.4. Regional Marine Heatwaves (MHWs) and The Relevant Circulation Anomalies
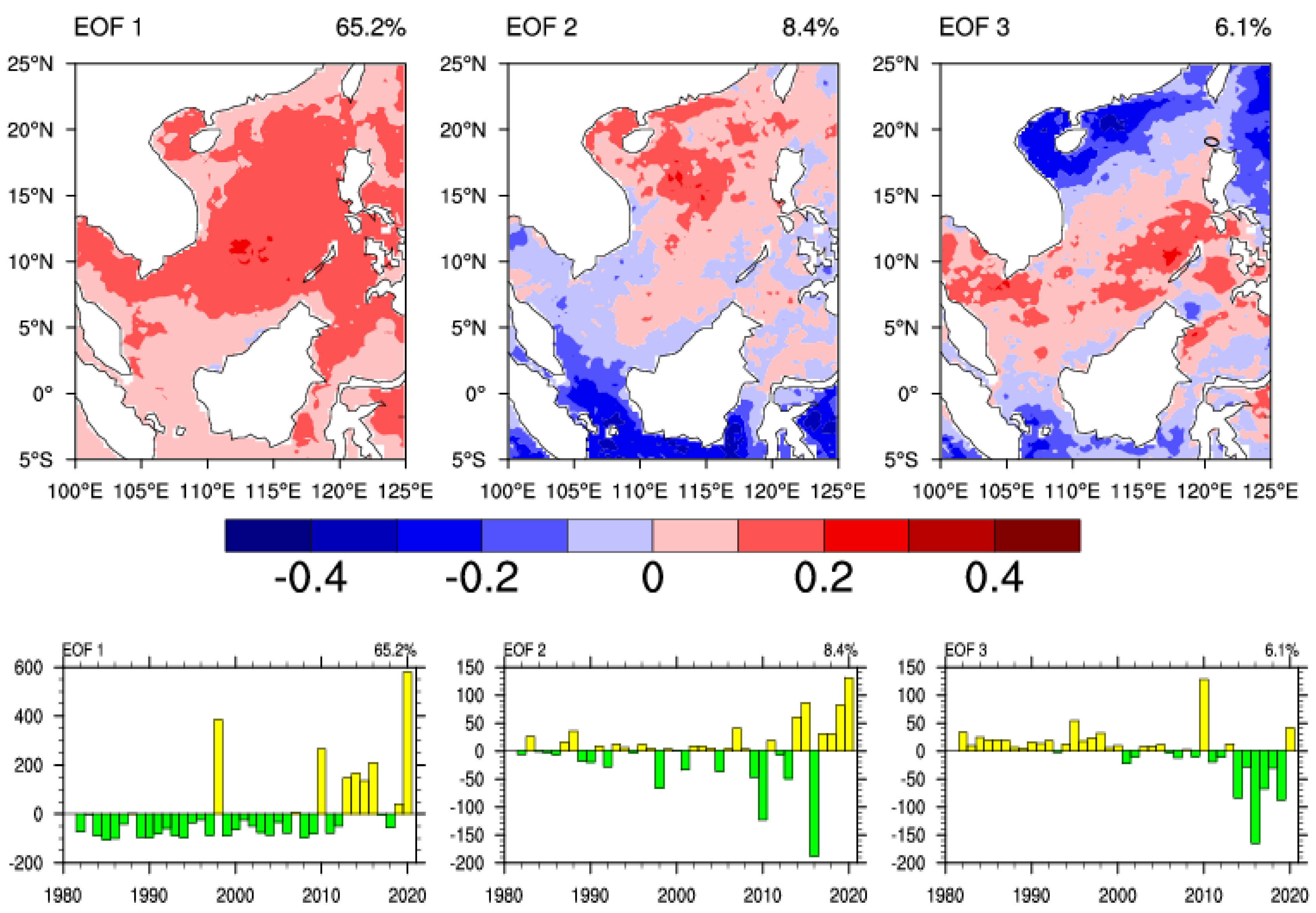
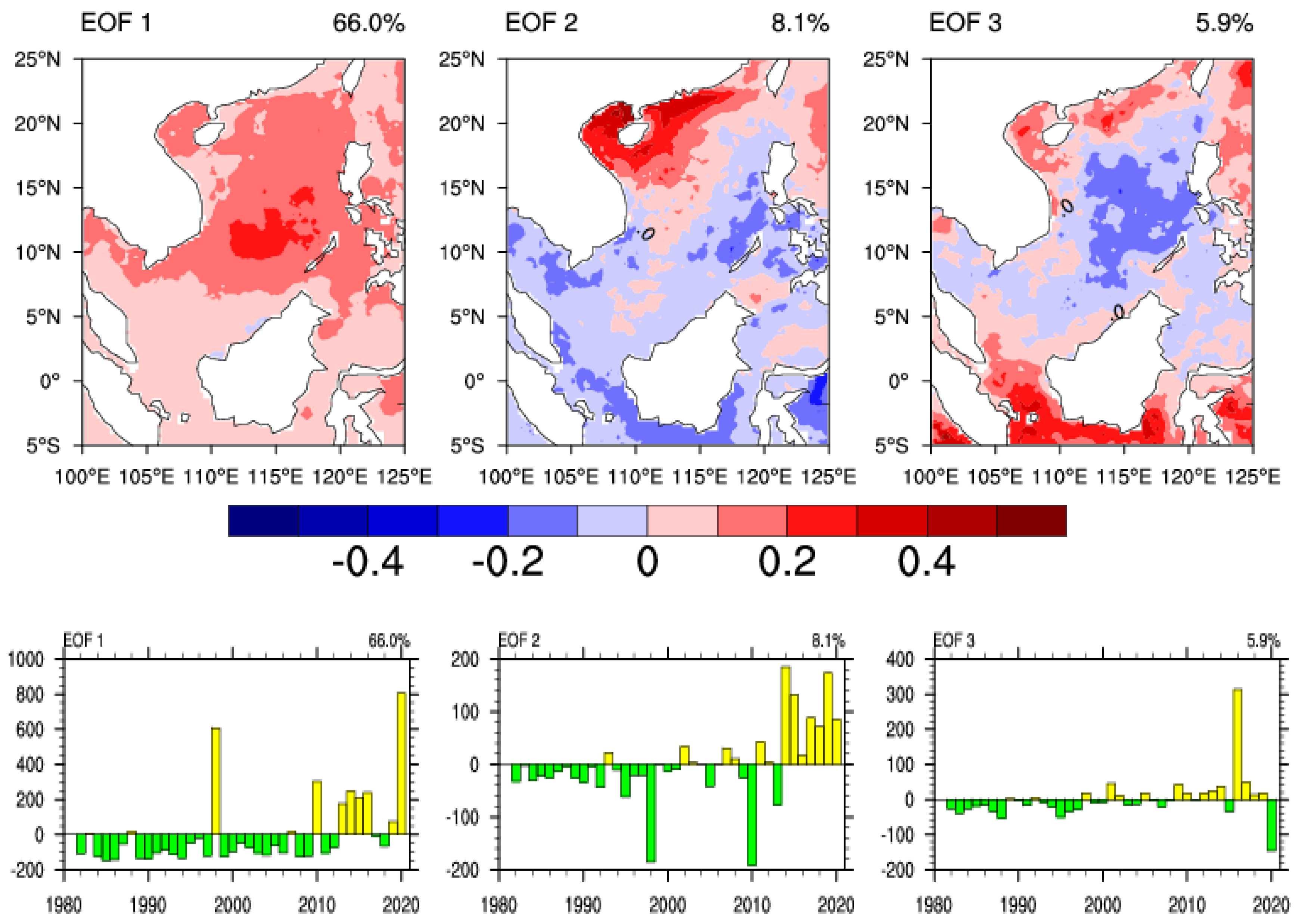
2.5. Empirical Orthogonal Function (EOF) Analysis
2.6. Testing for Significance of Correlations and Trends
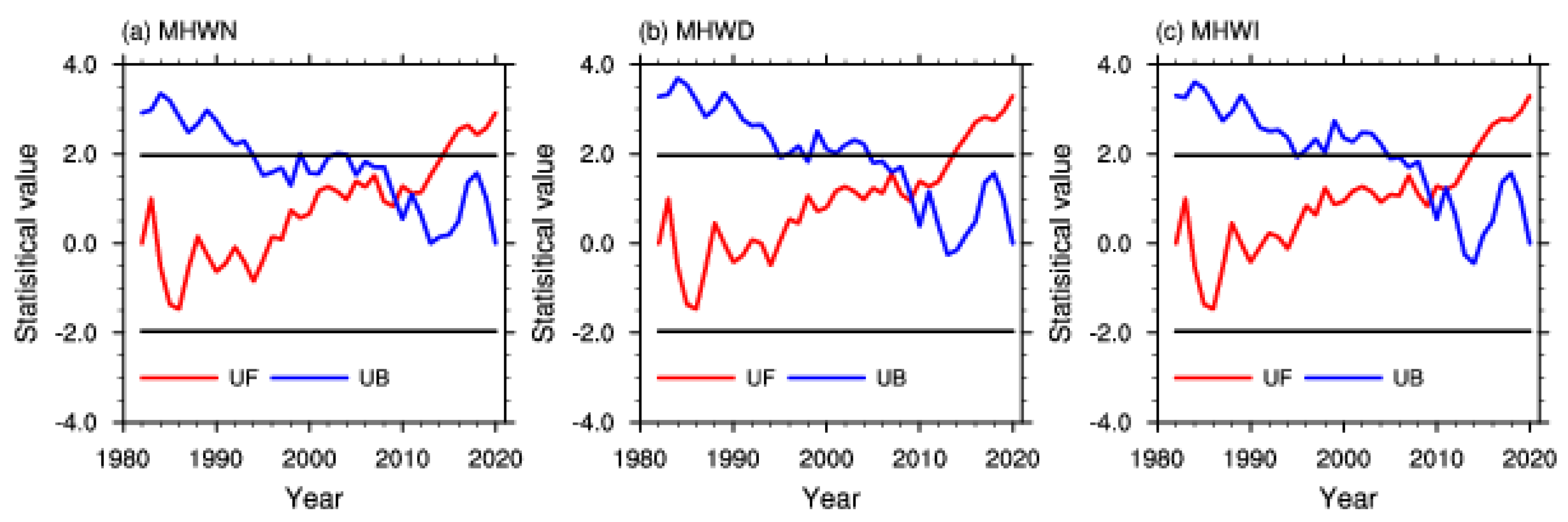
2.7. Mann–Kendall Abrupt Change Test
3. Results
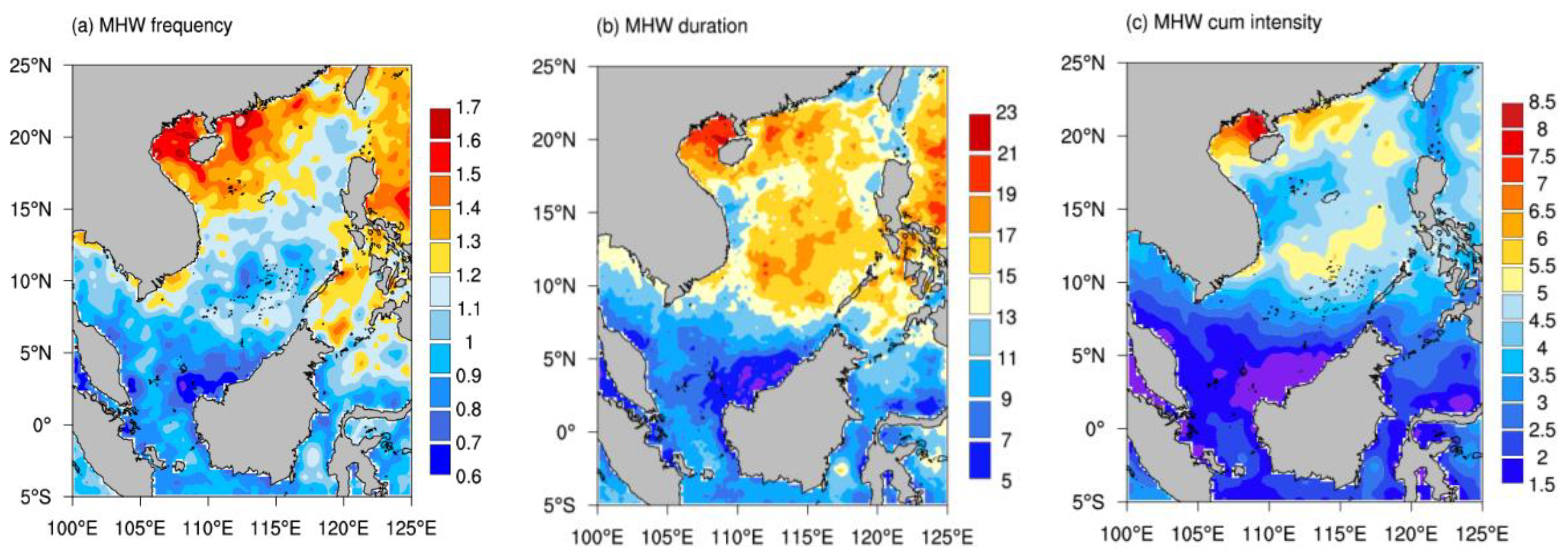
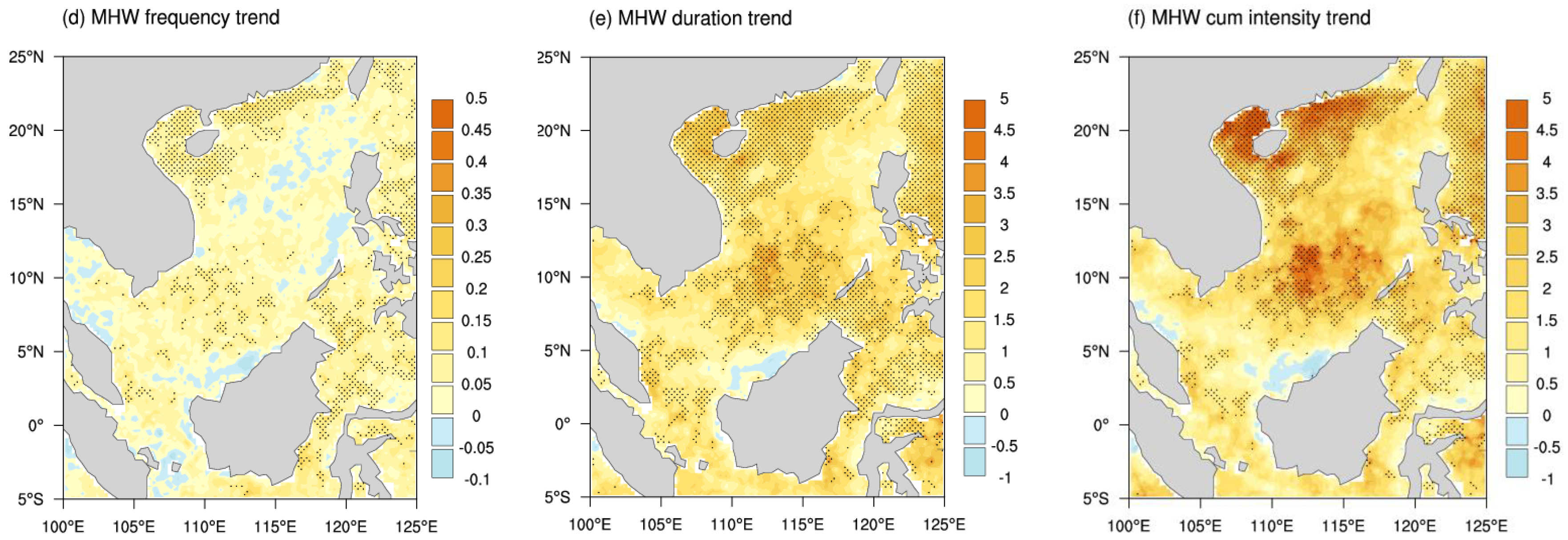
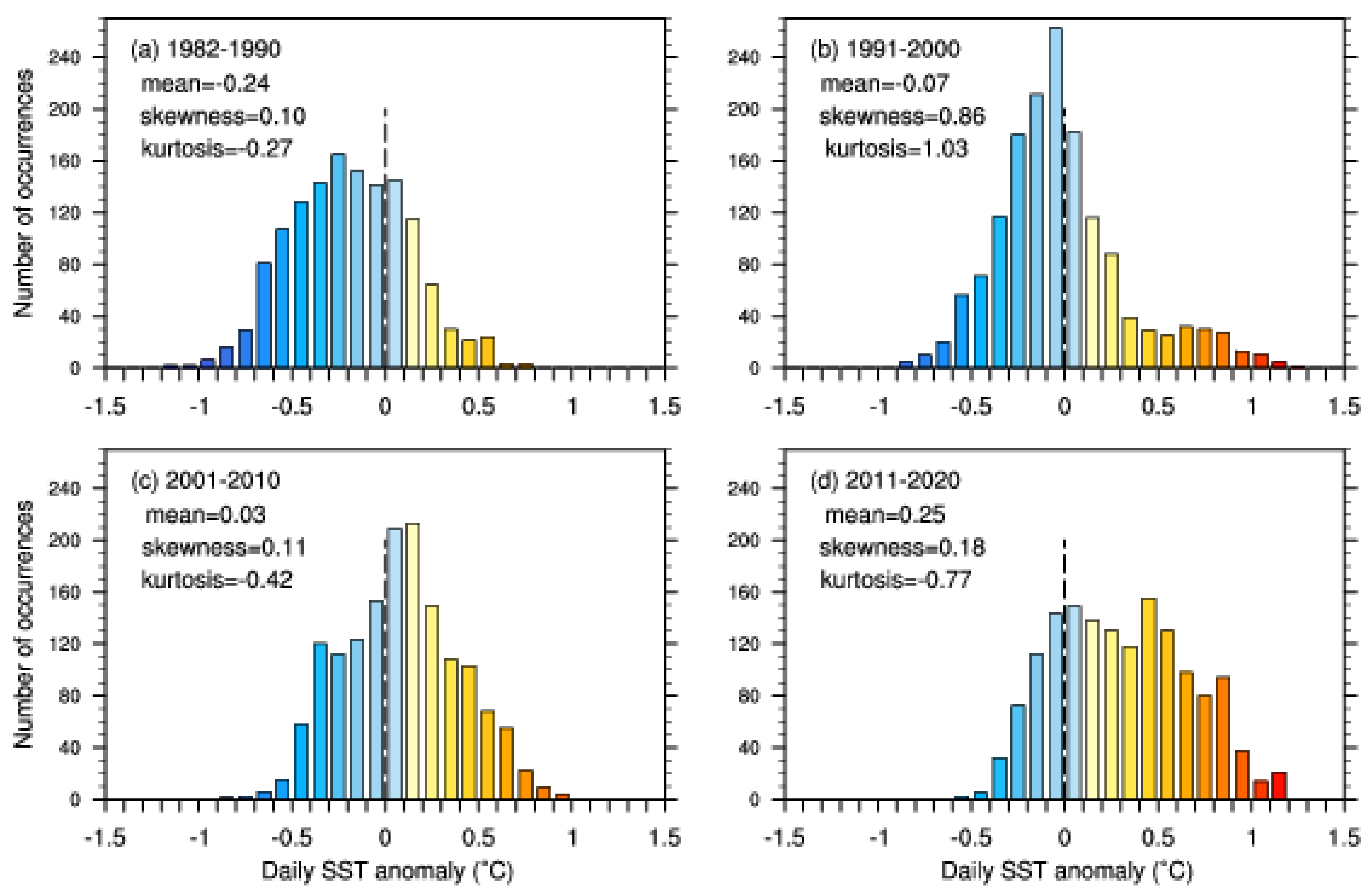
3.1. Climatology and Long-Term Trends in Annual MHWs Indices
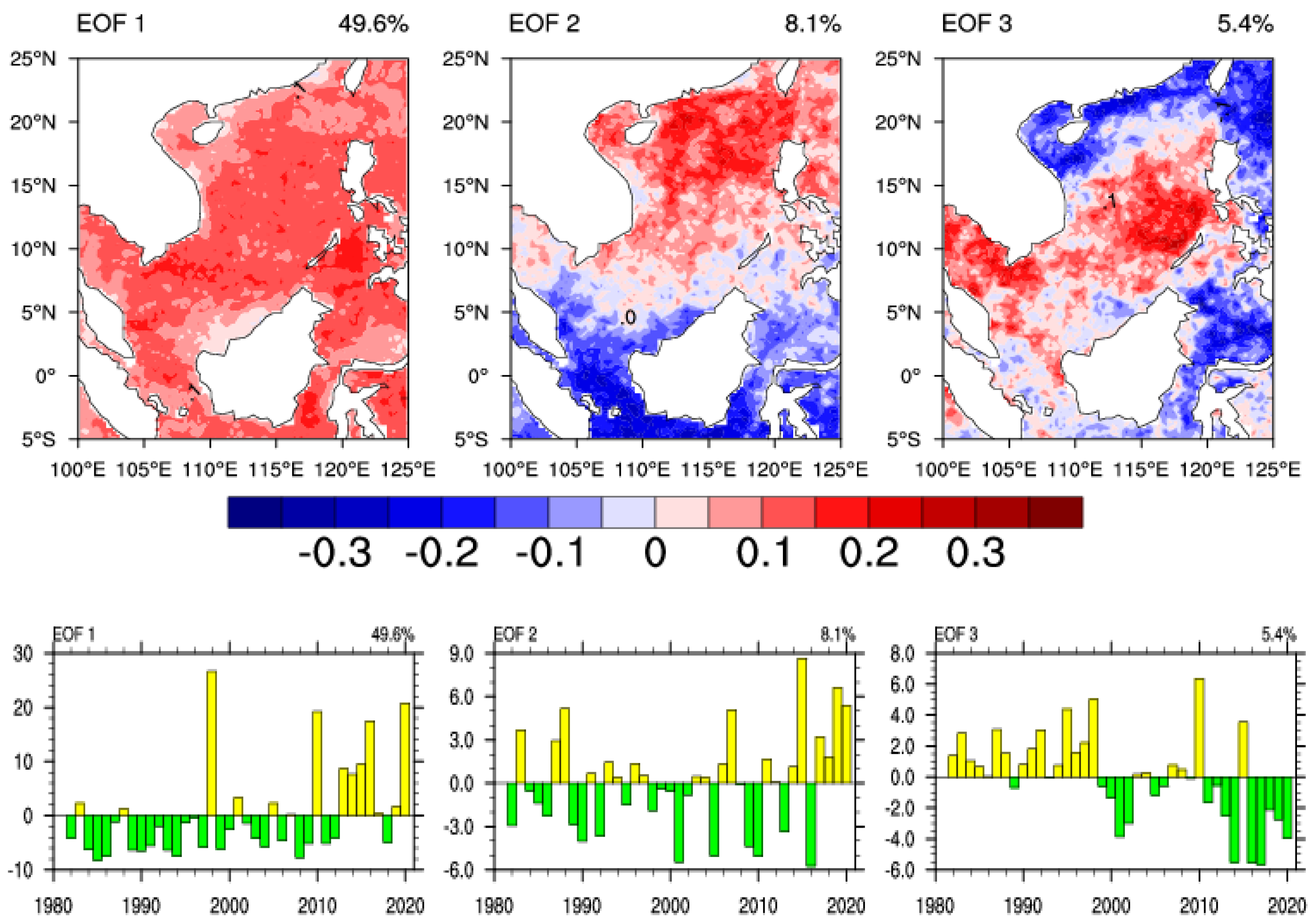
3.2. Dominant Modes of Marine Heatwave Variations
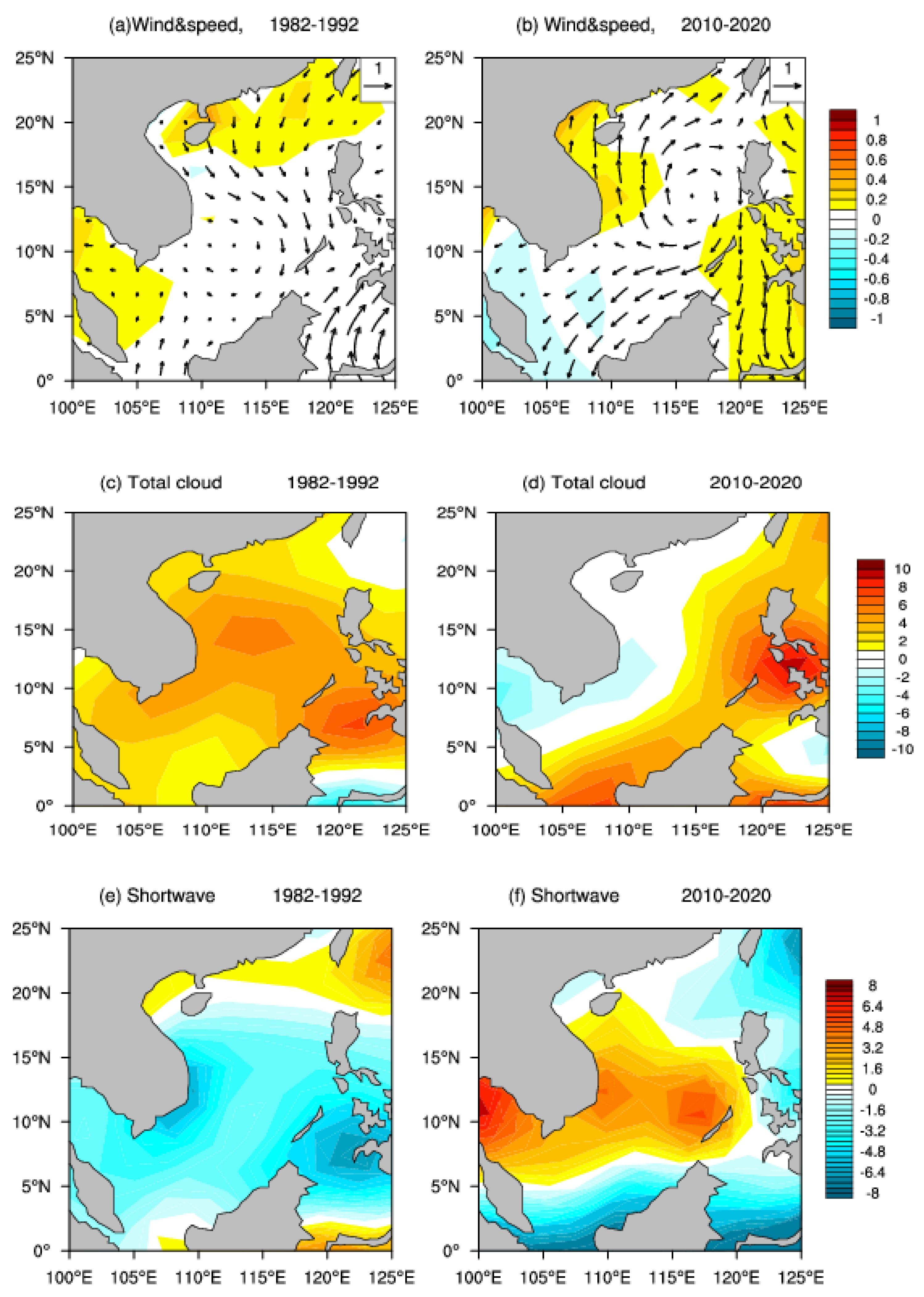
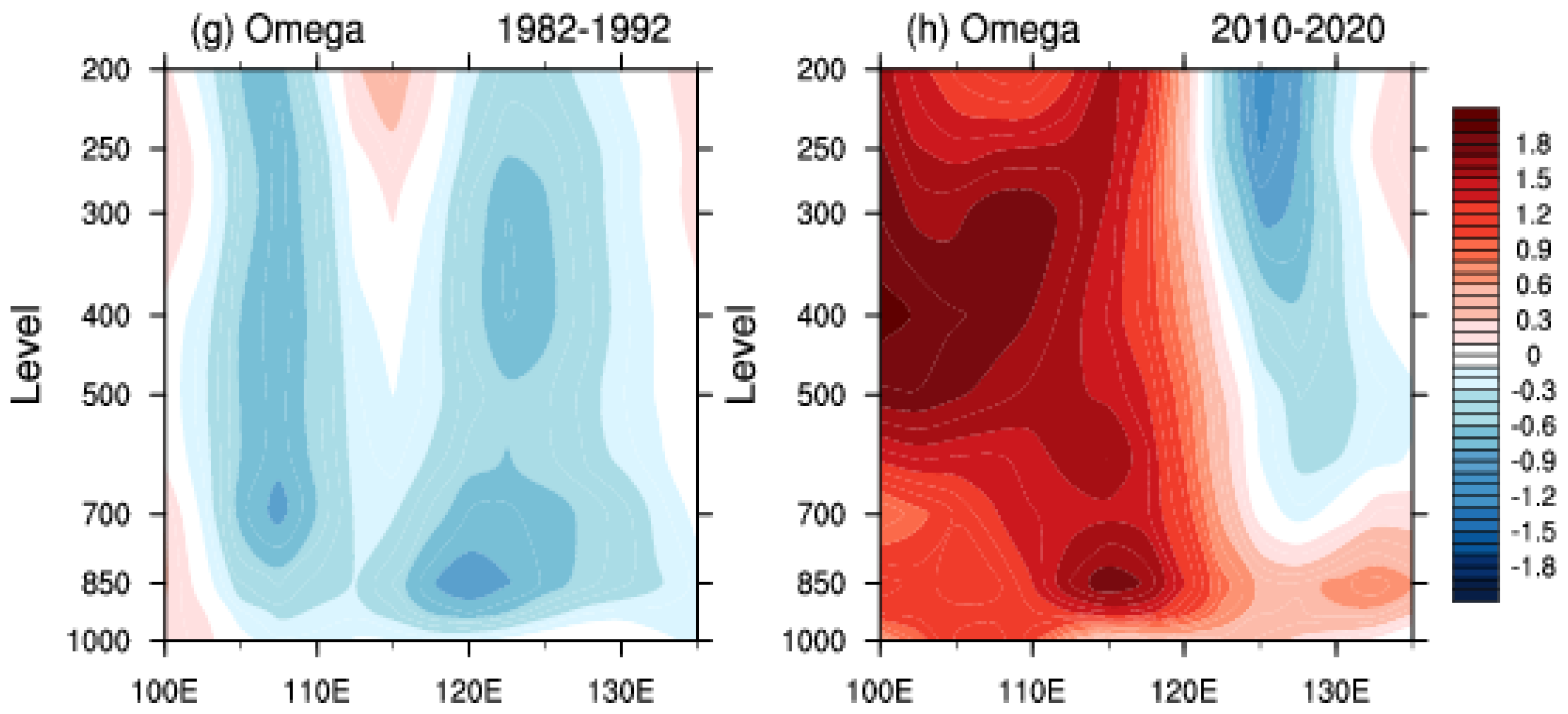
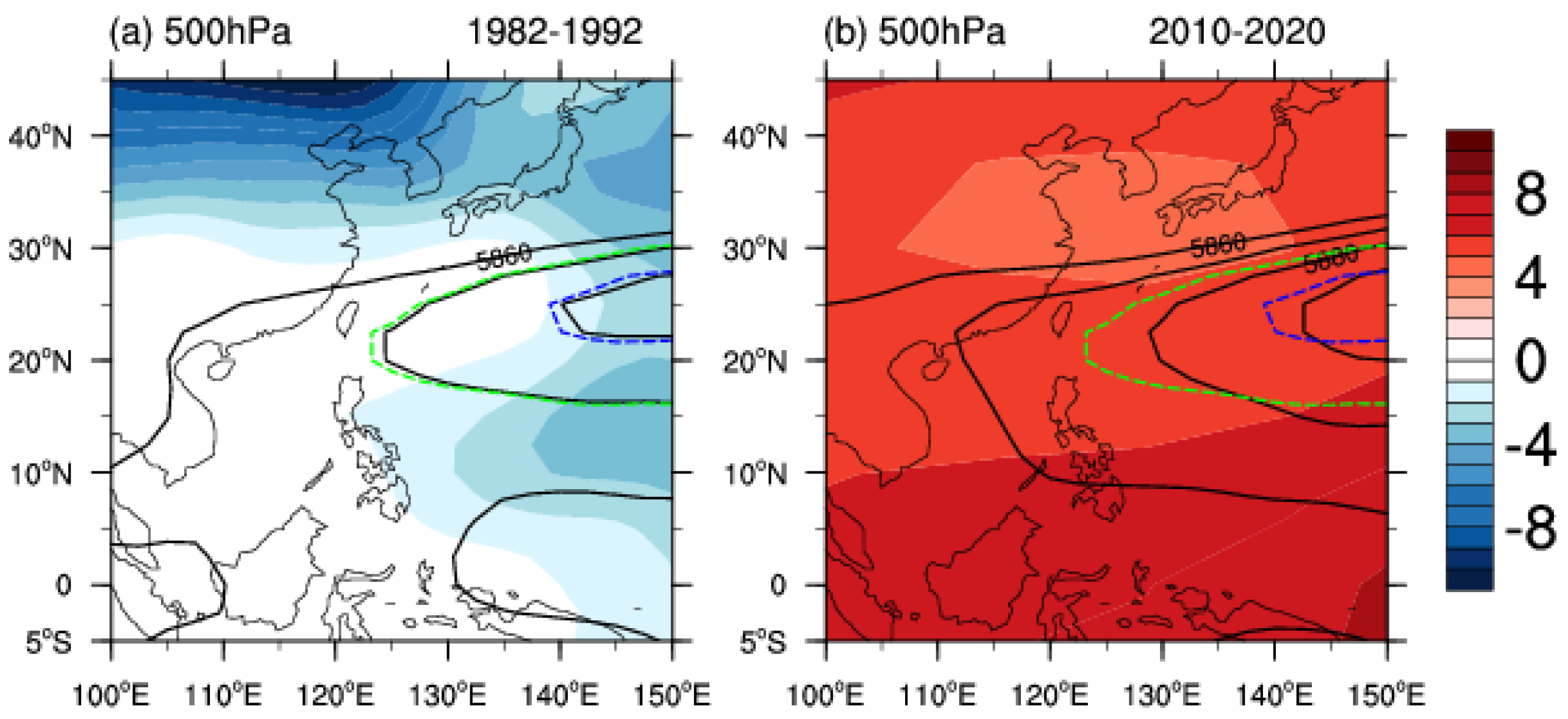
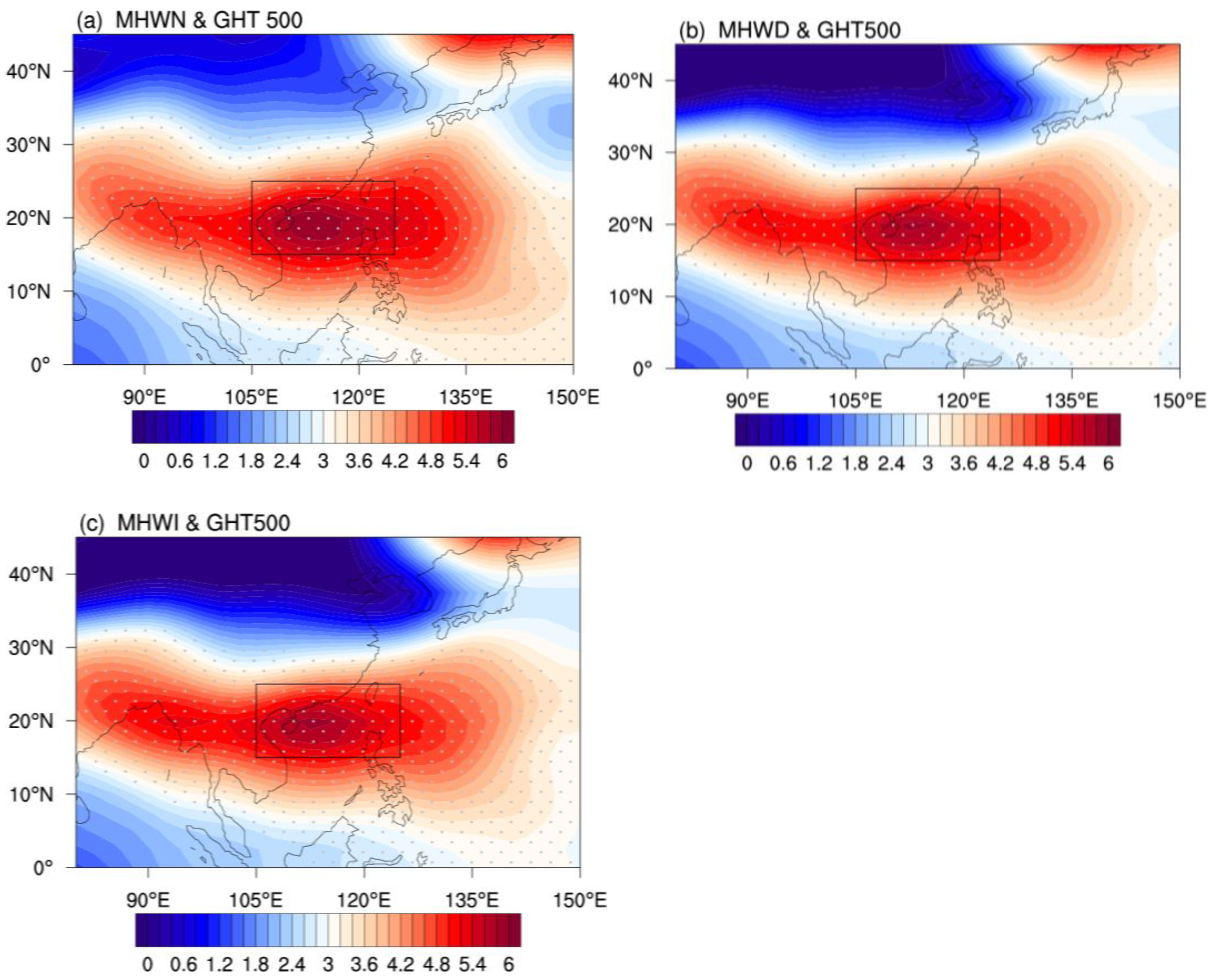
3.3. Connection with Large-Scale Atmospheric Circulation
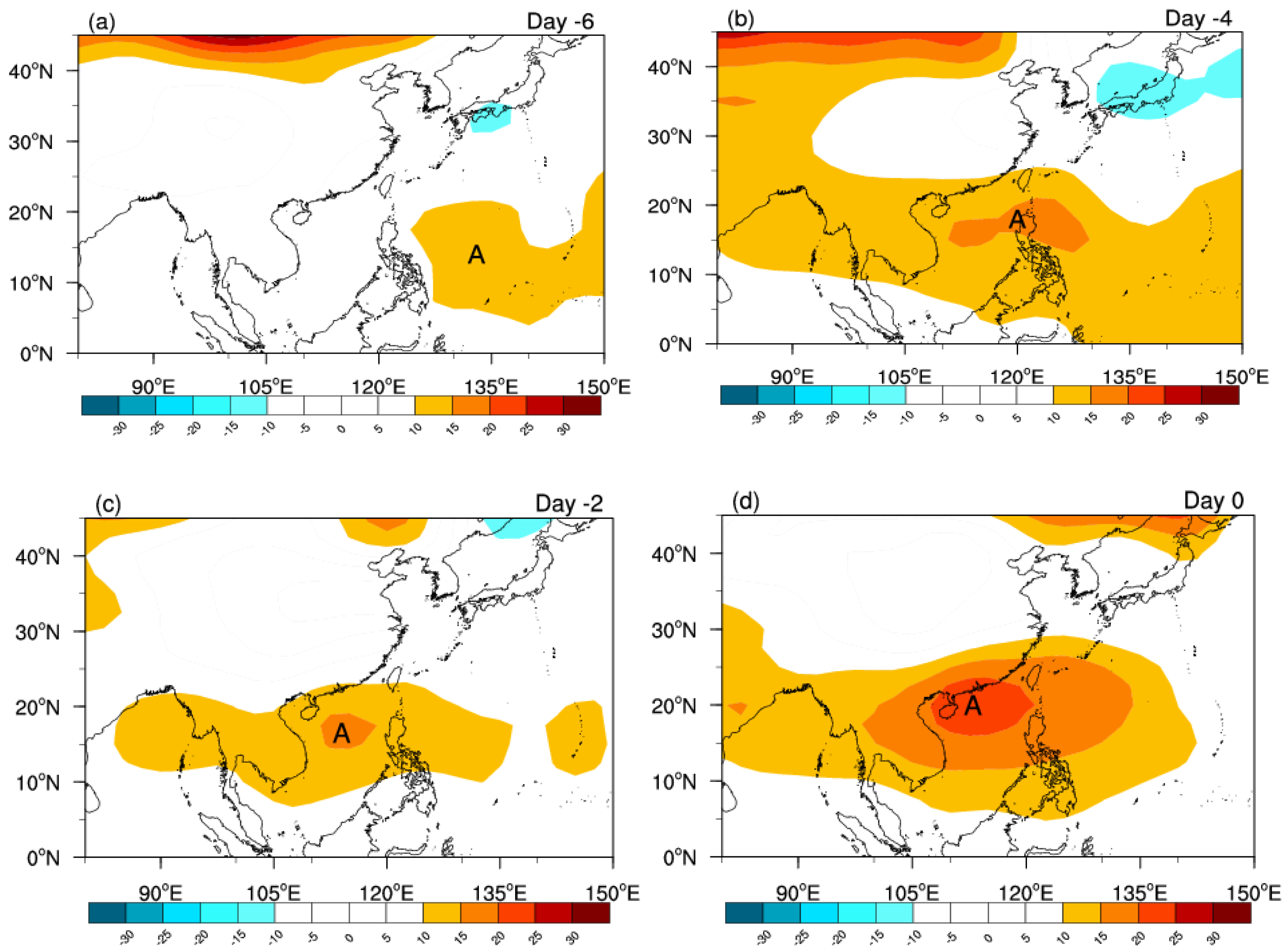
3.3.1. Abnormities of Atmospheric Circulation
3.3.2. Western North Pacific Subtropical High (WNPSH)
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, L.; Abraham, J.; Zhu, J.; Trenberth, K.E.; Fasullo, J.; Boyer, T.; Locarnini, R.; Zhang, B.; Yu, F.J.; Wan, L.Y.; et al. Record-setting ocean warmth continued in 2019. Adv. Atmos. Sci. 2020, 37, 137–142. [Google Scholar] [CrossRef]
- Ma, X.; Liu, W.; Allen, R.J.; Huang, G.; Li, X. Dependence of regional ocean heat uptake on anthropogenic warming scenarios. Sci. Adv. 2020, 6, eabc0303. [Google Scholar] [CrossRef] [PubMed]
- Laufkötter, C.; Zscheischler, J.; Frölicher, T.L. High-impact marine heatwaves attributable to human-induced global warming. Science 2020, 369, 1621–1625. [Google Scholar] [CrossRef] [PubMed]
- Oliver, E.C.J.; Benthuysen, J.A.; Darmaraki, S.; Donat, M.G.; Hobday, A.J.; Holbrook, N.J.; Schlegel, R.W.; Gupta, A.S. Marine Heatwaves. Annu. Rev. Mar. Sci. 2021, 13, 20.1–20.30. [Google Scholar] [CrossRef]
- Frölicher, T.L.; Fischer, E.M.; Gruber, N. Marine heatwaves under global warming. Nature 2018, 560, 360–364. [Google Scholar] [CrossRef]
- Darmaraki, S.; Somot, S.; Sevault, F.; Nabat, P.; Narvaez, W.D.C.; Cavicchia, L.; Djurdjevic, V.; Li, L.; Sannino, G.; V.Sein, D. Future evolution of marine heatwaves in the Mediterranean Sea. Clim. Dyn. 2019, 53, 1371–1392. [Google Scholar] [CrossRef]
- Kuroda, H.; Setou, T. Extensive marine heatwaves at the sea surface in the Northwestern Pacific Ocean in summer 2021. Remote Sens. 2021, 13, 3989. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). WMO Statement on the State of the Global Climate in 2020; WMO: Geneva, Switzerland, 2021; p. 56. [Google Scholar]
- Caputi, N.; Kangas, M.; Denham, A.; Feng, M.; Pearce, A.; Hetzel, Y.; Chandrapavan, A. Management adaptation of invertebrate fisheries to an extreme marine heat wave event at a global warming hot spot. Ecol. Evol. 2016, 6, 3583–3593. [Google Scholar] [CrossRef]
- Hughes, T.P.; Kerry, J.T.; Alvarez-Noriega, M.; Alvarez-Romero, J.G.; Anderson, K.D.; Andrew, H.B.; Babcock, R.C.; Beger, M.; Bellwood, D.R.; Berkelmans, R.; et al. Global warming and recurrent mass bleaching of corals. Nature 2017, 543, 373–377. [Google Scholar] [CrossRef]
- Holbrook, N.J.; Scannell, H.A.; Gupta, A.S.; Benthuysen, J.A.; Feng, M.; Oliver, E.C.J.; Alexander, L.V.; Burrows, M.T.; Donat, M.G.; Hobday, A.J.; et al. A global assessment of marine heatwaves and their drivers. Nat. Commun. 2019, 10, 2624. [Google Scholar] [CrossRef]
- Oliver, E.; Benthuysen, J.; Bindoff, N.; Hobday, A.J.; Holbrook, N.J.; Mundy, C.N.; Perkins-Kirkpatrick, S.E. The unprecedented 2015/16 Tasman Sea marine heatwave. Nat. Commun. 2017, 8, 16101. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Wang, C. Variations in summer marine heatwaves in the South China Sea. J. Geophys. Res. Oceans 2021, 126, e2021JC017792. [Google Scholar] [CrossRef]
- Tan, H.J.; Cai, R.S.; Wu, R.G. Summer marine heatwaves in the South China Sea: Trend, variability and possible causes. Adv. Clim. Chang. Res. 2022, 13, 323–332. [Google Scholar] [CrossRef]
- De Deckker, P. The Indo-Pacific Warm Pool: Critical to world oceanography and world climate. Geosci. Lett. 2016, 3, 20. [Google Scholar] [CrossRef]
- Huang, D.; Licuanan, W.Y.; Hoeksema, B.W.; Chen, C.A.; Ang, P.O.; Huang, H.; Lane, D.J.W.; Vo, S.T.; Waheed, Z.; Affendi, Y.A.; et al. Extraordinary diversity of reef corals in the South China Sea. Mar Biodiv. 2015, 45, 157–168. [Google Scholar] [CrossRef]
- Zhao, H.T.; Wang, L.R.; Yuan, J.Y. Sustainable development of the coral reefs in the South China Sea Islands. Trop. Geogr. 2016, 36, 55–65, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- DeCarlo, T.M.; Cohen, A.L.; Wong, G.T.F.; Davis, K.A.; Lohmann, P.; Soong, K. Mass coral mortality under local amplification of 2 °C ocean warming. Sci. Rep. 2017, 7, 44586. [Google Scholar] [CrossRef]
- China Meteorological Administration Climate Change Centre. Blue Book on Climate Change in China; Science Press: Beijing, China, 2021; p. 78.
- Wu, L.; Cai, W.; Zhang, L.; Nakamura, H.; Timmermann, A.; Joyce, T.; McPhaden, M.J.; Alexander, M.; Qiu, B.; Visbeck, M.; et al. Enhanced warming over the global subtropical western boundary currents. Nat. Clim. Chang. 2012, 2, 161–166. [Google Scholar] [CrossRef]
- Schlegel, R.W.; Oliver, E.C.J.; Sarah, P.K.; Andries, K.; Smit, A.J. Predominant Atmospheric and oceanic patterns during coastal marine heatwaves. Front. Mar. Sci. 2017, 4, 323. [Google Scholar] [CrossRef]
- Li, X.; Donner, S.D. Lengthening of warm periods increased the intensity of warm-season marine heatwaves over the past 4 decades. Clim. Dyn. 2022, 59, 2643–2654. [Google Scholar] [CrossRef]
- Park, Y.G.; Choi, A. Long-term changes of South China Sea surface temperatures in winter and summer. Cont. Shelf Res. 2017, 143, 185–193. [Google Scholar] [CrossRef]
- Banzon, V.; Smith, T.M.; Chin, T.M.; Liu, C.; Hankins, W. A long-term record of blended satellite and in situ sea-surface temperature for climate monitoring, modeling, and environmental studies. Earth Syst. Sci. Data 2016, 8, 165–176. [Google Scholar] [CrossRef]
- Benthuysen, J.A.; Oliver, E.C.J.; Feng, M.; Marshall, A.G. Extreme marine warming across tropical Australia during austral summer 2015–2016. J. Geophys. Res. Oceans 2018, 2, 1301–1326. [Google Scholar] [CrossRef]
- Lee, S.; Park, M.S.; Kwon, M.; Kim, Y.H.; Park, Y.G. Two major modes of east Asian marine heatwaves. Environ. Res. Lett. 2020, 15, 074008. [Google Scholar] [CrossRef]
- Kumar, C.; Podestá, G.; Kilpatrick, K.; Peter, M. A machine learning approach to estimating the error in satellite sea surface temperature retrievals. Remote Sens. Environ. 2021, 255, 112227. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Amer. Meteor. Soc. 1996, 77, 437–470. [Google Scholar] [CrossRef]
- You, Q.; Sanchez-Lorenzo, A.; Wild, M.; Folini, D.; Fraedrich, K.; Ren, G.Y.; Kang, S. Decadal variation of surface solar radiation in the Tibetan Plateau from observations, reanalysis and model simulations. Clim. Dyn. 2013, 40, 2073–2086. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Q.; Song, Z.; Sun, W.; Dong, W. A comparison of global surface temperature variability, extremes and warming trend using reanalysis datasets and CMST-Interim. Int. J. Climatol. 2022, 42, 5609–5628. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Li, W.J.; Ai, W.X.; Li, Q.Q. Reconstruction and Application of the Monthly Western Pacific Subtropical High Indices. J. Appl. Meteor. Sci. 2012, 23, 414–423, (In Chinese with English abstract). [Google Scholar]
- Hobday, A.J.; Alexander, L.V.; Perkins, S.E.; Smale, D.A.; Straub, S.C.; Oliver, E.C.J.; Benthuysen, J.A.; Burrows, M.T.; Donat, M.G.; Peng, M.; et al. A hierarchical approach to defining marine heatwaves. Prog. Oceanogr. 2016, 141, 227–238. [Google Scholar] [CrossRef]
- Skirving, W.; Marsh, B.; De La Cour, J.; Liu, G.; Harris, A.; Maturi, E.; Geiger, E.; Eakin, C.M. Coraltemp and the coral reef watch coral bleaching heat stress product suite version 3.1. Remote Sens. 2020, 12, 3856. [Google Scholar] [CrossRef]
- Schlegel, R.W.; Smit, J.A. HeatwaveR: A central algorithm for the detection of heatwaves and cold-spells. J. Open Source Softw. 2018, 3, 821. [Google Scholar] [CrossRef]
- Lorenz, E.N. Empirical Orthogonal Functions and Statistical Weather Prediction; Massachusetts Institute of Technology, Department of Meteorology: Cambridge, MA, USA, 1956; p. 52. [Google Scholar]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling errors in the estimation of empirical orthogonal functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research; Cambridge University Press: London, UK, 1999; p. 484. [Google Scholar]
- Berger, W.H.; Labeyrie, L.D. Abrupt Climatic Change Evidence and Implications; St. Hugues de Biviers: Biviers, France, 1985; p. 8. [Google Scholar]
- Hao, X.M.; Chen, Y.N.; Li, W.H. Impact of anthropogenic activities on the hydrologic characters of the mainstream of the Tarim River in Xinjiang durthe past 50 years. Environ. Geol. 2009, 57, 435–445. [Google Scholar] [CrossRef]
- Tabari, H.; Abghari, H.; Talaee, P.H. Temporal trends and spatial characteristics of drought and rainfall in arid and semiarid regions of Iran. Hydrol. Process. 2012, 26, 3351–3361. [Google Scholar] [CrossRef]
- Li, Y.; Ren, G.; Wang, Q.; You, Q. More extreme marine heatwaves in the China Seas during the global warming hiatus. Environ. Res. Lett. 2019, 14, 104010. [Google Scholar] [CrossRef]
- Fischer, E.M.; Schär, C. Consistent geographical patterns of changes in high-impact European heatwaves. Nat. Geosci. 2010, 3, 398–403. [Google Scholar] [CrossRef]
- Oliver, E.C.J. Mean warming not variability drives marine heatwave trends. Clim. Dyn. 2019, 53, 1653–1659. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V. The shifting probability distribution of global daytime and night-time temperatures. Geophys. Res. Lett. 2012, 39, L14707. [Google Scholar] [CrossRef]
- Holbrook, N.J.; Gupta, A.S.; Oliver, E.C.J.; Hobday, A.J.; Wernberg, T. Keeping pace with marine heatwaves. Nat. Rev. Earth Env. 2020, 1, 482–493. [Google Scholar] [CrossRef]
- Bond, N.A.; Cronin, M.F.; Freeland, H.; Mantua, N. Causes and impacts of the 2014 warm anomaly in the NE Pacific. Geophys. Res. Lett. 2015, 42, 3414–3420. [Google Scholar] [CrossRef]
- Salinger, M.J.; Renwick, J.; Behrens, E.; Mullan, A.B.; Diamond, H.J.; Sirguey, P.; Smith, R.O.; Trought, M.C.T.; Alexander V, L.; Cullen, N.J.; et al. The unprecedented coupled ocean-atmosphere summer heatwave in the New Zealand region 2017/18: Drivers, mechanisms and impacts. Environ. Res. Lett. 2019, 14, 044023. [Google Scholar] [CrossRef]
- Wu, R.; Wen, Z.; Yang, S.; Li, Y. An interdecadal change in southern China summer rainfall around 1992/93. J. Clim. 2010, 23, 2389–2403. [Google Scholar] [CrossRef]
- Luo, M.; Lau, N.C. Heat waves in southern China: Synoptic Behavior, long-term change, and urbanization effects. J. Clim. 2017, 30, 703–720. [Google Scholar] [CrossRef]
- Zhang, L.P.; Wu, L.X.; Lin, X.P.; Wu, D.X. Modes and mechanisms of sea surface temperature low-frequency variations over the coastal China seas. J. Geophys. Res. 2010, 115, C08031. [Google Scholar] [CrossRef]
- He, C.; Zhou, T.J.; Lin, A.L.; Wu, B.; Gu, D.; Li, C.H.; Zheng, B. Enhanced or weakened western North Pacific subtropical high under global warming? Sci. Rep. 2015, 5, 16771. [Google Scholar] [CrossRef]
- Choi, W.; Kim, K.-Y. Summertime variability of the western North Pacific subtropical high and its synoptic influences on the East Asian weather. Sci. Rep. 2019, 9, 7865. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Wernberg, T.; Smale, D.; Tuya, F.; Thomsen, M.; Langlois, T.; Bettignies, T.; Bennett, S.; Rousseaux, C. An extreme climatic event alters marine ecosystem structure in a global biodiversity hotspot. Nat. Clim. Chang. 2013, 3, 78–82. [Google Scholar] [CrossRef]
- Jacox, M.G.; Alexander, M.A.; Amaya, D.; Becker, E.; Bograd, S.J.; Brodie, S.; Hazen, E.L.; Buil, M.P.; Tommasi, D. Global seasonal forecasts of marine heatwaves. Nature 2022, 604, 486–490. [Google Scholar] [CrossRef]
- Xiang, B.; Wang, B.; Yu, W.; Xu, S. How can anomalous western North Pacific Subtropical High intensify in late summer? Geophys. Res. Lett. 2013, 40, 2349–2354. [Google Scholar] [CrossRef]
- Chen, Z.; Wen, Z.; Wu, R.; Lin, X.; Wang, J. Relative importance of tropical SST anomalies in maintaining the Western North Pacific anomalous anticyclone during El Niño to La Niña transition years. Clim. Dyn. 2016, 46, 1027–1041. [Google Scholar] [CrossRef]
- Chen, W.; Park, J.K.; Dong, B.; Jung, W.S. The relationship between El Niño and the western North Pacific summer climate in a coupled GCM: Role of the transition of El Niño decaying phases. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Chung, P.H.; Sui, C.H.; Li, T. Interannual relationships between the tropical sea surface temperature and summertime subtropical anticyclone over the western North Pacific. J. Geophys. Res. Atmos. 2011, 116, D13111. [Google Scholar] [CrossRef]
- Piton, V.; Delcroix, T. Seasonal and interannual (ENSO) climate variabilities and trends in the South China Sea over the last three decades. Ocean Sci. Discuss. 2018, preprint. [Google Scholar] [CrossRef]
- Francis, J.; Vavrus, S.J. Evidence linking arctic amplification to extreme weather in Mid-Latitudes. Geophys. Res. Lett. 2012, 39, L06801. [Google Scholar] [CrossRef]
| Index | Definition | Symbol or Formula | Unit |
|---|---|---|---|
| MHWN | Number of MHWs in the warm season in each year | N | Count |
| MHWD | Average duration of all MHWs in the warm season of each year | Days | |
| MHWI | Average cumulative intensity of all MHWs in the warm season of each year | °C•days |
| Index | r | r (Detrended) | ||||
|---|---|---|---|---|---|---|
| MHWN | MHWD | MHWI | MHWN | MHWD | MHWI | |
| Area index (AI) | 0.76 * | 0.76 * | 0.75 * | 0.70 * | 0.67 * | 0.66 * |
| Intensity index (INI) | 0.7 5 * | 0.77 * | 0.75 * | 0.69 * | 0.69 * | 0.68 * |
| Ridge line index (RI) | −0.27 | −0.19 | −0.20 | −0.36 | −0.28 | −0.27 |
| Westward ridge point index (WRI) | −0.75 * | −0.64 * | −0.63 * | −0.57 * | −0.51 * | −0.51 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Ren, G.; Wang, Q.; Mu, L.; Niu, Q. Marine Heatwaves in the South China Sea: Tempo-Spatial Pattern and Its Association with Large-Scale Circulation. Remote Sens. 2022, 14, 5829. https://doi.org/10.3390/rs14225829
Li Y, Ren G, Wang Q, Mu L, Niu Q. Marine Heatwaves in the South China Sea: Tempo-Spatial Pattern and Its Association with Large-Scale Circulation. Remote Sensing. 2022; 14(22):5829. https://doi.org/10.3390/rs14225829
Chicago/Turabian StyleLi, Yan, Guoyu Ren, Qingyuan Wang, Lin Mu, and Qianru Niu. 2022. "Marine Heatwaves in the South China Sea: Tempo-Spatial Pattern and Its Association with Large-Scale Circulation" Remote Sensing 14, no. 22: 5829. https://doi.org/10.3390/rs14225829
APA StyleLi, Y., Ren, G., Wang, Q., Mu, L., & Niu, Q. (2022). Marine Heatwaves in the South China Sea: Tempo-Spatial Pattern and Its Association with Large-Scale Circulation. Remote Sensing, 14(22), 5829. https://doi.org/10.3390/rs14225829











