Anomalous Zenith Total Delays for an Insular Tropical Location: The Tahiti Island Case
Abstract
1. Introduction
2. Methodology
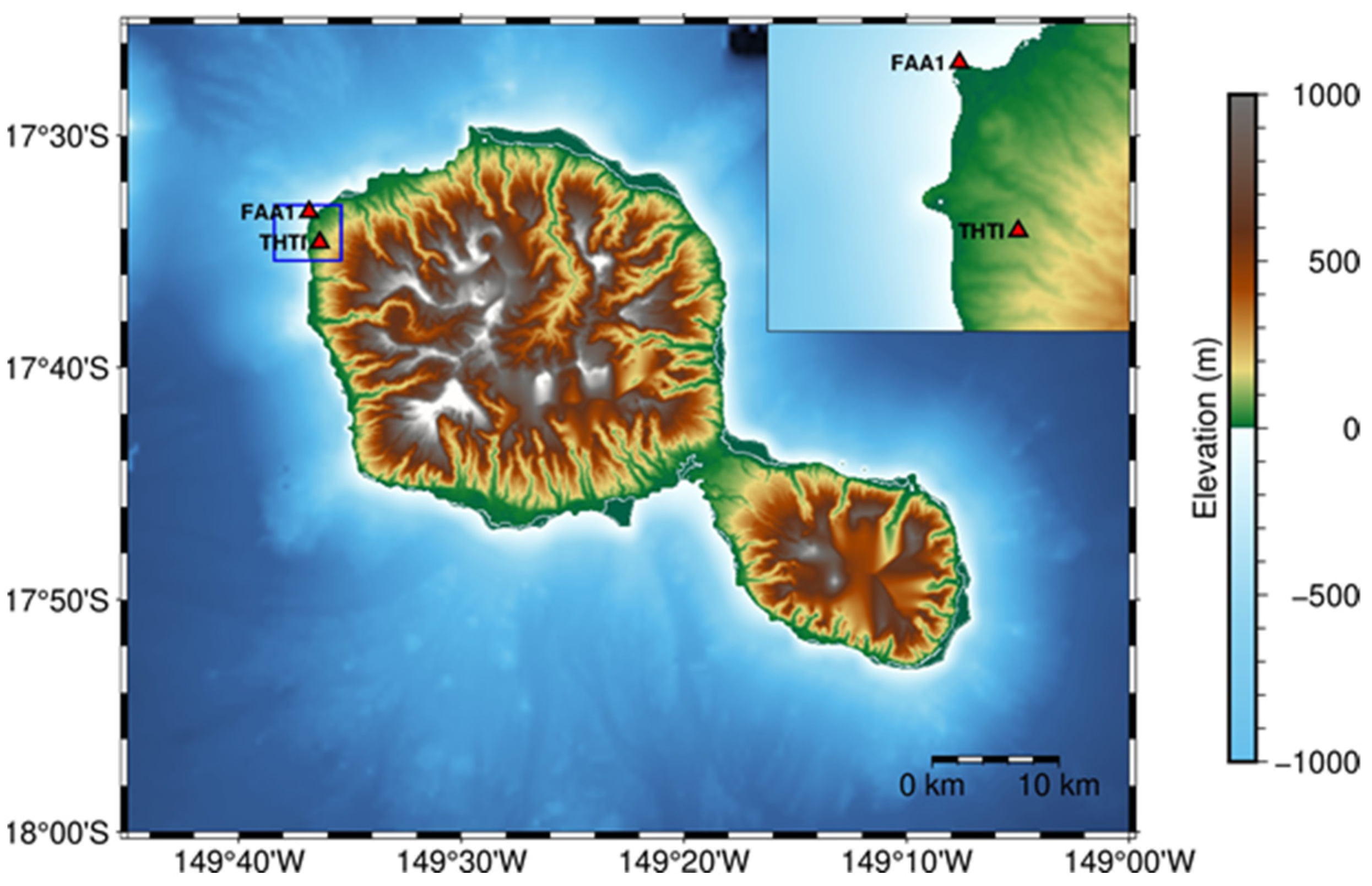
3. Datasets
4. Results
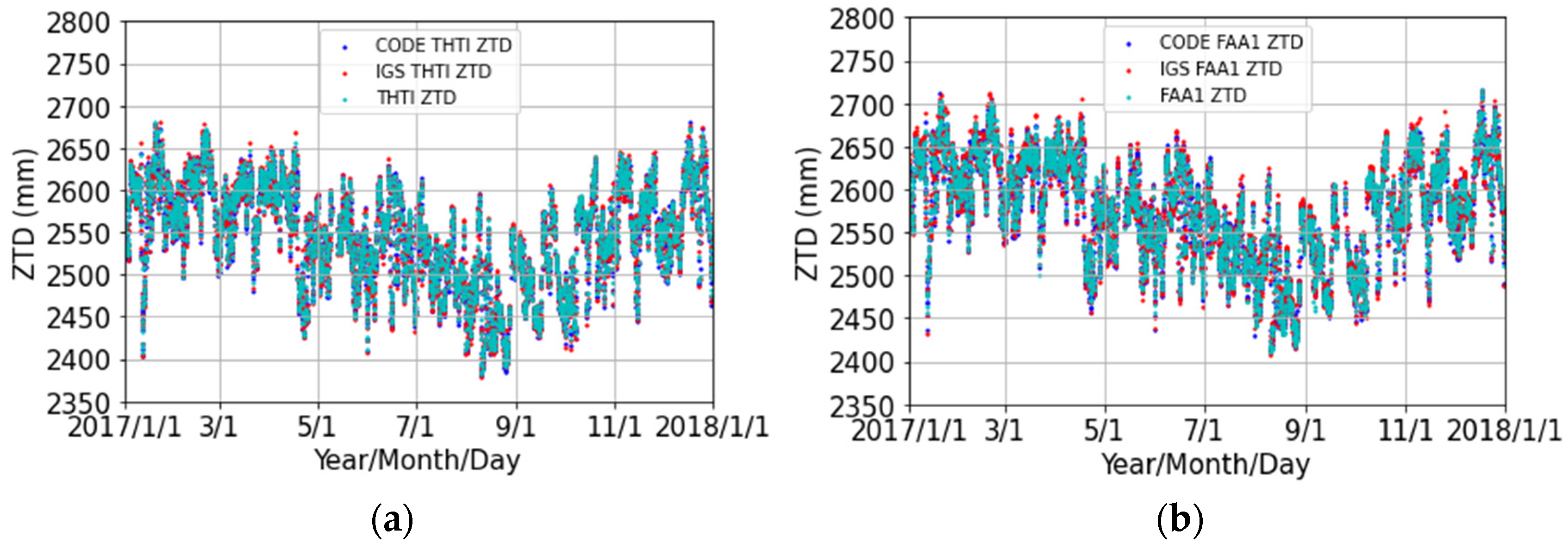
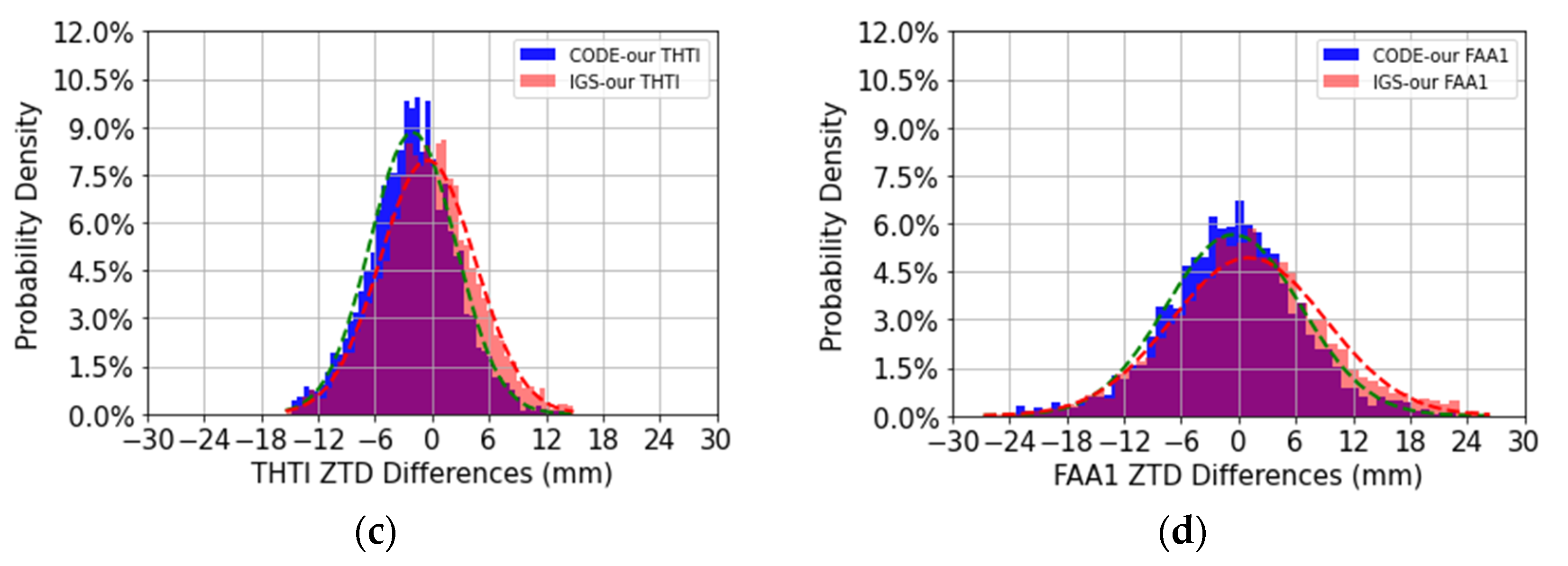
4.1. Comparisons of Our ZTD Estimates with CODE and IGS ZTD Estimates
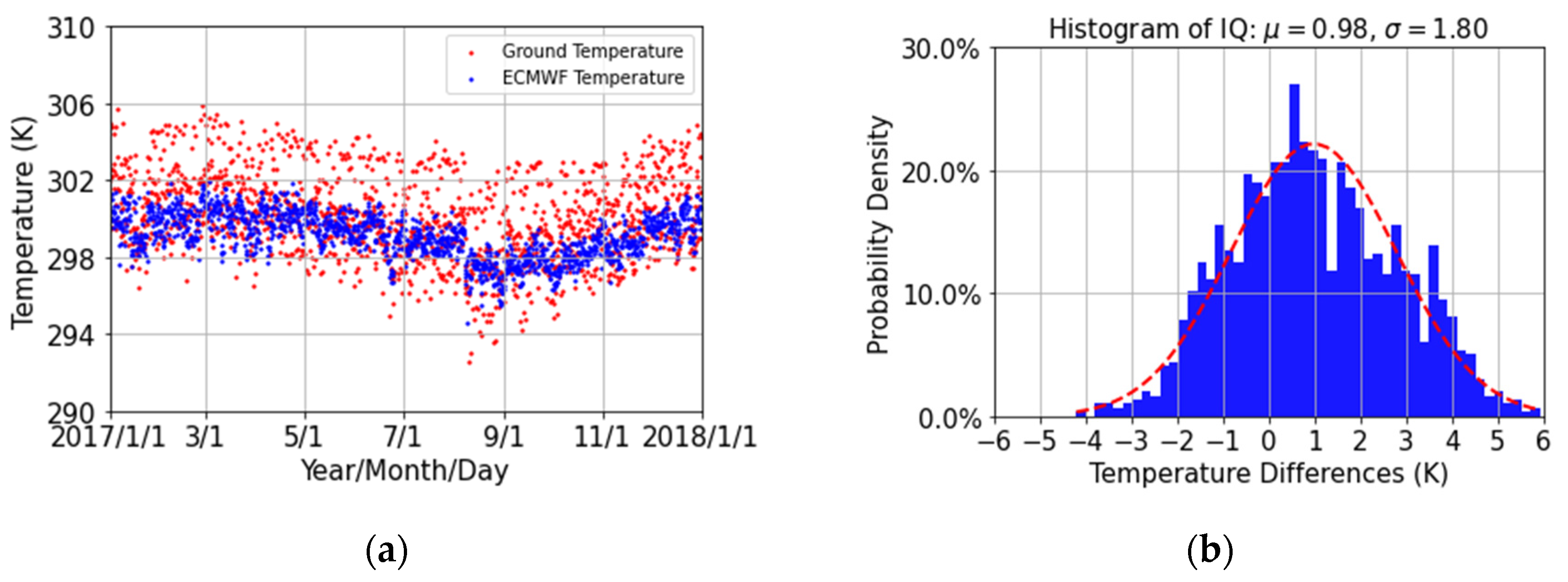
4.2. Comparison of the Surface Temperature from the FAA1 Ground Weather Station and the Site-Wise VMF1 Files
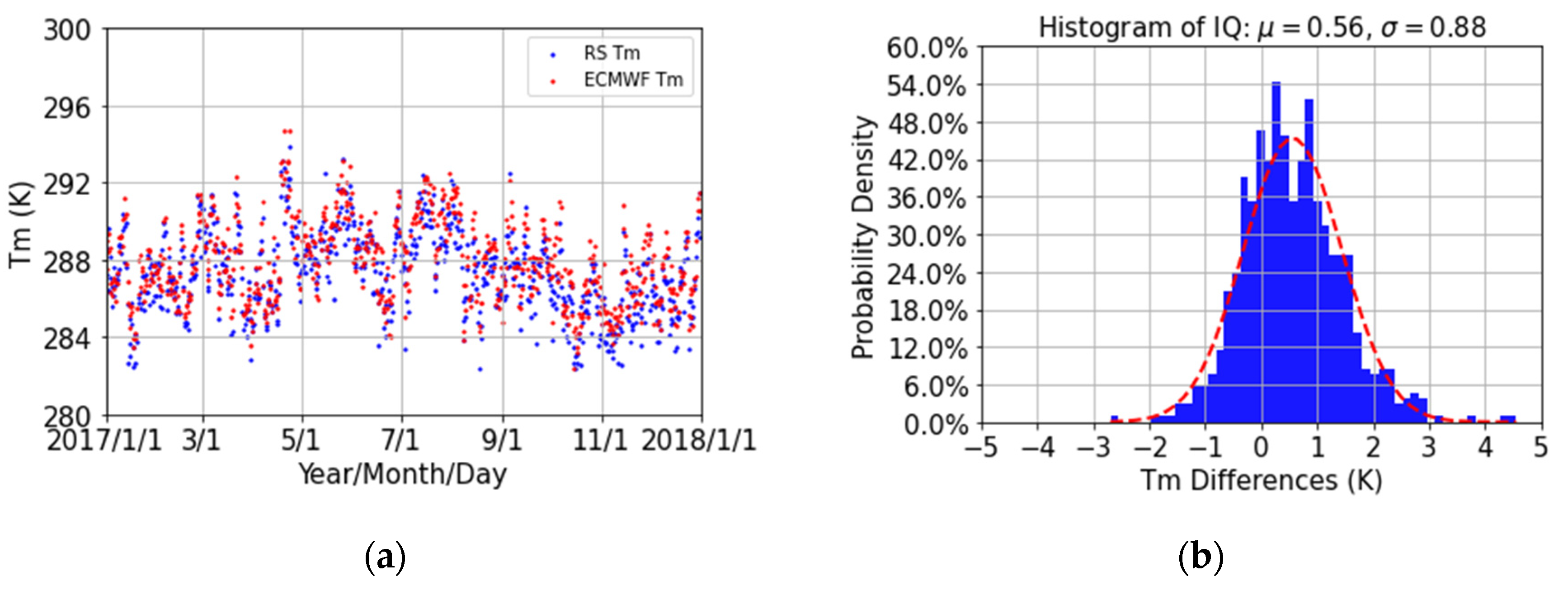
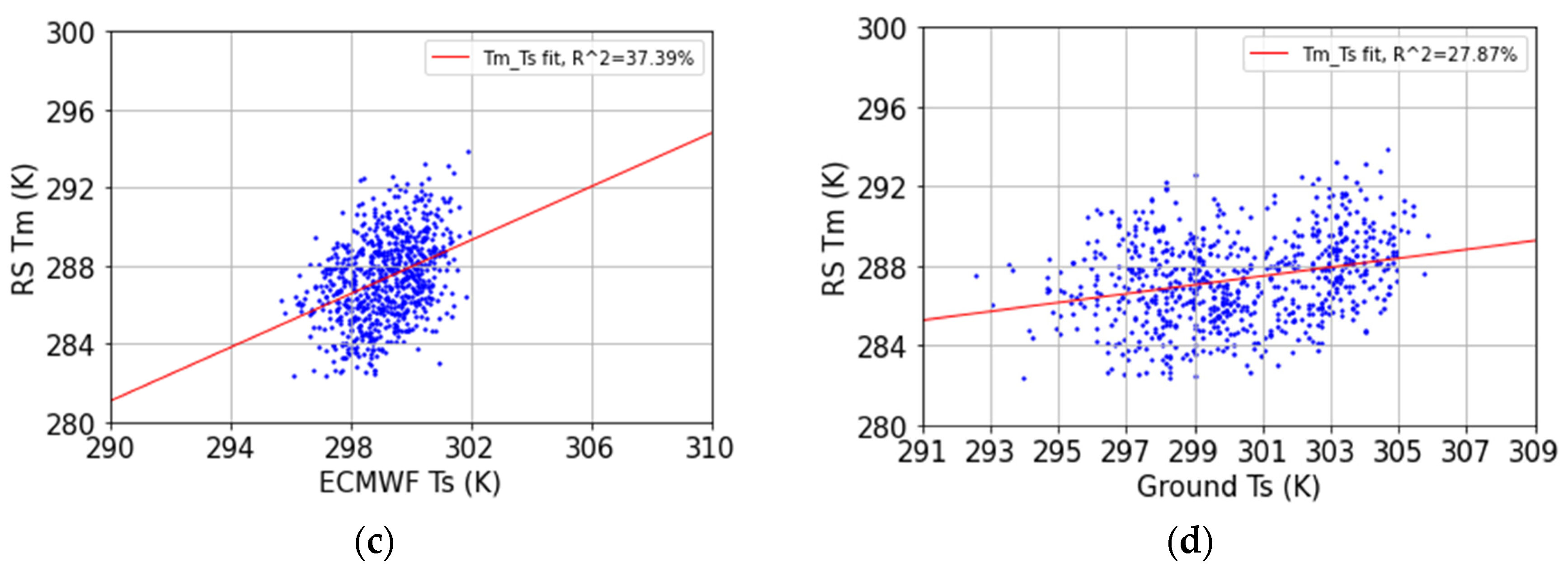
4.3. Comparison of Tm Estimates from RS Measurements and Site-Wise VMF1 Files
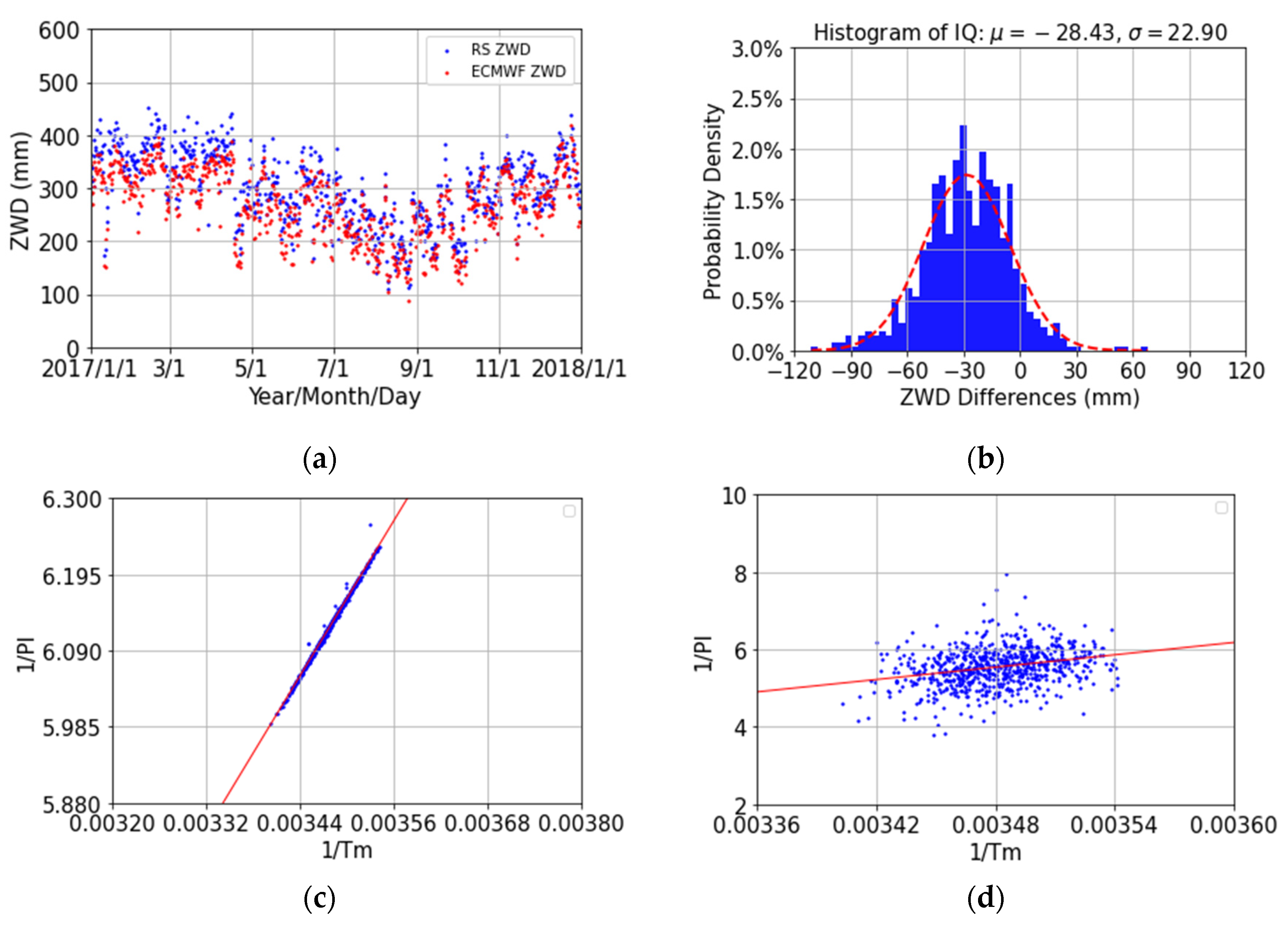
4.4. Comparison of the ZWD Estimates from RS Data with the ZWD Estimates from VMF1/ECMWF Files
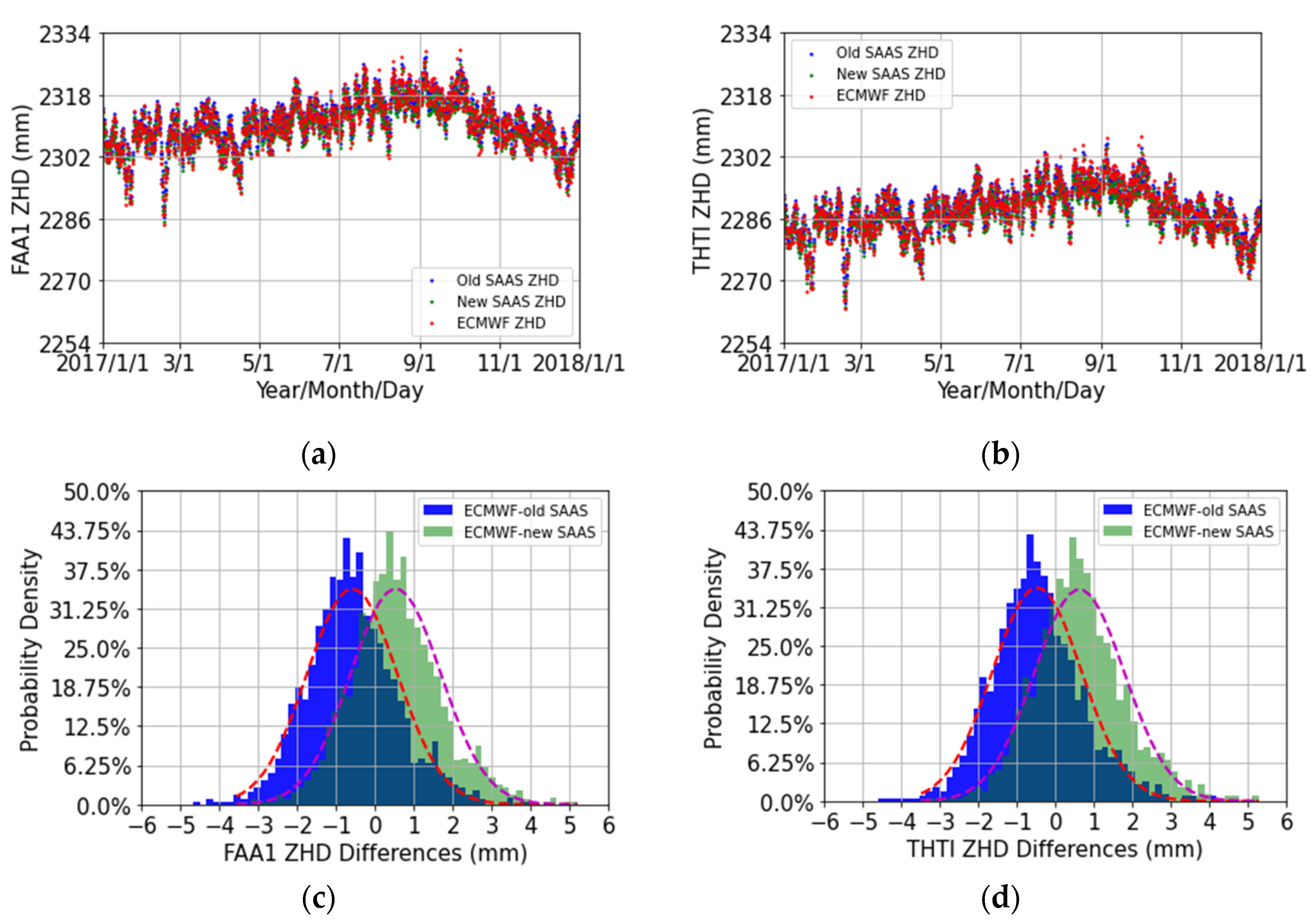
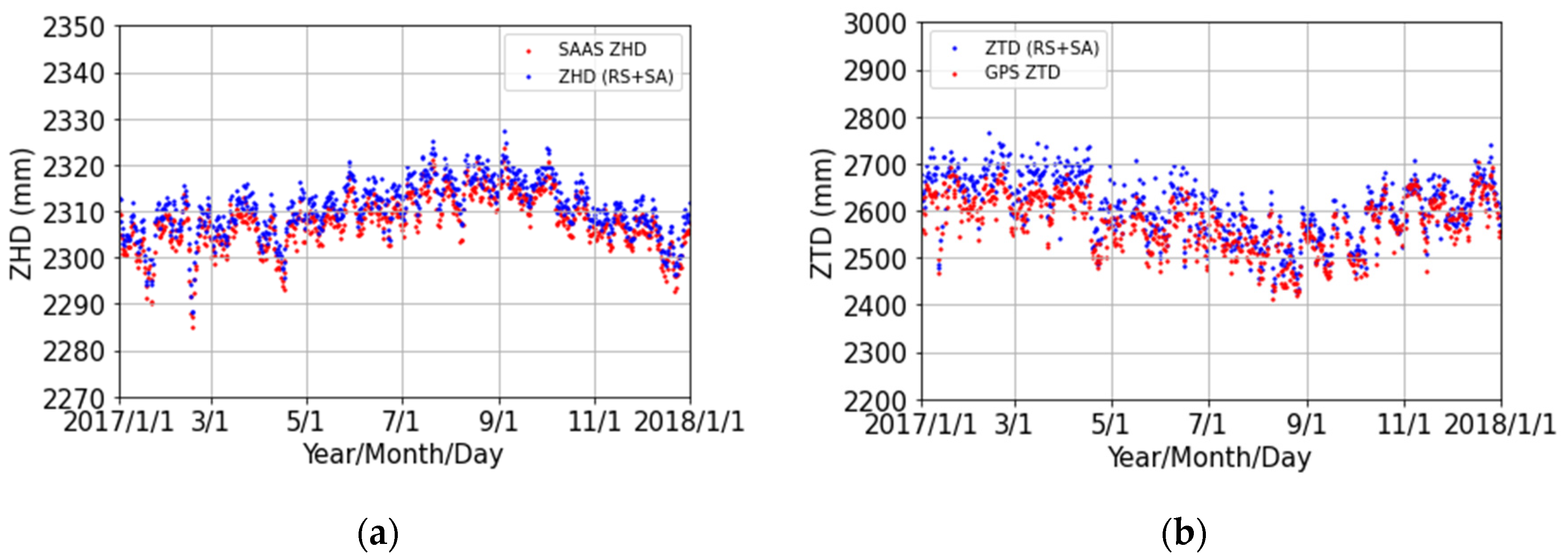
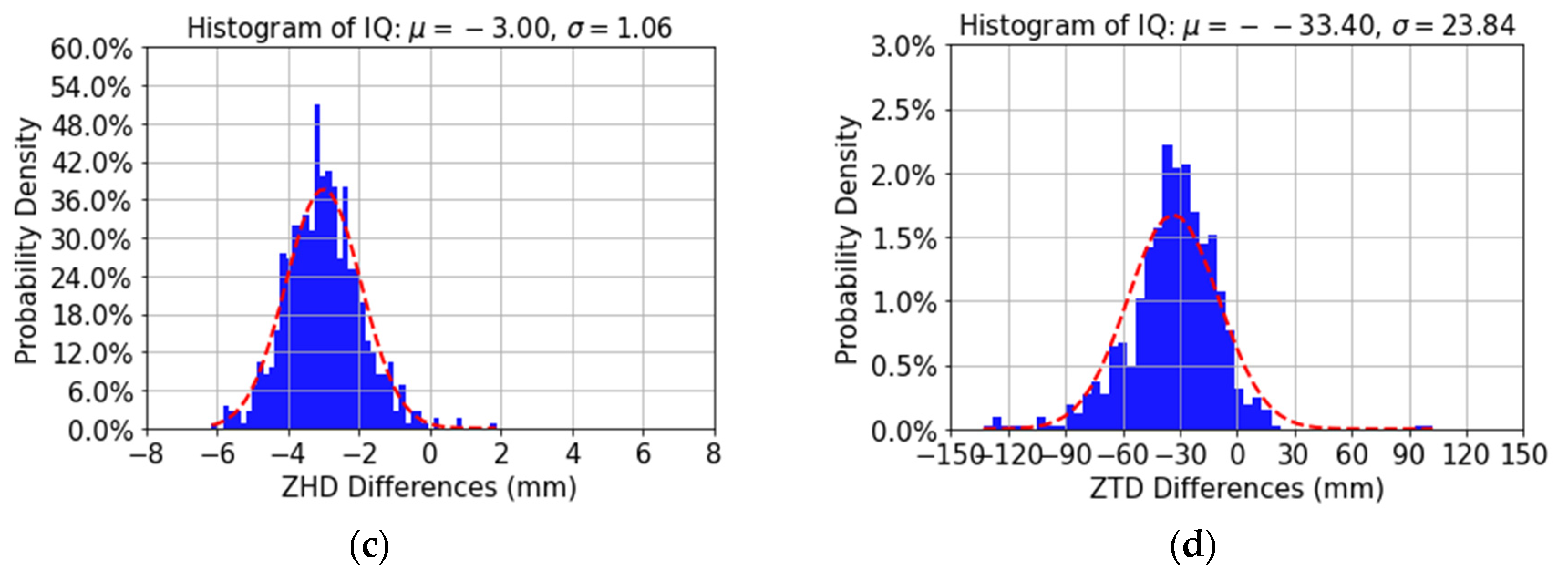
4.5. Comparison of ZHD Estimates Based on the Saastamoinen Model with ZHD Estimates Based on Davis’ Adapted Saastamoinen Model
4.6. Comparison of GPS ZTD Estimates with ZTD Estimates from RS Data and a Standard Atmosphere
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Zhang, F.; Barriot, J.-P.; Xu, G.; Hopuare, M. Modeling the Slant Wet Delays from One GPS Receiver as a Series Expansion with Respect to Time and Space: Theory and an Example of Application for the Tahiti Island. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7520–7532. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Y.; Ma, X.; Yao, W.; Yao, Y.; Li, X. An Improved Rainfall Forecasting Model Based on GNSS Observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4891–4900. [Google Scholar] [CrossRef]
- Xia, P.; Xia, J.; Ye, S.; Xu, C. A new method for estimating tropospheric zenith wet-component delay of gnss signals from surface meteorology data. Remote Sens. 2020, 12, 3497. [Google Scholar] [CrossRef]
- Elliott, W.P.; Gaffen, D.J. On the Utility of Radiosonde Humidity Archives for Climate Studies. Bull. Am. Meteorol. Soc. 1991, 72, 1507–1520. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Chen, G.; Wu, Z. Evaluation of HY-2A satellite-borne water vapor radiometer with shipborne GPS and GLONASS observations over the Indian Ocean. GPS Solut. 2019, 23, 1–9. [Google Scholar] [CrossRef]
- Campmany, E.; Bech, J.; Rodríguez-Marcos, J.; Sola, Y.; Lorente, J. A comparison of total precipitable water measurements from radiosonde and sunphotometers. Atmos. Res. 2010, 97, 385–392. [Google Scholar] [CrossRef]
- Guo, J.; Hou, R.; Zhou, M.; Jin, X.; Li, G. Detection of particulate matter changes caused by 2020 california wildfires based on gnss and radiosonde station. Remote Sens. 2021, 13, 4557. [Google Scholar] [CrossRef]
- Zhang, S.; Fang, L.; Wang, G.; Li, W. The impact of second-order ionospheric delays on the ZWD estimation with GPS and BDS measurements. GPS Solut. 2020, 24, 1–11. [Google Scholar] [CrossRef]
- Lou, Y.; Huang, J.; Zhang, W.; Liang, H.; Zheng, F.; Liu, J. A new zenith tropospheric delay grid product for real-time PPP applications over China. Sensors 2018, 18, 65. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Barriot, J.-P.; Xu, G.; Hopuare, M. Analysis and Comparison of GPS Precipitable Water Estimates between Two Nearby Stations on Tahiti Island. Sensors 2019, 19, 5578. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Y.; Yao, W.; Yao, Y. Hourly Rainfall Forecast Model Using Supervised Learning Algorithm. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–9. [Google Scholar] [CrossRef]
- Zhou, Y.; Lou, Y.; Zhang, W.; Wu, P.; Bai, J.; Zhang, Z. Tropospheric Second-Order Horizontal Gradient Modeling for GNSS PPP. Remote Sens. 2022, 14, 4807. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Li, W. Real-time wide-area precise tropospheric corrections (WAPTCs) jointly using GNSS and NWP forecasts for China. J. Geod. 2022, 96, 1–18. [Google Scholar] [CrossRef]
- Hopfield, H.S. Tropospheric effect on electromagnetically measured range: Prediction from surface weather data. Radio Sci. 1971, 6, 357–367. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géod. 1972, 105, 279–298. [Google Scholar] [CrossRef]
- Black, H.D. An Easily Implemented Range Correction for the Tropospheric Range Correction. Bull. Géod. 1978, 83, 1825–1828. [Google Scholar]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Huang, L.; Liu, L.; Chen, H.; Jiang, W. An improved atmospheric weighted mean temperature model and its impact on GNSS precipitable water vapor estimates for China. GPS Solut. 2019, 23, 51. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Zus, F.; Heinkelmann, R.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Improving BeiDou real-time precise point positioning with numerical weather models. J. Geod. 2017, 91, 1019–1029. [Google Scholar] [CrossRef]
- Emardson, T.R.; Elgered, G.; Johansson, J.M. Three months of continuous monitoring of atmospheric water vapor with a network of Global Positioning System receivers. J. Geophys. Res. Atmos. 1998, 103, 1807–1820. [Google Scholar] [CrossRef]
- Suresh Raju, C.; Saha, K.; Thampi, B.V.; Parameswaran, K. Empirical model for mean temperature for Indian zone and estimation of precipitable water vapor from ground based GPS measurements. Ann. Geophys. 2007, 25, 1935–1948. [Google Scholar] [CrossRef]
- Mekik, C.; Deniz, I. Modelling and validation of the weighted mean temperature for Turkey. Meteorol. Appl. 2017, 24, 92–100. [Google Scholar] [CrossRef]
- Zhang, F.; Barriot, J.-P.; Xu, G.; Yeh, T.-K. Metrology Assessment of the Accuracy of Precipitable Water Vapor Estimates from GPS Data Acquisition in Tropical Areas: The Tahiti Case. Remote Sens. 2018, 10, 758. [Google Scholar] [CrossRef]
- Huang, L.; Wang, X.; Xiong, S.; Li, J.; Liu, L.; Mo, Z.; Fu, B.; He, H. High-precision GNSS PWV retrieval using dense GNSS sites and in-situ meteorological observations for the evaluation of MERRA-2 and ERA5 reanalysis products over China. Atmos. Res. 2022, 276, 106247. [Google Scholar] [CrossRef]
- Ross, R.J.; Rosenfeld, S. Estimating mean weighted temperature of the atmosphere for Global Positioning System applications. J. Geophys. Res. 1997, 102, 719–730. [Google Scholar] [CrossRef]
- Yao, Y.; Zhu, S.; Yue, S. A globally applicable, season-specific model for estimating the weighted mean temperature of the atmosphere. J. Geod. 2012, 86, 1125–1135. [Google Scholar] [CrossRef]
- Huang, L.; Jiang, W.; Liu, L.; Chen, H.; Ye, S. A new global grid model for the determination of atmospheric weighted mean temperature in GPS precipitable water vapor. J. Geod. 2019, 93, 159–176. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. 1992, 97, 15787. [Google Scholar] [CrossRef]
- Thayer, G.D. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Owens, J.C. Optical Refractive Index of Air: Dependence on Pressure, Temperature and Composition. Appl. Opt. 1967, 6, 51. [Google Scholar] [CrossRef]
- Bolton, D. The computation of equivalent potential temperature. Mon. Weather Rev. 1980, 108, 1046–1053. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; Fan, S.; Cheng, Y. Water vapor- weighted mean temperature and its impact on the determination of precipitable water vapor and its linear trend. J. Geophys. Res. Atmos. 2016, 121, 833–852. [Google Scholar] [CrossRef]
- Barriot, J.-P.; Feng, P. Beyond Mapping Functions and Gradients. In Geodetic Sciences—Theory, Applications and Recent Developments; IntechOpen: London, UK, 2021. [Google Scholar]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Serafini, J.; Barriot, J.-P.; Sichoix, L. The evolution of precipitable water and precipitation over the Island of Tahiti from hourly to seasonal periods. Int. J. Remote Sens. 2014, 35, 6687–6707. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software, Version 5.2; University of Bern, Bern Open Publishing: Bern, Switzerland, 2015; ISBN 9783906813059.
- Zhang, B.; Chen, Y.; Yuan, Y. PPP-RTK based on undifferenced and uncombined observations: Theoretical and practical aspects. J. Geod. 2019, 93, 1011–1024. [Google Scholar] [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. Solid Earth 2006, 111, 1–9. [Google Scholar] [CrossRef]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products. Geod. Surv. Div. Nat. Resour. Canada Ottawa 2009, 6, 34. [Google Scholar]
- Ray, R.D.; Ponte, R.M. Barometric tides from ECMWF operational analyses. Ann. Geophys. 2003, 21, 1897–1910. [Google Scholar] [CrossRef]
- Durre, I.; Vose, R.S.; Wuertz, D.B. Overview of the integrated global radiosonde archive. J. Clim. 2006, 19, 53–68. [Google Scholar] [CrossRef]
- Feng, P.; Li, F.; Yan, J.; Zhang, F.; Barriot, J.P. Assessment of the accuracy of the saastamoinen model and vmf1/vmf3 mapping functions with respect to ray-tracing from radiosonde data in the framework of gnss meteorology. Remote Sens. 2020, 12, 3337. [Google Scholar] [CrossRef]
- Kouba, J. Implementation and testing of the gridded Vienna mapping function 1 (VMF1). J. Geod. 2008, 82, 193–205. [Google Scholar] [CrossRef]
- Vedel, H. Conversion of WGS84 Geogeometric Heights to NWP Model HIRLAM Geopotential Heights; Danish Meteorological Institute: Copenhagen, Danmark, 2000; pp. 1–16. [Google Scholar]
- U.S. Government. Standard Atmosphere; U.S. Government: Washington, DC, USA, 1976.
- Stull, R.B. Meteorology: For Scientists and Engineers; West Publishing: St. Paul, MN, USA, 1995. [Google Scholar]
- Abdelazeem, M.; El-Rabbany, A. Assessment of GNSS PPP-Based Zenith Tropospheric Delay. Artif. Satell. 2020, 55, 171–184. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Labib, B.; Yan, J.; Barriot, J.P.; Zhang, F.; Feng, P. Monitoring Zenithal Total Delays over the three different climatic zones from IGS GPS final products: A comparison between the use of the VMF1 and GMF mapping functions. Geod. Geodyn. 2019, 10, 93–99. [Google Scholar] [CrossRef]
- Szołucha, M.; Kroszczyński, K.; Kiliszek, D. Accuracy of Precise Point Positioning (PPP) with the use of different International GNSS Service (IGS) products and stochastic modelling. Geod. Cartogr. 2018, 67, 207–238. [Google Scholar] [CrossRef]
- Jin, S.; Su, K. PPP models and performances from single- to quad-frequency BDS observations. Satell. Navig. 2020, 1, 1–13. [Google Scholar] [CrossRef]
- Mccarthy, P.W.; Liu, Z.; Cascioli, V. Humidity Sensors: Advances in Reliability, Calibration ans Application; MDPI: Basel, Switzerland, 2019; ISBN 9783039211234. [Google Scholar]
- Snajdrova, K.; Boehm, J.; Willis, P.; Haas, R.; Schuh, H. Multi-technique comparison of tropospheric zenith delays derived during the CONT02 campaign. J. Geod. 2006, 79, 613–623. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, J.; Chen, M.; Shi, J.; Zhou, L. Quantitative assessment of meteorological and tropospheric Zenith Hydrostatic Delay models. Adv. Sp. Res. 2016, 58, 1033–1043. [Google Scholar] [CrossRef]
- Allinson, C.R.; Clarke, P.J.; Edwards, S.J.; King, M.A.; Baker, T.F.; Cruddace, P.R. Stability of direct GPS estimates of ocean tide loading. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Montenbruck, O. Springer Handbook of Global Navigation Satellite System; Springer International Publishing: New York, NY, USA, 2017; ISBN 9783319429267. [Google Scholar]
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Zhang, B.; Hou, P.; Zha, J.; Liu, T. Integer-estimable FDMA model as an enabler of GLONASS PPP-RTK. J. Geod. 2021, 95, 91. [Google Scholar] [CrossRef]
- Melachroinos, S.A.; Biancale, R.; Llubes, M.; Perosanz, F.; Lyard, F.; Vergnolle, M.; Bouin, M.N.; Masson, F.; Nicolas, J.; Morel, L.; et al. Ocean tide loading (OTL) displacements from global and local grids: Comparisons to GPS estimates over the shelf of Brittany, France. J. Geod. 2008, 82, 357–371. [Google Scholar] [CrossRef]
- Boy, J.P.; Chao, B.F. Precise evaluation of atmospheric loading effects on Earth’s time-variable gravity field. J. Geophys. Res. Solid Earth 2005, 110, 1–10. [Google Scholar] [CrossRef]
- Francis, O.; Mazzega, P. Global charts of ocean tide loading effects. J. Geophys. Res. 1990, 95, 411–424. [Google Scholar] [CrossRef]
- Hackman, C.; Guerova, G.; Byram, S. International GNSS Service ( IGS ) Troposphere Products and Working Group Activities. In Proceedings of the from the Wisdom of the Ages to the Challenges of the Modern World Sofia, Sofia, Bulgaria, 17–21 May 2015; pp. 17–21. [Google Scholar]
| Our ZTD Estimates | IGS | CODE | |
|---|---|---|---|
| Precise satellite orbits and clocks | CODE Final products | IGS Final products | CODE Final products |
| Approach | PPP | PPP | Relative positioning |
| Elevation angle cutoff | 3 degrees | 7 degrees | 3 degrees |
| Mapping function | VMF1 (Vienna Mapping Function 1) | GMF (Global Mapping Function) | VMF1 |
| A priori troposphere estimate | Dry VMF model | Dry Niell model | Dry VMF model |
| Ionosphere correction | Ionosphere-free linear combination of L1 and L2 | Ionosphere-free linear combination of L1 and L2 | Ionosphere-free linear combination of L1 and L2 |
| Temporal resolution | 1 h | 5 min | 2 h |
| Ocean tidal loading | FES 2004 | FES 2004 | FES 2014b |
| Atmospheric tidal loading | Ray and Ponte (2003) [41] | Ray and Ponte (2003) [41] | S1 + S2 tidal corrections from the Vienna atmospheric pressure model |
| Differences | Max (mm) | Min (mm) | Bias (mm) | RMS (mm) | STD (mm) | Data Points | |
|---|---|---|---|---|---|---|---|
| THTI | CODE-our | 14.53 | −14.72 | −2.02 | 4.96 | 4.52 | 4244 |
| IGS-our | 14.93 | −15.42 | −0.47 | 5.03 | 5.01 | 4244 | |
| FAA1 | CODE-our | 22.89 | −23.39 | −0.51 | 7.06 | 7.04 | 4149 |
| IGS-our | 26.36 | −26.71 | 1.09 | 8.15 | 8.08 | 4149 | |
| Differences | Max (K) | Min (K) | Bias (K) | RMS (K) | STD (K) | Data Points |
|---|---|---|---|---|---|---|
| T1-T2 | 5.93 | −4.20 | 0.98 | 2.04 | 1.80 | 1458 |
| Differences | Max (K) | Min (K) | Bias (K) | RMS (K) | STD (K) | Data Points |
|---|---|---|---|---|---|---|
| ECMWF—RS | 4.55 | −2.69 | 0.56 | 1.05 | 0.88 | 724 |
| ZWD Differences | Max (mm) | Min (mm) | Bias (mm) | RMS (mm) | STD (mm) | Data Points |
|---|---|---|---|---|---|---|
| VMF1-RS | 68.01 | −111.01 | −28.43 | 36.51 | 22.90 | 724 |
| Differences | Max (mm) | Min (mm) | Bias (mm) | RMS (mm) | STD (mm) | Data Points |
|---|---|---|---|---|---|---|
| ECMWF-old FAA1 | 4.08 | −4.68 | −0.59 | 1.30 | 1.16 | 1461 |
| ECMWF-new FAA1 | 5.20 | −3.56 | 0.53 | 1.28 | 1.16 | 1461 |
| ECMWF-old THTI | 4.18 | −4.60 | −0.48 | 1.26 | 1.16 | 1461 |
| ECMWF-new THTI | 5.28 | −3.49 | 0.62 | 1.32 | 1.17 | 1461 |
| Differences | Max (mm) | Min (mm) | Bias (mm) | RMS (mm) | STD (mm) | Data Points |
|---|---|---|---|---|---|---|
| ZHD2-ZHD1 | 1.87 | −6.14 | −3.00 | 3.18 | 1.06 | 724 |
| ZTD2-ZTD1 | 102.61 | −132.97 | −33.40 | 41.04 | 23.84 | 689 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Feng, P.; Xu, G.; Barriot, J.-P. Anomalous Zenith Total Delays for an Insular Tropical Location: The Tahiti Island Case. Remote Sens. 2022, 14, 5723. https://doi.org/10.3390/rs14225723
Zhang F, Feng P, Xu G, Barriot J-P. Anomalous Zenith Total Delays for an Insular Tropical Location: The Tahiti Island Case. Remote Sensing. 2022; 14(22):5723. https://doi.org/10.3390/rs14225723
Chicago/Turabian StyleZhang, Fangzhao, Peng Feng, Guochang Xu, and Jean-Pierre Barriot. 2022. "Anomalous Zenith Total Delays for an Insular Tropical Location: The Tahiti Island Case" Remote Sensing 14, no. 22: 5723. https://doi.org/10.3390/rs14225723
APA StyleZhang, F., Feng, P., Xu, G., & Barriot, J.-P. (2022). Anomalous Zenith Total Delays for an Insular Tropical Location: The Tahiti Island Case. Remote Sensing, 14(22), 5723. https://doi.org/10.3390/rs14225723






