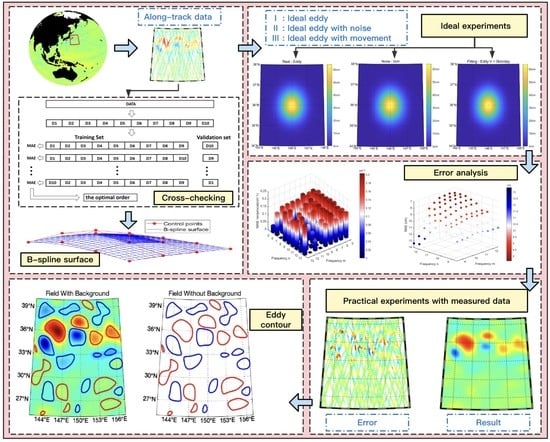
Oceanic Mesoscale Eddies Identification Using B-Spline Surface Fitting Model Based on Along-Track SLA Data
Abstract
1. Introduction
- Physical parameter method:
- 2.
- Sea surface geometry method:
- 3.
- Synthesis method:
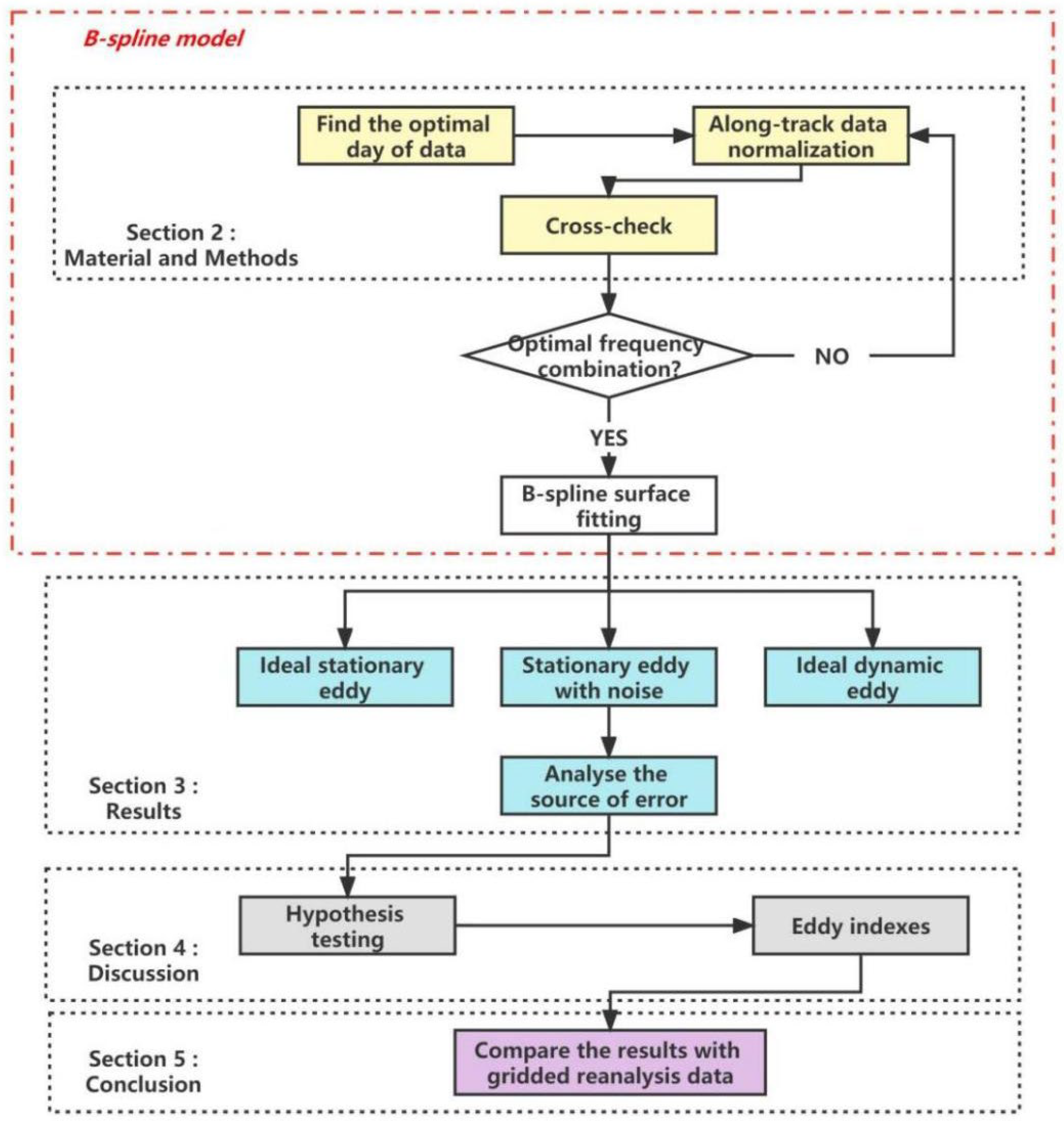
2. Materials and Methods
2.1. SLA Data
2.2. Methods
2.2.1. B-Spline Surface
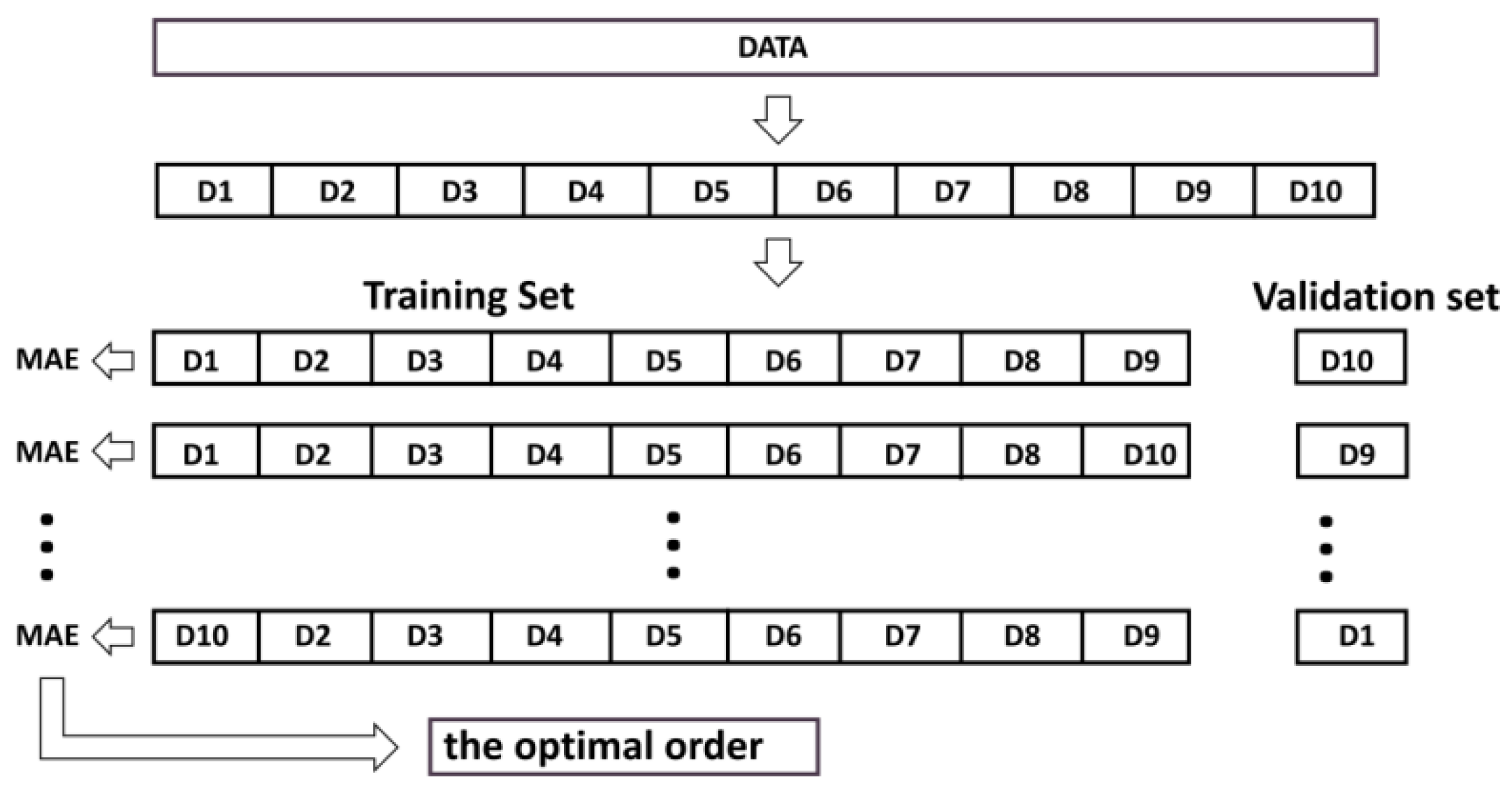
2.2.2. Cross-Checking
2.2.3. Surface Fitting
3. Results
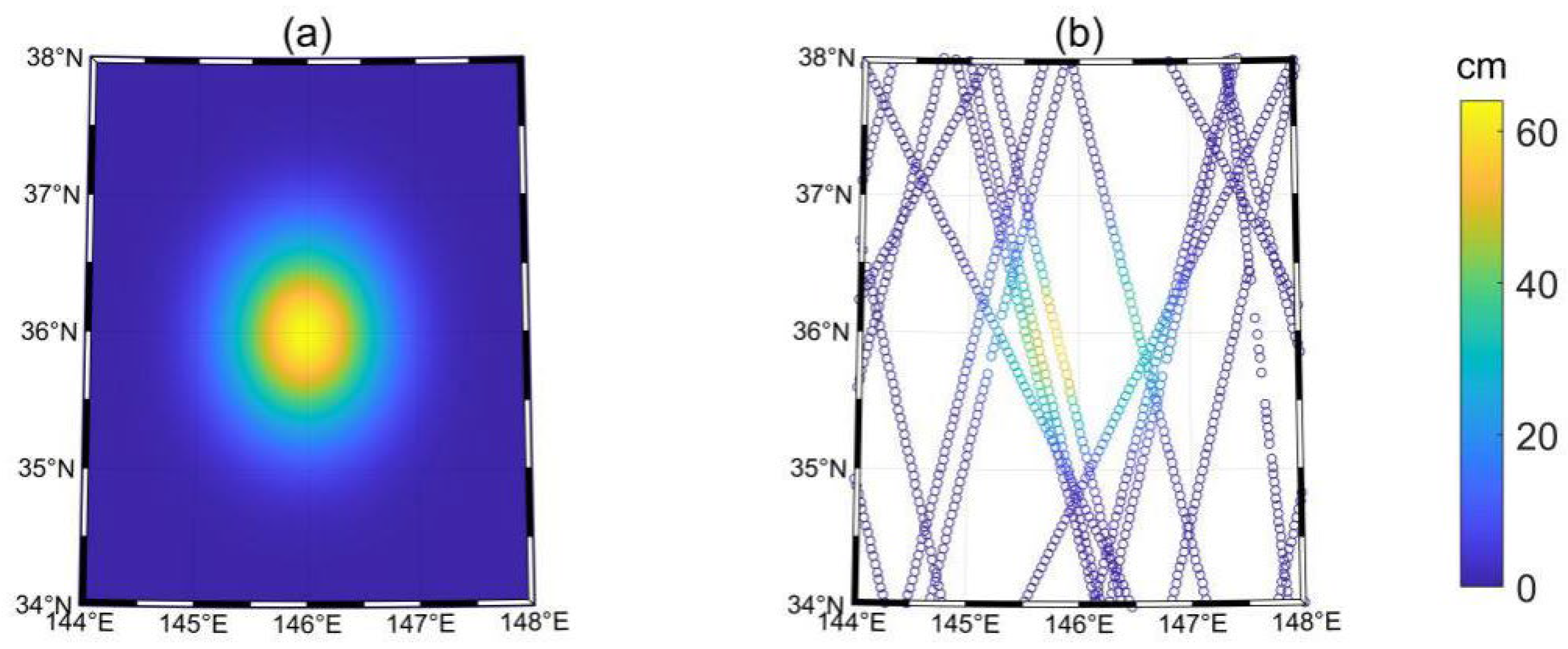
3.1. Ideal Experiment I: Ideal Stationary Eddy
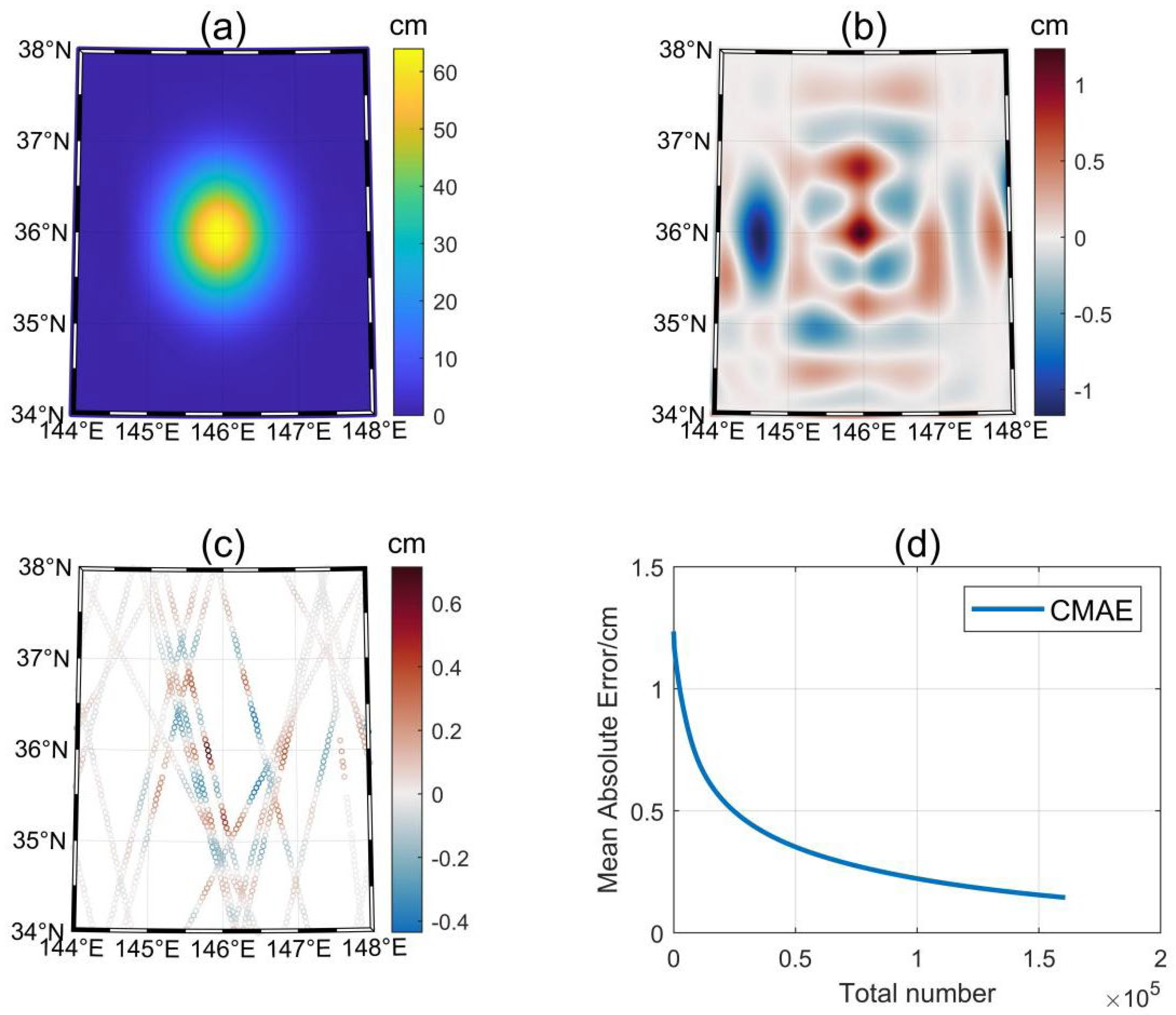
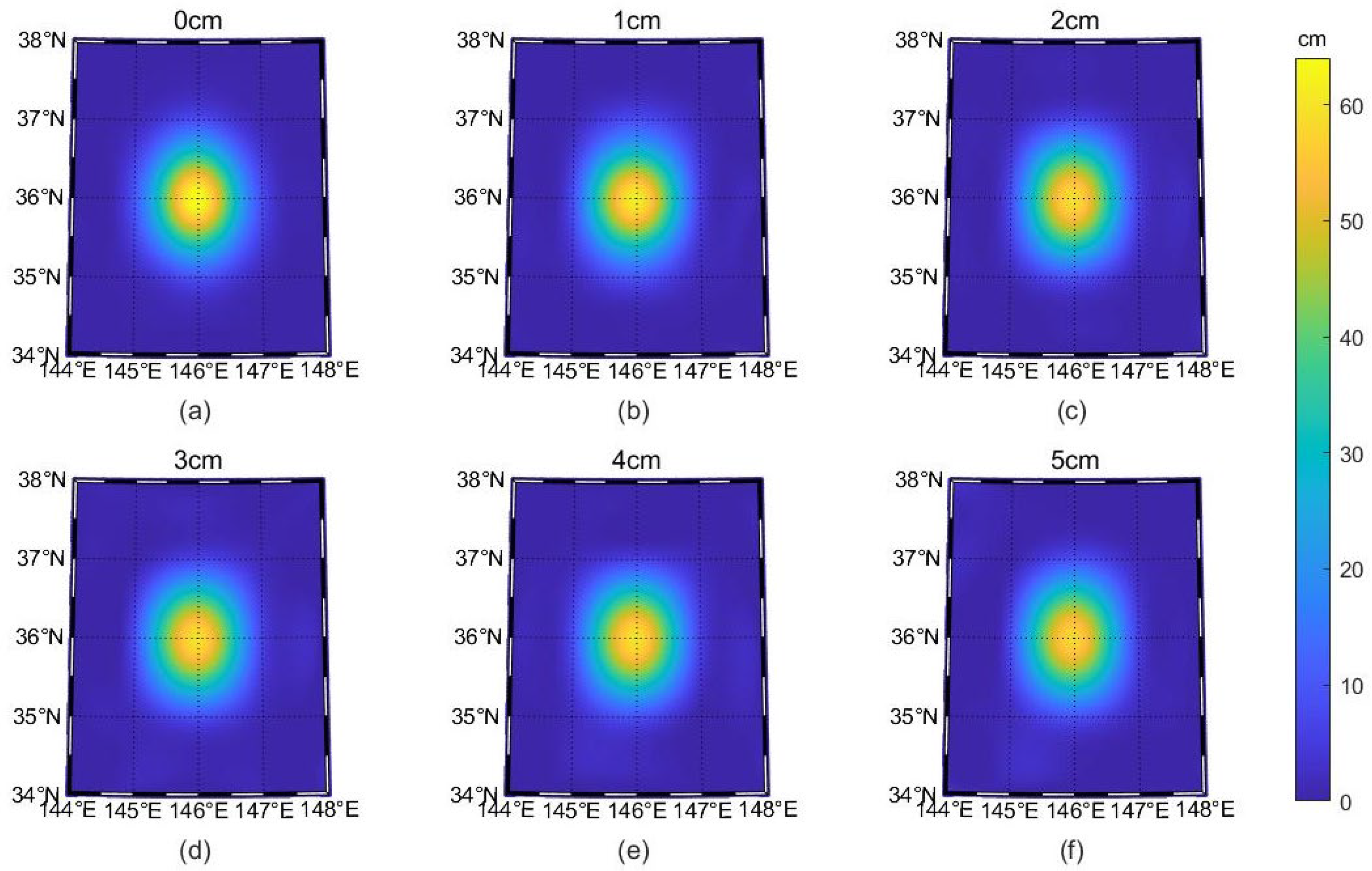
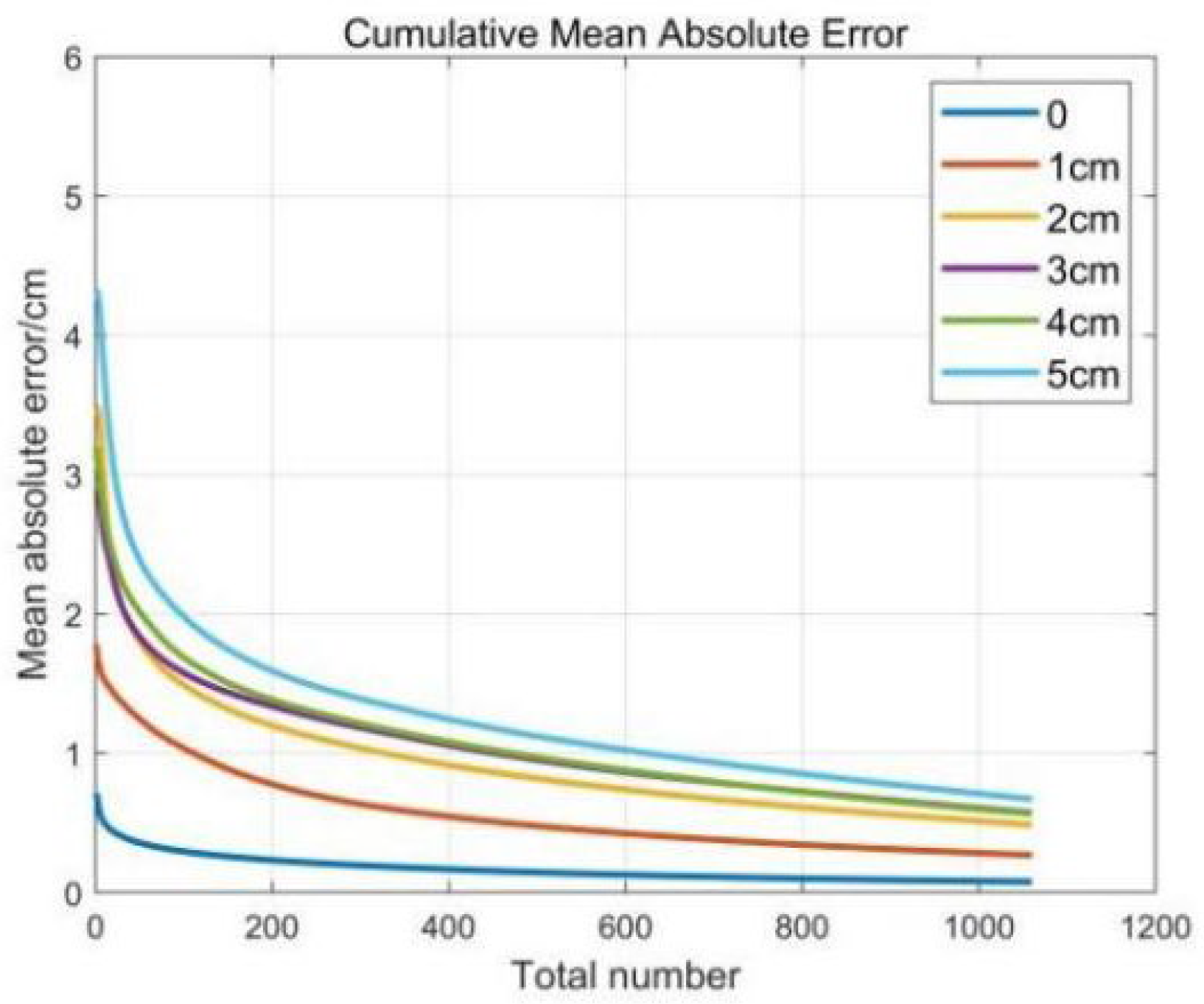
3.2. Ideal Experiment II: Stationary Eddy with Noise
3.3. Ideal Experiment III: Ideal Dynamic Eddy
4. Discussion
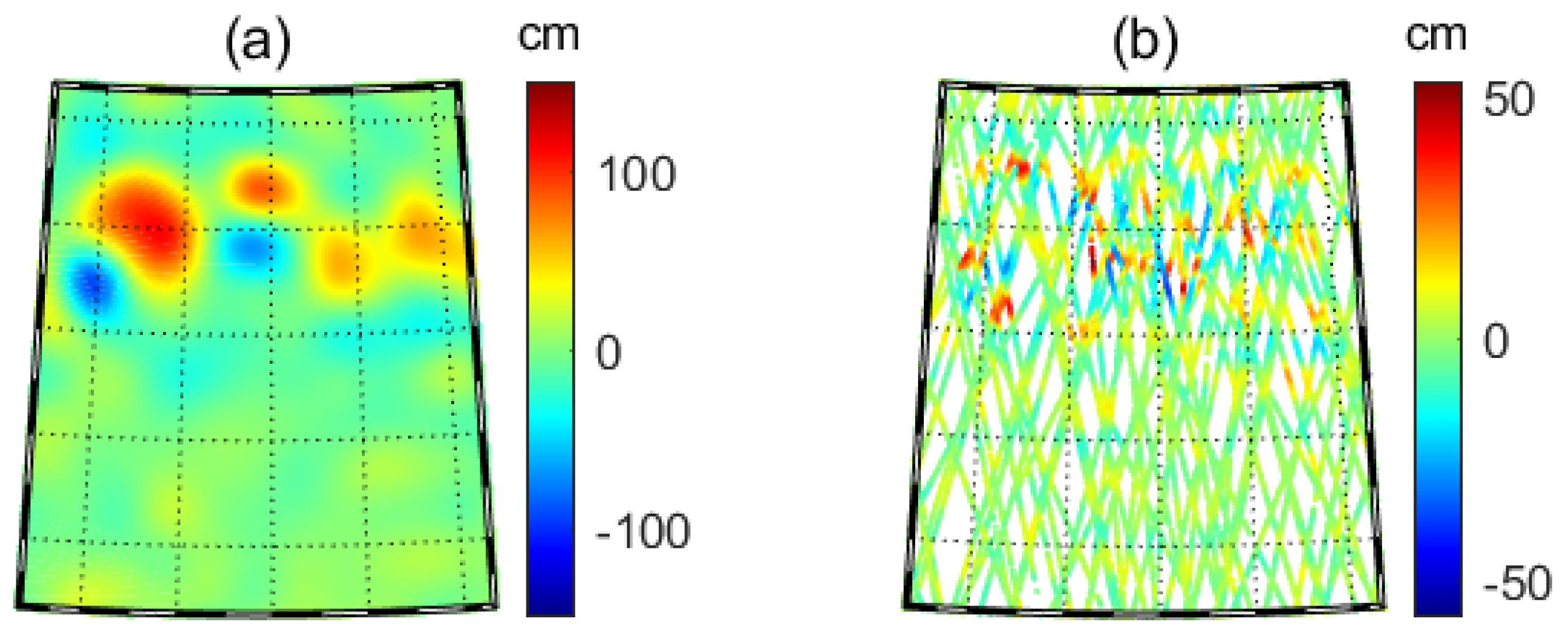
4.1. Practical Experiments with Measured Data
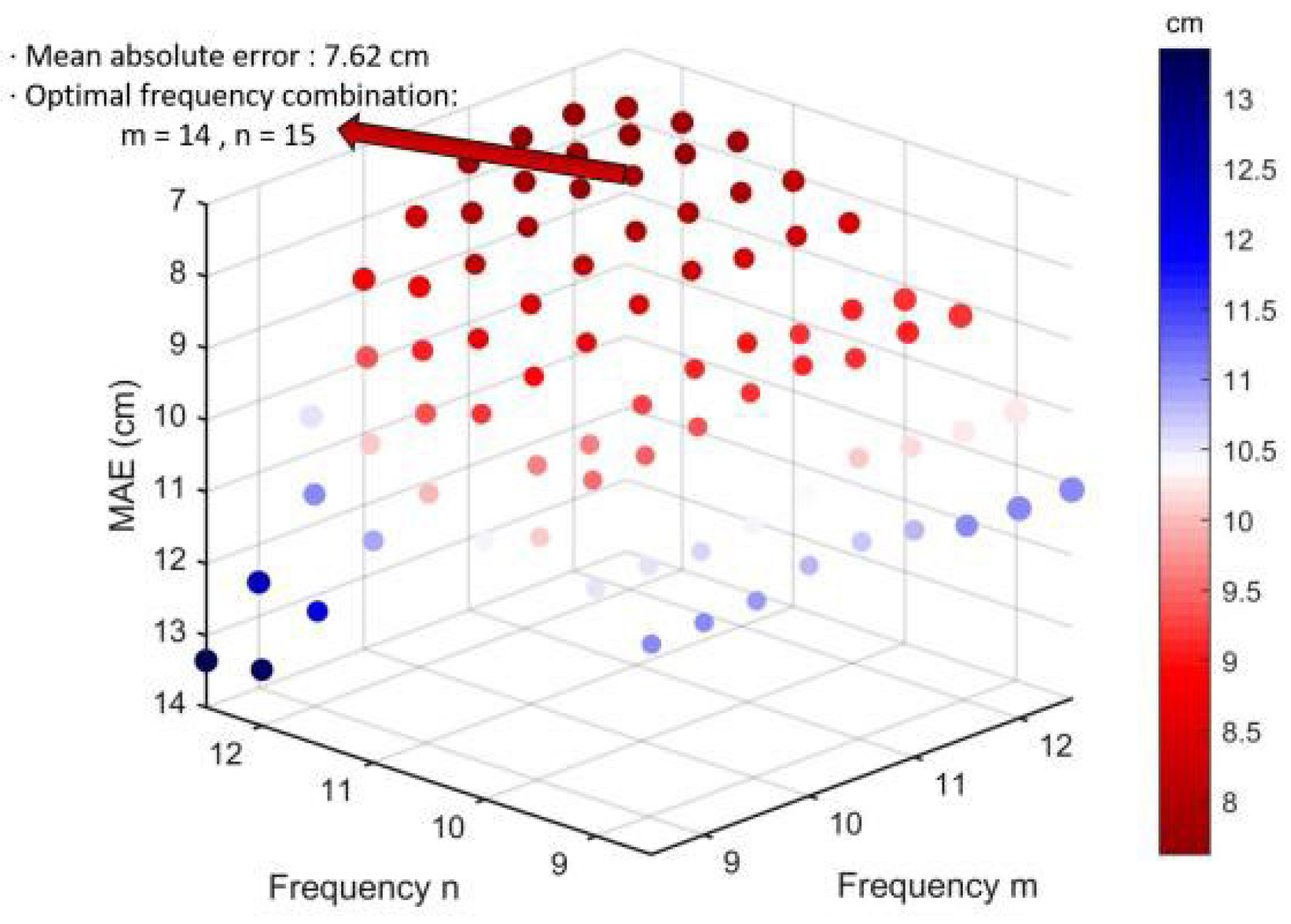
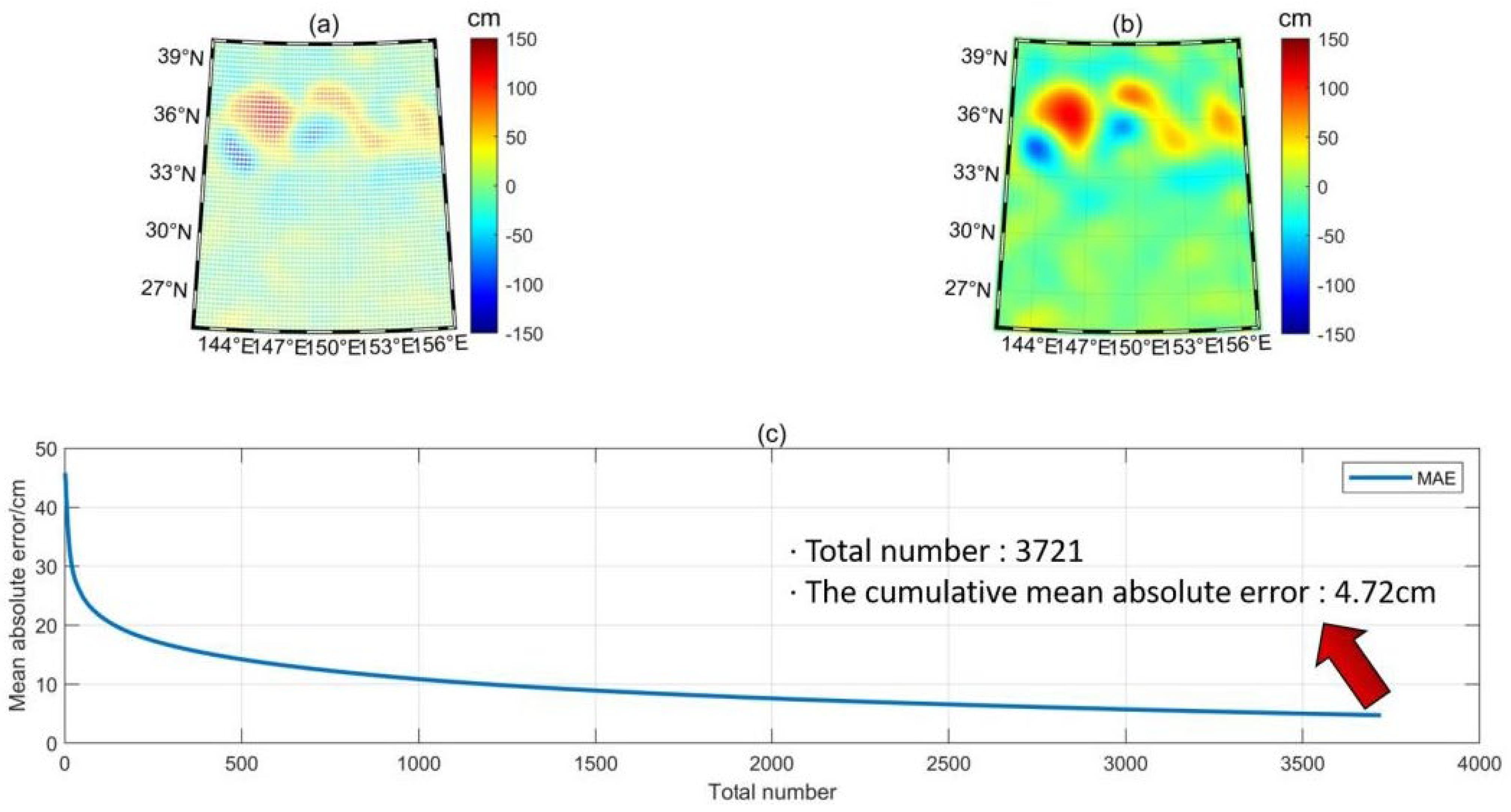
4.1.1. Determining the Optional Frequency Combination
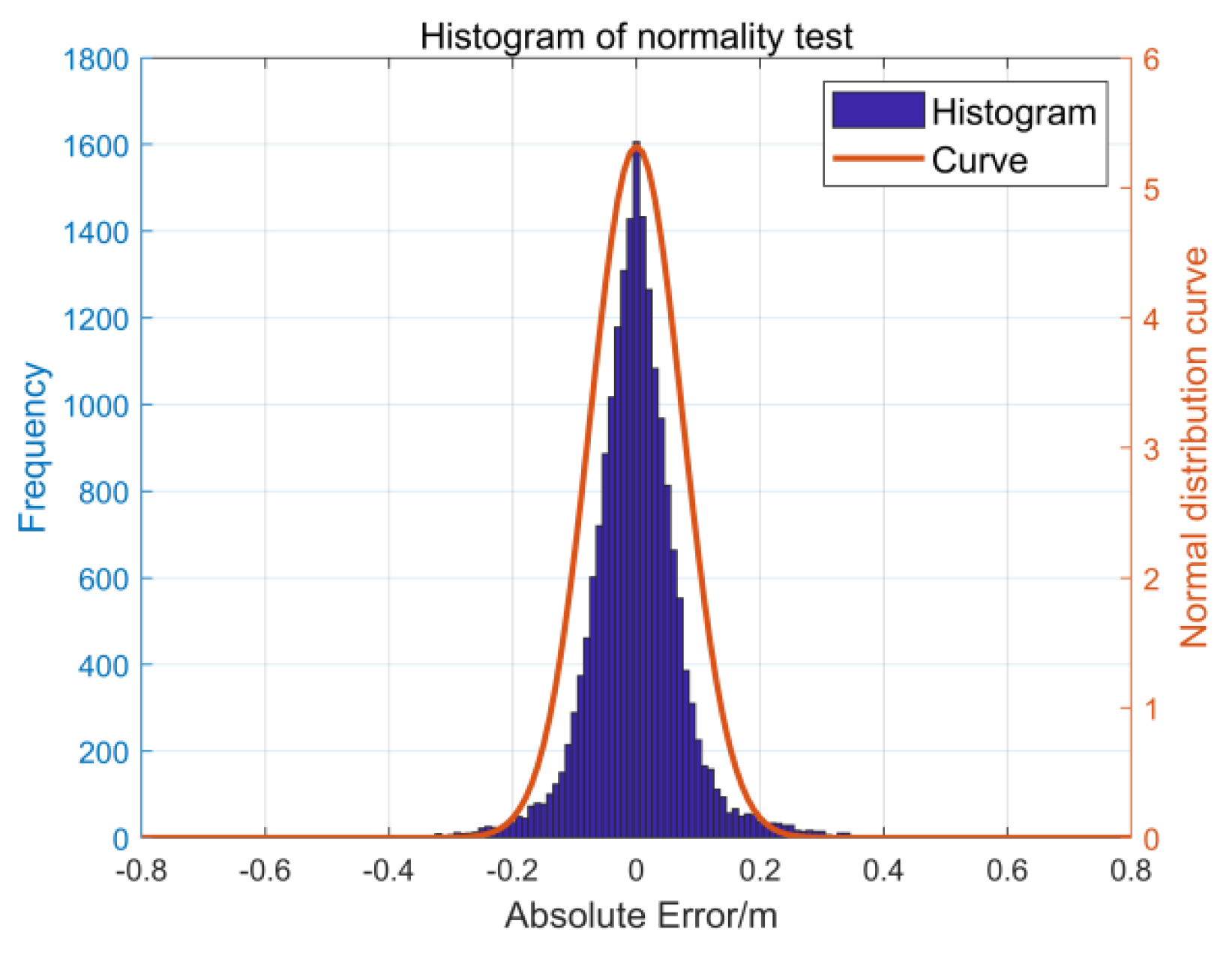
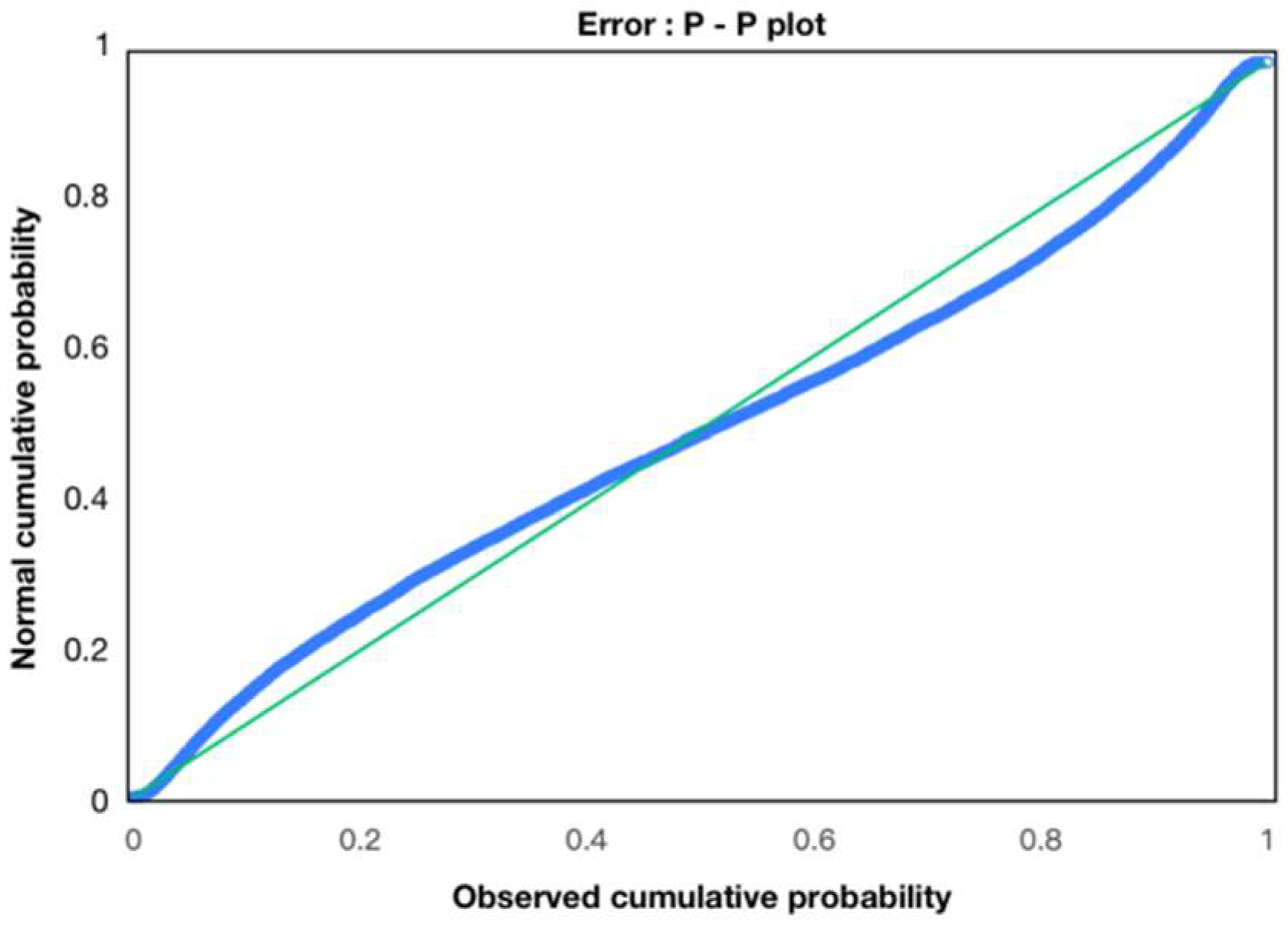
4.1.2. Hypothesis Testing
4.1.3. Mesoscale Eddy Indexes
- For an (anticyclone) cyclone eddy, the SLA data points inside the eddy are all (high) below a certain value.
- For an (anticyclone) cyclone eddy, there is at least one minimum (maximum) SLA value.
- The amplitude of the eddy is not less than 7.5 cm.
- The eddy boundary is a closed contour.
- The diameter of the eddy ranges from 50 to 400 km.
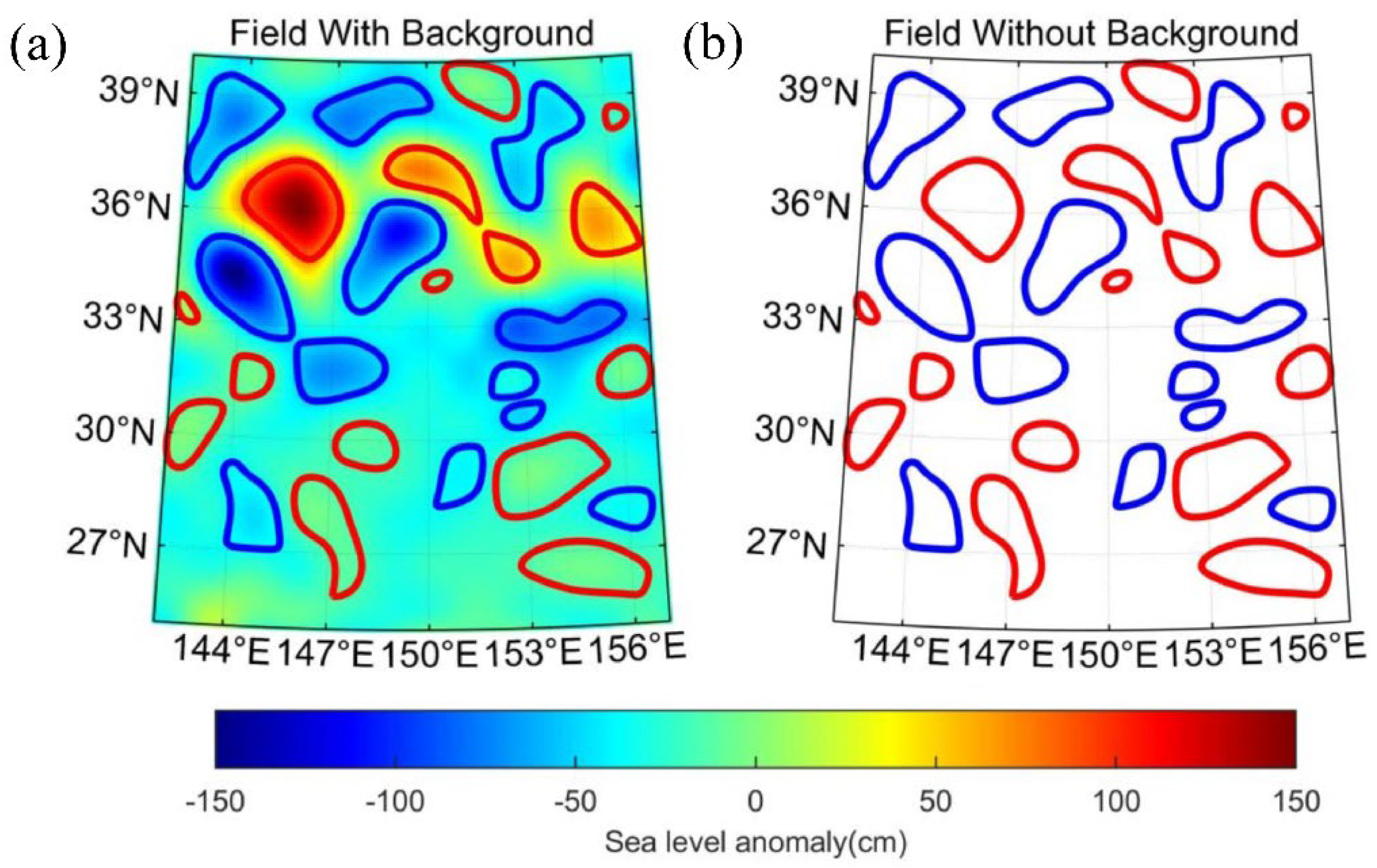
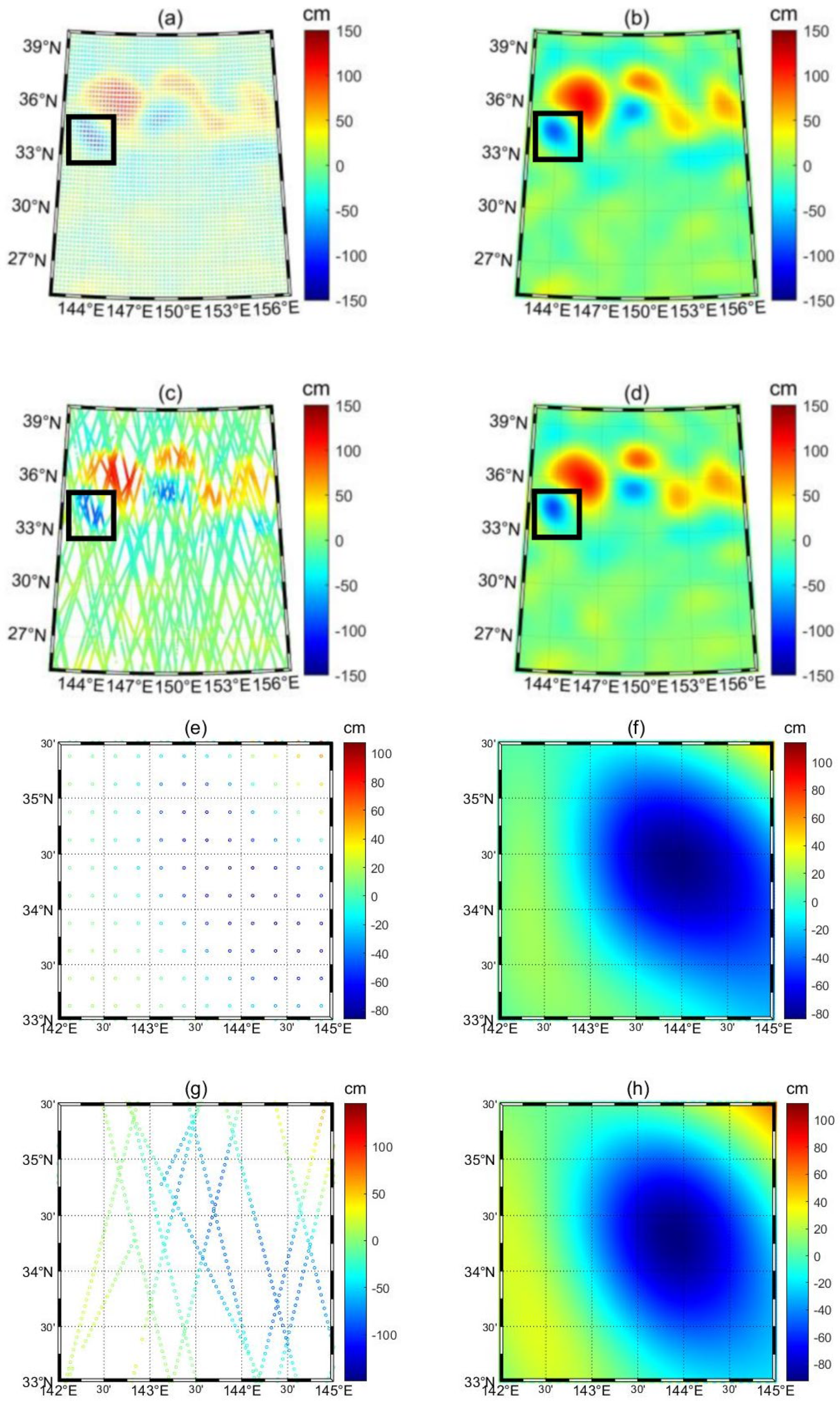
4.2. Eddy Contours
4.3. Compare and Analyze the Results of Gridded Data and Along-Track Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, G.; Yang, J.; Tian, F.; Chen, S.; Zhao, C.; Tang, J.; Liu, Y.; Wang, Y.; Yuan, Z.; He, Q.; et al. Remote sensing of oceanic eddies: Progresses and challenges. Natl. Remote Sens. Bull. 2021, 25, 302–322. [Google Scholar] [CrossRef]
- Gordon, A.L.; Giulivi, C.F. Ocean eddy freshwater flux convergence into the North Atlantic subtropics. J. Geophys. Res. Ocean. 2014, 119, 3327–3335. [Google Scholar] [CrossRef]
- Hausmann, U.; Czaja, A. The observed signature of mesoscale eddies in sea surface temperature and the associated heat transport. Deep Sea Res. Part I Oceanogr. Res. Pap. 2012, 70, 60–72. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; De Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34, 87–101. [Google Scholar] [CrossRef]
- Adams, D.K.; Mcgillicuddy, D.J.; Zamudio, L.; Thurnherr, A.M.; Liang, X.; Rouxel, O.; German, C.R.; Mullineaux, L.S. Surface-Generated Mesoscale Eddies Transport Deep-Sea Products from Hydrothermal Vents. Science 2011, 332, 580–583. [Google Scholar] [CrossRef]
- Siegel, D.A.; Granata, T.C.; Michaels, A.F.; Dickey, T.D. Mesoscale eddy diffusion, particle sinking, and the interpretation of sediment trap data. J. Geophys. Res. Ocean. 1990, 95, 5305–5311. [Google Scholar] [CrossRef]
- Wyrtki, K.; Magaard, L.; Hager, J. Eddy energy in the oceans. J. Geophys. Res. Atmos. 1976, 81, 2641–2646. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global heat and salt transports by eddy movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef]
- Duo, Z.; Wang, W.; Wang, H. Oceanic Mesoscale Eddy Detection Method Based on Deep Learning. Remote Sens. 2019, 11, 1921. [Google Scholar] [CrossRef]
- Nencioli, F.; Dong, C.; Dickey, T.; Washburn, L.; Mcwilliams, J.C. A Vector Geometry-Based Eddy Detection Algorithm and Its Application to a High-Resolution Numerical Model Product and High-Frequency Radar Surface Velocities in the Southern California Bight. J. Atmos. Ocean. Technol. 2010, 27, 564. [Google Scholar] [CrossRef]
- Okubo, A. Horizontal dispersion of floatable particles in vicinity of velocity singularities such as convergences. Deep Sea Res. Oceanogr. Abstr. 1970, 17, 445–454. [Google Scholar] [CrossRef]
- Weiss, J. The dynamics of enstrophy transfer in 2-dimensional hydrodynamics. Phys. D Nonlinear Phenom. 1991, 48, 273–294. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; Font, J.; Garcia-Ladona, E.; Emelianov, M.; Millot, C.; Taupier-Letage, I. Spatial structure of anticyclonic eddies in the Algerian basin (Mediterranean Sea) analyzed using the Okubo-Weiss parameter. Deep Sea Res. Part II 2004, 51, 3009–3028. [Google Scholar] [CrossRef]
- Mcwilliams, J.C. The emergence of isolated coherent vortices in turbulent flow. J. Fluid Mech. 1984, 146, 21–43. [Google Scholar] [CrossRef]
- Sadarjoen, I.A.; Post, F.H. Detection, quantification, and tracking of vortices using streamline geometry. Comput. Graph. 2000, 24, 333–341. [Google Scholar] [CrossRef]
- Viikmäe, B.; Torsvik, T. Quantification and characterization of mesoscale eddies with different automatic identification algorithms. J. Coast. Res. 2013, 2, 2077. [Google Scholar] [CrossRef]
- Halo, I.; Backeberg, B.; Penven, P.; Ansorge, I.; Reason, C.; Ullgren, J.E. Eddy properties in the Mozambique Channel: A comparison between observations and two numerical ocean circulation models. Deep Sea Res. Part II Top. Stud. Oceanogr. 2014, 100, 38–53. [Google Scholar] [CrossRef]
- Cox, M.G. The Numerical Evaluation of B-Splines. IMA J. Appl. Math. 1972, 10, 134–149. [Google Scholar] [CrossRef]
- Boor, C.D. On Calculating with B-Splines. J. Approx. Theory 1972, 6, 50–62. [Google Scholar] [CrossRef]
- Boor, C.D. A Practical Guide to Splines; Applied Mathematical Sciences; Springer: New York, NY, USA, 1978; Volume 27, p. 157. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M.; Jazar, R. Randomized Bidirectional B-Spline Parameterization Motion Planning. IEEE Trans. Intell. Transp. Syst. 2016, 17, 406–419. [Google Scholar] [CrossRef]
- Chen, X.; Wang, W.; Wei, H.; Dongqin, Y.E.; Mathematics, S.O. Shape adjustable C~2 continuous quasi-cubic Bézier spline curve. J. Hefei Univ. Technol. 2019, 42, 1431–1435. [Google Scholar] [CrossRef]
- Devroye, L.P.; Wagner, T.J. Distribution-free performance bounds for potential function rules. IEEE Trans. Inf. Theory 1979, 25, 601–604. [Google Scholar] [CrossRef]
- Geisser, S. A Predictive Approach to the Random Effect Model. Biometrika 1974, 61, 101–107. [Google Scholar] [CrossRef]
- Rao, C.R.; Wu, Y. Linear model selection by cross-validation. J. Stat. Plan. Inference 2009, 128, 231–240. [Google Scholar] [CrossRef]
- Geisser, S. The Predictive Sample Reuse Method with Application. J. Am. Stat. Assoc. 1975, 70, 320–328. [Google Scholar] [CrossRef]
- Zhang, X.; Jing, Z.; Zheng, R.; Huang, X.; Cao, H. Submesoscale characteristics of a typical anticyclonic mesoscale eddy in Kuroshio Extension. J. Trop. Oceanogr. 2021, 40, 31–40. [Google Scholar] [CrossRef]
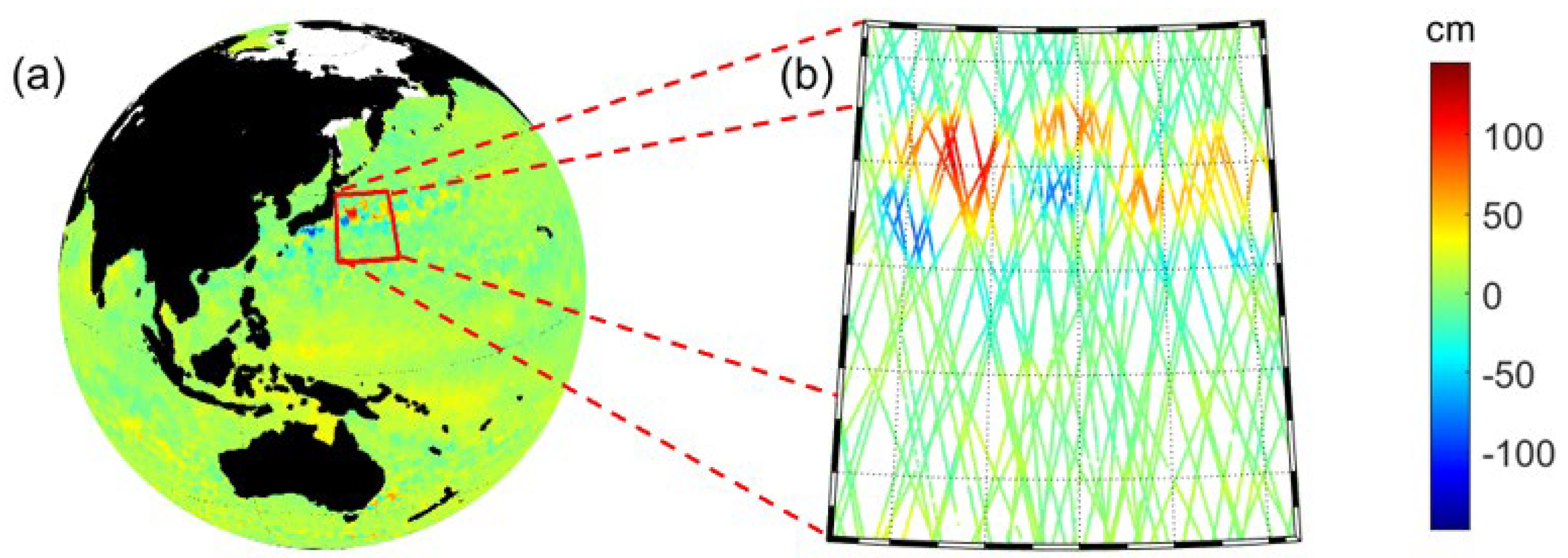


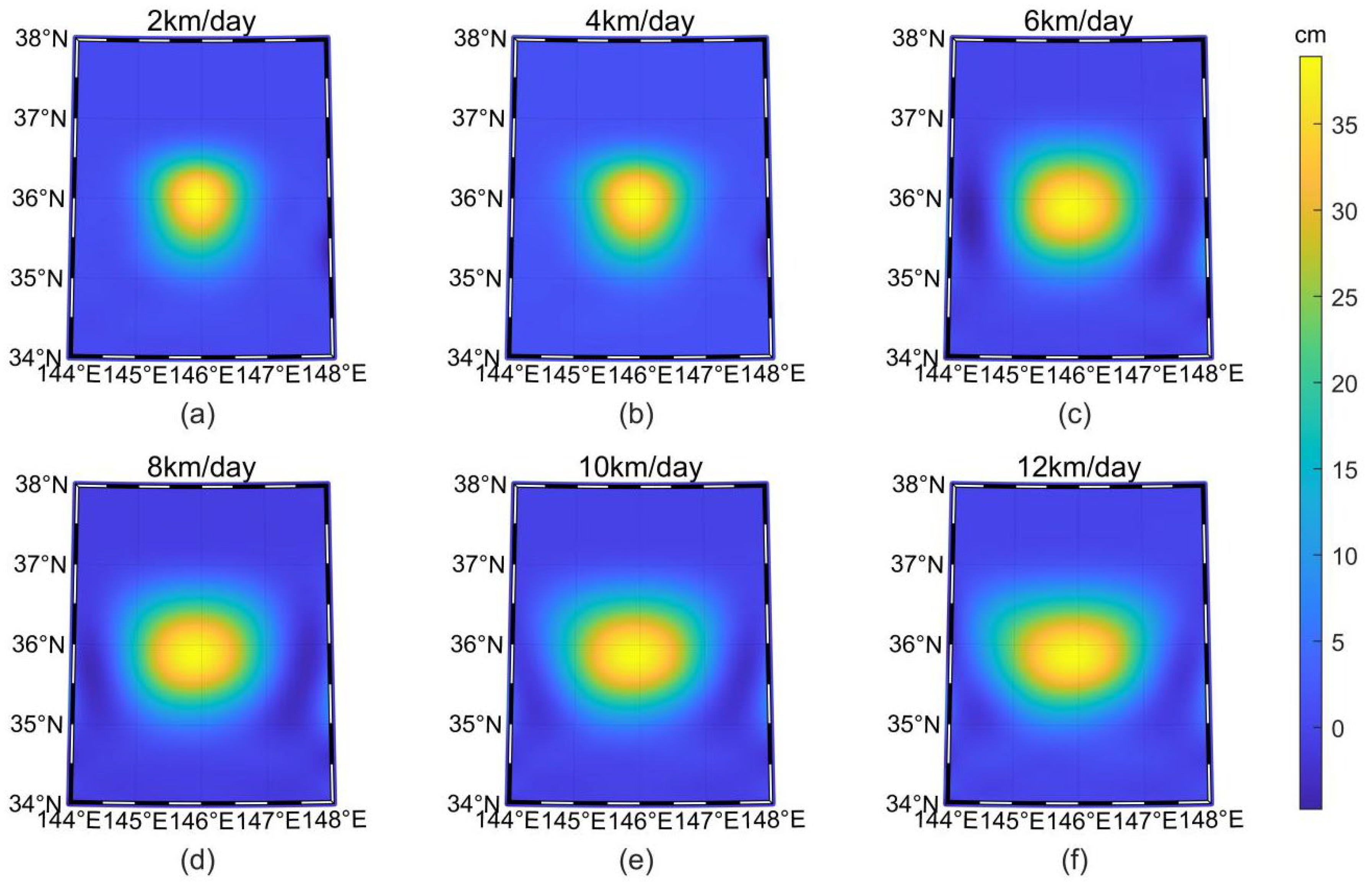
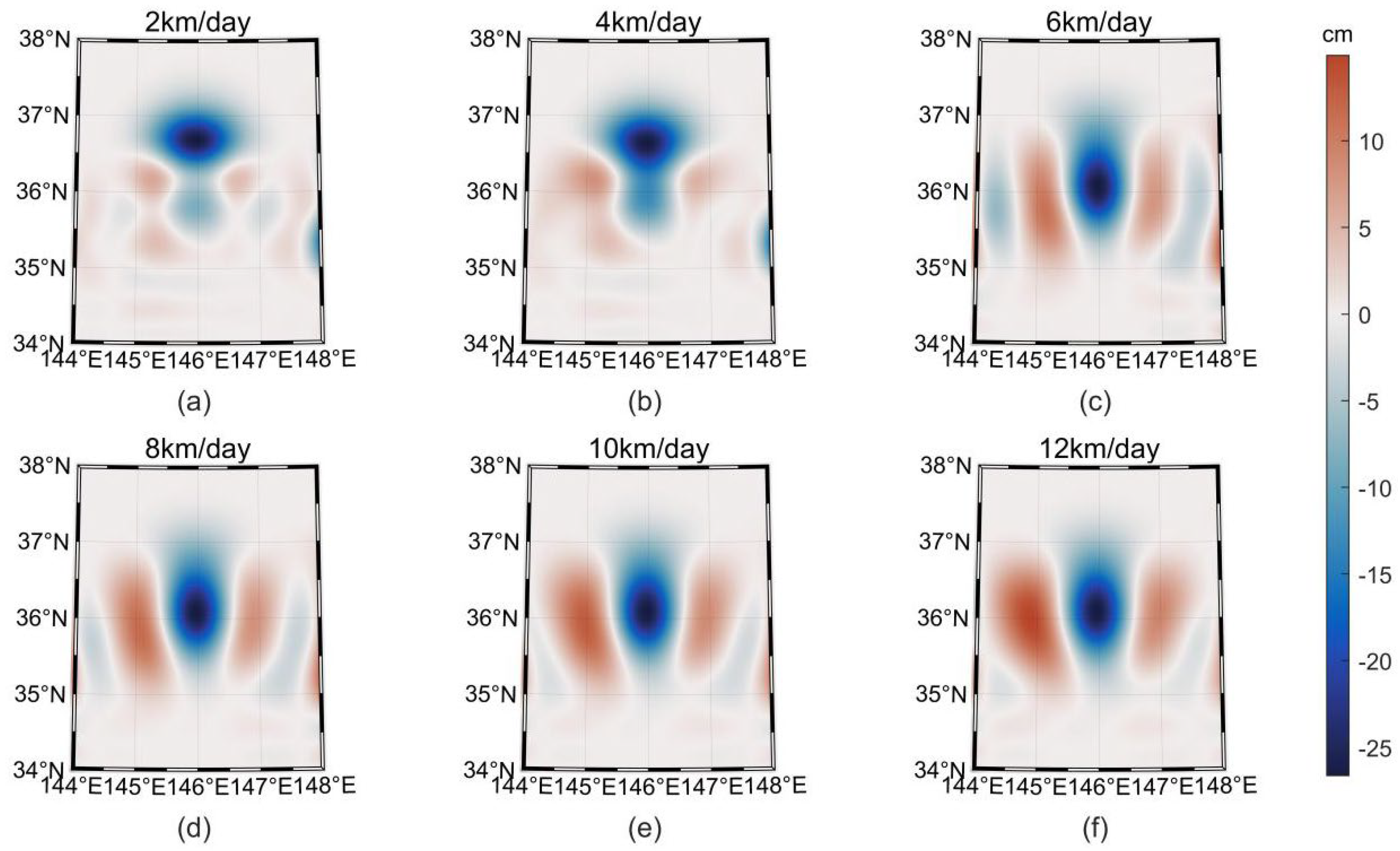
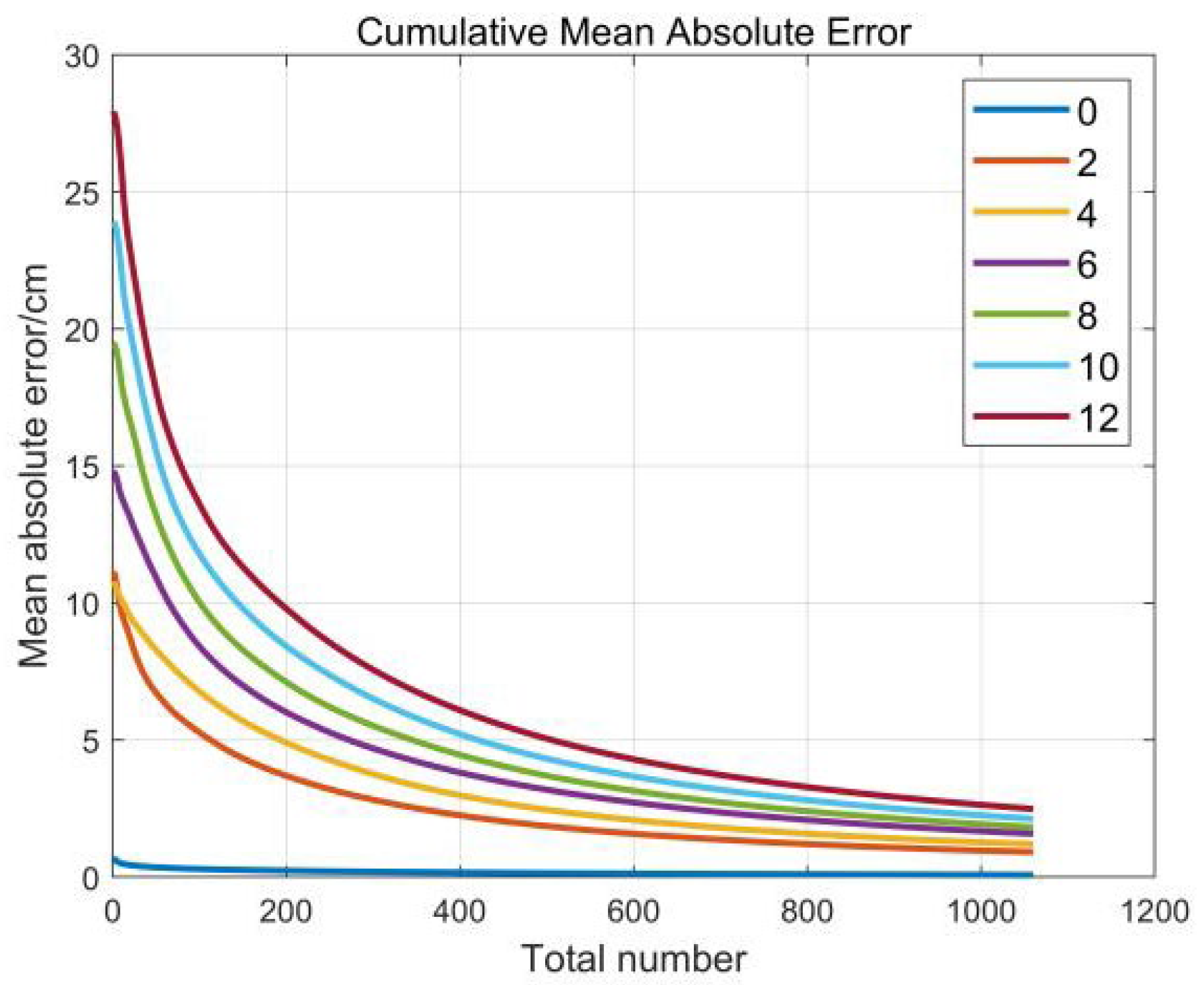
| Sample | Coverage | Range | Timer Series | Level | Type |
|---|---|---|---|---|---|
| SLA | North–West Pacific | 25–40°N 142–157°E | 2022,03,01–2022,03,09 | 3 | NRT |
| Frequency n | Frequency m | |||||
|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | 9 | 10 | |
| 7 | 5.84 | 5.34 | 6.40 | 6.70 | 7.53 | 28.01 |
| 8 | 5.86 | 5.03 | 5.86 | 4.95 | 5.41 | 22.79 |
| 9 | 5.65 | 5.04 | 6.30 | 5.52 | 7.04 | 14.18 |
| 10 | 5.63 | 5.02 | 6.30 | 4.93 | 5.69 | 10.32 |
| 11 | 6.12 | 5.00 | 6.31 | 5.12 | 8.79 | 13.95 |
| Noise (cm) | Total Number | |||||
|---|---|---|---|---|---|---|
| 10% | 20% | 40% | 60% | 80% | 100% | |
| 0 | 0.29 | 0.23 | 0.16 | 0.12 | 0.10 | 0.08 |
| 1 | 1.02 | 0.76 | 0.53 | 0.41 | 0.33 | 0.27 |
| 2 | 1.46 | 1.18 | 0.89 | 0.71 | 0.59 | 0.49 |
| 3 | 1.56 | 1.32 | 1.03 | 0.84 | 0.69 | 0.57 |
| 5 | 1.95 | 1.56 | 1.21 | 0.99 | 0.82 | 0.67 |
| V | Total Number | |||||
|---|---|---|---|---|---|---|
| 10% | 20% | 40% | 60% | 80% | 100% | |
| 0 | 0.29 | 0.23 | 0.16 | 0.12 | 0.10 | 0.08 |
| 2 | 5.14 | 3.56 | 2.14 | 1.50 | 1.14 | 0.91 |
| 4 | 6.62 | 4.74 | 2.84 | 1.97 | 1.50 | 1.20 |
| 6 | 8.20 | 5.82 | 3.64 | 2.58 | 1.97 | 1.58 |
| 8 | 9.76 | 6.87 | 4.25 | 2.98 | 2.27 | 1.82 |
| 10 | 11.49 | 8.14 | 4.97 | 3.48 | 2.65 | 2.12 |
| 12 | 13.25 | 9.47 | 5.80 | 4.07 | 3.10 | 2.49 |
| Days | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| Data Points | 8781 | 10,042 | 12,797 | 14,763 | 16,108 | 17,746 | 19,942 | 21,413 | 23,119 |
| MAE | 13.24 | 8.77 | 8.11 | 8.04 | 7.62 | 7.67 | 7.74 | 8.05 | 8.19 |
| Frequency n | Frequency m | |||||
|---|---|---|---|---|---|---|
| 11 | 12 | 13 | 14 | 15 | 16 | |
| 12 | 9.60 | 9.32 | 9.09 | 9.00 | 9.15 | 9.08 |
| 13 | 8.91 | 8.71 | 8.45 | 8.25 | 8.35 | 8.31 |
| 14 | 8.64 | 8.43 | 8.16 | 7.96 | 7.97 | 7.96 |
| 15 | 9.06 | 8.13 | 7.88 | 7.62 | 7.71 | 7.68 |
| 16 | 9.41 | 8.70 | 7.94 | 7.78 | 7.66 | 7.67 |
| 17 | 10.49 | 8.85 | 8.25 | 7.77 | 7.69 | 7.64 |
| Sample | Total | Average | Skewness | Kurtosis | S–W Inspection | K–S Inspection |
|---|---|---|---|---|---|---|
| ERROR | 16,108 | −0.075 | 0.427 | 4.453 | 0.942 (0.000 ***) | 0.067 (0.000 ***) |
| Test Value | Total | Standard Deviation | T | P |
|---|---|---|---|---|
| 0 | 16,108 | 0.427 | −1.398 | 0.162 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Gao, M.; Zhang, Y.; Guo, J.; Lv, X.; Zhang, A. Oceanic Mesoscale Eddies Identification Using B-Spline Surface Fitting Model Based on Along-Track SLA Data. Remote Sens. 2022, 14, 5713. https://doi.org/10.3390/rs14225713
Xu L, Gao M, Zhang Y, Guo J, Lv X, Zhang A. Oceanic Mesoscale Eddies Identification Using B-Spline Surface Fitting Model Based on Along-Track SLA Data. Remote Sensing. 2022; 14(22):5713. https://doi.org/10.3390/rs14225713
Chicago/Turabian StyleXu, Luochuan, Miao Gao, Yaorong Zhang, Junting Guo, Xianqing Lv, and Anmin Zhang. 2022. "Oceanic Mesoscale Eddies Identification Using B-Spline Surface Fitting Model Based on Along-Track SLA Data" Remote Sensing 14, no. 22: 5713. https://doi.org/10.3390/rs14225713
APA StyleXu, L., Gao, M., Zhang, Y., Guo, J., Lv, X., & Zhang, A. (2022). Oceanic Mesoscale Eddies Identification Using B-Spline Surface Fitting Model Based on Along-Track SLA Data. Remote Sensing, 14(22), 5713. https://doi.org/10.3390/rs14225713