Use of Airborne Radar Images and Machine Learning Algorithms to Map Soil Clay, Silt, and Sand Contents in Remote Areas under the Amazon Rainforest
Abstract
1. Introduction
2. Materials and Methods
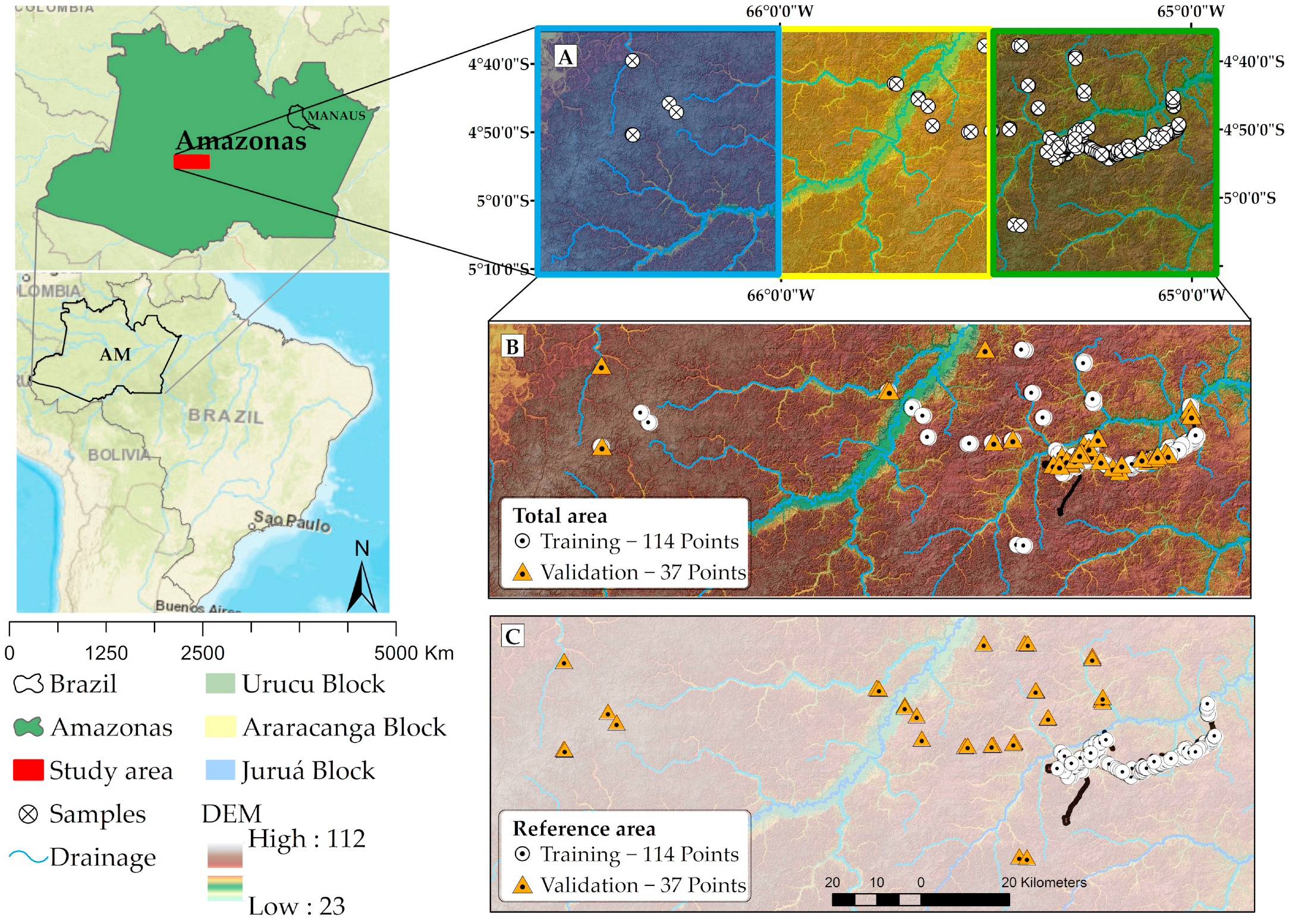
2.1. Study Area
2.2. Soil Sampling Designs
2.3. Soil Particle Size Fractions
2.4. Radar-Derived P-Band and Relief Covariates
2.5. Covariate Selection
2.6. Dissimilarities in Covariates between the Reference Area and Total Area
2.7. Model Training
2.8. Evaluation of the Accuracy of Interpolation Methods
2.9. Evaluation of the Importance of P-Band to Model’s Performance
3. Results
3.1. Summary Statistics
3.2. Similarity among the Reference Area and Exploration Blocks
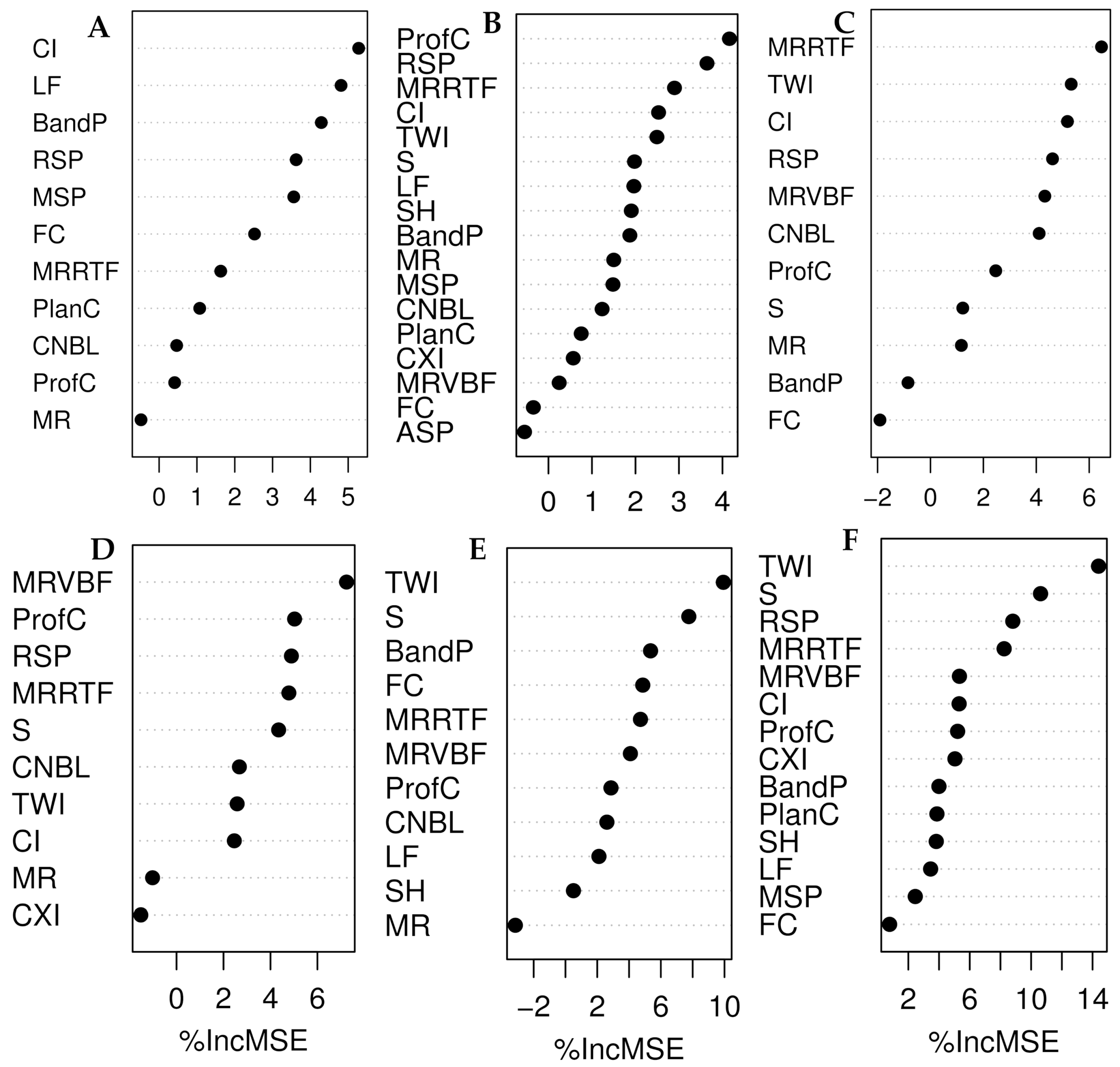
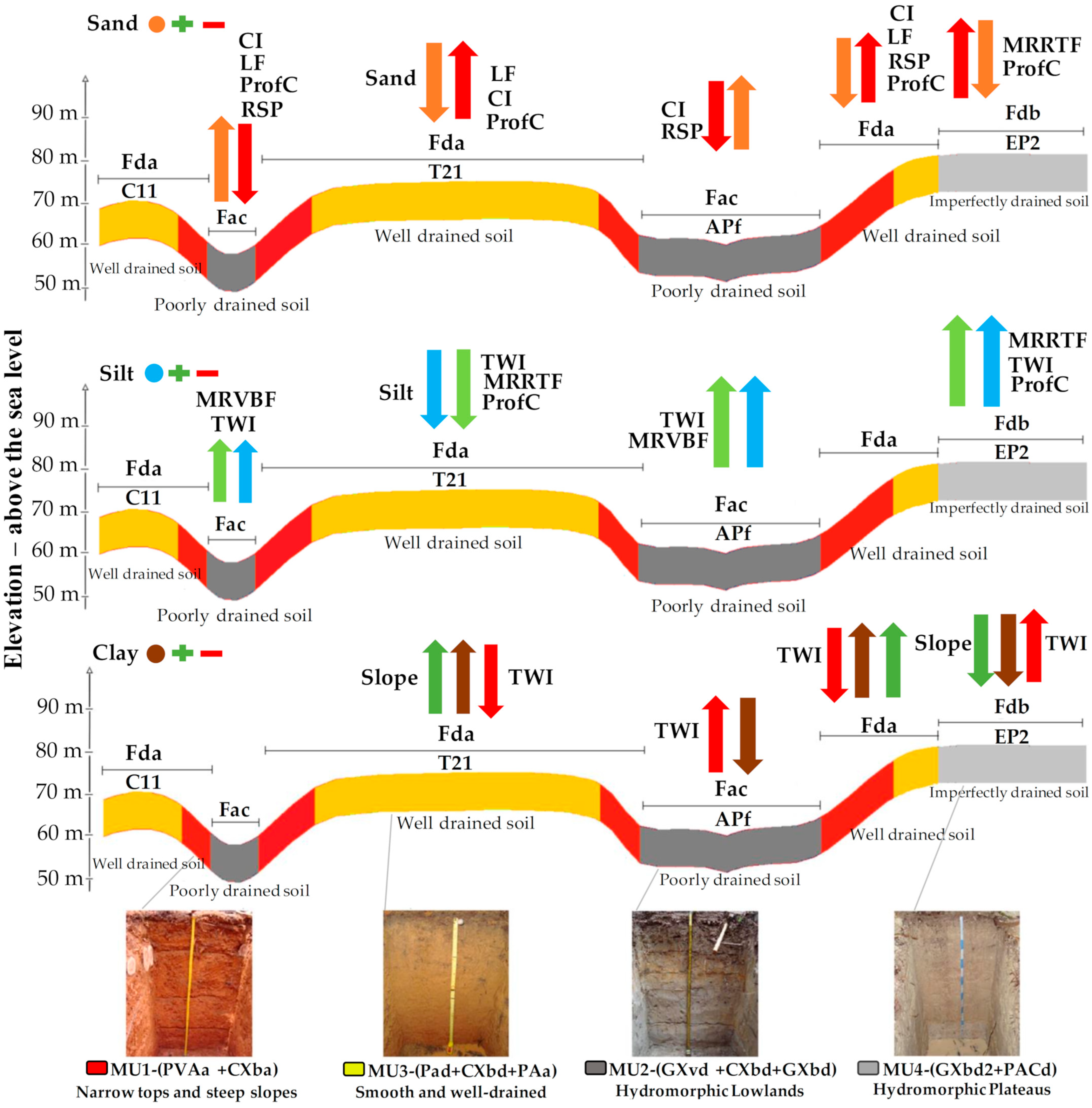
3.3. Remote Sensing Covariates and Soil Particle Size Fractions Relationships
3.4. Model Prediction Performance
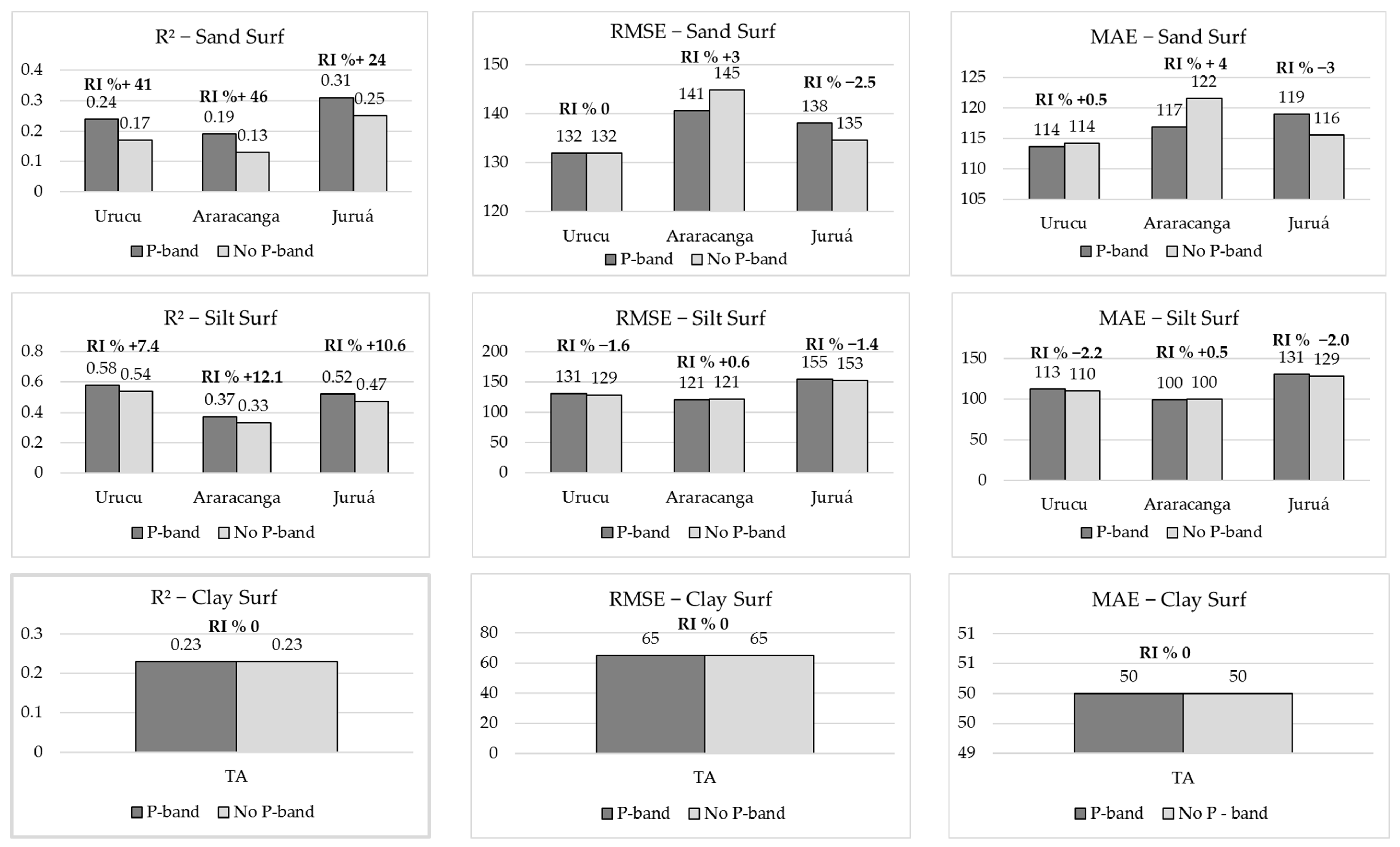
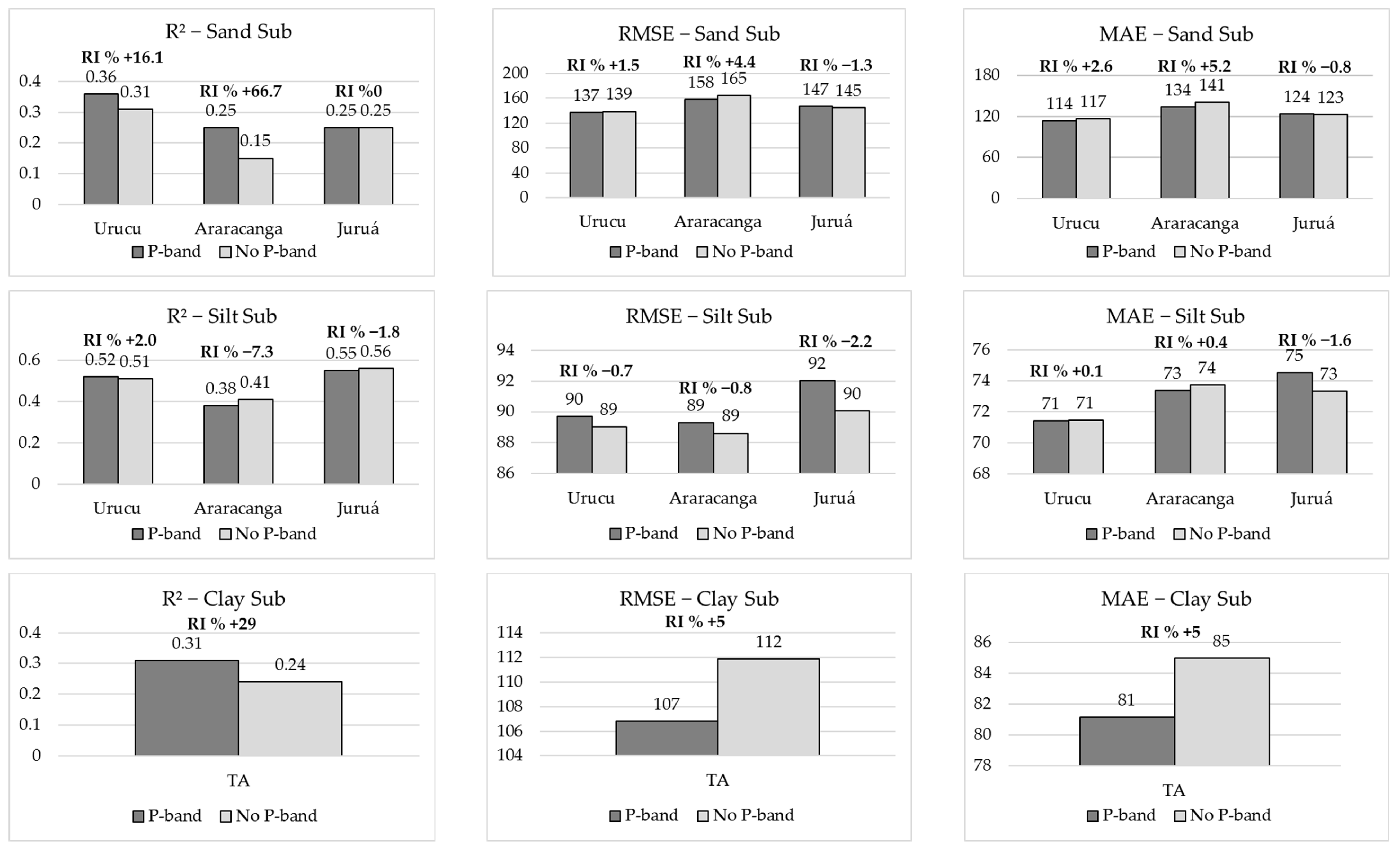
3.5. Relative Improvement (RI%) from Adding the Radar P-Band
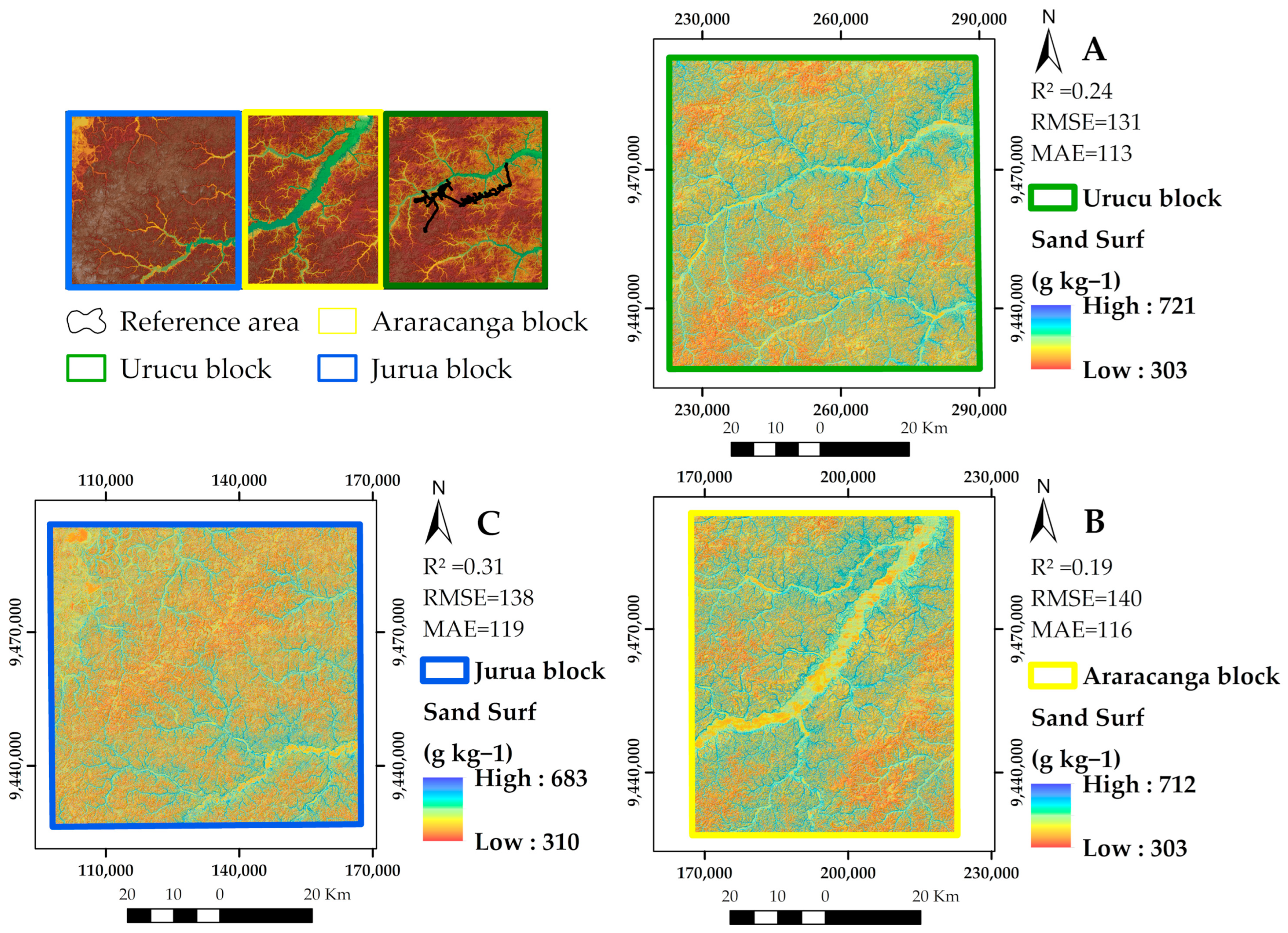
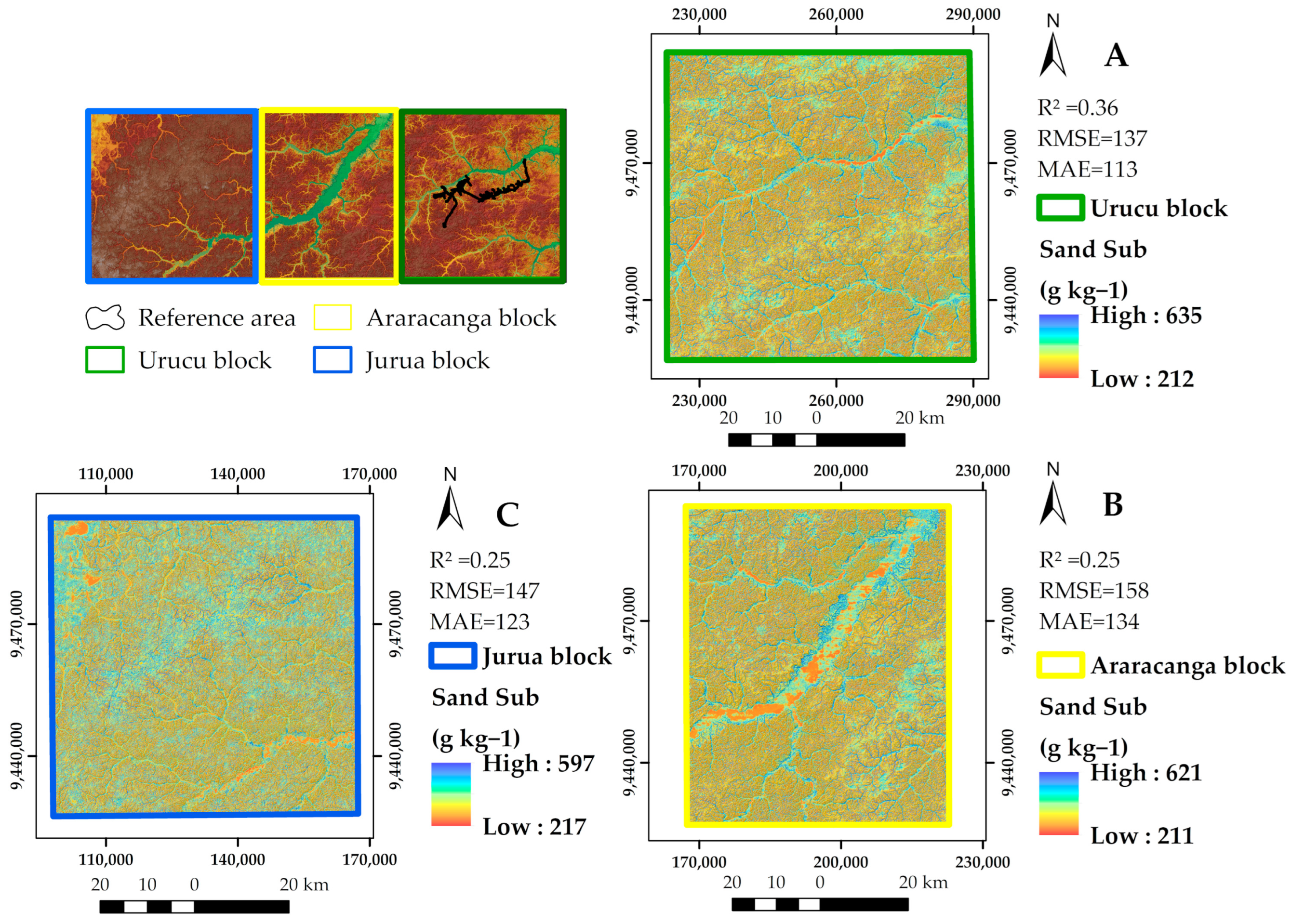
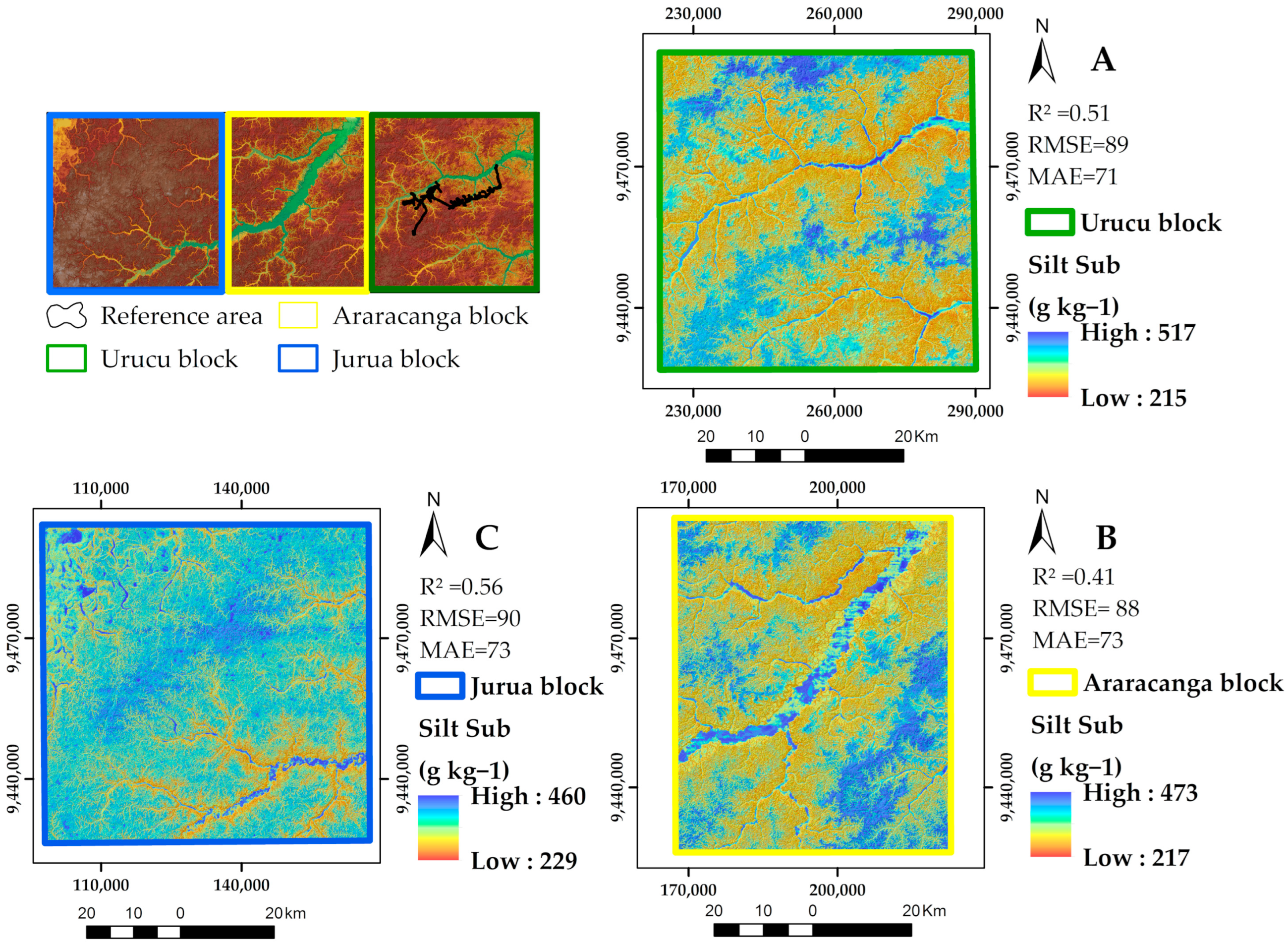
3.6. Soil Particle Size Fraction Maps
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akpa, S.I.C.; Odeh, I.O.A.; Bishop, T.F.A.; Hartemink, A.E. Digital Mapping of Soil Particle-Size Fractions for Nigeria. Soil Sci. Soc. Am. J. 2014, 78, 1953–1966. [Google Scholar] [CrossRef]
- Mehrabi-Gohari, E.; Matinfar, H.R.; Jafari, A.; Taghizadeh-Mehrjardi, R.; Triantafilis, J. The Spatial Prediction of Soil Texture Fractions in Arid Regions of Iran. Soil Syst. 2019, 3, 65. [Google Scholar] [CrossRef]
- Dos Santos, H.G.; Jacomine, P.K.T.; Dos Anjos, L.H.; De Oliveira, V.A.; Lumbreras, J.F.; Coelho, M.R.; De Almeida, J.A.; De Araujo Filho, J.C.; De Oliveira, J.B.; Cunha, T.J.F. Sistema Brasileiro de Classificação de Solos; Embrapa: Brasília, Brazil, 2018; ISBN 978-85-7035-817-2. [Google Scholar]
- Ließ, M.; Glaser, B.; Huwe, B. Uncertainty in the Spatial Prediction of Soil Texture: Comparison of Regression Tree and Random Forest Models. Geoderma 2012, 170, 70–79. [Google Scholar] [CrossRef]
- Minasny, B.; Hartemink, A.E. Predicting Soil Properties in the Tropics. Earth-Sci. Rev. 2011, 106, 52–62. [Google Scholar] [CrossRef]
- Amazônia Legal | IBGE. Available online: https://www.ibge.gov.br/geociencias/organizacao-do-territorio/estrutura-territorial/15819-amazonia-legal.html?=&t=o-que-e (accessed on 21 October 2022).
- Ceddia, M.B.; Villela, A.L.O.; Pinheiro, É.F.M.; Wendroth, O. Spatial Variability of Soil Carbon Stock in the Urucu River Basin, Central Amazon-Brazil. Sci. Total Environ. 2015, 526, 58–69. [Google Scholar] [CrossRef]
- Ceddia, M.B.; Gomes, A.S.; Vasques, G.M.; Pinheiro, É.F.M. Soil Carbon Stock and Particle Size Fractions in the Central Amazon Predicted from Remotely Sensed Relief, Multispectral and Radar Data. Remote Sens. 2017, 9, 124. [Google Scholar] [CrossRef]
- BRASIL Departamento Nacional de Produção Mineral. Projeto Radambrasil, 1973–1987. (Levantamento de Recursos Naturais, 38 volumes).
- Santos, J.; Spinelli-Araujo, L.; Kuplich, T.; Da Costa Freitas, D.; Dutra, L.; Sant’Anna, S.; Gama, F. Tropical Forest Biomass and Its Relationship with P-Band SAR Data. Rev. Bras. De Cartogr. 2006, 1, 58. [Google Scholar]
- Gama, F.; Santos, J.; Mura, J.; Rennó, C. Estimativa de Parâmetros Biofísicos de Povoamentos de Eucalyptus Através de Dados SAR Estimation of Biophysical Parameters in the Eucalyptus Stands by SAR Data. Ambiência 2009, 2, 29–42. [Google Scholar]
- Sambatti, J.B.M.; Leduc, R.; Lubeck, D.; Moreira, J.R.; dos Santos, J.R. Assessing Forest Biomass and Exploration in the Brazilian Amazon with Airborne InSAR: An Alternative for REDD. Open Remote Sens. J. 2012, 5, 21–36. [Google Scholar] [CrossRef]
- Saatchi, S.; Marlier, M.; Chazdon, R.L.; Clark, D.B.; Russell, A.E. Impact of Spatial Variability of Tropical Forest Structure on Radar Estimation of Aboveground Biomass. Remote Sens. Environ. 2011, 115, 2836–2849. [Google Scholar] [CrossRef]
- Freitas, C.D.C.; Soler, L.D.S.; Sant’Anna, S.J.S.; Dutra, L.V.; dos Santos, J.R.; Mura, J.C.; Correia, A.H. Land Use and Land Cover Mapping in the Brazilian Amazon Using Polarimetric Airborne P-Band SAR Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2956–2970. [Google Scholar] [CrossRef]
- Neeff, T.; Dutra, L.; Santos, J.; Da Costa Freitas, D.; Spinelli-Araujo, L. Tropical Forest Measurement by Interferometric Height Modeling and P-Band Radar Backscatter. For. Sci. 2005, 51, 585–594. [Google Scholar]
- Alemohammad, S.H.; Jagdhuber, T.; Moghaddam, M.; Entekhabi, D. Soil and Vegetation Scattering Contributions in L-Band and P-Band Polarimetric SAR Observations. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8417–8429. [Google Scholar] [CrossRef]
- Zribi, M.; Sahnoun, M.; Baghdadi, N.; Le Toan, T.; Ben Hamida, A. Analysis of the Relationship between Backscattered P-Band Radar Signals and Soil Roughness. Remote Sens. Environ. 2016, 186, 13–21. [Google Scholar] [CrossRef]
- Zribi, M.; Sahnoun, M.; Dusséaux, R.; Afifi, S.; Baghdadi, N.; Ben Hamida, A. Analysis of P Band Radar Signal Potential to Retrieve Soil Moisture Profile. In Proceedings of the 2016 2nd International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Monastir, Tunisia, 21 March 2016; pp. 591–595. [Google Scholar]
- Blumberg, D.G.; Freilikher, V.; Kaganovskii, Y.; Maradudin, A.A. Subsurface Microwave Remote Sensing of Soil-Water Content: Field Studies in the Negev Desert and Optical Modelling. Int. J. Remote Sens. 2002, 23, 4039–4054. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.S.; Moghaddam, M. Theoretical Modeling and Analysis of L- and P-Band Radar Backscatter Sensitivity to Soil Active Layer Dielectric Variations. Remote Sens. 2015, 7, 9450–9472. [Google Scholar] [CrossRef]
- Etminan, A.; Tabatabaeenejad, A.; Moghaddam, M. Retrieving Root-Zone Soil Moisture Profile From P-Band Radar via Hybrid Global and Local Optimization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5400–5408. [Google Scholar] [CrossRef]
- Tabatabaeenejad, A.; Burgin, M.; Duan, X.; Moghaddam, M. P-Band Radar Retrieval of Subsurface Soil Moisture Profile as a Second-Order Polynomial: First AirMOSS Results. IEEE Trans. Geosci. Remote Sens. 2015, 53, 645–658. [Google Scholar] [CrossRef]
- Srivastava, H.S.; Patel, P.; Navalgund, R.R. Incorporating Soil Texture in Soil Moisture Estimation from Extended Low-1 Beam Mode RADARSAT-1 SAR Data. Int. J. Remote Sens. 2006, 27, 2587–2598. [Google Scholar] [CrossRef]
- Lagacherie, P.; Robbez-Masson, J.M.; Nguyen-The, N.; Barthès, J.P. Mapping of Reference Area Representativity Using a Mathematical Soilscape Distance. Geoderma 2001, 101, 105–118. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Sheikhpour, R.; Zeraatpisheh, M.; Amirian-Chakan, A.; Toomanian, N.; Kerry, R.; Scholten, T. Semi-Supervised Learning for the Spatial Extrapolation of Soil Information. Geoderma 2022, 426, 116094. [Google Scholar] [CrossRef]
- Arruda, G.P.D.; Demattê, J.A.; Chagas, C.D.S.; Fiorio, P.R.; Fongaro, C.T. Digital Soil Mapping Using Reference Area and Artificial Neural Networks. Sci. Agric. 2016, 73, 266–273. [Google Scholar] [CrossRef]
- Grinand, C.; Arrouays, D.; Laroche, B.; Martin, M.P. Extrapolating Regional Soil Landscapes from an Existing Soil Map: Sampling Intensity, Validation Procedures, and Integration of Spatial Context. Geoderma 2008, 143, 180–190. [Google Scholar] [CrossRef]
- Chagas, C.D.S.; Junior, W.D.C.; Bhering, S.B.; Filho, B.C. Spatial Prediction of Soil Surface Texture in a Semiarid Region Using Random Forest and Multiple Linear Regressions. Catena 2016, 139, 232–240. [Google Scholar] [CrossRef]
- Bhering, S.B.; Chagas, C.D.S.; Junior, W.D.C.; Pereira, N.R.; Filho, B.C.; Pinheiro, H.S.K. Mapeamento digital de areia, argila e carbono orgânico por modelos Random Forest sob diferentes resoluções espaciais. Pesq. Agropec. Bras. 2016, 51, 1359–1370. [Google Scholar] [CrossRef]
- Wolski, M.S.; Dalmolin, R.S.D.; Flores, C.A.; Moura-Bueno, J.M.; Caten, A.T.; Kaiser, D.R. Digital Soil Mapping and Its Implications in the Extrapolation of Soil-Landscape Relationships in Detailed Scale. Pesqui. Agropecuária Bras. 2017, 52, 633–642. [Google Scholar] [CrossRef]
- Silva, S.H.G.; de Menezes, M.D.; Owens, P.R.; Curi, N. Retrieving Pedologist’s Mental Model from Existing Soil Map and Comparing Data Mining Tools for Refining a Larger Area Map under Similar Environmental Conditions in Southeastern Brazil. Geoderma 2016, 267, 65–77. [Google Scholar] [CrossRef]
- Wadoux, A.; Minasny, B.; Mcbratney, A. Machine Learning for Digital Soil Mapping: Applications, Challenges and Suggested Solutions. Earth-Sci. Rev. 2020, 210, 103359. [Google Scholar] [CrossRef]
- World Reference Base for Soil Resources 2014: International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; FAO: Rome, Italy, 2014; ISBN 978-92-5-108369-7.
- Keys to Soil Taxonomy | NRCS Soils. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/detail/soils/survey/class/taxonomy/?cid=nrcs142p2_053580 (accessed on 4 September 2022).
- Infoteca-e: Manual de Métodos de Análise de Solo. Available online: https://www.infoteca.cnptia.embrapa.br/handle/doc/1085209 (accessed on 5 September 2022).
- SAGA—System for Automated Geoscientific Analyses. Available online: https://saga-gis.sourceforge.io/en/index.html (accessed on 4 September 2022).
- Garson, G.D. Testing statistical assumptions; Blue Book Series; Statistical Associates Publishing: Hillsborough, CA, USA, 2012. [Google Scholar]
- Gower, J.C. A General Coefficient of Similarity and Some of Its Properties. Biometrics 1971, 27, 857. [Google Scholar] [CrossRef]
- Mallavan, B.P.; Minasny, B.; McBratney, A.B. Homosoil, a Methodology for Quantitative Extrapolation of Soil Information Across the Globe. In Digital Soil Mapping: Bridging Research, Environmental Application, and Operation; Boettinger, J.L., Howell, D.W., Moore, A.C., Hartemink, A.E., Kienast-Brown, S., Eds.; Progress in Soil Science; Springer: Dordrecht, The Netherlands, 2010; pp. 137–150. ISBN 978-90-481-8863-5. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, R.A. Classification and Regression Trees (CART); Wadsworth International: Belmont, CA, USA, 1984; Available online: https://www.routledge.com/Classification-and-Regression-Trees/Breiman-Friedman-Stone-Olshen/p/book/9780412048418 (accessed on 27 May 2021).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Nascimento, R.F.F.; Alcântara, E.H.; Kampel, M.; Stech, J.L.; Moraes, E.M.L.; Fonseca, L.M.G. O Algoritmo Support Vector Machines (SVM): Avaliação Da Separação Ótima de Classes Em Imagens CCD-CBERS-2. Available online: http://marte.sid.inpe.br/col/dpi.inpe.br/sbsr%4080/2008/10.20.10.59/doc/2079-2086.pdf (accessed on 7 January 2021).
- R Development Core Team. R: A Language and Environment for Statistical Computing. Version 3.1.1; R Foundation for Statistical Computing: Vienna, Austria, 2018; ISBN 3-900051-07-0. Available online: http://www.R-Project.Org (accessed on 1 June 2022).
- Maino, A.; Alberi, M.; Anceschi, E.; Chiarelli, E.; Cicala, L.; Colonna, T.; De Cesare, M.; Guastaldi, E.; Lopane, N.; Mantovani, F.; et al. Airborne Radiometric Surveys and Machine Learning Algorithms for Revealing Soil Texture. Remote Sens. 2022, 14, 3814. [Google Scholar] [CrossRef]
- Niang, M.A.; Nolin, M.C.; Jégo, G.; Perron, I. Digital Mapping of Soil Texture Using RADARSAT-2 Polarimetric Synthetic Aperture Radar Data. Soil Sci. Soc. Am. J. 2014, 78, 673–684. [Google Scholar] [CrossRef]
- Bousbih, S.; Zribi, M.; Pelletier, C.; Gorrab, A.; Lili-Chabaane, Z.; Baghdadi, N.; Ben Aissa, N.; Mougenot, B. Soil Texture Estimation Using Radar and Optical Data from Sentinel-1 and Sentinel-2. Remote Sens. 2019, 11, 1520. [Google Scholar] [CrossRef]
- Tomasella, J.; Hodnett, M.; Rossato, L. Pedotransfer Functions for the Estimation of Soil Water Retention in Brazilian Soils. Soil Sci. Soc. Am. J. 2000, 64, 327–338. [Google Scholar] [CrossRef]
- Villela, A.L.O. Mapeamento Digital de Solos da Formação Solimões Sob Floresta Tropical Amazônica. Ph.D. Thesis, Agronomia-Ciência do Solo, Universidade Federal Rural do Rio de Janeiro, Rio de Janeiro, Brazil, 2013. [Google Scholar]
- Adhikari, K.; Kheir, R.B.; Greve, M.B.; Bøcher, P.K.; Malone, B.P.; Minasny, B.; McBratney, A.B.; Greve, M.H. High-Resolution 3-D Mapping of Soil Texture in Denmark. Soil Sci. Soc. Am. J. 2013, 77, 860–876. [Google Scholar] [CrossRef]
- Santos, J.R.; Freitas, C.C.; Araujo, L.S.; Dutra, L.V.; Mura, J.C.; Gama, F.F.; Soler, L.S.; Sant’Anna, S.J.S. Airborne P-Band SAR Applied to the Aboveground Biomass Studies in the Brazilian Tropical Rainforest. Remote Sens. Environ. 2003, 87, 482–493. [Google Scholar] [CrossRef]
- Tiwari, R.; Singh, R.K.; Chauhan, D.S.; Singh, O.P.; Prakash, R.; Singh, D. Microwave Scattering for Soil Texture at X-Band and Its Retrieval Using Genetic Algorithm. Adv. Remote Sens. 2014, 3, 120–127. [Google Scholar] [CrossRef][Green Version]
- Prakash, R.; Singh, D.; Pathak, N.P. Microwave Specular Scattering Response of Soil Texture at X-Band. Adv. Space Res. 2009, 44, 801–814. [Google Scholar] [CrossRef]


| SiBCS a | Soil Taxonomy b | WRB b | n | Percent (%) |
|---|---|---|---|---|
| Argissolo Amarelo | Ultisols | Acrisols; Lixisols | 41 | 27.15 |
| Argissolo Vermelho | Utisols (Typic Rhodustults) | Acrisols; Lixisols | 2 | 1.32 |
| Argissolo Vermelho Amarelo | Ultisols | Acrisols; Lixisols | 29 | 19.20 |
| Argissolo Acizentado | Ultisol (Hapludult) | Haplic Lixisol | 3 | 1.98 |
| Cambissolo Háplico | Inceptisols | Cambisols | 49 | 32.45 |
| Cambissolo Flúvico | Entisols (Fluvents) | Fluvisols | 2 | 1.32 |
| Espodossolos Humilúvicos | Spodosols (Alorthods) | Podzols | 1 | 0.66 |
| Espodossolos Ferri-Humilúvicos | Spodosols (Orthods) | Podzols | 4 | 2.65 |
| Neossolo Quartzarênico | Entisols (Quartzipsamments) | Arenosols | 1 | 0.66 |
| Neossolos Flúvicos | Entisols (Fluvents) | Fluvisols | 2 | 1.32 |
| Planossolo Háplico | Ultisols (Albaquults) | Planosols | 2 | 1.32 |
| Gleissolos Háplicos | Entisols (Aquents) | Gleysols; Stagnosols | 14 | 9.27 |
| Gleissolos Melânicos | Entisols (Fluvaquentic Humaquepts) | Umbric Gleysols | 1 | 0.66 |
| Total | 151 | 100 |
| Algorithms | Hyperparameters | Definition | Tuning |
|---|---|---|---|
| RT | cp | A non-negative number for complexity parameter. | 0.001–0.01 |
| method | ANOVA | anova | |
| RF | mtry | number of variables used to produce each tree | 1–10 |
| ntree | the number of trees (default: 500) | 100–1000 | |
| nodesize | the minimum number of data points in each terminal node | 5 | |
| SVM | Kernel type | the kernel function | polynomial |
| type | svm can be used as a classification machine, as a regression machine, or for novelty detection. Depending on whether y is a factor or not, the default setting for type is C-classification or eps-regression, respectively, but may be overwritten by setting an explicit value. | ‘nu-regression’ or ‘eps-regression’ | |
| degree | parameter needed for kernel of type polynomial (default: 3) | 2–3 | |
| cost | The cost of predicting a sample within or on the wrong side of the margin. | 0–10 | |
| gamma | parameter needed for all kernels except linear (default: 1/(data dimension)) | 1 | |
| coef0 | parameter needed for kernels of type polynomial and sigmoid (default: 0) | 0 | |
| tolerance | tolerance of termination criterion (default: 0.001) | 0.001 |
| Variables | Dataset | n | Min | Max | Mean | Median | SD | Sk | K | CV (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| Sand Surf (g kg−1) | W | 151 | 80 | 918 | 458 | 437 | 156 | 0.36 | −0.11 | 34 |
| T(RA) | 114 | 182 | 918 | 468 | 450 | 154 | 0.48 | −0.07 | 32 | |
| V(RA) | 37 | 80 | 793 | 428 | 409 | 162 | 0.11 | −0.63 | 37 | |
| VU | 21 | 225 | 721 | 425 | 401 | 144 | 0.46 | −0.99 | - | |
| VA | 11 | 80 | 793 | 507 | 549 | 176 | −0.89 | 0.77 | - | |
| VJ | 5 | 151 | 360 | 267 | 273 | 75 | −0.36 | −1.38 | - | |
| T(TA) | 114 | 80 | 883 | 451 | 435 | 150 | 0.21 | −0.36 | 33 | |
| V(TA) | 37 | 208 | 918 | 481 | 460 | 173 | 0.59 | −0.19 | 35 | |
| Sand Sub (g kg−1) | W | 151 | 44 | 855 | 353 | 314 | 160 | 0.50 | −0.16 | 45 |
| T(RA) | 114 | 81 | 855 | 351 | 307 | 155 | 0.65 | 0.24 | 44 | |
| V(RA) | 37 | 44 | 695 | 357 | 338 | 178 | 0.16 | −1.09 | 49 | |
| VU | 21 | 86 | 674 | 342 | 314 | 169 | 0.41 | −1.00 | - | |
| VA | 11 | 44 | 695 | 460 | 493 | 172 | −0.97 | 0.51 | - | |
| VJ | 5 | 99 | 279 | 192 | 201 | 64 | −0.12 | −1.45 | - | |
| T(TA) | 114 | 44 | 695 | 337 | 308 | 145 | 0.24 | −0.75 | 43 | |
| V(TA) | 37 | 102 | 855 | 402 | 381 | 193 | 0.54 | −0.65 | 48 | |
| Silt Surf (g kg−1) | W | 151 | 26 | 792 | 389 | 375 | 145 | 0.16 | −0.27 | 37 |
| T(RA) | 114 | 26 | 687 | 364 | 351 | 131 | 0.03 | −0.12 | 36 | |
| V(RA) | 37 | 155 | 792 | 466 | 481 | 160 | −0.11 | −0.94 | 34 | |
| VU | 21 | 155 | 688 | 476 | 481 | 142 | −0.42 | −0.59 | - | |
| VA | 11 | 202 | 534 | 354 | 321 | 122 | 0.19 | −1.70 | - | |
| VJ | 5 | 597 | 792 | 668 | 643 | 78 | 0.56 | −1.59 | - | |
| T(TA) | 114 | 58 | 792 | 398 | 378 | 139 | 0.21 | −0.40 | 35 | |
| V(TA) | 37 | 26 | 696 | 364 | 350 | 160 | 0.17 | −0.32 | 44 | |
| Silt Sub (g kg−1) | W | 151 | 84 | 600 | 339 | 340 | 105 | 0.05 | −0.21 | 31 |
| T(RA) | 114 | 84 | 600 | 332 | 328 | 101 | −0.04 | 0.01 | 30 | |
| V(RA) | 37 | 168 | 570 | 361 | 349 | 115 | 0.14 | −1.05 | 32 | |
| VU | 21 | 191 | 570 | 359 | 343 | 113 | 0.39 | −0.87 | - | |
| VA | 11 | 168 | 486 | 309 | 303 | 104 | 0.19 | −1.42 | - | |
| VJ | 5 | 388 | 551 | 480 | 479 | 61 | −0.30 | −1.61 | - | |
| T(TA) | 114 | 84 | 600 | 349 | 349 | 100 | 0.07 | −0.21 | 29 | |
| V(TA) | 37 | 112 | 582 | 309 | 306 | 116 | 0.23 | −0.43 | 37 | |
| Clay Surf (g kg−1) | W | 151 | 4 | 500 | 152 | 140 | 86 | 0.87 | 1.12 | 56 |
| T(RA) | 114 | 34 | 500 | 169 | 155 | 82 | 0.79 | 1.08 | 48 | |
| V(RA) | 37 | 4 | 423 | 99 | 78 | 77 | 1.99 | 5.82 | 78 | |
| VU | 21 | 6 | 203 | 98 | 86 | 51 | 0.23 | −0.65 | - | |
| VA | 11 | 4 | 423 | 118 | 73 | 121 | 1.34 | 0.83 | - | |
| VJ | 5 | 27 | 130 | 64 | 57 | 40 | 0.66 | −1.37 | - | |
| T(TA) | 114 | 4 | 500 | 152 | 139 | 90 | 0.87 | 1.10 | 59 | |
| V(TA) | 37 | 39 | 351 | 154 | 142 | 74 | 0.81 | 0.33 | 48 | |
| Clay Sub (g kg−1) | W | 151 | 13 | 573 | 308 | 326 | 111 | −0.28 | −0.27 | 36 |
| T(RA) | 114 | 13 | 530 | 314 | 330 | 108 | −0.60 | 0.00 | 34 | |
| V(RA) | 37 | 70 | 573 | 288 | 267 | 120 | 0.52 | −0.43 | 42 | |
| VU | 21 | 70 | 573 | 298 | 288 | 131 | 0.36 | −0.76 | - | |
| VA | 11 | 150 | 532 | 250 | 200 | 117 | 1.12 | 0.20 | - | |
| VJ | 5 | 259 | 410 | 327 | 340 | 60 | 0.13 | −1.86 | - | |
| T(TA) | 114 | 70 | 573 | 314 | 327 | 105 | −0.09 | −0.57 | 33 | |
| V(TA) | 37 | 13 | 530 | 289 | 317 | 127 | −0.49 | −0.46 | 44 |
| Reference Area (199,167 Pixels) | Urucu (11,209,198 Pixels) | |||||||||
| Covariates (Unity) | Mean | Median | SD | Min | Max | Mean | Median | SD | Min | Max |
| CI (d) | 0.03 | 0.59 | 16.80 | −94.51 | 96.07 | −0.0002 | 0.54 | 16.41 | −98.08 | 98.91 |
| TWI (d) | 7.66 | 7.56 | 1.06 | 4.61 | 12.30 | 8.07 | 7.98 | 1.23 | 4.33 | 12.54 |
| RSP (0–1) | 0.48 | 0.51 | 0.30 | 0 | 1 | 0.44 | 0.45 | 0.30 | 0 | 1 |
| CND (m) | 6.40 | 6.15 | 4.01 | 0 | 25.39 | 5.41 | 4.88 | 3.95 | 0 | 29.64 |
| CNBL (m) | 61.72 | 61.16 | 5.95 | 46.56 | 79.59 | 63.47 | 64.07 | 7.16 | 23.03 | 83.16 |
| MRVBF (d) | 5.73 | 9.38 | 4.52 | 0 | 9.98 | 6.69 | 9.82 | 4.33 | 0 | 9.98 |
| MRRFT (d) | 2.84 | 1.97 | 2.67 | 0 | 7.93 | 4.02 | 4.76 | 3.09 | 0 | 7.99 |
| CXI (d) | 51.34 | 52.41 | 7.63 | 0.15 | 69.19 | 50.29 | 51.85 | 8.89 | 0 | 73.19 |
| ASP (°) | 177.10 | 175.22 | 106.81 | 0 | 360 | 173.78 | 171.04 | 107.03 | 0 | 360 |
| LF (d) | 5.32 | 5.00 | 2.41 | 1.00 | 10.00 | 5.18 | 5.00 | 2.11 | 1.00 | 10.00 |
| ProfC (m−1) | −0 | −0 | 0 | −0.009 | 0.01 | −0 | 0 | 0 | −0.013 | 0.011 |
| PlanC (m−1) | 0.0 | 3.40 | 0.0 | −0.007 | 0.01 | 0 | 0 | 0 | −0.010 | 0.013 |
| SH (m) | 4.08 | 3.55 | 1.85 | 1.47 | 18.94 | 3.84 | 3.36 | 1.79 | 1.13 | 25.51 |
| MSP (%) | 0.27 | 0.25 | 0.17 | 0.00 | 0.82 | 0.25 | 0.23 | 0.16 | 0.00 | 0.85 |
| S (%) | 6.23 | 5.15 | 4.87 | 0.00 | 48.86 | 5.16 | 3.70 | 4.77 | 0.00 | 67.20 |
| MR (d) | 0.25 | 0.16 | 0.29 | 0.00 | 2.49 | 0.21 | 0.10 | 0.27 | 0.00 | 2.95 |
| FC (d) | 2451 | 2996 | 3090 | 400 | 81207 | 2347 | 1449 | 2956 | 400 | 14170 |
| P-band (σ°) | 0.43 | 0.43 | 0.07 | 0 | 0.99 | 0.44 | 0.44 | 0.06 | 0 | 0.90 |
| Araracanga (9,364,993 Pixels) | Juruá (11,730,902 Pixels) | |||||||||
| Covariates (Unity) | Mean | Median | SD | Min | Max | Mean | Median | SD | Min | Max |
| CI (d) | 0 | 0.49 | 16.45 | −98.78 | 99.01 | 0.00 | 0.78 | 18.10 | −99.21 | 99.40 |
| TWI (d) | 7.92 | 7.72 | 1.41 | 4.36 | 12.37 | 7.58 | 7.38 | 1.28 | 3.86 | 12.01 |
| RSP (0–1) | 0.41 | 0.41 | 0.31 | 0 | 1 | 0.35 | 0.32 | 0.29 | 0 | 1 |
| CND (m) | 6.01 | 5.32 | 4.83 | 0 | 33.92 | 4.45 | 3.42 | 4.08 | 0 | 40.50 |
| CNBL (m) | 63.93 | 65.28 | 8.85 | 34.16 | 85.97 | 76.03 | 77.62 | 8.40 | 49.88 | 95.63 |
| MRVBF (d) | 4.96 | 4.77 | 4.13 | 0 | 9.96 | 3.70 | 3.89 | 2.82 | 0 | 9.65 |
| MRRFT (d) | 3.37 | 2.67 | 3.15 | 0 | 9.73 | 6.53 | 9.36 | 4.19 | 0 | 9.98 |
| CXI (d) | 48.32 | 50.92 | 11.07 | 0 | 73.40 | 39.58 | 41.13 | 8.27 | 0 | 63.48 |
| ASP (°) | 171.04 | 168.26 | 109.06 | 0 | 360 | 168.08 | 166.38 | 109.74 | 0 | 360 |
| LF (d) | 5.26 | 5.00 | 2.32 | 1.00 | 10.00 | 5.32 | 5.00 | 2.03 | 1.00 | 10.00 |
| ProfC (m−1) | −0.0 | 0.0 | 0.0 | −0.011 | 0.012 | −0.0 | −0.0 | 0 | −0.014 | 0.016 |
| PlanC (m−1) | 0.0 | 0.0 | 0 | −0.012 | 0.011 | 0.0 | 0.0 | 0 | −0.013 | 0.018 |
| SH (m) | 4.18 | 3.59 | 2.11 | 1.16 | 27.33 | 3.62 | 3.12 | 1.73 | 1.14 | 32 |
| MSP (%) | 0.31 | 0.29 | 0.20 | 0 | 0.88 | 0.22 | 0.18 | 0.16 | 0 | 0.89 |
| S (%) | 5.81 | 4.25 | 5.34 | 0 | 50.21 | 5.39 | 4.02 | 5.24 | 0 | 76.92 |
| MR (d) | 0.24 | 0.11 | 0.32 | 0 | 3.01 | 0.18 | 0.00 | 0.27 | 0 | 4.23 |
| FC (d) | 2332 | 1421 | 2993 | 400 | 13304 | 1609 | 1059 | 1735 | 400 | 6948 |
| P-band (σ°) | 0.45 | 0.45 | 0.11 | 0 | 0.93 | 0.43 | 0.43 | 0.10 | 0 | 0.94 |
| RT | RF | SVM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Atributtes | Data | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE |
| Sand Surf PCS | T | 0.34 | 124 | 96 | 0.93 | 67 | 53 | 0.47 | 113 | 91 |
| VU | 0.09 | 144 | 117 | 0.24 | 131 | 113 | 0.07 | 141 | 125 | |
| VUA | 0.03 | 165 | 129 | 0.19 | 140 | 116 | 0.01 | 162 | 140 | |
| V | 0.01 | 176 | 135 | 0.24 | 144 | 120 | 0.08 | 173 | 149 | |
| VUJ | 0.03 | 166 | 128 | 0.31 | 138 | 119 | 0.12 | 162 | 141 | |
| Sand Surf WM | T | 0.36 | 122 | 96 | 0.94 | 67 | 53 | 0.57 | 106 | 86 |
| VU | 0.21 | 132 | 103 | 0.20 | 132 | 114 | 0.04 | 144 | 129 | |
| VUA | 0.06 | 164 | 128 | 0.18 | 141 | 116 | 0.20 | 140 | 118 | |
| V | 0.03 | 175 | 132 | 0.19 | 148 | 123 | 0.19 | 145 | 123 | |
| VUJ | 0.09 | 157 | 113 | 0.22 | 143 | 125 | 0.08 | 151 | 134 | |
| Sand Sub PCS | T | 0.45 | 114 | 90 | 0.92 | 63 | 50 | 0.47 | 113 | 95 |
| VU | 0.09 | 161 | 137 | 0.24 | 147 | 126 | 0.20 | 148 | 126 | |
| VUA | 0.01 | 181 | 152 | 0.15 | 163 | 140 | 0.18 | 166 | 141 | |
| V | 0.00 | 190 | 155 | 0.11 | 165 | 143 | 0.24 | 168 | 139 | |
| VUJ | 0.02 | 179 | 145 | 0.17 | 154 | 132 | 0.21 | 155 | 127 | |
| Sand Sub WM | T | 0.48 | 111 | 87 | 0.92 | 64 | 51 | 0.57 | 105 | 86 |
| VU | 0.14 | 159 | 133 | 0.36 | 137 | 113 | 0.13 | 154 | 128 | |
| VUA | 0.05 | 181 | 155 | 0.25 | 158 | 134 | 0.15 | 173 | 146 | |
| V | 0.00 | 194 | 163 | 0.16 | 162 | 138 | 0.17 | 167 | 141 | |
| VUJ | 0.03 | 183 | 149 | 0.25 | 147 | 123 | 0.17 | 148 | 124 | |
| RT | RF | SVM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Atributtes | Data | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE |
| Silt Surf PCS | T | 0.49 | 93 | 72 | 0.91 | 56 | 43 | 0.50 | 93 | 71 |
| VU | 0.19 | 163 | 138 | 0.58 | 130 | 112 | 0.33 | 130 | 107 | |
| VUA | 0.07 | 154 | 129 | 0.37 | 120 | 99 | 0.17 | 175 | 123 | |
| V | 0.07 | 175 | 144 | 0.36 | 141 | 114 | 0.28 | 185 | 133 | |
| VUJ | 0.18 | 189 | 158 | 0.52 | 155 | 131 | 0.38 | 156 | 124 | |
| Silt Surf WM | T | 0.46 | 95 | 73 | 0.92 | 55 | 42. | 0.58 | 87 | 65 |
| VU | 0.26 | 163 | 144 | 0.46 | 139 | 120 | 0.24 | 143 | 122 | |
| VUA | 0.06 | 157 | 136 | 0.26 | 128 | 106 | 0.13 | 149 | 119 | |
| V | 0.08 | 174 | 149 | 0.26 | 149 | 122 | 0.22 | 159 | 128 | |
| VUJ | 0.26 | 186 | 161 | 0.42 | 164 | 140 | 0.26 | 158 | 134 | |
| Silt Sub PCS | T | 0.47 | 73 | 58 | 0.91 | 43 | 32 | 0.39 | 79 | 61 |
| VU | 0.36 | 90 | 72 | 0.51 | 89 | 71 | 0.38 | 91 | 77 | |
| VUA | 0.38 | 86 | 72 | 0.41 | 88 | 73 | 0.33 | 111 | 91 | |
| V | 0.26 | 99 | 80 | 0.46 | 89 | 74 | 0.39 | 131 | 101 | |
| VUJ | 0.22 | 106 | 83 | 0.56 | 90 | 73 | 0.39 | 126 | 93 | |
| Silt Sub WM | T | 0.49 | 72 | 57 | 0.92 | 43 | 32 | 0.53 | 72 | 56 |
| VU | 0.35 | 89 | 72 | 0.42 | 93 | 74 | 0.42 | 84 | 67 | |
| VUA | 0.33 | 89 | 73 | 0.31 | 93 | 76 | 0.39 | 91 | 76 | |
| V | 0.22 | 102 | 81 | 0.37 | 94 | 78 | 0.39 | 115 | 89 | |
| VUJ | 0.21 | 106 | 83 | 0.50 | 95 | 78 | 0.37 | 120 | 88 | |
| RT | RF | SVM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Atributtes | DATA | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE |
| Clay Surf PCS | T | 0.53 | 55 | 41 | 0.91 | 31 | 23 | 0.47 | 61 | 45 |
| VU | 0.09 | 73 | 59 | 0.24 | 71 | 59 | 0.21 | 67 | 53 | |
| VUA | 0.04 | 90 | 70 | 0.02 | 92 | 72 | 0.08 | 115 | 73 | |
| V | 0.03 | 90 | 73 | 0.02 | 92 | 73 | 0.04 | 111 | 73 | |
| VUJ | 0.06 | 78 | 65 | 0.19 | 76 | 64 | 0.17 | 69 | 57 | |
| Clay Surf WM | T | 0.54 | 54 | 40 | 0.92 | 31 | 23 | 0.56 | 56 | 41 |
| VU | 0.08 | 74 | 59 | 0.18 | 71 | 59 | 0.27 | 65 | 50 | |
| VUA | 0.04 | 89 | 70 | 0.02 | 91 | 71 | 0.17 | 82 | 61 | |
| V | 0.03 | 90 | 73 | 0.02 | 91 | 72 | 0.10 | 96 | 72 | |
| VUJ | 0.05 | 78 | 66 | 0.15 | 75 | 63 | 0.15 | 91 | 68 | |
| Clay Sub PCS | T | 0.61 | 67 | 53 | 0.91 | 39 | 30 | 0.58 | 70 | 52 |
| VU | 0.16 | 119 | 90 | 0.20 | 114 | 86 | 0.14 | 120 | 93 | |
| VUA | 0.02 | 136 | 101 | 0.08 | 122 | 95 | 0.17 | 117 | 95 | |
| V | 0.02 | 130 | 93 | 0.07 | 116 | 89 | 0.13 | 113 | 92 | |
| VUJ | 0.15 | 113 | 81 | 0.18 | 107 | 80 | 0.12 | 114 | 90 | |
| Clay Sub WM | T | 0.62 | 65 | 52 | 0.92 | 38 | 29 | 0.65 | 65 | 49 |
| VU | 0.02 | 138 | 103 | 0.18 | 115 | 87 | 0.07 | 128 | 99 | |
| VUA | 0.00 | 146 | 111 | 0.08 | 120 | 93 | 0.14 | 118 | 93 | |
| V | 0.00 | 141 | 104 | 0.07 | 114 | 88 | 0.03 | 152 | 116 | |
| VUJ | 0.03 | 131 | 95 | 0.17 | 108 | 81 | 0.02 | 170 | 131 | |
| RT | RF | SVM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Atributtes | Data | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE |
| Sand Surf PCS | T114 | 0.51 | 104 | 79 | 0.93 | 62 | 49 | 0.52 | 105 | 84 |
| V37 | 0.00 | 198 | 152 | 0.11 | 161 | 124 | 0.15 | 163 | 127 | |
| Sand Surf WM | T114 | 0.51 | 104 | 79 | 0.94 | 64 | 50 | 0.77 | 73 | 44 |
| V37 | 0.00 | 198 | 152 | 0.13 | 159 | 124 | 0.03 | 209 | 158 | |
| Sand Sub PCS | T114 | 0.54 | 97 | 80 | 0.93 | 58 | 47 | 0.40 | 113 | 94 |
| V37 | 0.03 | 202 | 148 | 0.23 | 174 | 137 | 0.21 | 180 | 138 | |
| Sand Sub WM | T114 | 0.55 | 97 | 80 | 0.95 | 59 | 48 | 0.81 | 64 | 41 |
| V37 | 0.03 | 202 | 148 | 0.22 | 177 | 145 | 0.19 | 207 | 162 | |
| Silt Surf PCS | T114 | 0.58 | 89 | 69 | 0.91 | 53 | 41 | 0.50 | 98 | 78 |
| V37 | 0.04 | 182 | 140 | 0.14 | 147 | 113 | 0.20 | 142 | 108 | |
| Silt Surf WM | T114 | 0.92 | 54 | 42 | 0.92 | 54 | 42 | 0.60 | 89 | 72 |
| V37 | 0.17 | 144 | 111 | 0.17 | 144 | 111 | 0.14 | 147 | 112 | |
| Silt Sub PCS | T114 | 0.49 | 71 | 57 | 0.91 | 39 | 31 | 0.42 | 76 | 61 |
| V37 | 0.06 | 123 | 97 | 0.03 | 120 | 98 | 0.29 | 102 | 79 | |
| Silt Sub WM | T114 | 0.51 | 69 | 55 | 0.92 | 38 | 30 | 0.55 | 69 | 54 |
| V37 | 0.04 | 126 | 99 | 0.06 | 116 | 94 | 0.21 | 107 | 84 | |
| Clay Surf PCS | T114 | 0.56 | 58 | 44 | 0.91 | 34 | 25 | 0.59 | 60 | 46 |
| V37 | 0.23 | 71 | 58 | 0.23 | 65 | 50 | 0.15 | 70 | 52 | |
| Clay Surf WM | T114 | 0.58 | 57 | 43 | 0.92 | 33 | 25 | 0.65 | 56 | 42 |
| V37 | 0.20 | 74 | 62 | 0.21 | 65 | 48 | 0.12 | 80 | 62 | |
| Clay Sub PCS | T114 | 0.54 | 70 | 55 | 0.93 | 38 | 30 | 0.57 | 70 | 56 |
| V37 | 0.19 | 117 | 94 | 0.31 | 107 | 81 | 0.29 | 114 | 92 | |
| Clay Sub WM | T114 | 0.51 | 73 | 58 | 0.93 | 39 | 30 | 0.61 | 68 | 53 |
| V37 | 0.21 | 116 | 93 | 0.30 | 107 | 82 | 0.26 | 122 | 94 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, A.C.d.S.; Ceddia, M.B.; Costa, E.M.; Pinheiro, É.F.M.; Nascimento, M.M.d.; Vasques, G.M. Use of Airborne Radar Images and Machine Learning Algorithms to Map Soil Clay, Silt, and Sand Contents in Remote Areas under the Amazon Rainforest. Remote Sens. 2022, 14, 5711. https://doi.org/10.3390/rs14225711
Ferreira ACdS, Ceddia MB, Costa EM, Pinheiro ÉFM, Nascimento MMd, Vasques GM. Use of Airborne Radar Images and Machine Learning Algorithms to Map Soil Clay, Silt, and Sand Contents in Remote Areas under the Amazon Rainforest. Remote Sensing. 2022; 14(22):5711. https://doi.org/10.3390/rs14225711
Chicago/Turabian StyleFerreira, Ana Carolina de S., Marcos B. Ceddia, Elias M. Costa, Érika F. M. Pinheiro, Mariana Melo do Nascimento, and Gustavo M. Vasques. 2022. "Use of Airborne Radar Images and Machine Learning Algorithms to Map Soil Clay, Silt, and Sand Contents in Remote Areas under the Amazon Rainforest" Remote Sensing 14, no. 22: 5711. https://doi.org/10.3390/rs14225711
APA StyleFerreira, A. C. d. S., Ceddia, M. B., Costa, E. M., Pinheiro, É. F. M., Nascimento, M. M. d., & Vasques, G. M. (2022). Use of Airborne Radar Images and Machine Learning Algorithms to Map Soil Clay, Silt, and Sand Contents in Remote Areas under the Amazon Rainforest. Remote Sensing, 14(22), 5711. https://doi.org/10.3390/rs14225711








