Coastal High-Temporal Sea-Surface Altimetry Using the Posterior Error Estimations of Ionosphere-Free PPP and Information Fusion for Multi-GNSS Retrievals
Abstract
1. Introduction
2. Materials and Methods
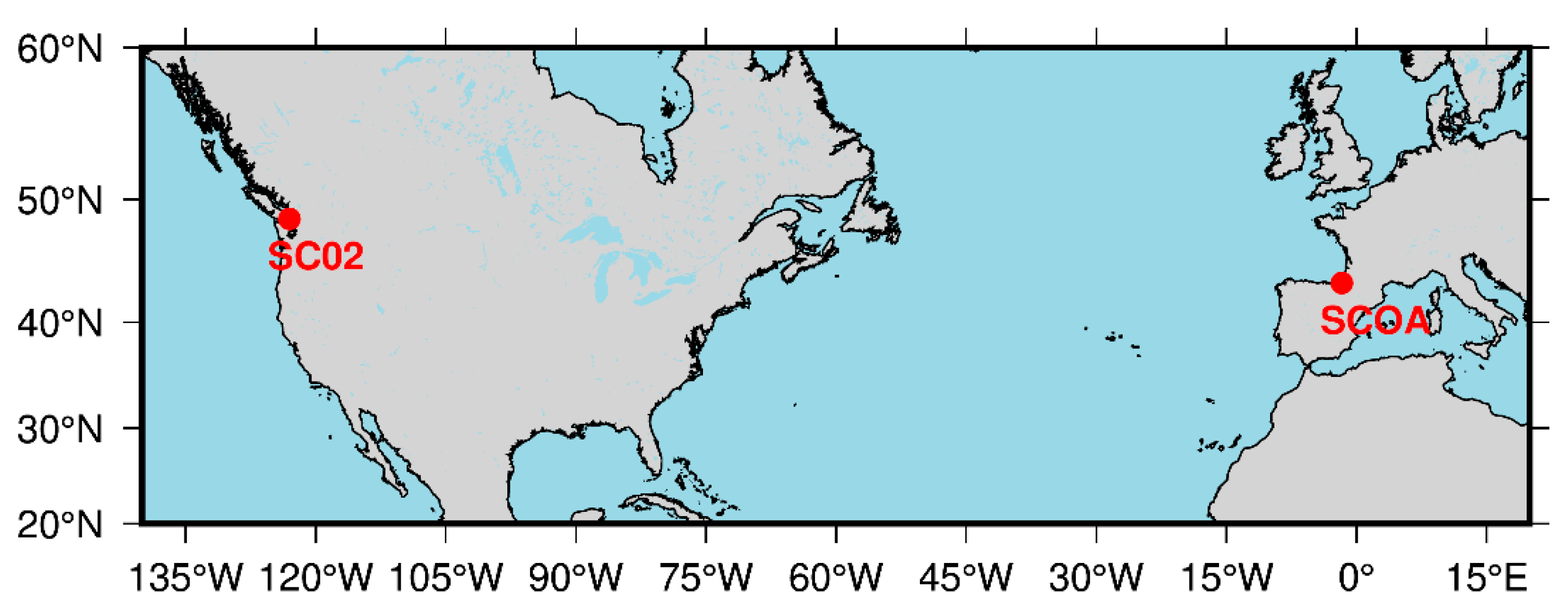
2.1. Site Description and Experimental Dataset
2.1.1. Site-Specific Summary

2.1.2. Characteristics of Signal
2.1.3. Selection of Azimuth and Elevation
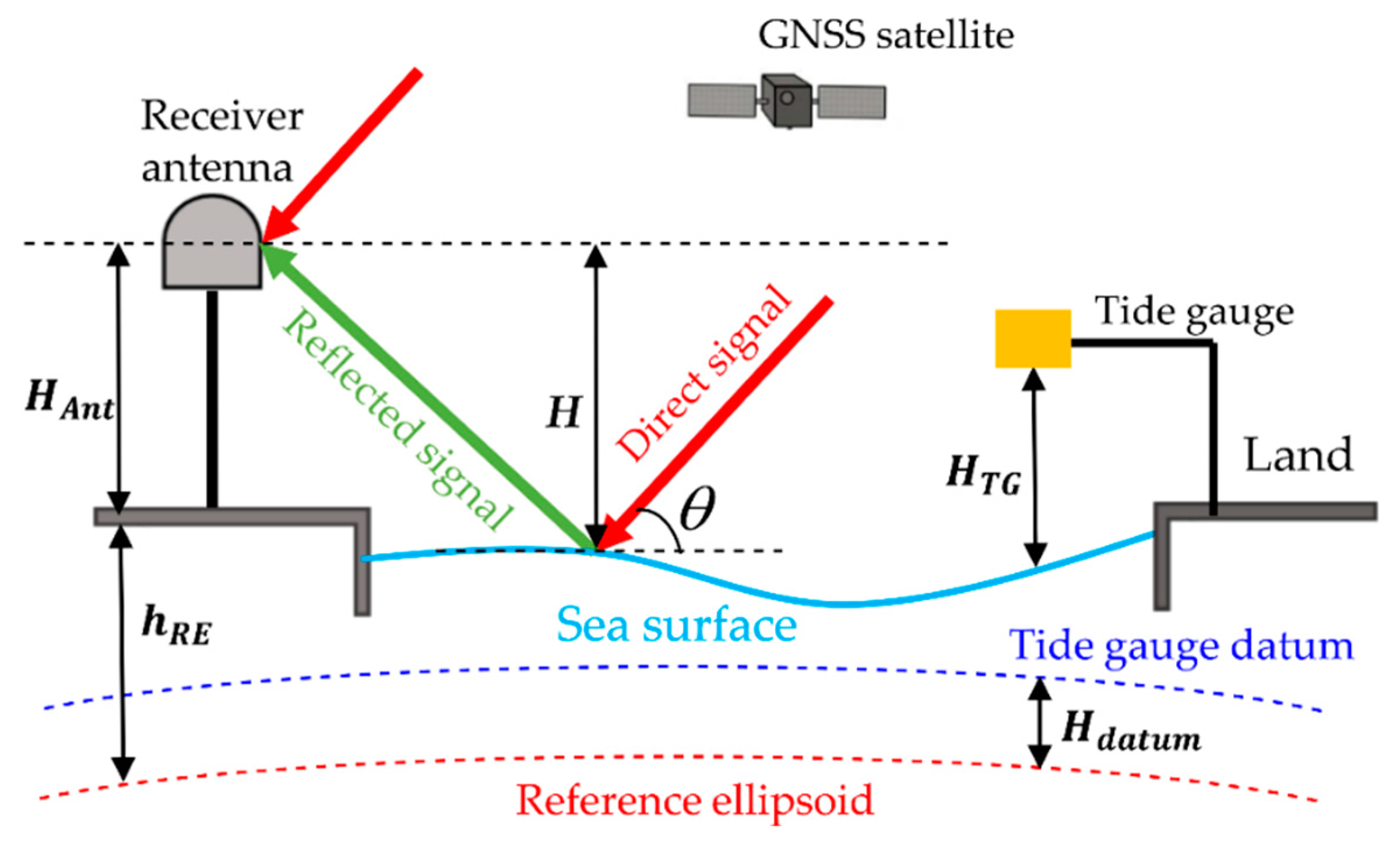
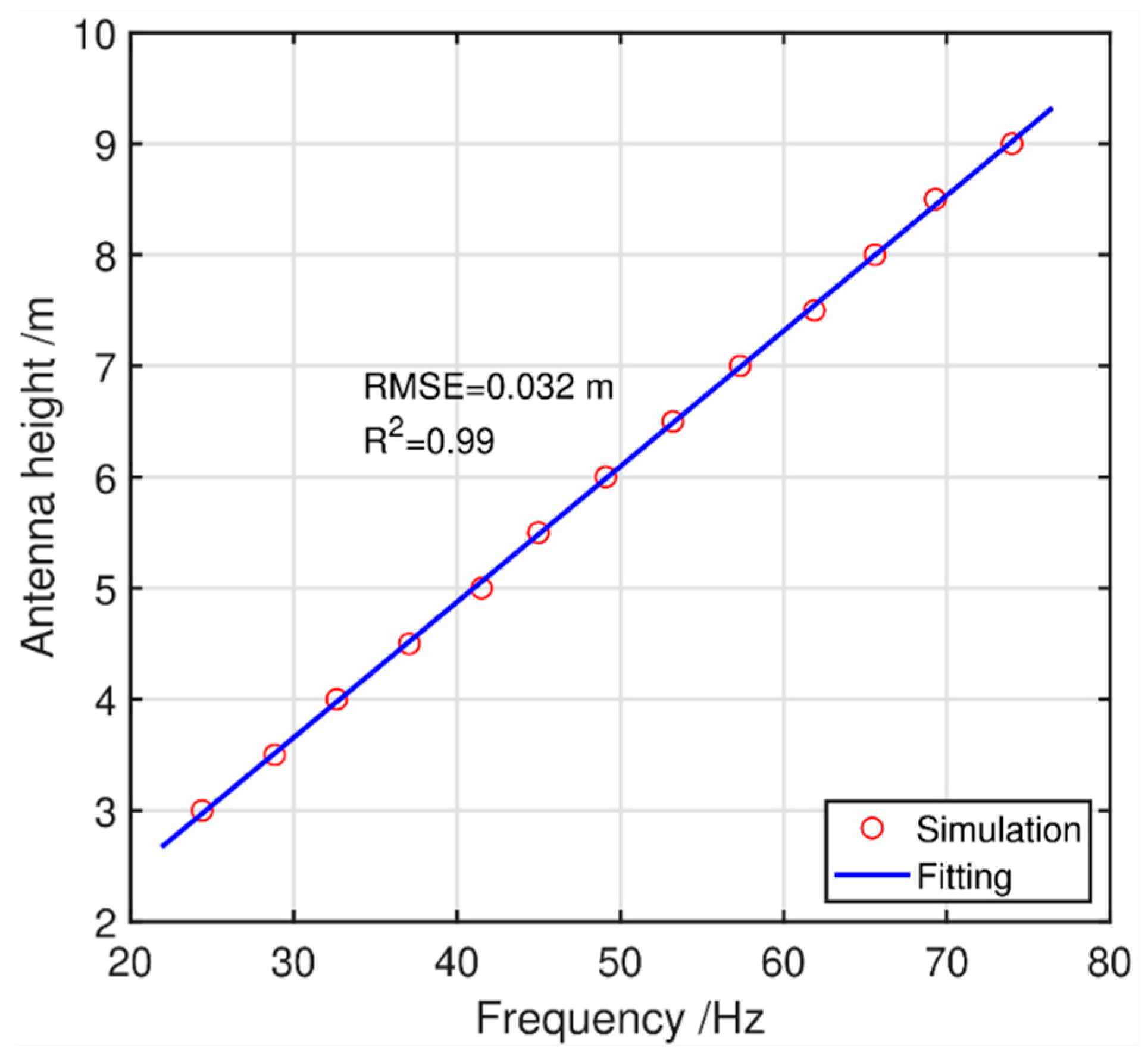
2.2. Basic Principle of GNSS-IR-Based Sea Surface Altimetry
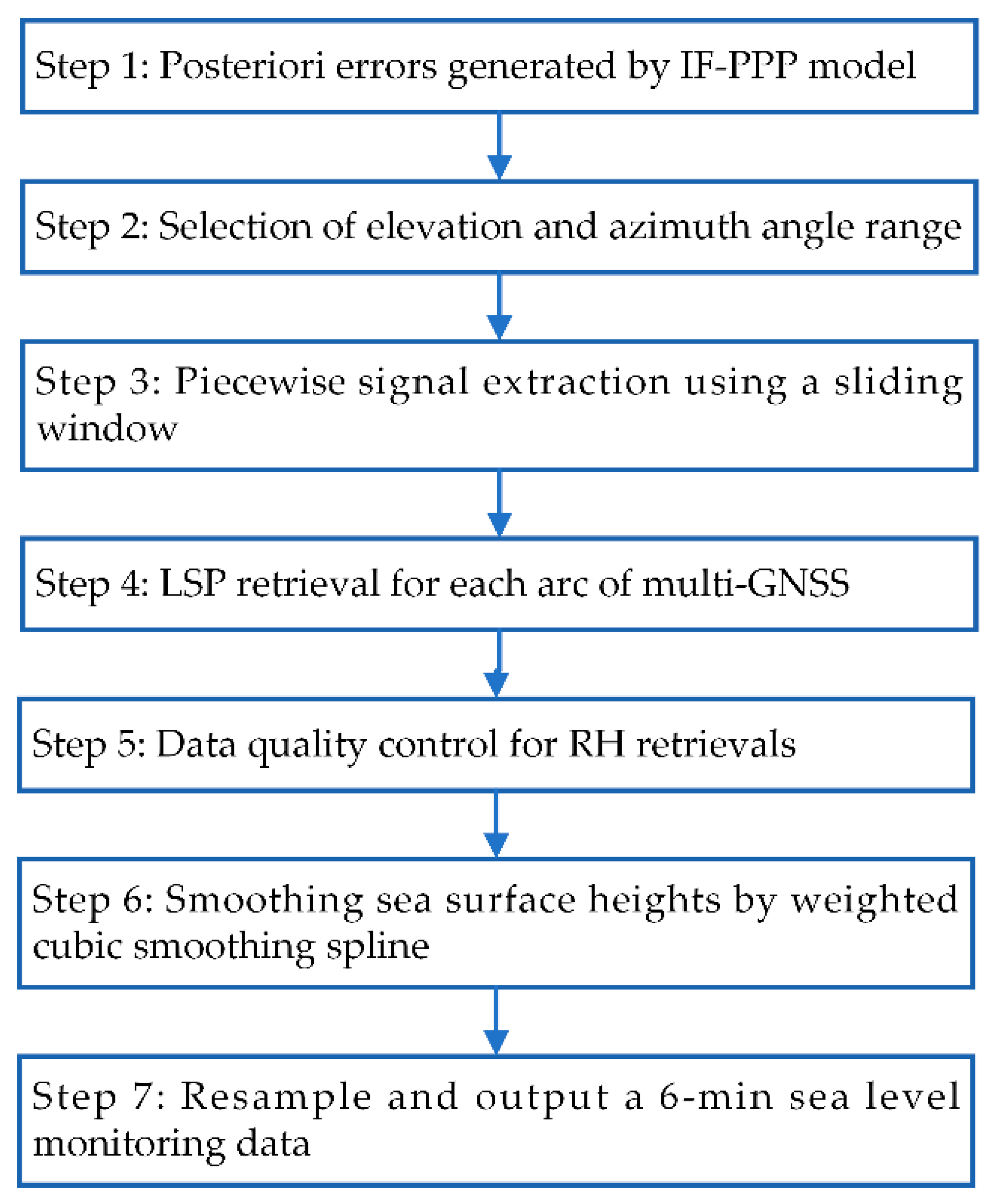
2.3. Strategy of Data Processing
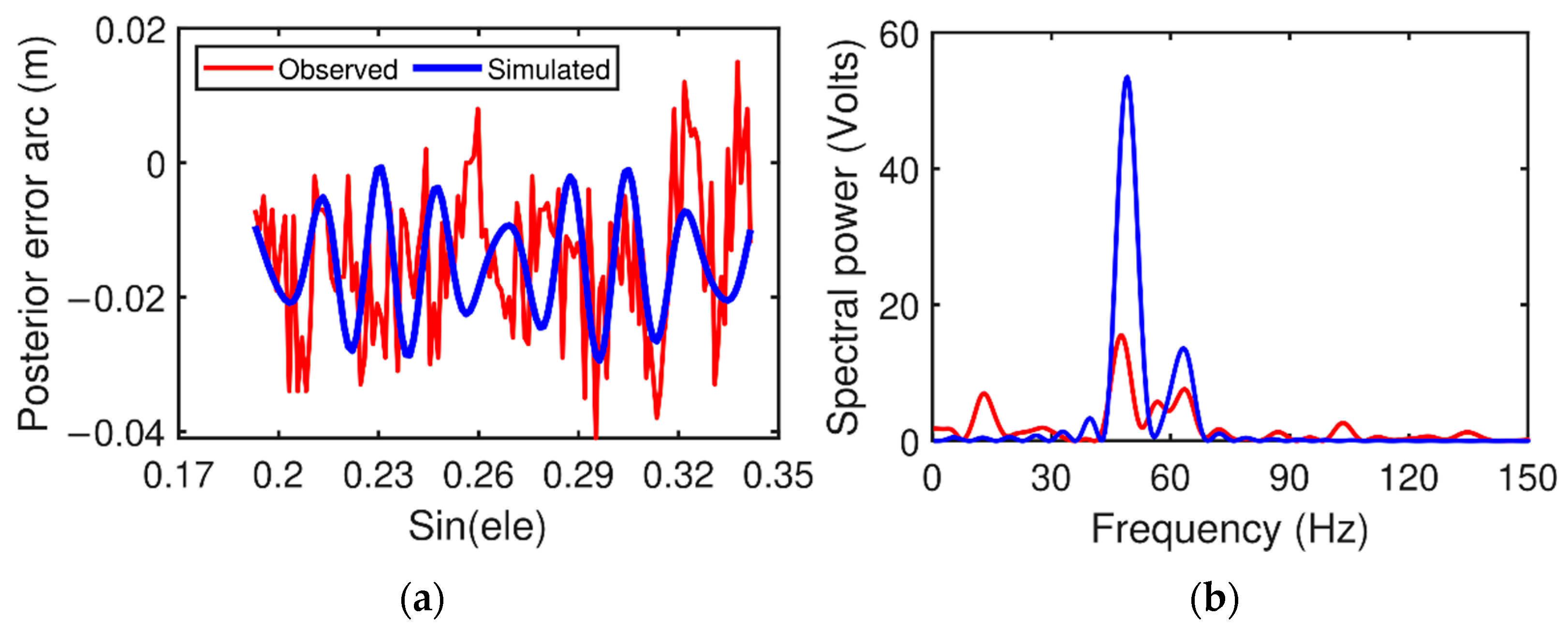
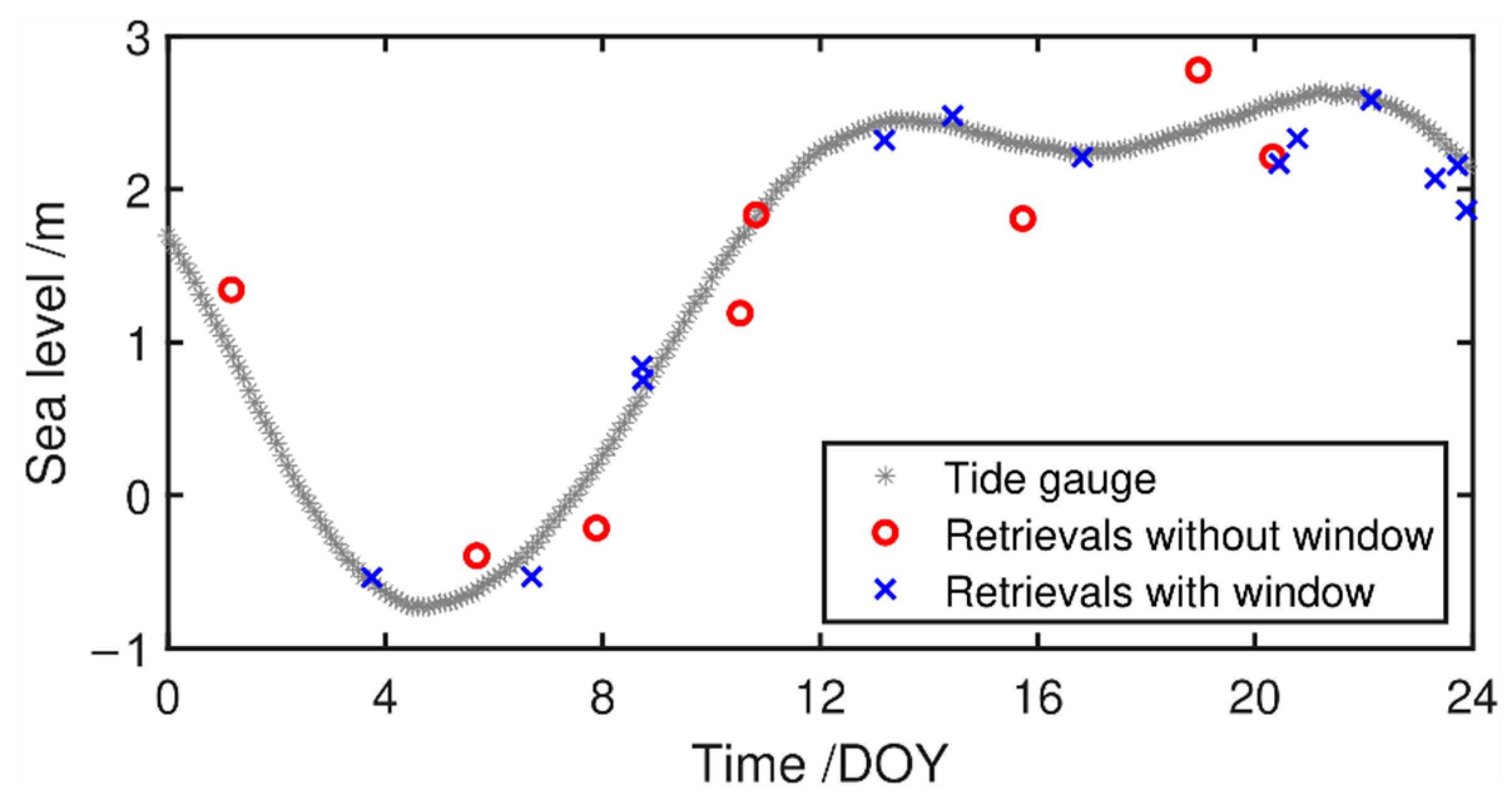
2.3.1. Signal Extraction Based on a Sliding Window
2.3.2. Data Quality Control for RH Retrievals
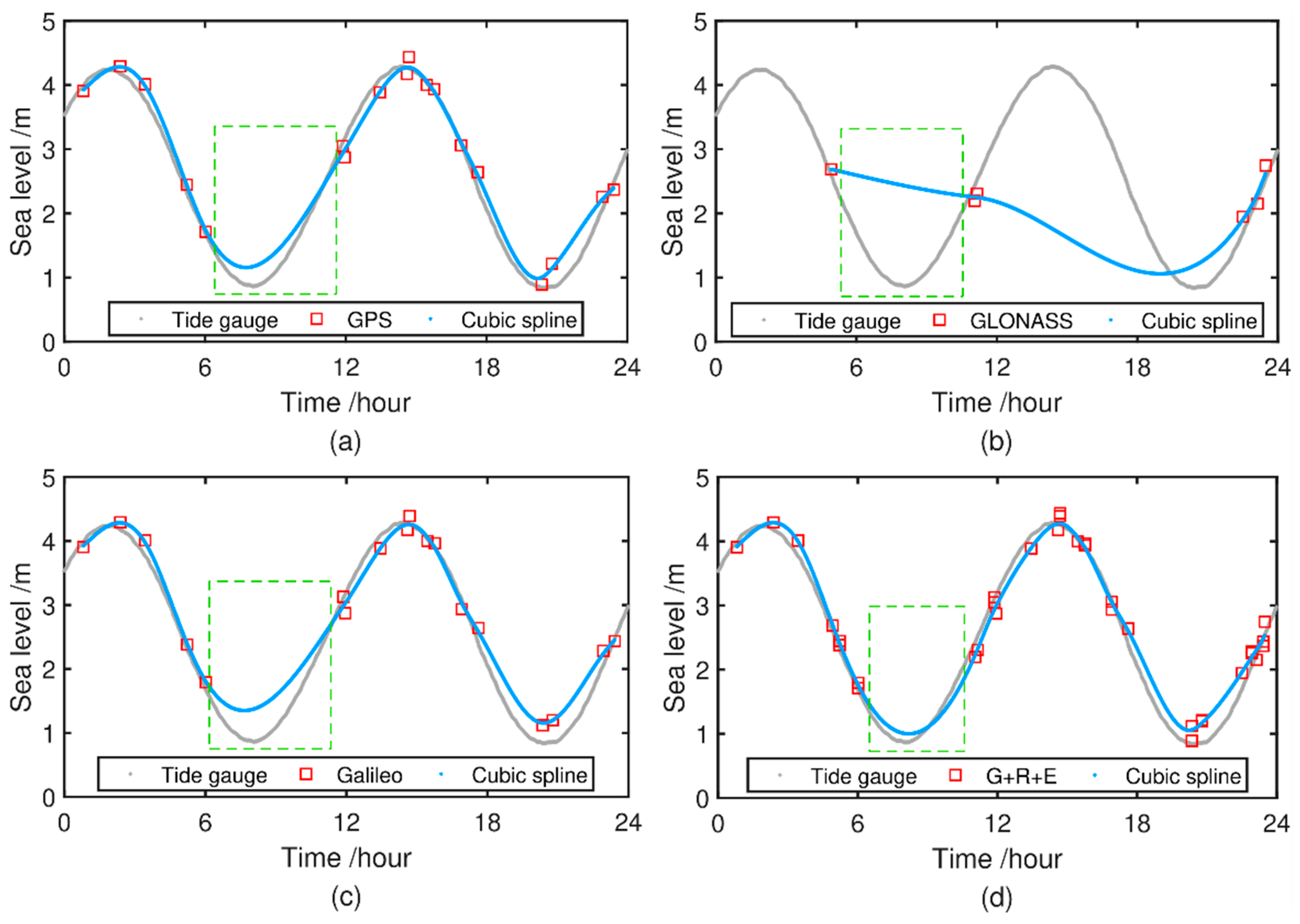
2.3.3. Smoothing Retrievals by Weighted Cubic Smoothing Spline
3. Results and Discussions
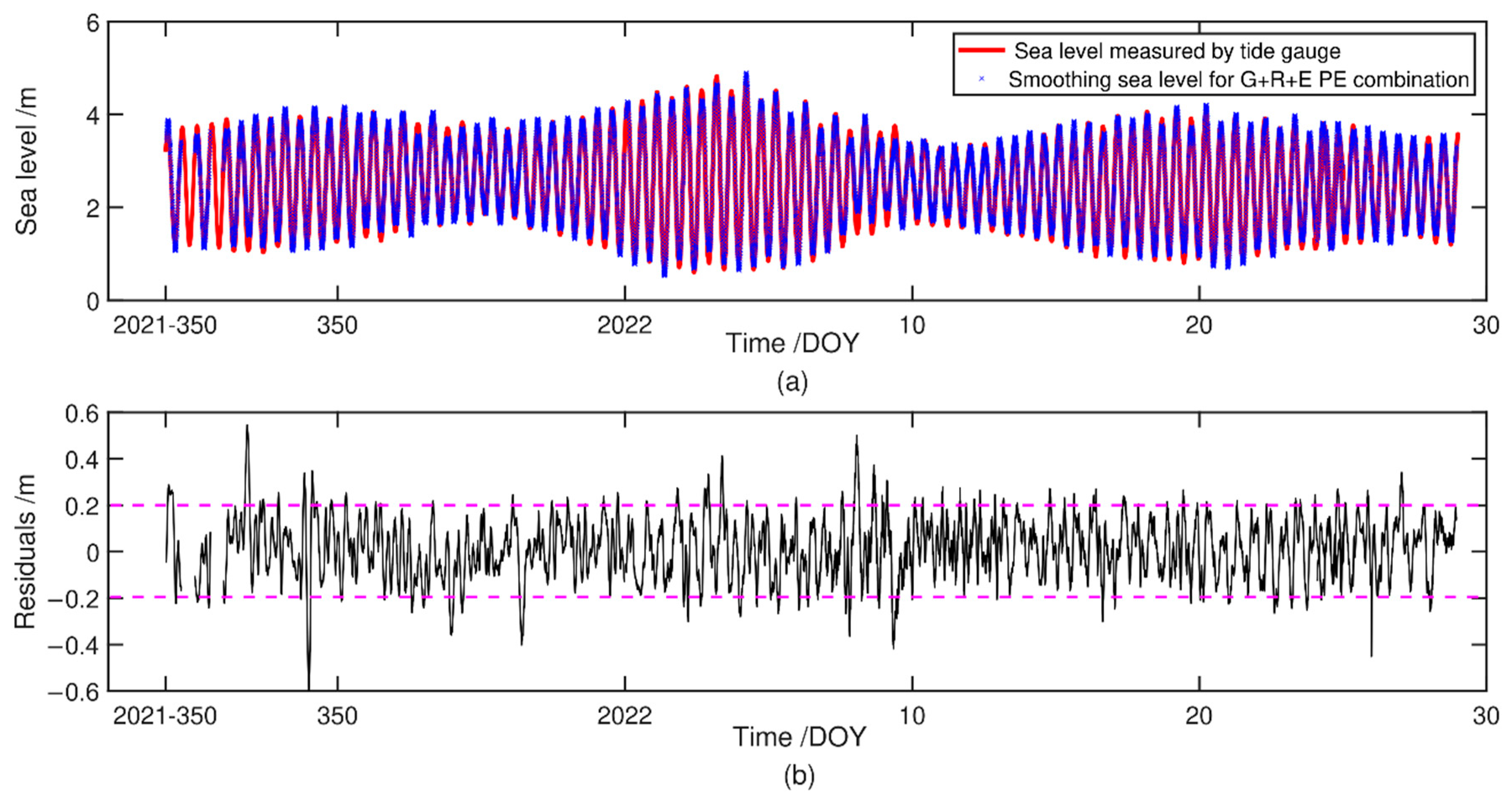
3.1. Experimental Results in Friday Harbor, USA
3.2. Experimental Results in Socoa, France
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, W.; Zhong, M. Global sea level variations from altimetry, GRACE and Argo data over 2005–2014. Geod. Geodyn. 2015, 6, 274–279. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Cazenave, A. Sea-level rise and its impact on coastal zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef] [PubMed]
- Cipollini, P.; Calafat, F.M.; Jevrejeva, S.; Melet, A.; Prandi, P. Monitoring Sea Level in the Coastal Zone with Satellite Altimetry and Tide Gauges. Surv. Geophys. 2017, 38, 33–57. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Shen, X.; Li, D.; Li, S. On Civil-Military Integrated Space-Based Real-Time Information Service System. Geomat. Inform. Sci. Wuhan Univ. Chin. 2017, 42, 1501–1505. [Google Scholar] [CrossRef]
- Huang, L.; Mo, Z.; Xie, S.; Liu, L.; Chen, J.; Kang, C.; Wang, S. Spatiotemporal characteristics of GNSS-derived precipitable water vapor during heavy rainfall events in Guilin, China. Satell. Navig. 2021, 2, 13. [Google Scholar] [CrossRef]
- Jin, S.; Qian, X.; Wu, X. Sea level change from BeiDou Navigation Satellite System-Reflectometry (BDS-R): First results and evaluation. Glob. Planet. Chang. 2017, 149, 20–25. [Google Scholar] [CrossRef]
- Garrison, J.L.; Komjathy, A.; Zavorotny, V.U.; Katzberg, S.J. Wind speed measurement using forward scattered GPS signals. IEEE Trans. Geosci. Remote Sens. 2002, 40, 50–65. [Google Scholar] [CrossRef]
- Löfgren, J.S.; Haas, R. Sea level measurements using multi-frequency GPS and GLONASS observations. EURASIP J. Adv. Signal Process 2014, 2014, 50. [Google Scholar] [CrossRef]
- Roussel, N.; Ramillien, G.; Frappart, F.; Darrozes, J.; Gay, A.; Biancale, R.; Striebig, N.; Hanquiez, V.; Bertin, X.; Allain, D. Sea level monitoring and sea state estimate using a single geodetic receiver. Remote Sens. Environ. 2015, 171, 261–277. [Google Scholar] [CrossRef]
- Song, M.; He, X.; Wang, X.; Jia, D.; Xiao, R.; Shi, H.; Wu, Y. Study on the Exploration of Spaceborne GNSS-R Raw Data Focusing on Altimetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6142–6154. [Google Scholar] [CrossRef]
- Martin-Neira, M. A pasive reflectometry and interferometry system (PARIS) application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Martin-Neira, M.; Caparrini, M.; Font-Rossello, J.; Lannelongue, S.; Vallmitjana, C.S. The PARIS concept: An experimental demonstration of sea surface altimetry using GPS reflected signals. IEEE Trans. Geosci. Remote Sens. 2001, 39, 142–150. [Google Scholar] [CrossRef]
- Löfgren, J.S.; Haas, R.; Scherneck, H.-G.; Bos, M.S. Three months of local sea level derived from reflected GNSS signals. Radio Sci. 2011, 46, RS0C05. [Google Scholar] [CrossRef]
- Anderson, K.D. Determination of Water Level and Tides Using Interferometric Observations of GPS Signals. J. Atmos. Ocean. Technol. 2000, 17, 1118–1127. [Google Scholar] [CrossRef]
- Yu, K.; Ban, W.; Zhang, X.; Yu, X. Snow Depth Estimation Based on Multipath Phase Combination of GPS Triple-Frequency Signals. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5100–5109. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.; Bilich, A.; Axelrad, P.; Braun, J. Using GPS multipath to measure soil moisture fluctuations: Initial results. GPS Solut. 2008, 12, 173–177. [Google Scholar] [CrossRef]
- Larson, K.M.; Gutmann, E.D.; Zavorotny, V.U.; Braun, J.J.; Williams, M.W.; Nievinski, F.G. Can we measure snow depth with GPS receivers? Geophys. Res. Lett. 2009, 36, L17502. [Google Scholar] [CrossRef]
- Larson, K.M.; Löfgren, J.S.; Haas, R. Coastal sea level measurements using a single geodetic GPS receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef]
- Larson, K.M.; Ray, R.D.; Nievinski, F.G.; Freymueller, J.T. The Accidental Tide Gauge: A GPS Reflection Case Study From Kachemak Bay, Alaska. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1200–1204. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Zhang, Q. Evaluation and combination of quad-constellation multi-GNSS multipath reflectometry applied to sea level retrieval. Remote Sens. Environ. 2019, 231, 111229. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II. Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- Strandberg, J.; Hobiger, T.; Haas, R. Improving GNSS-R sea level determination through inverse modeling of SNR data. Radio Sci. 2016, 51, 1286–1296. [Google Scholar] [CrossRef]
- Strandberg, J.; Hobiger, T.; Haas, R. Real-time sea-level monitoring using Kalman filtering of GNSS-R data. GPS Solut. 2019, 23, 61. [Google Scholar] [CrossRef]
- Ozeki, M.; Heki, K. GPS snow depth meter with geometry-free linear combinations of carrier phases. J. Geod. 2012, 86, 209–219. [Google Scholar] [CrossRef]
- Li, Y.; Chang, X.; Yu, K.; Wang, S.; Li, J. Estimation of snow depth using pseudorange and carrier phase observations of GNSS single-frequency signal. GPS Solut. 2019, 23, 118. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, F.; Zhang, X.; Pan, L. First result of GNSS-R-based sea level retrieval with CMC and its combination with the SNR method. GPS Solut. 2021, 26, 20. [Google Scholar] [CrossRef]
- Wang, N.; Xu, T.; Gao, F.; Xu, G. Sea Level Estimation Based on GNSS Dual-Frequency Carrier Phase Linear Combinations and SNR. Remote Sens. 2018, 10, 470. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, W.; Ji, B.; Yu, D.; Bian, S.; Gu, S.; Li, D. Effect of Stochastic Modeling for Inter-Frequency Biases of Receiver on BDS-3 Five-Frequency Undifferenced and Uncombined Precise Point Positioning. Remote Sens. 2022, 14, 3595. [Google Scholar] [CrossRef]
- Geng, J.; Yang, S.; Guo, J. Assessing IGS GPS/Galileo/BDS-2/BDS-3 phase bias products with PRIDE PPP-AR. Satell. Navig. 2021, 2, 17. [Google Scholar] [CrossRef]
- Huang, L.; Zhu, G.; Liu, L.; Chen, H.; Jiang, W. A global grid model for the correction of the vertical zenith total delay based on a sliding window algorithm. GPS Solut. 2021, 25, 98. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Zhang, S. Water levels measured with SNR using wavelet decomposition and Lomb–Scargle periodogram. GPS Solut. 2017, 22, 22. [Google Scholar] [CrossRef]
- Larson, K.M.; Nievinski, F.G. GPS snow sensing: Results from the EarthScope Plate Boundary Observatory. GPS Solut. 2013, 17, 41–52. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, S. An improved sea level retrieval method using the differential evolution of GNSS SNR data. Adv. Space Res. 2021, 67, 975–984. [Google Scholar] [CrossRef]
- Vu, P.L.; Ha, M.C.; Frappart, F.; Darrozes, J.; Ramillien, G.; Dufrechou, G.; Gegout, P.; Morichon, D.; Bonneton, P. Identifying 2010 Xynthia Storm Signature in GNSS-R-Based Tide Records. Remote Sens. 2019, 11, 782. [Google Scholar] [CrossRef]
- Roesler, C.; Larson, K.M. Software tools for GNSS interferometric reflectometry (GNSS-IR). GPS Solut. 2018, 22, 80. [Google Scholar] [CrossRef]
- Geremia-Nievinski, F.; Silva, M.F.E.; Boniface, K.; Monico, J.F.G. GPS Diffractive Reflectometry: Footprint of a Coherent Radio Reflection Inferred From the Sensitivity Kernel of Multipath SNR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4884–4891. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Zhang, S. Azimuth selection for sea level measurements using geodetic GPS receivers. Adv. Space Res. 2018, 61, 1546–1557. [Google Scholar] [CrossRef]
- Nievinski, F.G.; Larson, K.M. Forward modeling of GPS multipath for near-surface reflectometry and positioning applications. GPS Solut. 2013, 18, 309–322. [Google Scholar] [CrossRef]
- Aram, M.; El-Rabbany, A.; Krishnan, S.; Anpalagan, A. Single Frequency Multipath Mitigation Based on Wavelet Analysis. J. Navig. 2007, 60, 281–290. [Google Scholar] [CrossRef]
- Hobiger, T.; Haas, R.; Löfgren, J. Software-Defined Radio Direct Correlation GNSS Reflectometry by Means of GLONASS. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4834–4842. [Google Scholar] [CrossRef]
- Pan, H.; Lv, X.; Wang, Y.; Matte, P.; Chen, H.; Jin, G. Exploration of Tidal-Fluvial Interaction in the Columbia River Estuary Using S_TIDE. J. Geophys. Res. Oceans 2018, 123, 6598–6619. [Google Scholar] [CrossRef]
- Qian, X.; Jin, S. Estimation of Snow Depth from GLONASS SNR and Phase-Based Multipath Reflectometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4817–4823. [Google Scholar] [CrossRef]
- Larson, K.M.; Ray, R.D.; Williams, S.D.P. A 10-Year Comparison of Water Levels Measured with a Geodetic GPS Receiver versus a Conventional Tide Gauge. J. Atmos. Ocean. Technol. 2017, 34, 295–307. [Google Scholar] [CrossRef]
- Tabibi, S.; Geremia-Nievinski, F.; Dam, T.V. Statistical Comparison and Combination of GPS, GLONASS, and Multi-GNSS Multipath Reflectometry Applied to Snow Depth Retrieval. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3773–3785. [Google Scholar] [CrossRef]







| System | Frequency Band | Frequency (MHz) | Phase Code | SNR Code |
|---|---|---|---|---|
| GPS | L1 | 1575.42 | L1C | S1C |
| L2 | 1227.60 | L2X | S2X | |
| GLONASS | R1 | 1602 + k × 9/16 1 | L1C | S1C |
| R2 | 1246 + k × 7/16 | L2C | S2C | |
| Galileo | E1 | 1575.42 | L1X | S1X |
| E5a | 1176.45 | L5X | S5X |
| Terms | Data-Processing Strategy |
|---|---|
| Observations | GPS: L1/L2; GLONASS: G1/G2; Galileo: E1/E5a |
| Method | IF-PPP |
| Cut-off elevation angle | 5° |
| Estimator | Kalman filter (Backward and Forward) |
| Receiver position | Estimated from the PRIDE software [30] |
| Receiver clock | White noise model |
| Satellite orbit and clock | Precise ephemeris and clock products |
| Integer ambiguity | Constant model (each ambiguity parameter corresponds to one observation arc per satellite) |
| Inter-frequency biases | White noise model |
| Troposphere delays | Zenith Dry Delay (ZDD): Global Pressure and Temperature (GPT3) model; Zenith Wet Delay (ZWD): Random-walk model (5 × 10−8 m2/s) |
| Ionospheric delays | IF combination method |
| System | Frequency Combination | Fitting Coefficients | |
|---|---|---|---|
| a | b | ||
| GPS | L1 + L2 | 0.1222 | −0.011 |
| GLONASS | G1 + G2 | 0.1203 | −0.020 |
| Galileo | E1 + E5a | 0.1273 | −0.012 |
| System | Observation Code | Average Number of Retrievals per Day | RMSE (cm) | R2 |
|---|---|---|---|---|
| GPS | L1 + L2 | 19 | 20.8 | 0.973 |
| S2X | 40 | 16.5 | 0.972 | |
| GLONASS | R1 + R2 | 11 | 21.9 | 0.970 |
| S2C | 28 | 17.1 | 0.977 | |
| Galileo | E1 + E5a | 12 | 22.0 | 0.968 |
| S5X | 28 | 17.9 | 0.963 |
| GNSS Observation | Average Number of Retrievals per Day | Slope (m/m) | RMSE (cm) | R2 |
|---|---|---|---|---|
| PE combination | 35 | 0.952 | 18.4 | 0.973 |
| SNR combination | 45 | 0.976 | 16.5 | 0.988 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Bian, S.; Liu, Y.; Huang, L.; Liu, L.; Chen, C.; Li, H.; Zhai, G. Coastal High-Temporal Sea-Surface Altimetry Using the Posterior Error Estimations of Ionosphere-Free PPP and Information Fusion for Multi-GNSS Retrievals. Remote Sens. 2022, 14, 5599. https://doi.org/10.3390/rs14215599
Zhou W, Bian S, Liu Y, Huang L, Liu L, Chen C, Li H, Zhai G. Coastal High-Temporal Sea-Surface Altimetry Using the Posterior Error Estimations of Ionosphere-Free PPP and Information Fusion for Multi-GNSS Retrievals. Remote Sensing. 2022; 14(21):5599. https://doi.org/10.3390/rs14215599
Chicago/Turabian StyleZhou, Wei, Shaofeng Bian, Yi Liu, Liangke Huang, Lilong Liu, Cheng Chen, Houpu Li, and Guojun Zhai. 2022. "Coastal High-Temporal Sea-Surface Altimetry Using the Posterior Error Estimations of Ionosphere-Free PPP and Information Fusion for Multi-GNSS Retrievals" Remote Sensing 14, no. 21: 5599. https://doi.org/10.3390/rs14215599
APA StyleZhou, W., Bian, S., Liu, Y., Huang, L., Liu, L., Chen, C., Li, H., & Zhai, G. (2022). Coastal High-Temporal Sea-Surface Altimetry Using the Posterior Error Estimations of Ionosphere-Free PPP and Information Fusion for Multi-GNSS Retrievals. Remote Sensing, 14(21), 5599. https://doi.org/10.3390/rs14215599







