Analysis of Data-Derived SeaWinds Normalized Radar Cross-Section Noise
Abstract
1. Introduction
2. Data and Methods
2.1. Data
Quality Control (QC)
- frame_err_status is required to be 0. This requirement ensures that neither an unusual instrument condition applies, nor bad ephemeris, nor bad attitude.
- bit 4 (0-based) of frame_qual_flag is required to be 0; otherwise, bad data are present in the frame.
- bits 0–3 of frame_inst_status are required to be 0, while bits 4–6 are required to be “011”. Bits 0–1 account for the “Current Mode”, which can be “Wind Observation Mode”, “Calibration Mode”, “Standby Mode" or “Receive Only Mode”. Bit 2 accounts for the “First Pulse Count in the Frame” (Pulse A first or Pulse B first) and bit 3 accounts for the “Antenna Spin Rate” (Nominal or Alternate Rate). Finally, bits 4–6 account for the “Slice Resolution Mode”.
- bits 0, 4–9 of sigma0_qual_flag are required to be 0. This condition ensures that
- –
- The egg is usable (bit 0);
- –
- The scatterometer pulse is acceptable (bit 4);
- –
- The cell location algorithm converges (bit 5);
- –
- The frequency shift is within the range of the x factor table (bit 6);
- –
- The spacecraft temperature is within the calibration coefficient range (bit 7);
- –
- An applicable attitude record was found for this (bit 8);
- –
- Interpolated ephemeris data are acceptable for this (bit 9).
Bits 1, 2, and 3 account for the SNR level, the sign of , and the admitted range of s. None of these constraints is applied to the noise estimation of the slice . In fact, a fair estimate of the noise of the slice must take into account both low SNR measurements, negative values and s outside of the expected range; otherwise, the distribution of could be truncated and some artificial biases could be introduced.
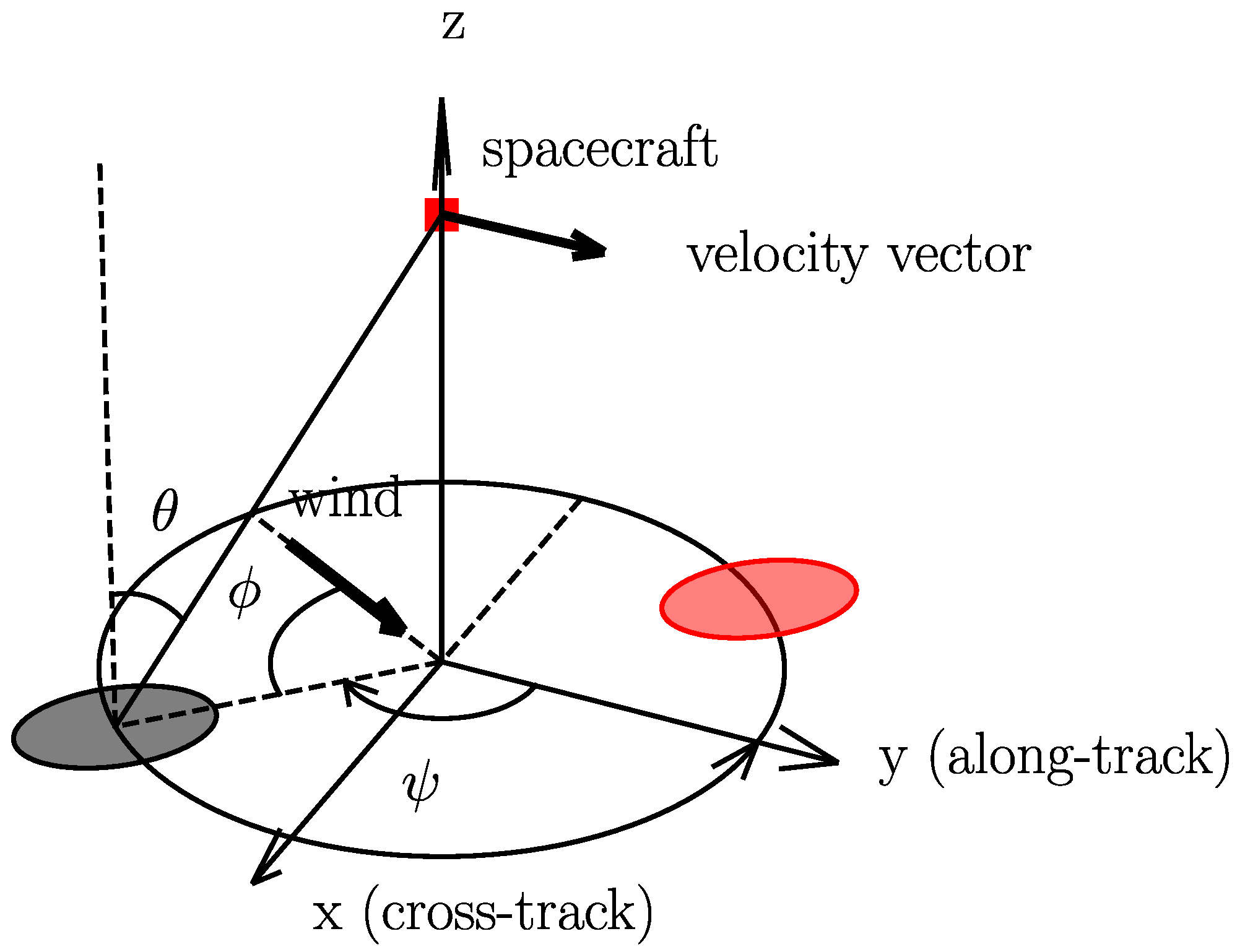
2.2. Methods
2.2.1. Estimate of the Expected ()
- The antenna beam polarization;
- The view (fore or aft);
- The slice index.
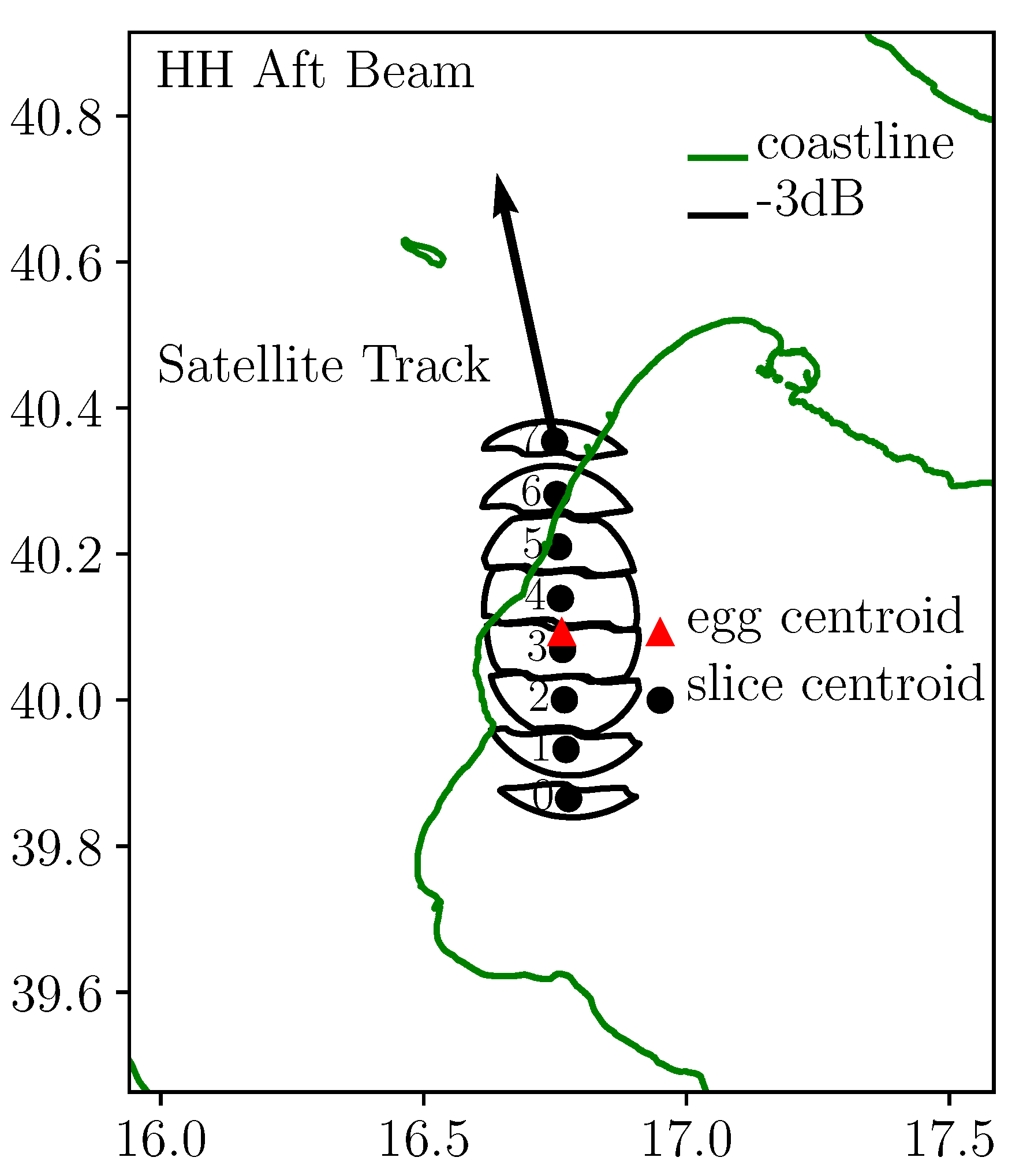
2.2.2. Impact of the Intra-Egg Bias on
2.2.3. Theoretical Model of the Distribution of
3. Results and Discussion
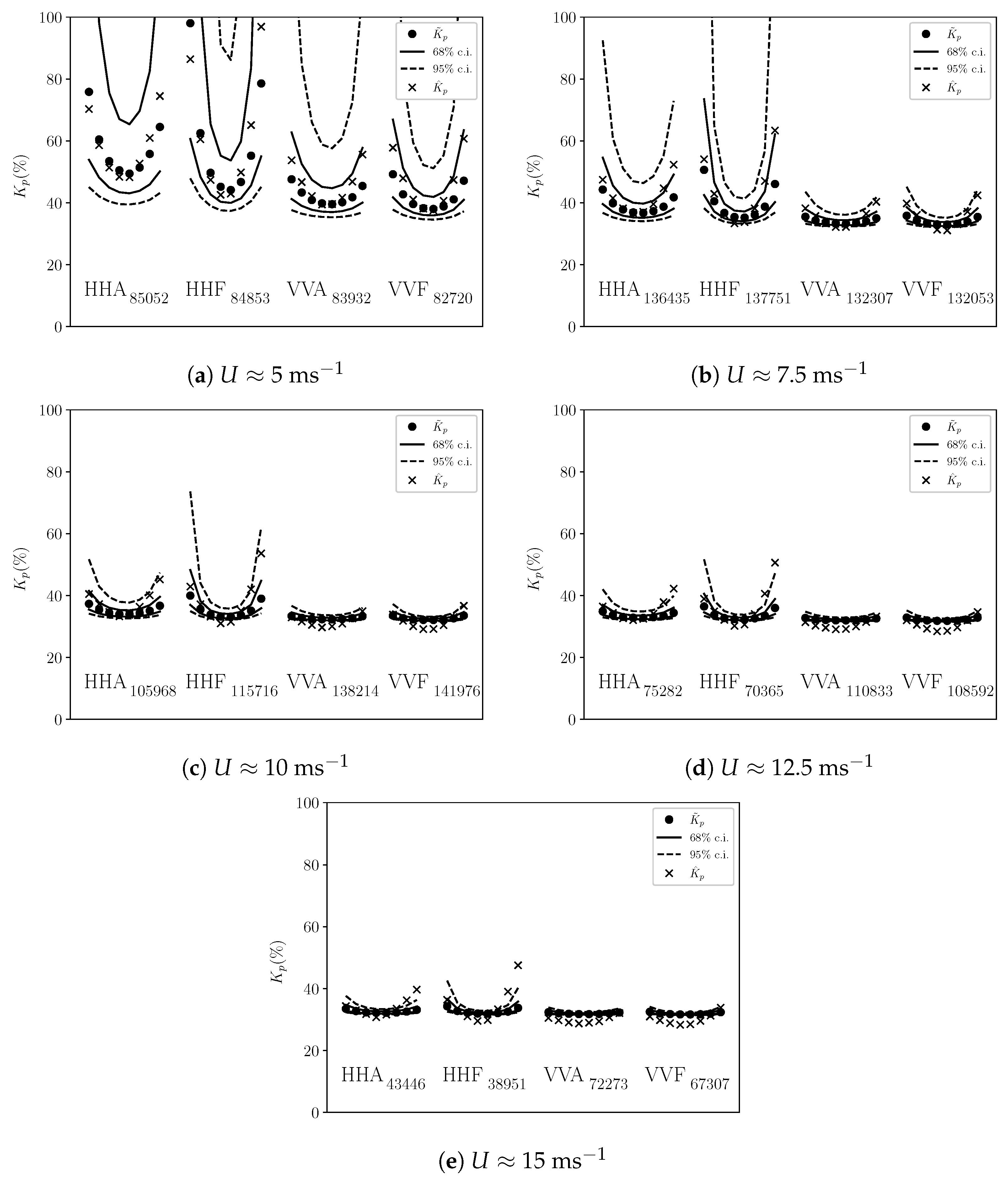
3.1. Comparison between and over Sea
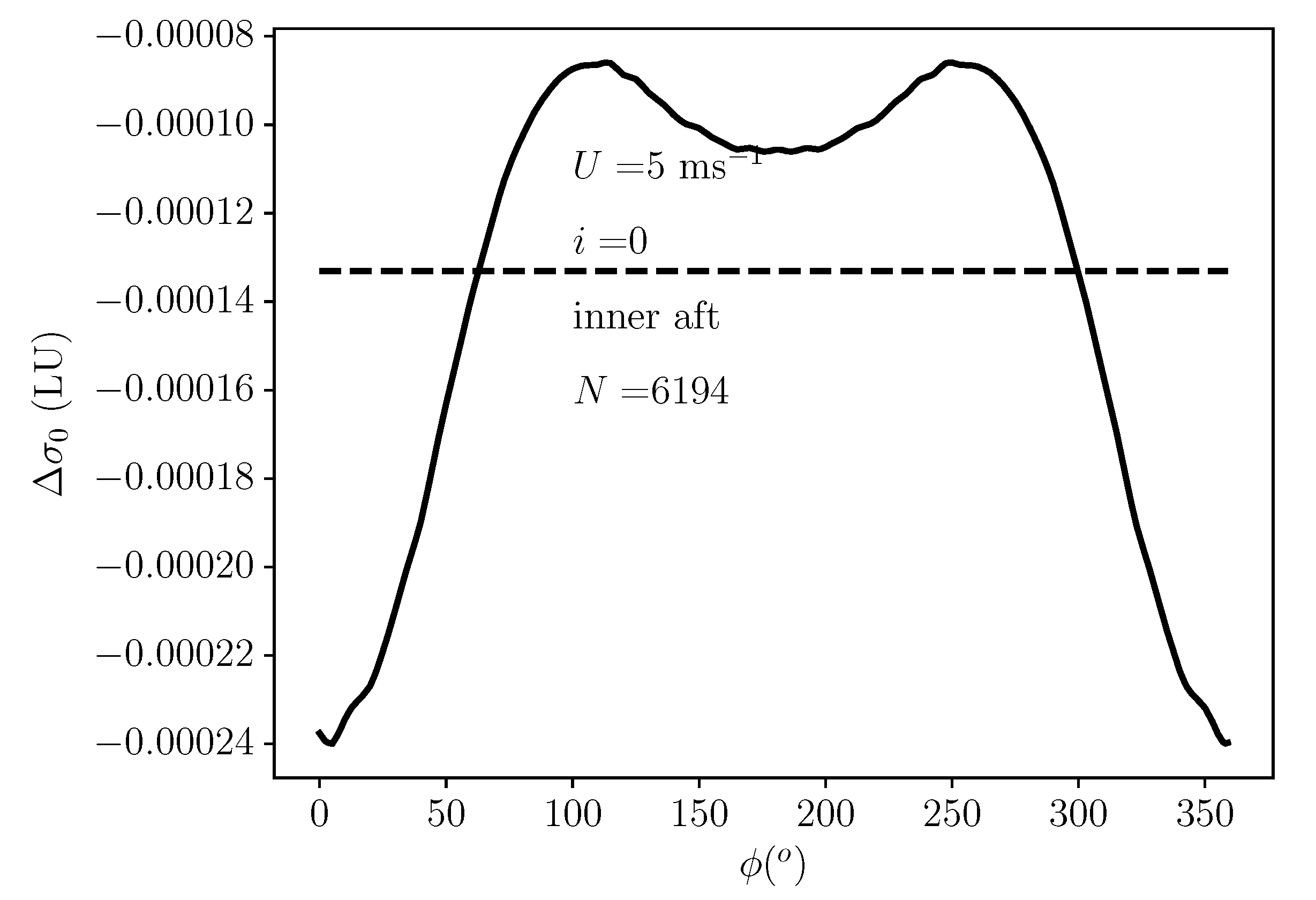
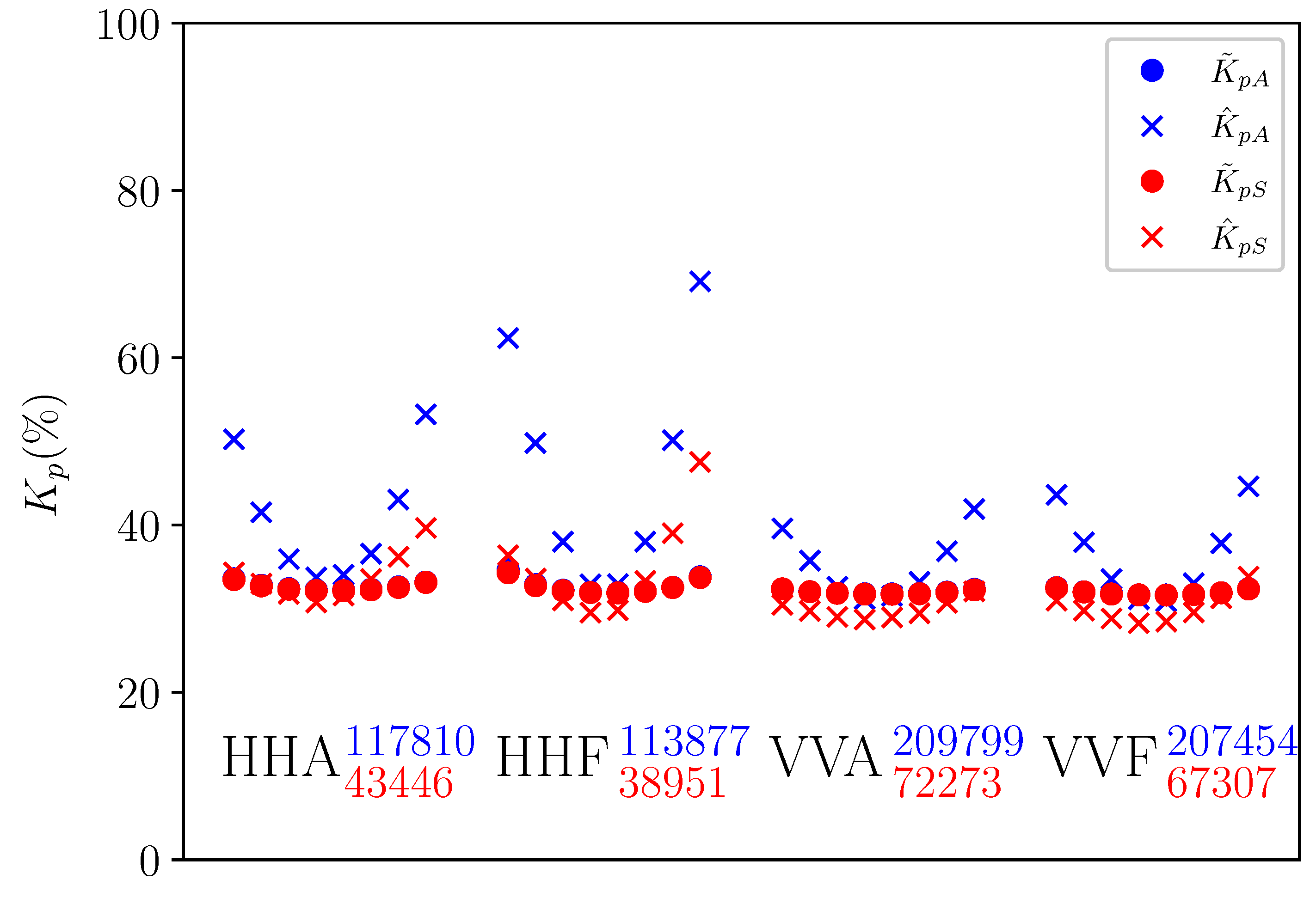
3.2. Impact of -Induced Intra-Egg Biases on
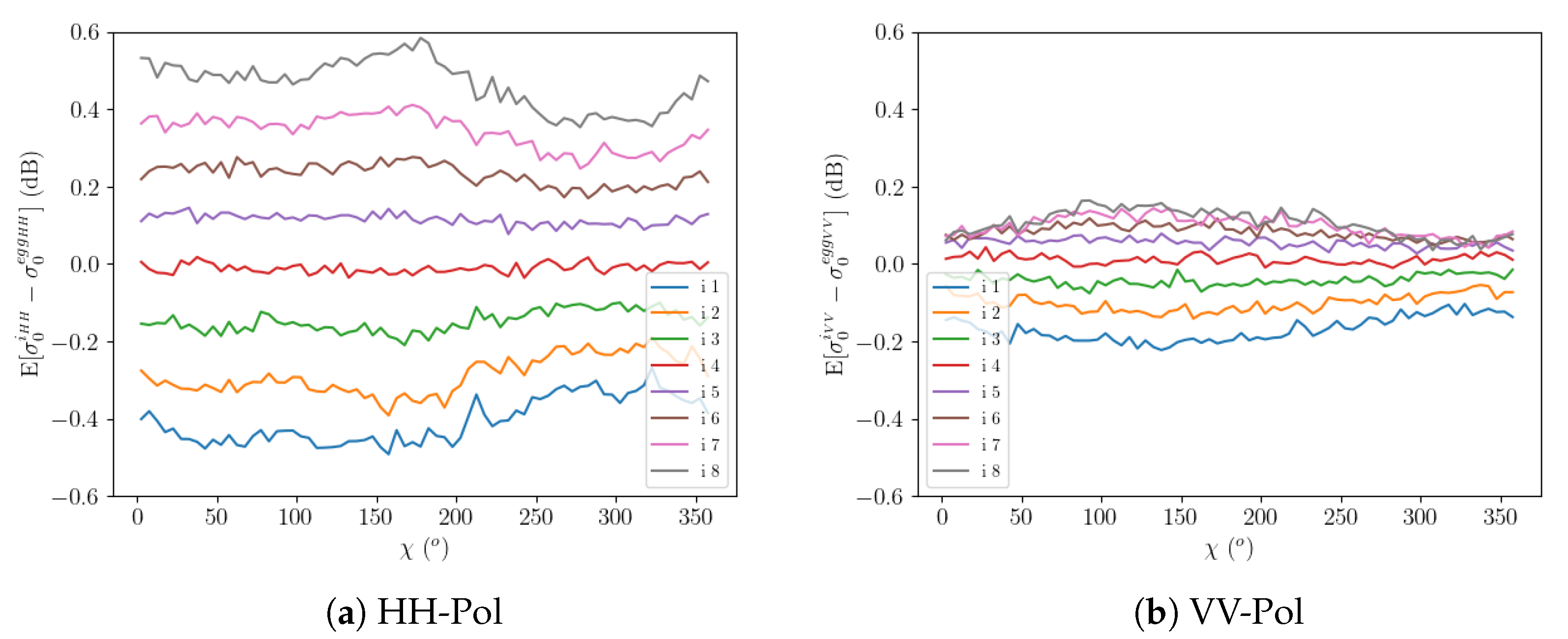
3.3. Sensitivity to the Type of Surface
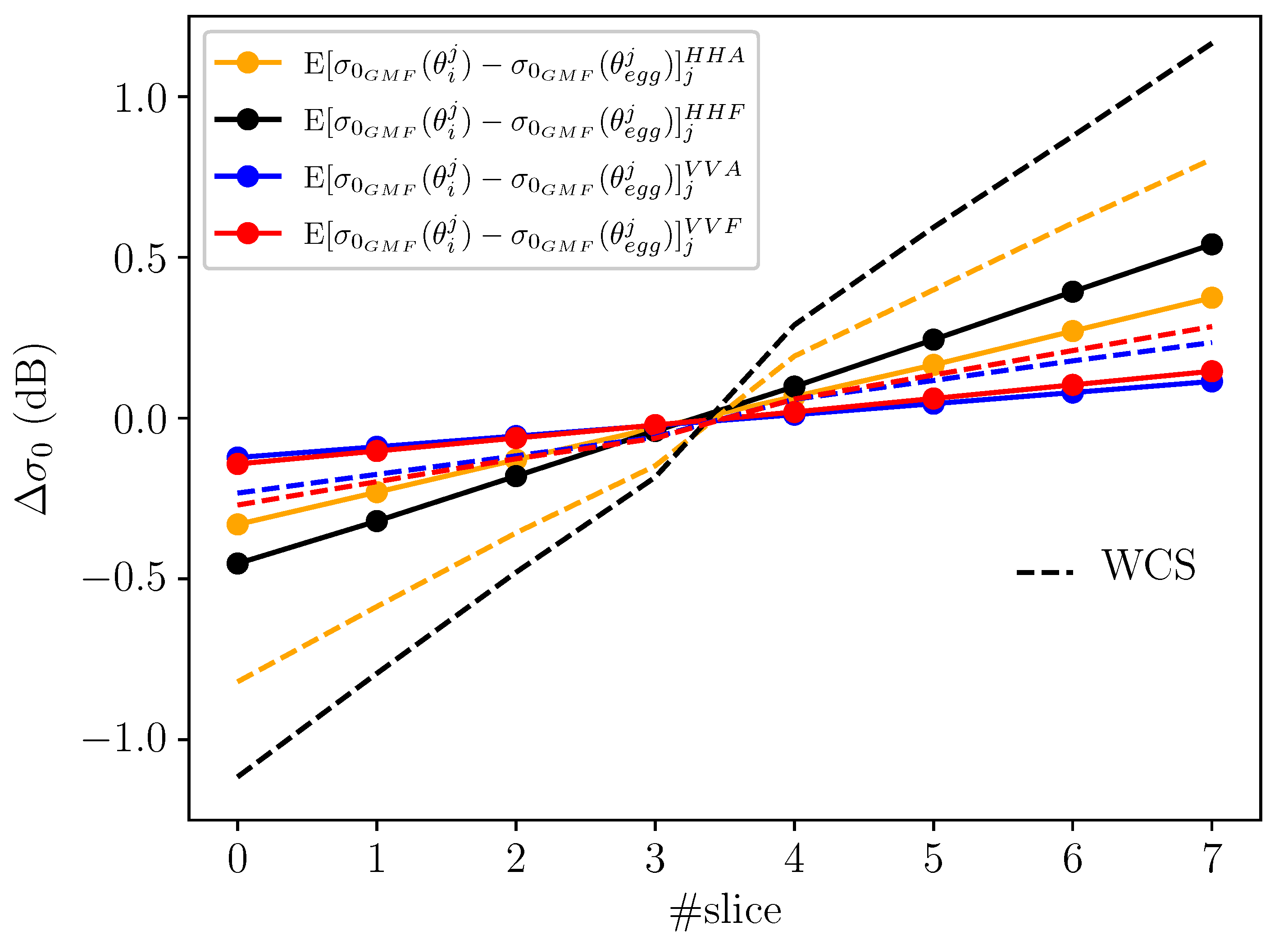
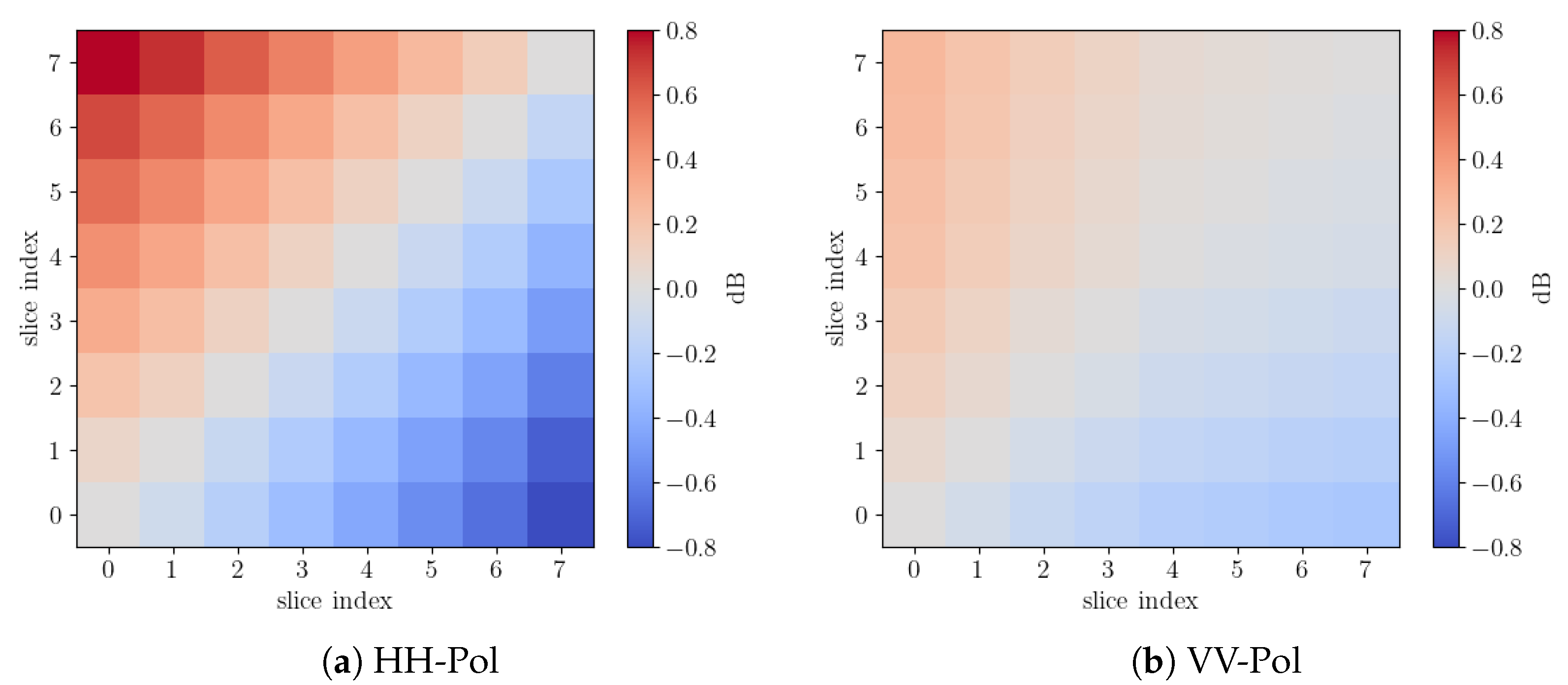
3.4. Inter-Slice Biases and Trends with Azimuth Angle
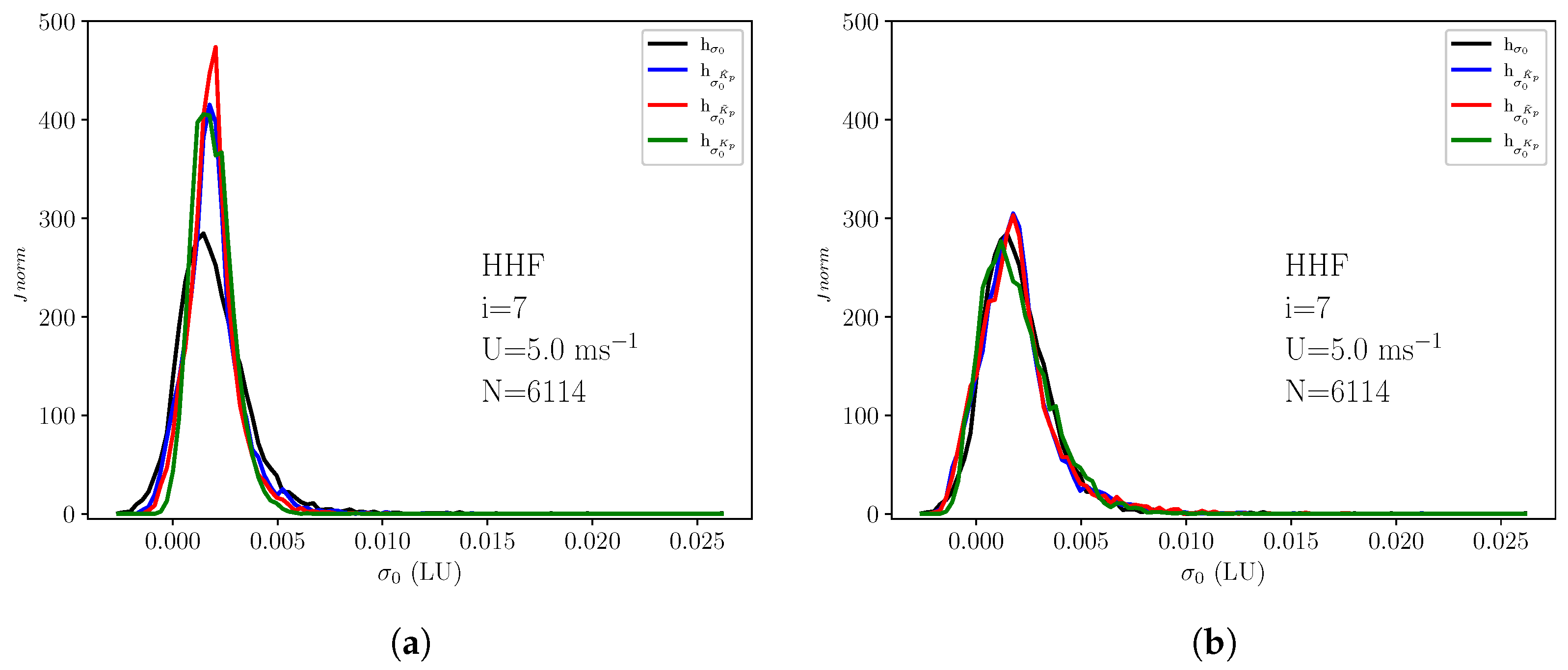
3.5. Simulation of Distribution
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Long, D.; Spencer, M. Radar backscatter measurement accuracy for a spaceborne pencil-beam wind scatterometer with transmit modulation. IEEE Trans. Geosci. Remote Sens. 1997, 35, 102–114. [Google Scholar] [CrossRef]
- Available online: https://scatterometer.knmi.nl/qscat_prod/ (accessed on 30 September 2022).
- Verhoef, A.; Vogelzang, J.; Verspeek, J.; Stoffelen, A. Long-Term Scatterometer Wind Climate Data Records. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2186–2194. [Google Scholar] [CrossRef]
- Available online: https://podaac-opendap.jpl.nasa.gov/opendap/ (accessed on 30 September 2022).
- Owen, M.P.; Long, D.G. Land-Contamination Compensation for QuikSCAT Near-Coastal Wind Retrieval. IEEE Trans. Geosci. Remote Sens. 2009, 47, 839–850. [Google Scholar] [CrossRef]
- Vogelzang, J.; Stoffelen, A. ASCAT Land Correction, Report for the EUMETSAT Ocean and Sea Ice SAF; Technical Report, SAF/OSI/CDOP3/KNMI/TEC/TN/384; Koninklijk Nederlands Meteorologisch Instituut: Utrecht, The Netherlands, 2020. [Google Scholar]
- Lindsley, R.D.; Blodgett, J.R.; Long, D.G. Analysis and Validation of High-Resolution Wind From ASCAT. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5699–5711. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar] [CrossRef]
- Stoffelen, A.; Portabella, M. On Bayesian scatterometer wind inversion. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1523–1533. [Google Scholar] [CrossRef]
- Fischer, R.E. Standard Deviation of Scatterometer Measurements from Space. IEEE Trans. Geosci. Electron. 1972, 10, 106–113. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing—Active and Passive; Addison-Wesley Pulishing Company: Boston, MA, USA, 1981; Volume 2. [Google Scholar]
- Portabella, M.; Stoffelen, A. Scatterometer Backscatter Uncertainty Due to Wind Variability. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3356–3362. [Google Scholar] [CrossRef]
- Thorlabs. QuikSCAT Science Data Product. User’s Manual; JPL NASA: Pasadena, CA, USA, 2006.
- Portabella, M.; Stoffelen, A. Rain Detection and Quality Control of SeaWinds. J. Atmos. Ocean. Technol. 2001, 18, 1171–1183. [Google Scholar] [CrossRef]
- Wang, Z.; Stoffelen, A.; Fois, F.; Verhoef, A.; Zhao, C.; Lin, M.; Chen, G. SST Dependence of Ku- and C-Band Backscatter Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2135–2146. [Google Scholar] [CrossRef]
- Spencer, M.; Wu, C.; Long, D. Tradeoffs in the design of a spaceborne scanning pencil beam scatterometer: Application to SeaWinds. IEEE Trans. Geosci. Remote Sens. 1997, 35, 115–126. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. Ocean. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Vogelzang, J.; Stoffelen, A. Quadruple Collocation Analysis of In-Situ, Scatterometer, and NWP Winds. J. Geophys. Res. Ocean. 2021, 126, e2021JC017189. [Google Scholar] [CrossRef]
- Vogelzang, J.; Stoffelen, A. On the Accuracy and Consistency of Quintuple Collocation Analysis of In Situ, Scatterometer, and NWP Winds. Remote Sens. 2022, 14, 4552. [Google Scholar] [CrossRef]
- Stoffelen, A. A Simple Method for Calibration of a Scatterometer over the Ocean. J. Atmos. Ocean. Technol. 1999, 16, 275–282. [Google Scholar] [CrossRef]


| Field | Shape | Full Name |
|---|---|---|
| sc_lat | (n_f,n_p,n_s) | sc latitude |
| sc_lon | (n_f,n_p,n_s) | sc longitude |
| sc_alt | (n_f,n_p,n_s) | sc altitude |
| x_pos | (n_f,n_p,n_s) | sc x-position ECEF |
| y_pos | (n_f,n_p,n_s) | sc y-position ECEF |
| z_pos | (n_f,n_p,n_s) | sc z-position ECEF |
| x_vel | (n_f,n_p,n_s) | sc x-velocity ECEF |
| y_vel | (n_f,n_p,n_s) | sc y-velocity ECEF |
| z_vel | (n_f,n_p,n_s) | sc z-velocity ECEF |
| cell_lat | (n_f,n_p) | cell latitude |
| cell_lon | (n_f,n_p) | cell longitude |
| cell_sigma0 | (n_f,n_p) | cell |
| cell_azimuth | (n_f,n_p) | cell azimuth |
| cell_incidence | (n_f,n_p) | cell incidence angle |
| ant_azimuth | (n_f,n_p) | antenna azimuth |
| slice_snr | (n_f,n_p,n_s) | slice SNR |
| slice_kpc_a | (n_f,n_p,n_s) | slice kp a coefficient |
| slice_kpc_b | 1 | slice kp b coefficient |
| slice_kpc_c | 1 | slice kp c coefficient |
| slice_azimuth | (n_f,n_p,n_s) | slice azimuth |
| slice_incidence | (n_f,n_p,n_s) | slice incidence angle |
| slice_sigma0 | (n_f,n_p,n_s) | slice |
| orbit_time | (n_f) | orbit time |
| Quality flag | Shape | Full name |
| frame_err_status | (n_f) | frame error status |
| frame_inst_status | (n_f) | frame instrument status |
| frame_qual_flag | (n_f) | frame quality flag |
| sigma0_mode_flag | (n_f,n_p) | mode flag |
| sigma0_qual_flag | (n_f,n_p) | quality flag |
| slice_qual_flag | (n_f,n_p) | slice quality flag |
| File attributes | ||
| EquatorCrossingLongitude | 1 | Equator Crossing Longitude |
| orbit_inclination | 1 | Orbit inclination |
| rev_orbit_period | 1 | Orbit revolution period |
| orbit_semi_major_axis | 1 | Orbit semi-major axis |
| orbit_eccentricity | 1 | Orbit eccentricity |
| Slice # | HHA | HHF | VVA | VVF |
|---|---|---|---|---|
| 0 | 0.68 ± 0.09 | 0.95 ± 0.15 | 0.56 ± 0.08 | 0.67 ± 0.09 |
| 1 | 0.48 ± 0.09 | 0.66 ± 0.13 | 0.40 ± 0.08 | 0.48 ± 0.09 |
| 2 | 0.26 ± 0.09 | 0.37 ± 0.12 | 0.24 ± 0.08 | 0.29 ± 0.08 |
| 3 | 0.05 ± 0.09 | 0.07 ± 0.11 | 0.08 ± 0.08 | 0.09 ± 0.08 |
| 4 | −0.16 ± 0.09 | −0.23 ± 0.12 | −0.08 ± 0.08 | −0.11 ± 0.08 |
| 5 | −0.38 ± 0.09 | −0.54 ± 0.13 | −0.24 ± 0.08 | −0.31 ± 0.08 |
| 6 | −0.60 ± 0.09 | −0.85 ± 0.16 | −0.41 ± 0.08 | −0.51 ± 0.08 |
| 7 | −0.82 ± 0.10 | −1.17 ± 0.19 | −0.57 ± 0.08 | −0.72 ± 0.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grieco, G.; Stoffelen, A.; Verhoef, A.; Vogelzang, J.; Portabella, M. Analysis of Data-Derived SeaWinds Normalized Radar Cross-Section Noise. Remote Sens. 2022, 14, 5444. https://doi.org/10.3390/rs14215444
Grieco G, Stoffelen A, Verhoef A, Vogelzang J, Portabella M. Analysis of Data-Derived SeaWinds Normalized Radar Cross-Section Noise. Remote Sensing. 2022; 14(21):5444. https://doi.org/10.3390/rs14215444
Chicago/Turabian StyleGrieco, Giuseppe, Ad Stoffelen, Anton Verhoef, Jur Vogelzang, and Marcos Portabella. 2022. "Analysis of Data-Derived SeaWinds Normalized Radar Cross-Section Noise" Remote Sensing 14, no. 21: 5444. https://doi.org/10.3390/rs14215444
APA StyleGrieco, G., Stoffelen, A., Verhoef, A., Vogelzang, J., & Portabella, M. (2022). Analysis of Data-Derived SeaWinds Normalized Radar Cross-Section Noise. Remote Sensing, 14(21), 5444. https://doi.org/10.3390/rs14215444







