A Calculation Model for Ground Surface Temperature in High-Altitude Regions of the Qinghai-Tibet Plateau, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Region and Data
2.1.1. Study Region
2.1.2. Data
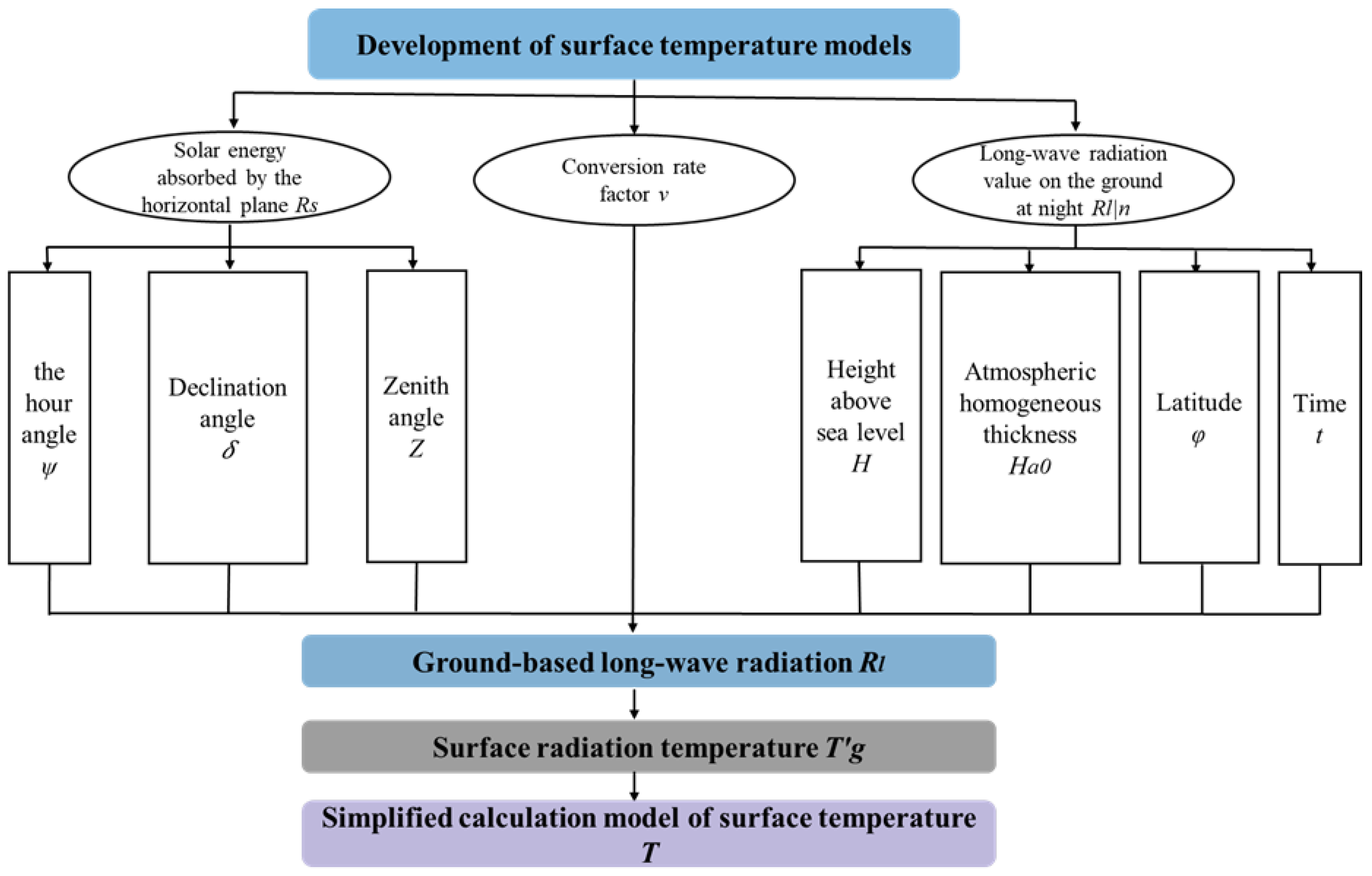
2.2. Ground Surface Temperature Calculation Model
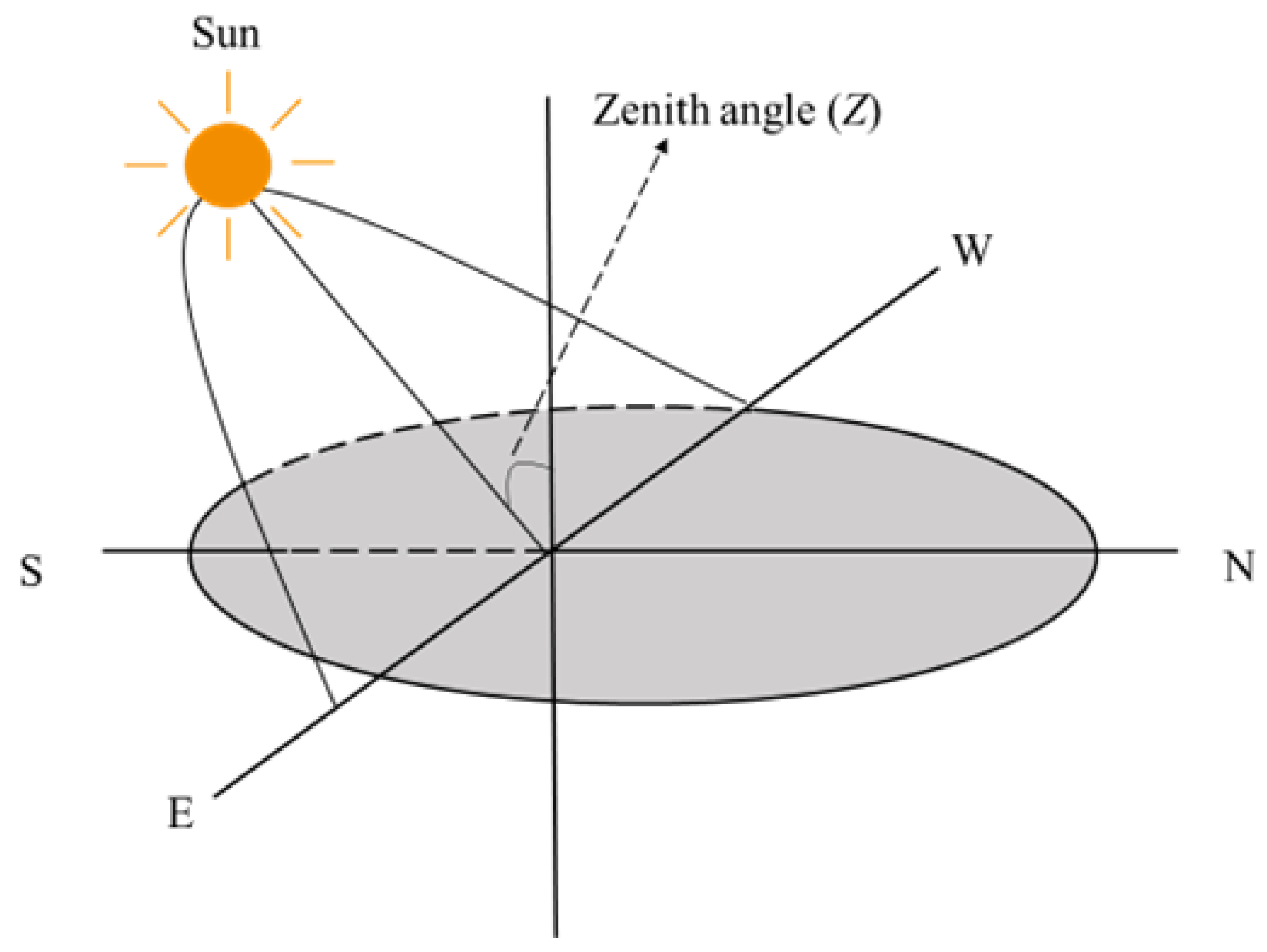
2.2.1. Direct Solar Radiation on Different Underlying Surfaces
2.2.2. Long-Wave Radiation on Different Underlying Surfaces
2.2.3. Thermal Boundary Model
2.2.4. Process of Surface Temperature Calculation
3. Results
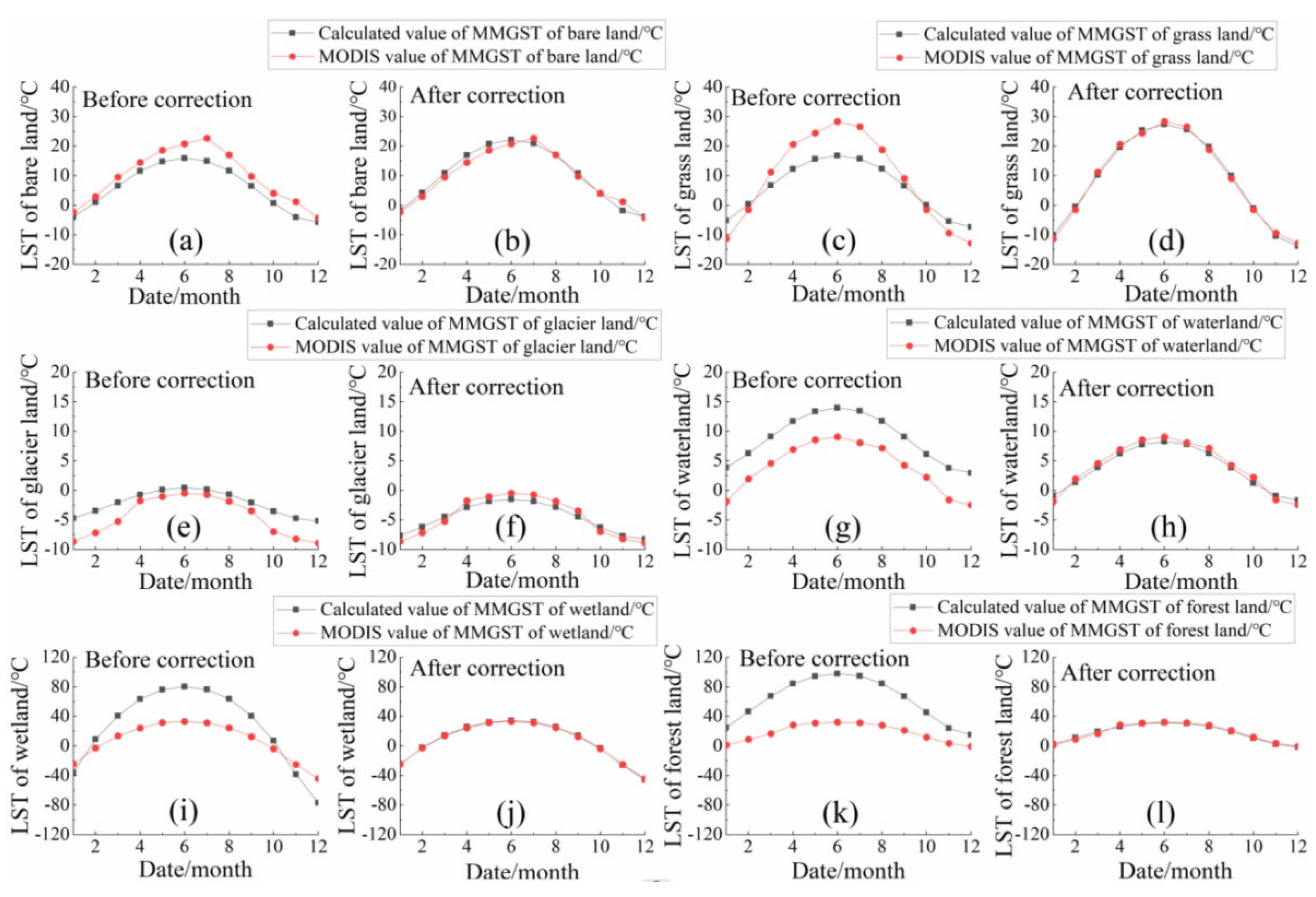
3.1. The Mean Monthly Ground Surface Temperature (MMGST)
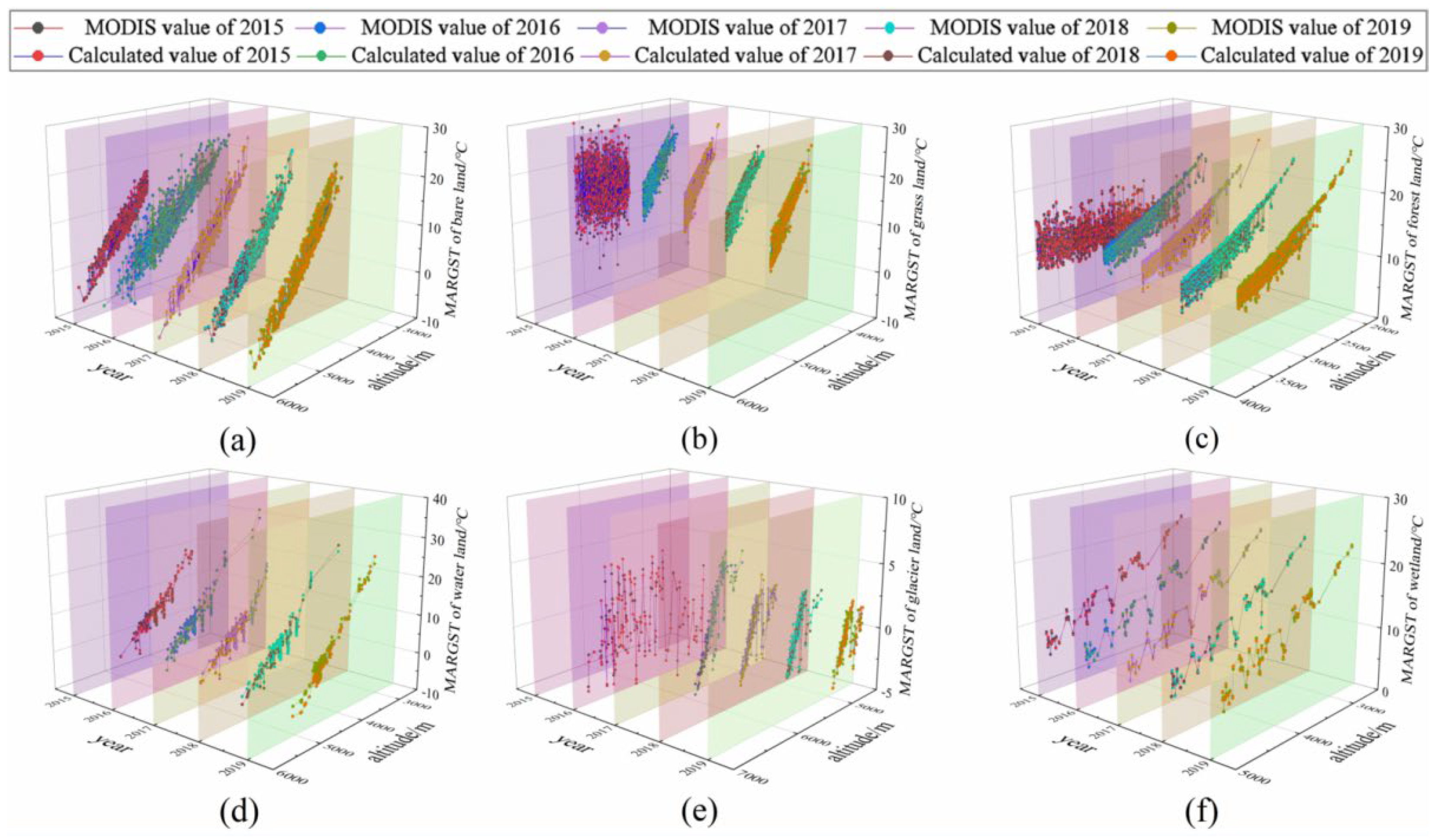
3.2. The Mean Annual Radiant Ground Surface Temperature (MARGST)
3.3. Results Validation
4. Discussion
5. Conclusions
- (1)
- In the Qinghai-Tibet Plateau, the absorbance capacity of solar radiation differs on different underlying surfaces, which represents the ground surface temperature. The reasons are mainly associated with the difference in the conversion ratio from total solar radiation to ground surface long-wave radiation on different underlying surfaces. Based on the calculation model, the order of conversion ratio coefficient is distributed as follows: grassland > wetland > forest > bare land > water body > glacier.
- (2)
- A simplified calculation model of ground surface temperature was built on different underlying surfaces, which considered latitude, altitude and solar radiation. The ground surface temperature can be approximately solved by the conversion coefficient and correction coefficient on different underlying surfaces. From the calculated results of MMGST and MARGST, the modified model has a high correlation with the MODIS data, which is higher than 0.85, and the RMSE and deviation were improved by the modified model. The inter-annual variation in MMGST has a unimodal curve trend with rising and falling.
- (3)
- The simplified and modified model presented in this paper can calculate the ground surface temperature at every hour of every day. By comparison with the MODIS data, the calculated results are found to have high precision. The application of the model will be expanded to other regions with different altitudes. The existing temperature calculation model mainly focuses on the Qinghai-Tibet Engineering Corridor, which is based on monitoring data. The calculation results represent the given condition and not all the underlying surfaces. The model presented in this manuscript has a higher resolution and wider application potential in ground surface analysis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Mao, K.; Mu, F.; Shi, J.; Yang, J.; Li, Z.; Qin, Z. A split window algorithm for retrieving land surface temperature from FY-3D MERSI-2 data. Remote Sens. 2019, 11, 2083. [Google Scholar] [CrossRef]
- Luo, J.; Zheng, J.Q.; Zhong, L.; Zhao, C.; Fu, Y. The Phenomenon of Diurnal Variations for Summer Deep Convective Precipitation over the Qinghai-Tibet Plateau and Its Southern Regions as Viewed by TRMM PR. Atmosphere 2021, 12, 745. [Google Scholar] [CrossRef]
- Schuur, E.A.G.; Bockheim, J.; Canadell, J.G.; Euskirchen, E.; Field, C.B.; Goryachkin, S.V.; Hagemann, S.; Kuhry, P.; Lafleur, P.M.; Lee, H.; et al. Vulnerability of Permafrost Carbon to Climate Change: Implications for the Global Carbon Cycle. Bioscience 2008, 58, 701–714. [Google Scholar] [CrossRef]
- Tian, J.; Chen, H.; Wang, Y.; Zhou, X. Methane production in relation with temperature, substrate and soil depth in Zoige wetlands on Tibetan Plateau. Acta Ecol. Sin. 2011, 31, 121–125. [Google Scholar] [CrossRef]
- Wang, J.; Wang, G.; Hu, H.; Wu, Q. The influence of degradation of the swamp and alpine meadows on CH4 and CO2 fluxes on the Qinghai-Tibetan Plateau. Environ. Earth Sci. 2010, 60, 537–548. [Google Scholar] [CrossRef]
- Zou, F.L.; Li, H.D.; Hu, Q.W. Responses of vegetation greening and land surface temperature variations to global warming on the Qinghai-Tibetan Plateau, 2001–2016. Ecol. Indic. 2020, 119, 106867. [Google Scholar] [CrossRef]
- Dumais, S.; Doré, G. An albedo based model for the calculation of pavement surface temperatures in permafrost regions. Cold Reg. Sci. Technol. 2016, 123, 44–52. [Google Scholar] [CrossRef]
- Wang, D.; Zhi, F.; Fang, J.; Li, H. Influence of solar radiation on surface thermal regime of different pavement types and its permafrost underlying embankment on the Qinghai-Tibetan Plateau. J. Highw. Transp. Res. Dev. 2008, 3, 38–43. [Google Scholar]
- Hu, Z.; Cheng, G.; Gu, L. Calculating method of global radiation and temperature on the roadbed surface of Qinghai-Xizang railway. Adv. Earth Sci. 2006, 21, 1304–1313. (In Chinese) [Google Scholar]
- Weng, Q.; Fu, P.; Gao, F. Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Hu, L.; Sun, Y.; Collins, G.; Fu, P. Improved estimates of monthly land surface temperature from MODIS using a diurnal temperature cycle (DTC) model. ISPRS J. Photogramm. Remote Sens. 2020, 168, 131–140. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, N.; He, J.; Jiang, X. Estimating mountain glacier surface temperatures from Landsat-ETM+ thermal infrared data: A case study of Qiyi glacier, China. Remote Sens. Environ. 2015, 1639, 286–295. [Google Scholar] [CrossRef]
- Shen, S.; Leptoukh, G.G. Estimation of surface air temperature over central and eastern Eurasia from MODIS land surface temperature. Environ. Res. Lett. 2011, 31, 8–13. [Google Scholar] [CrossRef]
- Zhou, S.; Cheng, J. An improved temperature and emissivity separation algorithm for the advanced Himawari imager. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7105–7124. [Google Scholar] [CrossRef]
- Hu, D.; Yu, W.; Yi, X.; Han, F.L. Boundary temperature features of the embankment in Qumar River region along the Qinghai-Tibet transportation engineering corridor. J. Glaciol. Geocryol. 2016, 38, 1332–1339. (In Chinese) [Google Scholar]
- Chou, Y.; Sheng, Y.; Zhu, Y. Study on the relationship between the shallow ground temperature of embankment and solar radiation in permafrost regions on Qinghai-Tibet Plateau. Cold Reg. Sci. Technol. 2012, 78, 122–130. [Google Scholar] [CrossRef]
- Huang, F.; Ma, W.; Li, M.S.; Ma, Y.M. Analysis on responses of land surface temperature on the Northern Tibetan Plateau to climate change. Plateau Meteorol. 2016, 35, 55–63. (In Chinese) [Google Scholar]
- Ma, W.; Mu, Y.; Zhang, J.; Yu, W.; Zhou, Z.; Chen, T. Lateral thermal influences of roadway and railway embankments in permafrost zones along the Qinghai-Tibet Engineering Corridor. Transp. Geotech. 2019, 21, 100285. [Google Scholar] [CrossRef]
- Luo, X.; Yu, Q.; Ma, Q.; Zhang, J.M. A prediction model on thermal boundary condition of embankment based on boundary layer theory. J. Cent. South Univ. 2019, 50, 168–178. (In Chinese) [Google Scholar]
- Li, R.; Zhao, L.; Wu, T.; Ding, Y.; Xin, Y.; Zou, D.; Xiao, Y.; Jiao, Y.; Qin, Y.; Sun, L. Temporal and spatial variations of global solar radiation over the Qinghai-Tibetan Plateau during the past 40 years. Theor. Appl. Climatol. 2013, 113, 573–583. [Google Scholar] [CrossRef]
- Wu, R.; Ma, Y. Comparative analyses on radiation characteristics in different areas over the Tibetan Plateau. Plateau Meteoro 2010, 29, 251–259. (In Chinese) [Google Scholar]
- Zhang, L.; Gao, L.; Chen, K. The variation characteristics of radiation balance and surface albedo in Wayanshan Wetland in the Qing-hai Lake watershed. J. Glaciol. Geocryol. 2018, 40, 1216–1222. (In Chinese) [Google Scholar]
- Zeng, J. The Characteristics and Parameterization of Land Surface Processes and Its Relationship with Climate over Northern China. Master’s Thesis, Chinese Academy of Meteorological Sciences, Beijing, China, 2011. (In Chinese). [Google Scholar]
- Li, Z.; Lyu, S.; Ao, Y.; Wen, L.; Zhao, L.; Wang, S. Long-term energy flux and radiation balance observations over Lake Ngoring, Tibetan Plateau. Atmos. Res. 2015, 155, 13–25. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, W.; Du, W.T.; Chen, J.Z.; Qin, X. Characteristics of energy budget under different weather conditions in the ablation area of the Lao hugou Glacier No. 12, Qilian Mountains. J. Glaciol. Geocryol. 2020, 42, 332–343. (In Chinese) [Google Scholar]
- Yi, X.; Hu, D.; Yu, W.B.; Liu, W.B. Study on the temperature boundary of embankment and its calculation model of the Qinghai-Tibet Highway in permafrost area. J. Glaciol. Geocryol. 2017, 39, 336–342. (In Chinese) [Google Scholar]
- Gu, X.; Ma, Y.; Ma, W.; Sun, F.L. Climatic characteristics of surface radiation flux over the Qinghai-Tibetan Plateau. Plateau Meteorol 2018, 37, 1458–1469. (In Chinese) [Google Scholar]
- Zeng, J.; Zhang, Q. A comparative study of the characteristics of the clear-sky land surface processes over the different underlying surfaces in the northern part of China during July-September 2008. Acta Meteorol. Sin. 2012, 70, 821–836. [Google Scholar]
- Chen, C.N.; Tian, L.; Zhu, L.Q.; Zhou, Y.K. The Impact of Climate Change on the Surface Albedo over the Qinghai-Tibet Plateau. Remote Sens. 2021, 13, 2336. [Google Scholar] [CrossRef]







| Code | Land Cover | Notes |
|---|---|---|
| 20 | Forest | Lands covered by arbor, where the crown coverage is larger than 30%. |
| 30 | Grassland | Lands covered by natural herbosa, where the coverage is larger than 10%. |
| 50 | Wetland | Lands located at the boundary between land and water, with wet soil, covered by helophyte or hygrophyte. |
| 60 | Water body | Lands covered by liquid water in land, including rivers, lakes and reservoirs. |
| 90 | Bare land | Lands with vegetation coverage less than 10%, including desert, gravel, bare rock, saline–alkaline land. |
| 100 | Glacier | Lands covered by snow, glaciers or ice sheets. |
| Underlying Surface | Total Solar Radiation Rs/(MJ·m−2) | Long-Wave Radiation on Ground Surface Rl/(MJ·m−2) | Equilibrium of Long-Wave Radiation at Night Rl|n/(MJ·m−2) | Conversion Ratio Coefficient v |
|---|---|---|---|---|
| Bare land | 1011.083 | 484.000 | 322.474 | 0.1598 |
| Alpine meadow (10 cm) | 1089.583 | 596.250 | 290.743 | 0.280 |
| Alpine meadow | 1023.333 | 448.508 | 281.949 | 0.163 |
| Wetland | 480.429 | 852.714 | 364.175 | 1.017 |
| Forest | 804.000 | 1011.000 | 323.722 | 0.855 |
| Water body | 453.150 | 359.083 | 319.835 | 0.087 |
| Glacier | 971.228 | 361.8432 | 323.722 | 0.0393 |
| Underlying Surface | Modified Equation of Ground Surface Temperature | R2 | RMSE | Bias |
|---|---|---|---|---|
| Bare land | Tg = 1.2 + 3 | 0.96 | 1.27 | 6.25 |
| Grassland | Tg = 1.7 − 1.2 | 0.93 | 1.33 | 4.86 |
| Wetland | Tg = 0.51 − 6.6 | 0.95 | 0.91 | 3.82 |
| Forest | Tg = 0.4 − 7.5 | 0.89 | 0.86 | 2.59 |
| Water body | Tg = 0.9 − 4.3 | 0.93 | 1.32 | 4.83 |
| Glacier | Tg = 1.2 − 2 | 0.87 | 1.14 | 3.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, M.; Li, N.; Liu, F.; Gao, Y.; Mu, Y.; Ma, W. A Calculation Model for Ground Surface Temperature in High-Altitude Regions of the Qinghai-Tibet Plateau, China. Remote Sens. 2022, 14, 5219. https://doi.org/10.3390/rs14205219
Chai M, Li N, Liu F, Gao Y, Mu Y, Ma W. A Calculation Model for Ground Surface Temperature in High-Altitude Regions of the Qinghai-Tibet Plateau, China. Remote Sensing. 2022; 14(20):5219. https://doi.org/10.3390/rs14205219
Chicago/Turabian StyleChai, Mingtang, Nan Li, Furong Liu, Yu Gao, Yanhu Mu, and Wei Ma. 2022. "A Calculation Model for Ground Surface Temperature in High-Altitude Regions of the Qinghai-Tibet Plateau, China" Remote Sensing 14, no. 20: 5219. https://doi.org/10.3390/rs14205219
APA StyleChai, M., Li, N., Liu, F., Gao, Y., Mu, Y., & Ma, W. (2022). A Calculation Model for Ground Surface Temperature in High-Altitude Regions of the Qinghai-Tibet Plateau, China. Remote Sensing, 14(20), 5219. https://doi.org/10.3390/rs14205219







