Analyses of the Impact of Soil Conditions and Soil Degradation on Vegetation Vitality and Crop Productivity Based on Airborne Hyperspectral VNIR–SWIR–TIR Data in a Semi-Arid Rainfed Agricultural Area (Camarena, Central Spain)
Abstract
1. Introduction
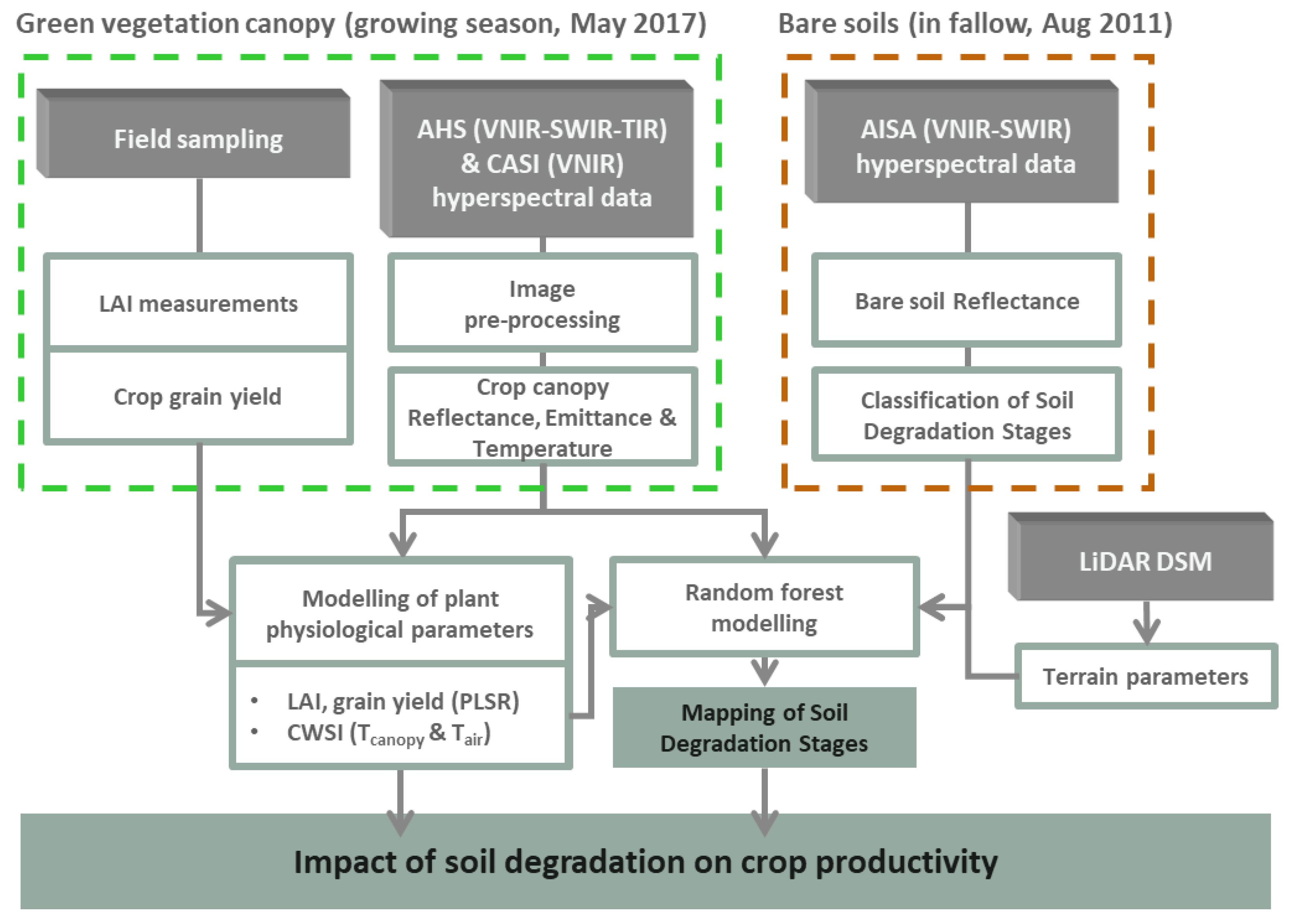
2. Materials and Methods
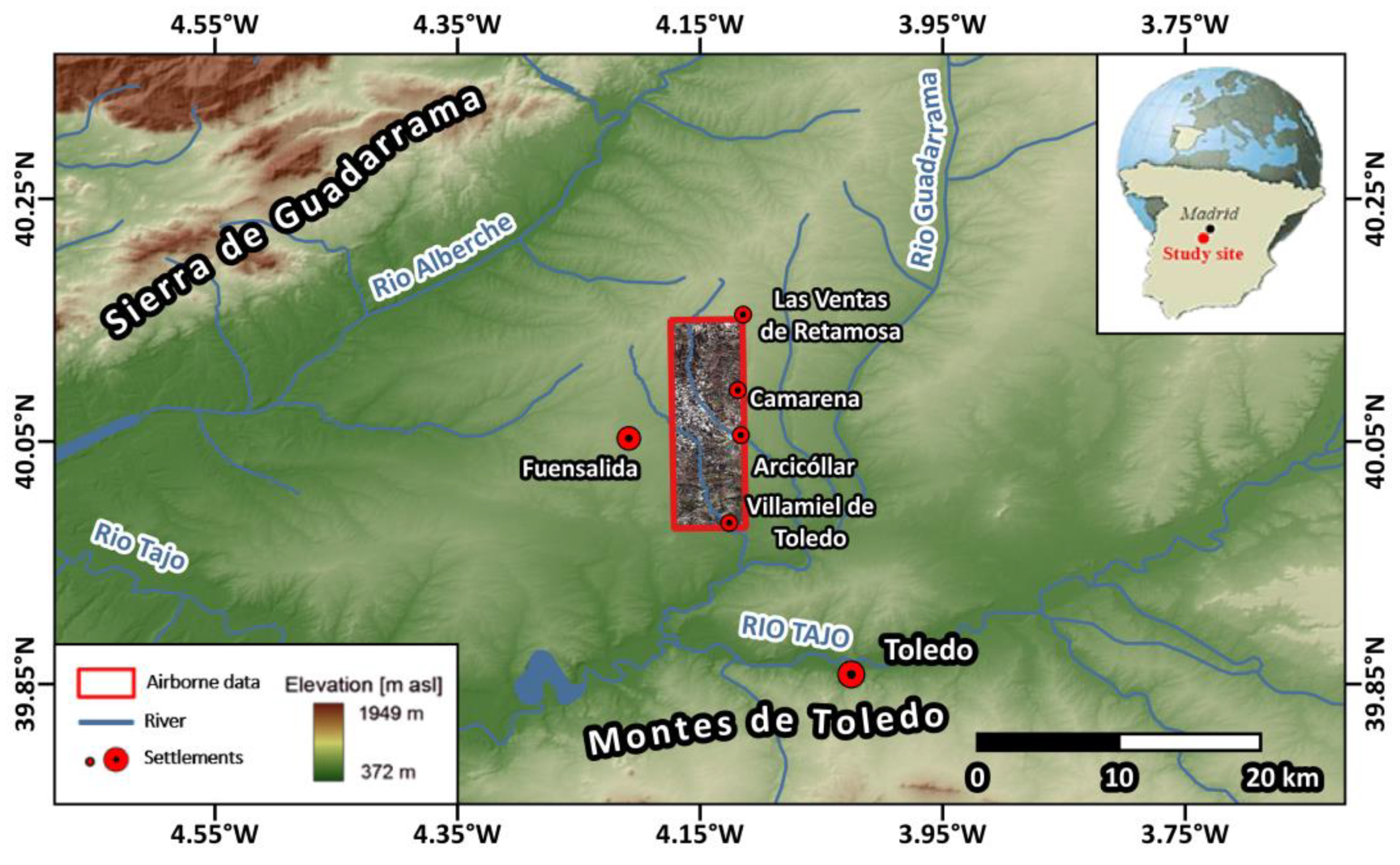
2.1. Study Site
2.2. Airborne Data Acquisition and Processing
2.3. Field Data Collection
2.4. Remote Sensing Data Analysis
2.4.1. Modeling of Crop Properties
2.4.2. CWSI
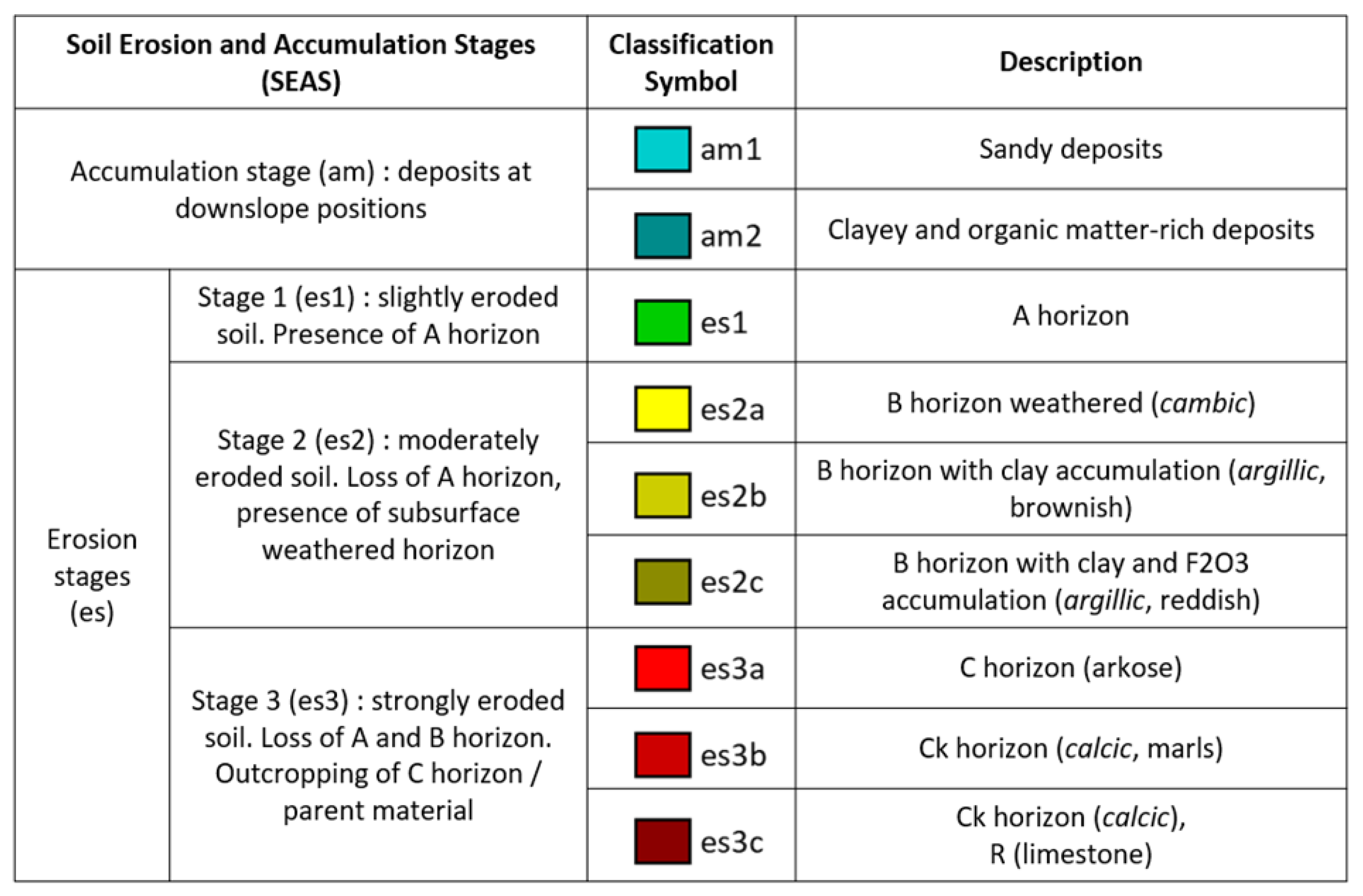
2.4.3. Prediction of SEAS Based on the Canopy Spectral Signal
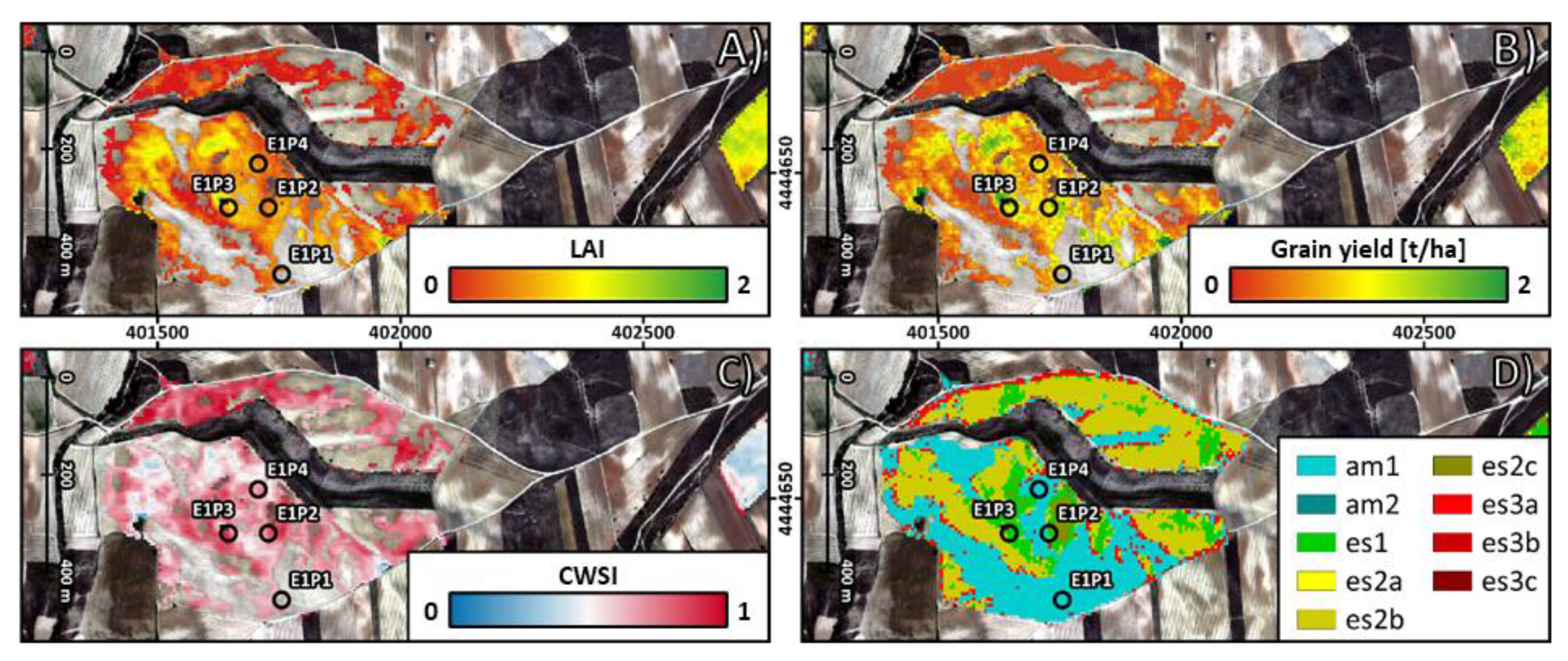
3. Results
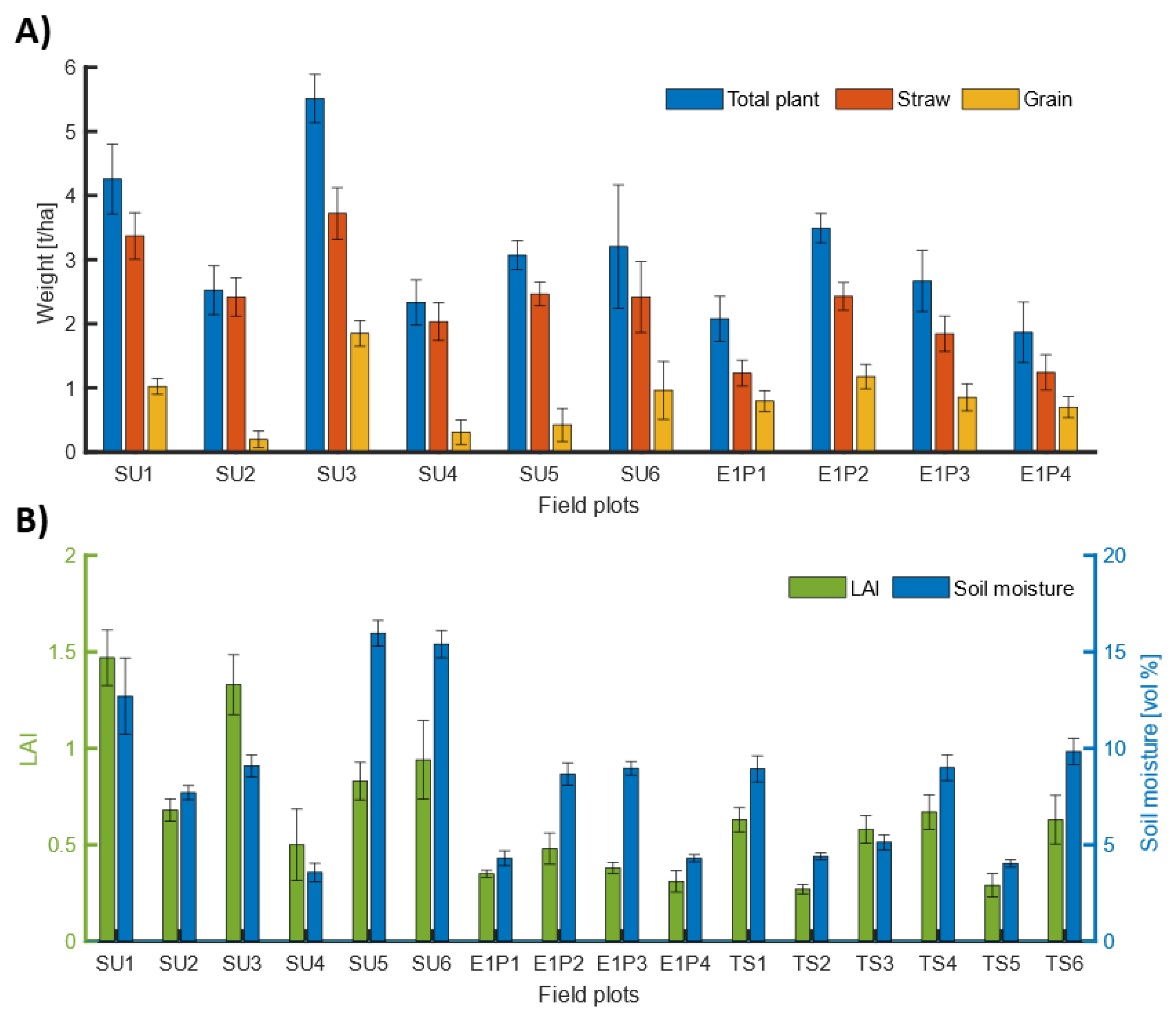
3.1. Field Data
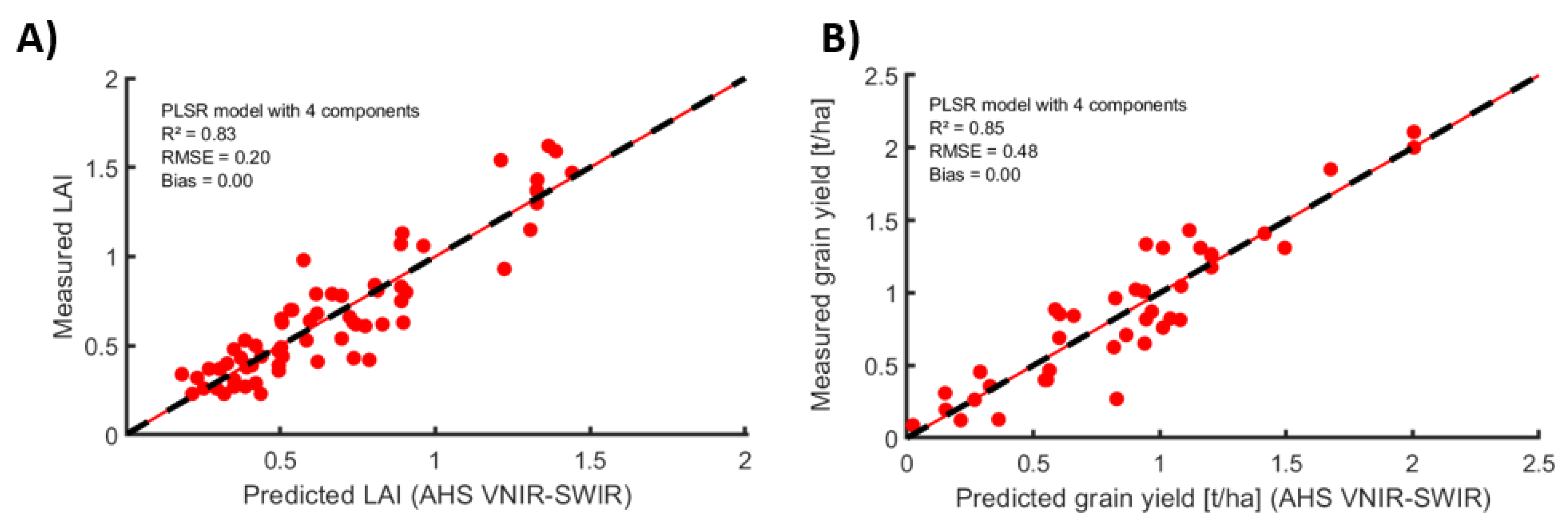
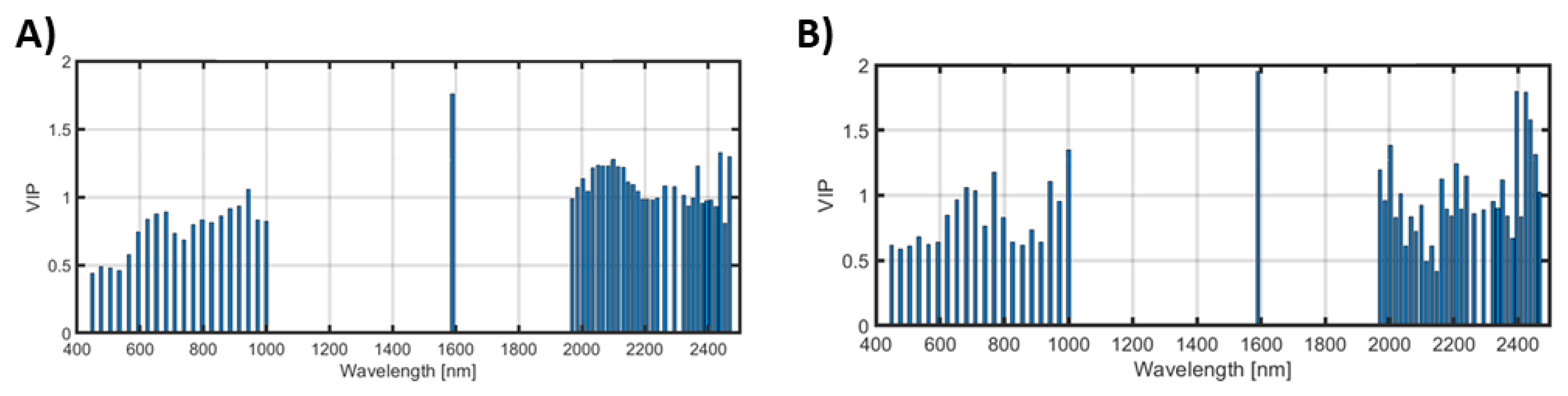
3.2. Prediction of Crop Properties
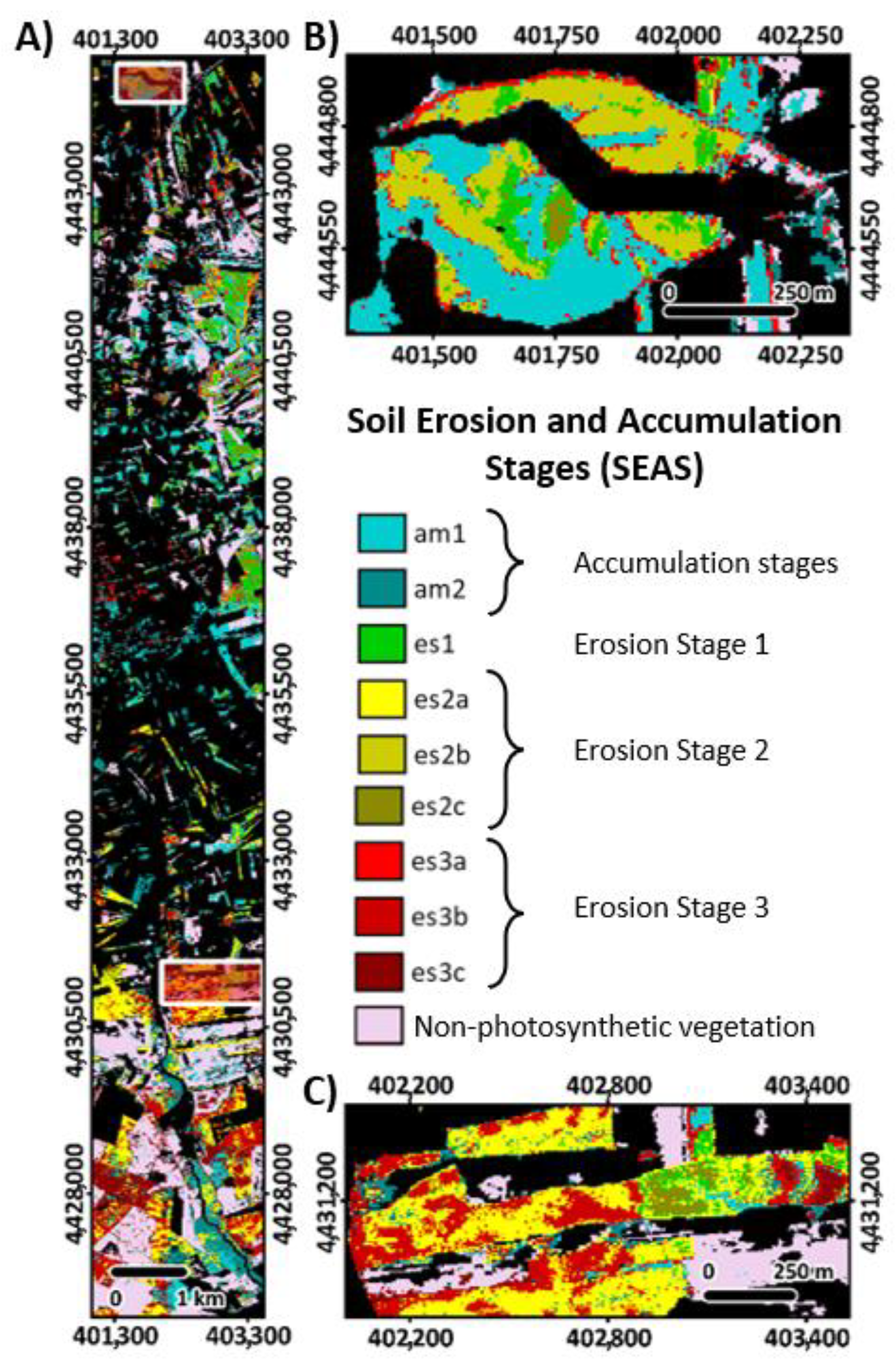
3.3. Prediction of SEAS Based on the Canopy Spectral Signal
4. Discussion
- Prediction of crop properties
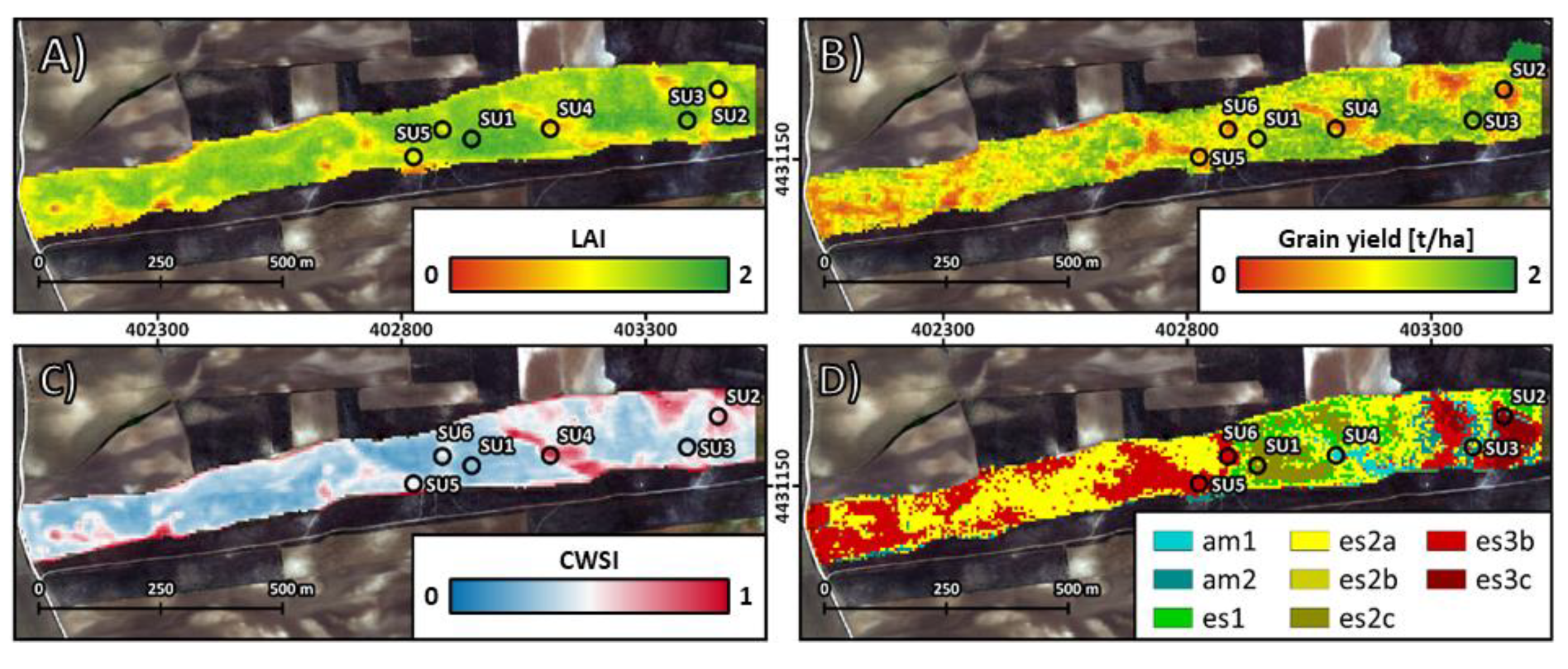
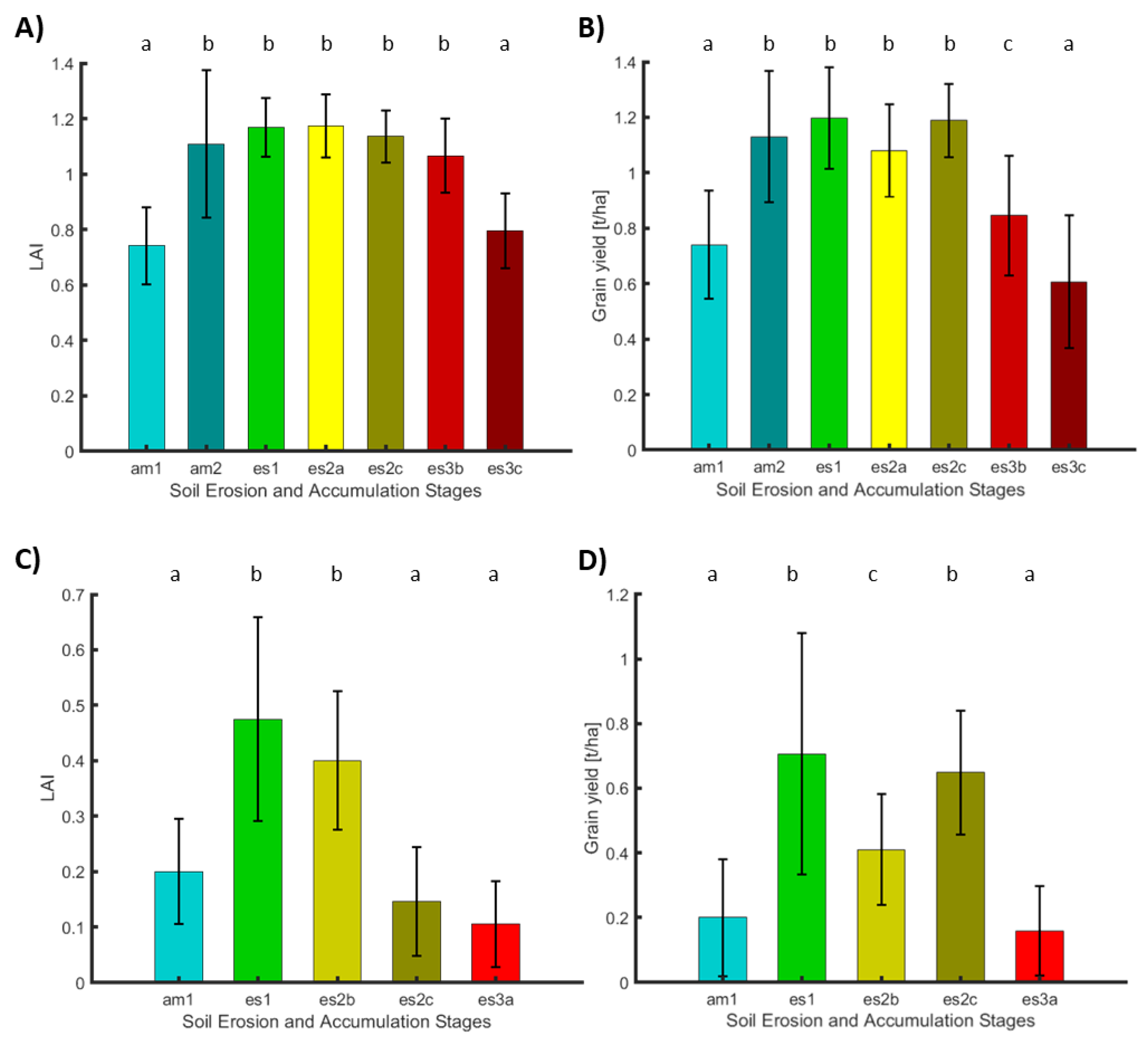
- Erosion stages in Camarena and their link to crop properties
- Prediction of SEAS based on the canopy spectral signal
5. Conclusions
- (1)
- The soil accumulation and degradation stages derived from hyperspectral remote sensing data are spatially related to crop vitality and yield.
- (2)
- The most severe stages of soil degradation with exposed bedrock, as well as sandy accumulation zones, do have a strong negative impact on plant vitality and crop yield across the study area.
- (3)
- The soil degradation status can be directly assessed based on spectral information of the vegetation canopy, using non-linear machine learning models such as a random forest classifier.
- (4)
- The exploitation of the spectral VNIR–SWIR and TIR information, as well as the auxiliary topographical information, increases the modeling potential for the complex relationship of the vegetation response to soil degradation. Furthermore, the reduction in the redundant spectral information, e.g., by applying an MNF transformation, is a crucial processing step that severely improves the overall classification accuracy.
- (5)
- Mapping SEAS zones could provide a tool for farmers to estimate the forthcoming yield and optimize field management (e.g., selection of suitable crop types, allocation of fertilizers, irrigation) by considering the detailed degradation status of their field plots.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lal, R.; Follett, R.F.; Stewart, B.A.; Kimble, J.M. Soil Carbon Sequestration to Mitigate Climate Change and Advance Food Security. Soil Sci. 2007, 172, 943–956. [Google Scholar] [CrossRef]
- Montanarella, L.; Pennock, D.J.; McKenzie, N.; Badraoui, M.; Chude, V.; Baptista, I.; Mamo, T.; Yemefack, M.; Singh Aulakh, M.; Yagi, K.; et al. World’s Soils Are under Threat. SOIL 2016, 2, 79–82. [Google Scholar] [CrossRef]
- Guerra, C.A.; Rosa, I.M.D.; Valentini, E.; Wolf, F.; Filipponi, F.; Karger, D.N.; Xuan, A.N.; Mathieu, J.; Lavelle, P.; Eisenhauer, N. Global Vulnerability of Soil Ecosystems to Erosion. Landsc. Ecol. 2020, 35, 823–842. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wu, B.; Ling, F.; Zeng, Y.; Yan, N.; Yuan, C. Identification of Priority Areas for Controlling Soil Erosion. CATENA 2010, 83, 76–86. [Google Scholar] [CrossRef]
- Lal, R. Soil Erosion and the Global Carbon Budget. Environ. Int. 2003, 29, 437–450. [Google Scholar] [CrossRef]
- Paustian, K.; Lehmann, J.; Ogle, S.; Reay, D.; Robertson, G.P.; Smith, P. Climate-Smart Soils. Nature 2016, 532, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Keesstra, S.D.; Bouma, J.; Wallinga, J.; Tittonell, P.; Smith, P.; Cerdà, A.; Montanarella, L.; Quinton, J.N.; Pachepsky, Y.; van der Putten, W.H.; et al. The Significance of Soils and Soil Science towards Realization of the United Nations Sustainable Development Goals. SOIL 2016, 2, 111–128. [Google Scholar] [CrossRef]
- García-Ruiz, J.M.; Nadal-Romero, E.; Lana-Renault, N.; Beguería, S. Erosion in Mediterranean Landscapes: Changes and Future Challenges. Geomorphology 2013, 198, 20–36. [Google Scholar] [CrossRef]
- Raclot, D.; Bissonnais, Y.L.; Annabi, M.; Sabir, M. Sub-Chapter 2.3.3. Challenges for Mitigating Mediterranean Soil Erosion under Global Change. In The Mediterranean Region under Climate Change; Moatti, J.-P., Thiébault, S., Eds.; IRD Éditions: Paris, France, 2016; pp. 311–318. ISBN 978-2-7099-2219-7. [Google Scholar]
- Gamon, J.A.; Somers, B.; Malenovský, Z.; Middleton, E.M.; Rascher, U.; Schaepman, M.E. Assessing Vegetation Function with Imaging Spectroscopy. Surv. Geophys. 2019, 40, 489–513. [Google Scholar] [CrossRef]
- Lausch, A.; Baade, J.; Bannehr, L.; Borg, E.; Bumberger, J.; Chabrilliat, S.; Dietrich, P.; Gerighausen, H.; Glässer, C.; Hacker, J.M.; et al. Linking Remote Sensing and Geodiversity and Their Traits Relevant to Biodiversity—Part I: Soil Characteristics. Remote Sens. 2019, 11, 2356. [Google Scholar] [CrossRef]
- Green, R.O. Lessons and Key Results from 30 Years of Imaging Spectroscopy. In Proceedings of the Imaging Spectrometry XIX. International Society for Optics and Photonics, San Diego, CA, USA, 19 September 2014; Volume 9222, p. 92220B. [Google Scholar]
- Sahoo, R.N.; Ray, S.S.; Manjunath, K.R. Hyperspectral Remote Sensing of Agriculture. Curr. Sci. 2015, 108, 848–859. [Google Scholar]
- Schaepman, M.E.; Ustin, S.L.; Plaza, A.J.; Painter, T.H.; Verrelst, J.; Liang, S. Earth System Science Related Imaging Spectroscopy—An Assessment. Remote Sens. Environ. 2009, 113, S123–S137. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and Biochemical Sources of Variability in Canopy Reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gitelson, A.A.; Jacquemoud, S.; Schaepman, M.; Asner, G.P.; Gamon, J.A.; Zarco-Tejada, P. Retrieval of Foliar Information about Plant Pigment Systems from High Resolution Spectroscopy. Remote Sens. Environ. 2009, 113, S67–S77. [Google Scholar] [CrossRef]
- Verrelst, J.; Malenovský, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.-P.; Lewis, P.; North, P.; Moreno, J. Quantifying Vegetation Biophysical Variables from Imaging Spectroscopy Data: A Review on Retrieval Methods. Surv. Geophys. 2019, 40, 589–629. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral Vegetation Indices and Their Relationships with Agricultural Crop Characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Chabrillat, S.; Demattê, J.A.M.; Taylor, G.R.; Hill, J.; Whiting, M.L.; Sommer, S. Using Imaging Spectroscopy to Study Soil Properties. Remote Sens. Environ. 2009, 113, S38–S55. [Google Scholar] [CrossRef]
- Chabrillat, S.; Ben-Dor, E.; Cierniewski, J.; Gomez, C.; Schmid, T.; van Wesemael, B. Imaging Spectroscopy for Soil Mapping and Monitoring. Surv. Geophys. 2019, 40, 361–399. [Google Scholar] [CrossRef]
- Paz-Kagan, T.; Zaady, E.; Salbach, C.; Schmidt, A.; Lausch, A.; Zacharias, S.; Notesco, G.; Ben-Dor, E.; Karnieli, A. Mapping the Spectral Soil Quality Index (SSQI) Using Airborne Imaging Spectroscopy. Remote Sens. 2015, 7, 15748–15781. [Google Scholar] [CrossRef]
- Schmid, T.; Rodriguez-Rastrero, M.; Escribano, P.; Palacios-Orueta, A.; Ben-Dor, E.; Plaza, A.; Milewski, R.; Huesca, M.; Bracken, A.; Cicuendez, V.; et al. Characterization of Soil Erosion Indicators Using Hyperspectral Data From a Mediterranean Rainfed Cultivated Region. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 845–860. [Google Scholar] [CrossRef]
- Žížala, D.; Zádorová, T.; Kapička, J. Assessment of Soil Degradation by Erosion Based on Analysis of Soil Properties Using Aerial Hyperspectral Images and Ancillary Data, Czech Republic. Remote Sens. 2017, 9, 28. [Google Scholar] [CrossRef]
- Goldshleger, N.; Goldshleger, N.; Livene, I.; Chudnovsky, A.; Ben-Dor, E. Integrating Passive and Active Remote Sensing Methods to Assess Soil Salinity: A Case Study from Jezre’el Valley, Israel. Soil Sci. 2012, 177, 392–401. [Google Scholar] [CrossRef]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent Advances of Hyperspectral Imaging Technology and Applications in Agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Hill, J.; Hostert, P.; Röder, A. Long-Term Observation of Mediterranean Ecosystems with Satellite Remote Sensing. In Recent Dynamics of the Mediterranean Vegetation and Landscape; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2004; pp. 33–43. ISBN 978-0-470-09371-9. [Google Scholar]
- Hill, J.; Schütt, B. Mapping Complex Patterns of Erosion and Stability in Dry Mediterranean Ecosystems. Remote Sens. Environ. 2000, 74, 557–569. [Google Scholar] [CrossRef]
- Yuzugullu, O.; Lorenz, F.; Fröhlich, P.; Liebisch, F. Understanding Fields by Remote Sensing: Soil Zoning and Property Mapping. Remote Sens. 2020, 12, 1116. [Google Scholar] [CrossRef]
- Pascucci, S.; Pignatti, S.; Casa, R.; Darvishzadeh, R.; Huang, W. Special Issue “Hyperspectral Remote Sensing of Agriculture and Vegetation”. Remote Sens. 2020, 12, 3665. [Google Scholar] [CrossRef]
- Ustin, S.L.; Roberts, D.A.; Gamon, J.A.; Asner, G.P.; Green, R.O. Using Imaging Spectroscopy to Study Ecosystem Processes and Properties. BioScience 2004, 54, 523–534. [Google Scholar] [CrossRef]
- Kokaly, R.F. Investigating a Physical Basis for Spectroscopic Estimates of Leaf Nitrogen Concentration. Remote Sens. Environ. 2001, 75, 153–161. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-Derived Land Surface Temperature: Current Status and Perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Heinemann, S.; Siegmann, B.; Thonfeld, F.; Muro, J.; Jedmowski, C.; Kemna, A.; Kraska, T.; Muller, O.; Schultz, J.; Udelhoven, T.; et al. Land Surface Temperature Retrieval for Agricultural Areas Using a Novel UAV Platform Equipped with a Thermal Infrared and Multispectral Sensor. Remote Sens. 2020, 12, 1075. [Google Scholar] [CrossRef]
- Gerhards, M.; Schlerf, M.; Mallick, K.; Udelhoven, T. Challenges and Future Perspectives of Multi-/Hyperspectral Thermal Infrared Remote Sensing for Crop Water-Stress Detection: A Review. Remote Sens. 2019, 11, 1240. [Google Scholar] [CrossRef]
- Calderón, R.; Navas-Cortés, J.A.; Lucena, C.; Zarco-Tejada, P.J. High-Resolution Airborne Hyperspectral and Thermal Imagery for Early Detection of Verticillium Wilt of Olive Using Fluorescence, Temperature and Narrow-Band Spectral Indices. Remote Sens. Environ. 2013, 139, 231–245. [Google Scholar] [CrossRef]
- O’Shaughnessy, S.A.; Evett, S.R.; Colaizzi, P.D.; Howell, T.A. A Crop Water Stress Index and Time Threshold for Automatic Irrigation Scheduling of Grain Sorghum. Agric. Water Manag. 2012, 107, 122–132. [Google Scholar] [CrossRef]
- Khanal, S.; Fulton, J.; Shearer, S. An Overview of Current and Potential Applications of Thermal Remote Sensing in Precision Agriculture. Comput. Electron. Agric. 2017, 139, 22–32. [Google Scholar] [CrossRef]
- Panigada, C.; Rossini, M.; Meroni, M.; Cilia, C.; Busetto, L.; Amaducci, S.; Boschetti, M.; Cogliati, S.; Picchi, V.; Pinto, F.; et al. Fluorescence, PRI and Canopy Temperature for Water Stress Detection in Cereal Crops. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 167–178. [Google Scholar] [CrossRef]
- Pinter, P.J., Jr.; Hatfield, J.L.; Schepers, J.S.; Barnes, E.M.; Moran, M.S.; Daughtry, C.S.T.; Upchurch, D.R. Remote Sensing for Crop Management. Photogramm. Eng. Remote Sens. 2003, 69, 647–664. [Google Scholar] [CrossRef]
- Loizzo, R.; Guarini, R.; Longo, F.; Scopa, T.; Formaro, R.; Facchinetti, C.; Varacalli, G. Prisma: The Italian Hyperspectral Mission. In Proceedings of the Igarss 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 175–178. [Google Scholar]
- Schickling, A.; Chabrillat, S.; Storch, T.; Fischer, S. Enmap: The German Spaceborne Imaging Spectroscopy Mission. In Proceedings of the OSA Optical Sensors and Sensing Congress 2021 (AIS, FTS, HISE, SENSORS, ES) (2021), Washington, DC, USA, 19–23 July 2021; p. HF4E.1. [Google Scholar]
- Rast, M.; Nieke, J.; Adams, J.; Isola, C.; Gascon, F. Copernicus Hyperspectral Imaging Mission for the Environment (Chime). In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 108–111. [Google Scholar]
- Thompson, D.R.; Bearden, D.; Brosnan, I.; Cawse-Nicholson, K.; Chrone, J.; Green, R.O.; Glenn, N.; Guild, L.; Hook, S.J.; Kokaly, R.; et al. NASA’s Surface Biology and Geology Concept Study: Status and Next Steps. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Brussels, Belgium, 11–16 July 2021; pp. 112–114. [Google Scholar]
- Keys to Soil Taxonomy; U.S. Department of Agriculture, Natural Resources Conservation Service, National Soil Survey Center: Lincoln, NE, USA, 2015.
- Michéli, E.; Schad, P.; Dent, D.; Nachtergaele, F.O.; Spaargaren, O.C. World Reference Base for Soil Resources, 2006; FAO (Food and Agriculture Organization of the United Nations), Ed.; Food and Agriculture Organization of the United Nations: Rome, Italy, 2006. [Google Scholar]
- Previtali, F. Pedoenvironments of the Mediterranean Countries: Resources and Threats. In Soil Security for Ecosystem Management: Mediterranean Soil Ecosystems 1; Kapur, S., Erşahin, S., Eds.; SpringerBriefs in Environment, Security, Development and Peace; Springer International Publishing: Cham, Switzerland, 2014; pp. 61–82. ISBN 978-3-319-00699-4. [Google Scholar]
- De Alba, S. Modeling the Effects of Complex Topography and Patterns of Tillage on Soil Translocation by Tillage with Mouldboard Plough. J. Soil Water Conserv. 2001, 56, 335–345. [Google Scholar]
- De Miguel, E.; Fernandez-Renau, A.; Prado, E.; Jimenez, M.; De La Camara, O.G.; Lines, C.; Gomez, J.A.; Martin, A.I.; Munoz, F. The Processing of CASI-1500i Data at INTA PAF. EARSeL eProc. 2014, 13, 30–37. [Google Scholar]
- De Miguel, E.; Fernandez-Renau, A.; Prado, E.; Jimenez, M.; De La Camara, O.G.; Lines, C.; Gomez, J.A.; Martin, A.I.; Munoz, F. A Review of INTA AHS PAF. EARSeL eProc. 2014, 13, 20–29. [Google Scholar]
- Schläpfer, D.; Richter, R. Geo-Atmospheric Processing of Airborne Imaging Spectrometry Data—Part 1: Parametric Orthorectification. Int. J. Remote Sens. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Richter, R.; Schläpfer, D. Atmospheric/Topographic Correction for Airborne Imagery (ATCOR-4 User Guide, Version 7.4, September 2021); ReSe Applications LLC: Wil, Switzerland, 2014. [Google Scholar]
- de Miguel, E.; Carrascosa, V.B.; Lagosr, M.G.; Michavila, M.J.; Schmid, T.; de la Cámara, Ó.G. Quality of INTA-AHS Images for Estimating Apparent Thermal Inertia in Soils. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3311–3314. [Google Scholar]
- Wold, H. Estimation of Principal Components and Related Models by Iterative Least Squares. In Multivariate Analysis; Academic Press: New York, NY, USA, 1966; pp. 391–420. [Google Scholar]
- Chen, J.; Gu, S.; Shen, M.; Tang, Y.; Matsushita, B. Estimating Aboveground Biomass of Grassland Having a High Canopy Cover: An Exploratory Analysis of in Situ Hyperspectral Data. Int. J. Remote Sens. 2009, 30, 6497–6517. [Google Scholar] [CrossRef]
- Feilhauer, H.; Asner, G.P.; Martin, R.E.; Schmidtlein, S. Brightness-Normalized Partial Least Squares Regression for Hyperspectral Data. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1947–1957. [Google Scholar] [CrossRef]
- Abdi, H. Partial Least Squares Regression and Projection on Latent Structure Regression (PLS Regression). WIREs Comput. Stat. 2010, 2, 97–106. [Google Scholar] [CrossRef]
- Otto, M. Chemometrics: Statistics and Computer Application in Analytical Chemistry, 3rd ed.; Wiley-VCH: Weinheim, Germany, 2016; ISBN 978-3-527-34097-2. [Google Scholar]
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a Test of Whether One of Two Random Variables Is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- McKight, P.E.; Najab, J. Kruskal-Wallis Test. In The Corsini Encyclopedia of Psychology; American Cancer Society, Wiley & Sons: New York, NY, USA, 2010; p. 1. ISBN 978-0-470-47921-6. [Google Scholar]
- Fisher, R.A. Statistical Methods for Research Workers. In Breakthroughs in Statistics: Methodology and Distribution; Kotz, S., Johnson, N.L., Eds.; Springer Series in Statistics; Springer: New York, NY, USA, 1992; pp. 66–70. ISBN 978-1-4612-4380-9. [Google Scholar]
- Fuchs, M. Infrared Measurement of Canopy Temperature and Detection of Plant Water Stress. Theor. Appl. Climatol. 1990, 42, 253–261. [Google Scholar] [CrossRef]
- Alghory, A.; Yazar, A. Evaluation of Crop Water Stress Index and Leaf Water Potential for Deficit Irrigation Management of Sprinkler-Irrigated Wheat. Irrig. Sci. 2019, 37, 61–77. [Google Scholar] [CrossRef]
- Rosenberg, O.; Cohen, Y.; Saranga, Y.; Levi, A.; Alchanatis, V. Comparison of Methods for Field Scale Mapping of Plant Water Status Using Aerial Thermal Imagery. In Precision Agriculture ’13; Stafford, J.V., Ed.; Academic Publishers: Wageningen, The Netherlands, 2013; pp. 185–192. [Google Scholar]
- Idso, S.B. Non-Water-Stressed Baselines: A Key to Measuring and Interpreting Plant Water Stress. Agric. Meteorol. 1982, 27, 59–70. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Krishna, G.; Sahoo, R.N.; Singh, P.; Patra, H.; Bajpai, V.; Das, B.; Kumar, S.; Dhandapani, R.; Vishwakarma, C.; Pal, M.; et al. Application of Thermal Imaging and Hyperspectral Remote Sensing for Crop Water Deficit Stress Monitoring. Geocarto Int. 2019, 36, 481–498. [Google Scholar] [CrossRef]
- Alchanatis, V.; Cohen, Y.; Cohen, S.; Moller, M.; Sprinstin, M.; Meron, M.; Tsipris, J.; Saranga, Y.; Sela, E. Evaluation of Different Approaches for Estimating and Mapping Crop Water Status in Cotton with Thermal Imaging. Precis. Agric. 2010, 11, 27–41. [Google Scholar] [CrossRef]
- Bian, J.; Zhang, Z.; Chen, J.; Chen, H.; Cui, C.; Li, X.; Chen, S.; Fu, Q. Simplified Evaluation of Cotton Water Stress Using High Resolution Unmanned Aerial Vehicle Thermal Imagery. Remote Sens. 2019, 11, 267. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Gambill, D.R.; Wall, W.A.; Fulton, A.J.; Howard, H.R. Predicting USCS Soil Classification from Soil Property Variables Using Random Forest. J. TerraMech. 2016, 65, 85–92. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.M.; Heuvelink, G.B.M.; Gonzalez, M.R.; Kilibarda, M.; Blagotic, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global Gridded Soil Information Based on Machine Learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- Ok, A.O.; Akar, O.; Gungor, O. Evaluation of Random Forest Method for Agricultural Crop Classification. Eur. J. Remote Sens. 2012, 45, 421–432. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Feng, H. Comparative of Remote Sensing Estimation Models of Winter Wheat Biomass Based on Random Forest Algorithm. Trans. Chin. Soc. Agric. Eng. 2016, 32, 175–182. [Google Scholar]
- Martín-Sotoca, J.J.; Saa-Requejo, A.; Moratiel, R.; Dalezios, N.; Faraslis, I.; Tarquis, A.M. Statistical Analysis for Satellite-Index-Based Insurance to Define Damaged Pasture Thresholds. Nat. Hazards Earth Syst. Sci. 2019, 19, 1685–1702. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N.; Li, Z.-L. A Comparative Study of Land Surface Emissivity Retrieval from NOAA Data. Remote Sens. Environ. 2001, 75, 256–266. [Google Scholar] [CrossRef]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A Transformation for Ordering Multispectral Data in Terms of Image Quality with Implications for Noise Removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Sharabian, V.R.; Noguchi, N.; Ishi, K. Significant Wavelengths for Prediction of Winter Wheat Growth Status and Grain Yield Using Multivariate Analysis. Eng. Agric. Environ. Food 2014, 7, 14–21. [Google Scholar] [CrossRef]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating Biomass of Barley Using Crop Surface Models (CSMs) Derived from UAV-Based RGB Imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop—The FAO Crop Model to Simulate Yield Response to Water: I. Concepts and Underlying Principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Xu, X.; Yang, G.; Wang, J. Estimation of Winter Wheat Biomass and Yield by Combining the AquaCrop Model and Field Hyperspectral Data. Remote Sens. 2016, 8, 972. [Google Scholar] [CrossRef]
- Jarmer, T.; Siegmann, B.; Lilienthal, H.; Höfle, B.; Selige, T.; Richter, N. LAI Assessing of Wheat Stands from AISA-Dual Imagery. In Proceedings of the EARSeL 8th EARSeL SIG-Imaging Spectroscopy Workshop, Nantes, France, 8–10 April 2013; p. 5. [Google Scholar]
- Marshall, M.; Thenkabail, P. Advantage of Hyperspectral EO-1 Hyperion over Multispectral IKONOS, GeoEye-1, WorldView-2, Landsat ETM+, and MODIS Vegetation Indices in Crop Biomass Estimation. ISPRS J. Photogramm. Remote Sens. 2015, 108, 205–218. [Google Scholar] [CrossRef]
- Wengert, M.; Piepho, H.-P.; Astor, T.; Graß, R.; Wijesingha, J.; Wachendorf, M. Assessing Spatial Variability of Barley Whole Crop Biomass Yield and Leaf Area Index in Silvoarable Agroforestry Systems Using UAV-Borne Remote Sensing. Remote Sens. 2021, 13, 2751. [Google Scholar] [CrossRef]
- Ceballos, A.; Martínez-Fernández, J.; Santos, F.; Alonso, P. Soil-Water Behaviour of Sandy Soils under Semi-Arid Conditions in the Duero Basin (Spain). J. Arid Environ. 2002, 51, 501–519. [Google Scholar] [CrossRef]
- Pinter, P.J.; Fry, K.E.; Guinn, G.; Mauney, J.R. Infrared Thermometry: A Remote Sensing Technique for Predicting Yield in Water-Stressed Cotton. Agric. Water Manag. 1983, 6, 385–395. [Google Scholar] [CrossRef]
- Olufayo, A.; Baldy, C.; Ruelle, P. Sorghum Yield, Water Use and Canopy Temperatures under Different Levels of Irrigation. Agric. Water Manag. 1996, 30, 77–90. [Google Scholar] [CrossRef]
- Wang, D.-C.; Zhang, G.-L.; Zhao, M.-S.; Pan, X.-Z.; Zhao, Y.-G.; Li, D.-C.; Macmillan, B. Retrieval and Mapping of Soil Texture Based on Land Surface Diurnal Temperature Range Data from MODIS. PLoS ONE 2015, 10, e0129977. [Google Scholar] [CrossRef] [PubMed]
- Berndtsson, R.; Larson, M. Spatial Variability of Infiltration in a Semi-Arid Environment. J. Hydrol. 1987, 90, 117–133. [Google Scholar] [CrossRef]
- Kosmas, C.; Gerontidis, S.; Marathianou, M.; Detsis, B.; Zafiriou, T.; Nan Muysen, W.; Govers, G.; Quine, T.; Vanoost, K. The Effects of Tillage Displaced Soil on Soil Properties and Wheat Biomass. Soil Tillage Res. 2001, 58, 31–44. [Google Scholar] [CrossRef]
- Cammarano, D.; Ronga, D.; Francia, E.; Akar, T.; Al-Yassin, A.; Benbelkacem, A.; Grando, S.; Romagosa, I.; Stanca, A.M.; Pecchioni, N. Genetic and Management Effects on Barley Yield and Phenology in the Mediterranean Basin. Front. Plant Sci. 2021, 12, 655406. [Google Scholar] [CrossRef]
- Serrano, L.; Filella, I.; Peñuelas, J. Remote Sensing of Biomass and Yield of Winter Wheat under Different Nitrogen Supplies. Crop Sci. 2000, 40, 723–731. [Google Scholar] [CrossRef]
- Cammarano, D.; Ceccarelli, S.; Grando, S.; Romagosa, I.; Benbelkacem, A.; Akar, T.; Al-Yassin, A.; Pecchioni, N.; Francia, E.; Ronga, D. The Impact of Climate Change on Barley Yield in the Mediterranean Basin. Eur. J. Agron. 2019, 106, 1–11. [Google Scholar] [CrossRef]
- Baret, F.; Houlès, V.; Guérif, M. Quantification of Plant Stress Using Remote Sensing Observations and Crop Models: The Case of Nitrogen Management. J. Exp. Bot. 2007, 58, 869–880. [Google Scholar] [CrossRef]
- Huntingford, C.; Hugo Lambert, F.; Gash, J.H.C.; Taylor, C.M.; Challinor, A.J. Aspects of Climate Change Prediction Relevant to Crop Productivity. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 1999–2009. [Google Scholar] [CrossRef] [PubMed]
- Jamieson, P.D.; Martin, R.J.; Francis, G.S.; Wilson, D.R. Drought Effects on Biomass Production and Radiation-Use Efficiency in Barley. Field Crop. Res. 1995, 43, 77–86. [Google Scholar] [CrossRef]
- Chabrillat, S.; Schmid, T.; Milewski, R.; Escribano, P.; Garcia, M.; Ben-Dor, E.; Guillaso, S.; Pelayo, M.; Reyes, A.; Sobejano-Paz, V.; et al. Mapping Crop Variability Related to Soil Quality and Crop Stress Within Rainfed Mediterranean Agroecosystems Using Hyperspectral Data. In 2018 9th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (Whispers); IEEE: New York, NY, USA, 2018; ISBN 978-1-72811-581-8. [Google Scholar]
- Chapman, G.W. The Relation of Iron and Manganese to Chlorosis in Plants. New Phytol. 1931, 30, 266–283. [Google Scholar] [CrossRef]
- Chan, J.C.-W.; Paelinckx, D. Evaluation of Random Forest and Adaboost Tree-Based Ensemble Classification and Spectral Band Selection for Ecotope Mapping Using Airborne Hyperspectral Imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the Random Forest Framework for Classification of Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Ibarrola-Ulzurrun, E.; Marcello, J.; Gonzalo-Martin, C. Assessment of Component Selection Strategies in Hyperspectral Imagery. Entropy 2017, 19, 666. [Google Scholar] [CrossRef]
- Zhang, C. Combining Hyperspectral and Lidar Data for Vegetation Mapping in the Florida Everglades. Photogramm. Eng. Remote Sens. 2014, 80, 733–743. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Neumann, C.; Förster, M.; Buddenbaum, H.; Ghosh, A.; Clasen, A.; Joshi, P.K.; Koch, B. Comparison of Feature Reduction Algorithms for Classifying Tree Species with Hyperspectral Data on Three Central European Test Sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2547–2561. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Atkinson, P.M.; Yao, H. Predicting Soil Organic Carbon Content in Spain by Combining Landsat TM and ALOS PALSAR Images. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102182. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random Forests for Land Cover Classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Kluczek, M.; Zagajewski, B.; Kycko, M. Airborne HySpex Hyperspectral Versus Multitemporal Sentinel-2 Images for Mountain Plant Communities Mapping. Remote Sens. 2022, 14, 1209. [Google Scholar] [CrossRef]
- Phan, T.N.; Kuch, V.; Lehnert, L.W. Land Cover Classification Using Google Earth Engine and Random Forest Classifier—The Role of Image Composition. Remote Sens. 2020, 12, 2411. [Google Scholar] [CrossRef]
- Stehman, S.V.; Foody, G.M. Key Issues in Rigorous Accuracy Assessment of Land Cover Products. Remote Sens. Environ. 2019, 231, 111199. [Google Scholar] [CrossRef]
- Heydari, S.S.; Mountrakis, G. Effect of Classifier Selection, Reference Sample Size, Reference Class Distribution and Scene Heterogeneity in per-Pixel Classification Accuracy Using 26 Landsat Sites. Remote Sens. Environ. 2018, 204, 648–658. [Google Scholar] [CrossRef]
- Gomez, C.; Oltra-Carrió, R.; Bacha, S.; Lagacherie, P.; Briottet, X. Evaluating the Sensitivity of Clay Content Prediction to Atmospheric Effects and Degradation of Image Spatial Resolution Using Hyperspectral VNIR/SWIR Imagery. Remote Sens. Environ. 2015, 164, 1–15. [Google Scholar] [CrossRef]



| VNIR | |
|---|---|
| Coverage [µm] | 0.38–1.05 |
| Bandwidth [FWHM] | 3 nm |
| Number of Bands | 288 (144 binned) |
| VNIR | SWIR I | SWIR II | TIR | |
|---|---|---|---|---|
| Coverage [µm] | 0.43–1.03 | 1.55–1.65 | 1.90–2.55 | 8.00–12.70 |
| Bandwidth [FWHM] | 28 nm | 90 nm | 18 nm | 450 nm |
| Number of Bands | 20 | 1 | 42 | 10 |
| Site Name | Total Grain [kg/ha] | Total Straw [kg/ha] | Total Plant [kg/ha] | LAI [m2/m2] | TDR Moisture [vol%] | |
|---|---|---|---|---|---|---|
| SU | Min | 14 | 1280 | 1294 | 0.33 | 3.20 |
| Max | 2108 | 4561 | 6669 | 1.64 | 19.73 | |
| Mean | 830 | 2777 | 3607 | 0.98 | 10.68 | |
| Std | 630 | 795 | 1338 | 0.38 | 4.61 | |
| E1 | Min | 237 | 584 | 820 | 0.23 | 3.60 |
| Max | 1509 | 2859 | 4269 | 0.63 | 10.07 | |
| Mean | 883 | 1699 | 2581 | 0.39 | 6.50 | |
| Std | 314 | 641 | 889 | 0.10 | 2.35 | |
| TS | Min | - | - | - | 0.22 | 3.43 |
| Max | - | - | - | 0.98 | 13.27 | |
| Mean | - | - | - | 0.52 | 6.85 | |
| Std | - | - | - | 0.19 | 2.54 |
| RF Data Basis | Overall Accuracy |
|---|---|
| MNF of (CASI VNIR + AHS SWIR–TIR) + DEM + MP * | 71.2 |
| MNF of (CASI VNIR + AHS SWIR–TIR) + DEM | 71.1 |
| MNF of (CASI VNIR + AHS SWIR–TIR) | 68.8 |
| MNF of (AHS VNIR–SWIR–TIR) + DEM | 68.0 |
| MNF of (AHS VNIR–SWIR–TIR) | 67.9 |
| AHS VNIR–SWIR–TIR + DEM | 63.9 |
| CASI VNIR + AHS SWIR–TIR | 62.5 |
| AHS VNIR–SWIR–TIR | 60.1 |
| AHS VNIR–SWIR | 56.3 |
| CASI VNIR | 55.8 |
| AHS VNIR | 51.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milewski, R.; Schmid, T.; Chabrillat, S.; Jiménez, M.; Escribano, P.; Pelayo, M.; Ben-Dor, E. Analyses of the Impact of Soil Conditions and Soil Degradation on Vegetation Vitality and Crop Productivity Based on Airborne Hyperspectral VNIR–SWIR–TIR Data in a Semi-Arid Rainfed Agricultural Area (Camarena, Central Spain). Remote Sens. 2022, 14, 5131. https://doi.org/10.3390/rs14205131
Milewski R, Schmid T, Chabrillat S, Jiménez M, Escribano P, Pelayo M, Ben-Dor E. Analyses of the Impact of Soil Conditions and Soil Degradation on Vegetation Vitality and Crop Productivity Based on Airborne Hyperspectral VNIR–SWIR–TIR Data in a Semi-Arid Rainfed Agricultural Area (Camarena, Central Spain). Remote Sensing. 2022; 14(20):5131. https://doi.org/10.3390/rs14205131
Chicago/Turabian StyleMilewski, Robert, Thomas Schmid, Sabine Chabrillat, Marcos Jiménez, Paula Escribano, Marta Pelayo, and Eyal Ben-Dor. 2022. "Analyses of the Impact of Soil Conditions and Soil Degradation on Vegetation Vitality and Crop Productivity Based on Airborne Hyperspectral VNIR–SWIR–TIR Data in a Semi-Arid Rainfed Agricultural Area (Camarena, Central Spain)" Remote Sensing 14, no. 20: 5131. https://doi.org/10.3390/rs14205131
APA StyleMilewski, R., Schmid, T., Chabrillat, S., Jiménez, M., Escribano, P., Pelayo, M., & Ben-Dor, E. (2022). Analyses of the Impact of Soil Conditions and Soil Degradation on Vegetation Vitality and Crop Productivity Based on Airborne Hyperspectral VNIR–SWIR–TIR Data in a Semi-Arid Rainfed Agricultural Area (Camarena, Central Spain). Remote Sensing, 14(20), 5131. https://doi.org/10.3390/rs14205131








