Impact of Atmospheric Correction Methods Parametrization on Soil Organic Carbon Estimation Based on Hyperion Hyperspectral Data
Abstract
1. Introduction
2. Materials and Methods
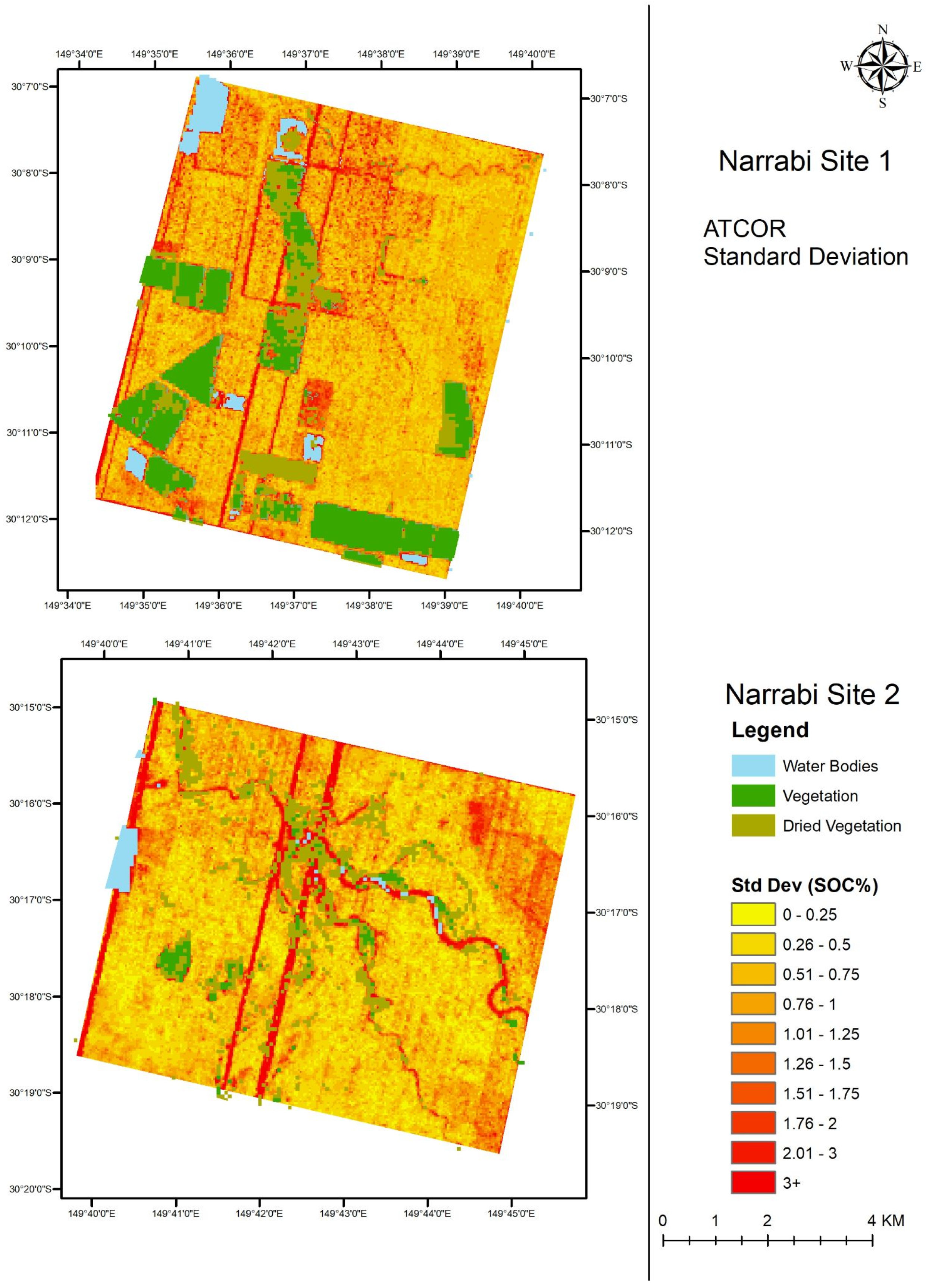
2.1. Study Area
2.2. Raw Hyperion Data
2.3. Soil Sampling
2.4. SOC Laboratory Measurements
2.5. Atmospheric Parameters
2.5.1. Water Vapor
2.5.2. Aerosol Optical Depth
2.6. Methodology
2.7. Atmospheric Correction Models
2.7.1. ATCOR Atmospheric Correction Model
2.7.2. Fast Line-of-Sight Atmospheric Analysis of Spectral Hypercubus (FLAASH) Atmospheric Correction Model
| Parameter | Selected Value |
|---|---|
| Atmospheric Model | Mid-Latitude Summer |
| Adjacency correction | No |
| Aerosol Model | Rural |
| Visibility | 30 kms |
| Region for water vapor retrieval | 820 nm |
| Spectral polishing | No |
| CO2 | 390 ppm |
| Aerosol optical depth | Ranges from 0.02 to 0.15 |
2.8. Bands Selection
2.9. Bare Soil Pixels Selection
2.10. Regression Model
2.10.1. Data Preparation
2.10.2. PLSR with Leave-One-Out Cross-Validation (LOOCV)
2.10.3. Model Evaluation
2.10.4. SOC Mapping
3. Results
3.1. Bare Soil Coverage Analysis
3.2. SOC Prediction Models Performances Using Hyperion Data Corrected by FLAASH
3.3. SOC Prediction Models Performances Using Hyperion Data Corrected by ATCOR
3.4. Significant Wavelengths for SOC Estimation
3.5. SOC Maps Using Hyperion Data Corrected by FLAASH
3.6. SOC Maps Using Hyperion Data Corrected by ATCOR
4. Discussions
4.1. Bare Soil Identification Variations Based on Atmospheric Parameters
4.2. Performance Analysis of PLSR Models after FLAASH AC Method
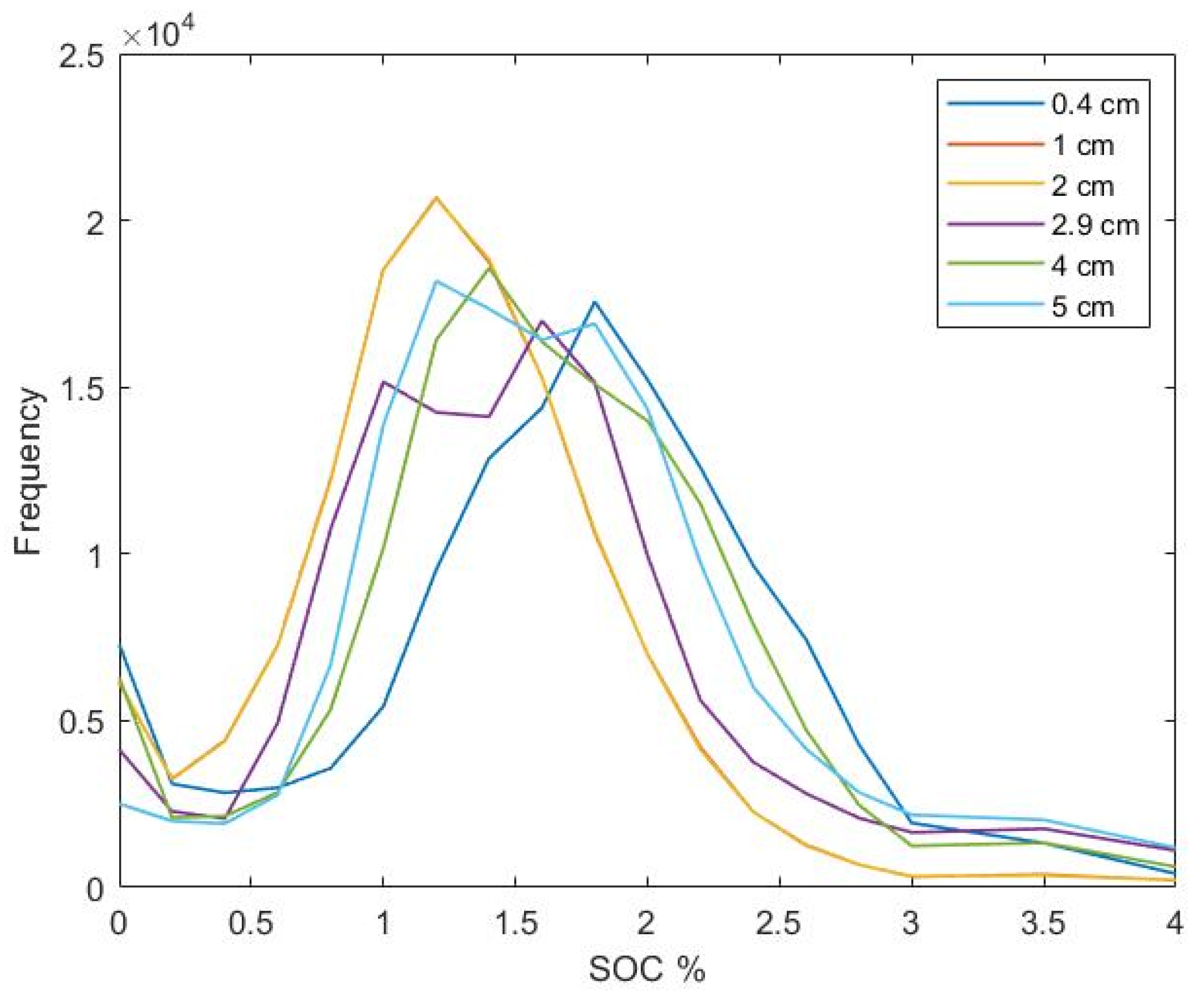
4.3. Performance Analysis of PLSR Models after ATCOR AC Method
4.4. ATCOR versus FLAASH for SOC Predictions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lal, R. Soil health and carbon management. Food Energy Secur. 2016, 5, 212–222. [Google Scholar] [CrossRef]
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F.; et al. Remote sensing of the terrestrial carbon cycle: A review of advances over 50 years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Sanchez, P.A.; Ahamed, S.; Carré, F.; Hartemink, A.E.; Hempel, J.; Huising, J.; Lagacherie, P.; McBratney, A.B.; McKenzie, N.J.; de Lourdes Mendonça-Santos, M.; et al. Digital soil map of the world. Science 2009, 325, 680–681. [Google Scholar] [CrossRef] [PubMed]
- Zaehle, S. Terrestrial nitrogen–carbon cycle interactions at the global scale. Philos. Trans. R. Soc. B Biol. Sci. 2013, 368, 20130125. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Borůvka, L.; Saberioon, M.; Vašát, R. Visible, near infrared, and mid-infrared spectroscopy applications for soil assessment with emphasis on soil organic matter content and quality: State-of-the-art and key issues. Appl. Spectrosc. 2013, 67, 1349–1362. [Google Scholar] [CrossRef]
- Chang, C.W.; Laird, D.A. Near-infrared reflectance spectroscopic analysis of soil C and N. Soil Sci. 2002, 167, 110–116. [Google Scholar] [CrossRef]
- Beyer, L.; Kahle, P.; Kretschmer, H.; Wu, Q. Soil organic matter composition of man-impacted urban sites in North Germany. J. Plant Nutr. Soil Sci. 2001, 164, 359–364. [Google Scholar] [CrossRef]
- Henderson, T.L.; Baumgardner, M.F.; Franzmeier, D.P.; Stott, D.E.; Coster, D.C. High dimensional reflectance analysis of soil organic matter. Soil. Sci. Soc. Am. J. 1992, 56, 865–872. [Google Scholar] [CrossRef]
- Stoner, E.R.; Baumgardner, M.F. Characteristic variations in reflectance of surface soils. Soil Sci. Soc. Am. J. 1981, 45, 1161–1165. [Google Scholar] [CrossRef]
- Shelukindo, H.B.; Semu, E.; Singh, B.R.; Munishi, P.K.T. Predictor variables for soil organic carbon contents in the Miombo woodlands ecosystem of Kitonga forest reserve, Tanzania. Int. J. Agric. Sci. 2014, 4, 222–231. [Google Scholar]
- Abdelhakim, B.; Tahar, G. Land use effect on soil and particulate organic carbon, and aggregate stability in some soils in Tunisia. Afr. J. Agric. Res. 2010, 5, 764–774. [Google Scholar]
- Gomez, C.; Viscarra Rossel, R.A.; McBratney, A.B. Soil organic carbon prediction by hyperspectral remote sensing and field vis-NIR spectroscopy: An Australian case study. Geoderma 2008, 146, 403–411. [Google Scholar] [CrossRef]
- Ayoubi, S.; Shahri, A.P.; Karchegani, P.M.; Sahrawat, K.L. Application of artificial neural network (ANN) to predict soil organic matter using remote sensing data in two ecosystems. Biomass Remote Sens. Biomass 2011, 181–196. [Google Scholar] [CrossRef]
- Stevens, A.; van Wesemael, B.; Vandenschrick, G.; Touré, S.; Tychon, B. Detection of Carbon Stock Change in Agricultural Soils Using Spectroscopic Techniques. Soil Sci. Soc. Am. J. 2006, 70, 844–850. [Google Scholar] [CrossRef]
- Hbirkou, C.; Pätzold, S.; Mahlein, A.-K.; Welp, G. Airborne hyperspectral imaging of spatial soil organic carbon heterogeneity at the field-scale. Geoderma 2012, 175, 21–28. [Google Scholar] [CrossRef]
- Bartholomeus, H.; Schaepman-Strub, G.; Blok, D.; Sofronov, R.; Udaltsov, S. Spectral estimation of soil properties in siberian tundra soils and relations with plant species composition. Appl. Environ. Soil Sci. 2012, 2012, 241535. [Google Scholar] [CrossRef]
- Ouerghemmi, W.; Gomez, C.; Naceur, S.; Lagacherie, P. Applying blind source separation on hyperspectral data for clay content estimation over partially vegetated surfaces. Geoderma 2011, 163, 227–237. [Google Scholar] [CrossRef]
- Chabrillat, S.; Ben-Dor, E.; Cierniewski, J.; Gomez, C.; Schmid, T.; van Wesemael, B. Imaging spectroscopy for soil mapping and monitoring. Surv. Geophys. 2019, 40, 361–399. [Google Scholar] [CrossRef]
- Thompson, D.R.; Guanter, L.; Berk, A.; Gao, B.C.; Richter, R.; Schläpfer, D.; Thome, K.J. Retrieval of atmospheric parameters and surface reflectance from visible and shortwave infrared imaging spectroscopy data. Surv. Geophys. 2019, 40, 333–360. [Google Scholar] [CrossRef]
- Gao, B.-C.; Montes, M.J.; Davis, C.O.; Goetz, A.F.H. Atmospheric correction algorithms for hyperspectral remote sensing data of land and ocean. Remote Sens. Environ. 2009, 113, S17–S24. [Google Scholar] [CrossRef]
- Souri, A.H.; Sharifi, M.A. Evaluation of scene-based empirical approaches for atmospheric correction of hyperspectral imagery. In Proceedings of the 33rd Asian Conference of Remote Sensing, Ambassador City Jomtien Hotel, Pattaya, Thailand, 26 November 2012. [Google Scholar]
- Song, C.; Woodcock, C.E.; Seto, K.C.; Lenney, M.P.; Macomber, S.A. Classification and change detection using Landsat TM data: When and how to correct atmospheric effects? Remote Sens. Environ. 2001, 75, 230–244. [Google Scholar] [CrossRef]
- Bernstein, L.S. Quick atmospheric correction code: Algorithm description and recent upgrades. Opt. Eng. 2012, 51, 111719. [Google Scholar] [CrossRef]
- Richter, R.; Schläpfer, D. Atmospheric/Topographic Correction for Satellite Imagery (ATCOR-2/3 User Guide, Version 8.3. 1, February 2014); ReSe Applications Schläpfer, Langeggweg: Wil, Switzerland, 2013. [Google Scholar]
- Adler-Golden, S.; Berk, A.; Bernstein, L.S.; Richtsmeier, S.; Acharya, P.K.; Matthew, M.W.; Chetwynd, J.H. FLAASH, a MODTRAN4 atmospheric correction package for hyperspectral data retrievals and simulations. In Proceedings of the 7th Annual JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 1 February 1988; Volume 97, pp. 9–14. [Google Scholar]
- Mazer, A.S.; Martin, M.; Lee, M.; Solomon, J.E. Image processing software for imaging spectrometry data analysis. Remote Sens. Environ. 1998, 24, 201–210. [Google Scholar] [CrossRef]
- Zheng, Q.; Kindel, B.C.; Goetz, A.F. The high accuracy atmospheric correction for hyperspectral data (HATCH) model. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1223–1231. [Google Scholar] [CrossRef]
- Katkovsky, L.V.; Martinov, A.O.; Siliuk, V.A.; Ivanov, D.A.; Kokhanovsky, A.A. Fast atmospheric correction method for hyperspectral data. Remote Sens. 2018, 10, 1698. [Google Scholar] [CrossRef]
- Gordon, H.R. Evolution of Ocean Color Atmospheric Correction: 1970–2005. Remote Sens. 2021, 13, 5051. [Google Scholar] [CrossRef]
- Rahman, H. Influence of atmospheric correction on the estimation of biophysical parameters of crop canopy using satellite remote sensing. Int. J. Remote Sens. 2001, 22, 1245–1268. [Google Scholar] [CrossRef]
- El Alem, A.; Lhissou, R.; Chokmani, K.; Oubennaceur, K. Remote Retrieval of Suspended Particulate Matter in Inland Waters: Image-Based or Physical Atmospheric Correction Models? Water 2021, 13, 2149. [Google Scholar] [CrossRef]
- Cetin, M.; Musaoglu, N.; Kocal, O.H. A comparison of Atmospheric correction methods on Hyperion imagery in forest areas. Uludag Universit. J. Fac. Eng. 2017, 22, 103–114. [Google Scholar] [CrossRef]
- Rani, N.; Mandla, V.R.; Singh, T. Evaluation of atmospheric corrections on hyperspectral data with special reference to mineral mapping. Geosci. Front. 2017, 8, 797–808. [Google Scholar] [CrossRef]
- Montes, M.J.J.; Fusina, R.A.; Donato, T.F.; Bachmann, C.M.; Gao, B.-C. The effects of atmospheric correction schemes on the hyperspectral imaging of littoral environments, IGARSS 2004. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium, Online. 26 September–2 October 2004; Volume 6, pp. 4187–4190. [Google Scholar] [CrossRef]
- Minu, S.; Shetty, A.; Minasny, B.; Gomez, C. The role of atmospheric correction algorithms in the prediction of soil organic carbon from Hyperion data. Int. J. Remote Sens. 2017, 38, 6435–6456. [Google Scholar] [CrossRef]
- Holzer-Popp, T. Retrieving aerosol optical depth and type in the boundary layer over land and ocean from simultaneous GOME spectrometer and ATSR-2 radiometer measurements 2. Case study application and validation. J. Geophys. Res. 2002, 107, AAC 16-1–AAC 16-17. [Google Scholar] [CrossRef]
- Bhatia, N.; Tolpekin, V.A.; Reusen, I.; Sterckx, S.; Biesemans, J.; Stein, A. Sensitivity of Reflectance to Water Vapor and Aerosol Optical Thickness. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3199–3208. [Google Scholar] [CrossRef]
- Mannschatz, T.; Pflug, B.; Borg, E.; Feger, K.H.; Dietrich, P. Uncertainties of LAI estimation from satellite imaging due to atmospheric correction. Remote Sens. Environ. 2014, 153, 24–39. [Google Scholar] [CrossRef]
- Griffin, M.K.; Burke, H.H.K. Compensation of hyperspectral data for atmospheric effects. Linc. Lab. J. 2013, 14, 29–54. [Google Scholar]
- Davaadorj, A. Evaluating Atmospheric Correction Methods Using Worldview-3 Image. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2019. [Google Scholar]
- Nazeer, M.; Nichol, J.E.; Yung, Y.K. Evaluation of atmospheric correction models and Landsat surface reflectance product in an urban coastal environment. Int. J. Remote Sens. 2014, 35, 6271–6291. [Google Scholar] [CrossRef]
- Bassani, C.; Cavalli, R.M.; Antonelli, P. Influence of aerosol and surface reflectance variability on hyperspectral observed radiance. Atmos. Meas. Tech. 2012, 5, 1193–1203. [Google Scholar]
- Folkman, M.A.; Pearlman, J.; Liao, L.B.; Jarecke, P.J. EO-1/Hyperion hyperspectral imager design, development, characterization, and calibration. Hyperspectral Remote Sens. Land Atmos. 2001, 4151, 40–51. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Kaufman, Y.J. Atmospheric effect on spatial resolution of surface imagery. Appl. Opt. 1984, 23, 3400–3408. [Google Scholar] [CrossRef]
- Platnick, S.T.; King, M.D.; Meyer, K.G.; Wind, G.A.; Amarasinghe, N.A.; Marchant, B.E.; Arnold, G.T.; Zhang, Z.H.; Hubanks, P.A.; Ridgway, B.I.; et al. MODIS cloud optical properties: User guide for the Collection 6 Level-2 MOD06/MYD06 product and associated Level-3 Datasets. Version. 2015, 1. Available online: https://modis-images.gsfc.nasa.gov/_docs/C6MOD06OPUserGuide.pdf (accessed on 11 September 2022).
- Berk, A.; Cooley, T.W.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lewis, P.E. MODTRAN5: A reformulated atmospheric band model with auxiliary species and practical multiple scattering options. In Proceedings of the Remote Sensing of Clouds and the Atmosphere IX, Maspalomas, Gran Canaria, Spain, 13–15 September 2004; Volume 5571, pp. 78–85. [Google Scholar]
- Berk, A.; Anderson, G.P. Impact of MODTRAN® 5.1 on atmospheric compensation. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2008; Volume 3, pp. III-127. [Google Scholar]
- Cooley, T.; Anderson, G.P.; Felde, G.W.; Hoke, M.L.; Ratkowski, A.J.; Chetwynd, J.H.; Lewis, P. FLAASH, a MODTRAN4-based atmospheric correction algorithm, its application and validation. IEEE Int. Geosci. Remote Sens. Symp. 2002, 3, 1414–1418. [Google Scholar]
- Lu, P.; Wang, L.; Niu, Z.; Li, L.; Zhang, W. Prediction of Soil Properties Using Laboratory VIS–NIR Spectroscopy and Hyperion Imagery. J. Geochem. Explor. 2013, 132, 26–33. [Google Scholar] [CrossRef]
- Jaber, S.M.; Lant, C.L.; Al-Qinna, M.I. Estimating spatial variations in soil organic carbon using satellite hyperspectral data and map algebra. Int. J. Remote Sens. 2011, 32, 5077–5103. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Singh, K.V.; Setia, R.; Sahoo, S.; Prasad, A.; Pateriya, B. Evaluation of NDWI and MNDWI for assessment of waterlogging by integrating digital elevation model and groundwater level. Geocarto Int. 2015, 30, 650–661. [Google Scholar] [CrossRef]
- Castaldi, F.; Chabrillat, S.; Don, A.; van Wesemael, B. Soil organic carbon mapping using LUCAS topsoil database and Sentinel-2 data: An approach to reduce soil moisture and crop residue effects. Remote Sens. 2019, 11, 2121. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard normal variate transformation and de-trending of near-infrared diffuse reflectance spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Chiang, J.H.; Hao, P.Y. A new kernel-based fuzzy clustering approach: Support vector clustering with cell growing. IEEE Trans. Fuzzy Syst. 2003, 11, 518–527. [Google Scholar] [CrossRef]
- Pearson, R.K. Outliers in process modeling and identification. IEEE Trans. Control. Syst. Technol. 2002, 10, 55–63. [Google Scholar] [CrossRef]
- Mark, H.L.; Tunnell, D. Qualitative near-infrared reflectance analysis using Mahalanobis distances. Anal. Chem. 1985, 57, 1449–1456. [Google Scholar] [CrossRef]
- Tenenhaus, M.; Amato, S.; Esposito Vinzi, V. A global goodness-of-fit index for PLS structural equation modelling. In Proceedings of the XLII SIS Scientific Meeting, Padova, Italy, 9 June 2004; Volume 1, Number 2. pp. 739–742. [Google Scholar]
- Nakagawa, S.; Schielzeth, H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 2013, 4, 133–142. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar]
- Malley, D.F.; Martin, P.D.; Ben-Dor, E. Application in analysis of soils. Near-Infrared Spectrosc. Agric. 2004, 44, 729–784. [Google Scholar]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. TrAC Trends Anal. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in partial least squares regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Vaudour, E.; Gomez, C.; Fouad, Y.; Lagacherie, P. Sentinel-2 image capacities to predict common topsoil properties of temperate and Mediterranean agroecosystems. Remote Sens. Environ. 2019, 223, 21–33. [Google Scholar] [CrossRef]
- Dvorakova, K.; Heiden, U.; van Wesemael, B. Sentinel-2 Exposed Soil Composite for Soil Organic Carbon Prediction. Remote Sens. 2021, 13, 1791. [Google Scholar] [CrossRef]
- Ben-Dor, E. Quality assessment of several methods to recover surface reflectance using synthetic imaging spectroscopy data. Remote Sens. Environ. 2004, 90, 389–404. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Inbar, Y.; Chen, Y. The reflectance spectra of organic matter in the visible near-infrared and short wave infrared region (400–2500 nm) during a controlled decomposition process. Remote Sens. Environ. 1997, 61, 1–15. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Wu, W.; Liu, H. Prediction of Soil Organic Carbon under Different Land Use Types Using Sentinel-1/-2 Data in a Small Watershed. Remote Sens. 2021, 13, 1229. [Google Scholar] [CrossRef]
- Gao, B.C.; Goetz, A.F.H. Column Atmospheric Water Vapor and Vegetation Liquid Water Retrievals from Airborne Imaging Spectrometer Data. J. Geo. Res. 1990, 95, 3549–3564. [Google Scholar] [CrossRef]
- Das, S.; Pandey, P.; Mohanty, S.; Nayak, S.K. Influence of NCO/OH and transesterified castor oil on the structure and properties of polyurethane: Synthesis and characterization. Mater. Express 2015, 5, 377–389. [Google Scholar] [CrossRef]
- Yusuf, F.R.; Santoso, K.B.; Ningam, M.U.L.; Kamal, M.; Wicaksono, P. Evaluation of atmospheric correction models and Landsat surface reflectance product in Daerah Istimewa Yogyakarta, Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2018, 169, 012004. [Google Scholar] [CrossRef]
- Marcello, J.; Eugenio, F.; Perdomo, U.; Medina, A. Assessment of Atmospheric Algorithms to Retrieve Vegetation in Natural Protected Areas Using Multispectral High Resolution Imagery. Sensors 2016, 16, 1624. [Google Scholar] [CrossRef] [PubMed]
- Manakos, I.; Manevski, K.; Kalaitzidis, C.; Edler, D. Comparison between atmospheric correction modules on the basis of worldview-2 imagery and in situ spectroradiometric measurements. In Proceedings of the 7th EARSeL SIG Imaging Spectroscopy Workshop, Edinburgh, UK, 11–13 April 2011; pp. 11–13. [Google Scholar]

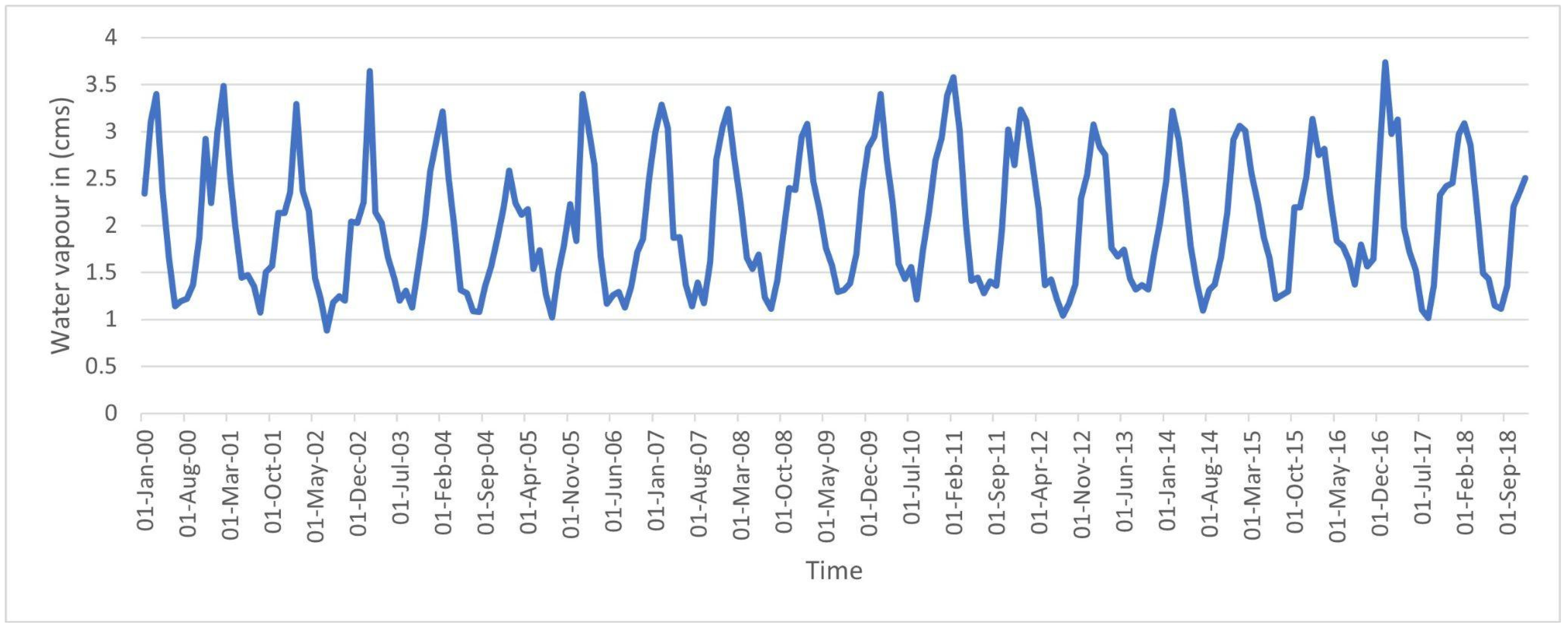
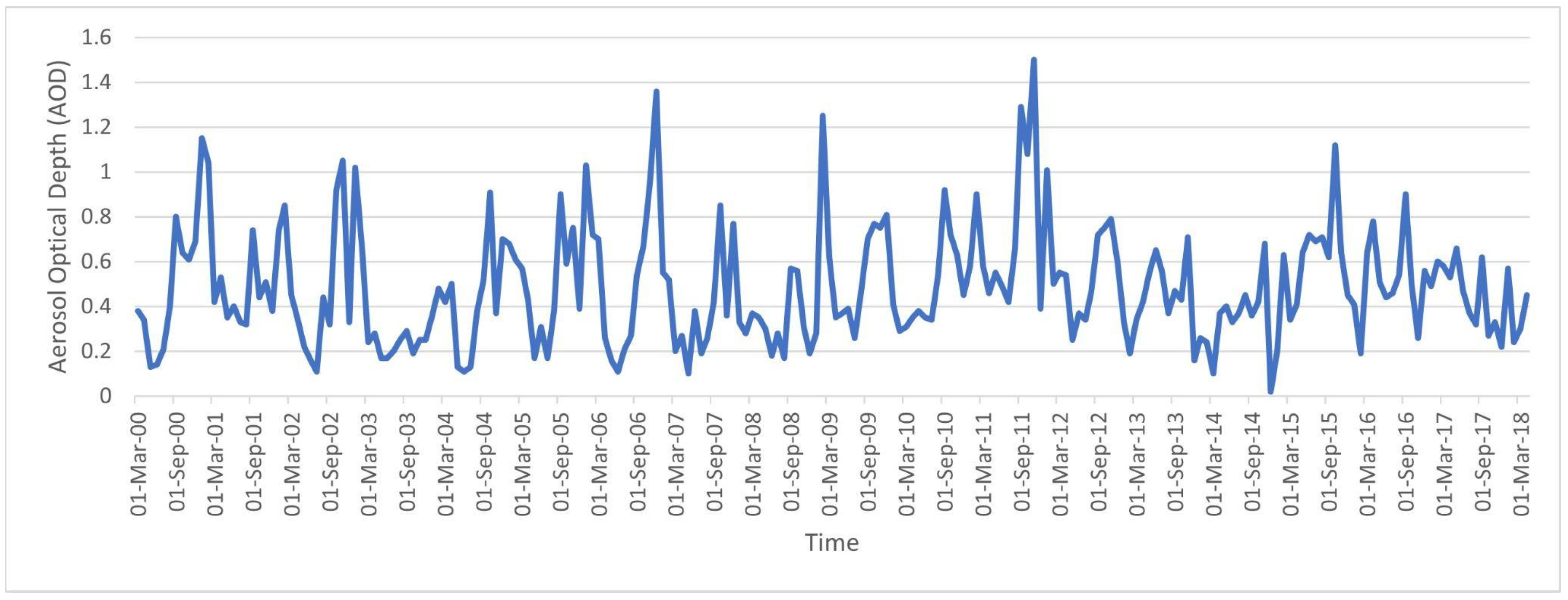

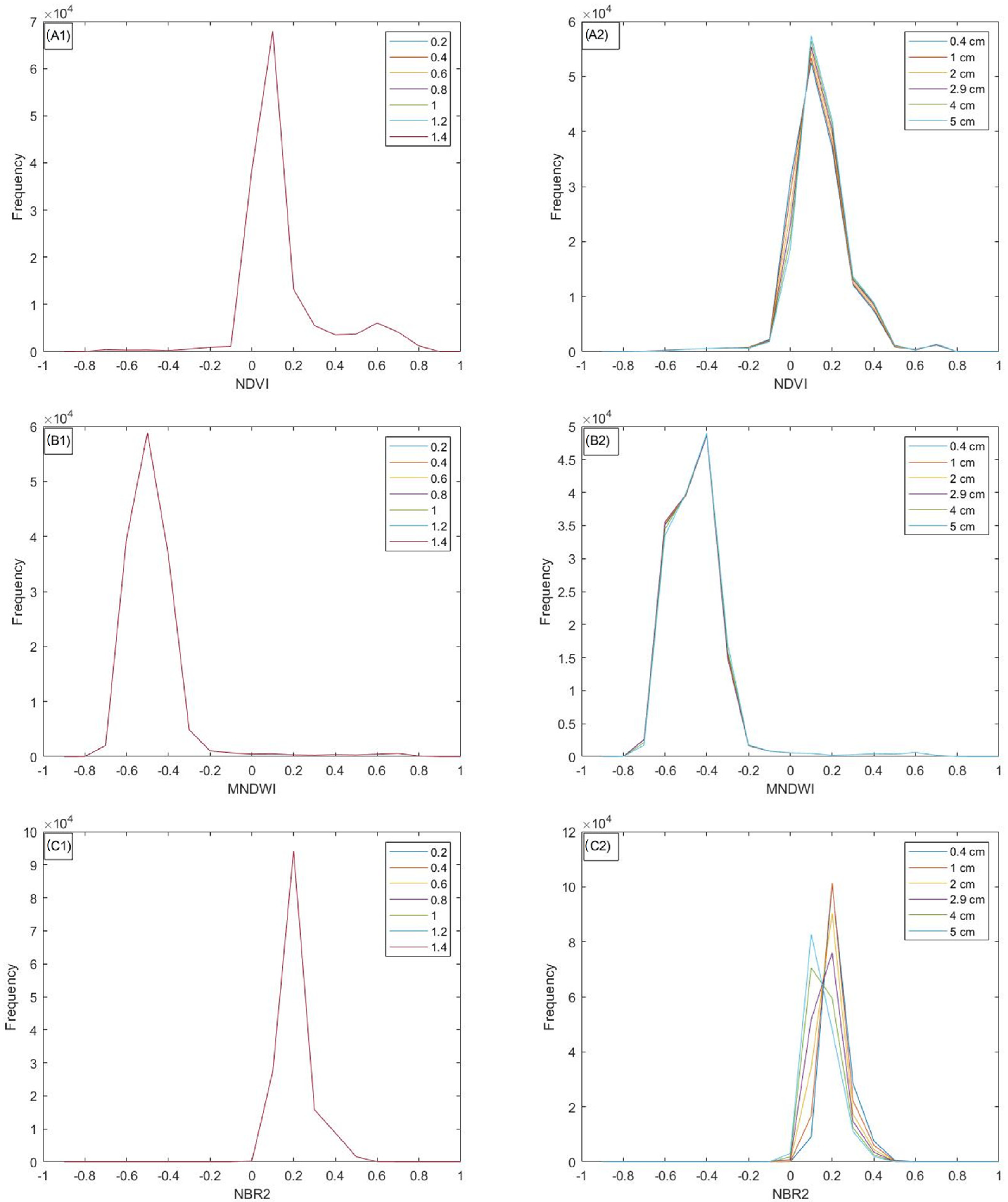
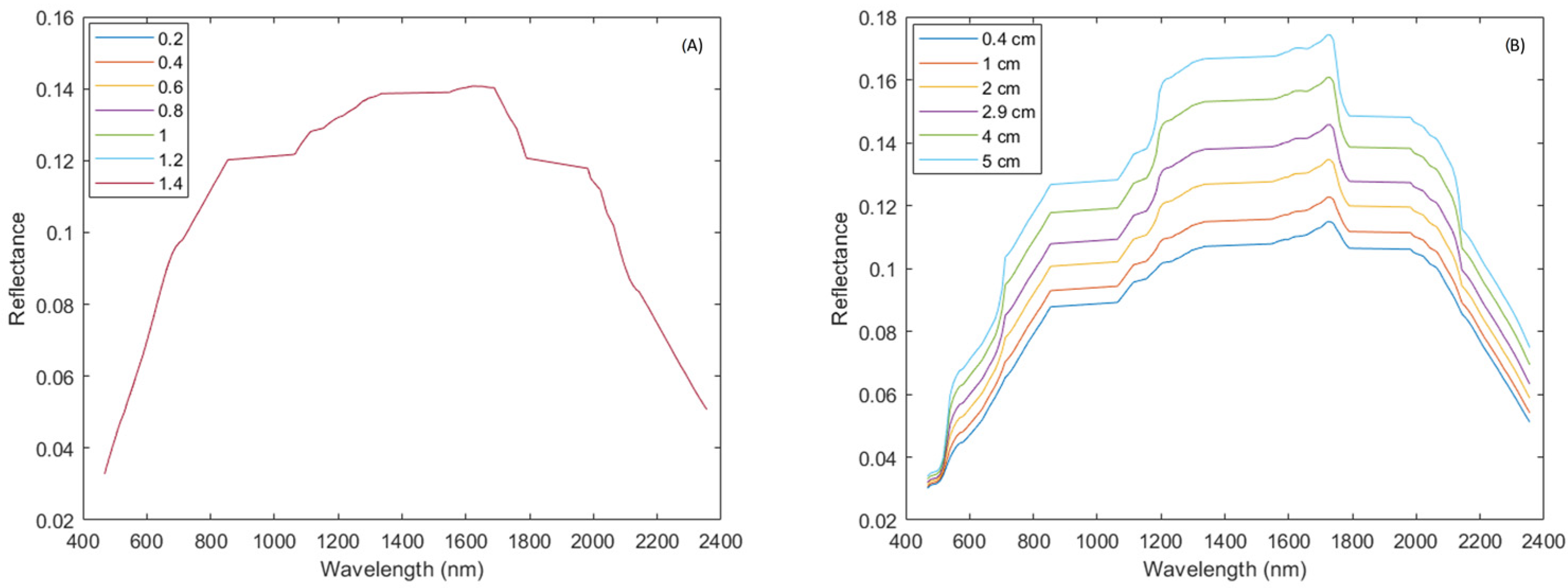
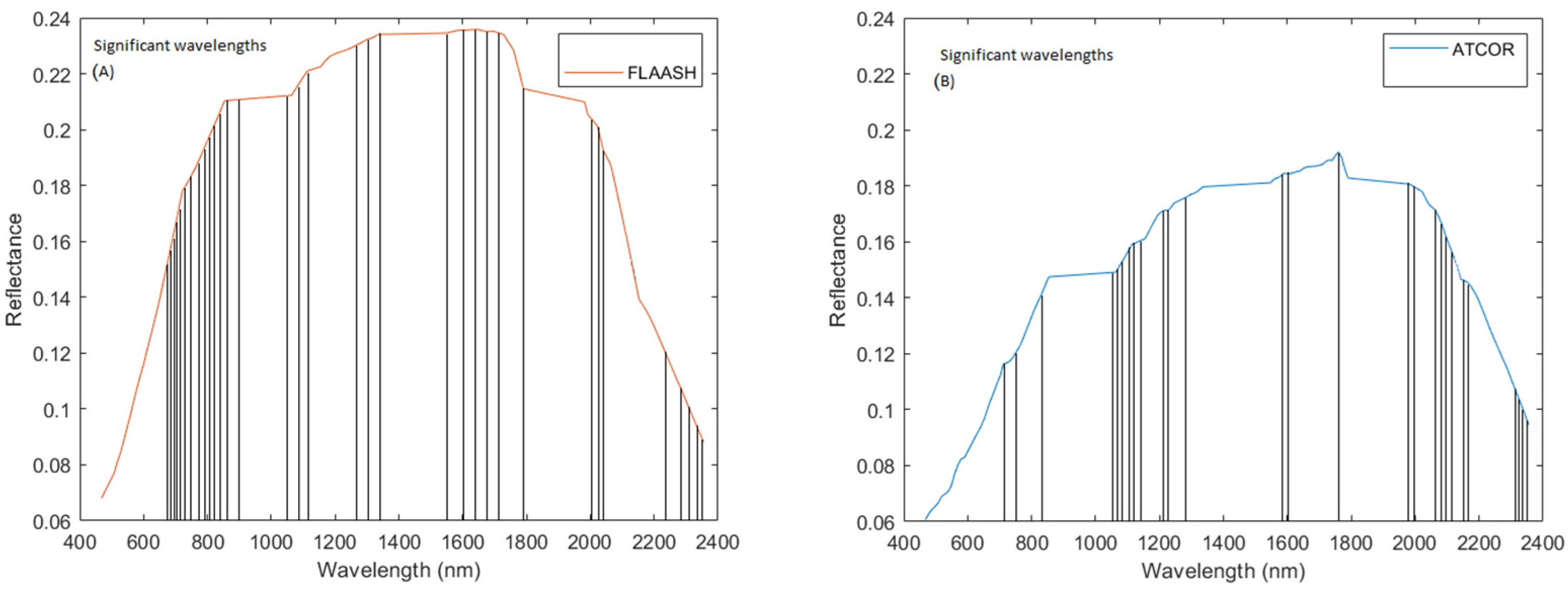


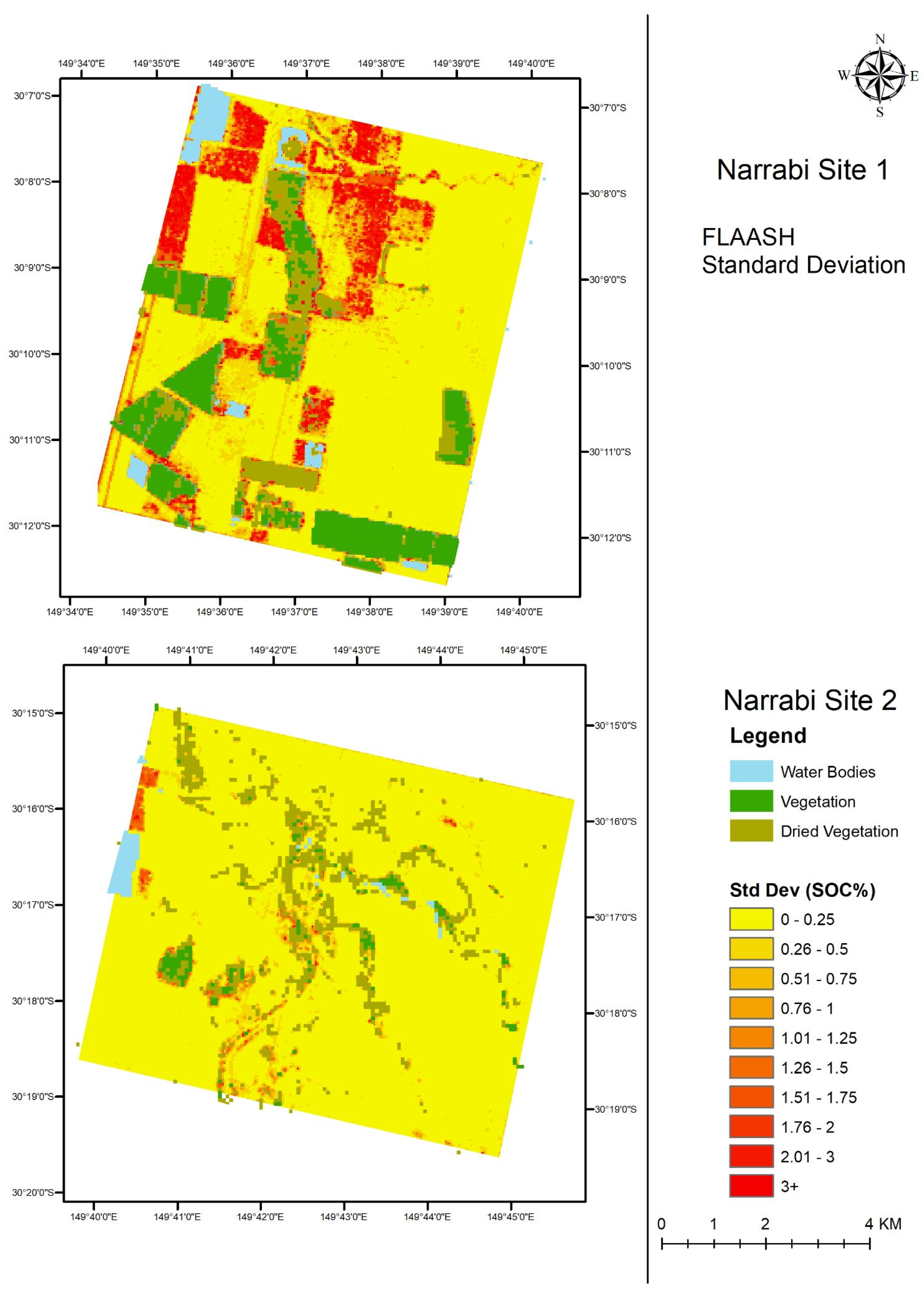
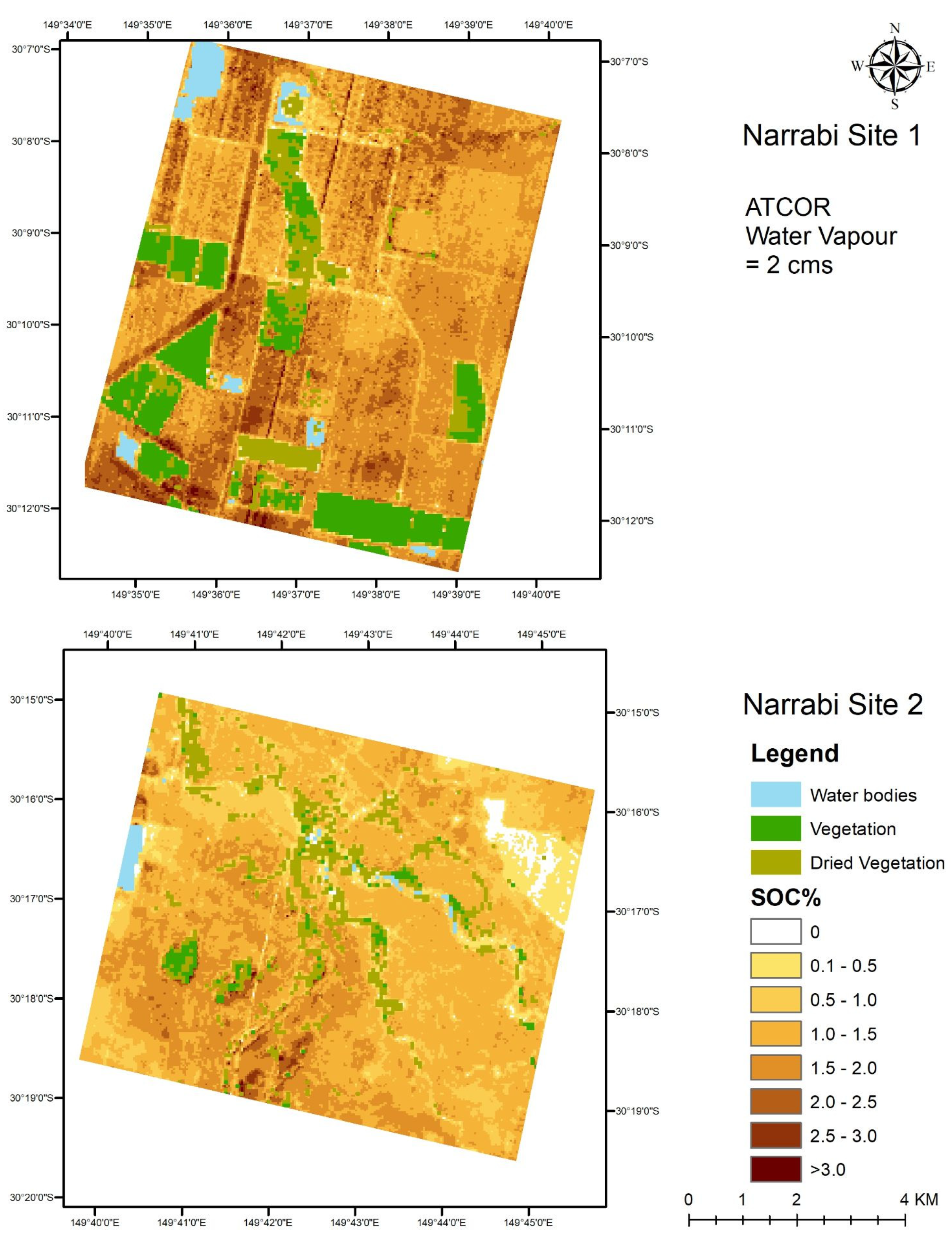
| Water Vapor (WV) (in cm) | Aerosol Optical Depth (AOD) | |
|---|---|---|
| Minimum | 0.9 | 0.02 |
| Maximum | 3.7 | 1.50 |
| Mean | 2 | 0.48 |
| Median | 1.9 | 0.42 |
| Standard Deviation | 0.7 | 0.25 |
| Parameter | Selected Value |
|---|---|
| Atmospheric Model | Mid-Latitude Summer |
| Adjacency correction | No |
| Aerosol Model | Rural |
| Visibility | 30 km |
| Region for water vapor retrieval | 820 nm |
| Spectral polishing | No |
| CO2 | 390 ppm |
| Water vapor | Ranges from 0.9 cm to 3.7 cm |
| AOD | 0.2 | 0.4 | 0.6 | 0.8 | 1 | 1.2 | 1.4 |
|---|---|---|---|---|---|---|---|
| Bare soil coverage (%) | 82.35 | 82.35 | 82.35 | 82.35 | 82.35 | 82.35 | 82.35 |
| R2cv | 0.79 | 0.79 | 0.79 | 0.79 | 0.79 | 0.79 | 0.79 |
| RMSEcv (%) | 0.40 | 0.41 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 |
| RPD | 2.23 | 2.21 | 2.22 | 2.23 | 2.23 | 2.23 | 2.23 |
| RPIQ | 3.26 | 3.24 | 3.25 | 3.26 | 3.27 | 3.26 | 3.26 |
| bias (%) | 0.32 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 |
| Number of Latent Variables | 2 | 2 | 2 | 2 | 4 | 2 | 2 |
| Water Vapor (in cm) | 0.4 | 1 | 2 | 2.9 | 4 | 5 |
|---|---|---|---|---|---|---|
| Bare soil coverage (%) | 75.04 | 80.54 | 84.04 | 83.50 | 83.17 | 82.85 |
| R2cv | 0.75 | 0.78 | 0.79 | 0.75 | 0.72 | 0.72 |
| RMSEcv (%) | 0.44 | 0.41 | 0.41 | 0.44 | 0.47 | 0.46 |
| RPD | 2.04 | 2.17 | 2.19 | 2.03 | 1.91 | 1.93 |
| RPIQ | 2.98 | 3.17 | 3.21 | 2.97 | 2.80 | 2.83 |
| bias (%) | 0.35 | 0.33 | 0.31 | 0.34 | 0.38 | 0.35 |
| Number of Latent Variables | 5 | 2 | 3 | 4 | 2 | 6 |
| AOD | Negative SOC Pixels % |
|---|---|
| 0.2 | 6.31 |
| 0.4 | 1.93 |
| 0.6 | 2.64 |
| 0.8 | 2.65 |
| 1.0 | 3.27 |
| 1.2 | 4.98 |
| 1.4 | 5.50 |
| Water Vapor (in cms) | Negative SOC Pixels % |
|---|---|
| 0.4 | 5.51 |
| 1.0 | 4.60 |
| 2.0 | 4.63 |
| 2.9 | 3.22 |
| 4.0 | 4.53 |
| 5.0 | 1.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mruthyunjaya, P.; Shetty, A.; Umesh, P.; Gomez, C. Impact of Atmospheric Correction Methods Parametrization on Soil Organic Carbon Estimation Based on Hyperion Hyperspectral Data. Remote Sens. 2022, 14, 5117. https://doi.org/10.3390/rs14205117
Mruthyunjaya P, Shetty A, Umesh P, Gomez C. Impact of Atmospheric Correction Methods Parametrization on Soil Organic Carbon Estimation Based on Hyperion Hyperspectral Data. Remote Sensing. 2022; 14(20):5117. https://doi.org/10.3390/rs14205117
Chicago/Turabian StyleMruthyunjaya, Prajwal, Amba Shetty, Pruthviraj Umesh, and Cécile Gomez. 2022. "Impact of Atmospheric Correction Methods Parametrization on Soil Organic Carbon Estimation Based on Hyperion Hyperspectral Data" Remote Sensing 14, no. 20: 5117. https://doi.org/10.3390/rs14205117
APA StyleMruthyunjaya, P., Shetty, A., Umesh, P., & Gomez, C. (2022). Impact of Atmospheric Correction Methods Parametrization on Soil Organic Carbon Estimation Based on Hyperion Hyperspectral Data. Remote Sensing, 14(20), 5117. https://doi.org/10.3390/rs14205117








