A Fusion-Based Defogging Algorithm
Abstract
:1. Introduction
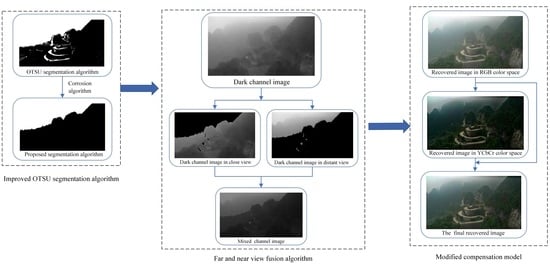
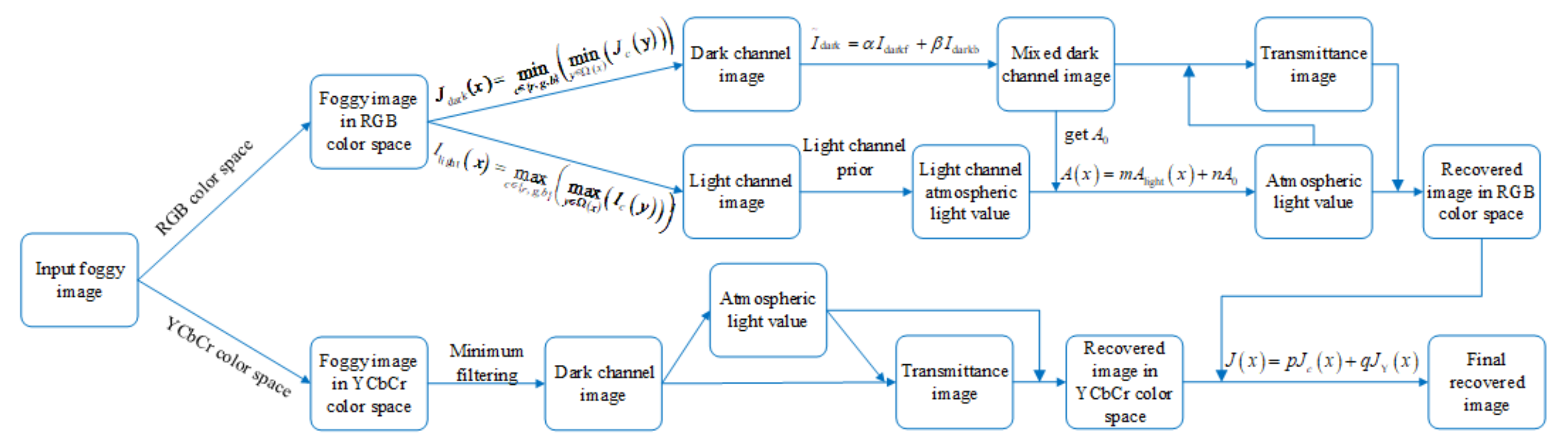
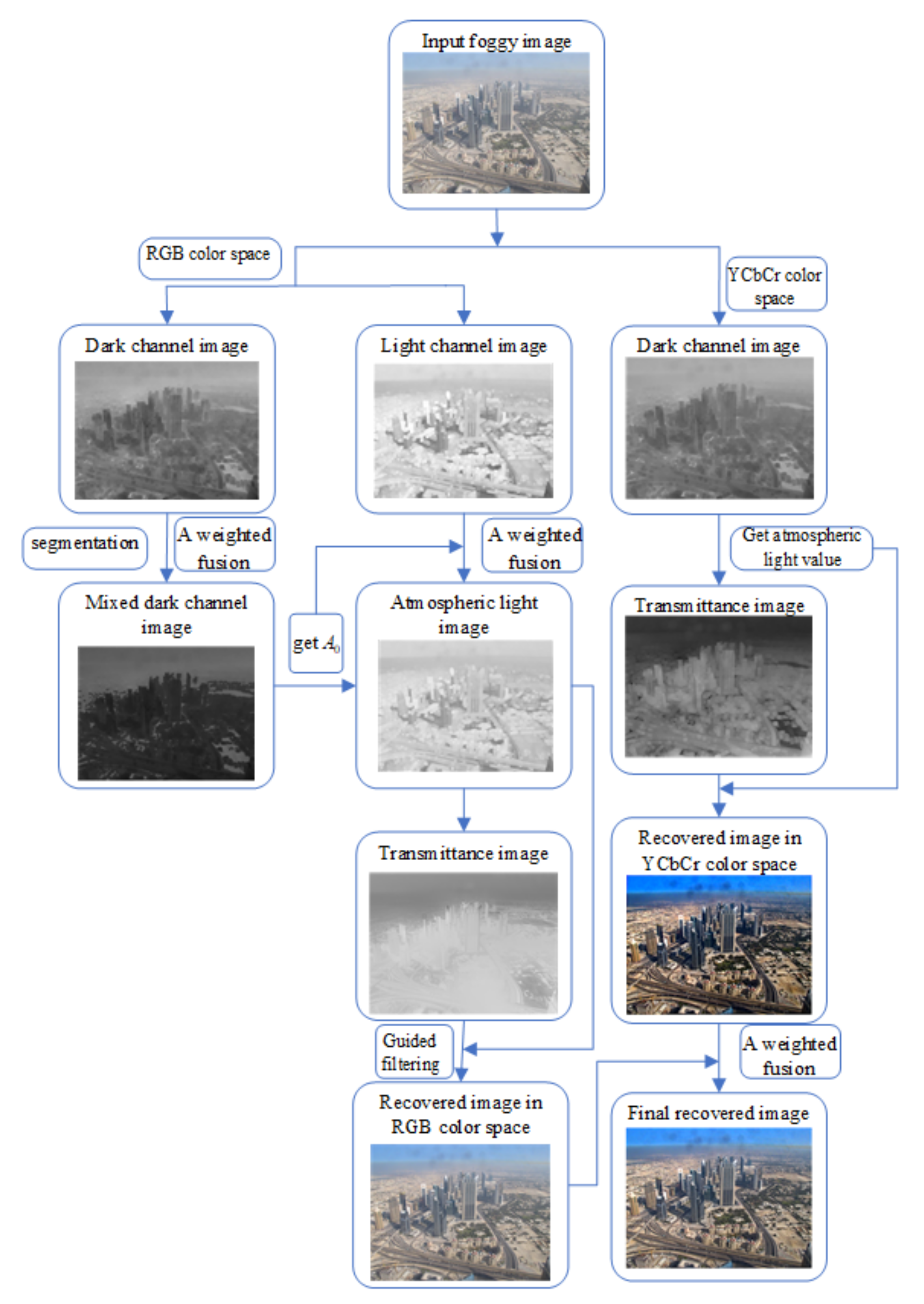
- To solve the problem of the inaccurate estimation of atmospheric light value and transmittance, we propose a novel atmospheric light scattering model. The light channel prior is introduced to obtain a more accurate atmospheric light and transmittance value.
- Aiming at the shortage that the dark channel prior theory is prone to distort in some regions of the image, an improved two-dimensional Otsu image segmentation algorithm is established. It mixes the dark channels in the near and distant areas and sets adaptive adjustment parameters of the mixed dark channel in the near and distant areas based on the optimal objective quality evaluation index.
- In order to overcome the drawback that the defogging parameters are single and fixed in the process of defogging, an adaptive parameter model is generated to calculate the defogging degree according to the atmospheric light value.
- Focusing on reducing the computational complexity of refining transmittance, we utilize gray images corresponding to foggy images as guiding images for guiding filtering. Meanwhile, a brightness/color compensation model based on visual perception is proposed to correct the restored images, which improves the contrast and color saturation of the restored images.
2. Related Work
2.1. Dark Channel Prior Theory
2.2. Guided Filtering Algorithm
3. The Proposed Algorithm
3.1. Two-Dimensional Otsu Remote Sensing Image Segmentation Algorithm
3.2. Mixed Dark Channel Algorithm
3.3. Dark-Light Channel Fusion Model
3.4. An Adaptive Defogging Intensity Parameter Model
3.5. Brightness/Color Compensation Model Based on Visual Perception
3.6. Restoration of Fog-Free Images
4. Integrated Performance and Discussion
4.1. Visual Effect Analysis
4.2. Image Defogging Evaluation Index
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Chen, G.; Zhou, J. Iterative optimization defogging algorithm using Gaussian weight decay. Acta Autom. Sin. 2019, 45, 819–828. [Google Scholar]
- Huang, W.; Li, J.; Qi, C. Dense haze scene image defogging algorithm based on low rank and dictionary expression decisions. J. Xi’an Jiaotong Univ. 2020, 54, 118–125. [Google Scholar]
- Yang, Y.; Lu, X. Image dehazing combined with adaptive brightness transformation inequality to estimate transmission. J. Xi’an Jiaotong Univ. 2021, 6, 69–76. [Google Scholar]
- Fan, T.; Li, C.; Ma, X.; Chen, Z.; Zhang, X.; Chen, L. An improved single image defogging method based on Retinex. In Proceedings of the 2017 2nd International Conference on Image, Vision and Computing (ICIVC), Chengdu, China, 2–4 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 410–413. [Google Scholar]
- Magudeeswaran, V.; Singh, J.F. Contrast limited fuzzy adaptive histogram equalization for enhancement of brain images. Int. J. Imaging Syst. Technol. 2017, 27, 98–103. [Google Scholar] [CrossRef] [Green Version]
- Fu, F.; Liu, F. Wavelet-Based Retinex Algorithm for Unmanned Aerial Vehicle Image Defogging. In Proceedings of the 2015 8th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 12–13 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 426–430. [Google Scholar]
- Ma, Z.; Wen, J. Single-scale Retinex sea fog removal algorithm based on fusion of edge information. J. Comput.-Aided Des. Graph. 2015, 27, 217–225. [Google Scholar]
- Liu, Y.; Yan, H.; Gao, S.; Yang, K. Criteria to evaluate the fidelity of image enhancement by MSRCR. IET Image Process. 2018, 12, 880–887. [Google Scholar] [CrossRef]
- Zhang, W.; Dong, L.; Pan, X.; Zhou, J.; Qin, L.; Xu, W. Single image defogging based on multi-channel convolutional MSRCR. IEEE Access 2019, 7, 72492–72504. [Google Scholar] [CrossRef]
- Liu, X. A defogging algorithm for ship video surveillance images under adaptive histogram equalization processing. Ship Sci. Technol. 2020, 42, 70–72. [Google Scholar]
- Wong, C.; Jiang, G.; Rahman, M.A.; Liu, S.; Lin, F.; Kwok, N.; Shi, H.; Yu, Y.; Wu, T. Histogram equalization and optimal profile compression based approach for colour image enhancement. J. Vis. Commun. Image Represent. 2016, 38, 802–813. [Google Scholar] [CrossRef]
- Fei, Y.; Shao, F. Contrast adjustment based on image retrieval. Prog. Laser Optoelectron. 2018, 55, 112–121. [Google Scholar]
- Huan, H.H.; Abduklimu, T.; He, X. Color image defogging method based on wavelet transform. Comput. Technol. Dev. 2020, 30, 60–64. [Google Scholar]
- Jia, J.; Yue, H. A wavelet-based approach to improve foggy image clarity. IFAC Proc. Vol. 2014, 47, 930–935. [Google Scholar] [CrossRef] [Green Version]
- Huan, H.H.; Abduklimu, T.; He, X. A method of traffic image defogging based on wavelet transform. Electron. Des. Eng. 2020, 28, 56–59. [Google Scholar]
- Wang, X. Research on Dehazing Algorithm of Light Field Image Based on Multi-Cues Fusion; Hefei University of Technology: Hefei, China, 2020. [Google Scholar]
- Zhang, Y. Research on Key Technologies of Haze Removal of Sea-Sky Background Image Based on Full Polarization Information Detection; University of Chinese Academy of Sciences: Beijing, China, 2020. [Google Scholar]
- Xu, Z.; Zhang, S.; Gu, L.; Huang, H.; Wang, H.; Liu, Q. A remote sensing image defogging method of UAV. Commun. Technol. 2020, 53, 2442–2446. [Google Scholar]
- Wang, W.; Chang, F.; Ji, T.; Wu, X. A Fast Single-Image Dehazing Method Based on a Physical Model and Gray Projection. IEEE Access 2018, 6, 5641–5653. [Google Scholar] [CrossRef]
- Jun, J.G.; Chu, Q.; Zhang, X.; Fan, Z. Image Dehazing Method Based on Light Field Depth Estimation and Atmospheric Scattering Model. Acta Photonica Sin. 2020, 49, 0710001. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Zhang, J.; Sun, R. Image dehazing algorithm by combining light field multi-cues and atmospheric scattering model. Opto-Electron. Eng. 2020, 47, 190634. [Google Scholar]
- You, J.; Liu, P.; Rong, X.; Li, B.; Xu, T. Dehazing and enhancement research of polarized image based on dark channel priori principle. Laser Infrared 2020, 50, 493–500. [Google Scholar]
- Namer, E.; Schechner, Y.Y. Advanced visibility improvement based on polarization filtered images. In Polarization Science and Remote Sensing II.; SPIE: San Diego, CA, USA, 2005; Volume 5888, p. 588805. [Google Scholar]
- Xia, P.; Liu, X. Real-Time Static Polarimetric Image Dehazing Technique Based on Atmospheric Scattering Correction. J. Beijing Univ. Posts Telecommun. 2016, 39, 33–36. [Google Scholar]
- Ueki, Y.; Ikehara, M. Weighted Generalization of Dark Channel Prior with Adaptive Color Correction for Defogging. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 24–28 August 2020; IEEE: Piscataway, NJ, USA, 2021; pp. 685–689. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Single image haze removal using dark channel prior. In Proceedings of the IEEE-Computer-Society Conference on Computer Vision and Pattern Recognition Workshops, Miami, FL, USA, 20–25 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1956–1963. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided image filtering. In Proceedings of the European Conference on Computer Vision (ECCV), Heraklion, Greece, 5–11 September 2010; Springer: Berlin, Germany, 2010; pp. 1–14. [Google Scholar]
- Xu, Y.; Guo, X.; Wang, H.; Zhao, F.; Peng, L. Single image haze removal using light and dark channel prior. In Proceedings of the 2016 IEEE/CIC International Conference on Communications in China (ICCC), Chengdu, China, 27–29 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Li, J.; Hu, Q.; Ai, M. Haze and thin cloud removal via sphere model improved dark channel prior. IEEE Geosci. Remote Sens. Lett. 2018, 16, 472–476. [Google Scholar] [CrossRef]
- Wang, F.; Wang, W. Road extraction using modified dark channel prior and neighborhood FCM in foggy aerial images. Multimed. Tools Appl. 2019, 78, 947–964. [Google Scholar]
- Engin, D.; Gen, A.; Eenel, H.K. Cycle-Dehaze: Enhanced CycleGAN for single image dehazing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 825–833. [Google Scholar]
- Li, J.; Li, G.; Fan, H. Image dehazing using residual-based deep CNN. IEEE Access 2018, 6, 26831–26842. [Google Scholar] [CrossRef]
- Zhang, H.; Patel, V.M. Densely connected pyramid dehazing network. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 3194–3203. [Google Scholar]
- Ren, W.; Ma, L.; Zhang, J.; Pan, J.; Cao, X.; Liu, W.; Yang, M. Gated fusion network for single image dehazing. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 3253–3261. [Google Scholar]
- Chen, D.; He, M.; Fan, Q.; Liao, J.; Zhang, L.; Hou, D.; Lu, Y.; Hua, G. Gated context aggregation network for image dehazing and deraining. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1375–1383. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Li, W. Two-dimensional Otsu automatic threshold segmentation for grayscale image. Acta Autom. Sin. 1993, 19, 101–105. [Google Scholar]
- Tarel, J.; Hautiere, N. Fast visibility restoration from a single color or gray level image. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 2201–2208. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Single image haze removal using dark channel prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 2341–2353. [Google Scholar]
- Tufail, Z.; Khurshid, K.; Salmana, A.; Nizami, I.F.; Khurshid, K.; Jeon, B. Improved dark channel prior for image defogging using RGB and YCbCr color space. IEEE Access 2018, 6, 32576–32587. [Google Scholar] [CrossRef]
- Gao, T.; Li, K.; Chen, T.; Liu, M.; Mei, S.; Xing, K. A Novel UAV Sensing Image Defogging Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2610–2625. [Google Scholar] [CrossRef]
- Yu, C.; Lin, H.; Xu, X.; Ye, X. Parameter estimation of fog degradation model and CUDA design. J. Comput.-Aided Des. Graph. 2018, 30, 327–335. [Google Scholar] [CrossRef]
- Fan, X.; Ye, S.; Shi, P.; Zhang, X.; Ma, J. An image dehazing algorithm based on improved atmospheric scattering model. J. Comput.-Aided Des. Graph. 2019, 31, 1148–1155. [Google Scholar] [CrossRef]
- Xiao, J.; Shen, M.; Lei, J.; Xiong, W.; Jiao, C. Image conversion algorithm of haze scene based on generative adversarial networks. J. Comput. Sci. 2020, 43, 165–176. [Google Scholar]
- Yao, T.; Liang, Y.; Liu, X.; Hu, Q. Video dehazing algorithm via haze-line prior with spatiotemporal correlation constraint. J. Electron. Inf. Technol. 2020, 42, 2796–2804. [Google Scholar]















| Tarel’s Algorithm | He’s Algorithm | Tufail’s Algorithm | Gao’s Algorithm | Proposed Algorithm | |
|---|---|---|---|---|---|
| UQI | 0.6996 | 0.7404 | 0.3848 | 0.7896 | 0.7954 |
| SSIM | 0.8219 | 0.8368 | 0.4749 | 0.8514 | 0.8828 |
| PSNR | 13.2775 | 15.1127 | 9.8925 | 14.2001 | 16.9181 |
| H | 7.4240 | 7.4163 | 6.6700 | 7.4926 | 7.5637 |
| Tarel’s Algorithm | He’s Algorithm | Tufail’s Algorithm | Gao’s Algorithm | Proposed Algorithm | |
|---|---|---|---|---|---|
| UQI | 0.5523 | 0.5811 | 0.1931 | 0.5384 | 0.6056 |
| SSIM | 0.6600 | 0.6449 | 0.2623 | 0.5392 | 0.6791 |
| PSNR | 11.9295 | 10.5063 | 8.2694 | 9.5916 | 12.1122 |
| H | 7.0385 | 6.5117 | 6.1015 | 6.3426 | 7.0759 |
| Tarel’s Algorithm | He’s Algorithm | Tufail’s Algorithm | Gao’s Algorithm | Proposed Algorithm | |
|---|---|---|---|---|---|
| UQI | 0.7055 | 0.6941 | 0.2912 | 0.7610 | 0.7780 |
| SSIM | 0.8420 | 0.7652 | 0.3646 | 0.8576 | 0.8723 |
| PSNR | 16.0496 | 10.4442 | 6.8214 | 16.1046 | 16.3206 |
| H | 7.3893 | 7.2419 | 6.8116 | 7.4419 | 7.6805 |
| Tarel’s Algorithm | He’s Algorithm | Tufail’s Algorithm | Gao’s Algorithm | Proposed Algorithm | |
|---|---|---|---|---|---|
| UQI | 0.7752 | 0.7439 | 0.2861 | 0.7173 | 0.7878 |
| SSIM | 0.8620 | 0.8681 | 0.3004 | 0.8283 | 0.8753 |
| PSNR | 16.5706 | 16.3768 | 7.8100 | 13.3087 | 16.9963 |
| H | 7.4138 | 7.3514 | 6.4437 | 7.4138 | 7.4954 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Liu, M.; Gao, T.; Cheng, P.; Mei, S.; Li, Y. A Fusion-Based Defogging Algorithm. Remote Sens. 2022, 14, 425. https://doi.org/10.3390/rs14020425
Chen T, Liu M, Gao T, Cheng P, Mei S, Li Y. A Fusion-Based Defogging Algorithm. Remote Sensing. 2022; 14(2):425. https://doi.org/10.3390/rs14020425
Chicago/Turabian StyleChen, Ting, Mengni Liu, Tao Gao, Peng Cheng, Shaohui Mei, and Yonghui Li. 2022. "A Fusion-Based Defogging Algorithm" Remote Sensing 14, no. 2: 425. https://doi.org/10.3390/rs14020425
APA StyleChen, T., Liu, M., Gao, T., Cheng, P., Mei, S., & Li, Y. (2022). A Fusion-Based Defogging Algorithm. Remote Sensing, 14(2), 425. https://doi.org/10.3390/rs14020425