Leaf Area Index Estimation of Pergola-Trained Vineyards in Arid Regions Based on UAV RGB and Multispectral Data Using Machine Learning Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
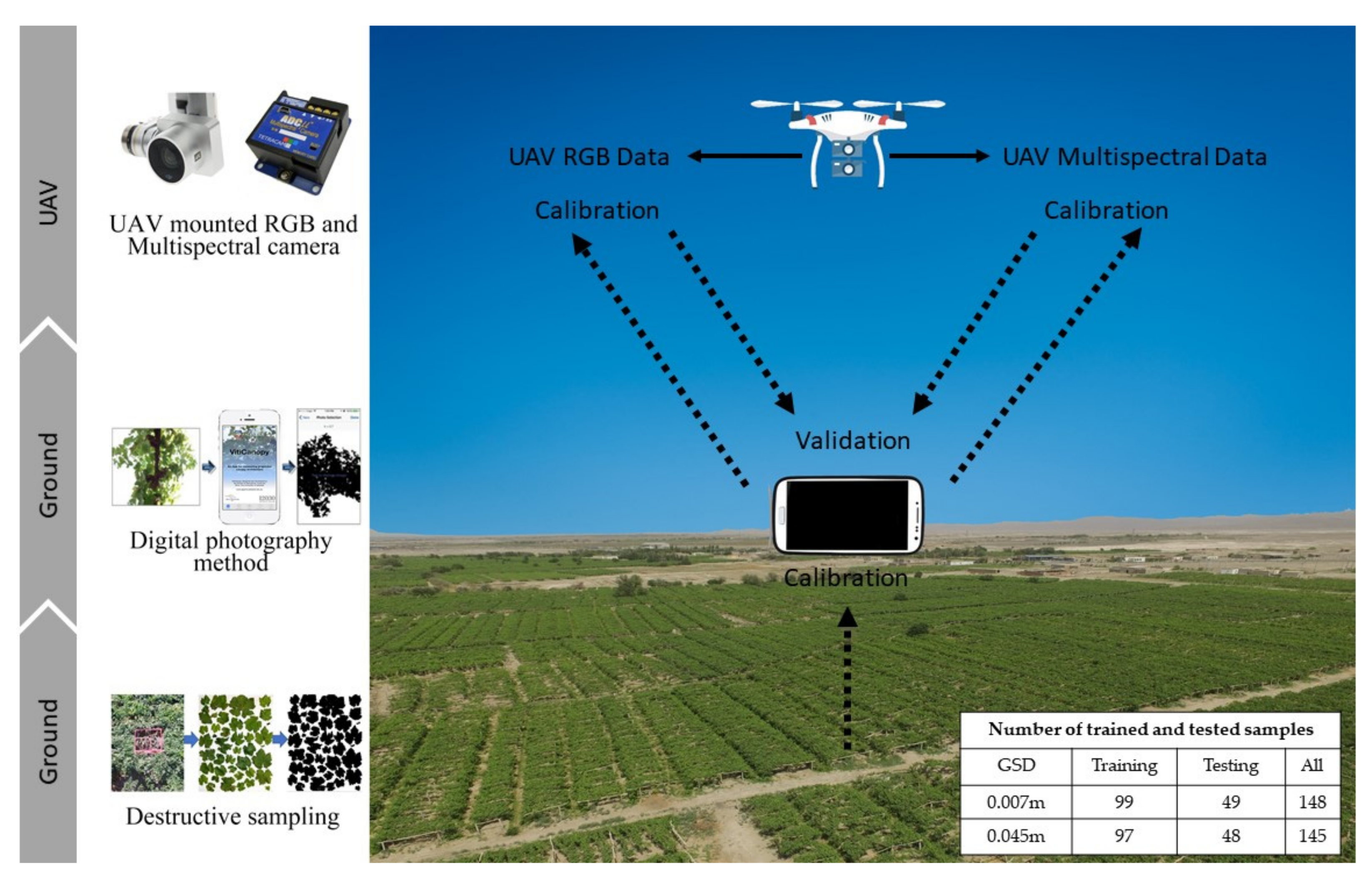
2.2. Data
2.2.1. Unmanned Aerial Vehicle (UAV) Data Acquisition
2.2.2. Leaf Area Index (LAI) Data Acquisition by Destructive Sampling
2.2.3. LAI Data Acquisition by Digital Cover Photography Method
2.3. Methods
2.3.1. Determination of Light Extinction Coefficient
2.3.2. Spectral Feature Extraction and Reduction
2.3.3. Ensemble Model Development
3. Results
3.1. Calibration Result of Light Extinction Coefficient
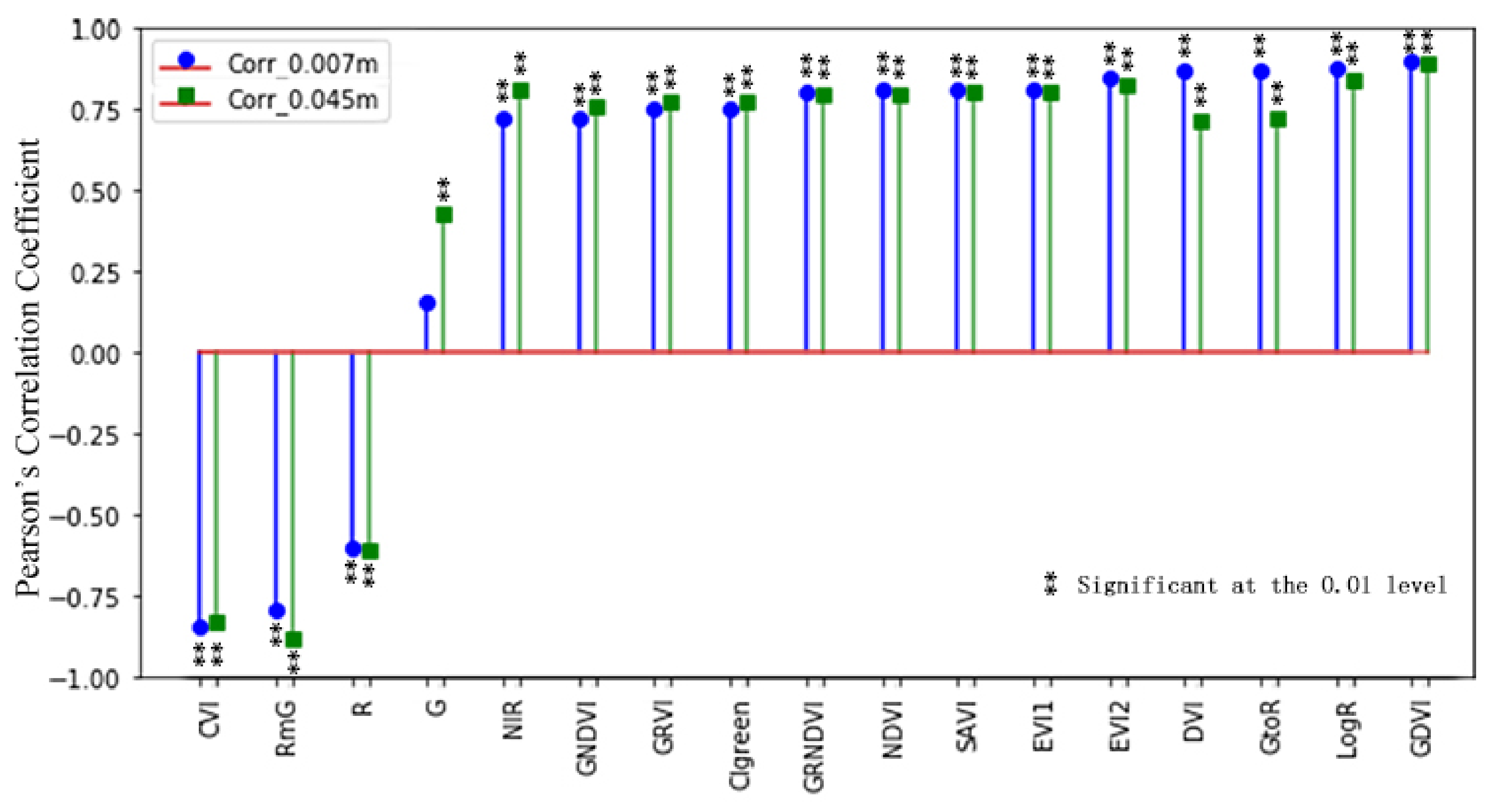
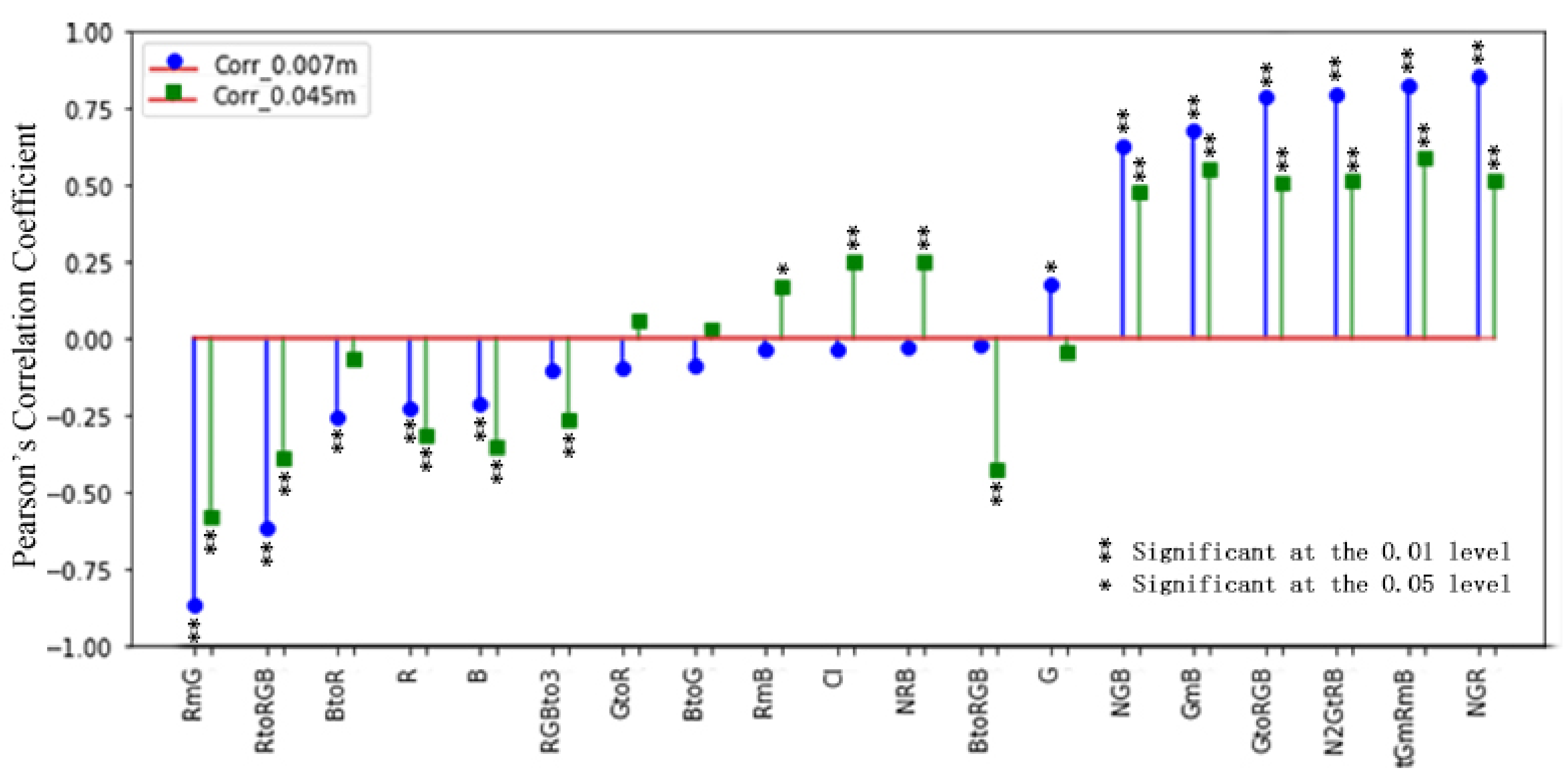
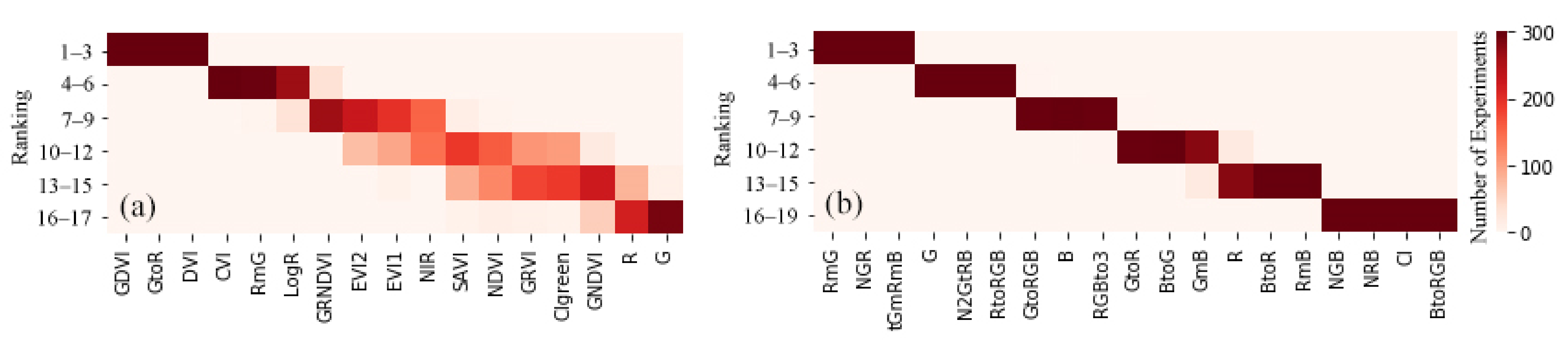
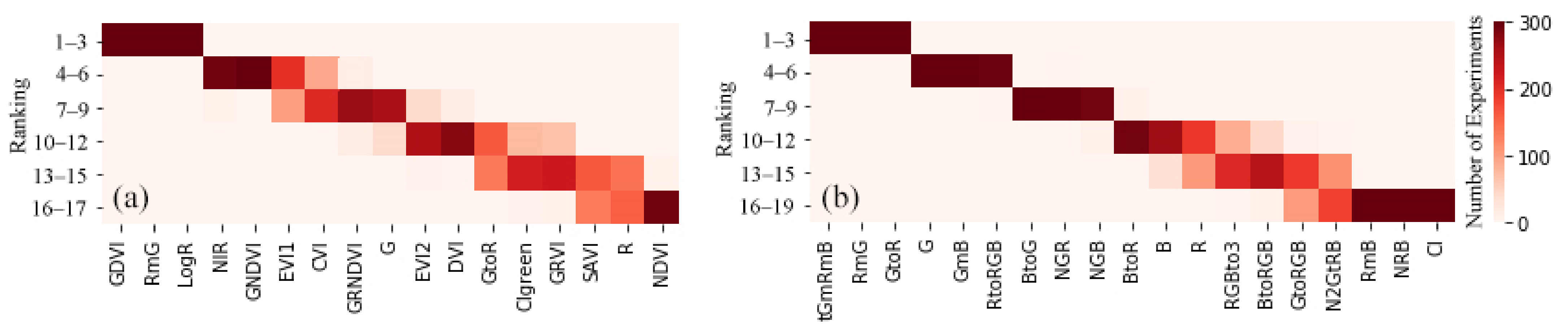
3.2. Vegetation Indices and Selection
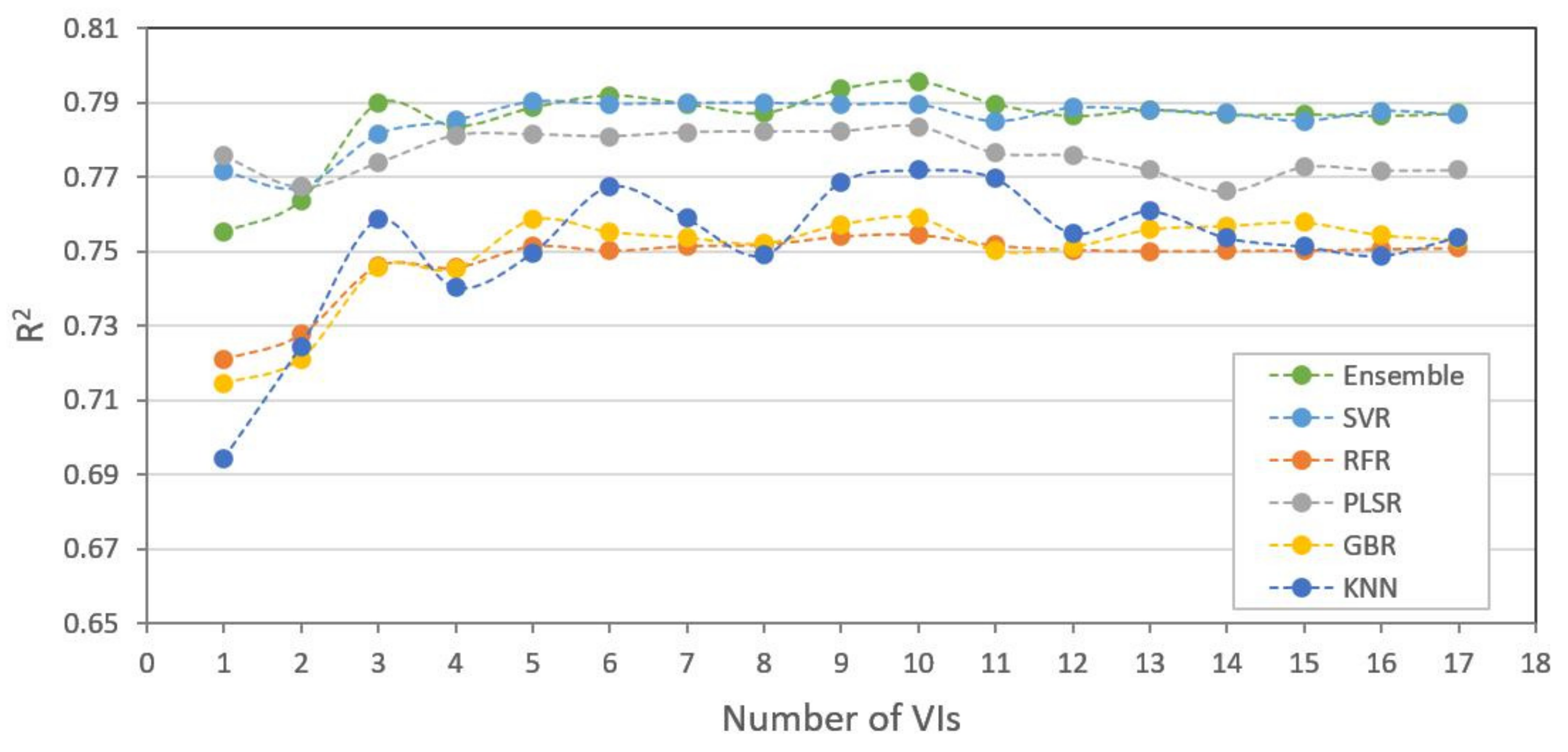
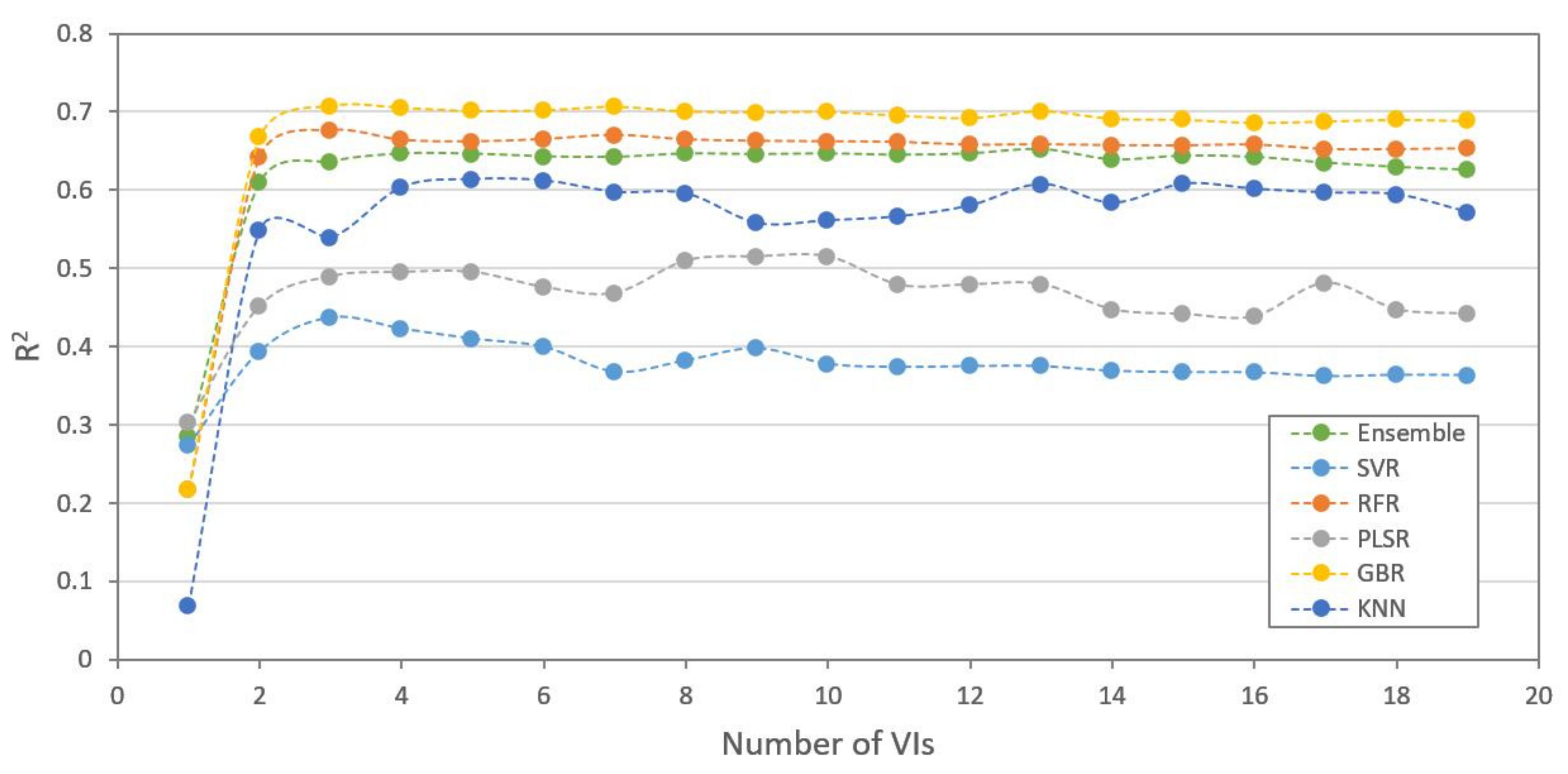
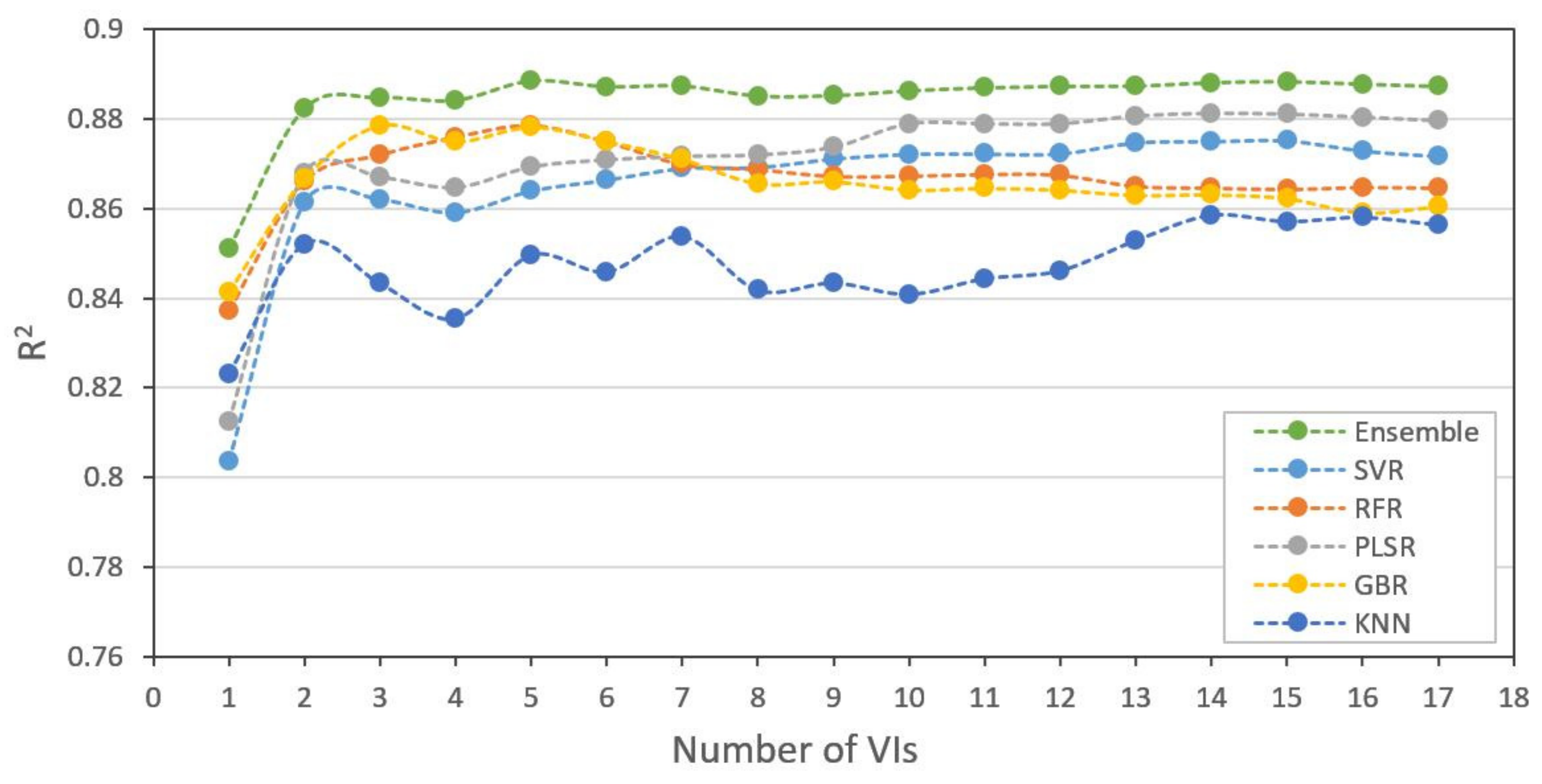
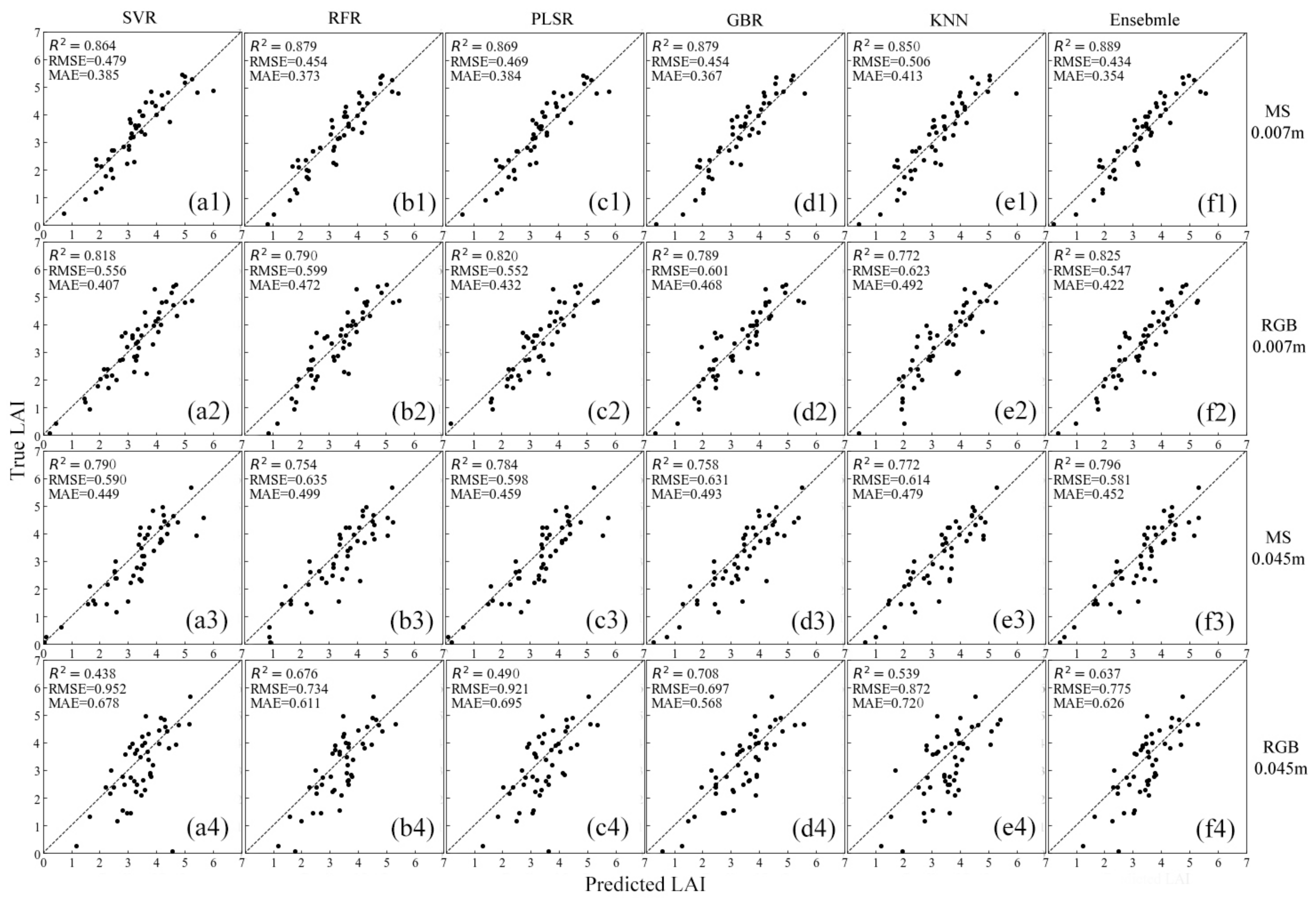
3.3. Model Comparison and Performance
3.4. Model Adaptability for Different Datasets
4. Discussion
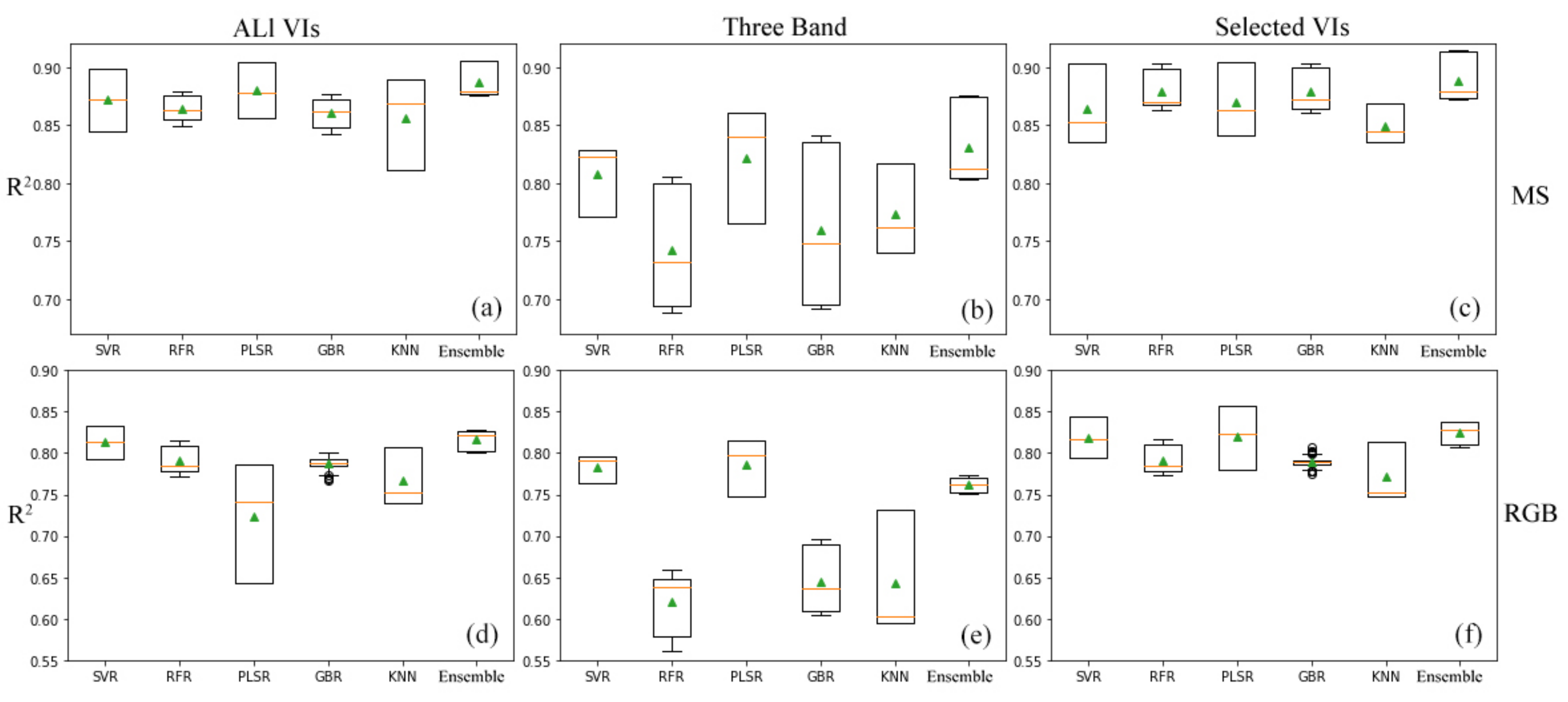
4.1. Contributions of Feature Selection for Datasets
4.2. Comparing Different Machine Learning Methods in Different Datasets
4.3. Effects of Different Ground Sample Distance (GSD) and Sensor Datasets
5. Conclusions
- (a)
- We proposed a light extinction coefficient that is suitable for estimating the LAI in pergola-trained vineyards. The LAI values estimated using the proposed light extinction coefficient of 0.41 were closer to the true LAI, using which in situ LAI values can be estimated quickly by the use of portable devices such as mobile phones or tablets.
- (b)
- We propose a robust VI-LAI estimation ensemble model that outperforms other base models. Among these, those using multispectral data-derived VIs showed higher potentiality than RGB data-derived ones. However, RGB data were also found to be a promising data source with an R2 reaching 0.825, RMSE 0.546, and MAE 0.421.
- (c)
- Feature selection improved the accuracy and efficiency of LAI estimation models by using the best combinations of VIs from both multispectral and RGB data.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ML Methods | Using All 19 VIs | Using Selected 18 VIs | Using 3 Bands | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | |
| SVR | 0.813 (0.016) | 0.565 (0.021) | 0.415 (0.020) | 0.818 (0.021) | 0.556 (0.028) | 0.407 (0.023) | 0.783 (0.014) | 0.608 (0.008) | 0.453 (0.011) |
| RFR | 0.790 (0.015) | 0.599 (0.029) | 0.471 (0.011) | 0.791 (0.015) | 0.598 (0.028) | 0.470 (0.010) | 0.623 (0.033) | 0.804 (0.052) | 0.610 (0.018) |
| PLSR | 0.723 (0.059) | 0.684 (0.069) | 0.485 (0.041) | 0.820 (0.032) | 0.552 (0.037) | 0.432 (0.045) | 0.787 (0.029) | 0.602 (0.027) | 0.447 (0.023) |
| GBR | 0.787 (0.007) | 0.604 (0.015) | 0.471 (0.014) | 0.790 (0.005) | 0.600 (0.015) | 0.467 (0.007) | 0.645 (0.034) | 0.779 (0.055) | 0.600 (0.023) |
| KNN | 0.766 (0.029) | 0.630 (0.028) | 0.496 (0.020) | 0.772 (0.030) | 0.623 (0.030) | 0.492 (0.023) | 0.643 (0.063) | 0.777 (0.058) | 0.602 (0.046) |
| Ensemble | 0.817 (0.011) | 0.560 (0.006) | 0.432 (0.016) | 0.825 (0.012) | 0.546 (0.007) | 0.421 (0.019) | 0.762 (0.008) | 0.638 (0.012) | 0.489 (0.020) |
| ML Methods | Using All 17 VIs | Using Selected 10 VIs | Using 3 Bands | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | |
| SVR | 0.787 (0.019) | 0.594 (0.018) | 0.451 (0.027) | 0.790 (0.018) | 0.590 (0.017) | 0.449 (0.024) | 0.768 (0.017) | 0.620 (0.030) | 0.475 (0.003) |
| RFR | 0.751 (0.044) | 0.638 (0.036) | 0.500 (0.028) | 0.754 (0.041) | 0.635 (0.032) | 0.499 (0.026) | 0.715 (0.074) | 0.679 (0.066) | 0.531 (0.040) |
| PLSR | 0.772 (0.025) | 0.614 (0.033) | 0.470 (0.034) | 0.783 (0.026) | 0.598 (0.030) | 0.459 (0.032) | 0.767 (0.017) | 0.622 (0.021) | 0.485 (0.034) |
| GBR | 0.754 (0.049) | 0.634 (0.041) | 0.496 (0.040) | 0.759 (0.037) | 0.629 (0.029) | 0.491 (0.028) | 0.730 (0.049) | 0.665 (0.037) | 0.534 (0.029) |
| KNN | 0.754 (0.025) | 0.638 (0.012) | 0.496 (0.017) | 0.772 (0.024) | 0.614 (0.010) | 0.479 (0.015) | 0.732 (0.055) | 0.662 (0.045) | 0.522 (0.029) |
| Ensemble | 0.787 (0.025) | 0.592 (0.019) | 0.453 (0.027) | 0.796 (0.023) | 0.581 (0.018) | 0.452 (0.021) | 0.777 (0.027) | 0.606 (0.015) | 0.478 (0.022) |
| ML Methods | Using All 19 VIs | Using Selected 3 VIs | Using 3 Bands | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | |
| SVR | 0.364 (0.144) | 1.025 (0.088) | 0.735 (0.031) | 0.438 (0.192) | 0.952 (0.152) | 0.678 (0.053) | 0.048 (0.393) | 1.239 (0.242) | 0.865 (0.007) |
| RFR | 0.653 (0.045) | 0.765 (0.075) | 0.626 (0.067) | 0.676 (0.058) | 0.734 (0.040) | 0.611 (0.029) | 0.495 (0.051) | 0.925 (0.081) | 0.757 (0.040) |
| PLSR | 0.442 (0.134) | 0.958 (0.090) | 0.713 (0.028) | 0.490 (0.096) | 0.921 (0.060) | 0.695 (0.024) | 0.214 (0.105) | 1.148 (0.069) | 0.897 (0.067) |
| GBR | 0.689 (0.037) | 0.724 (0.058) | 0.604 (0.048) | 0.708 (0.051) | 0.697 (0.032) | 0.568 (0.036) | 0.539 (0.096) | 0.882 (0.126) | 0.713 (0.064) |
| KNN | 0.572 (0.020) | 0.850 0.019) | 0.669 (0.006) | 0.539 (0.113) | 0.872 (0.070) | 0.720 (0.072) | 0.451 (0.111) | 0.957 (0.080) | 0.781 (0.088) |
| Ensemble | 0.626 (0.044) | 0.792 (0.015) | 0.622 (0.039) | 0.637 (0.077) | 0.775 (0.053) | 0.626 (0.039) | 0.466 (0.012) | 0.950 (0.042) | 0.767 (0.044) |

References
- FAO. The Future of Food and Agriculture: Trends and Challenges; FAO: Rome, Italy, 2017. [Google Scholar]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Chason, J.W.; Baldocchi, D.D.; Huston, M.A. A Comparison of Direct and Indirect Methods for Estimating Forest Canopy Leaf-Area. Agric. For. Meteorol. 1991, 57, 107–128. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L.; van den Brande, M.M.M. Using Sentinel-2 Data for Retrieving LAI and Leaf and Canopy Chlorophyll Content of a Potato Crop. Remote Sens. 2017, 9, 405. [Google Scholar] [CrossRef] [Green Version]
- Towers, P.C.; Strever, A.; Poblete-Echeverría, C. Comparison of Vegetation Indices for Leaf Area Index Estimation in Vertical Shoot Positioned Vine Canopies with and without Grenbiule Hail-Protection Netting. Remote Sens. 2019, 11, 1073. [Google Scholar] [CrossRef] [Green Version]
- Vélez, S.; Barajas, E.; Rubio, J.A.; Vacas, R.; Poblete-Echeverría, C. Effect of Missing Vines on Total Leaf Area Determined by NDVI Calculated from Sentinel Satellite Data: Progressive Vine Removal Experiments. Appl. Sci. 2020, 10, 3612. [Google Scholar] [CrossRef]
- Watson, D.J. Comparative Physiological Studies on the Growth of Field Crops: I. Variation in Net Assimilation Rate and Leaf Area between Species and Varieties, and within and between Years. Ann. Bot. 1947, 11, 41–76. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef] [Green Version]
- Hicks, S.K.; Lascano, R.J. Estimation of Leaf-Area Index for Cotton Canopies Using the Li-Cor Lai-2000 Plant Canopy Analyzer. Agron. J. 1995, 87, 458–464. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Smith, G.J.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Gates, D.J.; Westcott, M. A Direct Derivation of Miller Formula for Average Foliage Density. Aust. J. Bot. 1984, 32, 117–119. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Plant Canopy Gap-Size Analysis Theory for Improving Optical Measurements of Leaf-Area Index. Appl. Opt. 1995, 34, 6211–6222. [Google Scholar] [CrossRef] [Green Version]
- Lang, A.R.G.; Mcmurtrie, R.E. Total Leaf Areas of Single Trees of Eucalyptus-Grandis Estimated from Transmittances of the Suns Beam. Agric. For. Meteorol. 1992, 58, 79–92. [Google Scholar] [CrossRef]
- Lang, A.R.G.; Xiang, Y.Q. Estimation of Leaf-Area Index from Transmission of Direct Sunlight in Discontinuous Canopies. Agric. For. Meteorol. 1986, 37, 229–243. [Google Scholar] [CrossRef]
- Breda, N.J.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Costa, J.D.; Coelho, R.D.; Barros, T.H.D.; Fraga, E.F.; Fernandes, A.L.T. Leaf area index and radiation extinction coefficient of a coffee canopy under variable drip irrigation levels. Acta Sci. Agron. 2019, 41, e42703. [Google Scholar] [CrossRef]
- Macfarlane, C.; Hoffman, M.; Eamus, D.; Kerp, N.; Higginson, S.; McMurtrie, R.; Adams, M. Estimation of leaf area index in eucalypt forest using digital photography. Agric. For. Meteorol. 2007, 143, 176–188. [Google Scholar] [CrossRef]
- Müller-Linow, M.; Wilhelm, J.; Briese, C.; Wojciechowski, T.; Schurr, U.; Fiorani, F. Plant Screen Mobile: An open-source mobile device app for plant trait analysis. Plant Methods 2019, 15, 2. [Google Scholar] [CrossRef] [Green Version]
- Easlon, H.M.; Bloom, A.J. Easy Leaf Area: Automated Digital Image Analysis for Rapid and Accurate Measurement of Leaf Area. Appl. Plant Sci. 2014, 2, 1400033. [Google Scholar] [CrossRef]
- Orlando, F.; Movedi, E.; Coduto, D.; Parisi, S.; Brancadoro, L.; Pagani, V.; Guarneri, T.; Confalonieri, R. Estimating Leaf Area Index (LAI) in Vineyards Using the PocketLAI Smart-App. Sensors 2016, 16, 2004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Bei, R.; Fuentes, S.; Gilliham, M.; Tyerman, S.; Edwards, E.; Bianchini, N.; Smith, J.; Collins, C. VitiCanopy: A Free Computer App to Estimate Canopy Vigor and Porosity for Grapevine. Sensors 2016, 16, 585. [Google Scholar] [CrossRef] [Green Version]
- Poblete-Echeverria, C.; Fuentes, S.; Ortega-Farias, S.; Gonzalez-Talice, J.; Yuri, J.A. Digital Cover Photography for Estimating Leaf Area Index (LAI) in Apple Trees Using a Variable Light Extinction Coefficient. Sensors 2015, 15, 2860–2872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Turton, S.M. The relative distribution of photosynthetically active radiation within four tree canopies, Craigieburn Range, New Zealand. Aust. For. Res. 1985, 15, 383–394. [Google Scholar]
- Smith, F.W.; Sampson, D.A.; Long, J.N. Comparison of Leaf-Area Index Estimates from Tree Allometrics and Measured Light Interception. For. Sci. 1991, 37, 1682–1688. [Google Scholar]
- Smith, N.J. Estimating leaf area index and light extinction coefficients in stands of Douglas-fir (Pseudotsugamenziesii). Can. J. For. Res. 1993, 23, 317–321. [Google Scholar] [CrossRef]
- Pierce, L.L.; Running, S.W. Rapid Estimation of Coniferous Forest Leaf-Area Index Using a Portable Integrating Radiometer. Ecology 1988, 69, 1762–1767. [Google Scholar] [CrossRef]
- Jarvis, P.G.; Leverenz, J.W. Productivity of Temperate, Deciduous and Evergreen Forests, 1st ed.; Springer: Berlin, Germany, 1983; pp. 233–280. [Google Scholar]
- Vose, J.M.; Clinton, B.D.; Sullivan, N.H.; Bolstad, P.V. Vertical leaf area distribution, light transmittance, and application of the Beer-Lambert Law in four mature hardwood stands in the southern Appalachians. Can. J. For. Res. 1995, 25, 1036–1043. [Google Scholar] [CrossRef] [Green Version]
- Hassika, P.; Berbigier, P.; Bonnefond, J.M. Measurement and modelling of the photosynthetically active radiation transmitted in a canopy of maritime pine. Ann. Sci. For. 1997, 54, 715–730. [Google Scholar] [CrossRef] [Green Version]
- Turner, D.P.; Cohen, W.B.; Kennedy, R.E.; Fassnacht, K.S.; Briggs, J.M. Relationships between Leaf Area Index and Landsat TM Spectral Vegetation Indices across Three Temperate Zone Sites. Remote Sens. Environ. 1999, 70, 52–68. [Google Scholar] [CrossRef]
- Padalia, H.; Sinha, S.K.; Bhave, V.; Trivedi, N.K.; Kumar, A.S. Estimating canopy LAI and chlorophyll of tropical forest plantation (North India) using Sentinel-2 data. Adv. Space Res. 2020, 65, 458–469. [Google Scholar] [CrossRef]
- Sun, L.; Wang, W.Y.; Jia, C.; Liu, X.R. Leaf area index remote sensing based on Deep Belief Network supported by simulation data. Int. J. Remote Sens. 2021, 42, 7637–7661. [Google Scholar] [CrossRef]
- MODIS Web. Available online: http://modis.gsfc.nasa.gov/data/atbd/atbd_mod15.pdf (accessed on 3 November 2021).
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Nino, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION—Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Sozzi, M.; Kayad, A.; Marinello, F.; Taylor, J.A.; Tisseyre, B. Comparing vineyard imagery acquired from Sentinel-2 and Unmanned Aerial Vehicle (UAV) platform. Oeno One 2020, 54, 189–197. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Jia, M.M.; Wang, Z.M.; Zhou, Y.M.; Wen, X.; Tan, Y.; Cheng, L.N. A Comparison of Gaofen-2 and Sentinel-2 Imagery for Mapping Mangrove Forests Using Object-Oriented Analysis and Random Forest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4185–4193. [Google Scholar] [CrossRef]
- Kamal, M.; Sidik, F.; Prananda, A.R.A.; Mahardhika, S.A. Mapping Leaf Area Index of restored mangroves using WorldView-2 imagery in Perancak Estuary, Bali, Indonesia. Remote Sens. Appl. Soc. Environ. 2021, 23, 100567. [Google Scholar] [CrossRef]
- Kokubu, Y.; Hara, S.; Tani, A. Mapping Seasonal Tree Canopy Cover and Leaf Area Using Worldview-2/3 Satellite Imagery: A Megacity-Scale Case Study in Tokyo Urban Area. Remote Sens. 2020, 12, 1505. [Google Scholar] [CrossRef]
- Tian, J.Y.; Wang, L.; Li, X.J.; Gong, H.L.; Shi, C.; Zhong, R.F.; Liu, X.M. Comparison of UAV and WorldView-2 imagery for mapping leaf area index of mangrove forest. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 22–31. [Google Scholar] [CrossRef]
- Peng, X.S.; Han, W.T.; Ao, J.Y.; Wang, Y. Assimilation of LAI Derived from UAV Multispectral Data into the SAFY Model to Estimate Maize Yield. Remote Sens. 2021, 13, 1094. [Google Scholar] [CrossRef]
- Gong, Y.; Yang, K.L.; Lin, Z.H.; Fang, S.H.; Wu, X.T.; Zhu, R.S.; Peng, Y. Remote estimation of leaf area index (LAI) with unmanned aerial vehicle (UAV) imaging for different rice cultivars throughout the entire growing season. Plant Methods 2021, 17, 1–16. [Google Scholar] [CrossRef]
- Liu, Z.J.; Guo, P.J.; Liu, H.; Fan, P.; Zeng, P.Z.; Liu, X.Y.; Feng, C.; Wang, W.; Yang, F.Z. Gradient Boosting Estimation of the Leaf Area Index of Apple Orchards in UAV Remote Sensing. Remote Sens. 2021, 13, 3263. [Google Scholar] [CrossRef]
- Mathews, A.J.; Jensen, J.L.R. Visualizing and Quantifying Vineyard Canopy LAI Using an Unmanned Aerial Vehicle (UAV) Collected High Density Structure from Motion Point Cloud. Remote Sens. 2013, 5, 2164–2183. [Google Scholar] [CrossRef] [Green Version]
- Raj, R.; Walker, J.P.; Pingale, R.; Nandan, R.; Naik, B.; Jagarlapudi, A. Leaf area index estimation using top-of-canopy airborne RGB images. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102282. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Tanaka, Y.; Imachi, Y.; Yamashita, M.; Katsura, K. Feasibility of Combining Deep Learning and RGB Images Obtained by Unmanned Aerial Vehicle for Leaf Area Index Estimation in Rice. Remote Sens. 2021, 13, 84. [Google Scholar] [CrossRef]
- Yao, X.; Wang, N.; Liu, Y.; Cheng, T.; Tian, Y.C.; Chen, Q.; Zhu, Y. Estimation of Wheat LAI at Middle to High Levels Using Unmanned Aerial Vehicle Narrowband Multispectral Imagery. Remote Sens. 2017, 9, 1304. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.J.; Cheng, T.; Guo, W.; Xu, X.; Qiao, H.B.; Xie, Y.M.; Ma, X.M. Leaf area index estimation model for UAV image hyperspectral data based on wavelength variable selection and machine learning methods. Plant Methods 2021, 17, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Li, C.; Tang, L.; Ma, L. Retrieval and scale effect analysis of LAI over typical farmland from UAV-based hyperspectral data. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XXI, Strasbourg, France, 9–11 September 2019. [Google Scholar]
- Tian, L.; Qu, Y.H.; Qi, J.B. Estimation of Forest LAI Using Discrete Airborne LiDAR: A Review. Remote Sens. 2021, 13, 2408. [Google Scholar] [CrossRef]
- Pastonchi, L.; Di Gennaro, S.F.; Toscano, P.; Matese, A. Comparison between satellite and ground data with UAV-based information to analyse vineyard spatio-temporal variability. Oeno One 2020, 54, 919–934. [Google Scholar] [CrossRef]
- Xiao, X.X.; Zhang, T.J.; Zhong, X.Y.; Shao, W.W.; Li, X.D. Support vector regression snow-depth retrieval algorithm using passive microwave remote sensing data. Remote Sens. Environ. 2018, 210, 48–64. [Google Scholar] [CrossRef]
- Tobias, R.D. An Introduction to Partial Least Squares Regression. In Proceedings of the SUGI Proceedings, Orlando, FL, USA, April 1995. [Google Scholar]
- Wold, S.; Sjostrom, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemometr. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Filippi, A.M.; Guneralp, I.; Randall, J. Hyperspectral remote sensing of aboveground biomass on a river meander bend using multivariate adaptive regression splines and stochastic gradient boosting. Remote Sens. Lett. 2014, 5, 432–441. [Google Scholar] [CrossRef]
- Adsule, P.G.; Karibasappa, G.S.; Banerjee, K.; Mundankar, K. Status and prospects of raisin industry in India. In Proceedings of the International Symposium on Grape Production and Processing, Baramati, India, 13 May 2008. [Google Scholar]
- Caruso, G.; Tozzini, L.; Rallo, G.; Primicerio, J.; Moriondo, M.; Palai, G.; Gucci, R. Estimating biophysical and geometrical parameters of grapevine canopies (’Sangiovese’) by an unmanned aerial vehicle (UAV) and VIS-NIR cameras. Vitis 2017, 56, 63–70. [Google Scholar]
- Gullo, G.; Branca, V.; Dattola, A.; Zappia, R.; Inglese, P. Effect of summer pruning on some fruit quality traits in Hayward kiwifruit. Fruits 2013, 68, 315–322. [Google Scholar] [CrossRef] [Green Version]
- Shiozaki, Y.; Kikuchi, T. Fruit Productivity as Related to Leaf-Area Index and Tree Vigor of Open-Center Apple-Trees Trained by Traditional Japanese System. J. Jpn. Soc. Hortic. Sci. 1992, 60, 827–832. [Google Scholar] [CrossRef] [Green Version]
- Grantz, D.A.; Zhang, X.J.; Metheney, P.D.; Grimes, D.W. Indirect Measurement of Leaf-Area Index in Pima Cotton (Gossypium-Barbadense L) Using a Commercial Gap Inversion Method. Agric. For. Meteorol. 1993, 67, 1–12. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L. Using Hyperspectral Remote Sensing Data for Retrieving Canopy Chlorophyll and Nitrogen Content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 574–583. [Google Scholar] [CrossRef]
- Beeri, O.; Netzer, Y.; Munitz, S.; Mintz, D.F.; Pelta, R.; Shilo, T.; Horesh, A.; Mey-tal, S. Kc and LAI Estimations Using Optical and SAR Remote Sensing Imagery for Vineyards Plots. Remote Sens. 2020, 12, 3478. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, L.; Wang, W.; Chen, B. UAV Data as an Alternative to Field Sampling to Monitor Vineyards Using Machine Learning Based on UAV/Sentinel-2 Data Fusion. Remote Sens. 2021, 13, 457. [Google Scholar] [CrossRef]
- Hua, Y. Temperature Changes Characteristic of Turpan in Recent 60 Years. J. Arid Meteorol. 2012, 30, 630–634. [Google Scholar]
- Lv, T.; Wu, S.; Liu, Q.; Xia, S.; Ge, H.; Li, J. Variations of Extreme Temperature in Turpan City, Xinjiang during the Period of 1952–2013. Arid. Zone Res. 2018, 35, 606–614. [Google Scholar]
- Tetracam ADC Micro. Available online: https://tetracam.com/Products-ADC_Micro.htm (accessed on 10 October 2021).
- Sara, V.; Silvia, D.F.; Filippo, M.; Piergiorgio, M. Unmanned aerial vehicles and Geographical Information System integrated analysis of vegetation in Trasimeno Lake, Italy. Lakes Reserv. Sci. Policy Manag. Sustain. Use 2016, 21, 5–19. [Google Scholar]
- Candiago, S.; Remondino, F.; De Giglio, M.; Dubbini, M.; Gattelli, M. Evaluating Multispectral Images and Vegetation Indices for Precision Farming Applications from UAV Images. Remote Sens. 2015, 7, 4026–4047. [Google Scholar] [CrossRef] [Green Version]
- Hoffmann, C.M.; Blomberg, M. Estimation of leaf area index of Beta vulgaris L. based on optical remote sensing data. J. Agron. Crop. Sci. 2004, 190, 197–204. [Google Scholar]
- Gobron, N.; Pinty, B.; Verstraete, M.M.; Widlowski, J.L. Advanced vegetation indices optimized for up-coming sensors: Design, performance, and applications. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2489–2505. [Google Scholar]
- Pichon, L.; Taylor, J.A.; Tisseyre, B. Using smartphone leaf area index data acquired in a collaborative context within vineyards in southern France. Oeno One 2020, 54, 123–130. [Google Scholar] [CrossRef]
- Tongson, E.J.; Fuentes, S.; Carrasco-Benavides, M.; Mora, M. Canopy architecture assessment of cherry trees by cover photography based on variable light extinction coefficient modelled using artificial neural networks. Acta Hortic. 2019, 1235, 183. [Google Scholar] [CrossRef]
- Fuentes, S.; Chacon, G.; Torrico, D.D.; Zarate, A.; Viejo, C.G. Spatial Variability of Aroma Profiles of Cocoa Trees Obtained through Computer Vision and Machine Learning Modelling: A Cover Photography and High Spatial Remote Sensing Application. Sensors 2019, 19, 3054. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuentes, S.; Palmer, A.R.; Taylor, D.; Zeppel, M.; Whitley, R.; Eamus, D. An automated procedure for estimating the leaf area index (LAI) of woodland ecosystems using digital imagery, MATLAB programming and its application to an examination of the relationship between remotely sensed and field measurements of LAI. Funct. Plant Biol. 2008, 35, 1070–1079. [Google Scholar] [CrossRef]
- Leblanc, S.G. Correction to the plant canopy gap-size analysis theory used by the Tracing Radiation and Architecture of Canopies instrument. Appl. Opt. 2002, 41, 7667–7670. [Google Scholar] [CrossRef]
- Kawashima, S.; Nakatani, M. An algorithm for estimating chlorophyll content in leaves using a video camera. Ann. Bot. 1998, 81, 49–54. [Google Scholar] [CrossRef] [Green Version]
- Schell, J.A. Monitoring vegetation systems in the great plains with ERTS. Nasa Spec. Publ. 1973, 351, 309. [Google Scholar]
- Vincini, M.; Frazzi, E.; D’Alessio, P. Comparison of narrow-band and broad-band vegetation indices for canopy chlorophyll density estimation in sugar beet. In Proceedings of the 6th European Conference on Precision Agriculture, Skiathos, Greece, 3–6 June 2007; Wageningen Academic Publishers: Wageningen, The Netherlands, 2007; pp. 189–196. [Google Scholar]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Tucker, C.J.; Elgin, J.H.; Mcmurtrey, J.E.; Fan, C.J. Monitoring Corn and Soybean Crop Development with Hand-Held Radiometer Spectral Data. Remote Sens. Environ. 1979, 8, 237–248. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanre, D. Atmospherically Resistant Vegetation Index (Arvi) for Eos-Modis. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Wang, F.M.; Huang, J.F.; Tang, Y.L.; Wang, X.Z. New Vegetation Index and Its Application in Estimating Leaf Area Index of Rice. Rice Sci. 2007, 14, 195–203. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Ustin, S.L.; Whiting, M.L. Temporal and spatial relationships between within-field yield variability in cotton and high-spatial hyperspectral remote sensing imagery. Agron. J. 2005, 97, 641–653. [Google Scholar] [CrossRef] [Green Version]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef] [Green Version]
- Boegh, E.; Soegaard, H.; Broge, N.; Hasager, C.B.; Jensen, N.O.; Schelde, K.; Thomsen, A. Airborne multispectral data for quantifying leaf area index, nitrogen concentration, and photosynthetic efficiency in agriculture. Remote Sens. Environ. 2002, 81, 179–193. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Estimation of vegetation water content and photosynthetic tissue area from spectral reflectance: A comparison of indices based on liquid water and chlorophyll absorption features. Remote Sens. Environ. 2003, 84, 526–537. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Berjon, A.; Lopez-Lozano, R.; Miller, J.R.; Martin, P.; Cachorro, V.; Gonzalez, M.R.; de Frutos, A. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]
- Woebbecke, D.M.; Meyer, G.E.; Vonbargen, K.; Mortensen, D.A. Color Indexes for Weed Identification under Various Soil, Residue, and Lighting Conditions. Trans. ASAE 1995, 38, 259–269. [Google Scholar] [CrossRef]
- Escadafal, R.; Belghith, A.; Moussa, H.B. Indices spectraux pour la teledetection de la degradation des milieux naturels en tunisie aride. In Proceedings of the 6th International Symposium on Physical Measurements and Signatures in Remote Sensing, Val-d’Isère, France, 17–24 January 1994; pp. 253–259. [Google Scholar]
- Rivera-Caicedo, J.P.; Verrelst, J.; Munoz-Mari, J.; Camps-Valls, G.; Moreno, J. Hyperspectral dimensionality reduction for biophysical variable statistical retrieval. ISPRS J. Photogramm. Remote Sens. 2017, 132, 88–101. [Google Scholar] [CrossRef]
- Karegowda, A.G.; Manjunath, A.S.; Jayaram, M.A. Comparative study of attribute selection using gain ratio and correlation based feature selection. Int. J. Inf. Manag. 2010, 2, 271–277. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Zhao, J.Q.; Karimzadeh, M.; Masjedi, A.; Wang, T.J.; Zhang, X.W.; Crawford, M.M.; Ebert, D.S. FeatureExplorer: Interactive Feature Selection and Exploration of Regression Models for Hyperspectral Images. In Proceedings of the 2019 IEEE Visualization Conference (VIS), Vancouver, BC, Canada, 20–25 October 2019. [Google Scholar]
- Moghimi, A.; Yang, C.; Marchetto, P.M. Ensemble Feature Selection for Plant Phenotyping: A Journey From Hyperspectral to Multispectral Imaging. IEEE Access 2018, 6, 56870–56884. [Google Scholar] [CrossRef]
- Feng, L.W.; Zhang, Z.; Ma, Y.C.; Du, Q.Y.; Williams, P.; Drewry, J.; Luck, B. Alfalfa Yield Prediction Using UAV-Based Hyperspectral Imagery and Ensemble Learning. Remote Sens. 2020, 12, 2028. [Google Scholar] [CrossRef]
- Sylvester, E.V.A.; Bentzen, P.; Bradbury, I.R.; Clement, M.; Pearce, J.; Horne, J.; Beiko, R.G. Applications of random forest feature selection for fine-scale genetic population assignment. Evol. Appl. 2018, 11, 153–165. [Google Scholar] [CrossRef]
- Jin-Lei, L.I.; Zhu, X.L.; Zhu, H.Y. A Clustering Ensembles Algorithm Based on Voting Strategy. Comput. Simul. 2008, 3, 126–128. [Google Scholar]
- Lan, Y.B.; Huang, Z.X.; Deng, X.L.; Zhu, Z.H.; Huang, H.S.; Zheng, Z.; Lian, B.Z.; Zeng, G.L.; Tong, Z.J. Comparison of machine learning methods for citrus greening detection on UAV multispectral images. Comput. Electron. Agr. 2020, 171, 105234. [Google Scholar] [CrossRef]
- Azadbakht, M.; Ashourloo, D.; Aghighi, H.; Radiom, S.; Alimohammadi, A. Wheat leaf rust detection at canopy scale under different LAI levels using machine learning techniques. Comput. Electron. Agr. 2019, 156, 119–128. [Google Scholar] [CrossRef]
- Bahat, I.; Netzer, Y.; Grunzweig, J.M.; Alchanatis, V.; Peeters, A.; Goldshtein, E.; Ohana-Levi, N.; Ben-Gal, A.; Cohen, Y. In-Season Interactions between Vine Vigor, Water Status and Wine Quality in Terrain-Based Management-Zones in a ‘Cabernet Sauvignon’ Vineyard. Remote Sens. 2021, 13, 1636. [Google Scholar] [CrossRef]
- Yang, K.L.; Gong, Y.; Fang, S.H.; Duan, B.; Yuan, N.G.; Peng, Y.; Wu, X.T.; Zhu, R.S. Combining Spectral and Texture Features of UAV Images for the Remote Estimation of Rice LAI throughout the Entire Growing Season. Remote Sens. 2021, 13, 3001. [Google Scholar] [CrossRef]
- Susantoro, T.M.; Wikantika, K.; Saepuloh, A.; Harsolumakso, A.H. Selection of vegetation indices for mapping the sugarcane condition around the oil and gas field of North West Java Basin, Indonesia. Iop. C Ser. Earth Environ. 2018, 149, 012001. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.L.; Jia, K.; Xiao, C.C.; Wei, D.D.; Zhao, X.; Lan, J.H.; Wei, X.Q.; Yao, Y.J.; Wang, B.; Sun, Y.; et al. Leaf Area Index Estimation Algorithm for GF-5 Hyperspectral Data Based on Different Feature Selection and Machine Learning Methods. Remote Sens. 2020, 12, 2110. [Google Scholar] [CrossRef]
- Grabska, E.; Frantz, D.; Ostapowicz, K. Evaluation of machine learning algorithms for forest stand species mapping using Sentinel-2 imagery and environmental data in the Polish Carpathians. Remote Sens. Environ. 2020, 251, 112103. [Google Scholar] [CrossRef]
- Leuning, R.; Hughes, D.; Daniel, P.; Coops, N.C.; Newnham, G. A multi-angle spectrometer for automatic measurement of plant canopy reflectance spectra. Remote Sens. Environ. 2006, 103, 236–245. [Google Scholar] [CrossRef]






| Mission Date | Growth Period of Vine | Data Type | Flight Height | GSD |
|---|---|---|---|---|
| 4 May | Blooming stage | VitiCanopy, UAV data | 17 m | 0.007 m |
| 14 May | Fruit setting stage | VitiCanopy, UAV data | 100 m | 0.045 m |
| 29 June | Veraison stage | VitiCanopy, UAV data | 17 m, 100 m | 0.007 m, 0.045 m |
| 7 August | Post-harvest stage | True LAI, VitiCanopy, UAV data | 17 m, 91 m | 0.007 m, 0.045 m |
| Dataset | Number of Samples |
|---|---|
| 0.007 m GSD MS | 148 |
| 0.007 m GSD RGB | 145 |
| 0.045 m GSD MS | 148 |
| 0.045 m GSD RGB | 145 |
| Vegetation Index Name | Abbrev. | Formula | Used Sensor | Source |
|---|---|---|---|---|
| Near Infrared | NIR | NIR | MS | |
| Red | R | R | MS, RGB | [76] |
| Green | G | G | MS, RGB | [76] |
| Blue | B | B | RGB | [76] |
| Normalized Differential Vegetation Index | NDVI | (NIR − R)/(NIR + R) | MS | [77] |
| Chlorophyll Vegetation Index | CVI | NIR∗R/G2 | MS | [78] |
| Chlorophyll Index Green | CIgreen | (NIR/G) − 1 | MS | [79] |
| Green Difference Vegetation Index | GDVI | NIR − G | MS | [80] |
| Enhanced Vegetation Index 1 | EVI1 | 2.4∗(NIR − R)/(NIR + R + 1) | MS | [81] |
| Enhanced Vegetation Index 2 | EVI2 | 2.5∗(NIR − R)/(NIR + 2.4*R + 1) | MS | [82] |
| Green-Red NDVI | GRNDVI | (NIR − R − G)/(NIR + R + G) | MS | [83] |
| Green NDVI | GNDVI | (NIR − G)/(NIR + G) | MS | [84] |
| Green Ratio Vegetation Index | GRVI | NIR/G | MS | [85] |
| Difference Vegetation Index | DVI | NIR/R | MS | [86] |
| Log Ratio | LogR | Log(NIR/R) | MS | |
| Soil Adjusted Vegetation Index | SAVI | (1 + L)(NIR − R)/(NIR + R + L) | MS | [87] |
| Simple Ratio Green to Red | GtoR | G/R | MS, RGB | |
| Simple Ratio Blue to Green | BtoG | B/G | RGB | [88] |
| Simple Ratio Blue to Red | BtoR | B/R | RGB | [88] |
| Simple difference of green and blue | GmB | G − B | RGB | [76] |
| Simple difference of red and blue | RmB | R − B | RGB | [76] |
| Simple difference of red and green | RmG | R − G | MS, RGB | |
| Simple Ratio of Green and Red + Blue | tGmRmB | 2G − R − B | RGB | [89] |
| Mean RGB | RGBto3 | (R + G + B)/3 | RGB | |
| Red Percentage Index | RtoRGB | R/(R + G + B) | RGB | [76] |
| Green Percentage Index | GtoRGB | G/(R + G + B) | RGB | [76] |
| Blue Percentage Index | BtoRGB | B/(R + G + B) | RGB | [76] |
| Normalized Green-Red Index | NGR | (G − R)/(G + R) | RGB | [76,85] |
| Normalized Red-Blue Index | NRB | (R − B)/(R + B) | RGB | [76] |
| Normalized Green-Blue Index | NGB | (G − B)/(G + B) | RGB | [76] |
| Green Leaf Index | GLI | (2G − R − B)/(2G + R + B) | RGB | [70] |
| Coloration Index | CI | (Red - Blue)/Red | RGB | [90] |
| Model Type | Equation | R2 | RMSE |
|---|---|---|---|
| Linear | + 0.17 | 0.57 | 0.0591 |
| Exponential | 0.50 | 0.65 | 0.0593 |
| ML Methods | Using All 17 VIs | Using Selected 5 VIs | Using 3 Bands | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | |
| SVR | 0.872 (0.022) | 0.466 (0.030) | 0.372 (0.021) | 0.864 (0.029) | 0.479 (0.043) | 0.385 (0.038) | 0.807 (0.026) | 0.572 (0.026) | 0.466 (0.038) |
| RFR | 0.864 (0.009) | 0.481 (0.013) | 0.399 (0.019) | 0.879 (0.015) | 0.455 (0.022) | 0.373 (0.028) | 0.742 (0.045) | 0.661 (0.051) | 0.556 (0.054) |
| PLSR | 0.880 (0.020) | 0.451 (0.028) | 0.366 (0.027) | 0.869 (0.026) | 0.469 (0.039) | 0.384 (0.036) | 0.822 (0.041) | 0.547 (0.050) | 0.451 (0.052) |
| GBR | 0.860 (0.011) | 0.489 (0.018) | 0.398 (0.033) | 0.879 (0.016) | 0.454 (0.025) | 0.368 (0.034) | 0.759 (0.059) | 0.636 (0.073) | 0.524 (0.084) |
| KNN | 0.856 (0.033) | 0.492 (0.054) | 0.404 (0.046) | 0.850 (0.014) | 0.506 (0.018) | 0.413 (0.031) | 0.773 (0.032) | 0.621 (0.033) | 0.508 (0.043) |
| Ensemble | 0.887 (0.013) | 0.438 (0.018) | 0.358 (0.027) | 0.889 (0.018) | 0.434 (0.030) | 0.354 (0.039) | 0.830 (0.031) | 0.536 (0.042) | 0.449 (0.053) |
| Model | Metrics | 0.007 m GSD MS | 0.007 m GSD RGB | 0.045 m GSD MS | 0.045 m GSD RGB |
|---|---|---|---|---|---|
| SVR | R2 | 0.864 | 0.818 | 0.790 | 0.438 |
| RMSE | 0.479 | 0.556 | 0.590 | 0.952 | |
| MAE | 0.385 | 0.407 | 0.449 | 0.678 | |
| RFR | R2 | 0.879 | 0.791 | 0.754 | 0.676 |
| RMSE | 0.455 | 0.598 | 0.635 | 0.734 | |
| MAE | 0.373 | 0.470 | 0.499 | 0.611 | |
| PLSR | R2 | 0.869 | 0.820 | 0.783 | 0.490 |
| RMSE | 0.469 | 0.552 | 0.598 | 0.921 | |
| MAE | 0.384 | 0.432 | 0.459 | 0.695 | |
| GBR | R2 | 0.879 | 0.788 | 0.758 | 0.708 |
| RMSE | 0.454 | 0.602 | 0.630 | 0.697 | |
| MAE | 0.368 | 0.470 | 0.492 | 0.568 | |
| KNN | R2 | 0.850 | 0.772 | 0.772 | 0.539 |
| RMSE | 0.506 | 0.623 | 0.614 | 0.872 | |
| MAE | 0.413 | 0.492 | 0.479 | 0.720 | |
| Ensemble | R2 | 0.889 | 0.825 | 0.796 | 0.637 |
| RMSE | 0.434 | 0.547 | 0.581 | 0.775 | |
| MAE | 0.354 | 0.422 | 0.452 | 0.626 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilniyaz, O.; Kurban, A.; Du, Q. Leaf Area Index Estimation of Pergola-Trained Vineyards in Arid Regions Based on UAV RGB and Multispectral Data Using Machine Learning Methods. Remote Sens. 2022, 14, 415. https://doi.org/10.3390/rs14020415
Ilniyaz O, Kurban A, Du Q. Leaf Area Index Estimation of Pergola-Trained Vineyards in Arid Regions Based on UAV RGB and Multispectral Data Using Machine Learning Methods. Remote Sensing. 2022; 14(2):415. https://doi.org/10.3390/rs14020415
Chicago/Turabian StyleIlniyaz, Osman, Alishir Kurban, and Qingyun Du. 2022. "Leaf Area Index Estimation of Pergola-Trained Vineyards in Arid Regions Based on UAV RGB and Multispectral Data Using Machine Learning Methods" Remote Sensing 14, no. 2: 415. https://doi.org/10.3390/rs14020415
APA StyleIlniyaz, O., Kurban, A., & Du, Q. (2022). Leaf Area Index Estimation of Pergola-Trained Vineyards in Arid Regions Based on UAV RGB and Multispectral Data Using Machine Learning Methods. Remote Sensing, 14(2), 415. https://doi.org/10.3390/rs14020415






