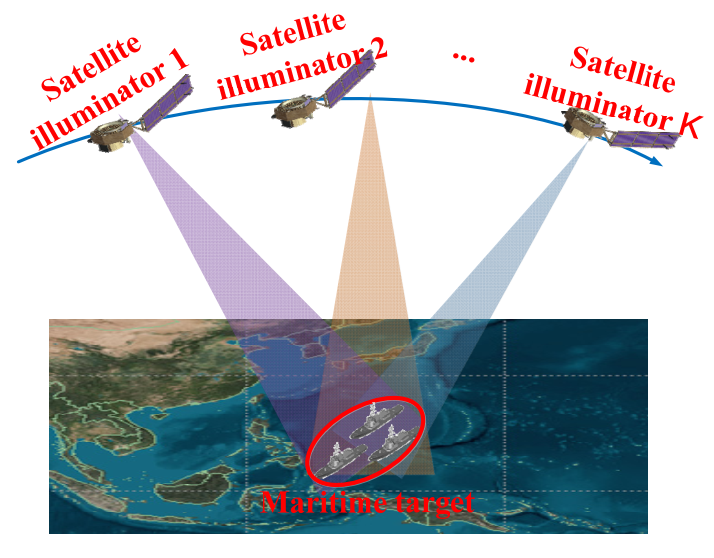
Suppose that the observation scene is covered with multiple beams, each generated by a LEO-based satellite illuminator, as shown in
Figure 1. Due to the distinct orbit parameters of different satellites, the echoes are concentrated over the dwell time and combined within an identical coordinate [
11,
12]. Accordingly, the enhanced multi-source fusion detection can be achieved.
For LEO satellites with different orbital velocity, moving direction and incident angle, there exists great differences in the range and Doppler history. This poses a considerable challenge for the robust fusion processing of multi-source echoes. Assume the echo of the
satellite can be expressed as
in range domain, where
,
is the monostatic range, and
stands for the platform number. In terms of back projection (BP) operation, the surveillance area in rectangular coordinate is divided into several cells, and the monostatic range of each cell can be calculated by utilizing the observation configurations. Therefore,
can be represented as
where
and
denote the satellite position vector and the target position vector, respectively,
are the corresponding coordinate value. To facilitate the subsequent processing, let the target locate on the earth’s surface, and its rectangular coordinate is given by
.
After the BP operation,
can be renewed as
. According to the above projection relationship, the echoes with multiple satellites can be combined in the Cartesian coordinate
. Here, the target signals corresponding to different satellites are presented as distinct iso-range lines, and the target position is located at the intersection of these iso-range lines. The multi-source fusion process [
12] can be summarized as
2.1. Pre-Compensation of Spaceborne Echo for LEO Satellite
In literature [
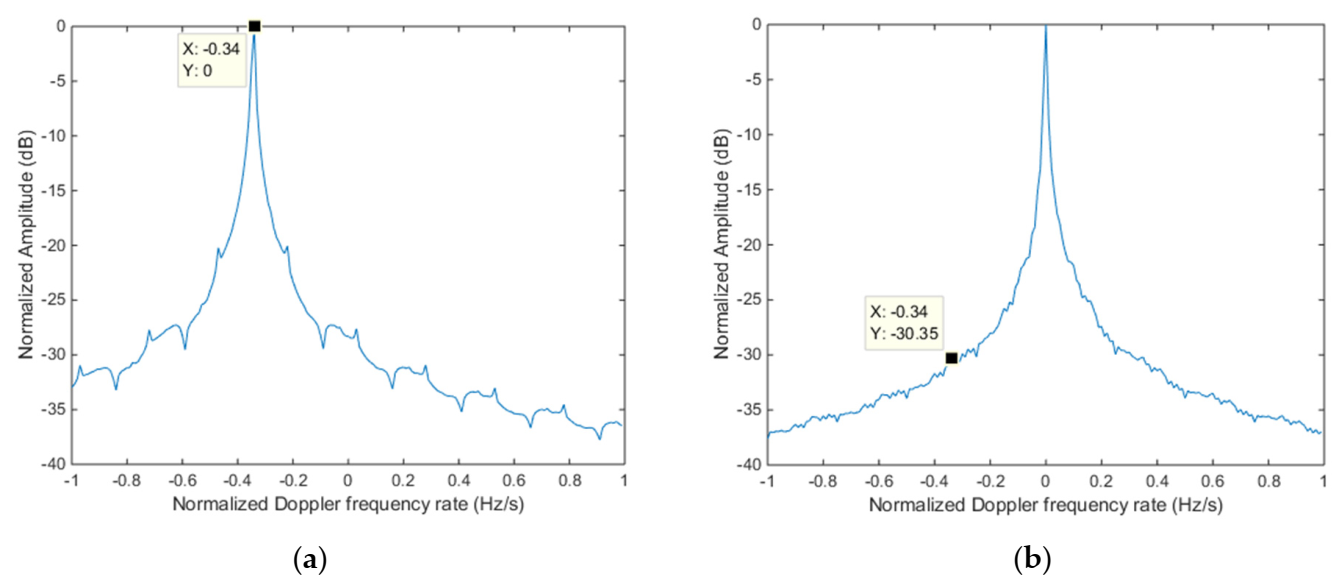
10], the moving target detection method is demonstrated with BeiDou satellites, in which the platform speeds are much lower than that of low orbit satellite, and the Doppler ambiguity problem can be ignored when integrating multiple echoes in DFR domain. However, this method is not applicable for the LEO constellation scenario. On one hand, the pulse repetition frequency (PRF) of the satellite illuminator is generally preset. Additionally, its adjustable dynamic range is limited. Thus, the high-speed movement of LEO satellites could apparently broaden the Doppler bandwidth (Bd) related to the observation scene and thus to reduce the target detectable interval, as indicated in
Figure 2a. On the other hand, the extended Doppler bandwidth may exceed the given PRF, which leads to the Doppler ambiguity issue, as indicated in
Figure 2b. In this case, the decoupling method, such as the KT transform [
13], is no longer applicable owing to the Doppler ambiguity of the observation scene.
On the other hand, the LEO satellites adopt the self-transmitting and self-receiving operation mode instead of the multiple-transmitting and single-receiving operation mode, where the configuration does not possess the extreme asymmetry in respect of the GEO (Geostationary Orbit) or MEO (Medium Earth Orbit) satellites. Thus, the LEO-based multi-source echoes cannot be concentrated on one cell in DFR domain. For the multiple-transmitting and single-receiving operation mode, DFR of a moving target can be defined as [
13]:
While that of the self-transmitting and self-receiving operation mode is given by:
In Equations (3) and (4), is the wavelength, and stand for the position vector of the transmitting platform and the receiving platform, respectively. and denote the corresponding velocity vector in turn. and are the position vector and the velocity vector of the target.
Under the condition of bistatic configuration with GEO or MEO satellite as its transmitter, Equation (3) can be approximately expressed as:
From Equation (5), the target DFR mainly depends on the position vector of the receiving platform under asymmetric configuration. Therefore, the multiple-transmitting and single-receiving operation mode is conducive to the fusion processing [
10]. However, the echoes related to multiple satellites cannot be directly integrated due to the distinct orbit parameters in respect of the self-transmitting and self-receiving operation mode, and the approximate Equation (4) is not valid here. To realize the universality of the multi-source fusion detection in respect of LEO-based satellite constellation, the robust fusion detection method should be presented to meet the application requirements of communication, navigation and radar with different orbital altitudes. In this section, the pre-compensation method of multi-source echoes is introduced based on the prior information, i.e., high-speed motion characteristic and spaceborne observation configuration.
By applying the Fast Fourier Transform (FFT) operation to the range-compressed signal, the echo of the
satellite can be expressed as:
where
and
represents the fast-frequency and slow-time,
is the dwell time,
is the carrier frequency.
denotes the Fourier transform of the range envelope.
stands for the monostatic range of the
satellite.
Since the ephemeris and the antenna beam directivity of each satellite are known, the pre-compensation of the whole observation scene can be carried out according to the range and Doppler history of the cell where the beam center is pointed. The pre compensation function is given by:
Based on the above pre-compensation operation, the Doppler band broadening caused by the high-speed motion platform as well as the DFR offset resulted from the observation configuration can be effectively alleviated.
2.2. Clutter Suppression Based on DFR Design
In view of the aforementioned pre-compensation strategy, the multi-source fusion process is performed in this section through setting the cell interval in DFR domain. On one hand, for the LEO-based satellites with different orbit elements and incident angles, although the DFR difference of clutter echoes can be corrected by employing the range and Doppler history of the cell where the beam center is pointed, the target velocity vector may still cause the dispersion of the target fusion energy in DFR domain. Therefore, there exists a theoretical lower bound for the DFR cell, where the multi-source echoes can be entirely integrated in the same cell. On the other hand, for the sake of the resolving ability in DFR domain, the echoes related to the target and the observation scene should be separated with an interval greater than the DFR cell, which possesses a theoretical upper bound accordingly.
Multiplying
by
, the compensated signal in range-DFR domain [
10] can be represented as
. Let the cell size of DFR be
, and the parameter selection technique of
should meet the following restrictions to achieve accurate information fusion as well as the effective clutter suppression.
(i) The DFR deviation of the target between any two satellites should be less than
, that is,
In Equation (8),
and
are DFRs of the
satellite and the
satellite, respectively.
and
satisfy
. According to Equation (4), Equation (8) can be described as:
where
and
stand for the position vectors of the
satellite and the
satellite.
and
denote the corresponding velocity vector.
(ii) The DFR deviation between the target and the observation scene should be greater than
, namely,
where
and
represent DFRs corresponding to the target and the clutter in turn.
Combined with the aforementioned constraint conditions, the optional internal of can be obtained.
2.3. Multi-Source Fusion CFAR Detection with LEO-Based Satellite Constellation
The accurate target echo focusing as well as the effective clutter suppression can be realized based on the above pre-compensation process and cell interval setting strategy. However, the direct CFAR detection procedure could result in the deterioration of target detection performance due to the target detection range difference with regard of multi-source satellites. In this section, the echo fusion and target detection processes are performed in the ENU (East North Up) coordinate through employing the coordinate system transformation operation. The main steps of multi-source fusion CFAR detection method are given below.
Step 1 Multi-source fusion of target echoes.
By performing the focusing operation in range-DFR domain, the
groups of echoes
from multiple satellites can be obtained in terms of their observation configurations, in which
denotes the cell position where the target is located, and
. Then,
can be reformulated as
through transforming the fused data from range coordinate to Cartesian coordinate. In this way, the multi-station echo fusion process can be completed by means of incoherent integration, as presented in Equation (2), and the multi-source fusion echo can be expressed as:
Step 2 Weight calculation of the contrast ratio based on the sliding window.
Assume that the sliding window is composed of
∗
cells, in which the central position is represented as
, and the edge region is described as
. The weight of the contrast ratio in respect of the sliding window center is indicated by:
where
and
satisfy
,
,
denotes the round down operation.
Step 3 Exponential weighted likelihood ratio modeling.
The exponential weighted likelihood ratio is given by:
where the natural constant
is set to 2.71828.
is the measured value of
after exponential operation, namely,
, where
stand for the exponential operation.
and
are the probability density functions corresponding to the cases that the target does or does not exist. That is,
As can be seen from Equation (14), the probability density functions become smaller as the cell under test gets farther from the target, where
and
are the target amplitude and the noise standard deviation. Here, the likelihood ratio detection statistic [
4] is more suitable for target fusion detection as a result of its joint detection property, compared with the amplitude detection statistic [
3]. That is, the amplitudes of the target cell and other background cells are directly employed to acquire a detection threshold when constructing the amplitude detection statistic. Hence, the former is employed to construct the multi-source fusion detection factor in this paper.
Step 4 Multi-source fusion CFAR detection.
The selection method of CFAR threshold [
14]
is given by
where
is the second-order statistics of the exponential weighted likelihood ratio.
represents the false alarm probability. Here, the difference between CA-CFAR method [
3] and the proposed method are chiefly as follows. For CA-CFAR method, the amplitudes of the target cell and other background cells are directly employed to acquire a threshold, which is suitable for point target detection. That is, the target occupies only one cell in the sliding window. While the presented detection method is applicable to distributed target detection, whose energy is located in distinct iso-range lines after the multi-source fusion process. In this case, the contrast ratio between the target cell and other background cells could be effectively enhanced in terms of the exponential weighted likelihood ratio.
Figure 3 demonstrates the flow chart of multi-source fusion CFAR detection algorithm with regard of the LEO-based satellite constellation.