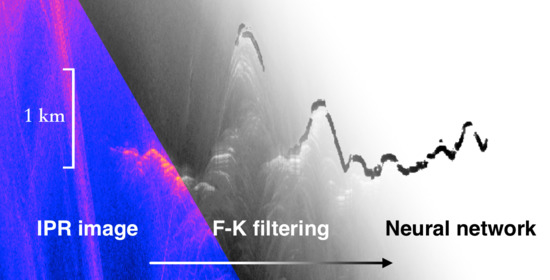
Noise Removal and Feature Extraction in Airborne Radar Sounding Data of Ice Sheets
Abstract
:1. Introduction
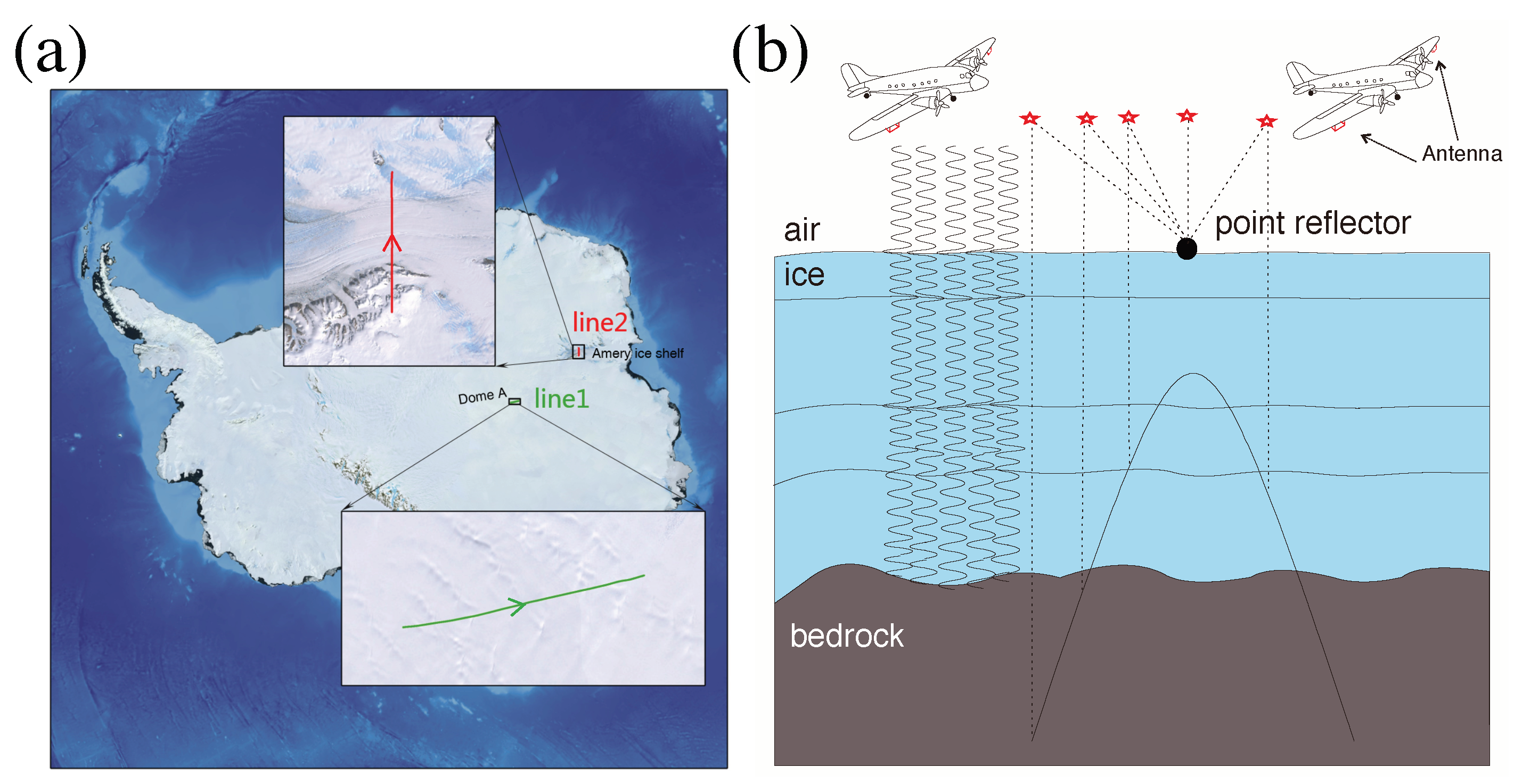
2. Data and Filtering Method
2.1. F–K and KL Filtering
2.2. Results of the Filtering Methods
3. Machine Learning Methods
3.1. K-SVD Algorithm
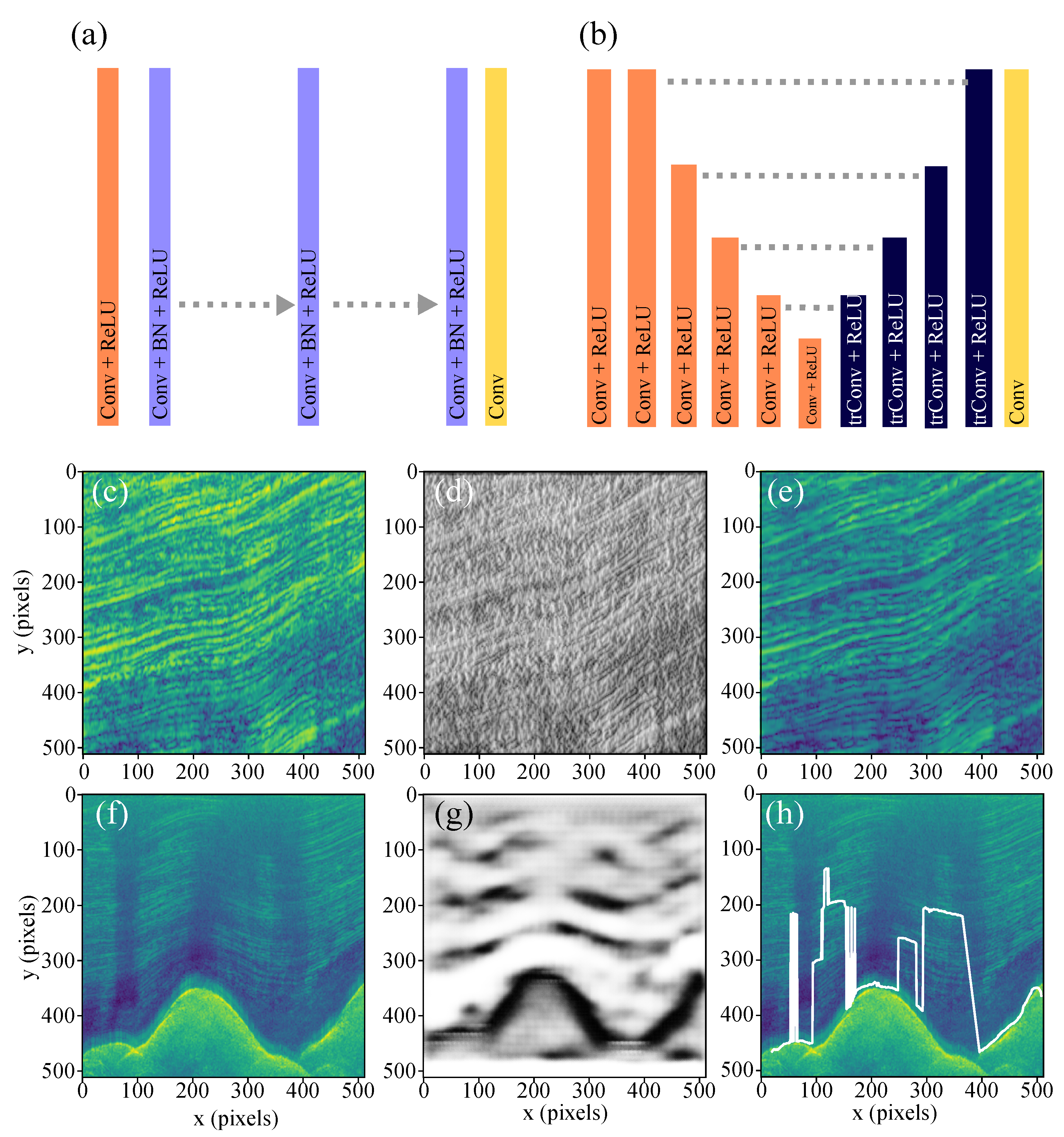
3.2. Artificial Neural Networks
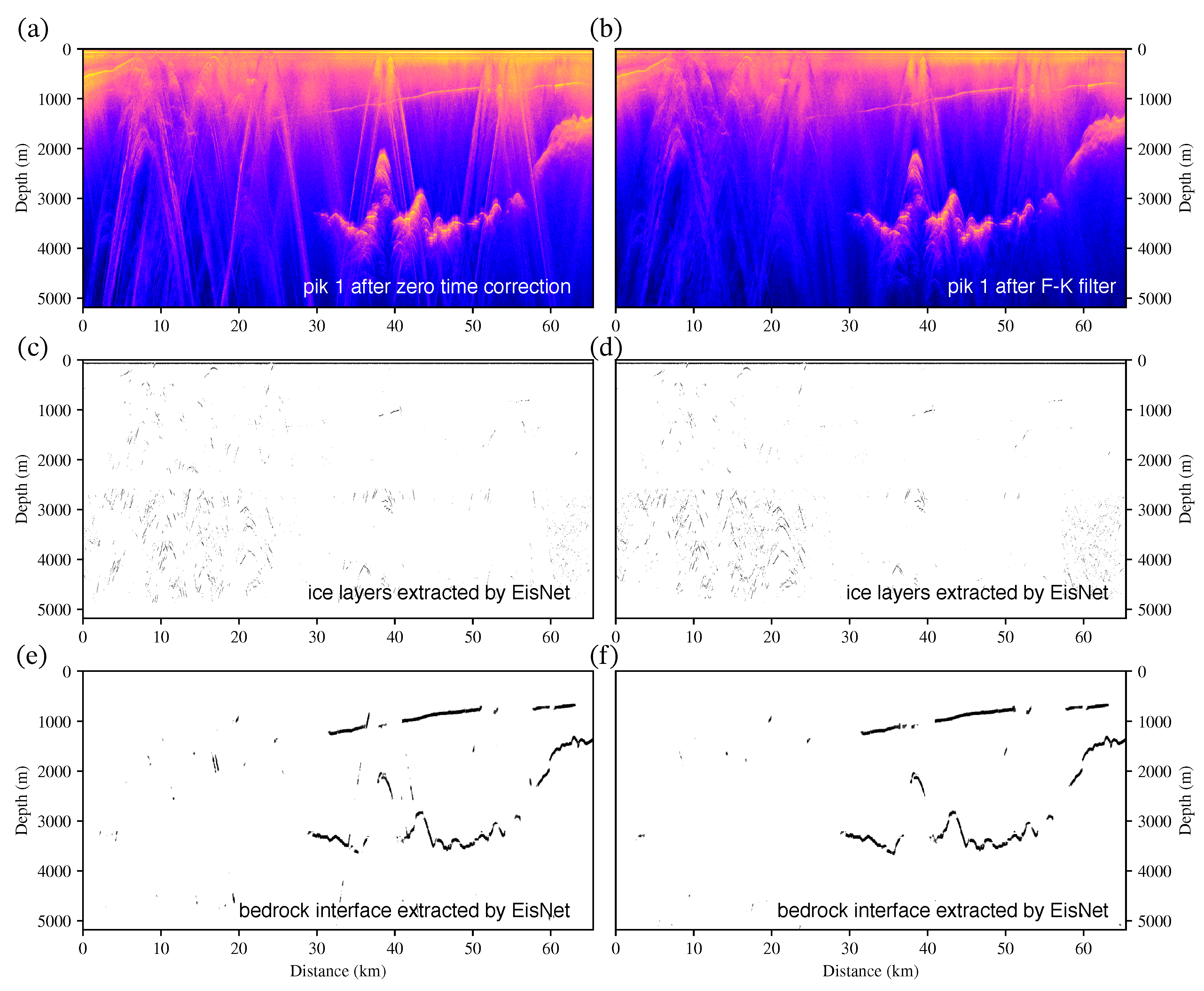
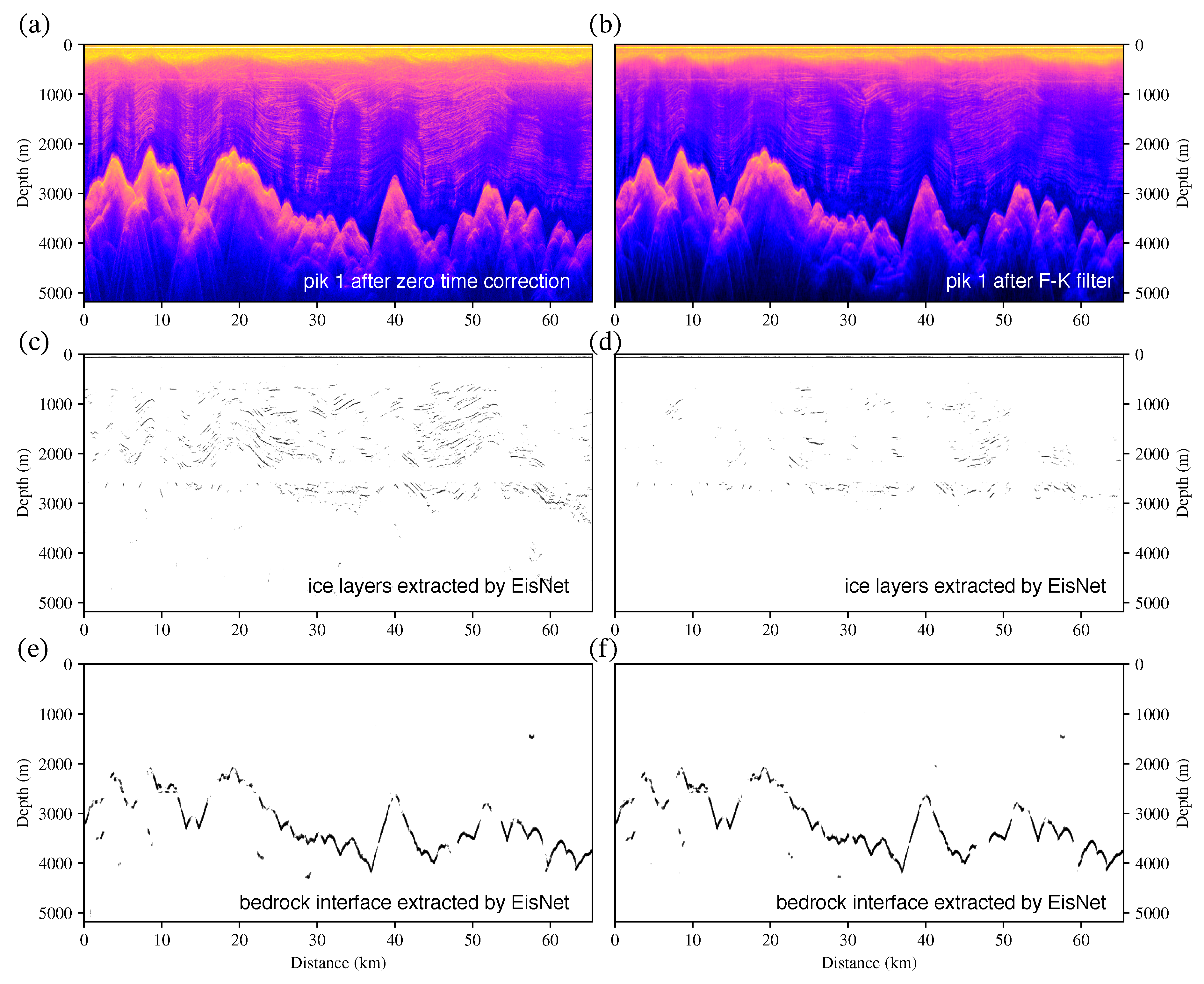
4. Fusion Applications of the Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hanna, E.; Pattyn, F.; Navarro, F.; Favier, V.; Goelzer, H.; van den Broeke, M.R.; Vizcaino, M.; Whitehouse, P.L.; Ritz, C.; Bulthuis, K.; et al. Mass balance of the ice sheets and glaciers–progress since AR5 and challenges. Earth-Sci. Rev. 2020, 201, 102976. [Google Scholar] [CrossRef]
- Poloczanska, E.; Mintenbeck, K.; Portner, H.O.; Roberts, D.; Levin, L.A. The IPCC special report on the ocean and cryosphere in a changing climate. In Proceedings of the 2018 Ocean Sciences Meeting, Portland, OR, USA, 11–16 February 2018. [Google Scholar]
- Mouginot, J.; Rignot, E.; Scheuchl, B. Sustained increase in ice discharge from the Amundsen Sea Embayment, West Antarctica, from 1973 to 2013. Geophys. Res. Lett. 2014, 41, 1576–1584. [Google Scholar] [CrossRef] [Green Version]
- Shepherd, A.; Ivins, E.; Rignot, E.; Smith, B.; Van Den Broeke, M.; Velicogna, I.; Whitehouse, P.; Briggs, K.; Joughin, I.; Krinner, G.; et al. Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature 2018, 558, 219–222. [Google Scholar]
- Rignot, E.; Mouginot, J.; Scheuchl, B.; Van Den Broeke, M.; Van Wessem, M.J.; Morlighem, M. Four decades of Antarctic Ice Sheet mass balance from 1979–2017. Proc. Natl. Acad. Sci. USA 2019, 116, 1095–1103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Winter, K.; Woodward, J.; Ross, N.; Dunning, S.A.; Hein, A.S.; Westoby, M.J.; Culberg, R.; Marrero, S.M.; Schroeder, D.M.; Sugden, D.E.; et al. Radar-detected englacial debris in the West Antarctic Ice Sheet. Geophys. Res. Lett. 2019, 46, 10454–10462. [Google Scholar]
- Bodart, J.A.; Bingham, R.G.; Ashmore, D.W.; Karlsson, N.B.; Hein, A.; Vaughan, D.G. Age-depth stratigraphy of Pine Island Glacier inferred from airborne radar and ice-core chronology. J. Geophys. Res. Earth Surf. 2021, 126, e2020JF005927. [Google Scholar] [CrossRef]
- Cavitte, M.G.; Young, D.A.; Mulvaney, R.; Ritz, C.; Greenbaum, J.S.; Ng, G.; Kempf, S.D.; Quartini, E.; Muldoon, G.R.; Paden, J.; et al. A detailed radiostratigraphic data set for the central East Antarctic Plateau spanning from the Holocene to the mid-Pleistocene. Earth Syst. Sci. Data 2021, 13, 4759–4777. [Google Scholar] [CrossRef]
- MacGREGOR, J.A.; Anandakrishnan, S.; Catania, G.A.; Winebrenner, D.P. The grounding zone of the Ross Ice Shelf, West Antarctica, from ice-penetrating radar. J. Glaciol. 2011, 57, 917–928. [Google Scholar] [CrossRef] [Green Version]
- Reese, R.; Gudmundsson, G.H.; Levermann, A.; Winkelmann, R. The far reach of ice-shelf thinning in Antarctica. Nat. Clim. Chang. 2018, 8, 53–57. [Google Scholar] [CrossRef]
- Robin, G.d.Q. Radio-echo sounding: Glaciological interpretations and applications. J. Glaciol. 1975, 15, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Fretwell, P.; Pritchard, H.D.; Vaughan, D.G.; Bamber, J.L.; Barrand, N.E.; Bell, R.; Bianchi, C.; Bingham, R.; Blankenship, D.D.; Casassa, G.; et al. Bedmap2: Improved ice bed, surface and thickness datasets for Antarctica. Cryosphere 2013, 7, 375–393. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, D.M.; Bingham, R.G.; Blankenship, D.D.; Christianson, K.; Eisen, O.; Flowers, G.E.; Karlsson, N.B.; Koutnik, M.R.; Paden, J.D.; Siegert, M.J. Five decades of radioglaciology. Ann. Glaciol. 2020, 61, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Matsuoka, K. Pitfalls in radar diagnosis of ice-sheet bed conditions: Lessons from englacial attenuation models. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Tang, X.; Sun, B.; Wang, T. Radar isochronic layer dating for a deep ice core at Kunlun Station, Antarctica. Sci. China Earth Sci. 2020, 63, 303–308. [Google Scholar] [CrossRef]
- Bons, P.D.; Jansen, D.; Mundel, F.; Bauer, C.C.; Binder, T.; Eisen, O.; Jessell, M.W.; Llorens, M.G.; Steinbach, F.; Steinhage, D.; et al. Converging flow and anisotropy cause large-scale folding in Greenland’s ice sheet. Nat. Commun. 2016, 7, 11427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cooper, M.; Jordan, T.; Siegert, M.; Bamber, J. Surface expression of basal and englacial features, properties, and processes of the Greenland ice sheet. Geophys. Res. Lett. 2019, 46, 783–793. [Google Scholar] [CrossRef] [Green Version]
- Bingham, R.G.; Rippin, D.M.; Karlsson, N.B.; Corr, H.F.; Ferraccioli, F.; Jordan, T.A.; Le Brocq, A.M.; Rose, K.C.; Ross, N.; Siegert, M.J. Ice-flow structure and ice dynamic changes in the Weddell Sea sector of West Antarctica from radar-imaged internal layering. J. Geophys. Res. Earth Surf. 2015, 120, 655–670. [Google Scholar] [CrossRef] [Green Version]
- Elsworth, C.W.; Schroeder, D.M.; Siegfried, M.R. Interpreting englacial layer deformation in the presence of complex ice flow history with synthetic radargrams. Ann. Glaciol. 2020, 61, 206–213. [Google Scholar] [CrossRef] [Green Version]
- Jordan, T.M.; Cooper, M.A.; Schroeder, D.M.; Williams, C.N.; Paden, J.D.; Siegert, M.J.; Bamber, J.L. Self-affine subglacial roughness: Consequences for radar scattering and basal water discrimination in northern Greenland. Cryosphere 2017, 11, 1247–1264. [Google Scholar] [CrossRef] [Green Version]
- Luo, K.; Liu, S.; Guo, J.; Wang, T.; Li, L.; Cui, X.; Sun, B.; Tang, X. Radar-Derived Internal Structure and Basal Roughness Characterization along a Traverse from Zhongshan Station to Dome A, East Antarctica. Remote Sens. 2020, 12, 1079. [Google Scholar] [CrossRef] [Green Version]
- Jordan, T.; Martin, C.; Ferraccioli, F.; Matsuoka, K.; Corr, H.; Forsberg, R.; Olesen, A.; Siegert, M. Anomalously high geothermal flux near the South Pole. Sci. Rep. 2018, 8, 16785. [Google Scholar] [CrossRef] [Green Version]
- Wolovick, M.; Moore, J.; Zhao, L. Joint Inversion for Surface Accumulation Rate and Geothermal Heat Flow from Ice-Penetrating Radar Observations at Dome A, East Antarctica. Part I: Model Description, Data Constraints, and Inversion Results. J. Geophys. Res. Earth Surf. 2021, 126, e2020JF005937. [Google Scholar] [CrossRef]
- Young, D.; Schroeder, D.; Blankenship, D.; Kempf, S.D.; Quartini, E. The distribution of basal water between Antarctic subglacial lakes from radar sounding. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2016, 374, 20140297. [Google Scholar] [CrossRef]
- Jordan, T.M.; Williams, C.N.; Schroeder, D.M.; Martos, Y.M.; Cooper, M.A.; Siegert, M.J.; Paden, J.D.; Huybrechts, P.; Bamber, J.L. A constraint upon the basal water distribution and thermal state of the Greenland Ice Sheet from radar bed echoes. Cryosphere 2018, 12, 2831–2854. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Sun, B.; Wang, J.; Greenbaum, J.; Guo, J.; Lindzey, L.; Cui, X.; Young, D.A.; Blankenship, D.D.; Siegert, M.J. Removal of ‘strip noise’ in radio-echo sounding data using combined wavelet and 2-D DFT filtering. Ann. Glaciol. 2020, 61, 124–134. [Google Scholar] [CrossRef] [Green Version]
- Heister, A.; Scheiber, R. Coherent large beamwidth processing of radio-echo sounding data. Cryosphere 2018, 12, 2969–2979. [Google Scholar] [CrossRef]
- Lilien, D.A.; Hills, B.H.; Driscol, J.; Jacobel, R.; Christianson, K. ImpDAR: An open-source impulse radar processor. Ann. Glaciol. 2020, 61, 114–123. [Google Scholar] [CrossRef]
- Partyka, G.; Gridley, J.; Lopez, J. Interpretational applications of spectral decomposition in reservoir characterization. Lead. Edge 1999, 18, 353–360. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Cheng, S.; Liu, S.; Guo, J.; Luo, K.; Zhang, L.; Tang, X. Data processing and interpretation of Antarctic ice-penetrating radar based on variational mode decomposition. Remote Sens. 2019, 11, 1253. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Zhang, S.; Zhao, H.; Chen, S. Target Identification with Improved 2D-VMD for Carrier-Free UWB Radar. Sensors 2021, 21, 2465. [Google Scholar] [CrossRef]
- Xiong, S.; Muller, J.P.; Carretero, R.C. A new method for automatically tracing englacial layers from MCoRDS data in NW Greenland. Remote Sens. 2018, 10, 43. [Google Scholar] [CrossRef] [Green Version]
- Berger, V.; Xu, M.; Chu, S.; Crandall, D.; Paden, J.; Fox, G.C. Automated tracking of 2D and 3D ice radar imagery using VITERBI and TRW-S. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; IEEE: Piscataway, NJ, USA, 2018; pp. 4162–4165. [Google Scholar]
- Donini, E.; Thakur, S.; Bovolo, F.; Bruzzone, L. An automatic approach to map refreezing ice in radar sounder data. In Image and Signal Processing for Remote Sensing XXV; International Society for Optics and Photonics: Strasbourg, France, 2019; Volume 11155, p. 111551B. [Google Scholar]
- Rahnemoonfar, M.; Yari, M.; Paden, J.; Koenig, L.; Ibikunle, O. Deep multi-scale learning for automatic tracking of internal layers of ice in radar data. J. Glaciol. 2021, 67, 39–48. [Google Scholar] [CrossRef]
- Castelletti, D.; Schroeder, D.M.; Hensley, S.; Grima, C.; Ng, G.; Young, D.; Gim, Y.; Bruzzone, L.; Moussessian, A.; Blankenship, D.D. An interferometric approach to cross-track clutter detection in two-channel VHF radar sounders. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6128–6140. [Google Scholar] [CrossRef]
- Delf, R.; Schroeder, D.M.; Curtis, A.; Giannopoulos, A.; Bingham, R.G. A comparison of automated approaches to extracting englacial-layer geometry from radar data across ice sheets. Ann. Glaciol. 2020, 61, 234–241. [Google Scholar] [CrossRef]
- Bergen, K.J.; Johnson, P.A.; Maarten, V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363. [Google Scholar] [CrossRef]
- Rahnemoonfar, M.; Fox, G.C.; Yari, M.; Paden, J. Automatic ice surface and bottom boundaries estimation in radar imagery based on level-set approach. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5115–5122. [Google Scholar] [CrossRef]
- Ibikunle, O.; Paden, J.; Rahnemoonfar, M.; Crandall, D.; Yari, M. Snow Radar Layer Tracking Using Iterative Neural Network Approach. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2960–2963. [Google Scholar] [CrossRef]
- Khami, N.; Imtiaz, O.; Abidi, A.; Aedavelli, A.; Goff, A.; Pisel, J.R.; Pyrcz, M.J. Automatic Feature Highlighting in Noisy RES Data With CycleGAN. arXiv 2021, arXiv:2108.11283. [Google Scholar]
- Dong, S.; Tang, X.; Guo, J.; Fu, L.; Chen, X.; Sun, B. EisNet: Extracting Bedrock and Internal Layers from Radiostratigraphy of Ice Sheets with Machine Learning. IEEE Trans. Geosci. Remote Sens. 2021, 1. [Google Scholar] [CrossRef]
- Young, D.A.; Wright, A.P.; Roberts, J.L.; Warner, R.C.; Young, N.W.; Greenbaum, J.S.; Schroeder, D.M.; Holt, J.W.; Sugden, D.E.; Blankenship, D.D.; et al. A dynamic early East Antarctic Ice Sheet suggested by ice-covered fjord landscapes. Nature 2011, 474, 72–75. [Google Scholar] [CrossRef]
- Greenbaum, J.; Blankenship, D.; Young, D.; Richter, T.; Roberts, J.; Aitken, A.; Legresy, B.; Schroeder, D.; Warner, R.; Van Ommen, T.; et al. Ocean access to a cavity beneath Totten Glacier in East Antarctica. Nat. Geosci. 2015, 8, 294–298. [Google Scholar] [CrossRef]
- Cavitte, M.G.; Blankenship, D.D.; Young, D.A.; Schroeder, D.M.; Parrenin, F.; Lemeur, E.; Macgregor, J.A.; Siegert, M.J. Deep radiostratigraphy of the East Antarctic plateau: Connecting the Dome C and Vostok ice core sites. J. Glaciol. 2016, 62, 323–334. [Google Scholar] [CrossRef] [Green Version]
- Lindzey, L.E.; Beem, L.H.; Young, D.A.; Quartini, E.; Blankenship, D.D.; Lee, C.K.; Lee, W.S.; Lee, J.I.; Lee, J. Aerogeophysical characterization of an active subglacial lake system in the David Glacier catchment, Antarctica. Cryosphere 2020, 14, 2217–2233. [Google Scholar] [CrossRef]
- Peters, M.E.; Blankenship, D.D.; Carter, S.P.; Kempf, S.D.; Young, D.A.; Holt, J.W. Along-track focusing of airborne radar sounding data from West Antarctica for improving basal reflection analysis and layer detection. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2725–2736. [Google Scholar] [CrossRef]
- Cui, X.; Jeofry, H.; Greenbaum, J.S.; Guo, J.; Li, L.; Lindzey, L.E.; Habbal, F.A.; Wei, W.; Young, D.A.; Ross, N.; et al. Bed topography of Princess Elizabeth Land in East Antarctica. Earth Syst. Sci. Data 2020, 12, 2765–2774. [Google Scholar] [CrossRef]
- Tzanis, A. matGPR Release 2: A freeware MATLAB® package for the analysis & interpretation of common and single offset GPR data. FastTimes 2010, 15, 17–43. [Google Scholar]
- Karhunen, K. Zur spektraltheorie stochastischer prozesse. Ann. Acad. Sci. Fennicae AI 1946, 34, 215–220. [Google Scholar]
- Loeve, M. Probability theory. Foundations. Random sequences. Van Nostrand 1955, 33, 5–16. [Google Scholar]
- Kawalec, A.; Owczarek, R.; Dudczyk, J. Karhunen-Loeve transformation in radar signal features processing. In Proceedings of the 2006 International Conference on Microwaves, Radar & Wireless Communications, Krakow, Poland, 22-24 May 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1168–1171. [Google Scholar]
- Haizhong, Y.; Xiaojian, Y. Derivative seismic processing method for GPR data. In IGARSS’97, Proceedings of the 1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings.; Remote Sensing—A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997; IEEE: Piscataway, NJ, USA, 1997; Volume 1, pp. 145–147. [Google Scholar]
- Wei, X.; Zhang, Y. Interference removal for autofocusing of GPR data from RC bridge decks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1145–1151. [Google Scholar] [CrossRef]
- Moreira, A. Improved multilook techniques applied to SAR and SCANSAR imagery. IEEE Trans. Geosci. Remote Sens. 1991, 29, 529–534. [Google Scholar] [CrossRef]
- Lang, S. Research on the Imaging and Signal Processing of High-Resolution Ice-Sounding Radar. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2015. [Google Scholar]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; IEEE: Piscataway, NJ, USA, 1993; pp. 40–44. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 770–778. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
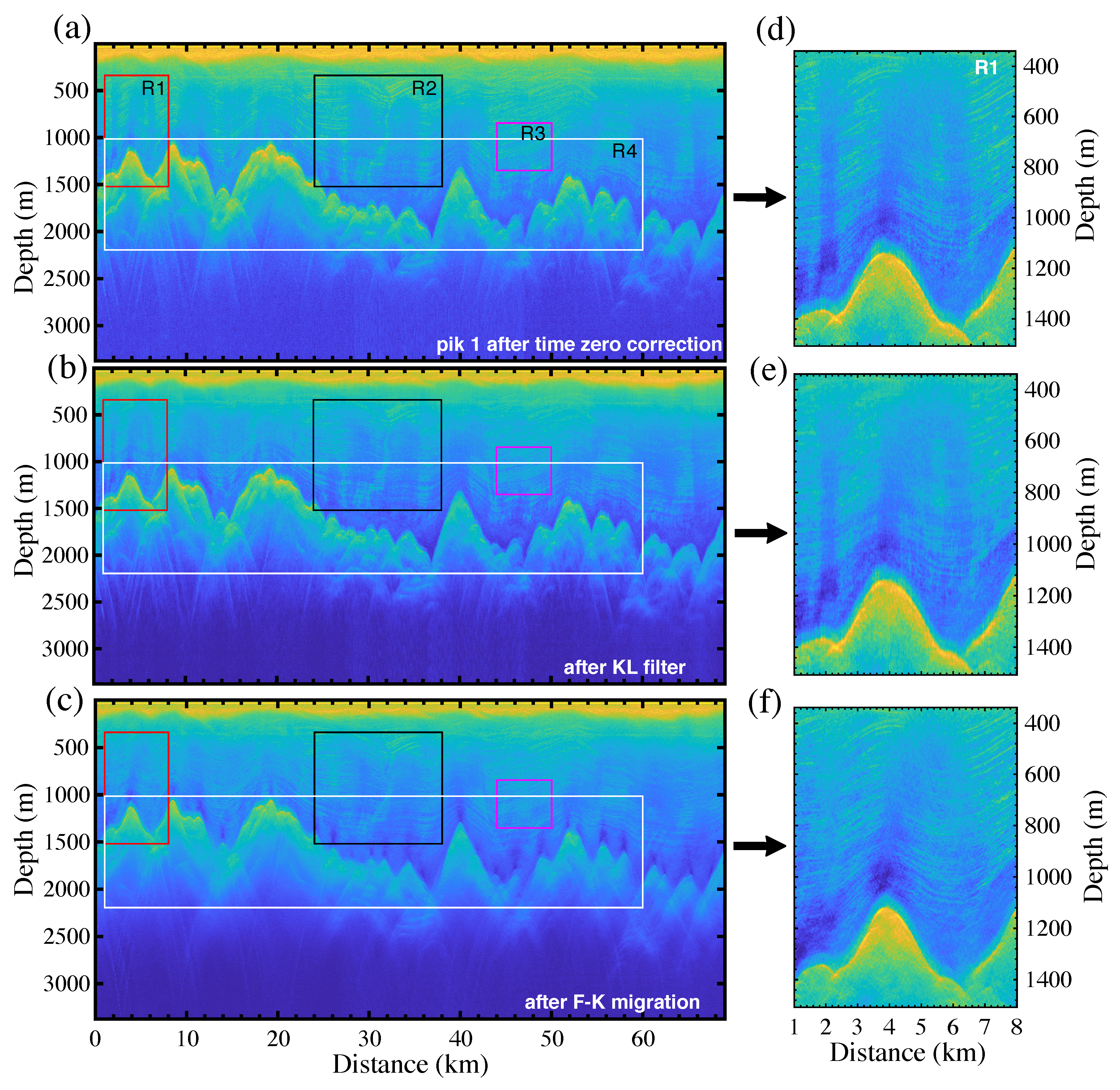


| Rectangle | ENL | EPI | PSNR (dB) | |||
|---|---|---|---|---|---|---|
| KL Filter | F–K Migration | KL Filter | F–K Migration | KL Filter | F–K Migration | |
| R1 (r) | 308.0 | 462.7 | 0.64 | 0.81 | 29.2 | 22.0 |
| R2 (k) | 307.8 | 347.6 | 0.66 | 0.75 | 25.3 | 20.7 |
| R3 (m) | 277.4 | 269.9 | 0.66 | 0.83 | 22.4 | 14.5 |
| R4 (w) | 105.5 | 139.6 | 0.66 | 0.64 | 27.4 | 22.5 |
| Rectangle | ENL | EPI | PSNR(dB) | |||
|---|---|---|---|---|---|---|
| F–K Filter | F–K Migration | F–K Filter | F–K Migration | F–K filter | F–K Migration | |
| R1 (r) | 13.3 | 79.0 | 0.87 | 0.75 | 23.0 | 15.9 |
| R2 (k) | 7.9 | 162.0 | 0.83 | 0.60 | 21.1 | 17.6 |
| R3 (m) | 47.3 | 102.8 | 0.88 | 0.43 | 26.8 | 20.1 |
| R4 (w) | 73.0 | 95.0 | 0.99 | 0.89 | 23.9 | 18.9 |
| Data | PSNR (dB) | Precision | Recall | F1-Score | ||||
|---|---|---|---|---|---|---|---|---|
| K-SVD | DnCNN | U-Net | DnCNN | U-Net | DnCNN | U-Net | DnCNN | |
| Line 1 (R1) | 16.401 | 35.757 | - | - | - | - | - | - |
| Line 1 (R3) | 7.548 | 32.420 | - | - | - | - | - | - |
| Test Dataset | - | - | 0.501 | 0.299 | 0.293 | 0.286 | 0.375 | 0.292 |
| Line | PSNR (dB) | |
|---|---|---|
| Before Filtering | After Filtering | |
| Line 2 (AMY) | 7.769 | 8.127 |
| Line 1 (TSH) | 9.384 | 7.277 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Dong, S.; Luo, K.; Guo, J.; Li, L.; Sun, B. Noise Removal and Feature Extraction in Airborne Radar Sounding Data of Ice Sheets. Remote Sens. 2022, 14, 399. https://doi.org/10.3390/rs14020399
Tang X, Dong S, Luo K, Guo J, Li L, Sun B. Noise Removal and Feature Extraction in Airborne Radar Sounding Data of Ice Sheets. Remote Sensing. 2022; 14(2):399. https://doi.org/10.3390/rs14020399
Chicago/Turabian StyleTang, Xueyuan, Sheng Dong, Kun Luo, Jingxue Guo, Lin Li, and Bo Sun. 2022. "Noise Removal and Feature Extraction in Airborne Radar Sounding Data of Ice Sheets" Remote Sensing 14, no. 2: 399. https://doi.org/10.3390/rs14020399
APA StyleTang, X., Dong, S., Luo, K., Guo, J., Li, L., & Sun, B. (2022). Noise Removal and Feature Extraction in Airborne Radar Sounding Data of Ice Sheets. Remote Sensing, 14(2), 399. https://doi.org/10.3390/rs14020399