Comparison of Winter Wheat Extraction Methods Based on Different Time Series of Vegetation Indices in the Northeastern Margin of the Qinghai–Tibet Plateau: A Case Study of Minhe, China
Abstract
:1. Introduction
2. Materials and Methods
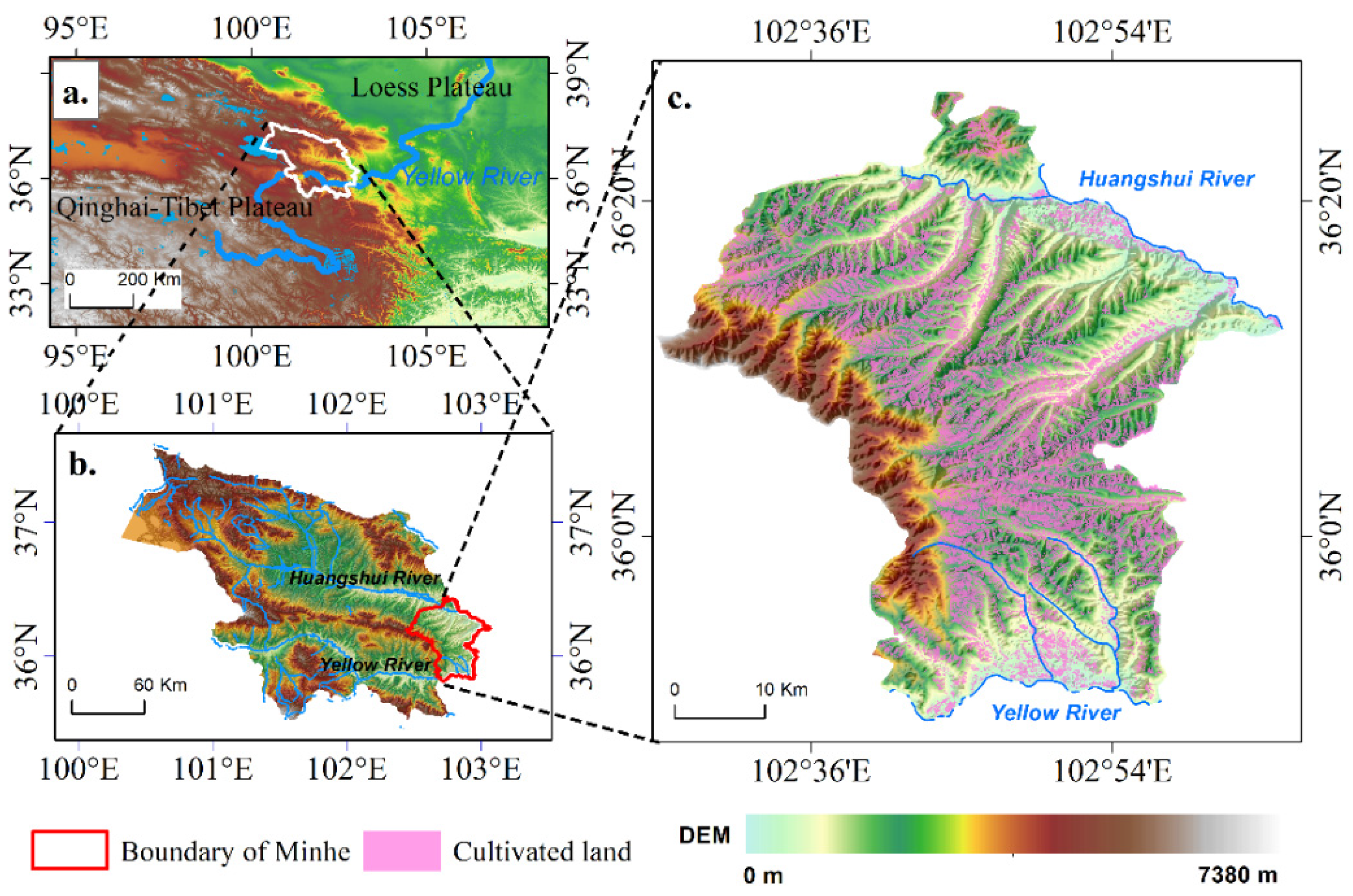
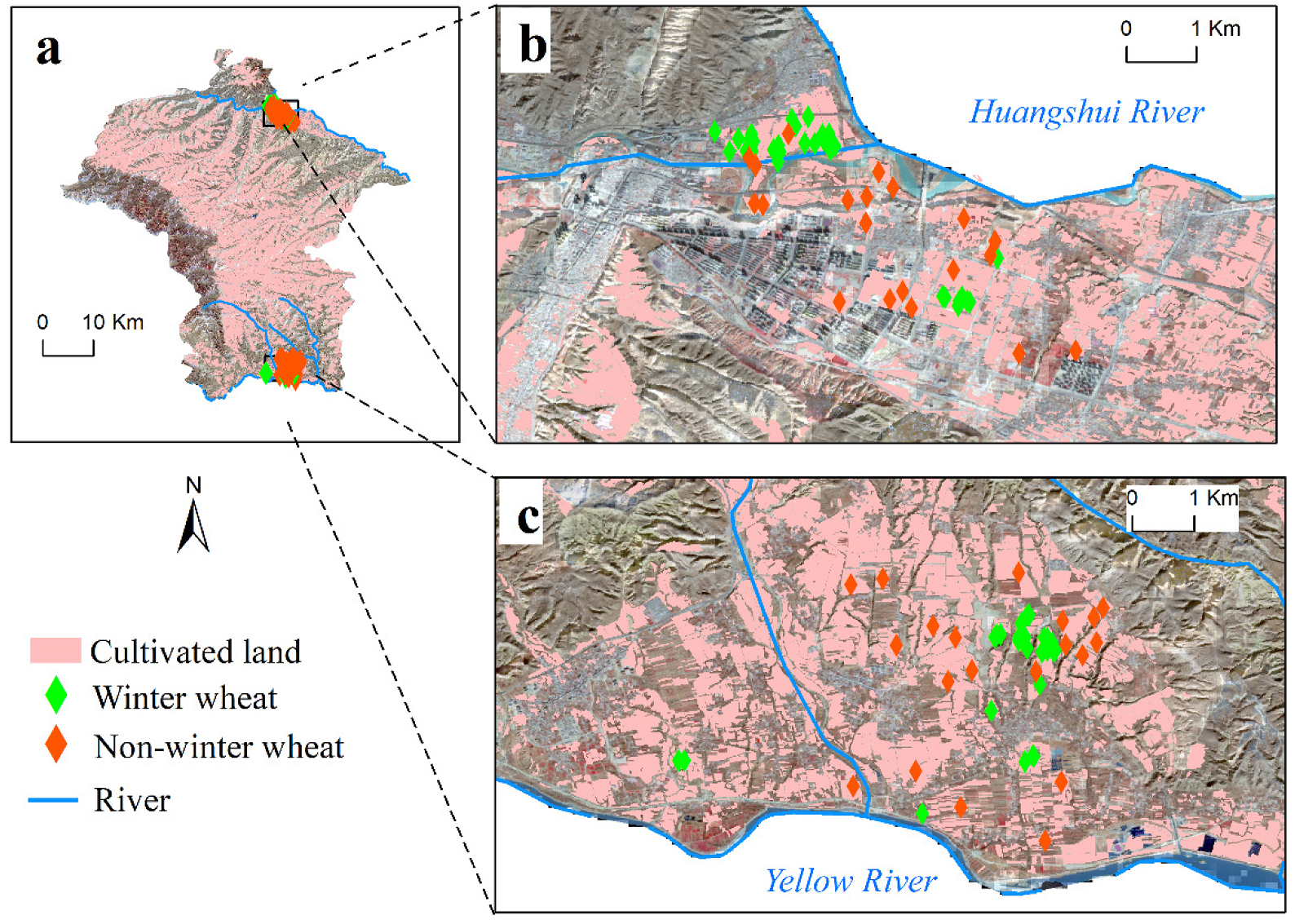
2.1. Study Area
2.2. Data
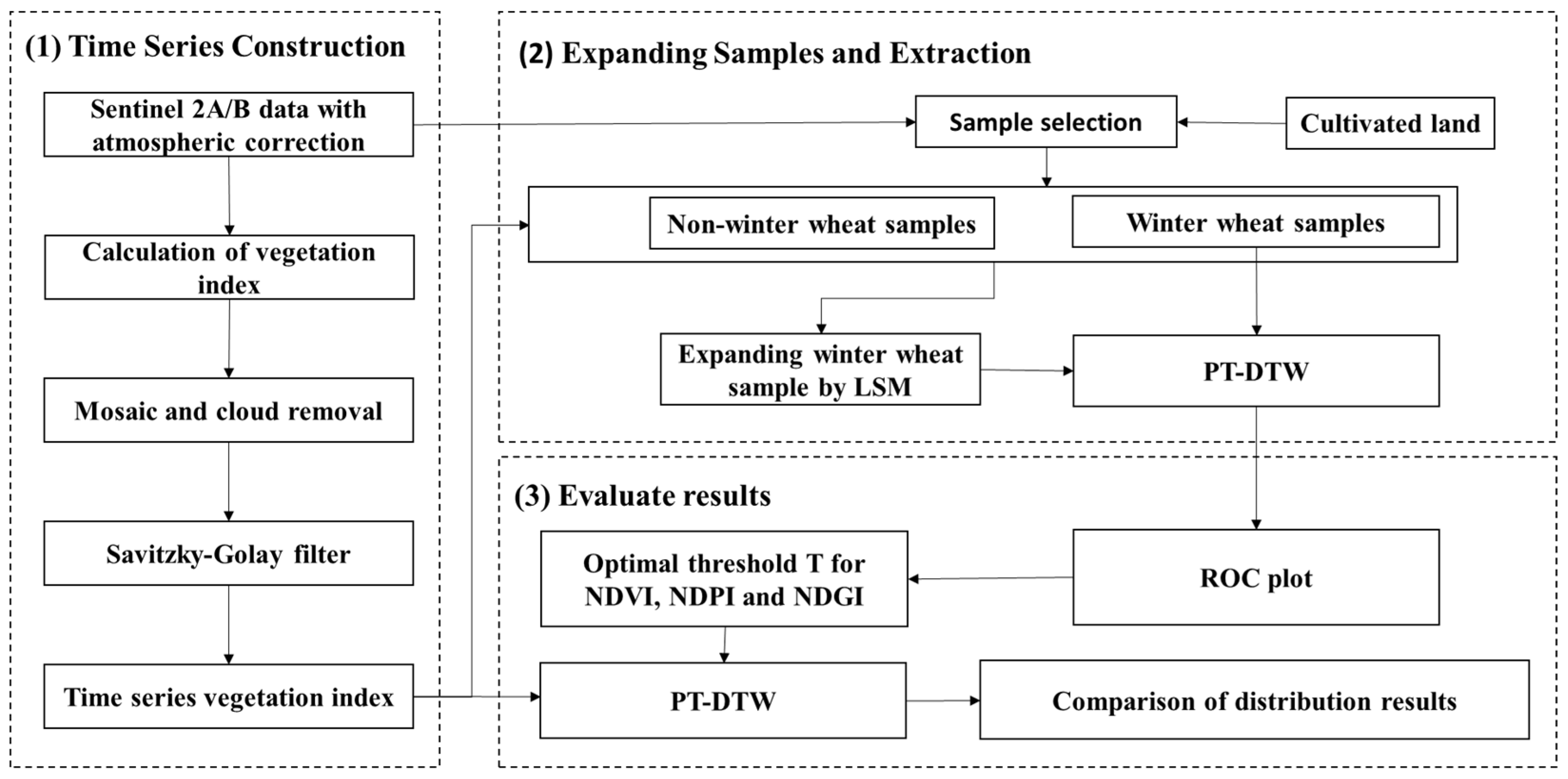
2.3. Technical Scheme
2.3.1. Time Series Construction
2.3.2. Expanding Samples and Extraction
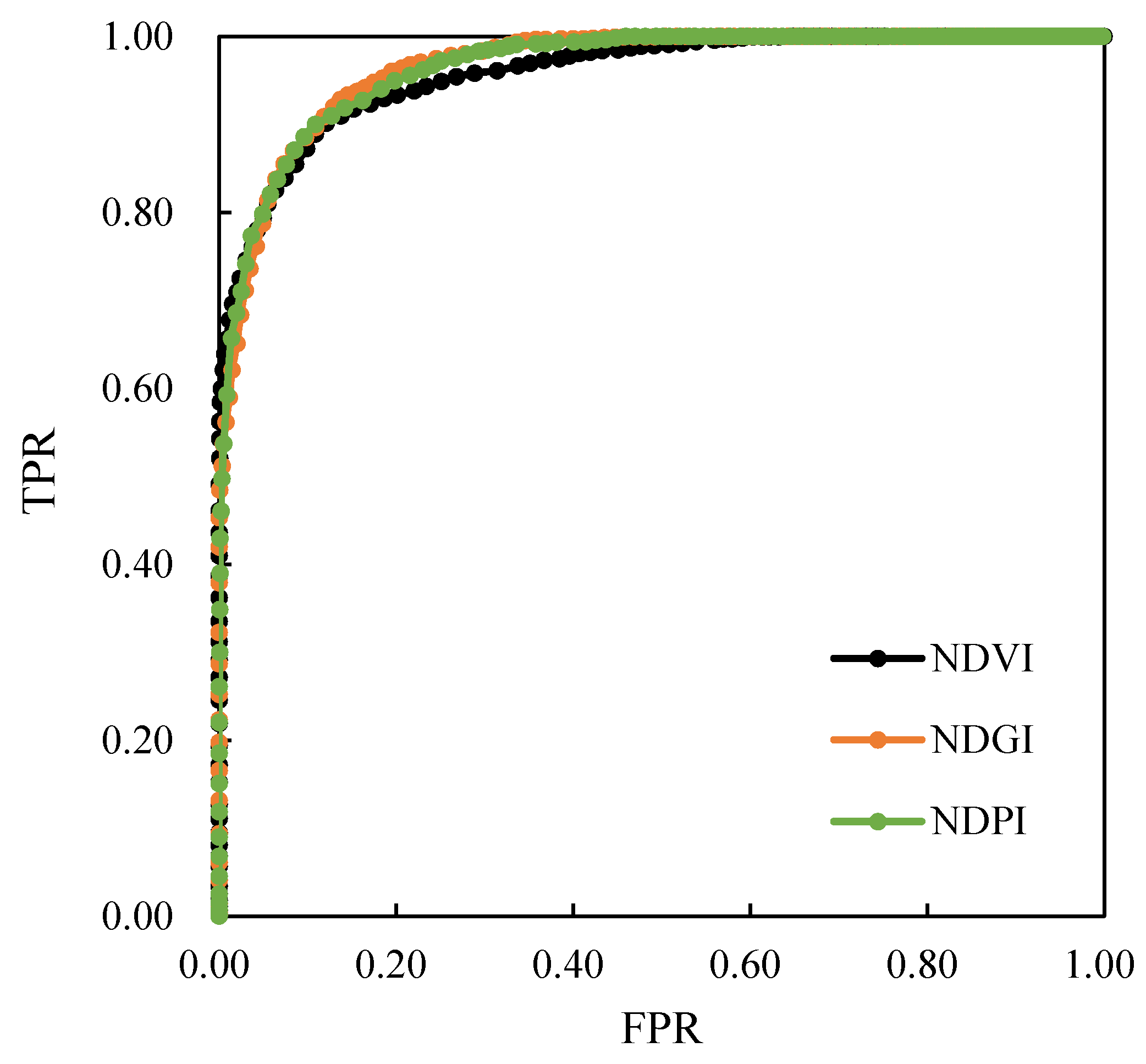
2.3.3. Accuracy Assessment via ROC and Optimal T
2.4. Vegetation Indices
2.5. Mosaic and Cloud Removal Algorithm
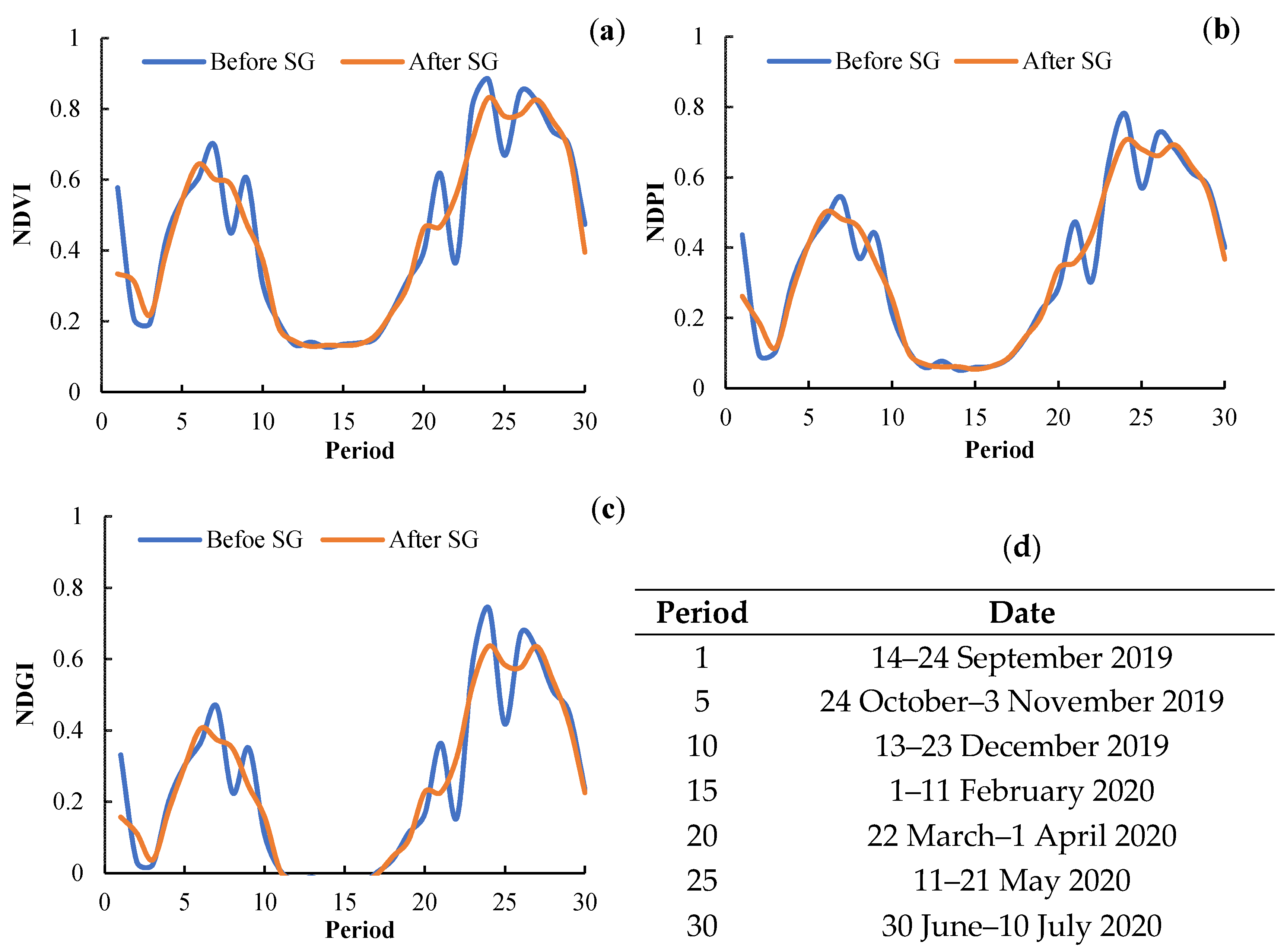
2.6. Savitzky–Golay Filter
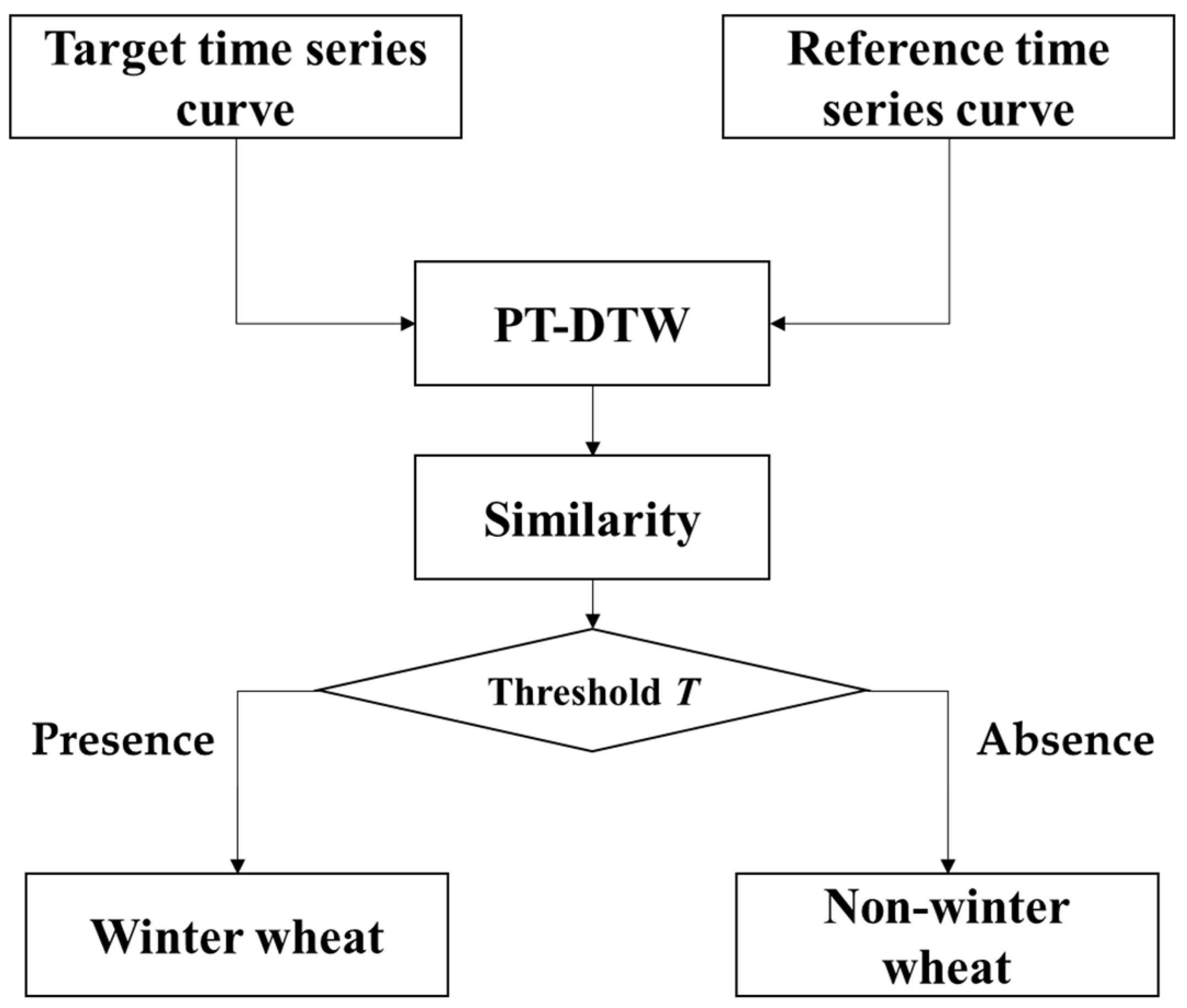
2.7. PT-DTW Algorithm
2.8. Accuracy Evaluation
3. Process and Results
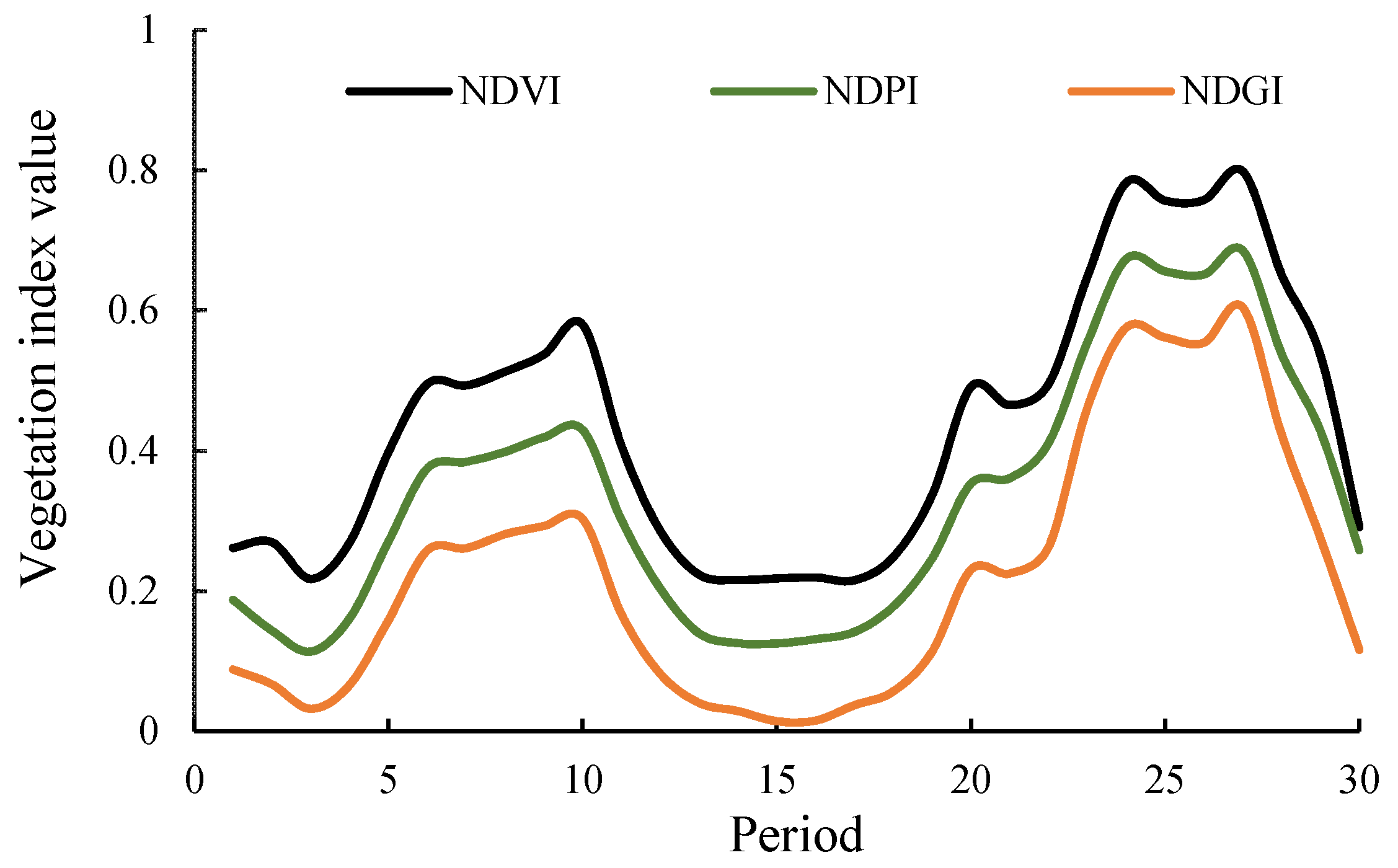
3.1. Time Series of Vegetation Indices
- (1)
- The vegetation indices were first calculated for all images. In GEE, the image expression interface was used to program and carry out the vegetation index algorithms according to Equations (1)–(3) by calling the 678 atmospheric corrected images covering Minhe from the Sentinel 2A/B dataset; afterwards, NDVI, NDPI, and NDGI were obtained.
- (2)
- Using the quality mosaic function within GEE, a 10-day time step, and NDVI was designated as the quality band, the multi-temporal images were mosaicked and cloud cover was removed, resulting in a total of 34 time series images. The corresponding bands of the three vegetation indices were then extracted from the mosaics and combined into three sets of time series vegetation index images for constructing a high-quality index curve.
- (3)
- According to the SG filtering principle [45], the filter function of three times 5-point fitting was programmed in GEE to smooth the time series of indices. This program eliminated the data of the initial and final periods, resulting in 30 time series images from 14 September 2019 to 7 October 2020.
3.2. Selection of Reference Curve and Threshold T
3.2.1. Sample Selection
3.2.2. Vegetation Indices Reference Curves
3.2.3. Selection of Threshold T
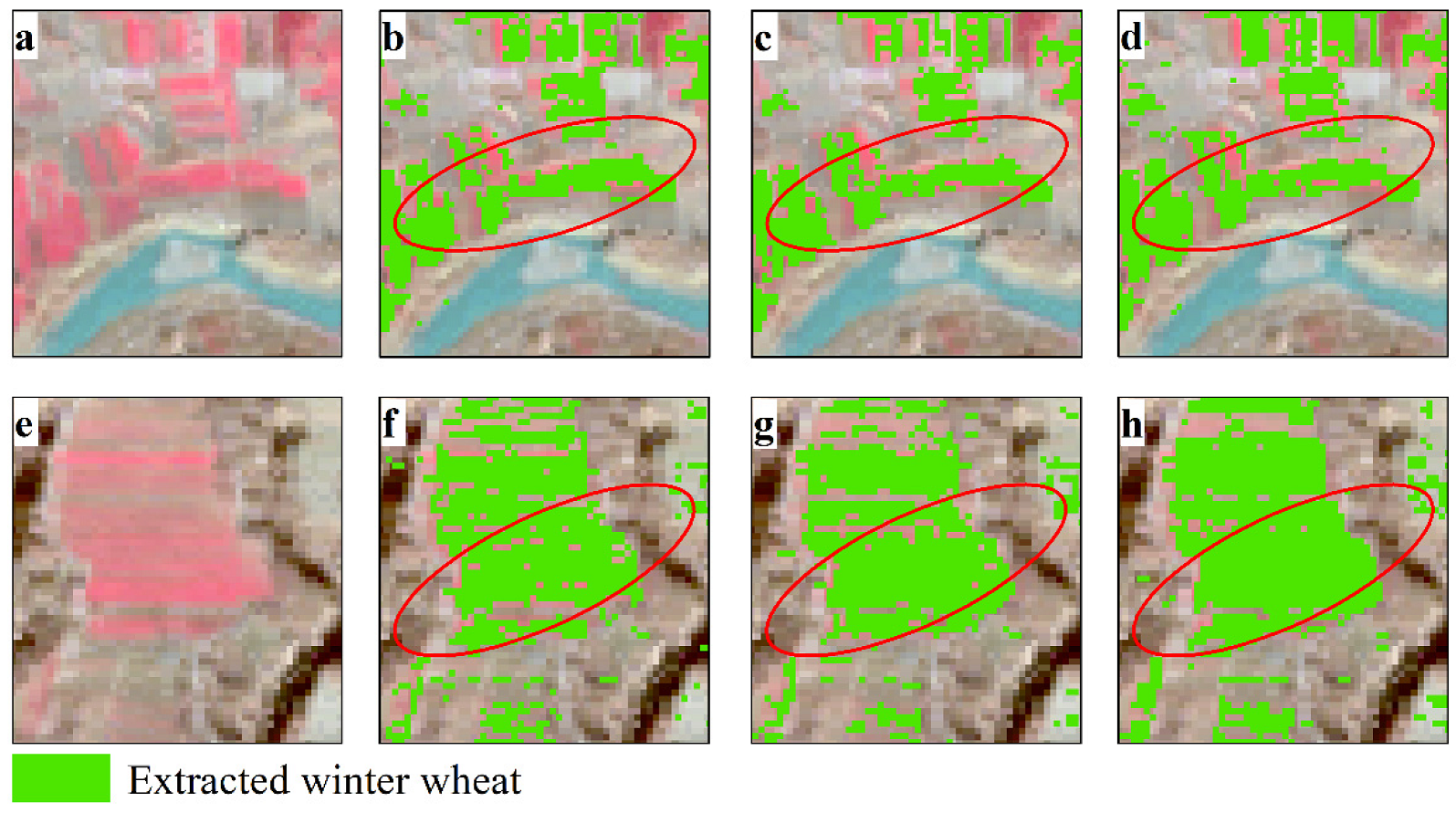
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| No. Winter Wheat | Longitude (°) | Latitude (°) | No. Winter Wheat | Longitude (°) | Latitude (°) |
|---|---|---|---|---|---|
| 1 | 102.8321991 | 36.34012101 | 31 | 102.8215339 | 36.33791838 |
| 2 | 102.8329072 | 36.33851354 | 32 | 102.8492914 | 36.31909747 |
| 3 | 102.8314678 | 36.33938116 | 33 | 102.8471242 | 36.31906289 |
| 4 | 102.829043 | 36.33893176 | 34 | 102.8487979 | 36.31800324 |
| 5 | 102.8256956 | 36.33860335 | 35 | 102.8502784 | 36.31847005 |
| 6 | 102.8250305 | 36.33805023 | 36 | 102.8673894 | 35.88064135 |
| 7 | 102.8225199 | 36.33917374 | 37 | 102.8657318 | 35.88057615 |
| 8 | 102.822198 | 36.34008982 | 38 | 102.8669388 | 35.88134548 |
| 9 | 102.8205458 | 36.3394503 | 39 | 102.8664976 | 35.88251362 |
| 10 | 102.8278629 | 36.3411096 | 40 | 102.8627154 | 35.88264401 |
| 11 | 102.8628656 | 35.88213114 | 41 | 102.8499259 | 36.31859709 |
| 12 | 102.8622648 | 35.88223545 | 42 | 102.8468145 | 36.31923679 |
| 13 | 102.8597081 | 35.88306055 | 43 | 102.848924 | 36.31855179 |
| 14 | 102.8588498 | 35.88267807 | 44 | 102.8538681 | 36.3241419 |
| 15 | 102.8645378 | 35.8653727 | 45 | 102.8313483 | 36.33999818 |
| 16 | 102.8632644 | 35.86459453 | 46 | 102.8303329 | 36.33885767 |
| 17 | 102.8636554 | 35.8858618 | 47 | 102.8323928 | 36.33806257 |
| 18 | 102.866505 | 35.88077895 | 48 | 102.8295158 | 36.34228171 |
| 19 | 102.8632671 | 35.88265455 | 49 | 102.8274237 | 36.34199652 |
| 20 | 102.8674006 | 35.88131822 | 50 | 102.8174997 | 36.34039149 |
| 21 | 102.8658503 | 35.88072301 | 51 | 102.8223066 | 36.33788167 |
| 22 | 102.8660586 | 35.88259989 | 52 | 102.8193938 | 36.33784398 |
| 23 | 102.8623315 | 35.88262329 | 53 | 102.858364 | 35.87200979 |
| 24 | 102.8635761 | 35.88107597 | 54 | 102.8654506 | 35.87580491 |
| 25 | 102.8638681 | 35.88585876 | 55 | 102.8591318 | 35.88298318 |
| 26 | 102.8483604 | 35.85708426 | 56 | 102.8676366 | 35.88072546 |
| 27 | 102.8644224 | 35.86548096 | 57 | 102.8672289 | 35.88178599 |
| 28 | 102.821937 | 36.33926221 | 58 | 102.8626812 | 35.88465212 |
| 29 | 102.8259041 | 36.33777124 | 59 | 102.8129411 | 35.86476349 |
| 30 | 102.8256573 | 36.33652671 | 60 | 102.8138048 | 35.86478088 |
| No. Non-Winter Wheat | Longitude (°) | Latitude (°) | No. Non-Winter Wheat | Longitude (°) | Latitude (°) |
| 1 | 102.8225883 | 36.33116338 | 21 | 102.8687295 | 35.88501014 |
| 2 | 102.8370508 | 36.3320277 | 22 | 102.8623717 | 35.89202697 |
| 3 | 102.8335317 | 36.31854326 | 23 | 102.8379958 | 35.89028862 |
| 4 | 102.8566631 | 36.31186933 | 24 | 102.8426306 | 35.89112303 |
| 5 | 102.8639587 | 36.31221515 | 25 | 102.8555911 | 35.87784088 |
| 6 | 102.8383095 | 35.86103466 | 26 | 102.8531878 | 35.8826394 |
| 7 | 102.8685648 | 35.86169548 | 27 | 102.8499263 | 35.88430838 |
| 8 | 102.8661999 | 35.85309907 | 28 | 102.852072 | 35.87624131 |
| 9 | 102.8445903 | 35.88152691 | 29 | 102.8691725 | 35.88154746 |
| 10 | 102.8746066 | 35.88693187 | 30 | 102.8648703 | 35.87768775 |
| 11 | 102.8716616 | 35.88003489 | 31 | 102.849542 | 36.32919305 |
| 12 | 102.8736786 | 35.88191256 | 32 | 102.853576 | 36.3262888 |
| 13 | 102.8732709 | 35.88556345 | 33 | 102.8529752 | 36.32449088 |
| 14 | 102.8474047 | 35.86326588 | 34 | 102.8346074 | 36.3315786 |
| 15 | 102.8539707 | 35.85797924 | 35 | 102.8237069 | 36.33095629 |
| 16 | 102.8427819 | 36.31772324 | 36 | 102.8385939 | 36.33521086 |
| 17 | 102.8400031 | 36.31880382 | 37 | 102.8404308 | 36.33316065 |
| 18 | 102.8416768 | 36.31988438 | 38 | 102.822755 | 36.33605531 |
| 19 | 102.8482343 | 36.32258948 | 39 | 102.8219181 | 36.33702329 |
| 20 | 102.8369678 | 36.32863987 | 40 | 102.8269607 | 36.34009998 |
References
- Shiferaw, B.; Smale, M.; Braun, H.; Duveiller, E.; Reynolds, M.; Muricho, G. Crops that feed the world 10. Past successes and future challenges to the role played by wheat in global food security. Food Secur. 2013, 5, 291–317. [Google Scholar] [CrossRef] [Green Version]
- Curtis, T.; Halford, N.G. Food security: The challenge of increasing wheat yield and the importance of not compromising food safety. Ann. Appl. Biol. 2014, 164, 354–372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vashisth, A.; Krishanan, P.; Joshi, D.K. Multi stage wheat yield estimation using different model under semiarid region of India. Int. Arch. Photogramm. 2019, XLII-3-W6, 263–267. [Google Scholar] [CrossRef] [Green Version]
- Mäkinen, H.; Kaseva, J.; Trnka, M.; Balek, J.; Kersebaum, K.C.; Nendel, C.; Gobin, A.; Olesen, J.E.; Bindi, M.; Ferrise, R.; et al. Sensitivity of European wheat to extreme weather. Field Crop. Res. 2018, 222, 209–217. [Google Scholar] [CrossRef]
- Porter, J.R.; Xie, L.; Challinor, A.J.; Cochrane, K.; Howden, S.M.; Iqbal, M.M.; Lobell, D.B.; Travasso, M.I. Food security and food production systems. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 485–533. [Google Scholar]
- Vannoppen, A.; Gobin, A.; Kotova, L.; Top, S.; De Cruz, L.; Vīksna, A.; Aniskevich, S.; Bobylev, L.; Buntemeyer, L.; Caluwaerts, S.; et al. Wheat yield estimation from NDVI and regional climate models in Latvia. Remote Sens. 2020, 12, 2206. [Google Scholar] [CrossRef]
- Hatfield, P.L.; Pinter, P.J., Jr. Remote sensing for crop protection. Crop Prot. 1993, 12, 403–413. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A.; Rundquist, D.C.; Keydan, G.; Leavitt, B.; Schepers, J. Monitoring maize (Zea mays L.) Phenology with remote sensing. Agron J. 2004, 96, 1139–1147. [Google Scholar] [CrossRef]
- Fang, P.; Zhang, X.; Wei, P.; Wang, Y.; Zhang, H.; Liu, F.; Zhao, J. The classification performance and mechanism of machine learning algorithms in winter wheat mapping using Sentinel-2 10 m resolution imagery. Appl. Sci. 2020, 10, 5075. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Feng, L.; Du, Q.; Runge, T. Combining multi-source data and machine learning approaches to predict winter wheat yield in the conterminous United States. Remote Sens. 2020, 12, 1232. [Google Scholar] [CrossRef] [Green Version]
- Song, D.; Zhang, C.; Yang, X.; Li, F.; Han, Y.; Gao, S.; Dong, H. Extracting winter wheat spatial distribution information from GF-2 image. J. Remote Sens. 2020, 24, 596–608. [Google Scholar]
- Dong, Q.; Chen, X.; Chen, J.; Zhang, C.; Liu, L.; Cao, X.; Zang, Y.; Zhu, X.; Cui, X. Mapping winter wheat in North China using Sentinel 2A/B data: A method based on phenology-time weighted dynamic time warping. Remote Sens. 2020, 12, 1274. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Tao, B.; Ren, W.; Zourarakis, D.P.; El Masri, B.; Sun, Z.; Tian, Q. An improved approach considering intraclass variability for mapping winter wheat using multitemporal MODIS EVI Images. Remote Sens. 2019, 11, 1191. [Google Scholar] [CrossRef] [Green Version]
- Zhong, L.; Hu, L.; Zhou, H.; Tao, X. Deep learning-based winter wheat mapping using statistical data as ground references in Kansas and northern Texas. U.S. Remote Sens. Environ. 2019, 233, 111411. [Google Scholar] [CrossRef]
- Huang, Q.; Wu, W.; Dend, H.; Zhang, L. Study on planting areas, extraction of remote sensing and monitoring of crop growth of winter wheat and rice in Jiangsu Province in 2009. Jiangsu Agric. Sci. 2010, 6, 508–511. [Google Scholar]
- Li, Y.; Chen, X.; Duan, H.; Shen, Y. Application of multi-source and multi-temporal remote sensing data in winter wheat identification. Geogr. Geo-Inf. Sci. 2010, 26, 47–49. [Google Scholar]
- Qin, Y.; Zhao, G.; Jiang, S.; Jinnan, C.; Yan, M.; Baihong, L.; Guochen, X.; Jiguang, H. Winter wheat yield estimation based on high and moderate resolution remote sensing data at county level. Trans. Chin. Soc. Agric. Engin. 2009, 25, 118–123. [Google Scholar]
- Yang, T.; Wang, Q.; Liu, Y.; Wan, Y.; Nie, X. A review of application of machine learning in wireline logging formation evaluation. J. Oil Gas Technol. 2020, 42, 27–38. [Google Scholar] [CrossRef]
- Cui, R.; Liu, Y.; Fu, J. Estimation of winter wheat biomass using visible spectral and BP based artificial neural networks. Spectrosc. Spect. Anal. 2015, 35, 2596–2601. [Google Scholar]
- Feng, M.; Yang, W.; Zhang, D.; Cao, L.; Wang, H.; Wang, Q. Monitoring planting area and growth situation of irrigation-land and dry-land winter wheat based on TM and MODIS data. Trans. Chin. Soc. Agric. Engin. 2009, 25, 103–109. [Google Scholar]
- He, Y.; Wang, C.; Jia, H.; Chen, F. Research on extraction of winter wheat based on random forest. Remote Sens. Technol. Appl. 2018, 33, 1132–1140. [Google Scholar]
- Yang, H.; Pan, Z.; Bai, W. Review of time series prediction methods. Comput. Sci. 2019, 46, 21–28. [Google Scholar]
- Song, Y.; Wang, J. Mapping winter wheat planting area and monitoring its phenology using sentinel-1 backscatter time series. Remote Sens. 2019, 11, 449. [Google Scholar] [CrossRef] [Green Version]
- Shi, F.; Gao, X.; Yang, L.; He, L.; Jia, W. Research on typical crop classification based on HJ-1A hyperspectral data in the Huangshui River Basin. Remote Sens. Technol. Appl. 2017, 32, 206–217. [Google Scholar]
- Zhang, J.; Zhang, X.; Tian, L.; Zhang, Q. The support vector machine method for RS images’ classification in northwest arid area. Sci. Surv. Mapp. 2017, 42, 49–52. [Google Scholar] [CrossRef]
- Mutanga, O.; Kumar, L. Google Earth Engine applications. Remote Sens. 2019, 11, 591. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Zhang, X.; Zeng, H.; Zhang, M.; Tian, F. Big data methods for environmental data. Bull. Chin. Acad. Sci. 2018, 33, 804–811. [Google Scholar]
- Xiao, W.; Xu, S.; He, T. Mapping paddy rice with Sentinel-1/2 and phenology-, object-based algorithm—An implementation in Hangjiahu Plain in China using GEE platform. Remote Sens. 2021, 13, 990. [Google Scholar] [CrossRef]
- He, Z.; Zhang, M.; Wu, B.; Xing, Q. Extraction of summer crop in Jiangsu based on Google Earth Engine. J. Geo-Inf. Sci. 2019, 21, 752–766. [Google Scholar]
- Yang, A.; Zhong, B.; Wu, J. Monitoring winter wheat in ShanDong province using Sentinel data and Google Earth Engine platform. In Proceedings of the 10th International Workshop on the Analysis of Multitemporal Remote Sensing Images (MultiTemp), IEEE, Shanghai, China, 5–7 August 2019. [Google Scholar]
- Zhao, B.; Zhao, D. Regional drought risk of winter wheat in Minhe County Qinghai Province. Sci. Technol. Qinghai Agri. Forest. 2018, 3, 18–23. [Google Scholar]
- Li, W.; Jiao, S.; Li, R. Effects of climate change on winter wheat in Minhe County. Sci. Technol. Qinghai Agri. Forest. 2018, 112, 6–11. [Google Scholar]
- National Catalogue Service for Geographic Information. 1:1,000,000 National Basic Geographic Database. Available online: https://www.webmap.cn/commres.do?method=result100W (accessed on 11 January 2021).
- Tian, Q.; Min, X. Advances in study on vegetation indices. Adv. Earth Sci. 1998, 13, 10–16. [Google Scholar]
- Miao, Z.; Liu, Z.; Wang, Z.; Song, K.; Du, J.; Zeng, L. Dynamic monitoring of vegetation fraction change in Jilin Province based on MODIS NDVI. Remote Sens. Technol. Appl. 2010, 25, 387–393. [Google Scholar]
- Liu, X.; Pan, Y.; Zhu, X.; Li, S. Spatiotemporal variation of vegetation coverage in Qinling-Daba Mountains in relation to environmental factors. Acta Geogr. Sinica 2015, 70, 705–716. [Google Scholar]
- Wang, X.; Hou, X. Variation of normalized difference vegetation index and its response to extreme climate in coastal China during 1982–2014. Geogr. Res. 2019, 38, 807–821. [Google Scholar]
- Costa, L.; Nunes, L.; Ampatzidis, Y. A new visible band index (vNDVI) for estimating NDVI values on RGB images utilizing genetic algorithms. Comp. Elect. Agric. 2020, 172, 105334. [Google Scholar] [CrossRef]
- Dong, C.; Zhao, G.; Qin, Y.; Wan, H. Area extraction and spatiotemporal characteristics of winter wheat–summer maize in Shandong Province using NDVI time series. PLoS ONE 2019, 14, e226508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, F.; Ren, J.; Wu, S.; Zhao, H.; Zhang, N. Comparison of regional winter wheat mapping results from different similarity measurement indicators of NDVI time series and their optimized thresholds. Remote Sens. 2021, 13, 1162. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.; Wu, J.; Tang, Y.; Shia, P.; Black, T.A.; Zhu, K. A snow-free vegetation index for improved monitoring of vegetation spring green-up date in deciduous ecosystems. Remote Sens. Environ. 2017, 196, 1–12. [Google Scholar] [CrossRef]
- Tian, J.; Zhu, X.; Shen, Z.; Wu, J.; Xu, S.; Liang, Z.; Wang, J. Investigating the urban-induced microclimate effects on winter wheat spring phenology using Sentinel-2 time series. Agric. Forest Meteorol. 2020, 294, 108153. [Google Scholar] [CrossRef]
- Yang, W.; Kobayashi, H.; Wang, C.; Shend, M.; Chen, J.; Matsushita, B.; Tang, Y.; Kim, Y.; Bret-Hartei, M.S.; Zona, D.; et al. A semi-analytical snow-free vegetation index for improving estimation of plant phenology in tundra and grassland ecosystems. Remote Sens. Environ. 2019, 228, 31–44. [Google Scholar] [CrossRef]
- Li, R.; Zhang, X.; Liu, B.; Zhang, B. Review on methods of remote sensing time-series data reconstruction. J. Remote Sens. 2009, 13, 335–341. [Google Scholar]
- Kai, Z.; Jönsson, P.; Jin, H.; Eklundh, L. Performance of smoothing methods for reconstructing NDVI time-series and estimating vegetation phenology from MODIS data. Remote Sens. 2017, 9, 1271. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Jönsson, P.; Tamura, M.; Gua, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Wang, L.; Qi, F.; Shen, X.; Huang, J. Monitoring multiple cropping index of Henan Province, China based on MODIS-EVI time series data and Savitzky-Golay Filtering algorithm. Comput. Model. Eng. Sci. 2019, 119, 331–348. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Zhang, X.; Huang, Y.; Hong, C.; Zhang, Z.; Huang, X.; Zeng, J.; Tang, J.; Zhang, R. Monitoring of winter wheat and summer corn phenology in Xiong’an new area based on NDVI time series. In Proceedings of the International Conference on Wireless Communication, Network and Multimedia Engineering (WCNME 2019), Guilin, China, 21–22 April 2019; Atlantis Press: Guilin, China, 2019; p. 21. [Google Scholar]
- Zhuo, W.; Huang, J.; Gao, X.; Ma, H.; Huang, H.; Su, W.; Meng, J.; Li, Y.; Chen, H.; Yin, D. Prediction of winter wheat maturity dates through assimilating remotely sensed leaf area index into crop growth model. Remote Sens. 2020, 12, 2896. [Google Scholar] [CrossRef]
- Chen, H.; Liu, C.; Sun, B. Survey on similarity measurement of time series data mining. Cont. Decis. 2017, 32, 1–11. [Google Scholar]
- Tu, G.; Geng, X. Research and implementation of similarity computation for spatiotemporal trajectories. Comp. Digit. Engin. 2020, 48, 1114–1120. [Google Scholar] [CrossRef]
- Wang, H.; Gong, Y.; Liu, W. Study on spatial-temporal multiscale adaptive method of gesture recognition. Comp. Sci. 2017, 44, 287–291. [Google Scholar]
- Maus, V.; Camara, G.; Cartaxo, R.; Sanchez, A.; Ramos, F.M.; de Queiroz, G.R. A time-weighted dynamic time warping method for land-use and land-cover mapping. IEEE J. Select. Topics Appl. Earth Obs. Remote Sens. 2016, 9, 3729–3739. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Spackman, K.A. Signal detection theory: Valuable tools for evaluating inductive learning. In Proceedings of the Sixth International Workshop on Machine Learning; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Dong, J.; Fu, Y.; Wang, J.; Tian, H.; Fu, S.; Niu, Z.; Han, W.; Zheng, Y.; Huang, J.; Yuan, W. Early-season mapping of winter wheat in China based on Landsat and Sentinel images. Earth Syst. Sci. Data 2020, 12, 3081–3095. [Google Scholar] [CrossRef]

| Band Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 8a | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Central wavelength (nm) | 433.9/ 442.3 | 496.6/ 492.1 | 560 /559 | 664.5/ 665 | 703.9/ 703.8 | 740.2/ 739.1 | 782.5/ 779.7 | 835.1/ 833 | 864.8/ 864 | 945/ 943.2 | 1373.5/ 1376.9 | 1613.7/ 1610.4 | 2202.4/ 2185.7 |
| Spatial resolution (m) | 60 | 10 | 10 | 10 | 20 | 20 | 20 | 10 | 20 | 60 | 60 | 20 | 20 |
| VI | T | TPR | FPR | ACC |
|---|---|---|---|---|
| NDVI | 0.060 | 76.66% | 0.0% | 88.33% |
| NDPI | 0.050 | 83.33% | 0.0% | 91.67% |
| NDGI | 0.051 | 80.00% | 0.0% | 90.00% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, F.; Xia, X.; Huang, Y.; Lv, S.; Chen, Q.; Pan, Y.; Zhu, X. Comparison of Winter Wheat Extraction Methods Based on Different Time Series of Vegetation Indices in the Northeastern Margin of the Qinghai–Tibet Plateau: A Case Study of Minhe, China. Remote Sens. 2022, 14, 343. https://doi.org/10.3390/rs14020343
Huang F, Xia X, Huang Y, Lv S, Chen Q, Pan Y, Zhu X. Comparison of Winter Wheat Extraction Methods Based on Different Time Series of Vegetation Indices in the Northeastern Margin of the Qinghai–Tibet Plateau: A Case Study of Minhe, China. Remote Sensing. 2022; 14(2):343. https://doi.org/10.3390/rs14020343
Chicago/Turabian StyleHuang, Fujue, Xingsheng Xia, Yongsheng Huang, Shenghui Lv, Qiong Chen, Yaozhong Pan, and Xiufang Zhu. 2022. "Comparison of Winter Wheat Extraction Methods Based on Different Time Series of Vegetation Indices in the Northeastern Margin of the Qinghai–Tibet Plateau: A Case Study of Minhe, China" Remote Sensing 14, no. 2: 343. https://doi.org/10.3390/rs14020343
APA StyleHuang, F., Xia, X., Huang, Y., Lv, S., Chen, Q., Pan, Y., & Zhu, X. (2022). Comparison of Winter Wheat Extraction Methods Based on Different Time Series of Vegetation Indices in the Northeastern Margin of the Qinghai–Tibet Plateau: A Case Study of Minhe, China. Remote Sensing, 14(2), 343. https://doi.org/10.3390/rs14020343







