Variational-Scale Segmentation for Multispectral Remote-Sensing Images Using Spectral Indices
Abstract
:1. Introduction
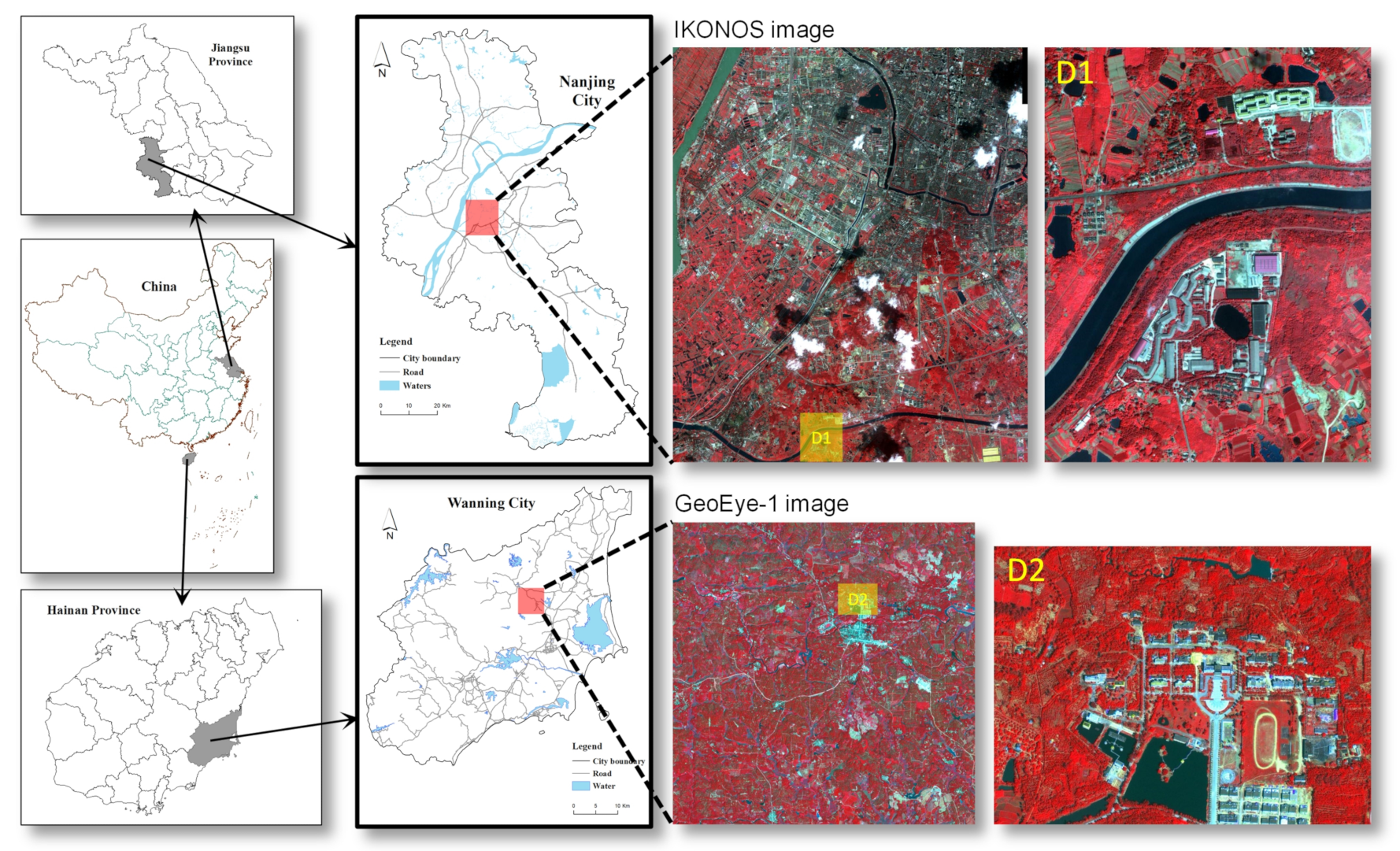
2. Study Area and Data
3. Methodology
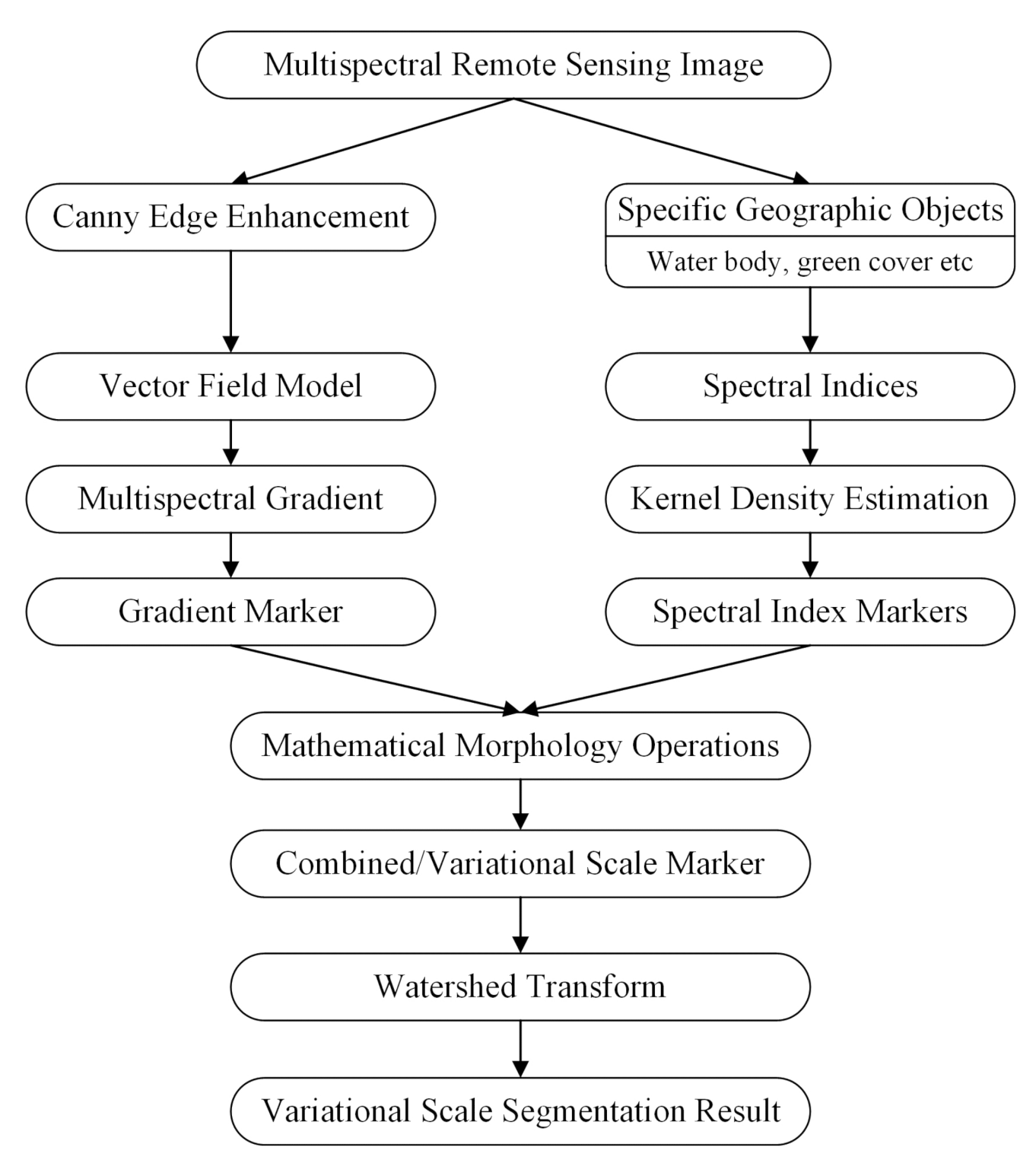
3.1. Overview
3.2. Marker Generation from Multispectral Gradient using the Vector Field Model
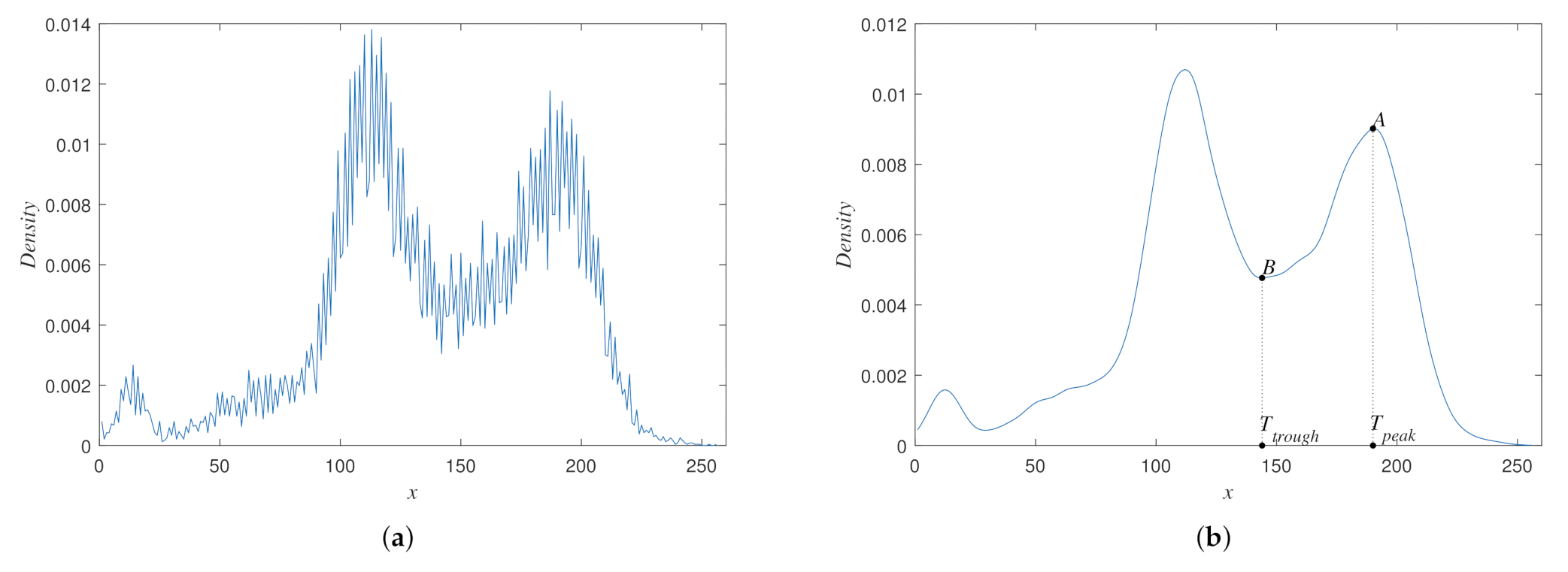
3.3. Marker Generation for Spectral Indices Based on a Histogram
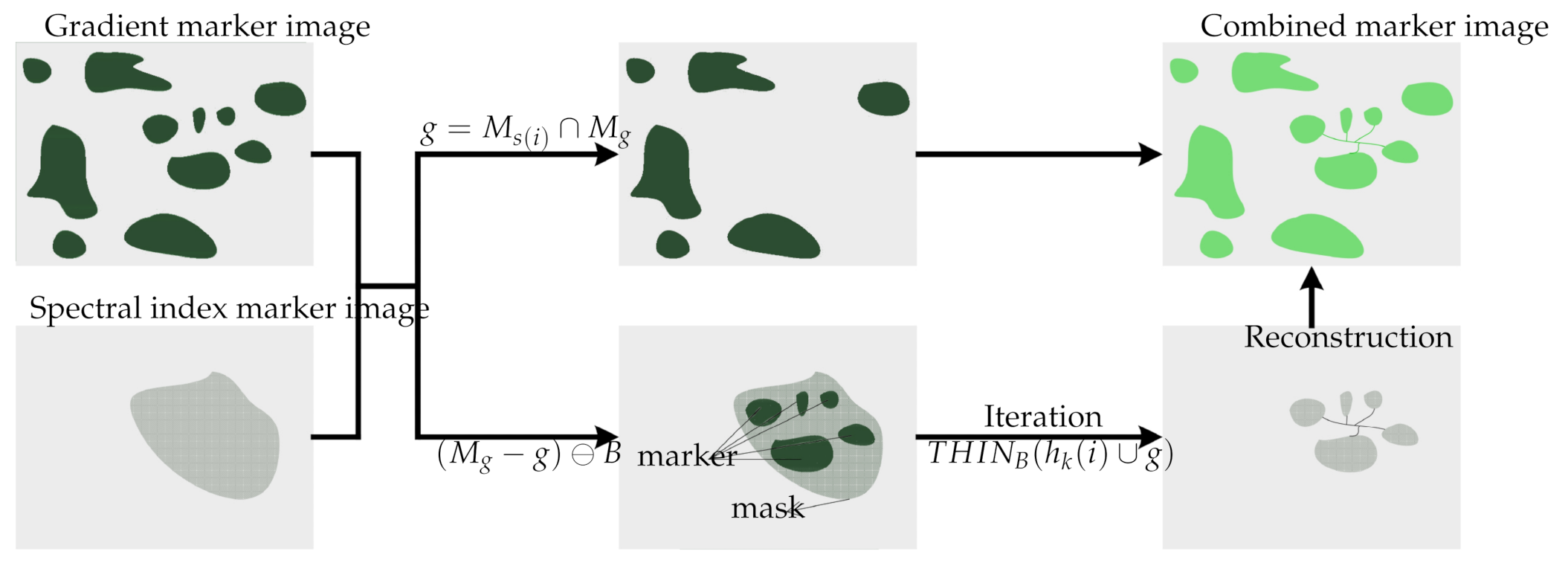
3.4. Segmentation via Combination of Markers from Spectral Indices and Gradient Markers
| Algorithm 1 Generating a combined marker image based on spectral indices and gradient markers. |
| Input: Gradient marker image Number of spectral index marker images N The ith spectral index marker image Output: Combined marker image
|
4. Experiments and Results
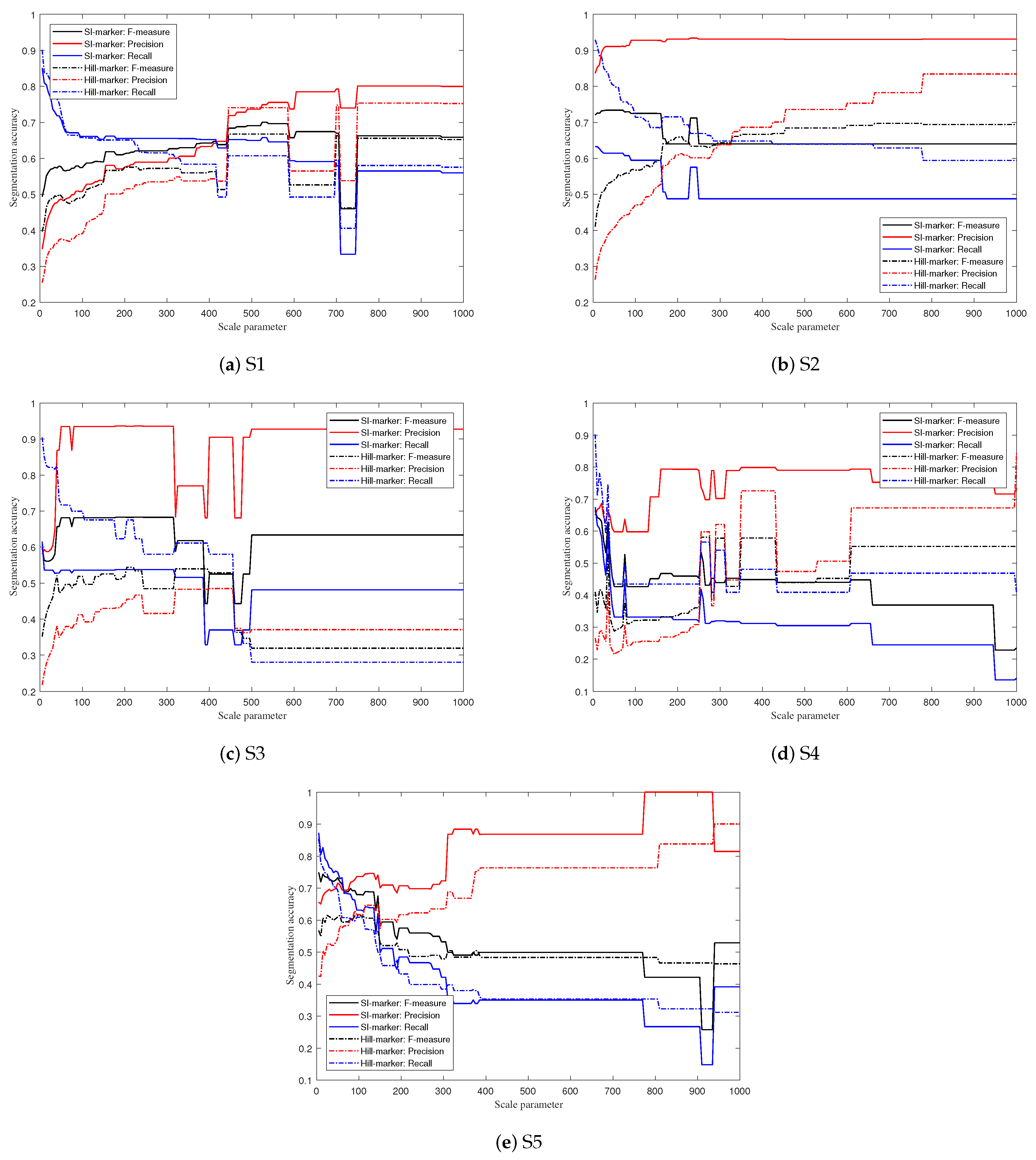
4.1. Performance Evaluation
4.2. Influence of the Threshold for Spectral Indices on Segmentation
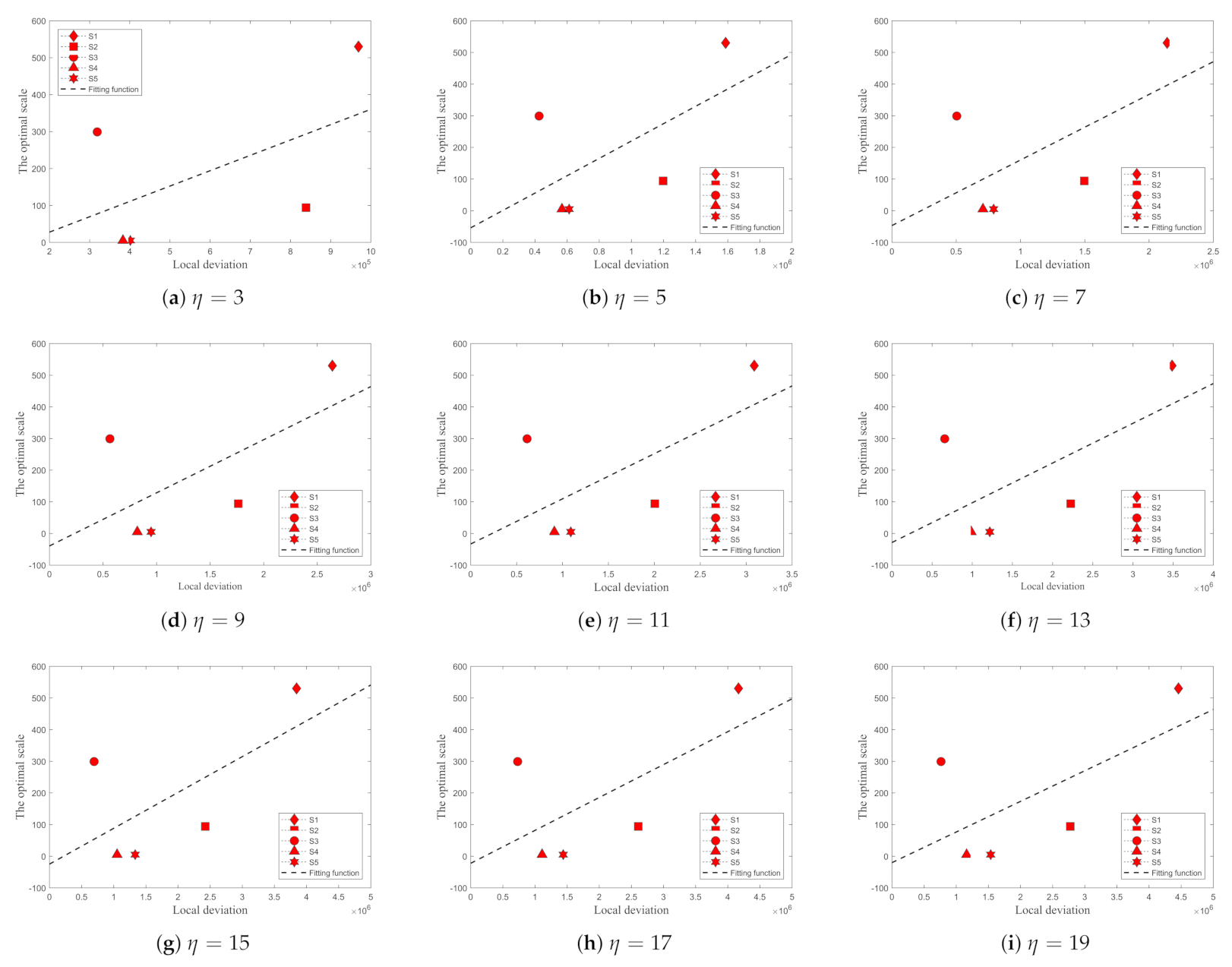
4.3. Automatic Selection of Optimal Segmentation Regions
| Algorithm 2 Obtaining the optimal thresholds of spectral indices for generating marker images. |
| Input: Multispectral band image T Output: Spectral index marker image
|
4.4. Influence of the Scale Parameter
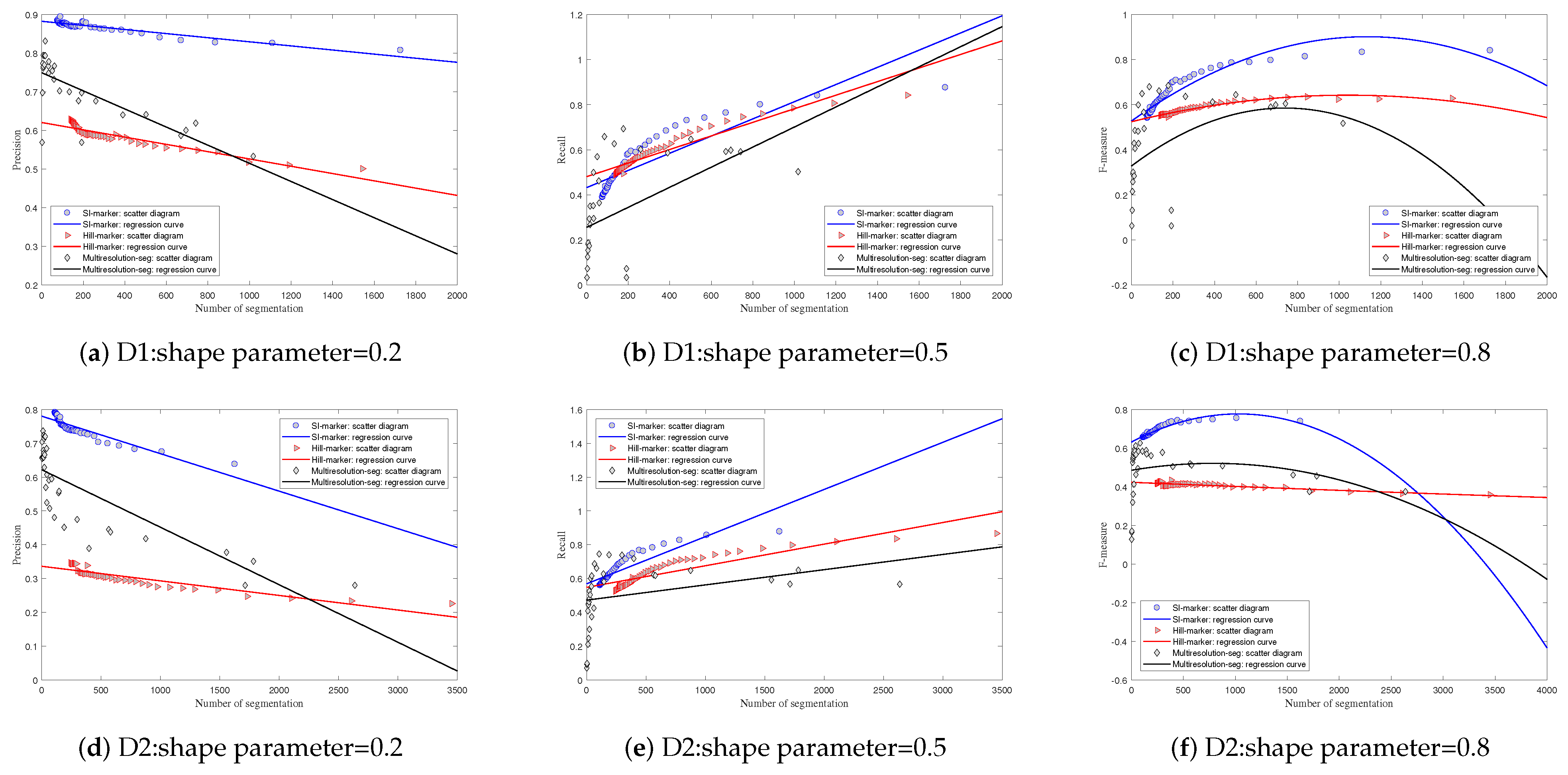
4.5. Comparision
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blaschke, T.; Hay, G.J. Object-oriented image analysis and scale-space: Theory and methods for modeling and evaluating multi-scale landscape structure. Int. Arch. Photogramm. Remote Sens. 1998, 34, 22–29. [Google Scholar]
- Blaschke, T.; Strobl, J.; Zeil, P. Object-oriented image processing in an integrated gis/remote sensing environment and perspectives for environmental applications. In Environmental Information for Planning, Politics and the Public; Cremers, A., Greve, K., Eds.; Metropolis: Marburg, Germany, 2000. [Google Scholar]
- Schiewe, J.; Tufte, L.; Ehlers, M. Potential and problems of multi-scale segmentation methods in remote sensing. GeoBIT/GIS 2001, 54, 34–39. [Google Scholar]
- Speake, T.; Mersereau, R.M. Segmentation of high-resolution remotely sensed data concepts, applications and problems. Jt. ISPRS Comm. Symp. Geospat. Theory Proc. Appl. 2002, 34, 380–385. [Google Scholar]
- Schiefer, F.; Kattenborn, T.; Frick, A.; Frey, J.; Schall, P.; Koch, B.; Schmidtlein, S. Mapping forest tree species in high resolution UAV-based RGB-imagery by means of convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2020, 170, 205–21539. [Google Scholar] [CrossRef]
- Nezami, S.; Khoramshahi, E.; Nevalainen, O.; Pölönen, I.; Honkavaara, E. Tree species classification of drone hyperspectral and rgb imagery with deep learning convolutional neural networks. Remote Sens. 2020, 12, 1070. [Google Scholar] [CrossRef] [Green Version]
- Grinias, I.; Panagiotakis, C.; Tziritas, G. MRF-based Segmentation and Unsupervised Classification for Building and Road Detection in Peri-urban Areas of High-resolution. ISPRS J. Photogramm. Remote Sens. 2016, 122, 145–166. [Google Scholar] [CrossRef]
- Marçal, A.R.S.; Borges, J.S.; Gomes, J.A.; Pinto da Costa, J.F. Land cover update by supervised classification of segmented aster images. Int. J. Remote Sens. 2005, 26, 1347–1362. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Li, X. Object-oriented classification for urban land cover mapping with aster imagery. Int. J. Remote Sens. 2007, 28, 4645–4651. [Google Scholar] [CrossRef]
- Duveiller, G.; Defourny, P.; Desclée, B.; Mayaux, P. Deforestation in central africa: Estimates at regional, national and landscape levels by advanced processing of systematically-distributed landsat extracts. Remote Sens. Environ. 2008, 112, 1969–1981. [Google Scholar] [CrossRef]
- Myint, S.W.; Yuan, M.; Cerveny, R.S.; Giri, C.P. Comparison of remote sensing image processing techniques to identify tornado damage areas from landsat tm data. Sensors 2008, 8, 1128–1156. [Google Scholar] [CrossRef] [Green Version]
- Jobin, B.; Labrecque, S.; Grenier, M.; Falardeau, G. Object-based classification as an alternative approach to the traditional pixel-based classification to identify potential habitat of the grasshopper sparrow. Environ. Manag. 2008, 41, 20–31. [Google Scholar] [CrossRef]
- Cufí, X.; Muñoz, X.; Freixenet, J.; Martí, J. A review of image segmentation techniques integrating region and boundary information. Adv. Imaging Electron Phys. 2003, 120, 1–39. [Google Scholar]
- Moghaddamzadeh, A.; Bourbakis, N. A fuzzy region growing approach for segmentation of color images. Pattern Recognit. 1997, 30, 867–881. [Google Scholar] [CrossRef]
- Xiao, P.; Feng, X.; An, R.; Zhao, S. Segmentation of multispectral high-resolution satellite imagery using log gabor filters. Int. J. Remote Sens. 2010, 31, 1427–1439. [Google Scholar] [CrossRef]
- Karantzalos, K.; Argialas, D. Improving edge detection and watershed segmentation with anisotropic diffusion and morphological levellings. Int. J. Remote Sens. 2006, 27, 5427–5434. [Google Scholar] [CrossRef]
- Baatz, M.; Schäpe, A. Multiresolution segmentation—An optimization approach for high quality multi-scale image segmentation. In Angewandte Geographische Informationsverarbeitung XII, Beiträge zum AGIT-Symposium Salzburg; Blaschke, T., Strobl, J., Greisebener, G., Eds.; Wichmann: Heidelberg, Germany, 2000. [Google Scholar]
- Evans, C.; Jones, R.; Svalbe, I.; Berman, M. Segmenting multispectral landsat tm images into field units. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1054–1064. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from eos-modis. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Li, Y.; Gong, P. An efficient texture image segmentation algorithm based on the gmrf model for classification of remotely sensed imagery. Int. J. Remote Sens. 2005, 26, 5149–5159. [Google Scholar] [CrossRef]
- Sarkar, A.; Biswas, M.K.; Kartikeyan, B.; Kumar, V.; Majumder, K.L.; Pal, D.K. A mrf model-based segmentation approach to classification for multispectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1102–1113. [Google Scholar] [CrossRef]
- Lizarazo, I.; Elsner, P. Fuzzy segmentation for object-based image classification. Int. J. Remote Sens. 2009, 30, 1643–1649. [Google Scholar] [CrossRef]
- Marr, D. Early processing of visual information. Phil. Trans. R. Soc. Lond. B 1976, 275, 483–524. [Google Scholar]
- Marr, D. Analyzing natural images: A computational theory of texture vision. Cold Spring Harbor Symp. Quant. Biol. 1976, 40, 647–662. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, P.; Feng, X. Object-specific optimization of hierarchical multiscale segmentations for high-spatial resolution remote sensing images. ISPRS J. Photogramm. Remote Sens. 2020, 159, 308–321. [Google Scholar] [CrossRef]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Object-oriented fuzzy analysis of remote sensing data for gis-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Zhang, H.; Fritts, J.E.; Goldman, S.A. Image segmentation evaluation: A survey of unsupervised methods. Comput. Vis. Image Underst. 2008, 110, 260–280. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Weng, Q.; Hay, G.J.; He, Y. Geographic object-based image analysis (geobia): Emerging trends and future opportunities. Gisci. Remote Sens. 2018, 55, 159–182. [Google Scholar] [CrossRef]
- Chen, G.; Ming, D.; Zhao, L.; Lv, B.; Zhou, K.; Qing, Y. Review on high spatial resolution remote sensing image segmentation evaluation. Photogramm. Eng. Remote Sens. 2018, 84, 629–646. [Google Scholar] [CrossRef]
- Espindola, G.M.; Camara, G.; Reis, I.A.; Monteiro, L.S.B.M. Parameter selection for region-growing image segmentation algorithms using spatial autocorrelation. Int. J. Remote Sens. 2006, 27, 3035–3040. [Google Scholar] [CrossRef]
- Corcoran, P.; Winstanley, A.; Mooney, P. Segmentation performance evaluation for object-based remotely sensed image analysis. Int. J. Remote Sens. 2010, 31, 617–645. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Ming, D.; Li, J.; Wang, J.; Zhang, M. Scale parameter selection by spatial statistics for geobia: Using mean-shift based multi-scale segmentation as an example. ISPRS J. Photogramm. Remote Sens. 2015, 106, 28–41. [Google Scholar] [CrossRef]
- Wang, Y.; Qi, Q.; Liu, Y.; Jiang, L.; Wang, J. Unsupervised segmentation parameter selection using the local spatial statistics for remote sensing image segmentation. Int. J. Appl. Earth Obs. GeoInf. 2011, 32, 2015–2024. [Google Scholar] [CrossRef]
- Dragut, L.; Tiede, D.; Levick, S.R. Esp: A tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar] [CrossRef]
- Dragut, L.; Csillik, O.; Eisank, C.; Tiede, D. Automated parameterisation for multiscale image segmentation on multiple layers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 119–127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; Li, P.; He, Y. A multi-band approach to unsupervised scale parameter selection for multi-scale image segmentation. ISPRS J. Photogramm. Remote Sens. 2014, 94, 13–24. [Google Scholar] [CrossRef]
- Zhang, X.; Du, S. Learning selfhood scales for urban land cover mapping with veryhigh-resolution satellite images. Remote Sens. Environ. 2016, 178, 172–190. [Google Scholar] [CrossRef]
- Yang, J.; He, Y.; Caspersen, J. Region merging using local spectral angle thresholds: A more accurate method for hybrid segmentation of remote sensing images. Remote Sens. Environ. 2017, 190, 137–148. [Google Scholar] [CrossRef]
- Dekavalla, M.; Argialas, D. A region merging segmentation with local scale parameters: Applications to spectral and elevation data. Remote Sens. 2018, 10, 2024. [Google Scholar] [CrossRef] [Green Version]
- Xiao, P.; Zhang, X.; Zhang, H.; Hu, R.; Feng, X. Multiscale optimized segmentation of urban green cover in high resolution remote sensing image. Remote Sens. 2018, 10, 1813. [Google Scholar] [CrossRef] [Green Version]
- Su, T. Scale-variable region-merging for high resolution remote sensing image segmentation. ISPRS J. Photogramm. Remote Sens. 2019, 147, 319–334. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Erdemir, M.Y.; Tonbul, H. Classification of semiurban landscapes from very high-resolution satellite images using a regionalized multiscale segmentation approach. J. Appl. Remote Sens. 2017, 11, 035016. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Lennert, M.; Vanhuysse, S.; Johnson, B.A.; Wolff, E. Scale matters: Spatially partitioned unsupervised segmentation parameter optimization for large and heterogeneous satellite images. Remote Sens. 2018, 10, 1440. [Google Scholar] [CrossRef] [Green Version]
- Vincent, L.; Soille, P. Watershed in digital spaces: An efficient algorithm based on immersion simulations. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 583–598. [Google Scholar] [CrossRef] [Green Version]
- Beucher, S.; Meyer, F. The morphological approach to segmentation: The watershed transformation. In Mathematical Morphology and its Applications to Image Processing; Dougherty, E.R., Ed.; Marcel Dekker: New York, NY, USA, 1993. [Google Scholar]
- Hill, P.R.; Canagarajah, C.N.; Bull, D.R. Image segmentation using a texture gradient based watershed transform. IEEE Trans. Image Process. 2003, 12, 1618–1633. [Google Scholar] [CrossRef]
- Sapiro, G.; Ringach, D.L. Anisotropic diffusion of multivalued images with applications to color filtering. IEEE Trans. Image Process. 1996, 5, 1582–1586. [Google Scholar] [CrossRef] [PubMed]
- Roberts, L.G. Monitoring the vernal advancements and retrogradation (greenwave effect) of nature vegetation. In NASA/GSFC Final Report; NASA: Greenbelt, Philippines, 1974. [Google Scholar]
- Work, E.A.; Gilmer, D.S. Utilization of satellite data for inventorying prairie ponds and lakes. Photogramm. Eng. Remote Sens. 1976, 42, 685–694. [Google Scholar]
- McFeeters, S.K. The use of normalized difference water index (ndwi) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Gao, B.C. Ndwi-a nomalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; van Leeuwen, W. A comparison of vegetation indices over a global set of tm images for eos-modis. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal application. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I. Hyperspectral vegetation indices and novel algorithms for predicting green lai of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for lai and apar assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanré, D. Atmospherically resistant vegetation index (arvi) for eos-modis. IEEE Trans. Geosci. Remote Sens. 1992, 30, 231–270. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Gong, P.; Pu, R.; Biging, G.S.; Larrieu, M.R. Estimation of forest leaf area index using vegetation indices derived from hyperion hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1355–1362. [Google Scholar] [CrossRef] [Green Version]
- Roy, P.S.; Sharma, K.P.; Jain, A. Stratification of density in dry deciduous forest using satellite remote sensing digital data—An approach based on spectral indices. J. Biosci. 1996, 21, 723–734. [Google Scholar] [CrossRef]
- Rosin, P.L. Unimodal thresholding. Pattern Recognit. 2001, 34, 2083–2096. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from grey-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Soille, P. Morphological Image Analysis-Principles and Applications; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Estrada, F.J.; Jepson, A.D. Quantitative evaluation of a novel image segmentation algorithm. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005. [Google Scholar]





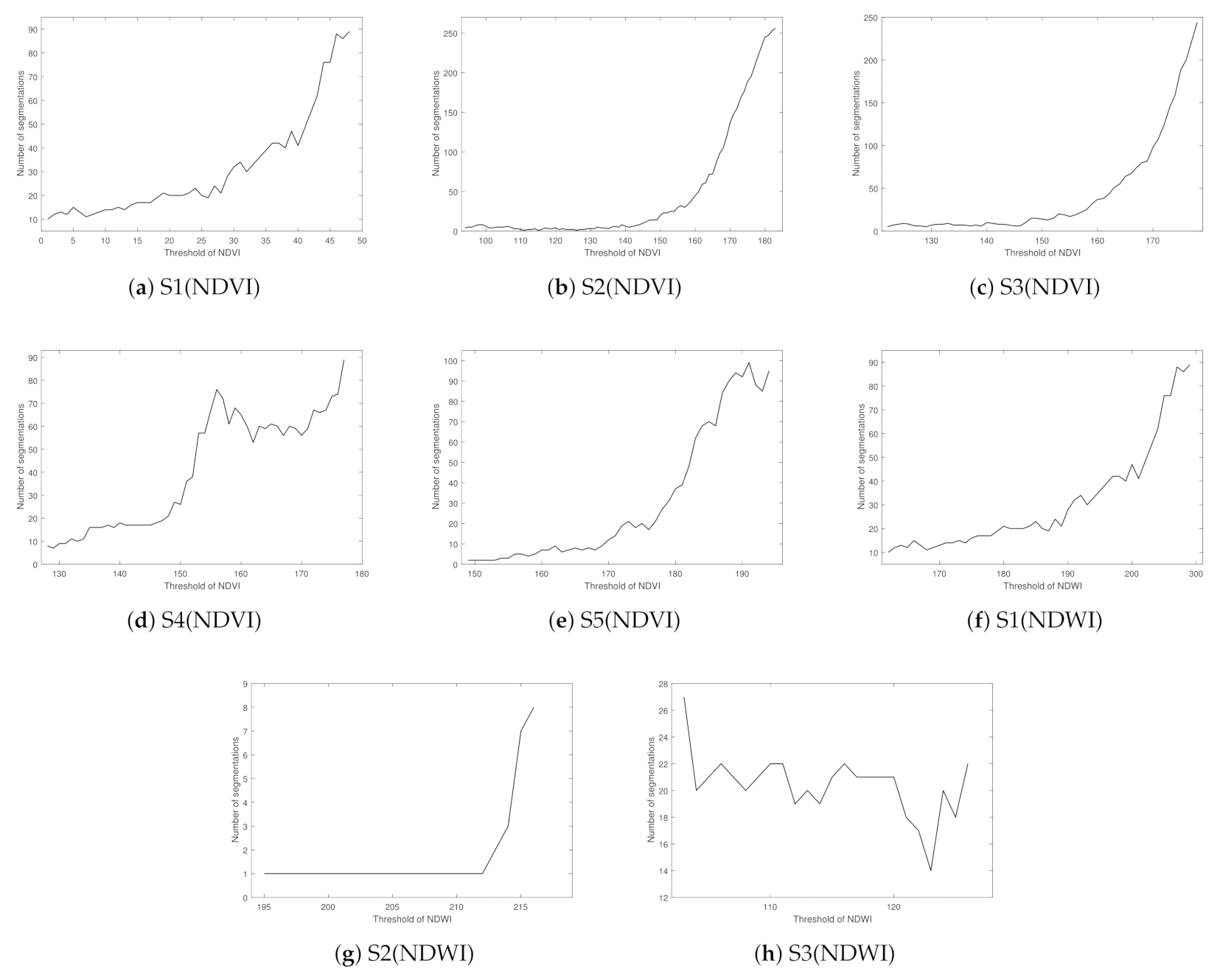




| NDVI | NDWI | |
|---|---|---|
| SI-1 | [161, 189] | [162, 209] |
| SI-2 | [94, 183] | − |
| SI-3 | [122, 178] | [195, 216] |
| SI-4 | [128, 177] | − |
| SI-5 | [149, 194] | [150, 154] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Chen, H.; Cheng, L.; Xiao, J. Variational-Scale Segmentation for Multispectral Remote-Sensing Images Using Spectral Indices. Remote Sens. 2022, 14, 326. https://doi.org/10.3390/rs14020326
Wang K, Chen H, Cheng L, Xiao J. Variational-Scale Segmentation for Multispectral Remote-Sensing Images Using Spectral Indices. Remote Sensing. 2022; 14(2):326. https://doi.org/10.3390/rs14020326
Chicago/Turabian StyleWang, Ke, Hainan Chen, Ligang Cheng, and Jian Xiao. 2022. "Variational-Scale Segmentation for Multispectral Remote-Sensing Images Using Spectral Indices" Remote Sensing 14, no. 2: 326. https://doi.org/10.3390/rs14020326
APA StyleWang, K., Chen, H., Cheng, L., & Xiao, J. (2022). Variational-Scale Segmentation for Multispectral Remote-Sensing Images Using Spectral Indices. Remote Sensing, 14(2), 326. https://doi.org/10.3390/rs14020326





