Research on Co-Channel Interference Cancellation for Underwater Acoustic MIMO Communications
Abstract
1. Introduction
- We propose a novel receiver for underwater acoustic MIMO communication. The proposed receiver consists of channel estimation with CoI cancellation and channel equalization with CoI cancellation.
- In Ref. [29], only two transmitters were considered for underwater acoustic MIMO channel estimation. Without loss of generality, in this paper, we extend the number of transmitters to more than two. Additionally, we analyze the performance of the proposed channel estimation method.
- We compare the difference between the proposed CE-DFE receiver and the traditional DA-DFE receiver in terms of analysis and experimental results. The results demonstrate that the proposed receiver achieves better communication performance, and the proposed receiver is not sensitive to parameters; therefore it provides an alternative to the design of a robust underwater acoustic MIMO MODEM.
2. MIMO System Design with CoI Cancellation
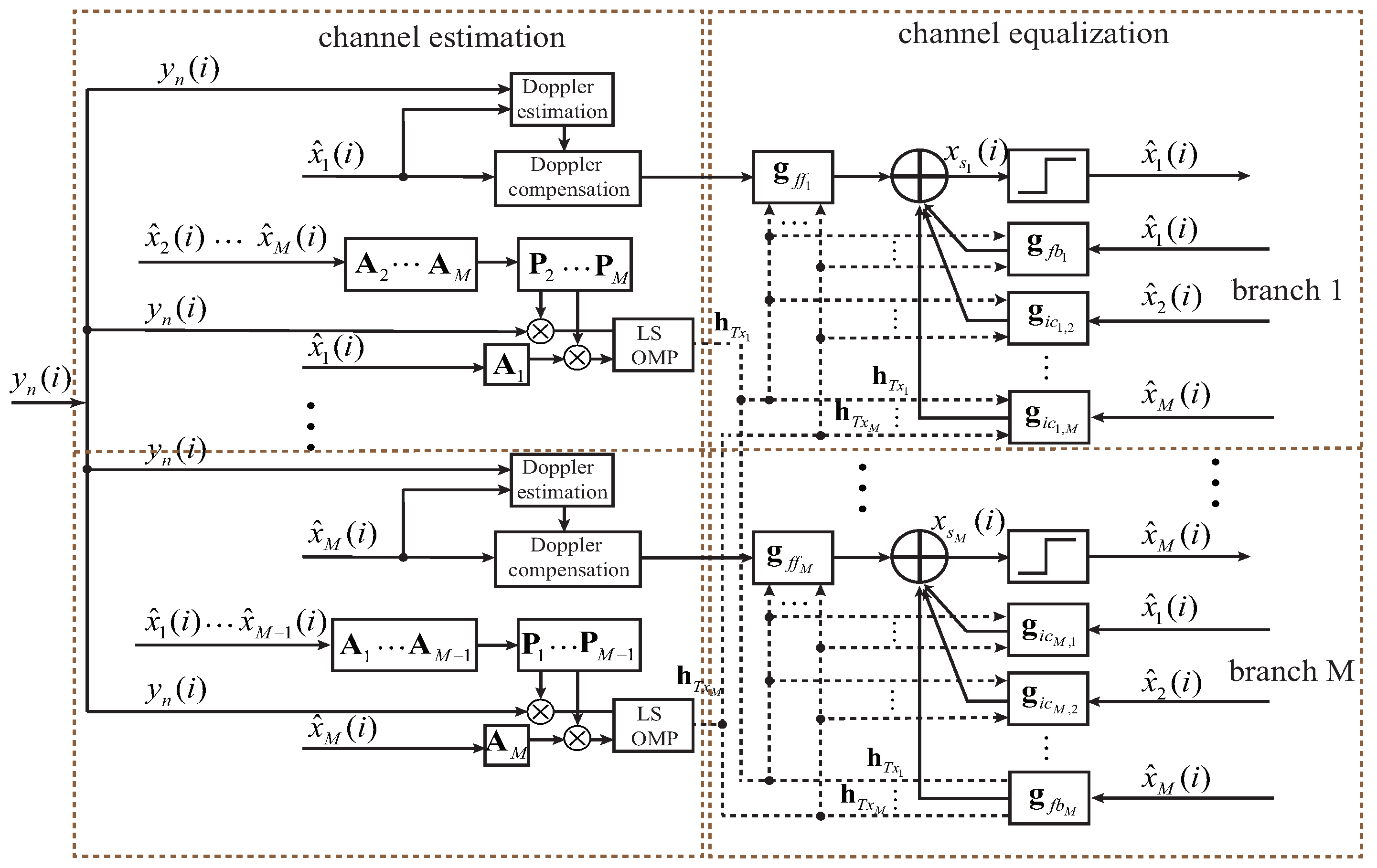
2.1. System Overview
2.2. Projection Based Channel Estimation
2.3. Channel Estimation Based Decision Feedback Equalization with IC
2.4. Performance Analysis
2.5. Computational Complexity Analysis
2.6. Relationship between CE-DFE and DA-DFE
- The biggest difference between the DA-DFE and the proposed CE-DFE is that the DA-DFE uses some criteria, such as least mean square or recursive least square, to train the filters, while the CE-DFE uses channel estimates to measure the filters directly. As the underwater acoustic channel is usually typically sparse, channel estimation can be performed using the compressed sensing method, which needs fewer training sequences, while the DA-DFE needs long sequences to achieve convergence.
- The CE-DFE always performs block by block. It is assumed that, within a data block, the channel is time-invariant, but varied in the next data block. The filters of CE-DFE will not change within one data block. In the decision-directed mode, some periodical training sequences are essential to prevent error propagation, because the decoding symbols are used for Doppler estimation and channel estimation, which may appear as erroneous symbols. Meanwhile, the DA-DFE iterates symbol by symbol, and the DA-DFE filters are updated symbol by symbol; thus, the filters can track the underwater acoustic channel. As a result, the computational complexity of DA-DFE is typically higher than that of CE-DFE, if the filter length relatively large.
- The Doppler estimation and compensation can be performed block by block for CE-DFE, while the DA-DFE utilizes the phase lock loop to track channel variance.
- The CE-DFE has fewer controlling parameters than DA-DFE, and DA-DFE is very sensitive to parameters such as the length of filters, forgotten factor and training length. Therefore, the CE-DFE is more robust to underwater acoustic channel.
3. Experimental Results
3.1. Experimental Setting
- 1
- RLS_DADFE. The receiver can be found in [9]. The filters were obtained by recursive least square.
- 2
- IPNLMS_DADFE. The receiver can be found in [12]. This is an improved normalized least mean square equalizer.
- 3
- 4
- CE_IC+DFE_NoIC. Channel estimation used the proposed channel model, which has the ability to eliminate interference, but channel equalization does not.
- 5
- CE_IC+DFE_NoIC. This is the opposite case to CE_IC+DFE_NoIC. The channel estimation used interference cancellation method, but channel equalization does not.
- 6
- CE_IC+DFE_IC. This is the proposed receiver. Both channel estimation and channel equalization can eliminate interference.
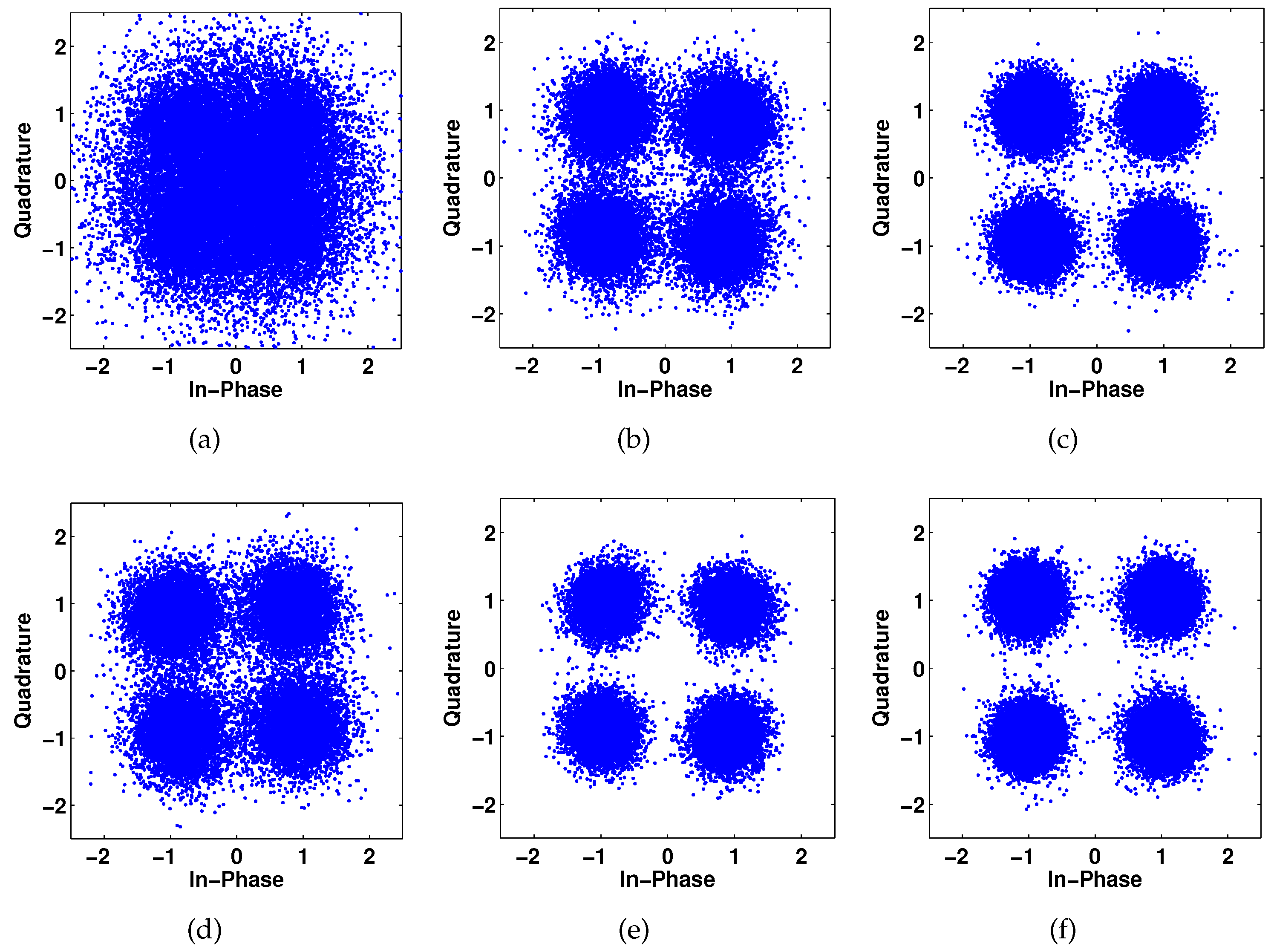
3.2. Results and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of (25)
References
- Dinakaran, R.; Zhang, L.; Li, C.T.; Bouridane, A.; Jiang, R. Robust and Fair Undersea Target Detection with Automated Underwater Vehicles for Biodiversity Data Collection. Remote Sens. 2022, 14, 3680. [Google Scholar] [CrossRef]
- Jiang, W.; Yang, X.; Tong, F.; Yang, Y.; Zhou, T. A Low-Complexity Underwater Acoustic Coherent Communication System for Small AUV. Remote Sens. 2022, 14, 3405. [Google Scholar] [CrossRef]
- Wu, W.; Gao, X.; Sun, C.; Li, G.Y. Shallow Underwater Acoustic Massive MIMO Communications. IEEE Trans. Signal Process. 2021, 69, 1124–1139. [Google Scholar] [CrossRef]
- Li, B.; Huang, J.; Zhou, S.; Ball, K.; Stojanovic, M.; Freitag, L.; Willett, P. MIMO-OFDM for high-rate underwater acoustic communications. IEEE J. Ocean. Eng. 2009, 34, 634–644. [Google Scholar]
- Han, J.; Zhang, L.; Leus, G. Partial FFT demodulation for MIMO-OFDM over time-varying underwater acoustic channels. IEEE Signal Process. Lett. 2015, 23, 282–286. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.R. Bandwidth-efficient frequency-domain equalization for single carrier multiple-input-multiple-output underwater acoustic communications. J. Acoust. Soc. Am. 2010, 128, 2910–2919. [Google Scholar] [CrossRef]
- Wang, L.; Tao, J.; Zheng, Y.R. Single-carrier frequency-domain turbo equalization without cyclic prefix or zero padding for underwater acoustic communications. J. Acoust. Soc. Am. 2012, 132, 3809–3817. [Google Scholar] [CrossRef]
- Yin, J.; Ge, W.; Han, X.; Guo, L. Frequency-domain equalization with interference rejection combining for single carrier multiple-input multiple-output underwater acoustic communications. J. Acoust. Soc. Am. 2020, 147, EL138–EL143. [Google Scholar] [CrossRef]
- Roy, S.; Duman, T.M.; McDonald, V.; Proakis, J.G. High-rate communication for underwater acoustic channels using multiple transmitters and space–time coding: Receiver structures and experimental results. IEEE J. Ocean. Eng. 2007, 32, 663–688. [Google Scholar] [CrossRef]
- Song, A.; Badiey, M. Time reversal multiple-input/multiple-output acoustic communication enhanced by parallel interference cancellation. J. Acoust. Soc. Am. 2012, 131, 281–291. [Google Scholar] [CrossRef]
- Song, A.; Badiey, M.; McDonald, V.K.; Yang, T.C. Time Reversal Receivers for High Data Rate Acoustic Multiple-Input—Multiple-Output Communication. IEEE J. Ocean. Eng. 2011, 36, 525–538. [Google Scholar] [CrossRef]
- Tao, J.; Wu, Y.; Han, X.; Pelekanakis, K. Sparse Direct Adaptive Equalization for Single-Carrier MIMO Underwater Acoustic Communications. IEEE J. Ocean. Eng. 2019, 45, 1622–1631. [Google Scholar] [CrossRef]
- Duan, W.; Tao, J.; Zheng, Y.R. Efficient Adaptive Turbo Equalization for Multiple-Input–Multiple-Output Underwater Acoustic Communications. IEEE J. Ocean. Eng. 2018, 43, 792–804. [Google Scholar] [CrossRef]
- Yang, Z.; Zheng, Y.R. Iterative channel estimation and turbo equalization for multiple-input multiple-output underwater acoustic communications. IEEE J. Ocean. Eng. 2015, 40, 232–242. [Google Scholar]
- Zhang, Y.; Zakharov, Y.V.; Li, J. Soft-decision-driven sparse channel estimation and turbo equalization for MIMO underwater acoustic communications. IEEE Access 2018, 6, 4955–4973. [Google Scholar] [CrossRef]
- Zhou, Y.; Tong, F.; Song, A.; Diamant, R. Exploiting spatial–temporal joint sparsity for underwater acoustic multiple-input–multiple-output communications. IEEE J. Ocean. Eng. 2020, 46, 352–369. [Google Scholar] [CrossRef]
- Ling, J.; Tan, X.; Yardibi, T.; Li, J.; Nordenvaad, M.L.; He, H.; Zhao, K. On Bayesian Channel Estimation and FFT-Based Symbol Detection in MIMO Underwater Acoustic Communications. IEEE J. Ocean. Eng. 2013, 39, 59–73. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Jiang, W.H.; Tong, F.; Zhang, G.Q. Exploiting joint sparsity for underwater acoustic MIMO communications. Appl. Acoust. 2017, 116, 357–363. [Google Scholar] [CrossRef]
- Stojanovic, M.; Catipovic, J.A.; Proakis, J.G. Phase-coherent digital communications for underwater acoustic channels. IEEE J. Ocean. Eng. 1994, 19, 100–111. [Google Scholar] [CrossRef]
- Song, A.; Abdi, A.; Badiey, M.; Hursky, P. Experimental demonstration of underwater acoustic communication by vector sensors. IEEE J. Ocean. Eng. 2011, 36, 454–461. [Google Scholar] [CrossRef]
- Yang, T.C. Relating the performance of time-reversal-based underwater acoustic communications in different shallow water environments. J. Acoust. Soc. Am. 2011, 130, 1995–2002. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Hovem, J.M.; Dong, H.; Liu, L. Coherent underwater communication using passive time reversal over multipath channels. Appl. Acoust. 2011, 72, 412–419. [Google Scholar] [CrossRef]
- Zhou, Y.; Song, A.; Tong, F.; Kastner, R. Distributed compressed sensing based channel estimation for underwater acoustic multiband transmissions. J. Acoust. Soc. Am. 2018, 143, 3985–3996. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Preisig, J.C. Estimation of rapidly time-varying sparse channels. IEEE J. Ocean. Eng. 2007, 32, 927–939. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Yan, S.; Shi, W.; Yang, X.; Guo, Y.; Gulliver, T.A. A novel underwater acoustic signal denoising algorithm for Gaussian/non-Gaussian impulsive noise. IEEE Trans. Veh. Technol. 2020, 70, 429–445. [Google Scholar] [CrossRef]
- Wang, S.; He, Z.; Niu, K.; Chen, P.; Rong, Y. New results on joint channel and impulsive noise estimation and tracking in underwater acoustic OFDM systems. IEEE Trans. Wirel. Commun. 2020, 19, 2601–2612. [Google Scholar] [CrossRef]
- Kuai, X.; Sun, H.; Zhou, S.; Cheng, E. Impulsive noise mitigation in underwater acoustic OFDM systems. IEEE Trans. Veh. Technol. 2016, 65, 8190–8202. [Google Scholar] [CrossRef]
- Chen, P.; Rong, Y.; Nordholm, S.; He, Z.; Duncan, A.J. Joint channel estimation and impulsive noise mitigation in underwater acoustic OFDM communication systems. IEEE Trans. Wirel. Commun. 2017, 16, 6165–6178. [Google Scholar] [CrossRef]
- Zhou, Y.; Diamant, R. A parallel decoding approach for mitigating near–far interference in internet of underwater things. IEEE Internet Things J. 2020, 7, 9747–9759. [Google Scholar] [CrossRef]
- Preisig, J.C. Performance analysis of adaptive equalization for coherent acoustic communications in the time-varying ocean environment. J. Acoust. Soc. Am. 2005, 118, 263–278. [Google Scholar] [CrossRef]
- Paige, C.C. and Saunders, M.A. LSQR: An algorithm for sparse linear equations and sparse least squares. ACM Trans. Math. Softw. 1982, 8, 43–71. [Google Scholar] [CrossRef]






| Methods | Limitations |
|---|---|
| frequency domain equalization [6,7,8] | In [6,8], CP or ZP are needed to prevent inter-block interference, thus degrading the bandwidth efficiency. In [7], if the reconstructed CoI is not correct, the error will propagate to the next iteration. |
| DA-DFE in [9,10,11,12] | Sensitive to parameters, and need long sequences to achieve convergence. |
| turbo and/or MMSE in [13,14,15] | Several iterations increase the computational complexity of turbo equalization, and the computation complexity of MMSE is exponential compared to the number of transmitters |
| CE-DFE in [16] | The channel estimation does not perform interference cancellation; the equalizers’ filter contains much noise. |
| Parameters | Value |
|---|---|
| Sampling frequency | 96,000 symbols/s |
| Bandwidth | 3200 symbols/s |
| Constellation Mapping | QPSK |
| = 18.7 ms | = 62.5 ms | |
|---|---|---|
| CE_IC+DFE_IC | 80.41 s | 80.78 s |
| RLS_DADFE | 45.85 s | 4408.8 s |
| IPNLMS_DADFE | 4.05 s | 25.70 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Tong, F.; Yang, X. Research on Co-Channel Interference Cancellation for Underwater Acoustic MIMO Communications. Remote Sens. 2022, 14, 5049. https://doi.org/10.3390/rs14195049
Zhou Y, Tong F, Yang X. Research on Co-Channel Interference Cancellation for Underwater Acoustic MIMO Communications. Remote Sensing. 2022; 14(19):5049. https://doi.org/10.3390/rs14195049
Chicago/Turabian StyleZhou, Yuehai, Feng Tong, and Xiaoyu Yang. 2022. "Research on Co-Channel Interference Cancellation for Underwater Acoustic MIMO Communications" Remote Sensing 14, no. 19: 5049. https://doi.org/10.3390/rs14195049
APA StyleZhou, Y., Tong, F., & Yang, X. (2022). Research on Co-Channel Interference Cancellation for Underwater Acoustic MIMO Communications. Remote Sensing, 14(19), 5049. https://doi.org/10.3390/rs14195049









