Evaluation of Real-time Precise Point Positioning with Ambiguity Resolution Based on Multi-GNSS OSB Products from CNES
Abstract
1. Introduction
2. Methodology
2.1. Dual-frequency Ionosphere-Free PPP Model
2.2. Method for Recovering the Integer Feature of Ambiguity
2.3. PPP-AR Process
3. Real-Time PPP-AR Performance
3.1. Data and Strategy
3.2. Quality Analysis of Phase Bias
3.3. Distribution of Ambiguity Residuals Using OSB Products
3.4. Performance Analysis of PPP-AR
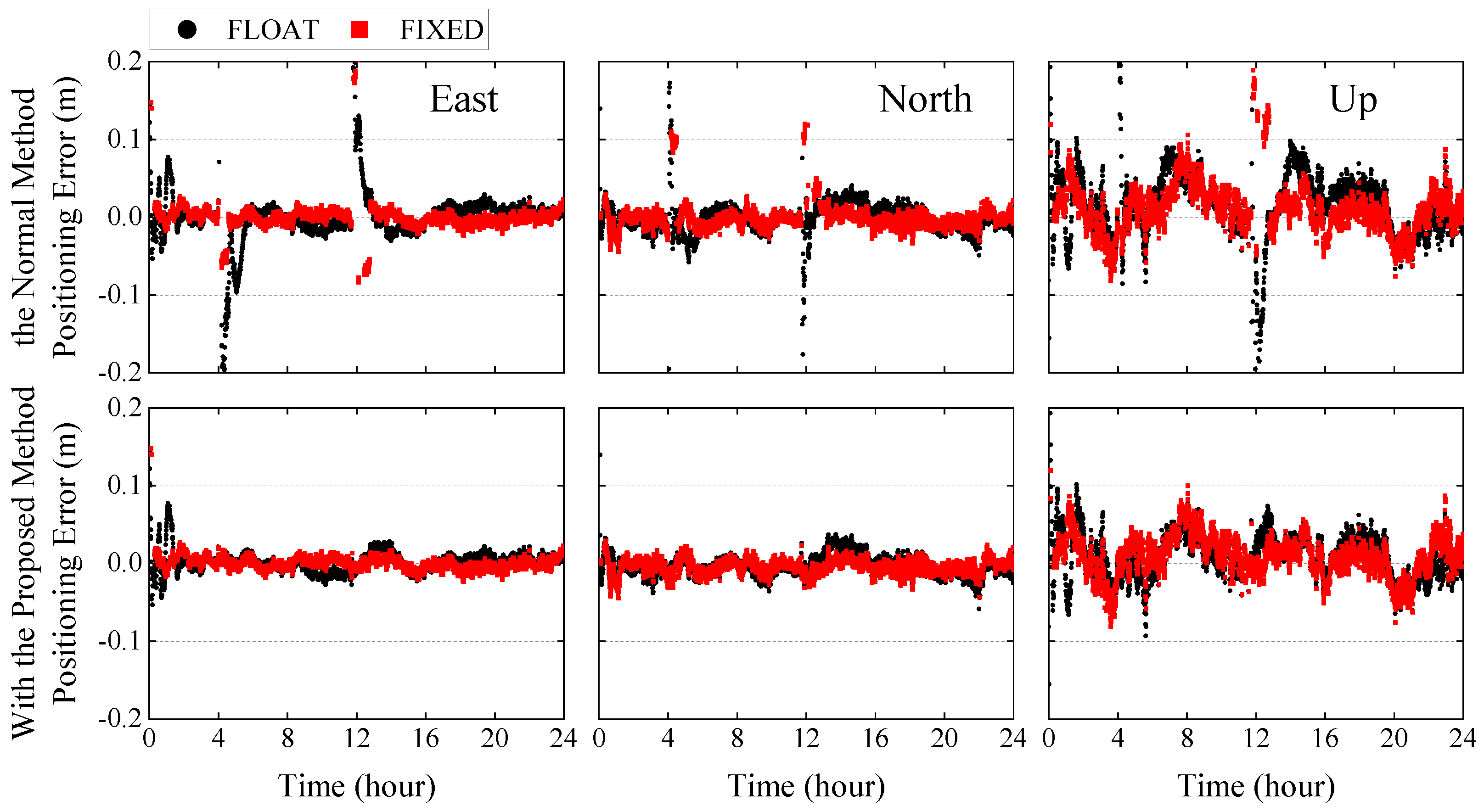
3.5. Dealing with the Missing Phase Bias
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. J. Geophys. Res. Soild Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Mercier, F.; Laurichesse, D. Zero-difference ambiguity blocking, Properties of satellite/receiver widelane biases. In Proceedings of the ENC-GNSS 2008, Toulouse, France, 23–25 April 2008. [Google Scholar]
- Laurichesse, D.; Mercier, F.; Berthias, J.-P.; Broca, P.; Cerri, L. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination. Navigation 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Collins, P.; Lahaye, F.; Héroux, P.; Bisnath, S. Precise Point Positioning with Ambiguity Resolution using the Decoupled Clock Model. In Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008; pp. 1315–1322. [Google Scholar]
- Collins, P.; Bisnath, S.; Lahaye, F.; Héroux, P. Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing. Navigation 2010, 57, 123–135. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef]
- Shi, J.; Gao, Y. A comparison of three PPP integer ambiguity resolution methods. GPS Solut. 2014, 18, 519–528. [Google Scholar] [CrossRef]
- Wang, J.; Huang, G.; Zhang, Q.; Gao, Y.; Gao, Y.; Luo, Y. GPS/BDS-2/Galileo Precise Point Positioning Ambiguity Resolution Based on the Uncombined Model. Remote Sens. 2020, 12, 1853. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, J.; Liu, S.; Tao, J.; Hu, Z.; Chen, G. A variant of raw observation approach for BDS/GNSS precise point positioning with fast integer ambiguity resolution. Satell. Navig. 2021, 2, 29. [Google Scholar] [CrossRef]
- Chen, C.; Xiao, G.; Chang, G.; Xu, T.; Yang, L. Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution Using Products from Different Analysis Centers. Remote Sens. 2021, 13, 3266. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, K. Performance Analysis of Precise Point Positioning Using Rea-Time Orbit and Clock Products. J. Glob. Position. Syst. 2004, 3, 95–100. [Google Scholar] [CrossRef]
- Capilla, R.M.; Berné-Valero, J.L.; Hermosilla-Rodrigo, A. Impact of multi-constellation products and ambiguity resolution in Precise Point Positioning for real-time measurements. Measurement 2017, 100, 183–193. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Wang, L.; Wang, X.; Yuan, H. Assessment of Multiple GNSS Real-Time SSR Products from Different Analysis Centers. ISPRS Int. J. Geo-Inf. 2018, 7, 85. [Google Scholar] [CrossRef]
- Alkan, R.M.; Erol, S.; İlçi, V.; Ozulu, İ.M. Comparative analysis of real-time kinematic and PPP techniques in dynamic environment. Measurement 2020, 163, 107995. [Google Scholar] [CrossRef]
- Zhao, X.; Ge, Y.; Ke, F.; Liu, C.; Li, F. Investigation of real-time kinematic multi-GNSS precise point positioning with the CNES products. Measurement 2020, 166, 108231. [Google Scholar] [CrossRef]
- Bulbul, S.; Bilgen, B.; Inal, C. The performance assessment of Precise Point Positioning (PPP) under various observation conditions. Measurement 2021, 171, 108780. [Google Scholar] [CrossRef]
- Ge, Y.; Chen, S.; Wu, T.; Fan, C.; Qin, W.; Zhou, F.; Yang, X. An analysis of BDS-3 real-time PPP: Time transfer, positioning, and tropospheric delay retrieval. Measurement 2021, 172, 108871. [Google Scholar] [CrossRef]
- Li, B.; Ge, H.; Bu, Y.; Zheng, Y.; Yuan, L. Comprehensive assessment of real-time precise products from IGS analysis centers. Satell. Navig. 2022, 3, 12. [Google Scholar] [CrossRef]
- El-Mowafy, A.; Deo, M.; Kubo, N. Maintaining real-time precise point positioning during outages of orbit and clock corrections. GPS Solut. 2017, 21, 937–947. [Google Scholar] [CrossRef]
- Fu, W.; Yang, Y.; Zhang, Q.; Huang, G. Real-time estimation of BDS/GPS high-rate satellite clock offsets using sequential least squares. Adv. Space Res. 2018, 62, 477–487. [Google Scholar] [CrossRef]
- Xie, W.; Huang, G.; Fu, W.; Li, P.; Cui, B. An efficient clock offset datum switching compensation method for BDS real-time satellite clock offset estimation. Adv. Space Res. 2021, 68, 1802–1813. [Google Scholar] [CrossRef]
- Fu, W.; Wang, L.; Chen, R.; Han, Y.; Zhou, H.; Li, T. Combined BDS-2/BDS-3 real-time satellite clock estimation with the overlapping B1I/B3I signals. Adv. Space Res. 2021, 68, 4470–4483. [Google Scholar] [CrossRef]
- Defraigne, P.; Bruyninx, C. On the link between GPS pseudorange noise and day-boundary discontinuities in geodetic time transfer solutions. GPS Solut. 2007, 11, 239–249. [Google Scholar] [CrossRef]
- Fu, W.; Huang, G.; Zhang, Q.; Gu, S.; Ge, M.; Schuh, H. Multi-GNSS real-time clock estimation using sequential least square adjustment with online quality control. J. Geod. 2019, 93, 963–976. [Google Scholar] [CrossRef]
- Laurichesse, D.; Langley, R. Handling the biases for improved triple frequency PPP convergence. In Proceedings of the GPS World 2015, Cleveland, OH, USA, 26 April 2015. [Google Scholar]
- Liu, T.; Chen, H.; Chen, Q.; Jiang, W.; Laurichesse, D.; An, X.; Geng, T. Characteristics of phase bias from CNES and its application in multi-frequency and multi-GNSS precise point positioning with ambiguity resolution. GPS Solut. 2021, 25, 58. [Google Scholar] [CrossRef]
- Shu, B.; Liu, H.; Wang, L.; Huang, G.; Zhang, Q.; Yang, Z. Performance improvement of real-time PPP ambiguity resolution using a regional integer clock. Adv. Space Res. 2021, 67, 1623–1637. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J.; Wang, C.; Zhang, Q. Satellite antenna phase center errors: Magnified threat to multi-frequency PPP ambiguity resolution. J. Geod. 2021, 95, 72. [Google Scholar] [CrossRef]
- Geng, J.; Yang, S.; Guo, J. Assessing IGS GPS/Galileo/BDS-2/BDS-3 phase bias products with PRIDE PPP-AR. Satell. Navig. 2021, 2, 17. [Google Scholar] [CrossRef]
- Shu, B.; Liu, H.; Xu, L.; Gong, X.; Qian, C.; Zhang, M.; Zhang, R. Analysis of satellite-induced factors affecting the accuracy of the BDS satellite differential code bias. GPS Solut. 2017, 21, 905–916. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Distributional Theory for the DIA Method. J. Geod. 2018, 92, 59–80. [Google Scholar] [CrossRef]
- Yang, L.; Shen, Y.; Li, B.; Rizos, C. Simplified Algebraic Estimation for the Quality Control of DIA Estimator. J. Geod. 2021, 95, 14. [Google Scholar] [CrossRef]
- Xie, W.; Huang, G.; Fu, W.; Shu, B.; Cui, B.; Li, M.; Yue, F. A Quality Control Method Based on Improved IQR for Estimating Multi-GNSS Real-Time Satellite Clock Offset. Measurement 2022, 201, 111695. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undiferenced and uncombined observations. GPS Solut. 2018, 22, 33. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the Theory of Atmospheric Refraction. J. Geod. 1972, 105, 279–298. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, H.; Gao, Y.; Yao, Y.; Xu, C. Evaluation and analysis of real-time precise orbits and clocks products from different IGS analysis centers. Adv. Space Res. 2018, 61, 2942–2954. [Google Scholar] [CrossRef]
- Ouyang, C.; Shi, J.; Huang, Y.; Guo, J.; Xu, C. Evaluation of BDS-2 real-time orbit and clock corrections from four IGS analysis centers. Measurement 2021, 168, 108441. [Google Scholar] [CrossRef]
- Li, X.; Liu, G.; Li, X.; Zhou, F.; Feng, G.; Yuan, Y.; Zhang, K. Galileo PPP rapid ambiguity resolution with fve-frequency observations. GPS Solut. 2020, 24, 24. [Google Scholar] [CrossRef]
- Wang, J.; Huang, G.; Yang, Y.; Zhang, Q.; Gao, Y.; Xiao, G. FCB estimation with three different PPP models: Equivalence analysis and experiment tests. GPS Solut. 2019, 23, 93. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Q.; Huang, G. Estimation of fractional cycle bias for GPS/BDS-2/Galileo based on international GNSS monitoring and assessment system observations using the uncombined PPP model. Satell. Navig. 2021, 2, 9. [Google Scholar] [CrossRef]
- Laurichesse, D. Phase Biases Estimation for Undifferenced Ambiguity Resolution. In Proceedings of the PPP-RTK & Open Standards Symposium, Toulouse, France, 12–13 March 2012. [Google Scholar]
- Banville, S.; Geng, J.; Loyer, S.; Schaer, S.; Springer, T.; Strasser, S. On the Interoperability of IGS Products for Precise Point Positioning with Ambiguity Resolution. J. Geod. 2020, 94, 10. [Google Scholar] [CrossRef]
- Li, Y.; Gao, Y.; Li, B. An Impact Analysis of Arc Length on Orbit Prediction and Clock Estimation for PPP Ambiguity Resolution. GPS Solut. 2015, 19, 201–213. [Google Scholar] [CrossRef]
- Kazmierski, K.; Sośnica, K.; Hadas, T. Quality Assessment of Multi-GNSS Orbits and Clocks for Real-Time Precise Point Positioning. GPS Solut. 2018, 22, 11. [Google Scholar] [CrossRef]
- Fujita, S.; Sato, Y.; Miya, M.; Ota, K.; Hirokawa, R.; Takiguchi, J. Design of Integrity Function on Centimeter Level Augmentation Service (CLAS) in Japanese Quasi-Zenith Satellite System. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 3258–3263. [Google Scholar]
- Weinbach, U.; Brandl, M.; Chen, X.; Landau, H.; Pastor, F.; Reussner, N.; Rodriguez-Solano, C. Integrity of the Trimble CenterPoint RTX Correction Service. In Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2018), Miami, Florida, 24–28 September 2018; pp. 1902–1909. [Google Scholar]
- Shu, B.; Liu, H.; Feng, Y.; Xu, L.; Qian, C.; Yang, Z. Analysis of Factors Affecting Asynchronous RTK Positioning with GNSS Signals. Remote Sens. 2019, 11, 1256. [Google Scholar] [CrossRef]
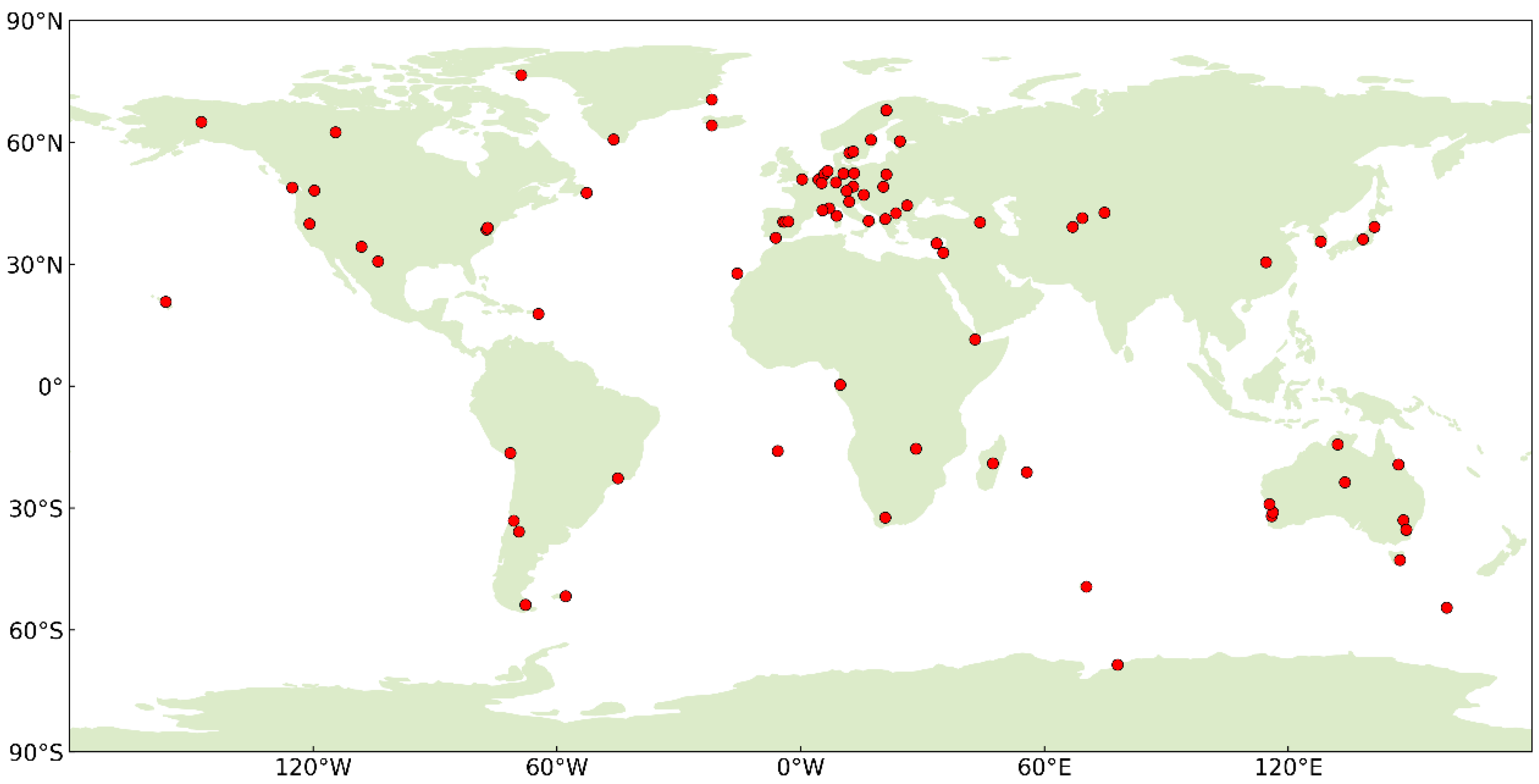
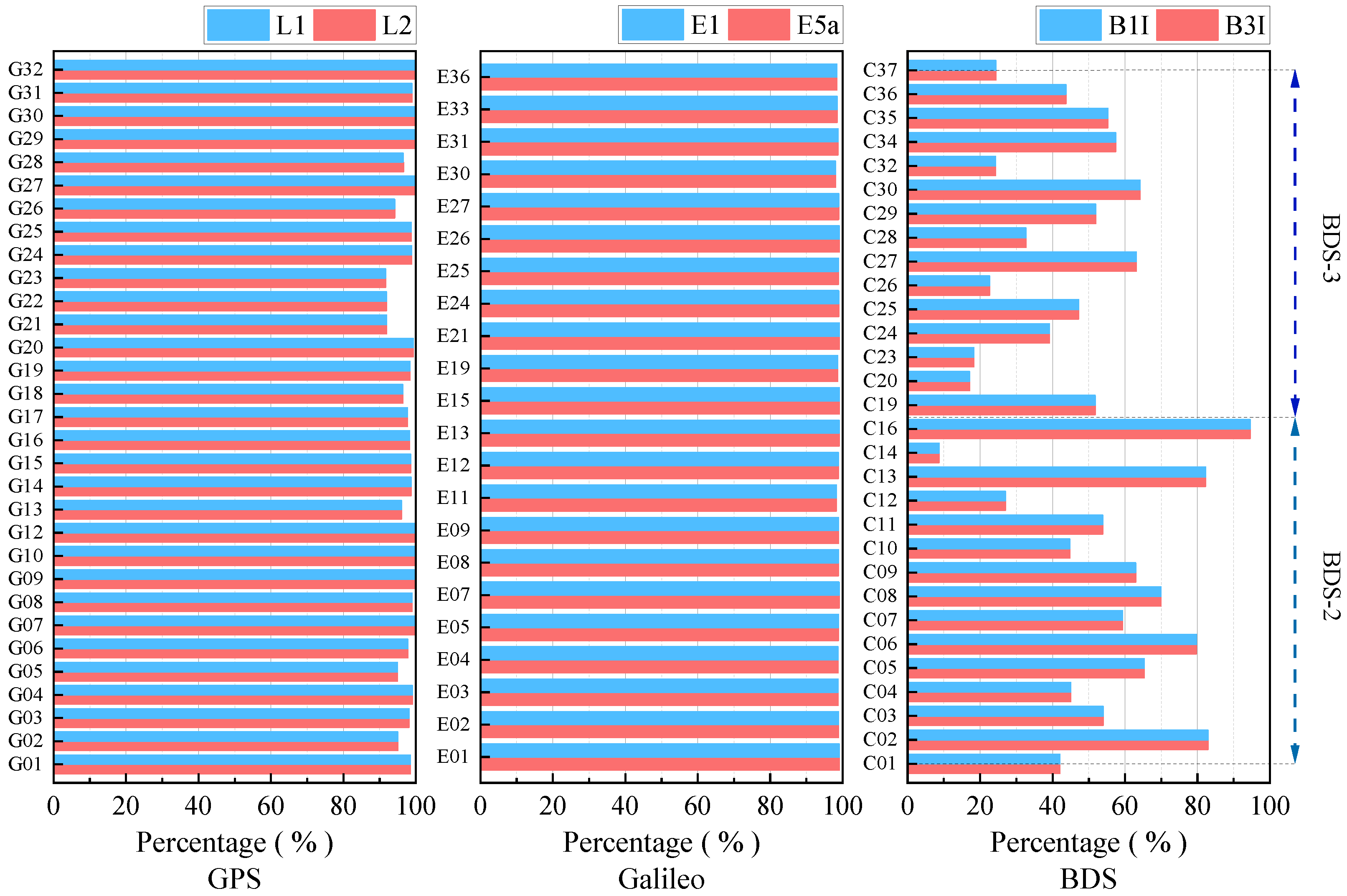
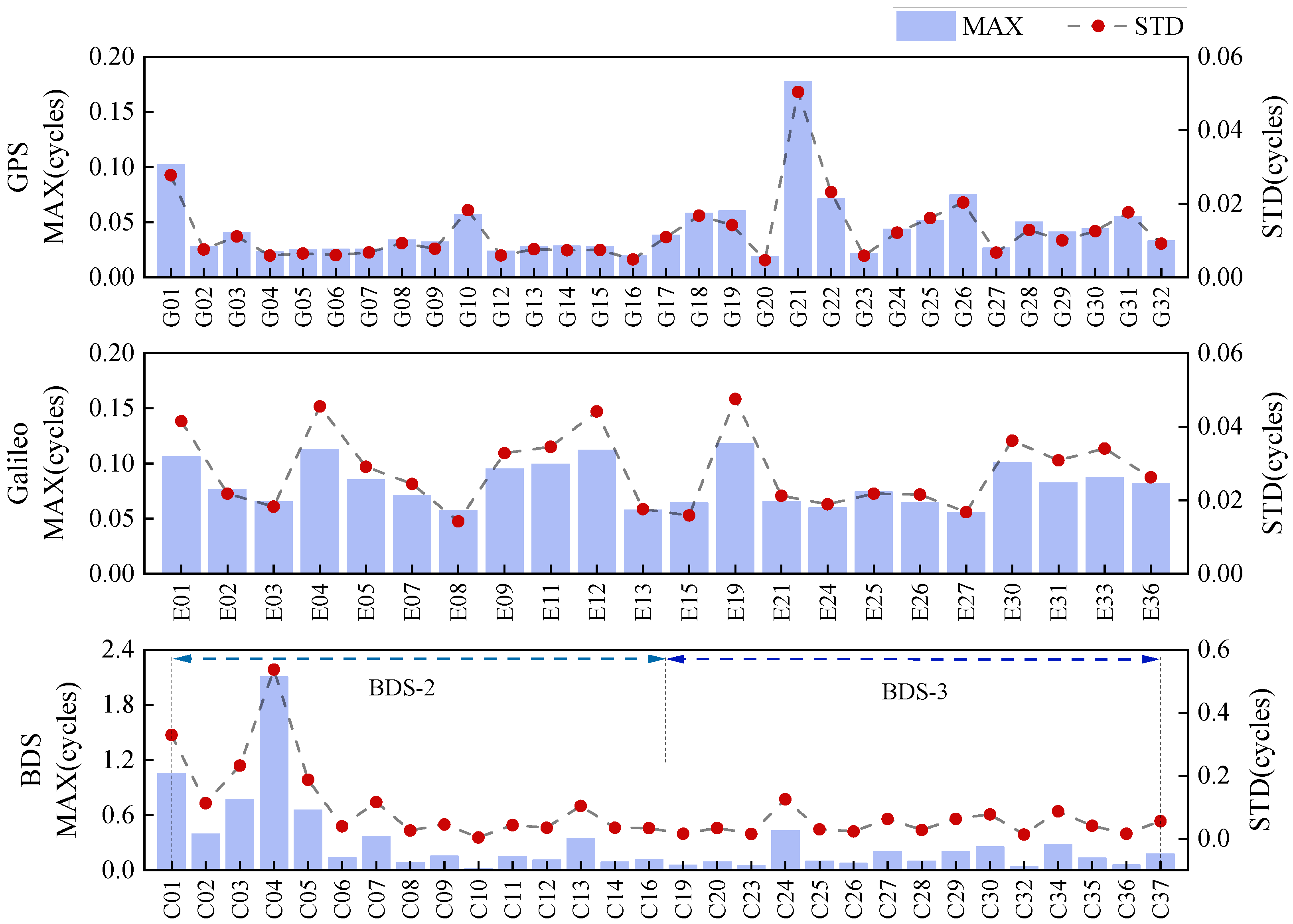
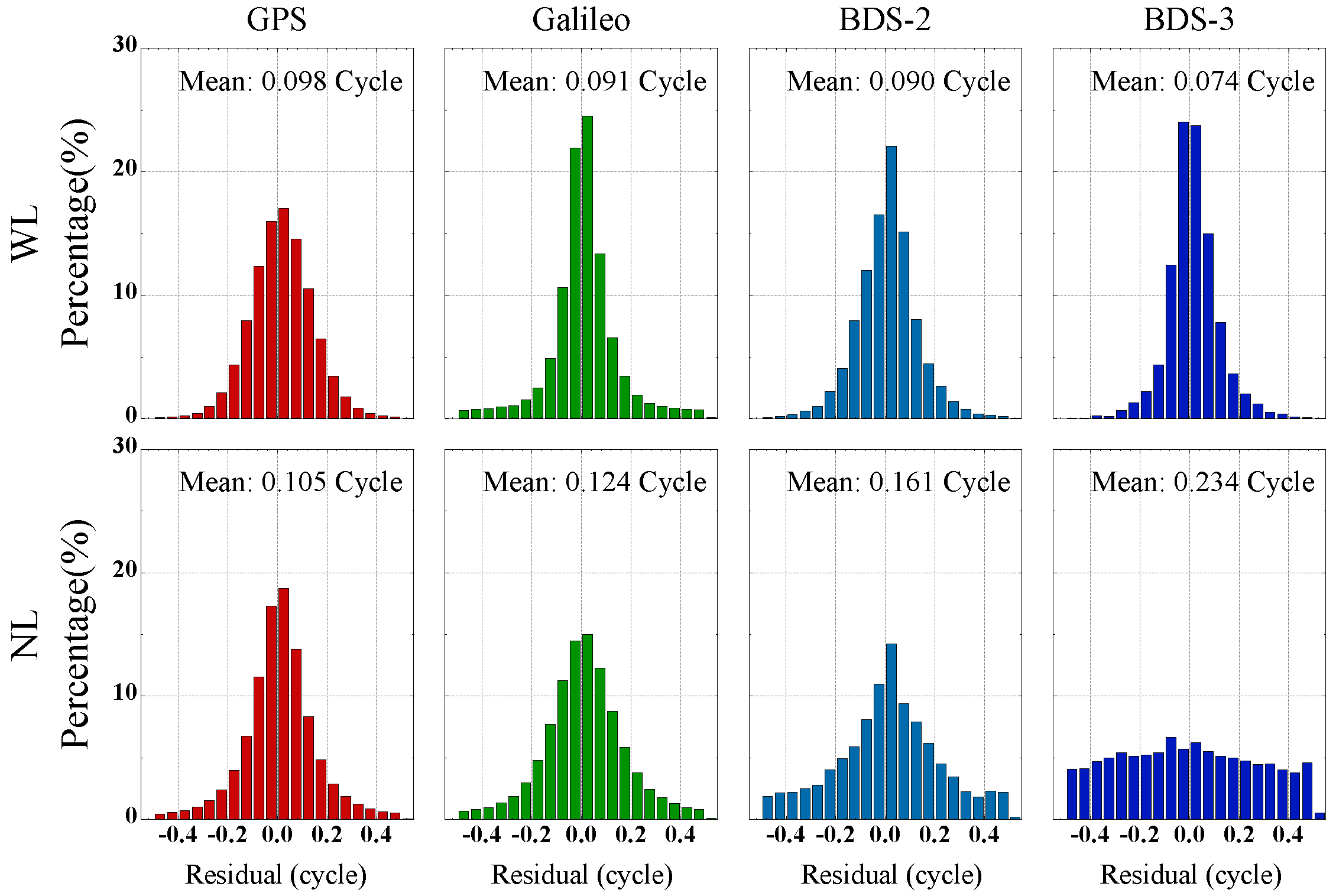


| System | Frequency Number | Frequency Type | Code Bias | Phase Bias |
|---|---|---|---|---|
| GPS | 1 | L1 | C1C C1P C1W | L1C |
| 2 | L2 | C2C C2S C2L C2X C2W | L2W | |
| GLONASS | 1 | G1 | C1C C1P | |
| 2 | G2 | C2C C2P | ||
| Galileo | 1 | E1 | C1C | L1C |
| 2 | E5a | C5Q | L5Q | |
| BDS | 1 | B1I | C2I | L2I |
| 2 | B3I | C6I | L6I |
| Parameter | Configurations |
|---|---|
| Estimator | Extended Kalman filter |
| Observations model | Ionosphere-free combinations |
| Frequency | GPS: L1/L2 Galileo: E1/E5a BDS: B1I/B3I |
| Observation weighting | 0.3 m and 0.003 m for GPS/Galileo/BDS code and phase, respectively |
| Sampling rate and cutoff angle | 30 s and 7° |
| Orbits and clocks | Real-time products from CNES |
| Code and phase biases | Corrected with the OSB products from CNES |
| Station coordinate | Kinematic mode: white noise Static mode: constant |
| Receiver clock | Estimated as white noise for each system |
| Tropospheric delay | A priori troposphere delay: Saastamoinen model [36] Zenith wet tropospheric delay: estimated as a random walk |
| AR validation | Bootstrapping success rate threshold: 95% Ratio test threshold: 2.0 |
| System | Frequency 1 | Frequency 2 |
|---|---|---|
| GPS | 97.6% | 97.6% |
| Galileo | 98.8% | 98.8% |
| BDS | 49.5% | 49.5% |
| System (Units: Cycles) | Frequency 1 | Frequency 2 | ||
|---|---|---|---|---|
| MAX | STD | MAX | STD | |
| GPS | 0.045 | 0.012 | 0.045 | 0.012 |
| Galileo | 0.081 | 0.028 | 0.083 | 0.028 |
| BDS | 0.292 | 0.085 | 0.293 | 0.085 |
| System | WL | NL | ||
|---|---|---|---|---|
| With ± 0.15 | With ± 0.25 | With ± 0.15 | With ± 0.25 | |
| GPS | 82.8% | 95.8% | 80.4% | 92.1% |
| Galileo | 84.3% | 92.3% | 74.3% | 88.7% |
| BDS-2 | 85.7% | 95.9% | 61.5% | 79.0% |
| BDS-3 | 89.3% | 97.2% | 39.8% | 60.1% |
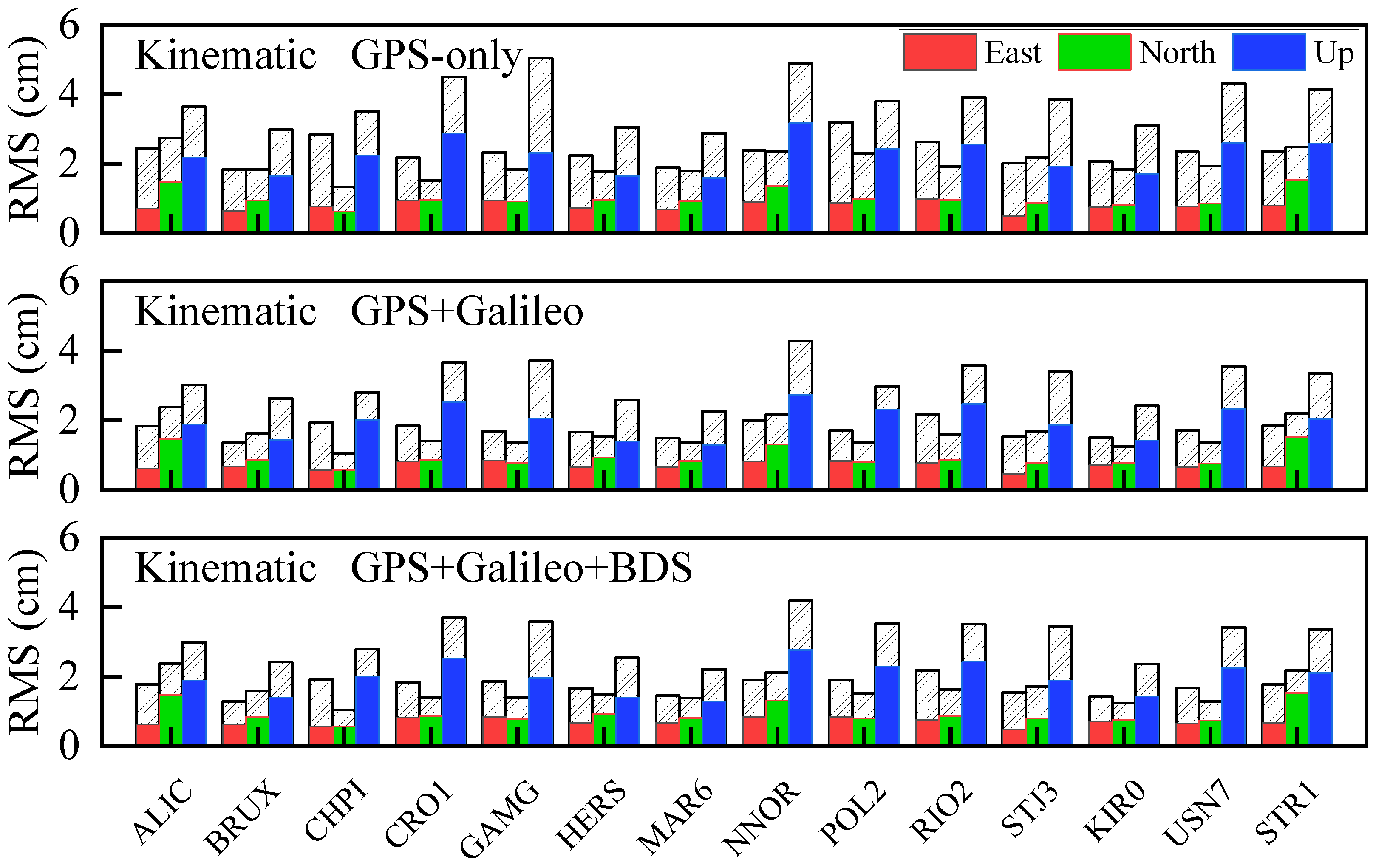
| Mode | System | Float (cm) | Fixed (cm) | Fixed Rate | ||||
|---|---|---|---|---|---|---|---|---|
| E | N | U | E | N | U | |||
| Kinematic | G | 2.44 | 2.03 | 4.13 | 1.15 (53%) | 1.38 (32%) | 3.14 (24%) | 97.8% |
| GE | 1.90 | 1.64 | 3.46 | 1.06 (44%) | 1.27 (23%) | 2.85 (17%) | 98.5% | |
| GEC | 1.89 | 1.64 | 3.43 | 1.06 (44%) | 1.27 (22%) | 2.85 (17%) | 98.3% | |
| Static | G | 1.42 | 1.14 | 1.73 | 0.79 (44%) | 0.95 (16%) | 1.48 (15%) | 98.8% |
| GE | 1.18 | 1.09 | 1.61 | 0.78 (34%) | 0.94 (14%) | 1.42 (12%) | 98.7% | |
| GEC | 1.18 | 1.09 | 1.59 | 0.77 (34%) | 0.94 (14%) | 1.41 (11%) | 98.3% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, S.; Shu, B.; Xie, W.; Huang, G.; Ge, Y.; Li, P. Evaluation of Real-time Precise Point Positioning with Ambiguity Resolution Based on Multi-GNSS OSB Products from CNES. Remote Sens. 2022, 14, 4970. https://doi.org/10.3390/rs14194970
Du S, Shu B, Xie W, Huang G, Ge Y, Li P. Evaluation of Real-time Precise Point Positioning with Ambiguity Resolution Based on Multi-GNSS OSB Products from CNES. Remote Sensing. 2022; 14(19):4970. https://doi.org/10.3390/rs14194970
Chicago/Turabian StyleDu, Shi, Bao Shu, Wei Xie, Guanwen Huang, Yulong Ge, and Pan Li. 2022. "Evaluation of Real-time Precise Point Positioning with Ambiguity Resolution Based on Multi-GNSS OSB Products from CNES" Remote Sensing 14, no. 19: 4970. https://doi.org/10.3390/rs14194970
APA StyleDu, S., Shu, B., Xie, W., Huang, G., Ge, Y., & Li, P. (2022). Evaluation of Real-time Precise Point Positioning with Ambiguity Resolution Based on Multi-GNSS OSB Products from CNES. Remote Sensing, 14(19), 4970. https://doi.org/10.3390/rs14194970






