Using UAV to Identify the Optimal Vegetation Index for Yield Prediction of Oil Seed Rape (Brassica napus L.) at the Flowering Stage
Abstract
1. Introduction
2. Materials and Methods
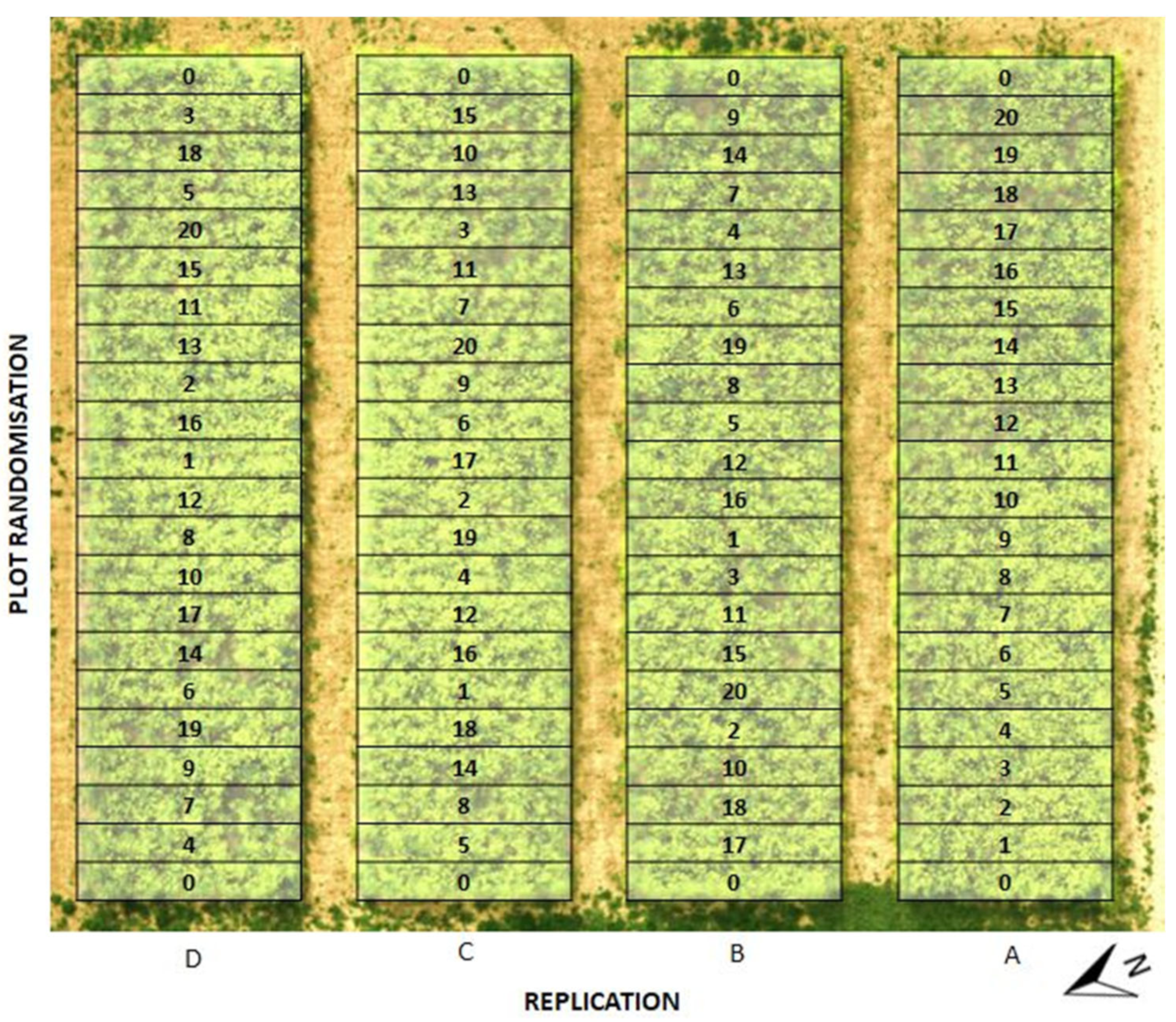
2.1. Field Experiment Localization
2.2. Establishment and Harvest of the Experiment
2.3. Vegetation Indices
2.4. Weather Conditions in 2019–2020
2.5. Statistical Analysis—Data Treatment
3. Results and Discussion
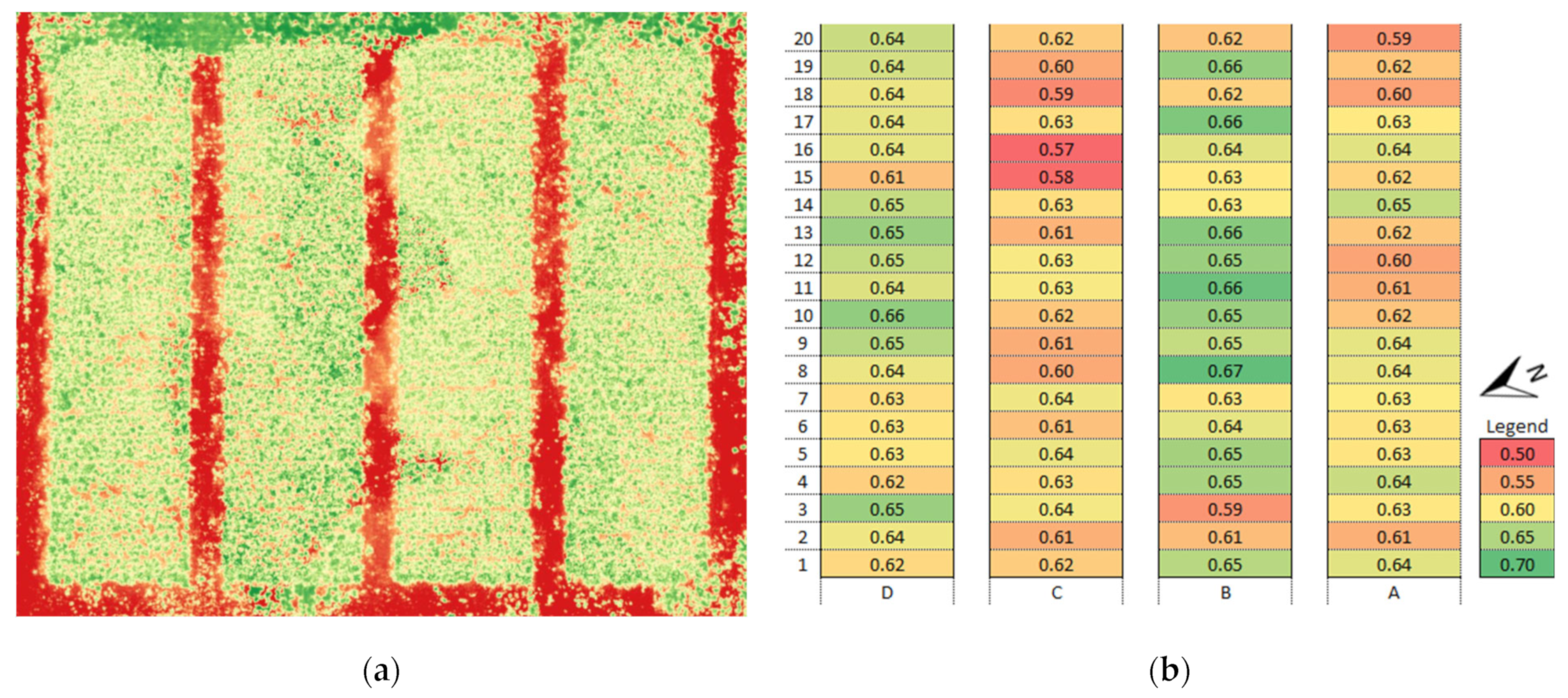
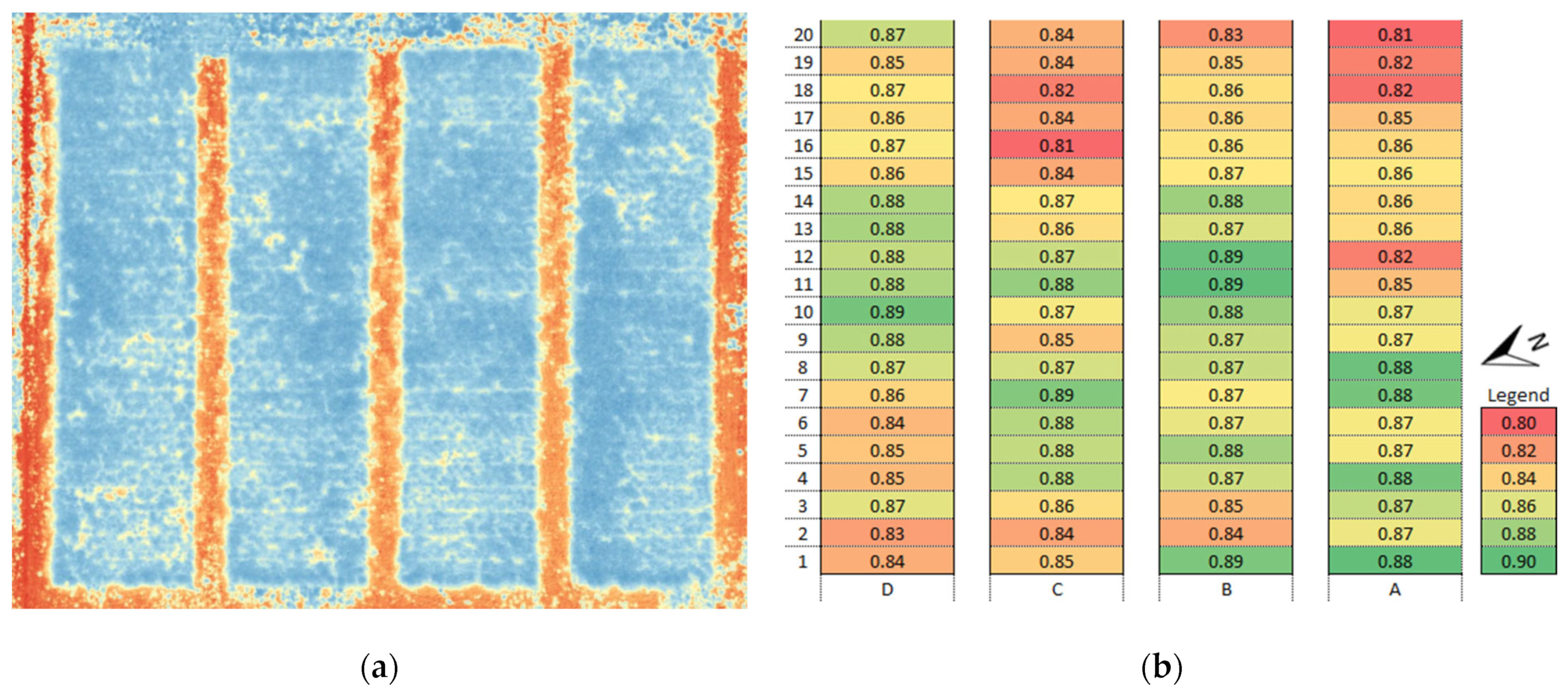
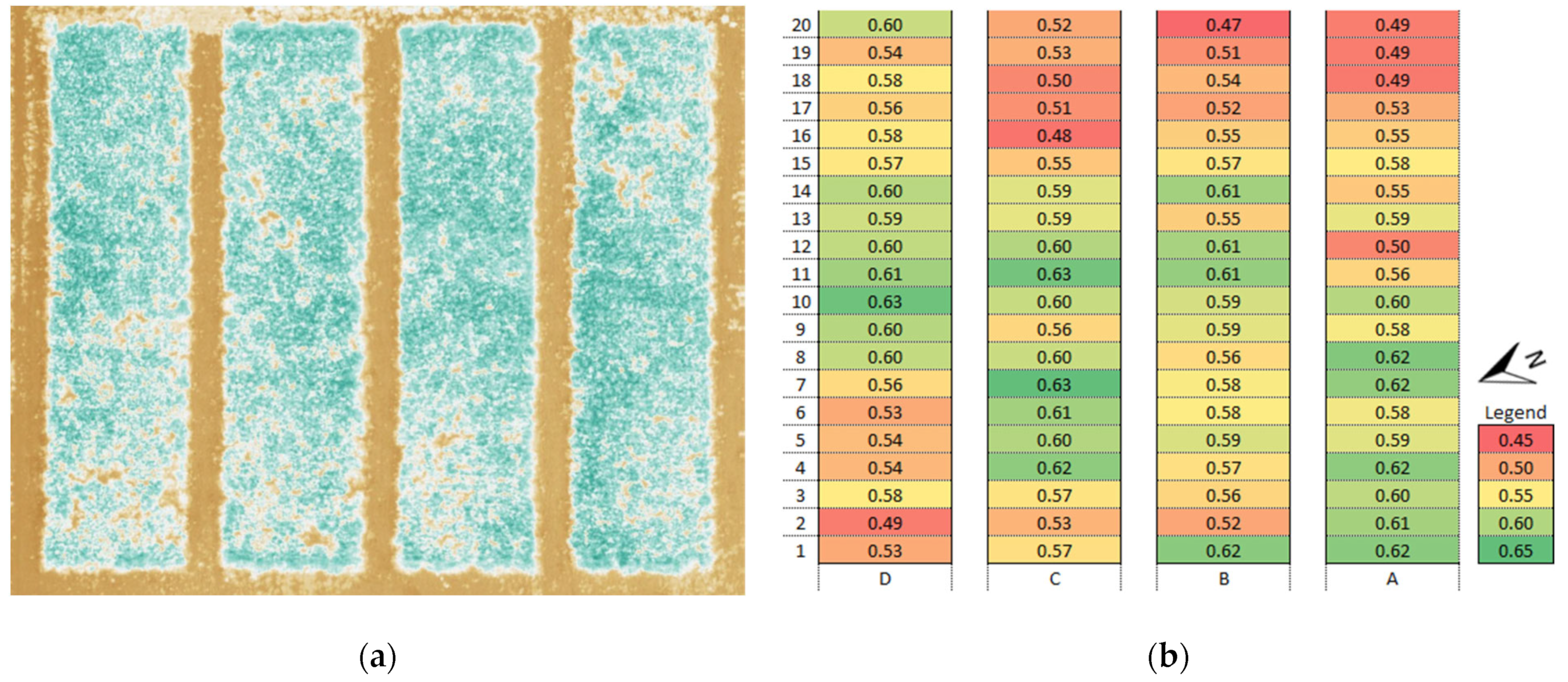
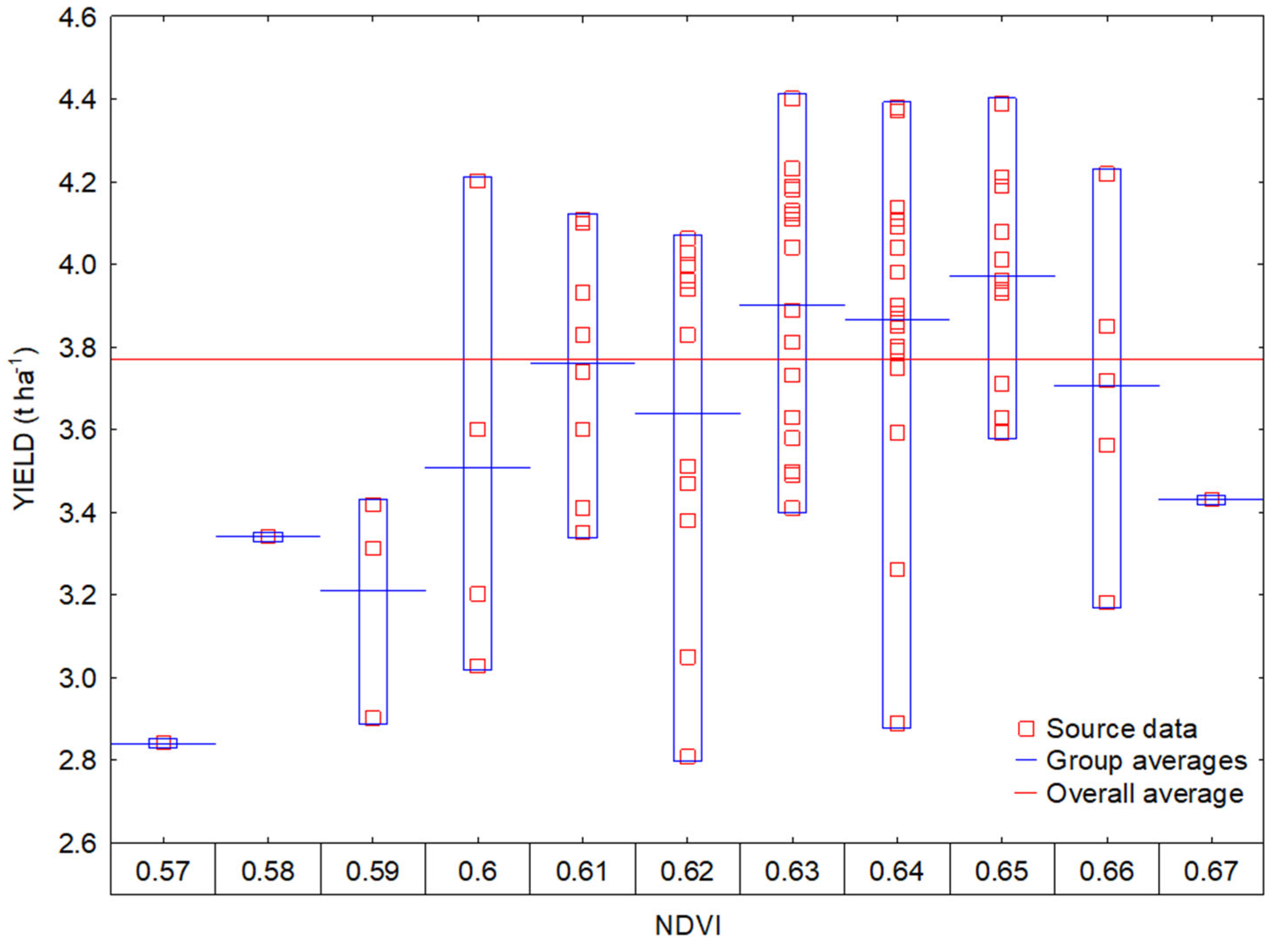
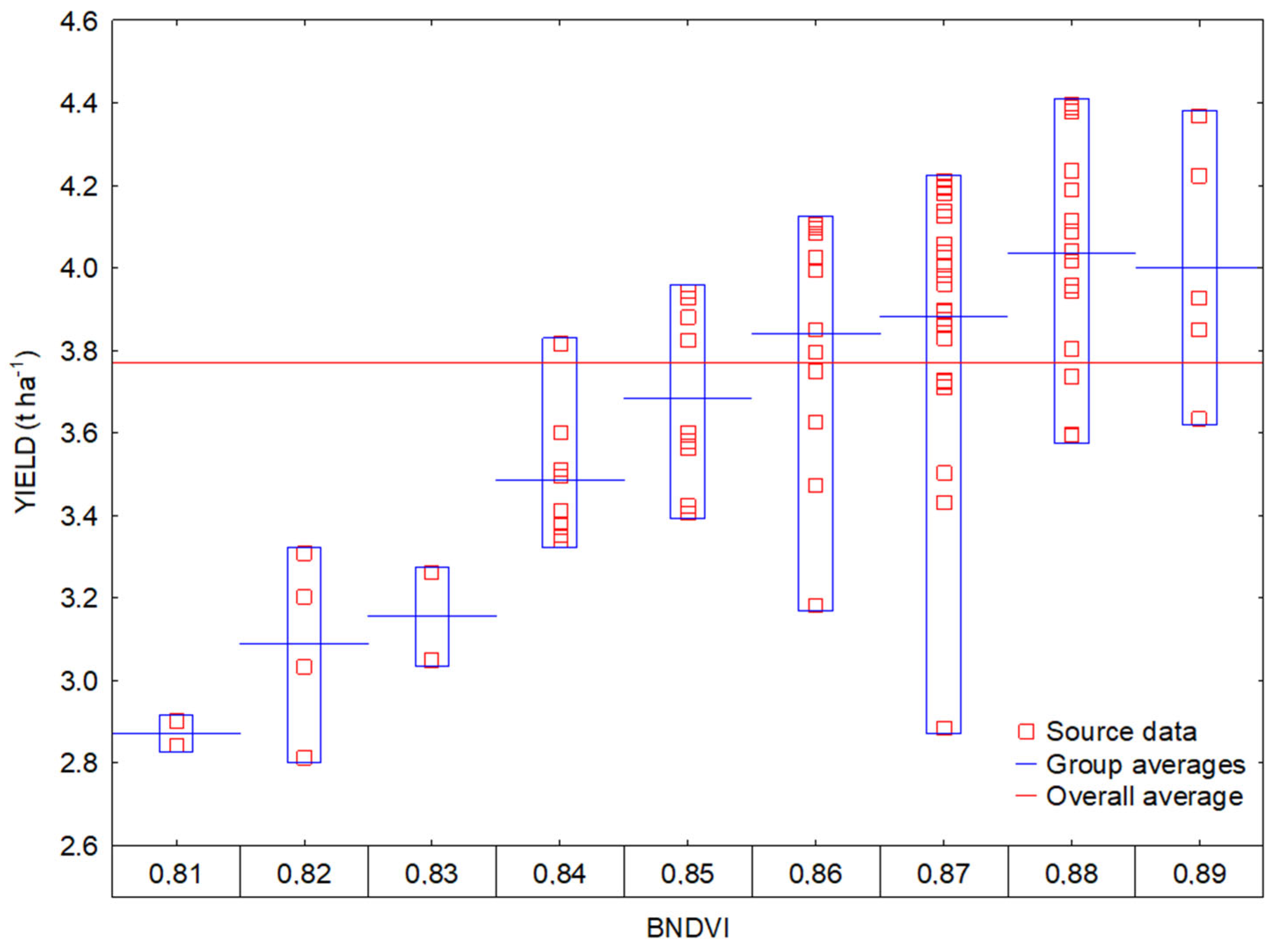
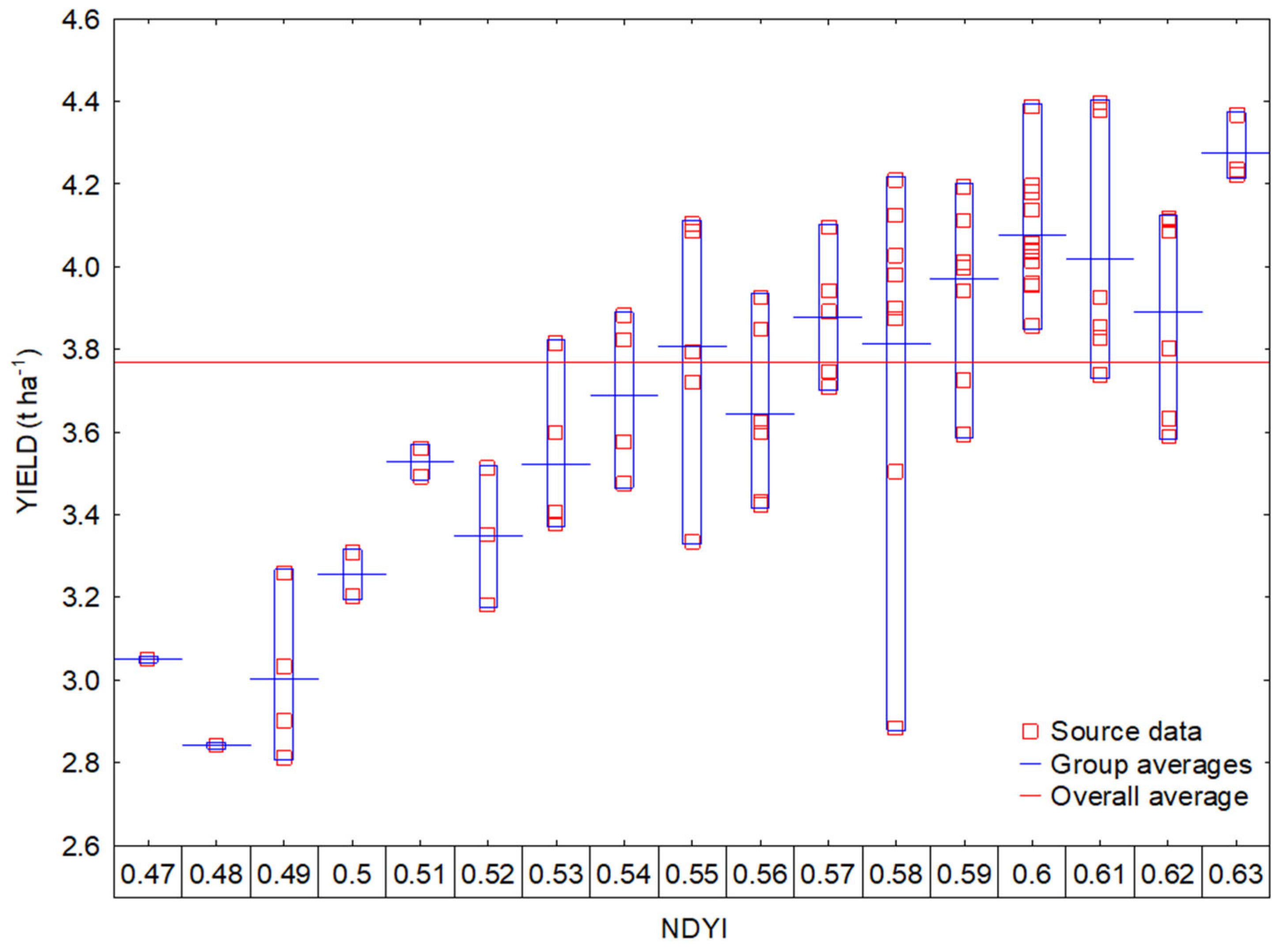
3.1. Vegetation Indices (VI)
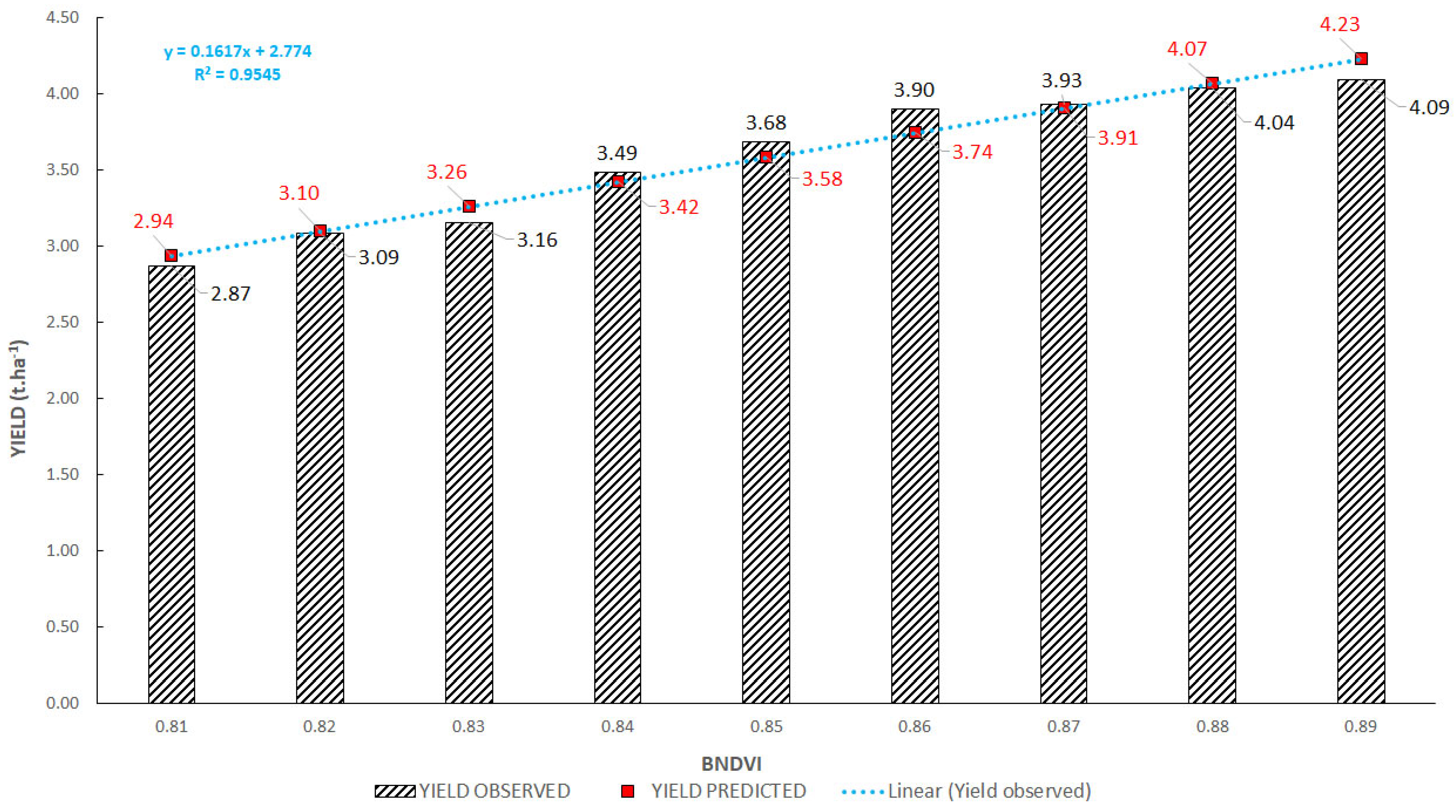
3.2. Interactions between Vegetation Indices and Yields
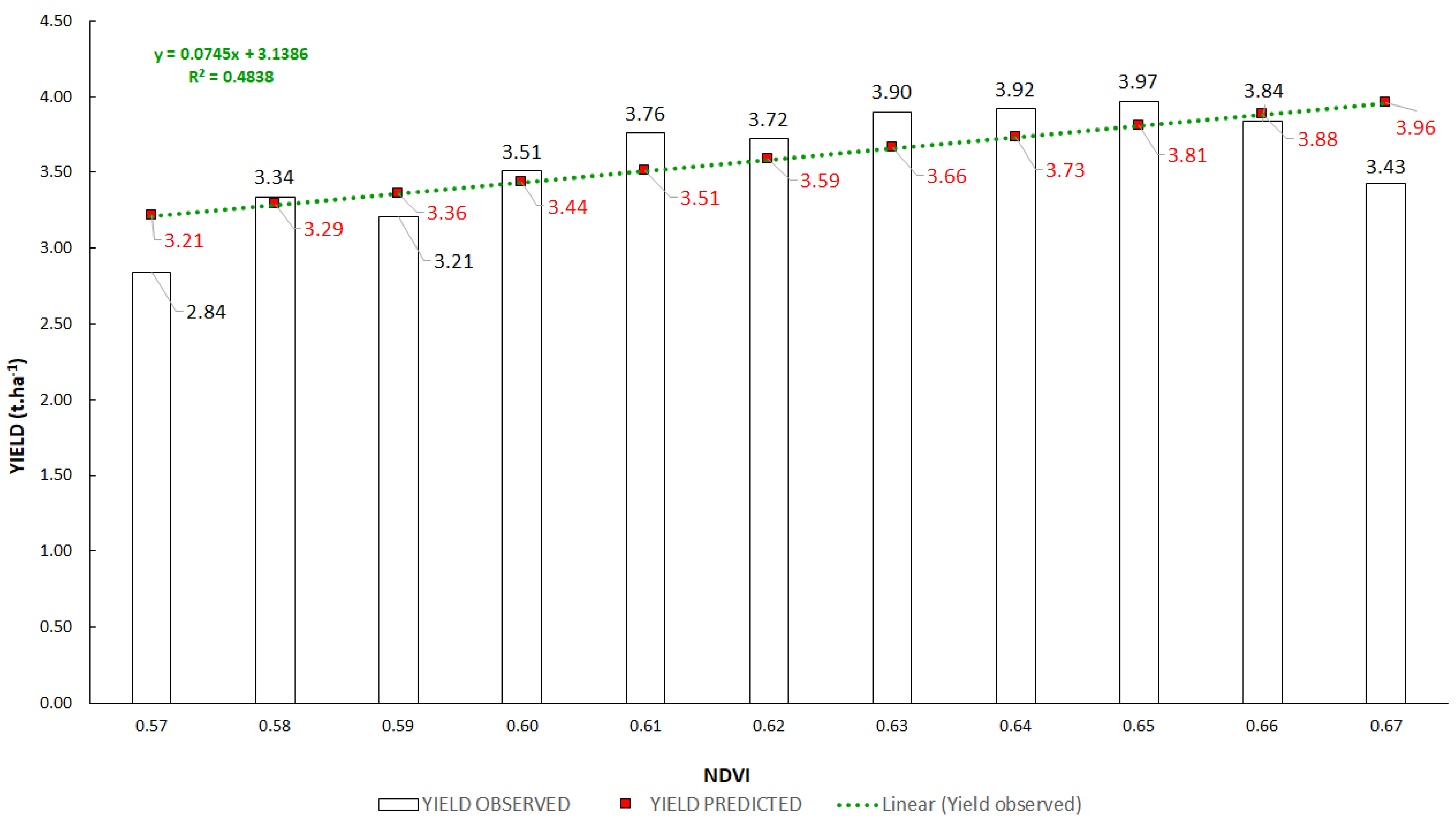
3.3. Regression Analysis of Vegetation Indices and Yield
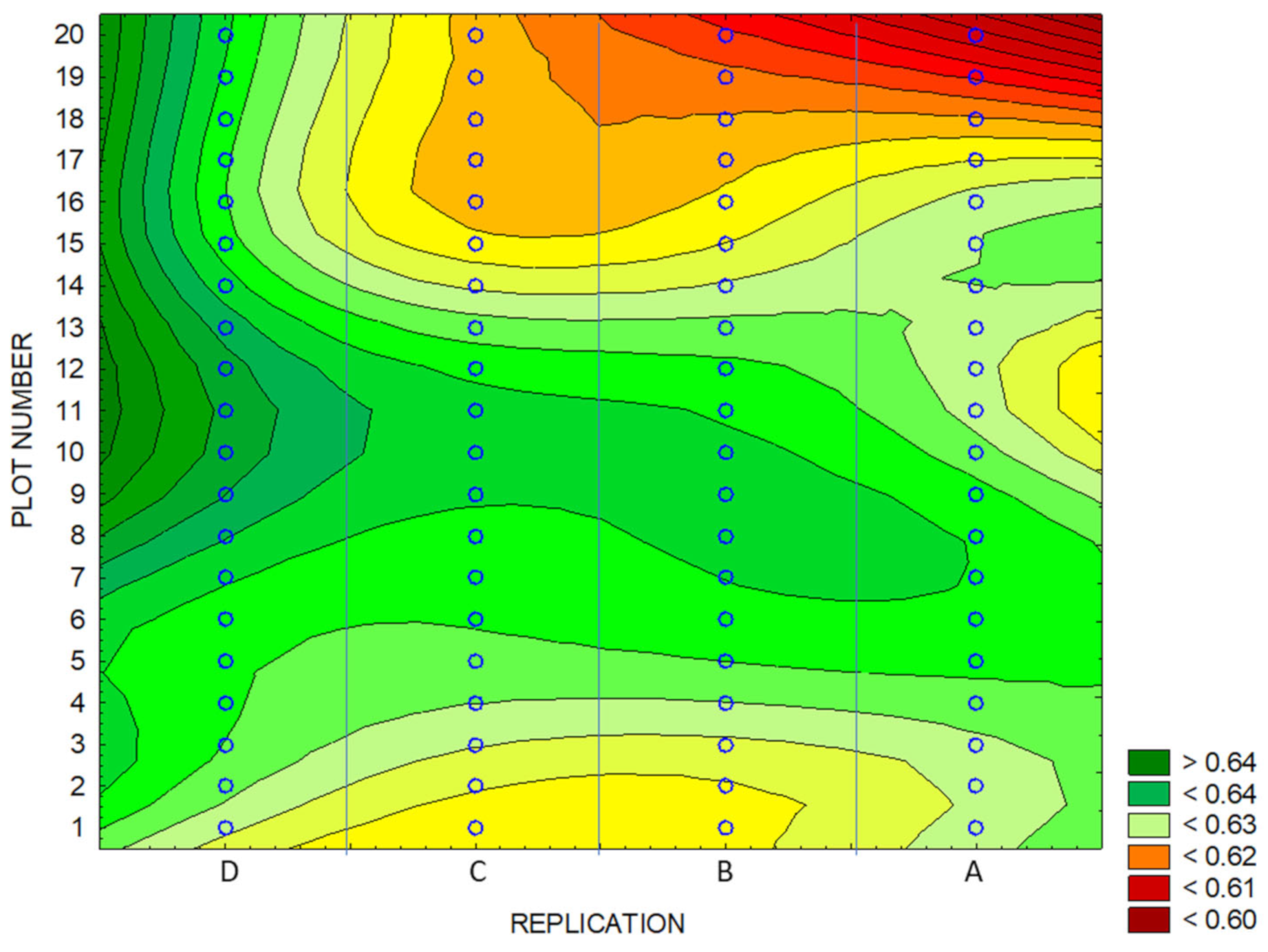
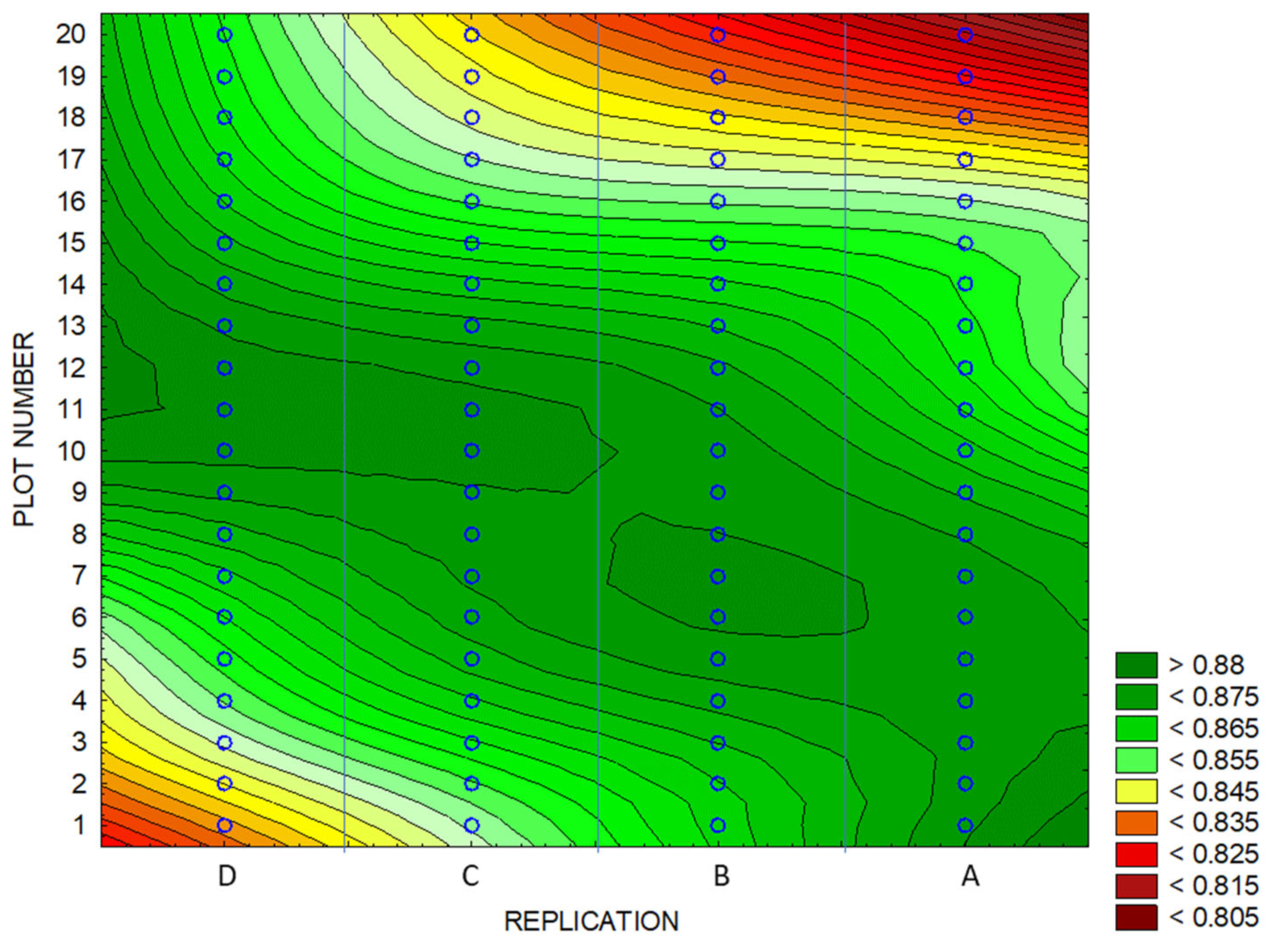
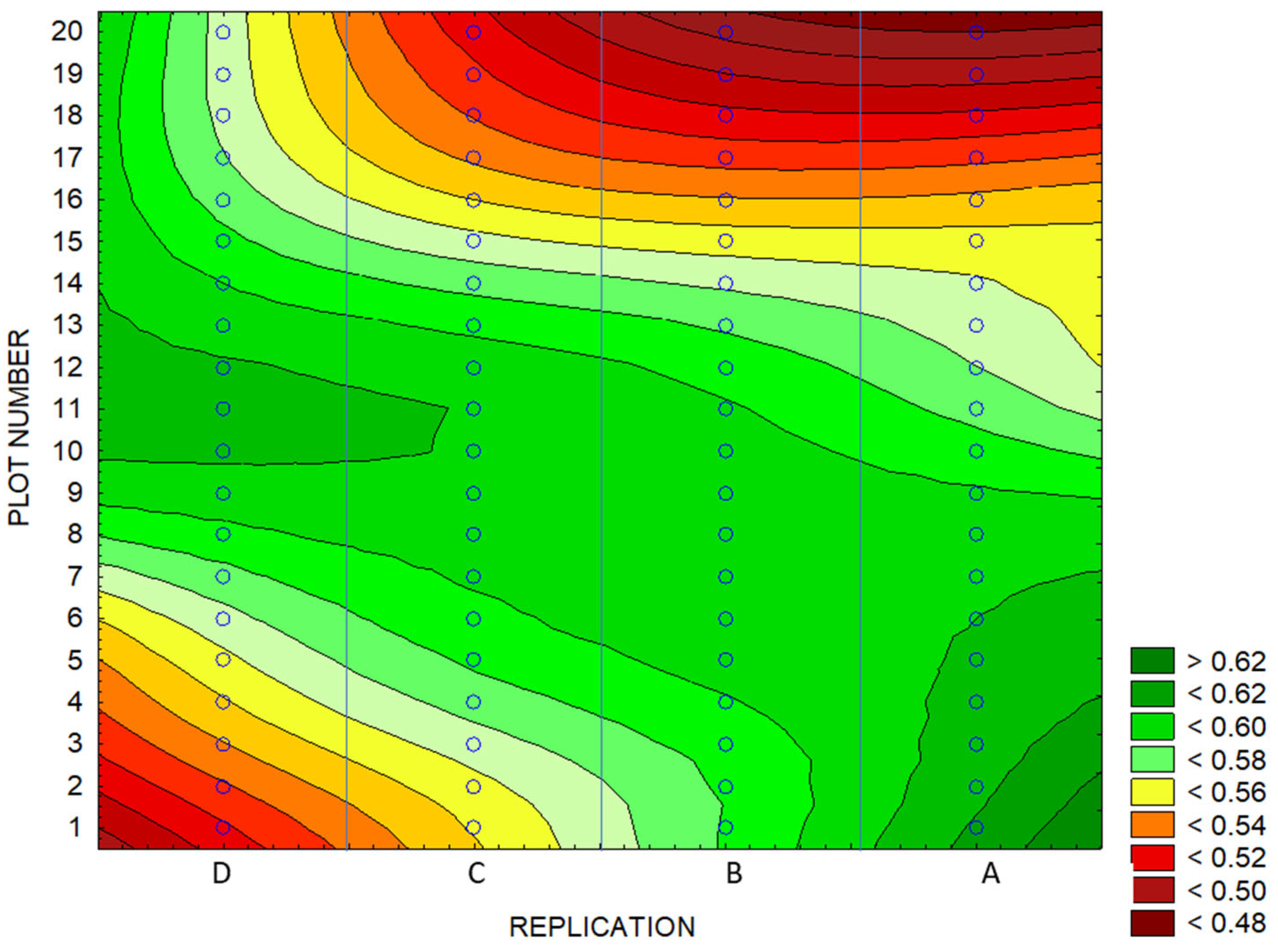
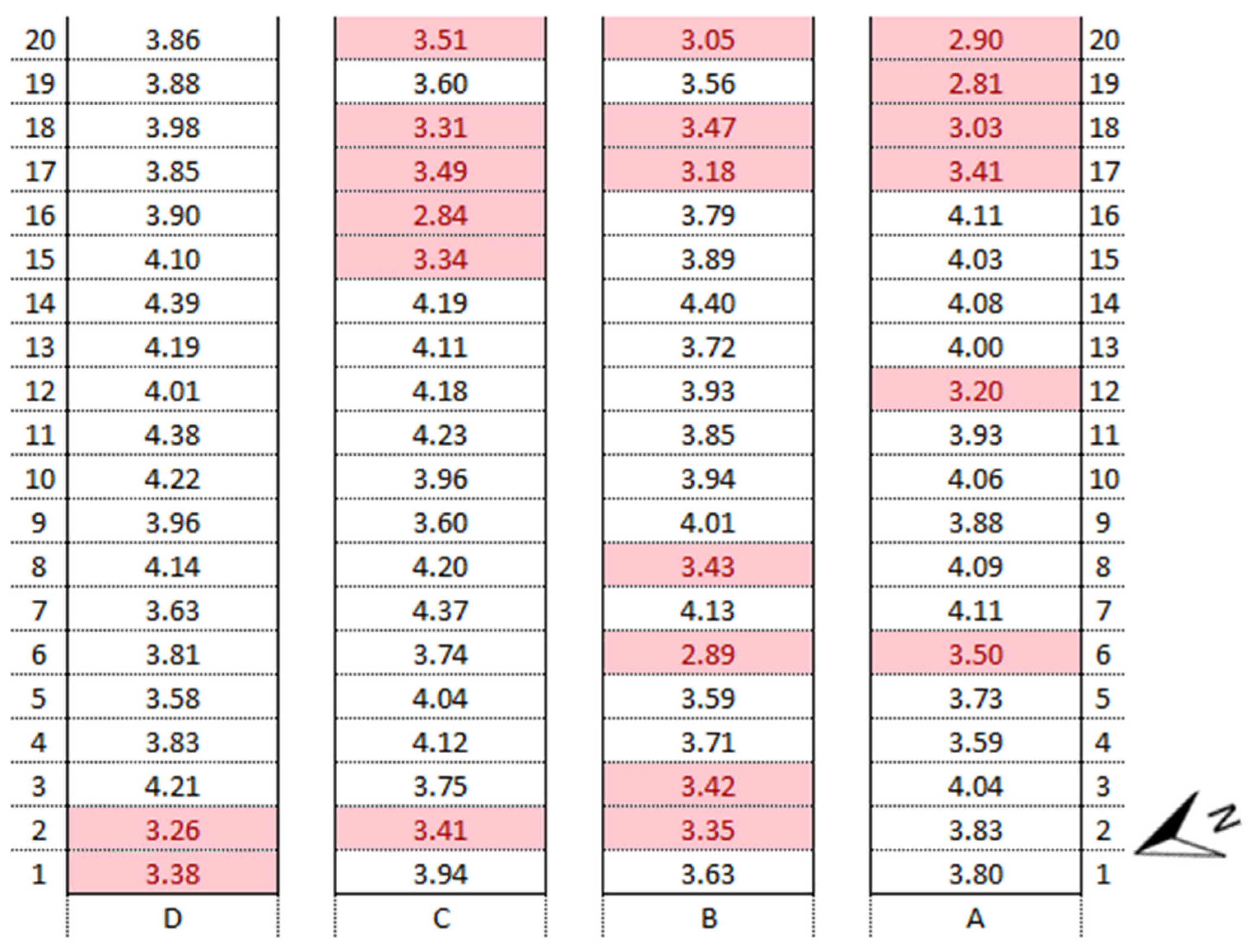
3.4. Identification of Anomalies in the Flowering Growth Condition Based on Vegetation Indices
- 1.
- LOW-YIELD AREAYIELD ≤ Q25;
- 2.
- HIGH-YIELD AREAYIELD > Q25.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cuaran, J.; Leon, J. Crop Monitoring using Unmanned Aerial Vehicles-A Review. Agric. Rev. 2021, 42, 121–132. [Google Scholar] [CrossRef]
- Mukherjee, A.; Misra, S.; Raghuwanshi, N.S. A survey of unmanned aerial sensing solutions in precision agriculture. J. Netw. Comput. Appl. 2019, 148, 102461. [Google Scholar] [CrossRef]
- Matese, A.; Toscano, P.; Gennaro, S.F.; Genesio, L.; Vaccari, F.P.; Primicerio, J.; Belli, C.; Zaldei, A.; Bianconi, R.; Gioli, B. Intercomparison of UAV, aircraft and satellite remote sensing platforms for precision viticulture. Remote Sens. 2015, 7, 2971–2990. [Google Scholar] [CrossRef]
- Chapman, S.C.; Merz, T.; Chan, A.; Jackway, P.; Hrabar, S.; Dreccer, M.F.; Holland, E.; Zheng, B.; Ling, T.J.; Jimenez-Berni, J. Pheno-copter: A low-altitude, autonomous remote sensing robotic helicopter for high-throughput field-based phenotyping. Agron. J. 2014, 4, 279–301. [Google Scholar] [CrossRef]
- Yang, C.; Hoffmann, W.C. Low-cost single-camera imaging system for aerial applicators. J. Appl. Remote Sens. 2015, 9, 096064. [Google Scholar] [CrossRef]
- Gebbers, R.; Adamchuk, V.I. Precision Agriculture and Food Security. Science 2010, 327, 828–831. [Google Scholar] [CrossRef] [PubMed]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating Biomass of Barley using Crop Surface Models (CSMs) Derived from UAV-Based RGB Imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- López-Granados, F. Weed detection for site-specific weed management: Mapping and real-time approaches: Weed detection for site-specific weed management. Weed Res. 2011, 51, 1–11. [Google Scholar] [CrossRef]
- Shi, Y.; Thomasson, J.A.; Murray, S.C.; Pugh, N.A.; Rooney, W.L.; Shafian, S.; Rajan, N.; Rouze, G.; Morgan, C.L.; Neely, H.L.; et al. Unmanned Aerial Vehicles for High-Throughput Phenotyping and Agronomic Research. PLoS ONE 2016, 11, e0159781. [Google Scholar] [CrossRef]
- Vega, F.A.; Ramírez, F.C.; Saiz, M.P.; Rosúa, F.O. Multi- temporal imaging using an unmanned aerial vehicle for monitoring a sunflower crop. Biosyst. Eng. 2015, 132, 19–27. [Google Scholar] [CrossRef]
- Sulik, J.J.; Long, D.S. Spectral considerations for modeling yield of canola. Remote Sens. Environ. 2016, 184, 161–174. [Google Scholar] [CrossRef]
- Kumar, N.; Singh, S.K.; Obi Reddy, G.P.; Mishra, V.N.; Bajpai, R.K. Remote Sensing and Geographic Information System in Water Erosion Assessment. Agric. Rev. 2020, 41, 116–123. [Google Scholar] [CrossRef]
- Gonzalez-de-Soto, M.; Emmi, L.; Perez-Ruiz, M.; Aguera, J.; Gonzalez-de-Santos, P. Autonomous systems for precise spraying–Evaluation of a robotised patch sprayer. Biosyst. Eng. 2016, 146, 165–182. [Google Scholar] [CrossRef]
- Huang, Y.; Hoffmann, C.W.; Lan, Y.; Wu, W.; Fritz, B.K. Development of a Spray System for an Unmanned Aerial Vehicle Platform. Appl. Eng. Agric. 2008, 25, 803–809. [Google Scholar] [CrossRef]
- Zhang, X.; He, Y. Rapid estimation of seed yield using hyperspectral images of oilseed rape leaves. Ind. Crop. Prod. 2013, 42, 416–420. [Google Scholar] [CrossRef]
- Zhang, T.; Vail, S.; Duddu, H.S.N.; Parkin, I.A.P.; Guo, X.; Johnson, E.N.; Shirtliffe, S.J. Phenotyping Flowering in Canola (Brassica napus L.) and Estimating Seed Yield Using an Unmanned Aerial Vehicle-Based Imagery. Front. Plant Sci. 2021, 12, 686332. [Google Scholar] [CrossRef]
- Leach, J.E.; Milford, G.F.J.; Mullen, L.A.; Scott, T.; Stevenson, H.J. Accumulation of Dry Matter in Oilseed Rape. Asp. Appl. Biol. 1989, 23, 117–123. [Google Scholar]
- Shukla, G.; Tiwari, P.; Dugesar, V.; Srivastava, P.K. Chapter 9-Estimation of evapotranspiration using surface energy balance system and satellite datasets. In Agricultural Water Management, 1st ed.; Srivastava, P.K., Gupta, M., Tsakiris, G., Quinn, N.W., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 157–183. [Google Scholar]
- Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression-based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
- Hancock, D.W.; Dougherty, C.T. Relationships between Blue- and Red-based Vegetation Indices and Leaf Area and Yield of Alfalfa. Crop Sci. 2007, 47, 2547. [Google Scholar] [CrossRef]
- Sulik, J.J.; Long, D.S. Spectral indices for yellow canola flowers. Int. J. Remote Sens. 2015, 36, 2751–2765. [Google Scholar] [CrossRef]
- Yates, D.J.; Steven, M.D. Reflexion and absorption of solar radiation by flowering canopies of oil-seed rape (Brassica napus L.). J. Agric. Sci. 1987, 109, 495–502. [Google Scholar] [CrossRef]
- Shen, M.; Chen, J.; Zhu, X.; Tang, Y. Yellow flowers can decrease NDVI and EVI values: Evidence from a field experiment in an alpine meadow. Can. J. Remote Sens. 2009, 35, 99–106. [Google Scholar] [CrossRef]
- Wan, L.; Cen, H.; Zhu, J.; Zhang, J.; Zhu, Y.; Sun, D.; Du, X.; Zhai, L.; Weng, H.; Li, Y.; et al. Grain yield prediction of rice using multi-temporal UAV-based RGB and multispectral images and model transfer—A case study of small farmlands in the South of China. Agric. For. Meteorol. 2020, 291, 108096. [Google Scholar] [CrossRef]
- Domínquez, J.A.; Kumhálová, J.; Novák, P. Winter oilseed rape and winter wheat growth prediction sensing remote sensing methods. Plant. Soil. Environ. 2015, 65, 410–416. [Google Scholar]
- Wan, L.; Li, Y.; Cen, H.; Zhu, J.; Yin, W.; Wu, W.; Zhu, H.; Sun, D.; Zhou, W.; He, Y. Combining UAV-Based Vegetation Indices and Image Classification to Estimate Flower Number in Oilseed Rape. Remote Sens. 2018, 10, 1484. [Google Scholar] [CrossRef]
- Peng, Y.; Zhu, T.; Li, Y.; Dai, C.; Fang, S.; Gong, Y.; Wu, X.; Zhu, R.; Liu, K. Remote prediction of yield based on LAI estimation in oilseed rape under different planting methods and nitrogen fertilizer applications. Agric. For. Meteorol. 2019, 271, 116–125. [Google Scholar] [CrossRef]
- FAO; IUSS. World Reference Base-Version 2015; 106; FAO: Rome, Italy, 2019; 197p, ISBN 978-92-5-131246-9. [Google Scholar]
- Meier, U. Growth Stages of Mono-and Dicotyledonous Plants; Federal Biological Research Centre for Agriculture and Forestry: Bonn, Germany, 2001. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1973. Goddard Space Flight Center, NASA SP-351. Science and Technical Information Office, NASA: Washington, DC, USA, 1974. pp. 309–317.
- Janoušek, J.; Jambor, V.; Marcoň, P.; Dohnal, P.; Synková, H.; Fiala, P. Using UAV-Based Photogrammetry to Obtain Correlation between the Vegetation Indices and Chemical Analysis of Agricultural Crops. Remote Sens. 2021, 13, 1878. [Google Scholar] [CrossRef]
- Tucker, C.J.; Holben, B.N.; Elgin, J.H., Jr.; McMurtrey, J.E. Relationship of spectral data to grain yield variation (within a winter wheat field). Photogramm. Eng. Remote Sens. 1980, 46, 657–666. [Google Scholar]
- Hodge, K.; Akhter, F.; Bainard, L.; Smith, A. Using an Unmanned Aerial Vehicle with Multispectral with RGB Sensors to Analyze Canola Yield in the Canadian Prairies. In Proceedings of the 14th International Conference on Precision Agriculture, Montreal, QC, Canada, 24–27 June 2018. [Google Scholar]
- d’Andrimont, R.; Taymans, M.; Lemoine, G.; Ceglar, A.; Yordanov, M.; van der Velde, M. Detecting flowering phenology in oil seed rape parcels with Sentinel-1 and -2 time series. Remote Sens. Environ. 2020, 239, 111660. [Google Scholar] [CrossRef]
- Barbosa, H.A.; Huete, A.R.; Baethgen, W.E. A 20-year study of NDVI variability over the Northeast Region of Brazil. J. Arid. Environ. 2006, 67, 288–307. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Shen, M.; Chen, J.; Zhu, X.; Tang, Y.; Chen, X. Do flowers affect biomass estimate accuracy from NDVI and EVI? Int. J. Remote Sens. 2010, 31, 2139–2149. [Google Scholar] [CrossRef]
- Behrens, T.; Müller, J.; Diepenbrock, W. Utilization of canopy reflectance to predict properties of oilseed rape (Brassica napus L.) and barley (Hordeum vulgare L.) during ontogenesis. Eur. J. Agron 2006, 25, 345–355. [Google Scholar] [CrossRef]
- Piekarczyk, J. Winter Oilseed-Rape Yield Estimates from Hyperspectral Radiometer Measurements. Quaest. Geogr. 2011, 30, 77–84. [Google Scholar] [CrossRef]
- Migdall, S.; Ohl, N.; Bach, H. Parameterisation of the Land Surface Reflectance Model SLC for Winter Rape Using Spaceborne Hyperspectral CHRIS Data. ESA SP-683. In Proceedings of the Hyperspectral Workshop, Frascati, Italy, 17–19 March 2010. [Google Scholar]
- Fan, H.; Liu, S.; Li, J.; Li, L.; Dang, L.; Ren, T.; Lu, J. Early prediction of the seed yield in winter oilseed rape based on the near-infrared reflectance of vegetation (NIRv). Comput. Electron. Agric. 2021, 186, 106166. [Google Scholar] [CrossRef]
- Mezera, J.; Lukas, V.; Horniaček, I.; Smutný, V.; Elbl, J. Comparison of Proximal and Remote Sensing for the Diagnosis of Crop Status in Site-Specific Crop Management. Sensors 2022, 22, 19. [Google Scholar] [CrossRef]
- Fischer, T.; Veste, M.; Eisele, A.; Bens, O.; Spyra, W.; Hüttl, R.F. Small scale spatial heterogeneity of Normalized Difference Vegetation Indices (NDVIs) and hot spots of photosynthesis in biological soil crusts. Flora Morphol. Distrib. Funct. Ecol. Plants 2012, 207, 159–167. [Google Scholar] [CrossRef]





| Year | Total Month Precipitation | Total Amount | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 9 | 10 | 11 | 12 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Vegetation Period | |
| 2019–2020 | 55.9 | 72.6 | 60.4 | 40.1 | 42.9 | 8.5 | 27.1 | 25.7 | 20.3 | 65.4 | 87.2 | 59.0 | 565.1 |
| 1981–2010 | 63.7 | 48.2 | 32.1 | 36.4 | 32.0 | 25.0 | 23.9 | 31.5 | 32.0 | 60.5 | 68.7 | 71.6 | 525.6 |
| Year | Average month temperature | Average | |||||||||||
| 8 | 9 | 10 | 11 | 12 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | vegetation period | |
| 2019–2020 | 20.8 | 14.6 | 9.9 | 5.2 | 0.6 | −0.2 | 4.6 | 5.3 | 9.9 | 12.6 | 18.0 | 19.2 | 10.0 |
| 1981–2010 | 18.8 | 14.1 | 8.8 | 3.5 | −0.6 | −1.7 | −0.3 | 3.8 | 9.5 | 14.6 | 17.4 | 19.5 | 9.0 |
| Equation (1) [30] | Normalized difference vegetation index (NDVI) | ||
| NDVI = | RNIR – RRed | ||
| RNIR + RRed | |||
| Equation (2) [20] | Blue normalized difference vegetation index (BNDVI) | ||
| BNDVI = | RNIR – Rblue | ||
| RNIR + Rblue | |||
| Equation (3) [21] | Normalized difference yellowness index (NDYI) | ||
| NDYI = | Rgreen – Rblue | ||
| Rgreen + Rblue | |||
| Variable | Mean | SD | N | Minimum | Maximum | Span |
|---|---|---|---|---|---|---|
| NDVI | 0.63 | 0.02 | 80.00 | 0.57 | 0.67 | 0.10 |
| BNDVI | 0.86 | 0.02 | 80.00 | 0.81 | 0.89 | 0.08 |
| NDYI | 0.57 | 0.04 | 80.00 | 0.47 | 0.63 | 0.16 |
| YIELD | 3.79 * | 0.38 | 77 * | 2.81 | 4.40 | 1.58 |
| Variable | NDVI | BNDVI | NDYI | YIELD (t/ha) |
|---|---|---|---|---|
| NDVI | 1.00 | 0.65 | 0.39 | 0.47 |
| BNDVI | 0.65 | 1.00 | 0.92 | 0.80 |
| NDYI | 0.39 | 0.92 | 1.00 | 0.84 |
| YIELD (t/ha) | 0.47 | 0.80 | 0.84 | 1.00 |
| Method of Calculation | From Yields of All Plots | From Average Yields of Plots with the Same Value of VI | ||||
|---|---|---|---|---|---|---|
| Parameter | NDVI | BNDVI | NDYI | NDVI | BNDVI | NDYI |
| Correlation coefficient R | 0.47 | 0.80 | 0.84 | 0.70 | 0.98 | 0.95 |
| Determination coefficient R2 | 0.22 | 0.64 | 0.70 | 0.48 | 0.95 | 0.90 |
| RMSE (t/ha) | 0.32 | 0.22 | 0.21 | 0.27 | 0.10 | 0.13 |
| Experimental Areas | NDVI | BNDVI | NDYI | Yield | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Q25 | Mean | Q25 | Mean | Q25 | Mean (t ha−1) | Q25 | |
| Whole Area | 0.63 | 0.62 | 0.86 | 0.85 | 0.57 | 0.54 | 3.77 | 3.51 |
| High-Yield Area | 0.65 | 0.88 | 0.59 | 3.94 | ||||
| Low-Yield Area | 0.61 | 0.84 | 0.52 | 3.24 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lukas, V.; Huňady, I.; Kintl, A.; Mezera, J.; Hammerschmiedt, T.; Sobotková, J.; Brtnický, M.; Elbl, J. Using UAV to Identify the Optimal Vegetation Index for Yield Prediction of Oil Seed Rape (Brassica napus L.) at the Flowering Stage. Remote Sens. 2022, 14, 4953. https://doi.org/10.3390/rs14194953
Lukas V, Huňady I, Kintl A, Mezera J, Hammerschmiedt T, Sobotková J, Brtnický M, Elbl J. Using UAV to Identify the Optimal Vegetation Index for Yield Prediction of Oil Seed Rape (Brassica napus L.) at the Flowering Stage. Remote Sensing. 2022; 14(19):4953. https://doi.org/10.3390/rs14194953
Chicago/Turabian StyleLukas, Vojtěch, Igor Huňady, Antonín Kintl, Jiří Mezera, Tereza Hammerschmiedt, Julie Sobotková, Martin Brtnický, and Jakub Elbl. 2022. "Using UAV to Identify the Optimal Vegetation Index for Yield Prediction of Oil Seed Rape (Brassica napus L.) at the Flowering Stage" Remote Sensing 14, no. 19: 4953. https://doi.org/10.3390/rs14194953
APA StyleLukas, V., Huňady, I., Kintl, A., Mezera, J., Hammerschmiedt, T., Sobotková, J., Brtnický, M., & Elbl, J. (2022). Using UAV to Identify the Optimal Vegetation Index for Yield Prediction of Oil Seed Rape (Brassica napus L.) at the Flowering Stage. Remote Sensing, 14(19), 4953. https://doi.org/10.3390/rs14194953







