A Novel Hybrid Attention-Driven Multistream Hierarchical Graph Embedding Network for Remote Sensing Object Detection
Abstract
1. Introduction
2. Related Work
2.1. Traditional Handcrafted-Feature-Based Object-Detection Approaches
2.2. Deep-Learning-Based Object-Detection Approaches
2.3. Attention-Mechanism-Based Object-Detection Approaches
2.4. Graph Convolutional Networks in Remote-Sensing Vision Applications
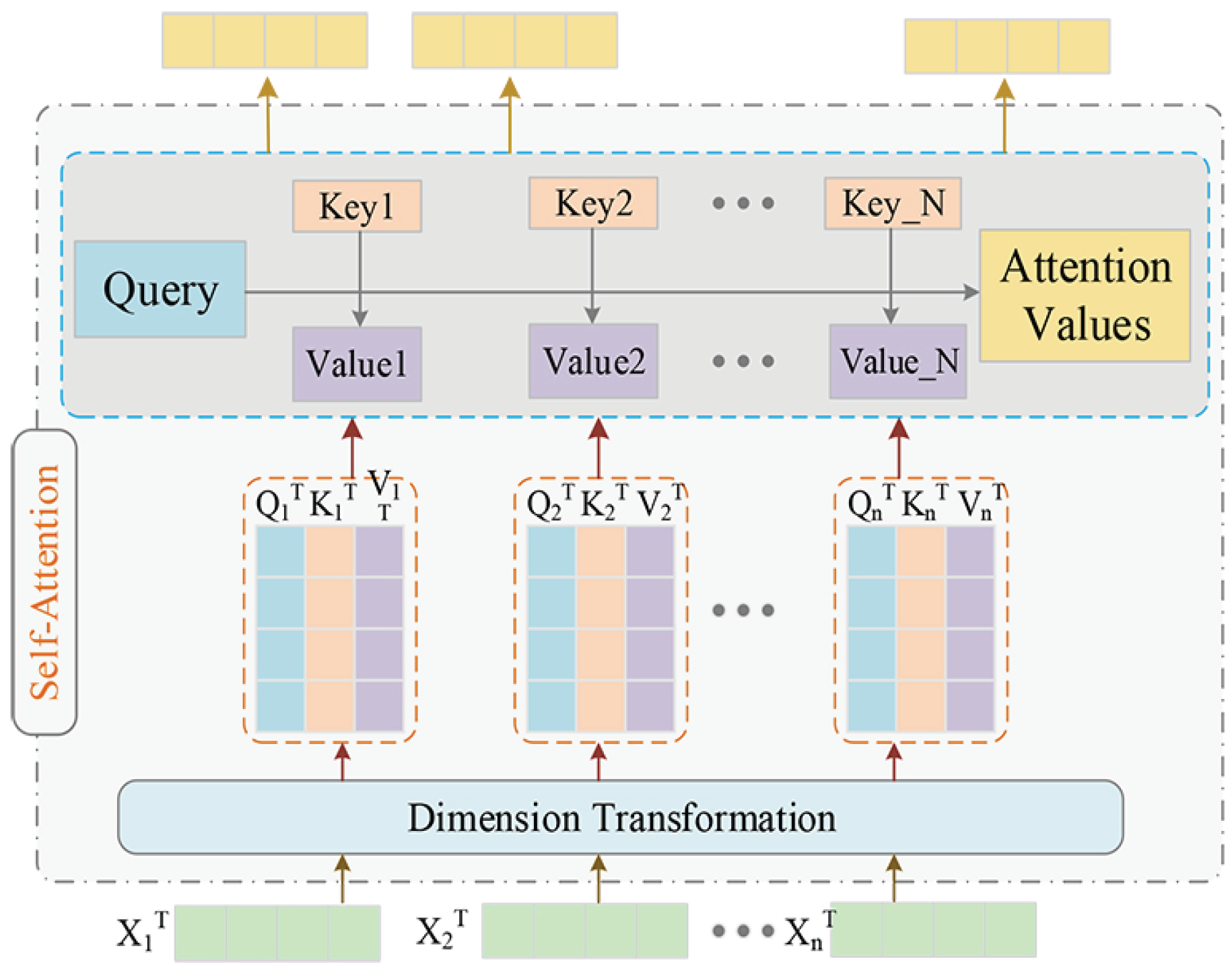
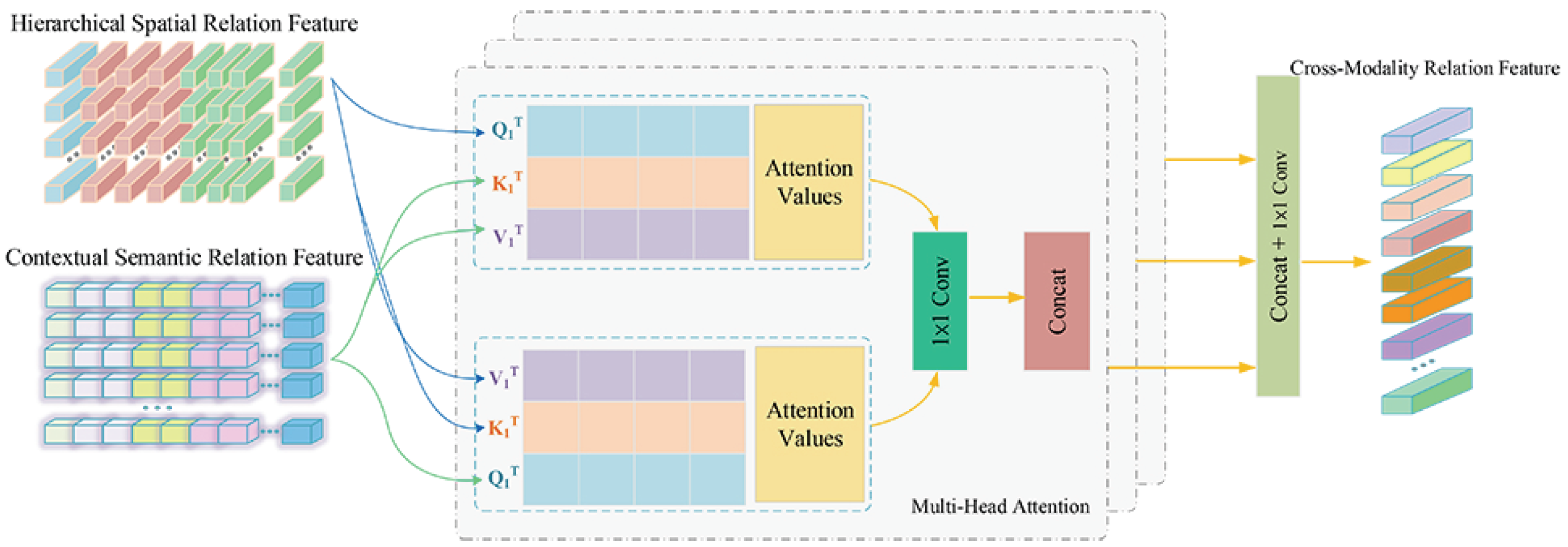
3. Proposed Method
3.1. Hierarchical Spatial Graph and Semantic Graph Construction
3.2. Hierarchical Spatial and Semantic Relation Learning
3.3. Objective Function of HA-MHGEN
4. Experiments
4.1. Datasets and Evaluation Metrics
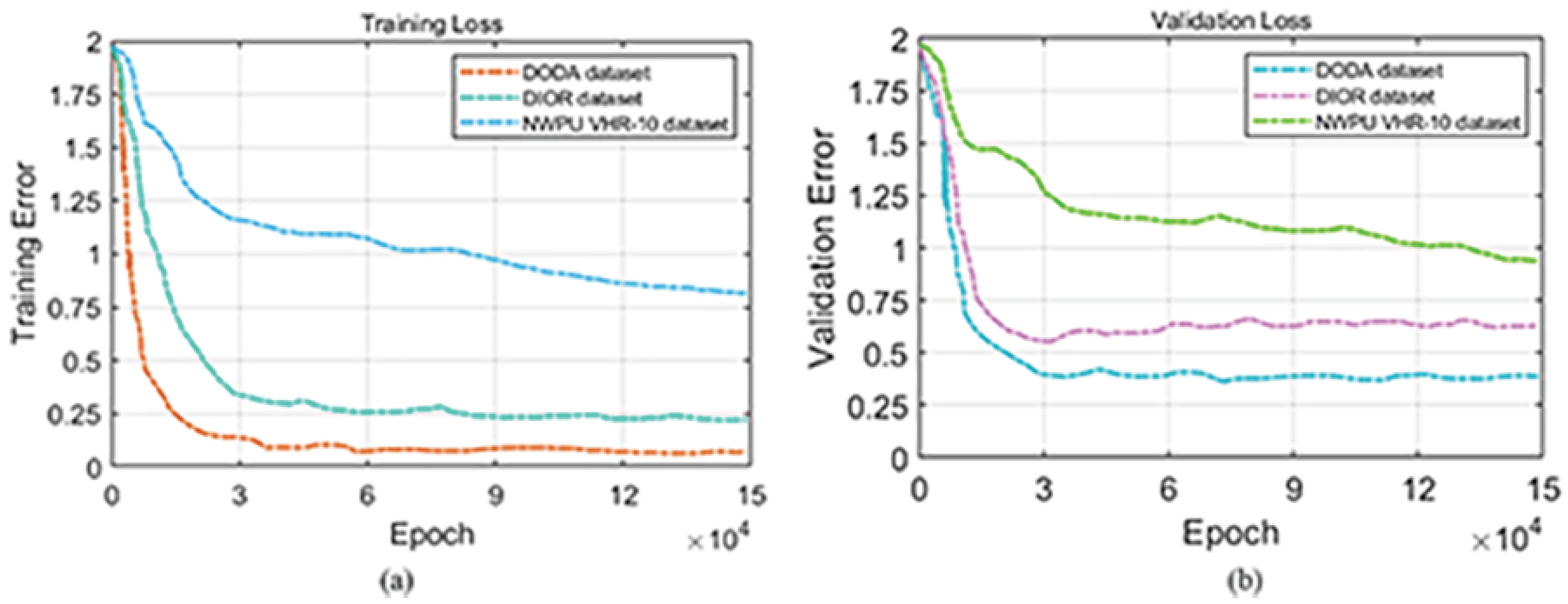
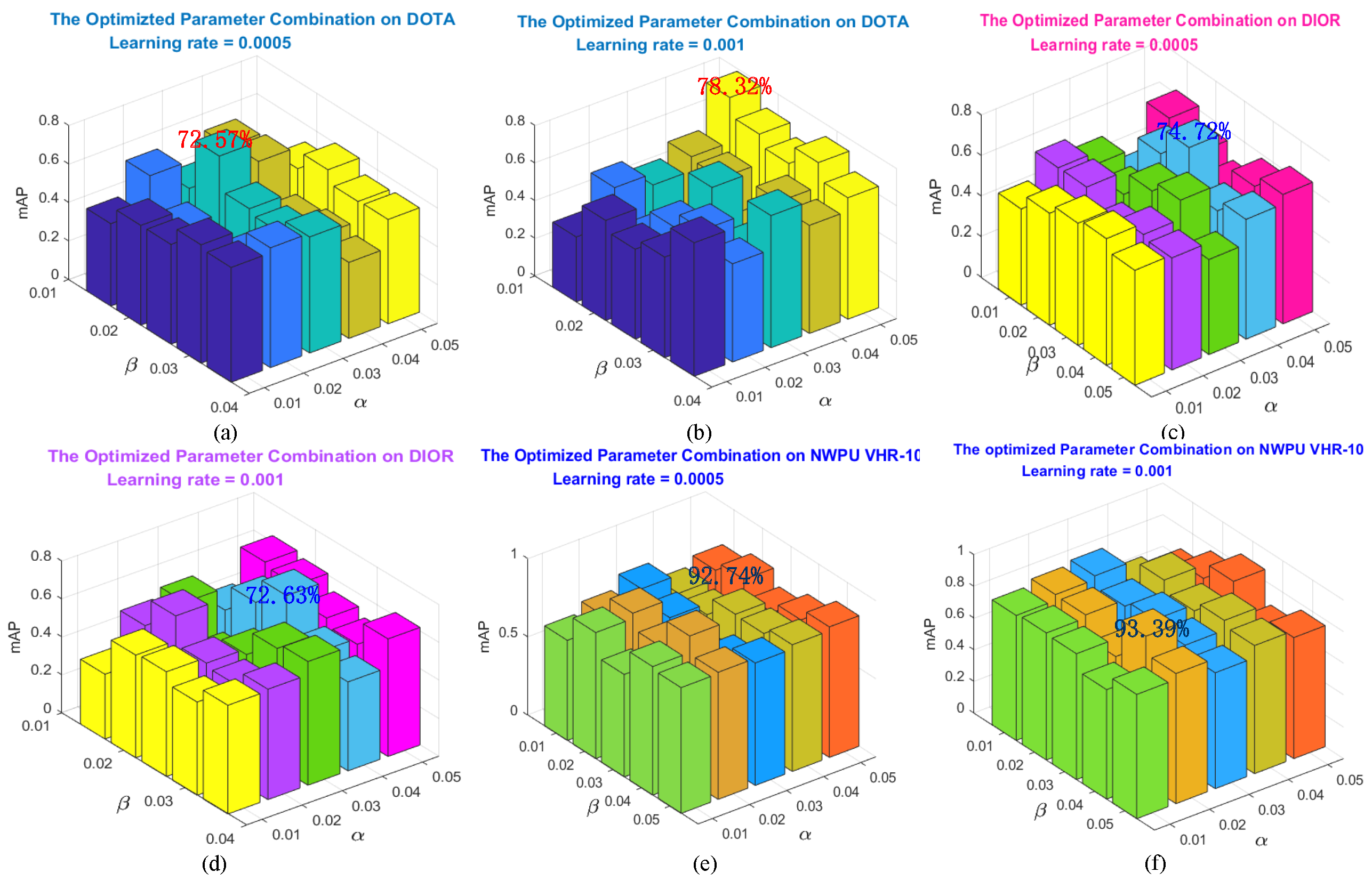
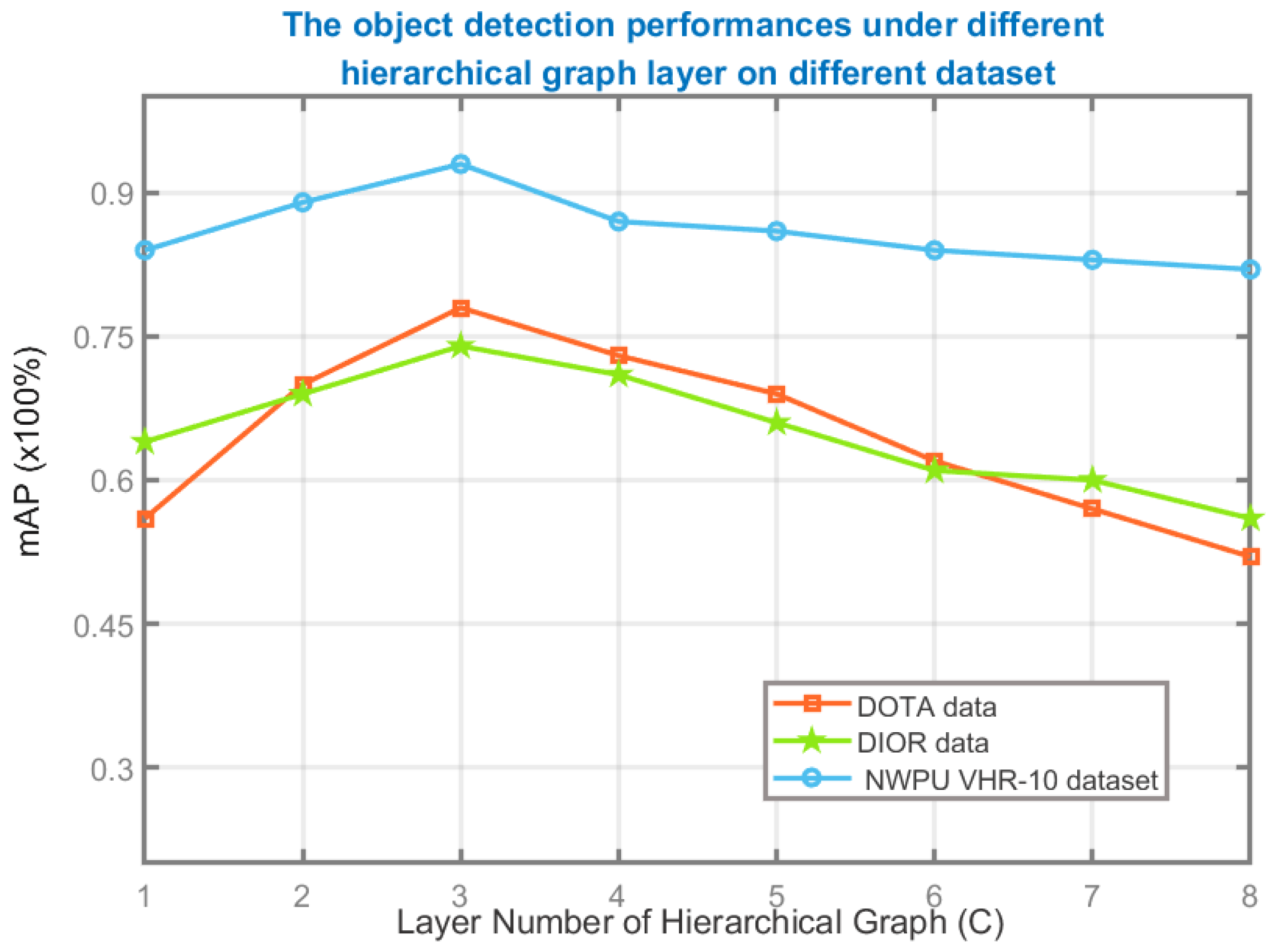
4.2. Implementation Details and Parameter Analysis
4.3. Comparisons and Analysis Using Different Network Configurations
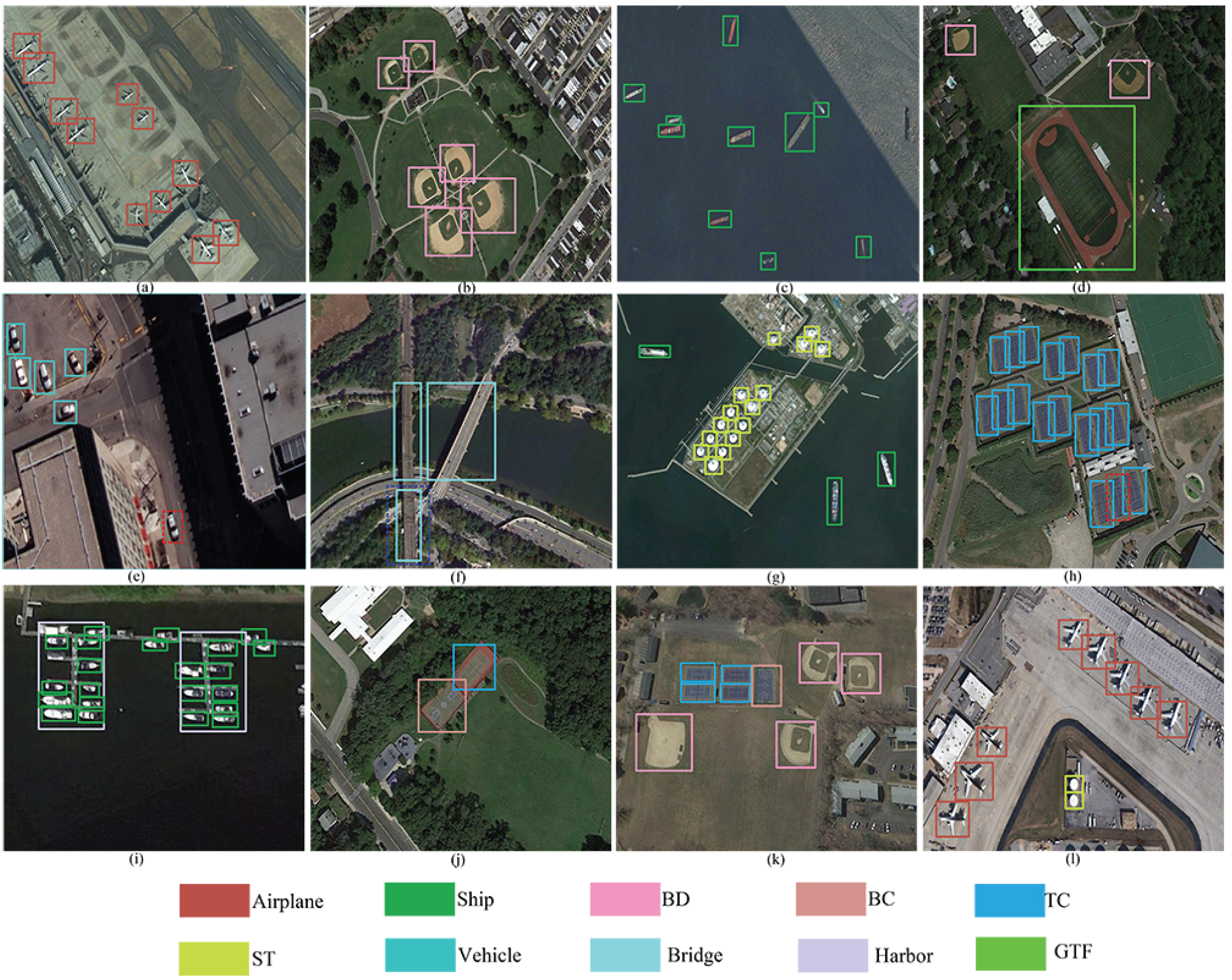
4.4. Quantitative and Qualitative Comparison and Analyses
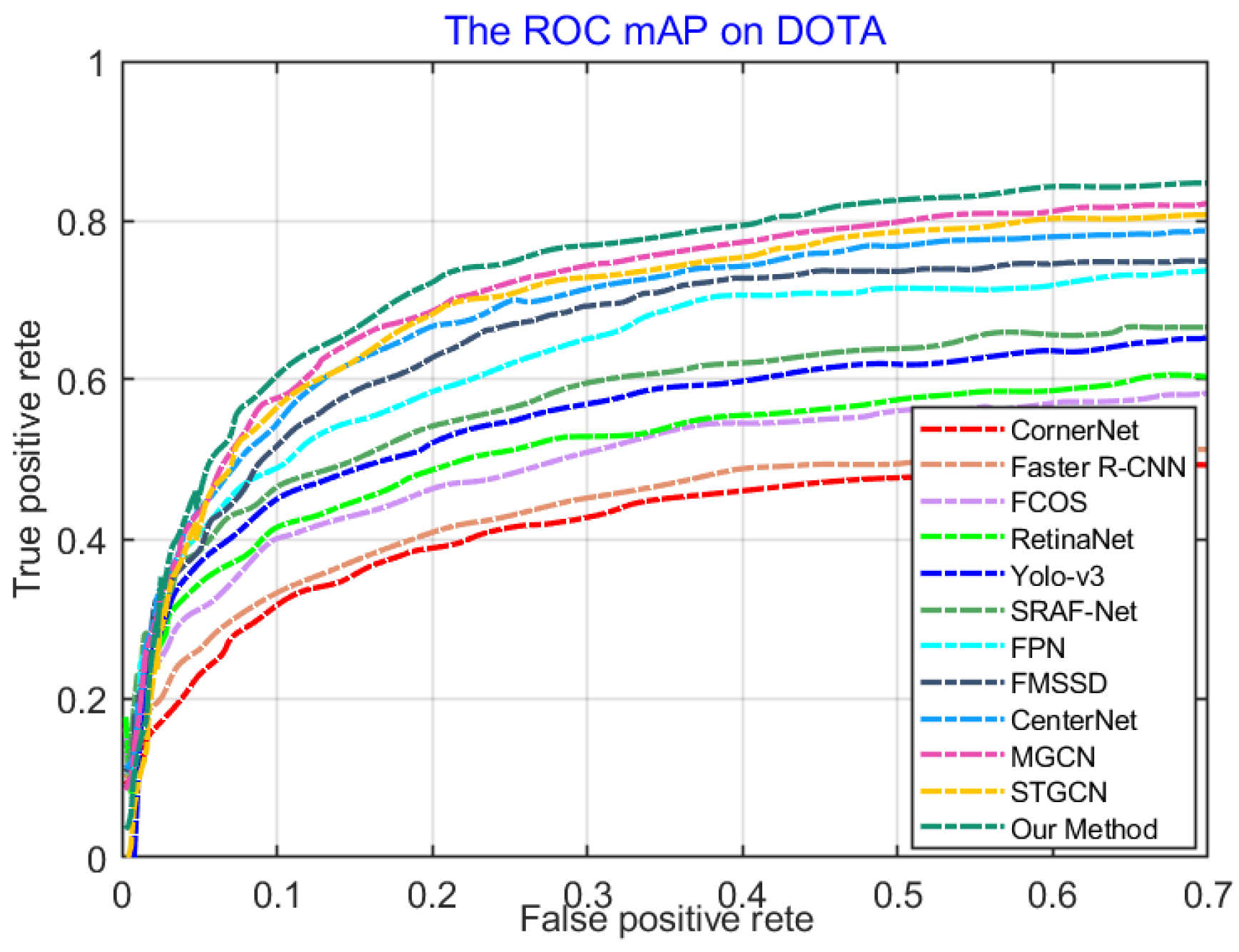
4.4.1. Comparison and Analysis on the DOTA Dataset
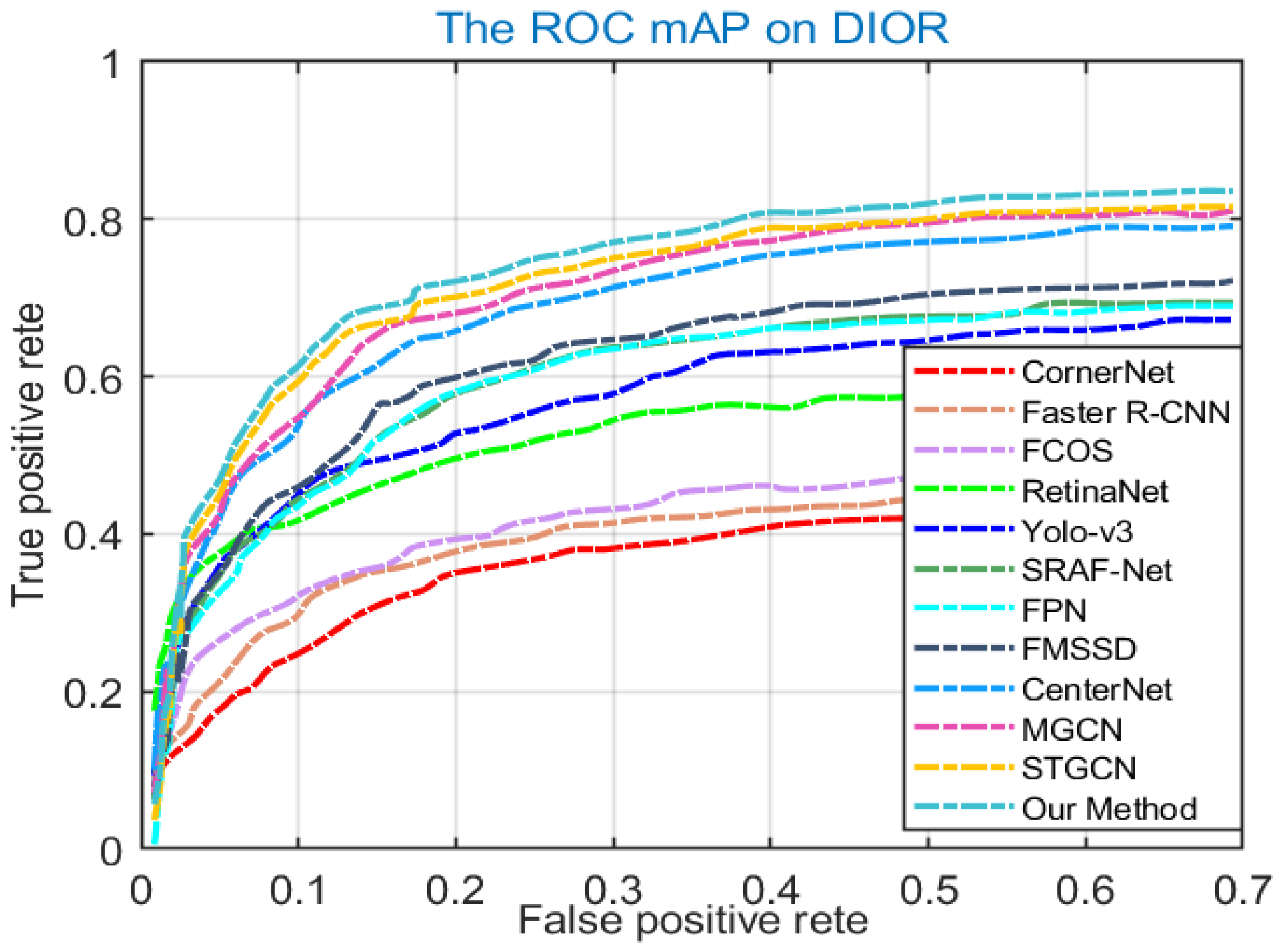
4.4.2. Comparisons and Analysis on the DIOR Dataset
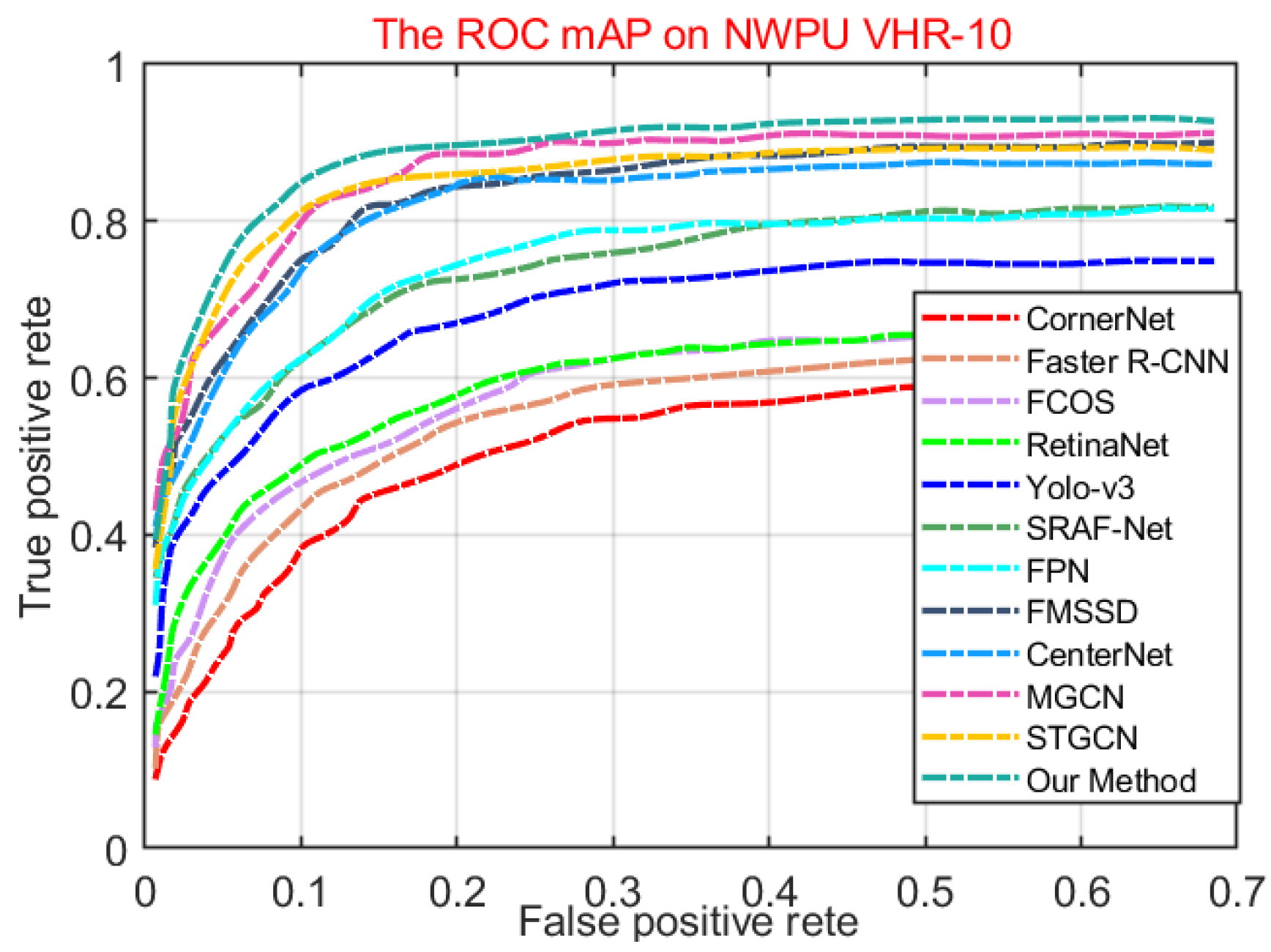
4.4.3. Comparisons and Analysis on the NWPU VHR-10 Dataset
4.4.4. Computational Cost Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Li, Y.; Chen, W.; Li, Y.; Dang, B. DNAS: Decoupling Neural Architecture Search for High-Resolution Remote Sensing Image Semantic Segmentation. Remote Sens. 2022, 14, 3864. [Google Scholar] [CrossRef]
- Ji, X.; Huang, L.; Tang, B.-H.; Chen, G.; Cheng, F. A Superpixel Spatial Intuitionistic Fuzzy C-Means Clustering Algorithm for Unsupervised Classification of High Spatial Resolution Remote Sensing Images. Remote Sens. 2022, 14, 3490. [Google Scholar] [CrossRef]
- Cheng, F.; Fu, Z.; Tang, B.; Huang, L.; Huang, K.; Ji, X. STF-EGFA: A Remote Sensing Spatiotemporal Fusion Network with Edge-Guided Feature Attention. Remote Sens. 2022, 14, 3057. [Google Scholar] [CrossRef]
- Qin, H.; Li, Y.; Lei, J.; Xie, W.; Wang, Z. A specially optimized one-stage network for object detection in remote sensing images. IEEE Geosci. Remote. Sens. Lett. 2021, 18, 401–405. [Google Scholar] [CrossRef]
- Ma, W.; Guo, Q.; Wu, Y.; Zhao, W.; Zhan, X.; Ji, L. A novel multi-model decision fusion network for object detection in remote sensing images. Remote Sens. 2019, 11, 737. [Google Scholar] [CrossRef]
- Qin, H.; Li, Y.; Lei, J.; Xie, W.; Wang, Z. Cross-scale feature fusion for object detection in optical remote sensing images. IEEE Geosci. Remote Sens. Lett. 2020, 18, 431–435. [Google Scholar]
- Ren, S.; He, K.; Gishick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- Cheng, G.; Yan, B.; Shi, P.; Li, K.; Yao, X.; Guo, L.; Han, J. Prototype-CNN for few-shot object detection in remote sensing images. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–10. [Google Scholar] [CrossRef]
- Long, Y.; Gong, Y.; Xiao, Z.; Liu, Q. Accurate object localization in remote sensing images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2486–2498. [Google Scholar] [CrossRef]
- Li, Q.; Wang, G.; Liu, J.; Chen, S. Robust scale-invariant feature matching for remote sensing image registration. IEEE Geosci. Remote Sens. Lett. 2009, 6, 287–291. [Google Scholar]
- Sirmacek, B.; Unsalan, C. Urban-area and building detection using SIFT keypoints and graph theory. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1156–1167. [Google Scholar] [CrossRef]
- Tao, C.; Tan, Y.; Cai, H.; Tian, J. Airport detection from large IKONOS images using clustered SIFT keypoints and region information. IEEE Geosci. Remote Sens. Lett. 2010, 8, 128–132. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Xiao, Z.; Liu, Q.; Tang, G.; Zhai, X. Elliptic Fourier transformation-based histograms of oriented gradients for rotationally invariant object detection in remote-sensing images. Int. J. Remote Sens. 2015, 36, 618–644. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Zhou, P.; Guo, L. Multi-class geospatial object detection and geographic image classification based on collection of part detectors. ISPRS J. Photogramm. Remote Sens. 2014, 98, 119–132. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, Y.; Feng, Y.; Lu, X. Hierarchical and robust convolutional neural network for very high-resolution remote sensing object detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5535–5548. [Google Scholar] [CrossRef]
- Meynberg, O.; Cui, S.; Reinartz, P. Detection of high-density crowds in aerial images using texture classification. Remote Sens. 2016, 8, 470. [Google Scholar] [CrossRef]
- Sun, H.; Sun, X.; Wang, H.; Li, Y.; Li, X. Automatic target detection in high-resolution remote sensing images using spatial sparse coding bag-of-words model. IEEE Geosci. Remote Sens. Lett. 2011, 9, 109–113. [Google Scholar] [CrossRef]
- Cheng, G.; Zhou, P.; Han, J. Learning rotation-invariant convolutional neural networks for object detection in VHR optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7405–7415. [Google Scholar] [CrossRef]
- Liu, J.; Yang, D.; Hu, F. Multiscale Object Detection in Remote Sensing Images Combined with Multi-Receptive-Field Features and Relation-Connected Attention. Remote Sens. 2022, 14, 427. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, H. Multi-Stage Feature Enhancement Pyramid Network for Detecting Objects in Optical Remote Sensing Images. Remote Sens. 2022, 14, 579. [Google Scholar] [CrossRef]
- Han, X.; Zhou, Y.; Zhang, L. An efficient and robust integrated geospatial object detection framework for high spatial resolution remote sensing imagery. Remote Sens. 2017, 9, 666. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Zhou, P.; Xu, D. Learning rotation-invariant and fisher discriminative convolutional neural networks for object detection. IEEE Trans. Image Process. 2018, 28, 265–278. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Zhuang, Y.; Chen, H.; Liu, X.; Zhang, T.; Li, L.; Dong, S.; Sang, Q. Rotation-insensitive and context-augmented object detection in remote sensing images. IEEE Trans. Geosci. Remote Sens. 2017, 56, 2337–2348. [Google Scholar]
- Deng, Z.; Sun, H.; Zhou, S.; Zhao, J.; Lei, L.; Zou, H. Multi-scale object detection in remote sensing imagery with convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2018, 145, 3–22. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, T.; Ouyang, C. End-to-end airplane detection using transfer learning in remote sensing images. Remote Sens. 2018, 10, 139. [Google Scholar] [CrossRef]
- Wang, G.; Zhuang, Y.; Chen, H.; Liu, X.; Zhang, T.; Li, L.; Dong, S.; Sang, Q. FSoD-Net: Full-scale object detection from optical remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, Y.; Wang, J.; Wang, Y.; Wang, Q. Semantic Context-Aware Network for Multiscale Object Detection in Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, Y.; Wang, J.; Wang, Y.; Wang, Q. Few-shot object detection via feature reweighting. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 8420–8429. [Google Scholar]
- Wang, P.; Sun, X.; Diao, W.; Fu, K.; Zhang, T.; Li, L.; Dong, S.; Sang, Q. FMSSD: Feature-merged single-shot detection for multiscale objects in large-scale remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3377–3390. [Google Scholar] [CrossRef]
- Chen, S.; Dai, B.; Tang, J.; Luo, B.; Wang, W.; Lv, K.; Dong, S.; Sang, Q. A refined single-stage detector with feature enhancement and alignment for oriented object. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8898–8908. [Google Scholar] [CrossRef]
- Li, X.; Drng, J.; Fang, Y. Enhanced TabNet: Attentive Interpretable Tabular Learning for Hyperspectral Image Classification. Remote Sens. 2022, 14, 716. [Google Scholar]
- Pan, F.; Wu, Z.; Liu, Q.; Xu, Y.; Wei, Z. DCFF-Net: A Densely Connected Feature Fusion Network for Change Detection in High-Resolution Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11974–11985. [Google Scholar] [CrossRef]
- Li, X.; Deng, J.; Fang, Y. Few-shot object detection on remote sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Chen, J.; Wan, J.; Zhu, G.; Xu, G.; Deng, M. Multi-scale spatial and channel-wise attention for improving object detection in remote sensing imagery. IEEE Geosci. Remote Sens. Lett. 2019, 17, 681–685. [Google Scholar] [CrossRef]
- Yang, X.; Yang, J.; Yan, J.; Zhang, Y.; Zhang, T.; Guo, Z.; Sun, X.; Fu, K. Scrdet: Towards more robust detection for small, cluttered and rotated objects. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 8232–8241. [Google Scholar]
- Wang, C.; Bai, X.; Wang, S.; Zhou, J.; Ren, P. Multiscale visual attention networks for object detection in VHR remote sensing images. IEEE Geosci. Remote Sens. Lett. 2018, 16, 310–314. [Google Scholar] [CrossRef]
- Lu, X.; Ji, J.; Xing, Z.; Miao, Q. Attention and feature fusion SSD for remote sensing object detection. IEEE Trans. Geosci. Remote Sens. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Yang, L.; Zhan, X.; Chen, D.; Yan, J.; Lov, C.; Lin, D. Learning to cluster faces on an affinity graph. In Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 2298–2306. [Google Scholar]
- Yang, L.; Zhan, X.; Chen, D.; Yan, J.; Lov, C.; Lin, D. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Shi, L.; Zhang, Y.; Cheng, J.; Lu, H. Two-stream adaptive graph convolutional networks for skeleton-based action recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 12026–12035. [Google Scholar]
- He, C.; Lai, S.; Lam, K. Improving object detection with relation graph inference. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 2537–2541. [Google Scholar]
- Chaudhuri, U.; Banerjee, B.; Bhattacharya, A. Siamese graph convolutional network for content based remote sensing image retrieval. Comput. Vis. Image Underst. 2019, 184, 22–30. [Google Scholar] [CrossRef]
- Khan, N.; Chaudhuri, U.; Banerjee, B.; Chaudhuri, S. Graph convolutional network for multi-label VHR remote sensing scene recognition. Neurocomputing 2019, 357, 36–46. [Google Scholar] [CrossRef]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.-S.; Dean, J. Distributed representations of words and phrases and their compositionality. Adv. Neural Inf. Process. Syst. 2013, 26. [Google Scholar]
- Hammond, D.K.; Vandergheynst, P.; Gribonval, R. Wavelets on graphs via spectral graph theory. Appl. Comput. Harmon. Anal. 2011, 30, 129–150. [Google Scholar] [CrossRef]
- Kopf, T.N.; Welling, X. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.-N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Xiao, L.; Wu, X.; Wu, W.; Yang, J.; He, L. Multi-Channel Attentive Graph Convolutional Network with Sentiment Fusion for Multimodal Sentiment Analysis. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 4578–4582. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1440–1448. [Google Scholar]
- Hsieh, T.-I.; Lo, Y.-C.; Chen, H.-T.; Liu, J.T.-L. One-shot object detection with co-attention and co-excitation. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Xia, G.; Bai, X.; Ding, J.; Zhu, Z.; Belongie, S.; Luo, J.; Datcu, M.; Pelillo, M.; Zhang, L. DOTA: A large-scale dataset for object detection in aerial images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 3974–3983. [Google Scholar]
- Li, K.; Wan, G.; Cheng, G.; Meng, L.; Han, J. Object detection in optical remote sensing images: A survey and a new benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 159, 296–307. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, M.; Wang, Y.; Zhu, Y.; Zhang, Z. Object detection in high resolution remote sensing imagery based on convolutional neural networks with suitable object scale features. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2104–2114. [Google Scholar] [CrossRef]
- He, C.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Piotr, D.; Ross, G.; He, K.; Bharah, H.; Serge, B. Feature pyramid networks for object detection. In Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Remon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2017, arXiv:1804.02767. [Google Scholar]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Piotr, D. Focal Loss for Dense Object Detection. In Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2980–2988. [Google Scholar]
- Tian, Z.; Shen, C.; Chen, H.; He, T. Fcos: Fully convolutional one-stage object detection. In Proceedings of the International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 9627–9636. [Google Scholar]
- Liu, J.; Li, S.; Zhou, C.; Cao, X.; Gao, Y.; Wang, B. SRAF-Net: A Scene-Relevant Anchor-Free Object Detection Network in Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Law, H.; Deng, J. Cornernet: Detecting objects as paired keypoints. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 734–750. [Google Scholar]
- Duan, K.; Bai, S.; Xie, L.; Qi, H.; Huang, Q.; Tian, Q. Centernet: Keypoint triplets for object detection. In Proceedings of the International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 6569–6578. [Google Scholar]
- Jiang, B.; Jiang, X.; Tang, J.; Luo, B.; Huang, S. Multiple graph convolutional networks for co-saliency detection. In Proceedings of the International Conference on Multimedia and Expo (ICME), Shanghai, China, 8-12 July 2019; pp. 332–337. [Google Scholar]
- Yan, S.; Xiong, Y.; Lin, D. Spatial temporal graph convolutional networks for skeleton-based action recognition. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence (AAAI), New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]





| HA -MHGEN | Configuration | DOTA | DIOR | NWPU VHR-10 | ||||
| Spa-Ra | Sem-Ra | SA-Spa-Ra | SA-Sem-Ra | MH-SS-Ra | mAP | mAP | mAP | |
| ✔ | - | - | - | - | 69.34 | 67.92 | 86.35 | |
| ✔ | ✔ | - | - | - | 72.13 | 69.15 | 89.78 | |
| ✔ | ✔ | ✔ | - | - | 74.02 | 71.42 | 90.47 | |
| ✔ | ✔ | ✔ | ✔ | - | 74.39 | 72.35 | 91.96 | |
| ✔ | ✔ | ✔ | ✔ | ✔ | 78.32 | 74.72 | 93.39 | |
| Methods | Airplane | BD | Bridge | Ship | GTF | BC | SV | LV | TC | ST | SBF | RA | SP | Harbor | HC | mAP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CornerNet | 67.85 | 78.94 | 53.59 | 27.08 | 68.05 | 63.75 | 31.39 | 46.52 | 87.96 | 53.57 | 62.46 | 69.79 | 43.06 | 58.79 | 23.94 | 55.78 |
| Faster R-CNN | 76.15 | 63.70 | 29.60 | 67.70 | 54.86 | 50.10 | 67.70 | 62.59 | 86.89 | 67.33 | 55.84 | 40.91 | 43.64 | 65.71 | 48.34 | 56.13 |
| FCOS | 88.81 | 71.63 | 56.35 | 68.92 | 40.86 | 67.31 | 49.37 | 74.58 | 89.56 | 70.77 | 44.63 | 70.97 | 42.71 | 66.90 | 36.97 | 62.69 |
| RetinaNet | 72.99 | 68.17 | 65.96 | 68.59 | 76.22 | 62.33 | 25.51 | 62.78 | 84.20 | 51.31 | 57.78 | 80.87 | 57.81 | 65.96 | 48.50 | 63.27 |
| Yolo-v3 | 93.91 | 68.78 | 45.93 | 85.56 | 51.92 | 66.82 | 50.12 | 60.67 | 93.88 | 83.47 | 52.45 | 45.01 | 55.85 | 74.03 | 56.68 | 65.67 |
| SRAF-Net | 88.93 | 72.76 | 50.10 | 83.77 | 45.93 | 70.32 | 59.51 | 75.69 | 93.00 | 67.08 | 55.63 | 62.69 | 47.36 | 71.45 | 41.80 | 65.73 |
| FPN | 88.70 | 75.10 | 52.60 | 84.50 | 59.20 | 81.30 | 69.40 | 78.80 | 90.60 | 82.60 | 52.50 | 62.10 | 66.30 | 76.60 | 60.10 | 72.00 |
| FMSSD | 89.11 | 81.51 | 48.22 | 76.87 | 67.94 | 82.67 | 69.23 | 73.56 | 90.71 | 73.33 | 52.65 | 67.52 | 80.57 | 72.37 | 60.15 | 72.43 |
| CenterNet | 97.37 | 78.56 | 49.39 | 90.30 | 53.39 | 66.11 | 62.16 | 80.24 | 94.58 | 85.75 | 64.86 | 69.02 | 75.63 | 78.86 | 66.82 | 73.94 |
| MGCN | 98.13 | 82.74 | 56.15 | 90.46 | 57.14 | 67.98 | 66.85 | 83.76 | 96.17 | 86.98 | 65.78 | 72.54 | 78.19 | 80.62 | 67.26 | 76.71 |
| STGCN | 90.42 | 79.87 | 63.39 | 86.42 | 76.54 | 80.08 | 77.46 | 87.87 | 86.83 | 82.45 | 68.19 | 69.43 | 65.08 | 81.41 | 57.17 | 76.84 |
| Our Method | 94.57 | 81.07 | 61.76 | 88.67 | 78.16 | 81.98 | 79.15 | 88.62 | 88.79 | 82.13 | 69.87 | 70/17 | 67.67 | 83.15 | 58.98 | 78.32 |
| Methods | Airplane | BF | Bridge | GTF | Ship | STM | TC | BC | ST | Harbor | Airport | ESA | Chimney | Dam | VE | GC | TS | OP | ETS | WM | mAP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Faster R-CNN | 51.40 | 62.20 | 27.00 | 61.80 | 56.10 | 41.80 | 73.90 | 80.70 | 39.60 | 43.70 | 61.60 | 53.40 | 74.20 | 37.30 | 34.30 | 69.60 | 44.70 | 49.00 | 45.10 | 65.30 | 53.60 |
| Yolo-v3 | 67.50 | 65.80 | 34.20 | 68.90 | 86.80 | 40.30 | 83.90 | 86.80 | 67.80 | 54.30 | 54.70 | 55.70 | 73.50 | 34.30 | 49.10 | 67.30 | 32.30 | 51.70 | 49.60 | 73.60 | 59.90 |
| FCOS | 73.60 | 84.30 | 32.10 | 17.10 | 51.10 | 71.40 | 77.40 | 46.70 | 63.10 | 73.20 | 62.00 | 76.60 | 52.40 | 39.70 | 71.90 | 80.80 | 37.20 | 46.10 | 58.40 | 82.70 | 60.00 |
| Center -Net | 64.00 | 65.70 | 34.80 | 66.00 | 81.30 | 53.50 | 80.90 | 86.30 | 63.70 | 45.30 | 66.30 | 60.80 | 73.10 | 41.10 | 46.30 | 73.00 | 44.10 | 53.30 | 54.20 | 78.80 | 61.60 |
| Retina -Net | 63.40 | 83.30 | 48.20 | 59.10 | 72.00 | 82.40 | 90.10 | 78.40 | 80.70 | 47.60 | 47.80 | 53.20 | 67.90 | 49.40 | 47.70 | 66.30 | 55.00 | 45.70 | 73.60 | 92.00 | 63.40 |
| Corner -Net | 68.50 | 85.20 | 46.90 | 16.80 | 34.50 | 89.10 | 84.70 | 78.40 | 40.00 | 68.60 | 77.10 | 73.90 | 76.90 | 60.20 | 45.00 | 79.10 | 52.30 | 58.90 | 74.80 | 70.10 | 64.10 |
| FPN | 54.00 | 63.30 | 44.80 | 76.80 | 71.80 | 68.30 | 81.10 | 80.70 | 53.80 | 46.40 | 74.50 | 76.50 | 72.50 | 60.00 | 43.10 | 76.00 | 59.50 | 57.20 | 62.30 | 81.20 | 65.10 |
| SRAF -Net | 88.40 | 92.60 | 83.80 | 16.20 | 59.40 | 80.90 | 87.90 | 90.60 | 55.60 | 76.40 | 76.50 | 86.80 | 83.80 | 58.60 | 53.20 | 82.80 | 90.60 | 58.00 | 66.80 | 91.00 | 69.70 |
| FMSSD | 85.60 | 75.80 | 40.70 | 78.60 | 84.90 | 76.70 | 87.90 | 89.50 | 65.30 | 62.00 | 82.40 | 67.10 | 77.60 | 64.70 | 44.50 | 80.80 | 62.40 | 58.00 | 61.70 | 76.30 | 71.10 |
| MGCN | 87.19 | 73.97 | 52.34 | 80.13 | 86.14 | 79.15 | 89.24 | 91.09 | 68.13 | 68.65 | 85.92 | 72.09 | 79.23 | 66.16 | 47.33 | 83.16 | 66.19 | 53.89 | 67.45 | 73.98 | 73.57 |
| STGCN | 88.13 | 72.54 | 49.76 | 85.32 | 86.76 | 77.91 | 88.15 | 90.12 | 70.16 | 69.73 | 83.17 | 74.11 | 79.57 | 67.98 | 44.54 | 85.90 | 67.23 | 54.17 | 68.12 | 71.25 | 73.73 |
| Our Method | 88.93 | 77.13 | 52.34 | 81.51 | 87.24 | 78.09 | 89.53 | 92.08 | 72.23 | 71.42 | 85.17 | 74.17 | 75.32 | 71.23 | 46.87 | 86.78 | 69.18 | 52.46 | 71.86 | 70.98 | 74.72 |
| Methods | Airplane | Ship | BD | BC | TC | ST | Vehicle | Bridge | Harbor | GTF | mAP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CornerNet | 72.10 | 53.67 | 44.13 | 83.16 | 67.79 | 56.51 | 77.25 | 92.67 | 49.17 | 99.96 | 69.64 |
| CenterNet | 73.09 | 71.97 | 87.41 | 73.37 | 65.12 | 59.91 | 55.75 | 53.76 | 75.48 | 95.27 | 71.11 |
| Yolo-v3 | 92.50 | 62.90 | 59.48 | 47.99 | 64.08 | 56.12 | 72.59 | 59.48 | 70.06 | 92.17 | 71.32 |
| RetinaNet | 99.56 | 78.16 | 99.55 | 65.18 | 83.37 | 82.29 | 71.91 | 40.25 | 65.66 | 95.38 | 78.13 |
| Faster R-CNN | 97.83 | 78.66 | 89.99 | 58.80 | 80.85 | 90.68 | 73.09 | 63.33 | 80.68 | 95.47 | 80.94 |
| SRAF-Net | 94.59 | 83.80 | 53.99 | 92.38 | 88.39 | 72.84 | 89.21 | 96.95 | 63.53 | 98.95 | 83.45 |
| STGCN | 95.76 | 94.82 | 93.45 | 86.92 | 85.83 | 95.03 | 87.39 | 73.41 | 84.86 | 87.62 | 88.50 |
| FMSSD | 99.70 | 89.90 | 98.20 | 96.80 | 86.00 | 90.30 | 88.20 | 80.10 | 75.60 | 99.60 | 90.40 |
| FPN | 100 | 90.86 | 96.84 | 95.05 | 90.67 | 99.99 | 90.19 | 50.86 | 93.67 | 100 | 90.80 |
| MGCN | 98.36 | 92.15 | 99.16 | 97.24 | 86.87 | 91.02 | 89.86 | 81.34 | 77.19 | 97.67 | 91.08 |
| FCOS | 99.99 | 85.21 | 97.75 | 80.34 | 95.80 | 96.94 | 88.92 | 88.92 | 95.04 | 99.67 | 92.14 |
| Our Method | 97.19 | 88.86 | 98.68 | 83.09 | 94.17 | 98.97 | 90.54 | 87.64 | 97.65 | 97.13 | 93.39 |
| Methods | Backbone | map@DOTA | map@DIOR | map@NWPU VHR-10 | Params (M) | GFLOPs | Inference Times (ms) |
|---|---|---|---|---|---|---|---|
| Faster R-CNN | ResNet-101 | 56.17 | 55.24 | 82.37 | 60.7 | 81.6 | 67 |
| Yolo-v3 | DarkNet-53 | 66.92 | 58.97 | 72.16 | 60.04 | 82.4 | 28 |
| FCOS | ResNet-101 | 61.73 | 61.37 | 92.39 | 51.2 | 70.65 | 55 |
| CenterNet | ResNet-101 | 74.08 | 62.51 | 72.07 | 52.7 | 75.2 | 44 |
| RetinaNet | ResNet-101 | 64.19 | 63.27 | 79.6 | 56.9 | 81.3 | 91 |
| CornerNet | Hourglass-54 | 55.82 | 64.59 | 71.84 | 112.7 | 287.6 | 127 |
| FPN | ResNet-101 | 72.43 | 66.18 | 91.34 | 50.7 | 112.3 | 69 |
| SRAF-Net | ResNet-101 | 66.37 | 70.39 | 84.55 | 62.9 | 87.2 | 46 |
| FMSSD | VGG-16 | 74.76 | 72.37 | 91.17 | 61.3 | 84.2 | 42 |
| MGCN | ResNet-101 | 77.92 | 72.94 | 91.39 | 62.4 | 87.2 | 52 |
| STGCN | ResNet-101 | 76.18 | 73.15 | 92.07 | 64.6 | 90.1 | 56 |
| Our Method | ResNet-101 | 78.79 | 74.96 | 93.27 | 51.4 | 67.9 | 33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, S.; Cao, L.; Kang, L.; Xing, X.; Tian, J.; Du, K.; Sun, K.; Fan, C.; Fu, Y.; Zhang, Y. A Novel Hybrid Attention-Driven Multistream Hierarchical Graph Embedding Network for Remote Sensing Object Detection. Remote Sens. 2022, 14, 4951. https://doi.org/10.3390/rs14194951
Tian S, Cao L, Kang L, Xing X, Tian J, Du K, Sun K, Fan C, Fu Y, Zhang Y. A Novel Hybrid Attention-Driven Multistream Hierarchical Graph Embedding Network for Remote Sensing Object Detection. Remote Sensing. 2022; 14(19):4951. https://doi.org/10.3390/rs14194951
Chicago/Turabian StyleTian, Shu, Lin Cao, Lihong Kang, Xiangwei Xing, Jing Tian, Kangning Du, Ke Sun, Chunzhuo Fan, Yuzhe Fu, and Ye Zhang. 2022. "A Novel Hybrid Attention-Driven Multistream Hierarchical Graph Embedding Network for Remote Sensing Object Detection" Remote Sensing 14, no. 19: 4951. https://doi.org/10.3390/rs14194951
APA StyleTian, S., Cao, L., Kang, L., Xing, X., Tian, J., Du, K., Sun, K., Fan, C., Fu, Y., & Zhang, Y. (2022). A Novel Hybrid Attention-Driven Multistream Hierarchical Graph Embedding Network for Remote Sensing Object Detection. Remote Sensing, 14(19), 4951. https://doi.org/10.3390/rs14194951












