Abstract
The use of multi-mode remote sensing data for biomass prediction is of potential value to aid planting management and yield maximization. In this study, an advanced biomass estimation approach for sugarcane fields is proposed based on multi-source remote sensing data. Since feature interpretability in agricultural data mining is significant, a feature extraction method of deep archetypal analysis (DAA) that has good model interpretability is introduced and aided by principal component analysis (PCA) for feature mining from the multi-mode multispectral and light detection and ranging (LiDAR) remote sensing data pertaining to sugarcane. In addition, an integrated regression model integrating random forest regression, support vector regression, K-nearest neighbor regression and deep network regression is developed after feature extraction by DAA to precisely predict biomass of sugarcane. In this study, the biomass prediction performance achieved using the proposed integrated learning approach is found to be predominantly better than that achieved by using conventional linear methods in all the time periods of plant growth. Of more significance, according to model interpretability of DAA, only a small set of informative features maintaining their physical meanings (four informative spectral indices and four key LiDAR metrics) can be extracted which eliminates the redundancy of multi-mode data and plays a vital role in accurate biomass prediction. Therefore, the findings in this study provide hands-on experience to planters with indications of the key or informative spectral or LiDAR metrics relevant to the biomass to adjust the corresponding planting management design.
1. Introduction
The issue of food production is a constant concern for governments, businesses, consumers, and other sectors because of its importance for national food security and individual living standards [1]. With the increasing demand for agricultural products due to the growing world population, how to increase crop yields has become one of the great challenges needing to be urgently addressed [2]. Among the various measures to increase crop yield, early biomass prediction on the field/farm scale plays an important role in providing guidance for adjusting crop management regimes. In other words, it can maximize crop yields and generate greater profit while reducing input resources and environmental pollution [3]. Non-destructive prediction of crop biomass is especially important for use as a guide for national food policy formulation, price control, and foreign food trade [4].
The rapid development of remote sensing technology in recent years has made it possible to achieve timeous, reliable, and cost-effective early biomass prediction. Among the different methods of remote sensing, unmanned aerial vehicle (UAV)-based remote sensing imaging is preferred as the primary means of data acquisition in agricultural production, accounting for the limitations of low resolution, high cost, and adverse influence of weather conditions in satellite remote sensing [5]. With collected remote sensing data using UAV, different vegetation indices (VIs) have been explored for crop biomass prediction. The normalized difference vegetation index (NDVI) proposed by Tucker et al. [6] was found to be very effective in characterizing the growth status of crops. It has a positive correlation with crop biomass. Based on this fact, more VI metrics were explored for trial use in agricultural biomass prediction activities for different crops. Among those are the enhanced vegetation index (EVI), the difference red edge index (NDRE), the green normalized difference vegetation index (GNDVI), etc. With calculation of these abundant VI features, the assessment of the crop biomass is mainly realized by finding the optimal VI. For example, Sulik and Long [7] used the normalized difference yellowness index (NDYI) to estimate flowering yield of oilseed rape which provided a better performance than NDVI. As more VI metrics were proposed, to address the limitations of individual VI metrics, multiple VIs can be combined as predictor variables to improve the effectiveness of biomass prediction methods. For example, Da et al. [8] found that a combination of soil-adjusted vegetation index (SAVI) and NDVI indices made a significant contribution in predicting soybean yield. Kouadio et al. [9] found that using EVI and NDVI could significantly reduce the errors of predicting wheat yield by extracting multiple VIs. Despite the encouraging results obtained using VIs, the intrinsic yield drivers have not been fully explored in the modelling.
Nowadays, using data from multiple sources to predict crop biomass is attracting much attention. Imaging with VIs-NIR sensors often suffers from saturation of data information, especially when applied on high density vegetation [10]. Therefore, it is necessary to use other sensors to acquire crop information as a supplement to the spectral information. Unlike multispectral information that can be quantified through VIs, the use of UAV-based light detection and ranging (LiDAR) sensors in agricultural research is relatively limited. In fact, studies conducted by Christiansen et al. [11] and Sofonia et al. [12] on wheat and sugarcane crops have revealed significant correlations between LiDAR-derived crop attributes and biomass. Therefore, the combination of spectral information conveyed in multispectral data and three-dimensional structural information of crops conveyed in LiDAR data to obtain more comprehensive information on crops has the potential to improve the estimation of plant traits in various agricultural applications.
With multi-source remote sensing data utilized for biomass prediction, many VI features can be obtained, with varying degrees of importance to the biomass prediction task. With limited training samples, simple concatenation or stacking of different feature objects may contain redundant information or result in overfitting models [13]. Therefore, feature dimensionality reduction is necessary when using multi-source remote sensing multispectral and LiDAR indicator data feature metrics [14]. For example, Cao et al. [15] used exploratory data analysis to select variables significantly associated with wheat yield. Li et al. [16] used the ReliefF feature selection algorithm to select two narrow-band vegetation indices for predicting potato yield. Zhang et al. [17] used a total of three methods of stepwise regression analysis, recursive feature elimination and Boruta analysis to select features for forest height estimation, all with relatively good results. There are also other feature transformation methods performing good feature learning for biomass estimation, such as principal component analysis (PCA) [18]. In fact, model interpretability is a key focus for feature learning in applications for agriculture and the forestry industry [19,20]. The lack of interpretability of the learning process make it difficult to find effective reference information to constrain and improve optimization of existing problems. Nowadays, the deep learning network is well known as a first choice for feature learning; however, limited model interpretability is a major problem when it is used for multi-source remote-sensing-based biomass prediction without being capable of providing features that have physical meaning. Moreover, most available deep learning networks are supervised. Archetypal analysis (AA) [21,22] aims to find data archetypes with extreme properties and shows great potential for feature learning. Given its ability to deliver good model interpretation, its kernel extension has been explored for extracting multi-source remote sensing metrics to facilitate forest age attribute evaluation by modification with fast implementation [13]. As with the probabilistic realization of AA by Seth [23], Keller et al. [24] proposed a deep archetypal analysis (DAA) in their latest research, which presents a significant ability to achieve unsupervised non-linear feature learning in potential space and is especially useful for applications with small training sets. Moreover, DAA allows use of a priori auxiliary information to guide the search for interpretable archetypal features. DAA, shows great potential for mining informative interpretable features in abundant multisource remote sensing data for biomass prediction through unsupervised non-linear deep learning by adding proper guiding information.
In addition to the use of informative VIs, another important aspect of estimation of crop biomass requires precise and robust regression models [25]. Multiple linear regression (MLR) is the most popular regression modelling method due to its simplicity and efficiency. For example, Stateras et al. [26] used MLR to develop an olive tree yield prediction model including factors such as NDVI and ground slope. Zhou et al. [1] used MLR to establish the relationship between rice yield and variables of NDVI and visible atmospherically resistant index (VARI) at different stages of its growth, which achieved a coefficient of determination exceeding 0.7. However, when there are complex relationships between predictor variables and biomass, linear regression models have limited performance [27]. There have been several non-linear regression models reported that are able to handle non-linear fitting tasks, such as random forest regression (RFR) [28], support vector regression (SVR) [29] and K-nearest neighbor regression (KNN) [30]. Zhang et al. [31] achieved good results in predicting winter wheat yield using SVR with hyperspectral data. Xu et al. [32] used RFR to estimate maize biomass and found that it was very helpful for precise estimation. Han et al. [33] used both SVR and RFR to predict winter wheat yield and achieved an of greater than 0.75. A deep neural network (DNN) was demonstrated to have powerful non-linear learning ability in different applications including regression tasks [34]. For example, Kross [35] used neural networks to model crop yields. Yang et al. [36] used deep convolutional networks for regression, and it was found to be significantly better than traditional regression models. Compared to those individual models, in recent years, integrated learning methods that integrate multiple underlying learners have received much attention [37,38,39]. Through use of integrated approaches, for example, the stacked regression method of superimposed regression [40], heterogeneous learners have been combined to exploit their different merits for regression accuracy improvement in forest cover estimation [41], PM2.5 monitoring [42] and predicting the yield of alfalfa [37] with hyperspectral data. However, integration of general regression models including DNN regression has rarely been explored for precise biomass prediction.
In light of the above facts, the aim of this study is to propose a deep-learning-based biomass prediction approach for sugarcane fields using UAV-based multi-source remote sensing data. Specific objectives include: (1) proposing a PCA-aided DAA interpretable remote sensing feature selection method for biomass prediction; (2) establishing an integrated regression model including DNN regression; and (3) evaluating the potential of the proposed approach for sugarcane biomass prediction.
2. Materials and Methods
2.1. Data Source
The dataset used in this study was created by Yuri et al. [18] for sugarcane biomass prediction. Data acquisition was conducted in the sugarcane fields using both UAV-based LiDAR and multispectral imaging sensors in six sessions during the growing season from November 2017 to June 2018. The sugarcane fields were sampled at two sites in north-east Queensland, each of which consisted of 10 m × 30 m blocks covering six rows of sugarcane. Nitrogen treatments (0, 70, 110, 150, 190 kg N/ha) were applied to each block by using randomized groups of categories. There were in total 56 randomly distributed sugarcane plots of size 2 m × 2 m that were finally collected for biomass evaluation during the last season. Manual weighing and recording of the mass of sugarcane from each of the 56 designated sampling plots were conducted. This biomass collection was used as reference to learn the proper biomass prediction model through relating to the remote sensed predictors calculated from multispectral and LiDAR data collected from these 56 field plots during six periods; biomass prediction at all locations of the planting site could then be achieved.
Yuri et al. [18] summarized and used 116 indices from multispectral and LiDAR data for predicting sugarcane biomass. Specifically, 10 vegetation indices, NDVI, NDRE, GNDVI, EVI, modified anthocyanin content index (MACI), optimized soil-adjusted vegetation index (OSAVI), simplified canopy chlorophyll content index (SCCCI), transformed chlorophyll absorption and reflectance index (TCARI), triangular greenness index and VARI, were calculated using multispectral images. On this basis, the maximum (max), minimum (min), mean (avg), standard deviation (std), 25th percentile (p25), 50th percentile (p50) and 75th percentile (p75) of each vegetation index of all pixels of each biomass sampling plot were derived, and a total of 70 multispectral features were obtained. In addition, a total of 46 LiDAR indicators were generated using LiDAR point cloud data. Maximum height (), average height (), average square height (), standard deviation of height (), height skewness (), height kurtosis (), 5th to 95th height percentiles (p05 to p95), 5th to 95th bincentiles (fraction of points between ground and the height percentile) (b05 to b95) and percentage of height points for 0 to 0.1 m, 0.1 m to 0.5 m, 0.5 m to 1 m and 1 m to 10 m (d00 to d03) (threshold values for d00, d01, d02 and d03 are defined to represent penetration of laser pulses at different sheights of sugarcane) were included. In this study, the same set of 116 metrics could be used to mine the key metrics important to sugarcane biomass prediction.
2.2. Method
The aim of this study is to investigate an advanced sugarcane biomass prediction method including potential feature mining and prediction modelling using UAV-based multi-source remote sensing. The workflow of the proposed approach is presented in Figure 1. As seen from Figure 1, with the fused multi-source remote sensing data metrics, interpretable feature selection was first conducted using a PCA-aided DAA. This network works to generate representative archetypes and then enables the elimination of an informative subset from the original 116 feature indicators. Then, an integrated regression model combining RFR, SVR, KNN and DNN is used to model the fitness between selected feature indicators and biomass to obtain the final biomass prediction model.
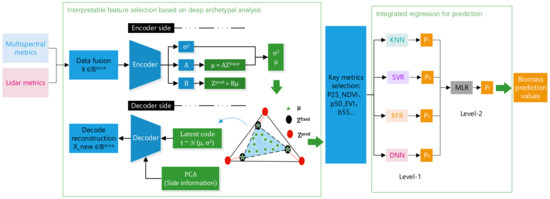
Figure 1.
Workflow diagram of the proposed biomass prediction method with the number of archetype parameters set to three as an example. , (i = 1, 2, 3, 4) are regression model predictions.
2.2.1. Interpretable Feature Selection
Feature selection is essential to reduce data dimensionality and extract more informative features before model development. Model interpretability is especially important for the intelligent processing of remote sensing information applied to agricultural applications [19,20]. To provide good model interpretability, a deep learning network of DAA [24] was deployed in this study to achieve representative feature learning from 116 remote sensed metrics of sugarcane to mine key metrics used for further biomass prediction.
The linear AA model can be regarded as a variant of non-negative matrix factorization. AA obtains low-dimensional potential factors called archetypes, endowed with geometric interpretation by imposing convex and non-negative constraints [22]. Mathematically, the objective of AA is to determine weight matrices A and B for a given data matrix X which enables obtaining a small set of k extreme/representative archetypes and can represent the data points using those archetypes. This leads to the following optimization problem formulated as Equation (1)
where is the input data with n features. The new features are known as archetypes which are generated as linear combinations of observations weighted by the index matrix B. The observations are reconstructed using these archetypes and the corresponding coefficients A.
The goal of DAA, as in linear AA, is to find K convex packets that best describe the components of the original data (i.e., the smallest convex set containing data X) and obtain extreme data patterns. DAA is established by adopting deep variational information bottleneck theory which combines the information bottleneck with the variational autoencoders approach. Different from AA, DAA identifies archetypes in a potential feature space. This is realized by transforming the original data X via a non-linear transformation into new representation . As deep variational information, bottleneck theory utilizes information bottleneck theory which optimizes the objective function (Equation (2)) to find the random variable T
where is the Lagrangian multiplier, and the function I denotes the mutual information domain. This formulation indicates that it enables T to retain as much information as possible from an auxiliary information matrix Y. Thus, in addition to good model interpretability, DAA also uses extra side information to guide the representative feature learning [24]. To constrain the feature learning process with extra benign property, PCA feature property and the advanced feature learning capability of DAA are combined in this study. Specifically, the auxiliary information Y is generated through PCA by setting the cumulative contribution of the principal component variance to 0.9. Using PCA principal components as auxiliary information is assumed to guide the data decomposition process to determine valuable archetypes in the potential space independent of each other as the principal components are orthogonal to each other. Moreover, approaching PCA decomposition is better to force the new data distribution with maximum cumulative variance. Another intention is to combine those advantages realized in the non-linear mapping space which can be taken as an indirect realization of PCA in the non-linear way but being imposed as more physical constraints.
By using a parametric form of Equation (2) with parametric conditionals and , and assuming IB Markov chain , the above formulation is revised thus
The non-linear transformation to achieve the new representation feature in DAA is realized through first sampling by means of the probabilistic AA following Equation (4)
where the mean and variance given by are non-linear transformations of data point learned by the encoder, and is a convex combination of the archetype , j = 1, …, k weighted by vector . The archetype is further considered to be a convex combination of , i = 1, …, m weighted by . Then, through learning the weight matrices A and B subjected to the convex constraints and Gaussian parameterization, DAA can learn, in a non-linear manner, the latent archetypes in the latent space and realize the transformation of X as a convex combination of those archetypes.
There is no absolute reference system in the potential space, so the k archetypes need to be positioned at the low-dimensional simplex, and matrix is used to collect the coordinates. This results in the loss of additional distance-dependent archetypes that need to be minimized:
where is the predicted archetype position given the learning weight matrices A and B. The optimal archetype structure is obtained if (i.e., the loss function is minimized) and the constraints on A and B can be guaranteed by using softmax layers. Therefore, the complete objective function of DAA is finally represented as Equation (6). More optimization details of DAA can be found elsewhere [24].
To acquire key original features rather than archetypes as mathematical generated features, this study mines the key metrics from the combination components of the archetypes. That means the most informative metric that contributes to each archetype is extracted. This must utilize the index matrix B of the archetypes as it indicates which original features contribute to the generation of the archetypes. Therefore, those original input feature metrics, which contribute the most to the generation of each archetype, are finally selected as the most explanatory physical features following Equation (7):
where represents the index vector corresponding to a certain archetype.
2.2.2. Biomass Prediction with an Integrated Regression Model
An appropriate regression model is important for biomass prediction. For example, the KNN method [30], an instance-based learning method that predicts the unknown sample by averaging the data of the k samples closest to the target sample, can tolerate noise and uncorrelated properties. Linear RFR [28] is a model that combines a large number of regression trees where each decision tree is constructed with a random set of features and samples and is learned independently of each other. The results of each tree are then combined to make the final prediction. Therefore, RFR can reduce overfitting. With respect to the non-linear regression methods, SVR [29] uses kernel functions to map data inputs to a high-dimensional feature space and realize non-linear regression. Those independent regression models have been widely explored for prediction tasks. Nowadays, as the powerful learning ability of a neural network, a deep regression network is of more potential to be constructed for regression. In addition, integrated learning that uses a sequence of learners to learn independently and then integrates the individual learning results following some rules can achieve more promising learning results. Therefore, in this study, an integrated learning model based on a stacking strategy proposed by Wolpert et al. [40] was used to integrate the abovementioned four regression models developed using different principles, while their power for biomass prediction has been demonstrated in many studies [25,27,43]. MLR was utilized to combine those base learners linearly for the sake of model diversity and complementary information. Specifically, the DNN regression network in this study was constructed with three fully connected hidden layers and 10 neurons for each layer. The entire neural network was trained by adjusting the weights of each hidden layer to establish an end-to-end relationship between the input and output. The non-linear Levenberg–Marquardt training algorithm was chosen for optimization as it is insensitive to over-parameterization problems and can reduce the possibility of falling into local minima.
2.3. Model Evaluation
To achieve acceptable accuracy and robustness when using such a small number of data samples, leave-one-out cross-validation was adopted for model training. In detail, 55 out of the total of 56 samples were selected at a time to train the model, and the remaining sample was used to validate the model performance, and the prediction performance of the model was characterized using the average of 56 test results.
To assess the predictive performance of the proposed model for crop biomass in a quantitative manner, the evaluation metrics in terms of , root mean square error (RMSE), and mean absolute deviation (MAE), were applied. The , RMSE, and MAE were calculated separately in the following equations:
where n is the number of samples, and are the observed and predicted values of the samples, respectively, and represents the mean of all observations. The higher the value of , the lower the RMSE and MAE, and the better the prediction achieved by the model.
3. Results
3.1. Multi-Source Data Feature Selection
Feature selection by DAA is unsupervised learning which requires manual settings of the generated representative archetypal features. To determine the optimal number of archetypes, features for biomass prediction with different parameter configurations were selected in this study, and the classic MLR model was used to quantify the effectiveness of those configurations of features for biomass estimation.
Figure 2 presents the biomass regression performance with varied number of archetypes in terms of . The number of archetype parameters is shown to increase; the prediction accuracy using the proposed feature selection methods shows an upward trend. To obtain the proper number of valuable predictors, the optimal number of archetypes for different periods of data was determined using the cut-off criterion of slow growth in model performance. For example, for Periods 2 and 3, the optimal archetype numbers can be obtained directly from the peak performance of the model, both with a value of 15. For Periods 1, 4, 5 and 6, since there is no significant peak in prediction performance, the archetype numbers at which the predicted performance begins to approach a plateau are selected as values of 15, 12, 14 and 12, respectively. Figure 3 displays fitted scatter plots of observed and predicted biomass values obtained using the respective best predictors for each of the six periods.
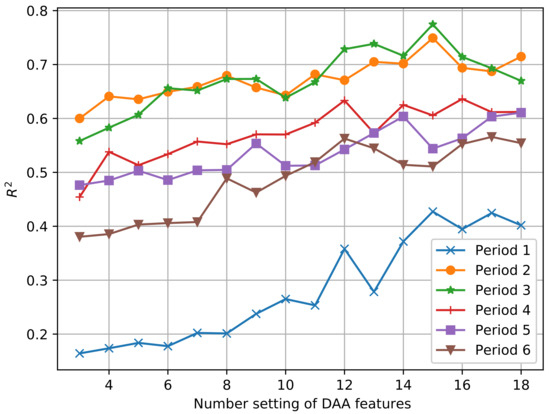
Figure 2.
Biomass prediction accuracy using MLR models with varied archetype settings.
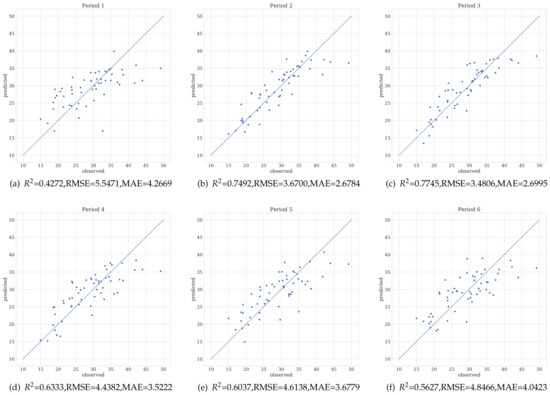
Figure 3.
Scatter plots of observed versus predicted values fitted using the best predictors for the six periods.
With the best subset of features achieved with PCA-aided DAA for biomass prediction in each period, prediction results compared to those using PCA-based feature learning and linear AA-based feature selection are illustrated in Figure 4. Prediction with PCA features was achieved according to the experimental setting by Yuri [18]. With the variance percentage set at 0.9, a total of seven-dimensional principal component features can be obtained with PCA for the biomass prediction using MLR in six different periods, and the values obtained are 0.1955, 0.6163, 0.6269, 0.5257, 0.4910 and 0.3695, respectively. When the feature learning of PCA is replaced by the proposed PCA-aided DAA feature selection in this study, the values of the fitting results show significant improvement over PCA in all six periods. In fact, it ranks first almost among all the counterpart methods during the whole growth period. It achieves the highest value of 0.7745 in the third period which obtains an improvement of 0.1476 compared to 0.6269 using a PCA approach in the same period. An average increase of at least 0.1076 can be achieved throughout the growth period. More increases are found in the early and late stages. Thus, those results confirm the validity of deep-learning-based feature selection method proposed in this study for predicting sugarcane biomass. Moreover, this figure also suggests that even though the linear AA is not as competitive as DAA in most periods except Period 5, it deserves higher recommendation compared to PCA in feature selection for biomass prediction.
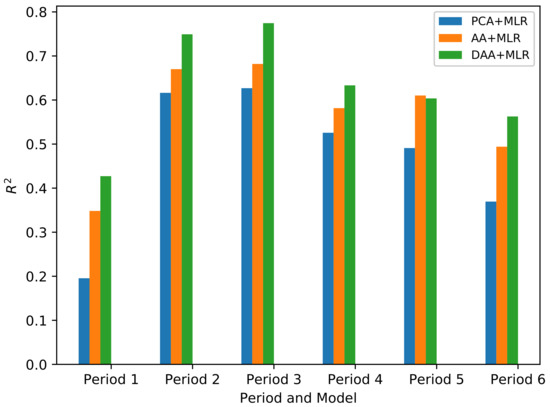
Figure 4.
Comparison of obtained with different feature selection methods for biomass prediction in six periods.
Table 1 summarizes the evaluation of the best subset of features selected by PCA-aided DAA for biomass prediction with the MLR model in six periods. The best metrics derived for biomass prediction in different periods are shown to differ. They were selected following Equation (7), and their specific weights in the generation of corresponding archetypes are presented in Figure 5. Combining the characteristics of the six periods of feature selection, the spectral indicators of , , , and and the LiDAR indicators , , p70 and b55 appear more frequently. Thus, these remote sensing metrics are considered as predictors with more potential value for biomass prediction. Table 1 also shows that during the whole growing process, the best prediction result arises in Period 3 with the highest of 0.7745, lowest RMSE of 3.4806 and an MAE of 2.6995. The growing status at the beginning and last period obtains much poorer predictions; therefore, around 120 days after application of fertilizer is the best time to predict sugarcane biomass. Using the metric data from this time period as an example, all the indicator metrics are visualized based on the data from this period (Figure 6). The biomass mapping results in Figure 6n imply that the growing statuses distribution represented by those 13 metrics including both spectra- and elevation-related, have different correlations with the final biomass distribution.

Table 1.
Selection of key indicators from multispectral and LiDAR data features.
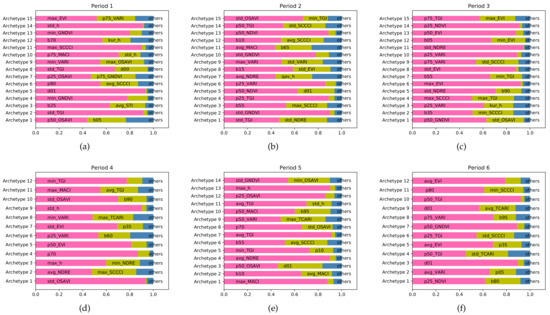
Figure 5.
The composition weight of the selected features in the respective archetype, with larger weights implying that the features are more capable of characterizing the extreme properties possessed by the archetype: (a) period 1; (b) period 2; (c) period 3; (d) period 4; (e) period 5; (f) period 6.
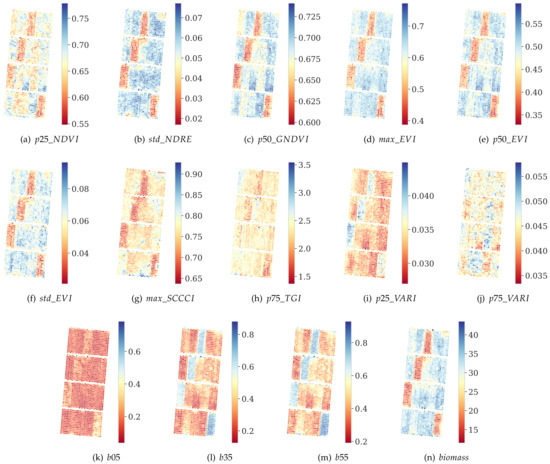
Figure 6.
Visualization of the growth status of the whole planted area with respect to each selected key metric. The final biomass map shows that most of the selected key indicators are correlated with crop biomass.
Figure 7 further presents the correlation between the above selected 13 predictors and the biomass data through a correlation matrix. As can be seen in the figure, the variables , , , , , , and are positively correlated with each other and with the biomass, while , , b05, b35 and b55 are negatively correlated with the previous variables and also negatively correlated with the biomass. This result is in fact along with the natural phenomena. For example, because the three LiDAR metrics of b05, b35 and b55 are defined as the fraction of points between the ground and the height percentile, the higher and denser growing of sugarcane means less points could arrive at the ground, and more points would be received at a higher height. Consequently, smaller values are calculated for those metrics, but more biomass would be achieved with higher and denser sugarcane.
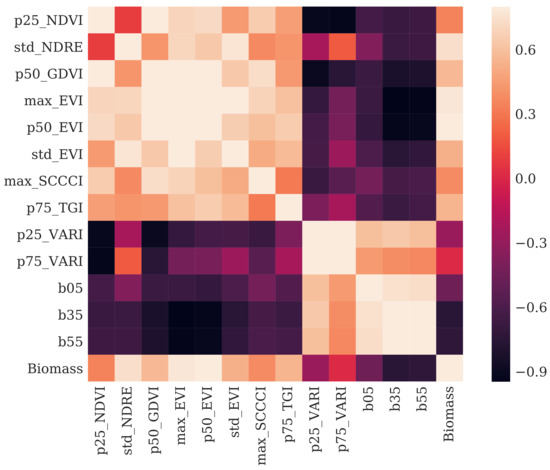
Figure 7.
Correlation matrix between selected features and biomass in Period 3.
3.2. Biomass Prediction with Different Regression Models
With the potential subset of biomass predictors, the four mentioned regression models introduced in Section 2.2.2 are first deployed for biomass prediction independently. Then, to evaluate the effectiveness of the stacking method, different combinations of the base learners are adopted to predict biomass for each of the six stages in the changing fertility of sugarcane. The biomass prediction results obtained are shown in Figure 8. The sugarcane biomass predicted by each individual regression model presents different performances on each prediction task. KNN and RFR do not maintain a high prediction accuracy in the whole growing periods and only have better results in a particular period. The highest achieved using SVR exceeds 0.7, but in some periods, the results are significantly inferior to those predicted by KNN or RFR algorithms. Obviously, the deep learning regression method behaves best among all methods assessed herein. Overall, the integrated regression models outperform every independent learning mode for predicting sugarcane biomass in all six periods; in general, the more the base learners are included, the more promising the prediction results are. The best results in all the periods are obtained by using the integrated learning with the four base learners. Compared to the best result of 0.7745 achieved using conventional MLR in Table 1, the integrated learning enables the much higher value of 0.8722 in the third period when the four base learners are integrated.
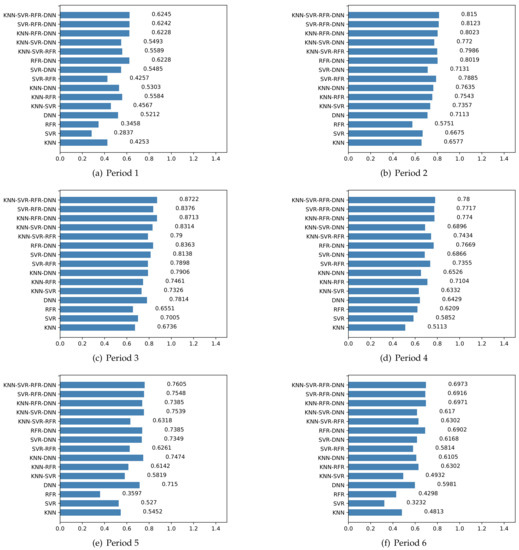
Figure 8.
comparison of different superimposed regression models for six periods.
Table 2 further displays the combination coefficients for the four base learners in the secondary integration learning layer with MLR. The higher the regression coefficient of a particular base learner is, the more significant its contribution to the final prediction performance will be. The effect of linear KNN on the performance of the stacking model has a positive correlation in the early periods and shows a negative correlation in the later stages, but the overall contribution is small with the regression coefficient being stable around 0.2. Interestingly, the trend of the integration coefficient of the non-linear SVR model is opposite that of KNN. It witnessed a steady decline, followed by a sharp fluctuation, first increasing, then decreasing. It maintains negative contributions in the integration for biomass prediction in the first three early stages and the final period. A positive coefficient for integration is only found in two stages. Over the six periods of the forecasting task, the RFR model shows a more stable performance, with regression coefficients fluctuating between 0.3 and 0.5. The DNN model makes the greatest contribution among all the base learners in all periods.

Table 2.
Distribution of regression coefficients within the second level model (MLR).
Figure 9 displays the scatter plots of observed versus predicted values obtained with the best predictors using the best integrated learning approach. In accordance with the best illustration of regression accuracy in Figure 8, the best visualization using fitting results is also obtained in Period 3. With respect to the regression models shown in Figure 9, the sugarcane biomass mapping of whole planting area in different periods using PCA-aided DAA feature selection and the best integrated regression learning including DNN is presented in Figure 10. Apparently, the predicted biomass distribution map learned with early or late period data obtains a prediction result violating the natural growing phenomenon. Figure 10c,d also show the discrete distribution of plant biomass, matching practical conditions on farmland. In contrast, the biomass of plants in a plant area shows more continuous and natural variations as shown in Figure 10b,c. In referring to the biomass prediction accuracy obtained on the sampled plots data as displayed in Figure 8, the biomass mapping of the whole plant area in Figure 10c is more promising in terms of its use in the evaluation of the growing status of such plants.
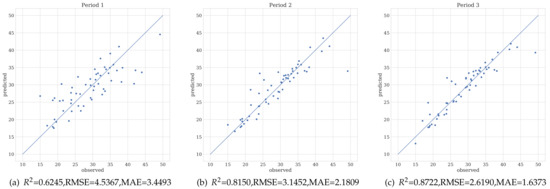
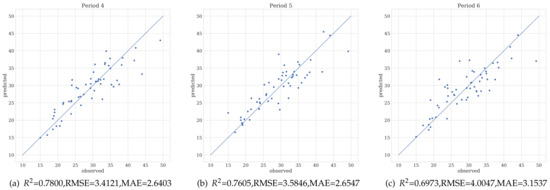
Figure 9.
Scatter plots of observed versus predicted biomass values achieved by the integrated regression model.
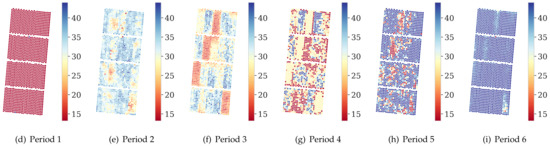
Figure 10.
Total biomass predicted using the proposed method for six periods. The color bars denote total biomass estimates from 10 to 40 in unit of kg.
4. Discussion
To establish a biomass prediction model with higher prediction accuracy through mining informative physical interpretable features to guide crop management interventions, this study proposes an effective deep-learning-based approach for feature selection based on a PCA-aided DAA network and using an integrated regression model. The proposed method archives much more promising results compared to traditional methods.
Appropriate feature processing of the data is an important step before regression modelling to obtain higher predictive performance. Feature processing algorithms such as recursive feature elimination [37] and PCA [18] have been applied to biomass prediction analysis with good results. In ecological studies, it is particularly important to select the most informative features from the original dataset, rather than use virtual mathematical features. Different from those widely used feature learning methods, our PCA-aided DAA network enables dimensionality reduction of the data features in a non-linear mapping space. Figure 4 shows that this non-linear method predominantly surpasses PCA and linear AA dimensionality reduction methods in feature mining for biomass prediction. Moreover, it allows easy extraction with clues to finding informative features while maintaining the original physical meaning of the data.
To address the challenge of precise biomass prediction, it is important to know the key influencing factors associated with yield to inform crop management interventions. In fact, it is of great significance to expound the implicit relationship between the physico-chemical characteristics of the object and those selected metrics. A study proves that remotely sensed vegetation indices can reflect the physiological characteristics of crops at different growth stages [44]. The higher values are usually associated with faster growth rates or higher biomass accumulation in crops [44,45]. In our study, different sets of VIs were found to exhibit potential for biomass prediction in different periods (Table 1). Figure 6 presents the 13 key metrics distribution of the whole planted area in the most representative period (Period 3). Most of the selected metrics that represent the growth status of the plants the most are also highly correlated with the biomass prediction results referring to Figure 6n, and those are mainly generated from spectral data. In contrast, three LiDAR metrics show a negative correlation with biomass. In fact, those three metrics are also in line with the natural phenomena because they are the fractions of points between ground and the corresponding height percentile. The higher and denser growing of sugarcane means that less points can arrive at the ground, and more points will be received at a higher height. Consequently, smaller values are calculated for b05, b35 and b55. This presents the potential value of our feature-selection method to extract interpretable remote sensing metrics which are important to reflect their relationship with final biomass. Moreover, the results also show that accurate prediction of the biomass relies on VIs of both spectral indices and LiDAR indicators. In fact, prediction of biomass using spectral indices alone encounters the problem of easy saturation in dense vegetation [10]. Combining spectral indices with LiDAR indicators carrying structural information about the crop (e.g., and b55) can benefit from the goodness of multi-source information to realize better predictions. Moreover, the traditional practice applies equal amounts of fertilizer indiscriminately to all planting areas at the beginning of the growing season. According to the information in Table 1 and Figure 6, proper adjustment measures to local conditions may allow better crop nutrient uptake and reduce environmental impacts through monitoring the key influencing factors and implementation of subsequent adjustments.
Many studies on crop biomass prediction have been performed using different regression methods, all of which have achieved promising prediction results [25,27,37,39,43]. In this study, Figure 8 shows most of the independent regression methods fail to achieve overall good prediction performance in different periods. Therefore, it is difficult for a single machine learning model to maintain a general high prediction performance in crop biomass estimation with different periods of remote sensing data. It is essential to develop a method that can integrate the advantages of multiple models to improve the accuracy of sugarcane biomass prediction under different growth conditions. Figure 8 demonstrates that the integrated learning combines the strengths of multiple machine learning models in obtaining greater prediction accuracy. It returns a more stable performance than the independent regression method which shows greater fluctuations over different periods; therefore, combining all suitable base learners by stacked regression methods as far as possible is an effective way in which to obtain an optimal model for sugarcane biomass prediction. Given the outstanding performance of the DNN shown in the present study, it deserves consideration for use in biomass estimation no matter whether used in independent or integrated learning cases.
The overall experimental results in this study show that the new approach proposed in this paper is very effective in improving the accuracy of biomass prediction based on early crop data. In terms of a temporal comparison, the prediction performance of the model peaks at the early periods of the season (i.e., the second and third periods in Figure 8) regardless of which method is used, and then the prediction accuracy gradually decreases. This finding suggests that the best time point for biomass prediction is around 120 days after crop fertilization, which is early in the entire growth cycle of sugarcane. The most likely reason for this result is that the differences in crop structure and vegetation index between the different N-fertilizer treatments are gradually decreasing with the increase in the crop growing period [18]. This is very important as it conforms to the practice that predicting crop biomass plays a significant role in adjustment of planting management practices to maximize yield. If the biomass could only be accurately predicted until late in the growing season, it would restrict the ability to take, and efficacy of, prompt actions or adjustments.
5. Conclusions
This study indicates that compared to the traditional biomass prediction technique using PCA, traditional AA and MLR, interpretable feature selection using the proposed PCA-aided DAA method and regression using an integrated regression model can further improve the biomass prediction performance. The prediction performance in terms of increased from 0.6269 in one available study [18] to 0.8722 using the method proposed here. The experimental results for six different periods of multi-source data pertaining to sugarcane plants indicate that our deep learning feature selection method enables users to achieve more informative VIs or LiDAR metrics than the PCA method in terms of feature interpretability. The multiple remote sensing metrics of , , , and and the LiDAR indicators , , p70 and b55 show potential value in sugarcane biomass estimation. This provides practical experience to growers with regard to the key or informative spectral or LiDAR indicators related to biomass, which allows them to adjust planting management plans accordingly.
Author Contributions
Conceptualization, Z.W. and Y.L.; methodology, Z.W., Y.L. and G.Z.; writing—original draft preparation, Z.W. and Y.L.; writing—review and editing, Z.W., G.Z., C.S., F.Z. and S.H.; funding acquisition, Z.W., G.Z., C.S., F.Z. and S.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was sponsored in part by National Natural Science Foundation of Guangdong under Grant 2020A1515011409, in part by Provincial Agricultural Science and Technology Innovation and Extension Project of Guangdong Province under Grant 2022KJ147, in part by the Guangzhou Fundamental and Applied Research 202201010273, in part by Key-Area Research and Development Program of Guangdong Province under Grant 2021B0101190003, in part by Special Project of Science and Technology Innovation Strategy of Guangdong Province under Grant 2021A1414030004, in part by Key Program of NSFC-Guangdong Joint Funds under Grant U1801263, U2001201, and in part by Guangdong Provincial Key Laboratory of Cyber-Physical System under Grant 2020B1212060069.
Institutional Review Board Statement
The study did not require ethical approval.
Informed Consent Statement
The study did not involve humans.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, X.; Zheng, H.; Xu, X.; He, J.; Ge, X.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.; Tian, Y. Predicting grain yield in rice using multi-temporal vegetation indices from UAV-based multispectral and digital imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 246–255. [Google Scholar] [CrossRef]
- Yu, N.; Li, L.; Schmitz, N.; Tian, L.F.; Greenberg, J.A.; Diers, B.W. Development of methods to improve soybean yield estimation and predict plant maturity with an unmanned aerial vehicle based platform. Remote Sens. Environ. 2016, 187, 91–101. [Google Scholar] [CrossRef]
- Panda, S.S.; Ames, D.P.; Panigrahi, S. Application of vegetation indices for agricultural crop yield prediction using neural network techniques. Remote Sens. 2010, 2, 673–696. [Google Scholar] [CrossRef]
- Wang, L.; Tian, Y.; Yao, X.; Zhu, Y.; Cao, W. Predicting grain yield and protein content in wheat by fusing multi-sensor and multi-temporal remote-sensing images. Field Crop. Res. 2014, 164, 178–188. [Google Scholar] [CrossRef]
- Wan, L.; Cen, H.; Zhu, J.; Zhang, J.; Zhu, Y.; Sun, D.; Du, X.; Zhai, L.; Weng, H.; Li, Y.; et al. Grain yield prediction of rice using multi-temporal UAV-based RGB and multispectral images and model transfer—A case study of small farmlands in the South of China. Agric. For. Meteorol. 2020, 291, 108096. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Sulik, J.J.; Long, D.S. Spectral considerations for modeling yield of canola. Remote Sens. Environ. 2016, 184, 161–174. [Google Scholar] [CrossRef]
- da Silva, E.E.; Baio, F.H.R.; Teodoro, L.P.R.; da Silva Junior, C.A.; Borges, R.S.; Teodoro, P.E. UAV-multispectral and vegetation indices in soybean grain yield prediction based on in situ observation. Remote Sens. Appl. Soc. Environ. 2020, 18, 100318. [Google Scholar] [CrossRef]
- Kouadio, L.; Newlands, N.K.; Davidson, A.; Zhang, Y.; Chipanshi, A. Assessing the performance of MODIS NDVI and EVI for seasonal crop yield forecasting at the ecodistrict scale. Remote Sens. 2014, 6, 10193–10214. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Ghulam, A.; Sidike, P.; Hartling, S.; Maimaitiyiming, M.; Peterson, K.; Shavers, E.; Fishman, J.; Peterson, J.; Kadam, S.; et al. Unmanned Aerial System (UAS)-based phenotyping of soybean using multi-sensor data fusion and extreme learning machine. ISPRS J. Photogramm. Remote Sens. 2017, 134, 43–58. [Google Scholar] [CrossRef]
- Christiansen, M.P.; Laursen, M.S.; Jørgensen, R.N.; Skovsen, S.; Gislum, R. Designing and testing a UAV mapping system for agricultural field surveying. Sensors 2017, 17, 2703. [Google Scholar] [CrossRef] [PubMed]
- Sofonia, J.; Shendryk, Y.; Phinn, S.; Roelfsema, C.; Kendoul, F.; Skocaj, D. Monitoring sugarcane growth response to varying nitrogen application rates: A comparison of UAV SLAM LiDAR and photogrammetry. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101878. [Google Scholar] [CrossRef]
- Zhao, G.; Sanchez-Azofeifa, A.; Laakso, K.; Sun, C.; Fei, L. Hyperspectral and Full-Waveform LiDAR Improve Mapping of Tropical Dry Forest’s Successional Stages. Remote Sens. 2021, 13, 3830. [Google Scholar] [CrossRef]
- de Almeida, C.T.; Galvao, L.S.; Ometto, J.P.H.B.; Jacon, A.D.; de Souza Pereira, F.R.; Sato, L.Y.; Lopes, A.P.; de Alencastro Graça, P.M.L.; de Jesus Silva, C.V.; Ferreira-Ferreira, J.; et al. Combining LiDAR and hyperspectral data for aboveground biomass modeling in the Brazilian Amazon using different regression algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, Z.; Tao, F.; Zhang, L.; Luo, Y.; Han, J.; Li, Z. Identifying the contributions of multi-source data for winter wheat yield prediction in China. Remote Sens. 2020, 12, 750. [Google Scholar] [CrossRef]
- Li, B.; Xu, X.; Zhang, L.; Han, J.; Bian, C.; Li, G.; Liu, J.; Jin, L. Above-ground biomass estimation and yield prediction in potato by using UAV-based RGB and hyperspectral imaging. ISPRS J. Photogramm. Remote Sens. 2020, 162, 161–172. [Google Scholar] [CrossRef]
- Zhang, N.; Chen, M.; Yang, F.; Yang, C.; Yang, P.; Gao, Y.; Shang, Y.; Peng, D. Forest Height Mapping Using Feature Selection and Machine Learning by Integrating Multi-Source Satellite Data in Baoding City, North China. Remote Sens. 2022, 14, 4434. [Google Scholar] [CrossRef]
- Shendryk, Y.; Sofonia, J.; Garrard, R.; Rist, Y.; Skocaj, D.; Thorburn, P. Fine-scale prediction of biomass and leaf nitrogen content in sugarcane using UAV LiDAR and multispectral imaging. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102177. [Google Scholar] [CrossRef]
- Shi, Y.; Han, L.; Huang, W.; Chang, S.; Dong, Y.; Dancey, D.; Han, L. A Biologically Interpretable Two-Stage Deep Neural Network (BIT-DNN) for Vegetation Recognition From Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–20. [Google Scholar] [CrossRef]
- Hong, D.; He, W.; Yokoya, N.; Yao, J.; Gao, L.; Zhang, L.; Chanussot, J.; Zhu, X. Interpretable hyperspectral artificial intelligence: When nonconvex modeling meets hyperspectral remote sensing. IEEE Geosci. Remote Sens. Mag. 2021, 9, 52–87. [Google Scholar] [CrossRef]
- Mørup, M.; Hansen, L.K. Archetypal analysis for machine learning and data mining. Neurocomputing 2012, 80, 54–63. [Google Scholar] [CrossRef]
- Cutler, A.; Breiman, L. Archetypal analysis. Technometrics 1994, 36, 338–347. [Google Scholar] [CrossRef]
- Seth, S.; Eugster, M.J. Probabilistic archetypal analysis. Mach. Learn. 2016, 102, 85–113. [Google Scholar] [CrossRef]
- Keller, S.M.; Samarin, M.; Arend Torres, F.; Wieser, M.; Roth, V. Learning extremal representations with deep archetypal analysis. Int. J. Comput. Vis. 2021, 129, 805–820. [Google Scholar] [CrossRef]
- Xu, J.X.; Ma, J.; Tang, Y.N.; Wu, W.X.; Shao, J.H.; Wu, W.B.; Wei, S.Y.; Liu, Y.F.; Wang, Y.C.; Guo, H.Q. Estimation of sugarcane yield using a machine learning approach based on uav-lidar data. Remote Sens. 2020, 12, 2823. [Google Scholar] [CrossRef]
- Stateras, D.; Kalivas, D. Assessment of olive tree canopy characteristics and yield forecast model using high resolution UAV imagery. Agriculture 2020, 10, 385. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Feng, L.; Du, Q.; Runge, T. Combining multi-source data and machine learning approaches to predict winter wheat yield in the conterminous United States. Remote Sens. 2020, 12, 1232. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Aha, D.W.; Kibler, D.; Albert, M.K. Instance-based learning algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, Q.; Ren, H.; Sun, Y.; Li, M.; Zhang, T.; Ren, S. Optimal hyperspectral characteristics determination for winter wheat yield prediction. Remote Sens. 2018, 10, 2015. [Google Scholar] [CrossRef]
- Xu, C.; Ding, Y.; Zheng, X.; Wang, Y.; Zhang, R.; Zhang, H.; Dai, Z.; Xie, Q. A Comprehensive Comparison of Machine Learning and Feature Selection Methods for Maize Biomass Estimation Using Sentinel-1 SAR, Sentinel-2 Vegetation Indices, and Biophysical Variables. Remote Sens. 2022, 14, 4083. [Google Scholar] [CrossRef]
- Han, J.; Zhang, Z.; Cao, J.; Luo, Y.; Zhang, L.; Li, Z.; Zhang, J. Prediction of winter wheat yield based on multi-source data and machine learning in China. Remote Sens. 2020, 12, 236. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks, a Comprehensive Foundation; Prentice-Hall Inc.: New Jersey, NJ, USA, 1999; Volume 7458, pp. 161–175. [Google Scholar]
- Kross, A.; Znoj, E.; Callegari, D.; Kaur, G.; Sunohara, M.; Lapen, D.R.; McNairn, H. Using artificial neural networks and remotely sensed data to evaluate the relative importance of variables for prediction of within-field corn and soybean yields. Remote Sens. 2020, 12, 2230. [Google Scholar] [CrossRef]
- Yang, Q.; Shi, L.; Han, J.; Zha, Y.; Zhu, P. Deep convolutional neural networks for rice grain yield estimation at the ripening stage using UAV-based remotely sensed images. Field Crop. Res. 2019, 235, 142–153. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, Z.; Ma, Y.; Du, Q.; Williams, P.; Drewry, J.; Luck, B. Alfalfa yield prediction using UAV-based hyperspectral imagery and ensemble learning. Remote Sens. 2020, 12, 2028. [Google Scholar] [CrossRef]
- Zhang, Z.; Pasolli, E.; Crawford, M.M. An adaptive multiview active learning approach for spectral–spatial classification of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2557–2570. [Google Scholar] [CrossRef]
- Fei, S.; Hassan, M.A.; He, Z.; Chen, Z.; Shu, M.; Wang, J.; Li, C.; Xiao, Y. Assessment of ensemble learning to predict wheat grain yield based on UAV-multispectral reflectance. Remote Sens. 2021, 13, 2338. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Healey, S.P.; Cohen, W.B.; Yang, Z.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.; Hughes, M.J.; Kennedy, R.E.; et al. Mapping forest change using stacked generalization: An ensemble approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Feng, L.; Li, Y.; Wang, Y.; Du, Q. Estimating hourly and continuous ground-level PM2. 5 concentrations using an ensemble learning algorithm: The ST-stacking model. Atmos. Environ. 2020, 223, 117242. [Google Scholar] [CrossRef]
- Cai, Y.; Guan, K.; Lobell, D.; Potgieter, A.B.; Wang, S.; Peng, J.; Xu, T.; Asseng, S.; Zhang, Y.; You, L.; et al. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
- Son, N.; Chen, C.; Chen, C.; Minh, V.; Trung, N. A comparative analysis of multitemporal MODIS EVI and NDVI data for large-scale rice yield estimation. Agric. For. Meteorol. 2014, 197, 52–64. [Google Scholar] [CrossRef]
- Hatfield, J. Remote sensing estimators of potential and actual crop yield. Remote Sens. Environ. 1983, 13, 301–311. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).