Abstract
This work provides a mathematical description of a process game for the safe driving of a ship that encounters other ships. State and control constraint variables, as well as a set of acceptable ship tactics, are taken into consideration. Multi-criteria optimization operations are developed as positional and matrix games, based on cooperative, non-cooperative, and classical (non-game) optimal steering control. Adequate algorithms for ship collision avoidance, relating to the above operations, are developed and verified through digital simulation of a real navigational situation using MATLAB/Simulink.
1. Introduction
A key problem with optimal control in maritime transport and logistics processes is the cost of the process: the control function is ambiguous and may be based on the control method and/or some stochastic situation with a fixed stochastic model, or it must be calculated using a specific control method and other undefined parameters [1].
Such a solution to this problem is the analysis of the process with the use of artificial intelligence methods [2] or the methods of game theory [3]. However, a more accurate representation of the actual process of safe ship motion control in collision situations is treating it as the controlling process that gamers use. The main game control methods in sea transport processes concern the control of the locations of moving objects, including the functioning of feedback, which can be represented by positional and matrix games. Such methods can be used to determine the safe control of a ship, avoiding collisions with other ships at sea.
In general, the entire process is performed first by the collision avoidance guidance algorithm and then by the ship motion control algorithm. This article deals with the synthesis methods of collision avoidance guidance algorithms, taking into account the game properties of the process.
However, for the synthesis of ship motion control algorithms, optimal, adaptive, and fuzzy control methods are used [4,5,6,7,8,9]. Then, it becomes important to take into account the influence of wind and sea waves on the ship’s movement [10,11].
Thus, previous publications on the application of game theory elements concerned both cooperative operations—autonomous surface vehicles (ASVs), and autonomous underwater vehicles (AUVs) [12,13,14,15,16,17]—and non-cooperative operations [18,19,20]. Other applications concerned fishery management [21,22], target defense [23], and power systems [20].
The use of game theory methods for the synthesis of collision avoidance guidance algorithms has so far been neglected in the literature; therefore, it has become the aim of this review paper.
This review presents the formulation of various types of algorithms for safe ship control in collision situations, developing the author’s earlier works [24,25,26].
Radar remote sensing data are used to describe and computationally implement various types of game control methods to avoid collisions with multiple objects.
The algorithms developed by the author include an innovative formulation of the control process of a group of ships as a multi-person, multistep matrix game and multistage positional game, then the optimization of this control task using dual linear programming.
For this purpose, Section 2 presents a mathematical game control process model containing: conditions of the control process, state and control limitations, and sets of allowable ship tactics.
Then, in Section 3, on the basis of the formulated model, two basic control algorithms are synthesized—positional and risk game control, in three possible versions—as a multi-stage cooperative game, as a non-cooperative game, and as optimal control outside the game.
Section 4 presents the results of the simulation tests of six algorithms in the navigational situation of passing a dozen or so ships.
The research results are discussed in Section 5, and detailed conclusions are included in Chapter 6, indicating the scope of work to be performed in the future.
2. The Game Control Process Model
A significant feature of the positional game is that the motion of each object depends on the position p(tk) of the other objects it passes at time k, as shown in Figure 1.
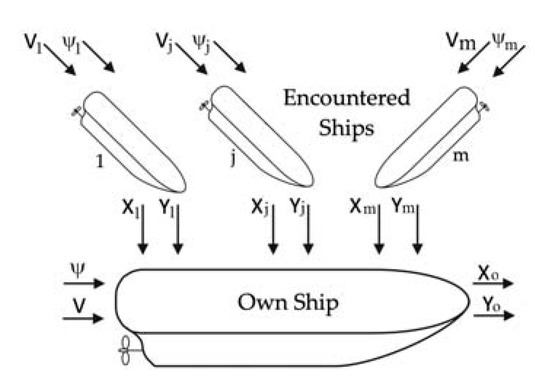
Figure 1.
The process of controlling moving ships: (V, ψ)—speed and course of own ship, (Vj, ψj)—speed and course of encountered j ship, (X0, Y0)—coordinates of own ship position p, (Xj, Yj)—coordinates of j encountered ship position p.
In the process model, possible variations in the speeds and directions of the encountered objects are considered [27,28,29,30,31,32].
2.1. The Condition of the Control Process
The considered ship’s position x0 (Equation (1)), as well as those of the encountered objects xj (Equation (2)), determine the present condition of the control process:
The control system begins to operate at moment tk, depending on the data the radar anti-collision system send to it regarding the present positions of the objects being traced:
Based on the overall notion of multi-stage games, it is expected that the considered object identifies the positions of other passing objects at time tk [33,34,35,36,37,38,39].
2.2. State and Control Limitations
Managers of vessel traffic must take into account the actual navigation constraints C, including the outline of the coastline or fairway, permanent obstacles, and waters closed to navigation, which constitute the limitations of the process state (Figure 2):
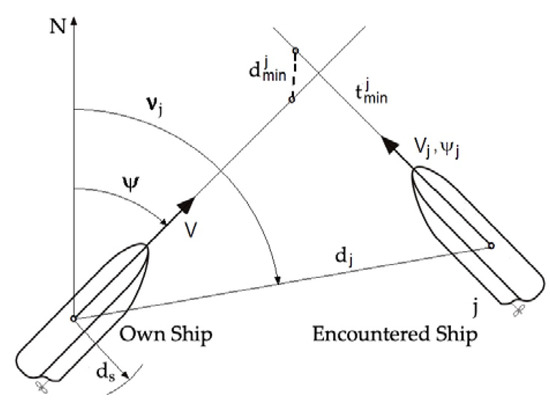
Figure 2.
State variables x0(djmin, tjmin), xj(dj, νj) and control variables u0(V, ψ), uj(Vj, ψj) describing the process of moving ships.
The control constraints consider the kinematics of ship movements, in terms of the rules recommended by COLREGs, in order to maintain a safe distance ds between ships [40]:
2.3. Sets of Allowable Ship Tactics
The sets of acceptable tactics for the participants in the game depend on those of each other, that is, the steering method chosen by ship j alters the admissible tactics set U0,j for the considered ship, consisting of possible changes in its course to port S01,j or starboard S02,j:
Figure 3 depicts the method used to determine the sets S01,j and S02,j of acceptable tactics for the considered ship during the passing of the encountered ship j at speed Vj and with course ψj.
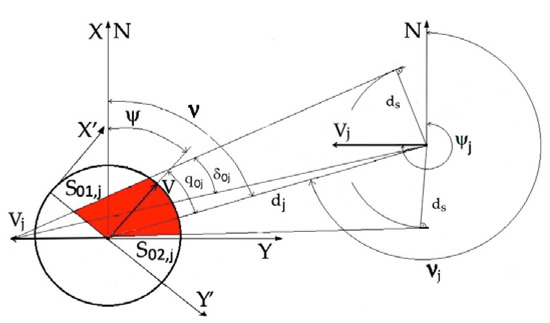
Figure 3.
Sets of acceptable tactics S01,j and S02,j for the considered ship to keep a safe passing distance ds from the encountered ship j.
Inequalities related to the tangents of a circle with radius ds define the set U0,j, as follows:
as well as that confining the arc of a circle with radius V:
The equations below describe the inequality components:
Individual COLREGs can be assigned a certain logical function Wj and, then, its specific value w0,j. The value of the variable w0, j is assigned to the COLREGs rules regarding the obligation to give way to ships approaching from starboard, or waiting for a ship approaching from port side to give way:
Similarly, the steering method chosen for the considered ship alters the set of permissible strategies Uj,0 of the encountered ship j, consisting of the possible changes in its course to port Sj1,0 or starboard Sj2,0:
Figure 4 depicts the method for determining the sets Sj1,0 and Sj2,0 of acceptable strategies for the encountered ship j during the passing of the considered ship with speed V and course Ψ.
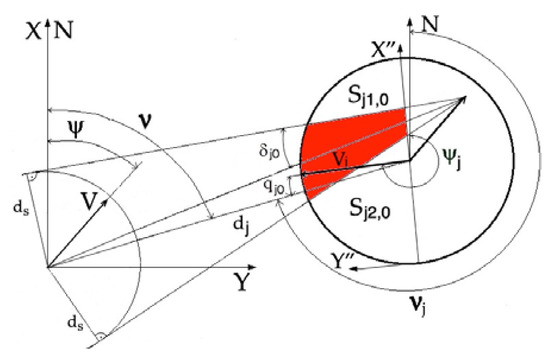
Figure 4.
Sets of permissible strategies Sj1,0 and Sj2,0 for the encountered ship j, in order to maintain a safe passing distance ds from the considered ship.
The set Uj,0 is defined by the inequalities. Tangents of a circle with radius ds define the set U0,j, as follows:
as well as that confining the arc of a circle with radius Vj:
The components of the inequalities are described by the following equations:
3. Multi-Criteria Game Control Algorithms
Safe and optimal ship control, in relation to all encountered ships, can be determined from the total set of admissible controls:
Optimal steering of a ship’s movement u0*(t) at time t is related to its current position p(t) and constitutes optimal position control u0*(p).
Two sets of admissible tactics can be formulated: firstly, the admissible tactics Uj,0[p(tk)] of the j ships encountered, relative to the considered ship; and second, the set of admissible tactics U0,j[p(tk)] for the considered ship, with respect to the j met ships.
Based on each j-th encountered ship, the steering u0,j and uj,0 are calculated, as well as the optimal positional tactics u0* for the considered ship, using the condition Q*, denoting control optimality [41,42,43,44,45,46,47].
3.1. Algorithm ANCPGC of Non-Cooperative Positional Game Control
The optimization criterion is used by the multi-stage positional game control:
where d0 is the distance from the considered vessel to the nearest turning point Pk along the pre-determined voyage route of the vessel.
First, the ship’s steering is calculated, in order to ensure that it has shortest transient course; that is, there should be minimal path loss (criterion: min) for non-cooperative met ships. This contributes greatly to extending the trajectory (criterion: max) of the ship.
Finally, from the controls set for the considered ship with regard to the j distinct encountered ships, the ship control sets are calculated for all met ships, in order to ensure there are the least path losses (criterion: min).
In the control algorithm, a triple linear programming method is utilized, based on the three optimization conditions described above (criterion: min, max, min).
The smallest losses in the considered ship’s path while safely evading the encountered ships are obtained through the maximum projection of the velocity vector onto the given ship’s course.
The simplex method is used to calculate the optimal control multiple times at each discrete stage of motion.
3.2. Algorithm ACPGC of Cooperative Positional Game Control
An optimization criterion is used for the multi-stage positional cooperative game control, as follows:
The modified ACPGC algorithm takes into account interactions between ships, in order to prevent the collision of any ships, and to replace the second condition (i.e., max to min).
3.3. Algorithm ANGPC of Non-Game Positional Control
The following optimization criterion is used for the multi-stage non-game control:
The criteria given in Equations (24)–(26) make it possible to determine the optimal changes in the course and speed values that form the considered ship’s optimal trajectory in a collision situation. This ensures the smallest loss of the path for the safe passage of the met ships at a distance no less than reference value ds. The dynamic properties of the ship, while implementing course and speed changes, are taken into account through consideration of the maneuver advance time tm [48,49,50].
To develop the ACPGC, ANGPC, and ANCPGC algorithms, the lp linear programming function from the Optimization Toolbox of the MATLAB/Simulink software was used (Algorithm A1) (Figure 5).
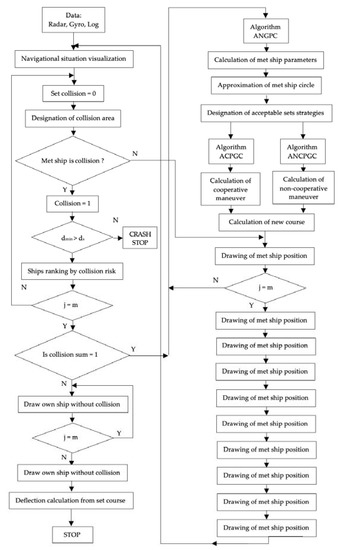
Figure 5.
Algorithm flowchart of the positional game control for safe passing of ships.
Appendix A shows the MATLAB/Simulink software used to calculate the optimal maneuver.
3.4. Algorithm ANCRGC of Non-Cooperative Risk Game Control
The ship collision risk concept (Equation (27)) can be defined using the present condition of the approach, explained by the parameters djmin and tjmin, in order to evaluate whether the situation can be assumed to be safe. The situation is considered safe if the ships pass at a distance no smaller than the pre-determined safe value ds and in a time no shorter than ts:
The values of the parameters k1 and k2 are influenced by the state of visibility at sea and the dimensions of the ship (i.e., its length ld and breadth bd), as follows:
The formula below is used for the control goal:
Then, some form of the probability matrix P = [pj(u0, uj)] can be formulated for the use of pure tactics [51].
The highest probability tactic can be used to solve the control problem:
3.5. Algorithm ACRGC of Cooperative Risk Game Control
The following optimization criterion is used in the cooperative risk game control:
3.6. Algorithm ANGRC of Non-Game Risk Control
The above criterion is usually reduced for non-game control, as follows:
To develop the ANCRGC, ACRGC, and ANGRC algorithms, the lp linear programming function from the Optimization Toolbox of the MATLAB/Simulink software was used (Algorithm A2) (Figure 6).
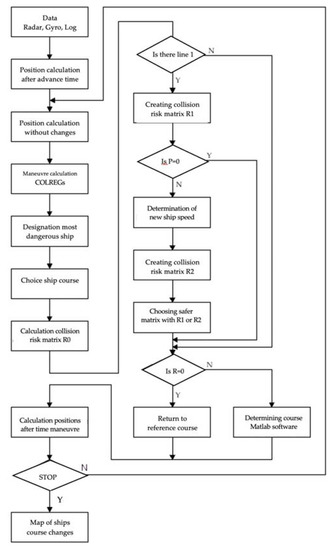
Figure 6.
Algorithm flowchart of the risk game control for safe passing ships.
Appendix B shows the MATLAB/Simulink program used to create COLREG rules.
4. Computer Simulation of Control Algorithms
The multi-criteria optimization algorithms were used to determine a ship’s safe trajectories under the conditions of encountering 15 other ships in the Skagerrak Strait, under restricted visibility at sea of ds = 1.4 nm (nautical miles); see Table 1 and Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14.

Table 1.
Motion variables of the considered ship and 15 encountered ships.
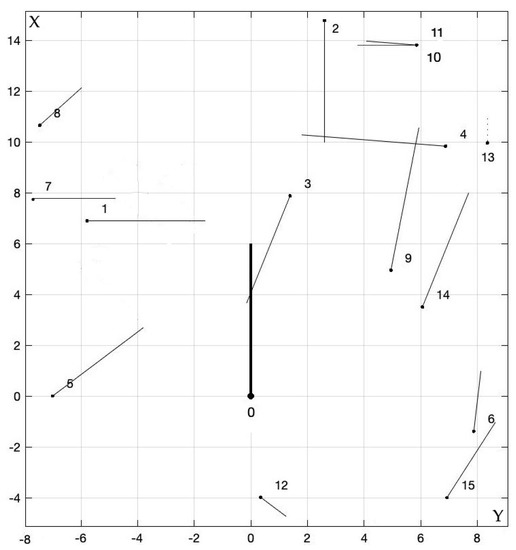
Figure 7.
Visualization of the navigation situation in the Skagerrak Strait in the form of 18 min vectors denoting the speeds of the considered ship and the 15 met ships.
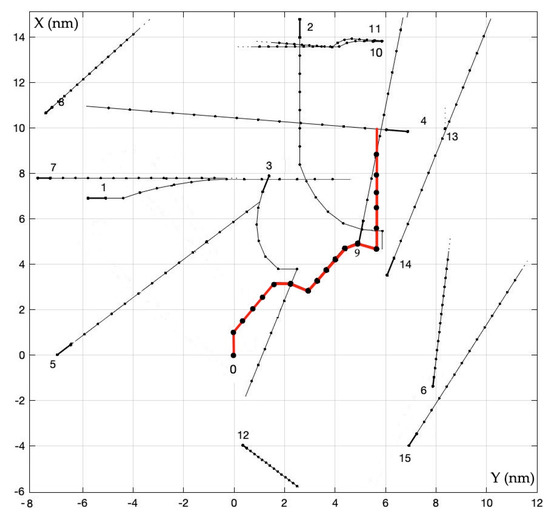
Figure 8.
Trajectories of ships in non-cooperative positional game ANCPGC.
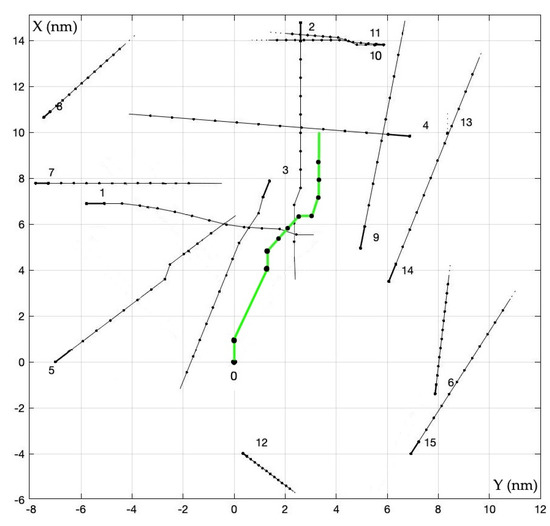
Figure 9.
Trajectories of ships in cooperative positional game ANCPGC.
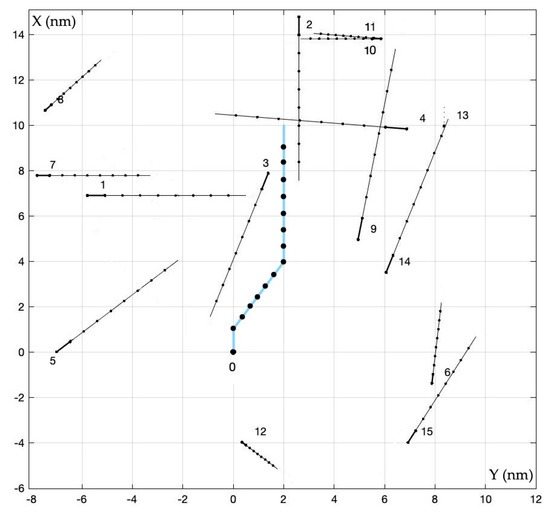
Figure 10.
Trajectories of ships in non-game positional control ANGPC.
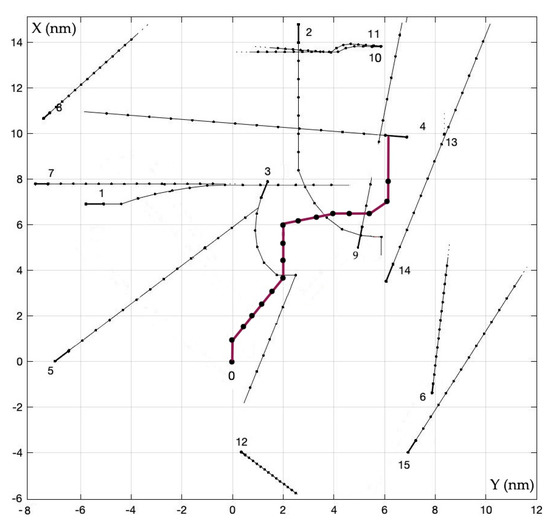
Figure 11.
Trajectories of ships in non-cooperative matrix game ANCRGC.
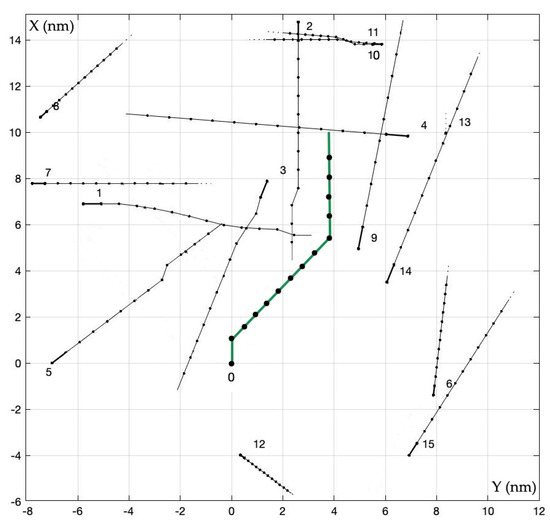
Figure 12.
Trajectories of ships in cooperative matrix game ACRGC.
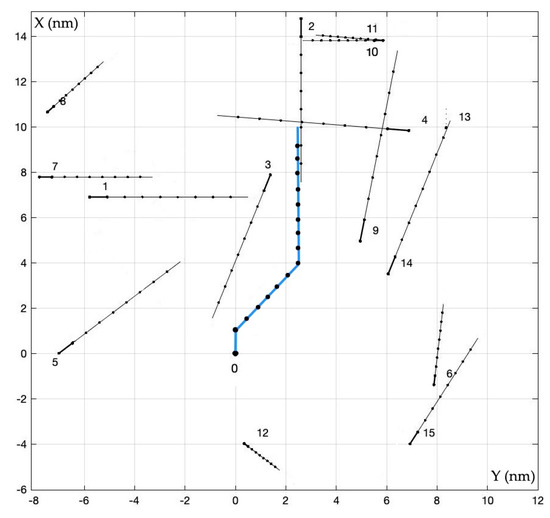
Figure 13.
Trajectories of ships in non-game matrix control ANGRC.
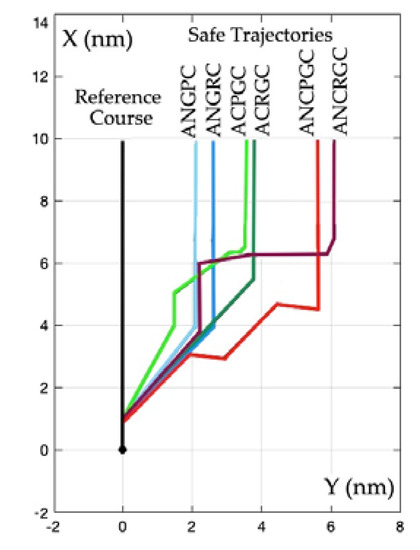
Figure 14.
Runs of optimal trajectories for the considered ship in the situation of safely passing 15 ships encountered in the Skagerrak Strait.
5. Discussion
The courses of individual safe trajectories differed mainly in terms of the final deviation from the initial course of the ship. This deviation is a measure of the extension of the ship’s route, which entails an increase in the operational costs of the ship, through additional fuel consumption by the ship’s propulsion system.
The deviation of the safe trajectory from its initial direction, with restricted visibility at sea, for which the adopted safe distance of passing ships with the value ds = 1.4 nm ranges from 3.8 nm for the cooperative position game ACPGC to 6.1 nm for the non-cooperative matrix game ANCRGC. On the other hand, trajectories for non-game control are characterized by a smaller final deviation of about 2.2 nm, but they do not take into account the possible risk of collision due to subjective erroneous maneuvering decisions of other ships.
The risk game control algorithm, both cooperative ACRGC and non-cooperative ANCRGC, is more sensitive and careful to ensure safe passing of ships.
In further studies, it is necessary to compare safe trajectories in different states of visibility at sea, good visibility for the safe passing distance of ships from 0.1 nm to 1.0 nm and for restricted visibility at sea in the range of safe passing from 1.1 to 3.0 nm.
6. Conclusions
The aim of the presented review of multi-criteria optimization algorithms used for the ship collision avoidance process was to determine the best solutions that simultaneously satisfy a set of many—often contradictory—optimization criteria. Similar examples include profit maximization and risk minimization.
Multi-stage optimization deals with problems that change over time; that is, practical optimization operations where the objective control function depends on the state of the transport process changing over time.
Due to the high complexity of the general model for the differential game related to the process of controlling moving objects, simplified models were used for the synthesis of practical control algorithms. Optimization of individual process models allowed for appropriate algorithms for determining the safe trajectory of a ship when it is very close to other (stationary and moving) ships to be obtained, which can be used for the computer-aided decision-making of the captain of the ship.
When developing a mathematical description of the control process in the form of a model of the appropriate type of game, to be used for safely controlling a ship that passing many other ships, one must take into account the degree of ambiguity of the situation caused by imperfect priority rules and the subjectivity of the navigator who makes the final decision to avoid a collision.
In light of this, multi-criteria optimization of safe ship control allowed for the synthesis of appropriate algorithms for cooperative, non-cooperative, and non-game control.
In future studies, the use of selected methods of computational intelligence can be analyzed; in particular, fuzzy control, allowing for better adjustment of control to the environmental conditions, and neural network, allowing for more accurate mapping of objects encountered as mobile obstacles.
The potential application of the research presented in this article is especially indicated for the improvement of maritime autonomous surface ship (MASS) control software.
Funding
This research was funded by a research project of the Electrical Engineering Faculty, Gdynia Maritime University, Poland, no. WE/2022/PZ/02: “Simulation models of optimal control of moving dynamic objects”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The study did not report any data.
Conflicts of Interest
The author declares no conflict of interest regarding the publication of this paper. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
| Algorithm A1. Calculating optimal maneuver. |
 |
 |
Appendix B
| Algorithm A2. COLREGs rules. |
 |
 |
 |
 |
 |
References
- Lisowski, J. The dynamic game models of safe navigation. TRANSNAV Int. J. Mar. Nav. Safety Sea Transp. 2007, 1, 11–18. [Google Scholar]
- Lisowski, J. The optimal and safe ship trajectories for different forms of neural state constraints. Mechatr. Syst. Mech. Mater. 2012, 180, 64–69. [Google Scholar] [CrossRef]
- Lisowski, J. Comparison of dynamic games in application to safe ship control. Pol. Marit. Res. 2014, 21, 3–12. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Liu, C.; Zhang, W. COLREGs-constrained adaptive fuzzy event-triggered control for underactuated surface vessels with the actuator failures. IEEE Trans. Fuzzy Syst. 2020, 29, 3822–3832. [Google Scholar] [CrossRef]
- Zhang, G.; Li, J.; Liu, C.; Zhang, W. A robust fuzzy speed regulator for unmanned sailboat robot via the composite ILOS guidance. Nonlinear 2022, 8, 1–16. [Google Scholar] [CrossRef]
- Śmierzchalski, R.; Witkowska, A. Advanced ship control methods. In Automatic Control, Robotics, and Information Processing; Kulczycki, P., Korbicz, J., Kacprzyk, J., Eds.; Springer Series on Studies in Systems; Decision and Control: Berlin/Heidelberg, Germany, 2021; Volume 296, pp. 617–643. [Google Scholar] [CrossRef]
- Szlapczynski, R.; Szlapczynska, J. Review of ship safety domains: Models and applications. Ocean. Eng. 2017, 145, 277–289. [Google Scholar] [CrossRef]
- Tomera, M.; Alfuth, L. Waypoint path controller for ships. TRANSNAV Int. J. Mar. Nav. Safety Sea Transp. 2020, 14, 375–383. [Google Scholar] [CrossRef]
- Lebkowski, A. Design of an autonomous transport system for coastal areas. TRANSNAV Int. J. Mar. Nav. Safety Sea Transp. 2018, 12, 117–124. [Google Scholar] [CrossRef]
- Gao, Q.; Song, L.; Yao, J. RANS prediction of wave-induced ship motions and steady wave forces and moments in regular waves. J. Mar. Sci. Eng. 2021, 9, 1459. [Google Scholar] [CrossRef]
- Borkowski, P. Numerical modeling of wave disturbances in the process of ship movement control. Algorithms 2018, 11, 130. [Google Scholar] [CrossRef]
- Hinostroza, M.A.; Xu, H.; Soares, C.G. Cooperative operation of autonomous surface vehicles for maintaining formation in complex marine environment. Ocean Eng. 2019, 183, 132–154. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, H.; Li, P.; Zou, J. Self-organizing cooperative pursuit strategy for multi-USV with dynamic obstacle ships. J. Mar. Sci. Eng. 2022, 10, 562. [Google Scholar] [CrossRef]
- Engwerda, J. Stabilization of an uncertain simple fishery management game. Fish. Res. 2018, 203, 63–73. [Google Scholar] [CrossRef]
- Singh, S.K.; Reddy, P.V. Dynamic network analysis of a target defense differential game with limited observations. arXiv 2021, arXiv:2101.05592. [Google Scholar]
- Mu, C.; Wang, K.; Ni, Z.; Sun, C. Cooperative differential game-based optimal control and its application to power systems. IEEE Trans. Ind. Inform. 2020, 16, 5169–5179. [Google Scholar] [CrossRef]
- Hagen, I.B.; Kufoalor, K.M.; Brekke, E.F.; Johansen, T.A. MPC-based collision avoidance strategy for existing marine vessel guidance systems. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, T.; Zhu, Q. The inverse problem of linear-quadratic differential games: When is a control strategies profile Nash? arXiv 2022, arXiv:2207.05303. [Google Scholar]
- Braquet, M.; Bakolas, E. Vector field-based collision avoidance for moving obstacles with time-varying elliptical shape. arXiv 2022, arXiv:2207.01747. [Google Scholar]
- Chen, Y.; Georgiou, T.T.; Pavon, M. Covariance steering in zero-sum linear-quadratic two-player differential games. arXiv 2019, arXiv:1909.05468. [Google Scholar]
- Gronbaek, L.; Lindroos, M.; Munro, G.; Pintassilgo, P. Cooperative games in fisheries with more than two players. In Game Theory and Fisheries Management; Springer: Cham, Switzerland, 2020; pp. 81–105. ISBN 978-3-030-40112-2. [Google Scholar]
- Gromova, E.V.; Petrosyan, L.A. On an approach to constructing a characteristic function in cooperative differential games. Project: Cooperative differential games with applications to ecological management. Autom. Remote Control. 2017, 78, 1680–1692. [Google Scholar] [CrossRef]
- Basar, T.; Olsder, G.J. Dynamic Non-Cooperative Game Theory; Siam: Philadelphia, PA, USA, 2013; ISBN 978-0-898-714-29-6. [Google Scholar]
- Lisowski, J. Synthesis of a path-planning algorithm for autonomous robots moving in a game environment during collision avoidance. Electronics 2021, 10, 675. [Google Scholar] [CrossRef]
- Lisowski, J. Multi-criteria multi-stage game optimization. J. Autom. Electron. Electr. Eng. 2022, 4, 37–42. [Google Scholar] [CrossRef]
- Lisowski, J. Game control methods comparison when avoiding collisions with multiple objects using radar remote sensing. Remote Sens. 2020, 12, 1573. [Google Scholar] [CrossRef]
- Ehrgott, M.; Gandibleux, X. Multiple Criteria Optimization: State of the Art Annotated Bibliographic Surveys; Kluwer Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Engwerda, J.C. LQ Dynamic Optimization and Differential Games; John Wiley & Sons: New York, NY, USA, 2005; ISBN 978-0-470-01524-7. [Google Scholar]
- Falcone, M.; Ferretti, R. Semi-Lagrangian Approximation Schemes for Linear and Hamilton-Jacobi Equations; Sian: Philadelphia, PA, USA, 2014. [Google Scholar]
- Guenin, B.; Konemann, J.; Tuncel, L. A Gentle Introduction to Optimization; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Hermes, H.; Isaacs, R. Differential games. Math. Comput. 1965, 19, 700. [Google Scholar] [CrossRef]
- Li, Y.; Vorobeychik, Y. Path planning games. Multiagent Syst. arXiv 2019, arXiv:1910.13880. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Osborne, M.J. An Introduction to Game Theory; Oxford University Press: New York, NY, USA, 2004; ISBN 978-0-19-512895-6. [Google Scholar]
- Speyer, J.L.; Jacobson, D.H. Primer on Optimal Control Theory; Siam: Toronto, ON, Canada, 2010; ISBN 978-0-898716-94-8. [Google Scholar]
- Spica, R.; Cristofalo, E.; Wang, Z.; Montijano, E.; Schwager, M. A real-time game theoretic planner for autonomous two-player drone racing. IEEE Trans. Robot. 2020, 36, 1389–1403. [Google Scholar] [CrossRef]
- Wells, D. Game and Mathematics; Cambridge University Press: London, UK, 2003; ISBN 978-1-78326-752-1. [Google Scholar]
- Yong, J. Optimization Theory—A Concise Introduction; World Scientific: New Jersey, NJ, USA, 2018; ISBN 978-981-3237-64-3. [Google Scholar]
- Lazarowska, A. Safe Trajectory Planning for Maritime Surface Ships; Springer Series on Naval Architecture, Marine Engineering; Shipbuilding and Shipping: Berlin/Heidelberg, Germany, 2022; Volume 13, pp. 1–185. [Google Scholar] [CrossRef]
- Isaacs, R. Differential Games; John Wiley & Sons: New York, NY, USA, 1965; ISBN 0-48640-682-2. [Google Scholar]
- Kim, I.Y.; de Weck, O.L. Adaptive weighted sum method for bi-objective optimization: Pareto front generation. Struct. Multidiscip. Opt. 2005, 29, 149–158. [Google Scholar] [CrossRef]
- Koksalan, M.; Wallenius, J.; Zionts, S. Early history of multiple criteria decision making. J. Multi-Criteria Decis. Anal. 2013, 20, 87–94. [Google Scholar] [CrossRef]
- Legriel, J. Multicriteria Optimization and Its Application to Multi-Processor Embedded Systems. Ph.D. Thesis, Grenoble University, Grenoble, France, 2011. [Google Scholar]
- Millington, I.; Funge, J. Artificial Intelligence for Games; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Nicotra, M.M.; Liao-McPherson, D.; Kolmanovsky, I.V. Embedding constrained model predictive control in a continuous-time dynamic feedback. IEEE Trans. Autom. Control 2019, 64, 1932–1946. [Google Scholar] [CrossRef]
- Nisan, N.; Roughgarden, T.; Tardos, E.; Vazirani, V.V. Algorithmic Game Theory; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Odu, G.O.; Charles-Owaba, O.E. Review of multi-criteria optimization methods—Theory and applications. IOSR J. Eng. 2013, 3, 1–14. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Garone, E.; Schenato, L. A Distributed method for linear programming problems with box constraints and time-varying inequalities. IEEE Control. Syst. Lett. 2018, 3, 404–409. [Google Scholar] [CrossRef]
- Messac, A.; Mattson, C.A. Generating well-distributed sets of Pareto points for engineering design using physical programming. J. Optim. Eng. 2002, 3, 431–450. [Google Scholar] [CrossRef]
- Messac, A.; Sukam, C.P.; Melachrinoudis, E. Agregate objective functions and Pareto frontiers: Required relationships and practical implications. J. Optim. Eng. 2000, 1, 171–188. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, Z.; Zheng, Z. A cooperative game approach for assessing the collision risk in multi-vessel encountering. Ocean Eng. 2019, 187, 106175. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).