An Improved RANSAC Outlier Rejection Method for UAV-Derived Point Cloud
Abstract
1. Introduction
Related Works
- number of inliers found;
- lower number of iterations;
- increased convergence rate;
- the refinement of the final inlier output (reducing the remaining outliers in the last stage of the loop).
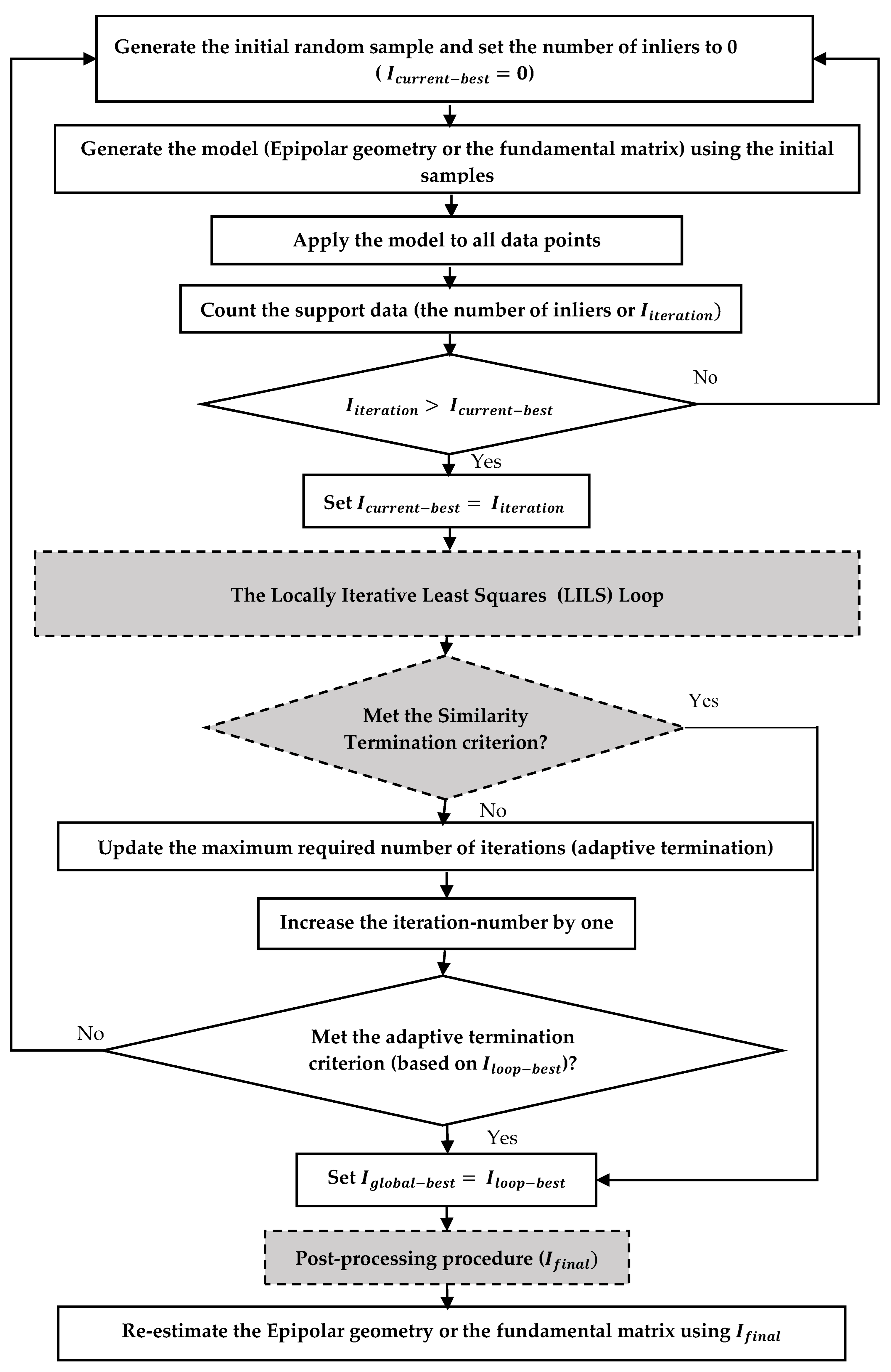
2. Methods
2.1. An Overview of the RANSAC-Based Methods
| Algorithm 1: Standard RANSAC procedure. |
| Inputs: M: all tie points, s: minimum number of points required to solve the unknown parameters of the model, and : a predefined threshold. |
| Output: : global-best-inliers |
| , |
| While < |
| Select an initial random sample (s points) |
| Generate the hypothesis using the initial sample (collinearity equations) |
| Evaluate the hypothesis (i.e., Euclidian distance for all tie data points (M)) |
| Count the supporting points () |
| If > |
| Update N based on the new (Equation (2)) |
| End If |
| + 1 |
| End While |
Re-estimate the Collinearity equations or the Fundamental matrix using |
2.2. ELISAC: Empowered Locally Iterative SAmple Consensus
2.3. Locally Iterative Least Squares (LILS) Loop
2.3.1. Basic LILS
| Algorithm 2: Basic LILS. |
| Inputs: M: all match points, s: minimum number of points required to solve the unknown parameters of a model, and : a predefined threshold. |
| Output: : global-best-inliers |
| , , |
| While < |
| Select an initial random sample (s points) |
| Generate a hypothesis using the initial sample |
| Evaluate the hypothesis (evaluation procedure against all data points (M)) |
| Count the support data () |
| If > |
| While ( > OR ) |
| If ≠ 0 |
| End If |
| Select all inliers () as initial sample |
| Generate a hypothesis (least-squares-based) using the initial sample |
| Evaluate the hypothesis (evaluation procedure against all data points (M)) |
| Count the supporting data () |
| End While |
| If ≥ |
| = |
| Else |
| = |
| End If |
| Check the ST criterion (optional) and terminate the program if it is satisfied. |
| Update N based on the new (AT-Basic criterion) |
| End If |
| + 1 |
| End While |
Re-estimate the Collinearity equations or the Fundamental matrix using |
2.3.2. Aggregated LILS
| Algorithm 3: Aggregated LILS. |
| Inputs: M: all match points, s: minimum number of points required to solve the unknown parameters of a model, and : a predefined threshold. |
| Output: : global-best-inliers |
| , , , |
| While < |
| Select an initial random sample (s points) |
| Generate a hypothesis using the initial sample |
| Evaluate the hypothesis (evaluation procedure against all data points (M)) |
| Count the support data () |
| If > |
| While ( > OR ) |
| If ≠ 0 |
| End If |
| Select all inliers () as the initial sample |
| Generate a hypothesis (least-squares-based) using the initial sample |
| Evaluate the hypothesis (evaluation procedure against all data points (M)) |
| Count the supporting data () |
| End While |
| If ≥ |
| If |
| Check the ST criterion (optional) and terminate the program if it is satisfied. |
| = |
| Else If |
| = |
| = |
| End If |
| Else |
| Check the ST criterion (optional) and terminate the program if it is satisfied. |
| = |
| End If |
| Update N based on the new (AT-Basic criterion) or (AT-Improved) |
| End If |
| + 1 |
| End While |
Re-estimate the Collinearity equations or the Fundamental matrix using obtained |
2.4. The Similarity Termination (ST) Criterion
2.5. Post-Processing Procedure
3. Experiments and Results
3.1. Dataset
3.2. Performance Evaluation
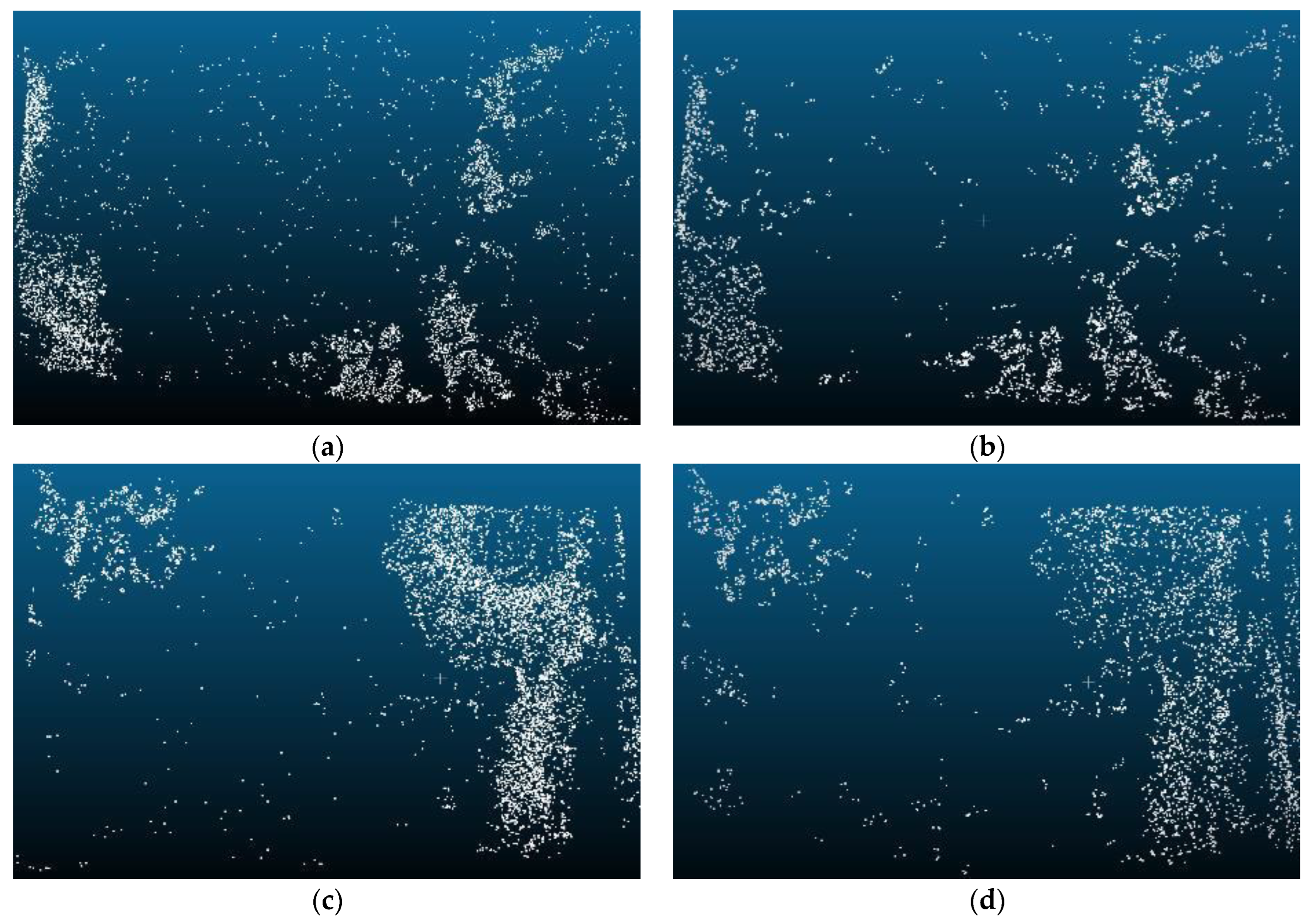
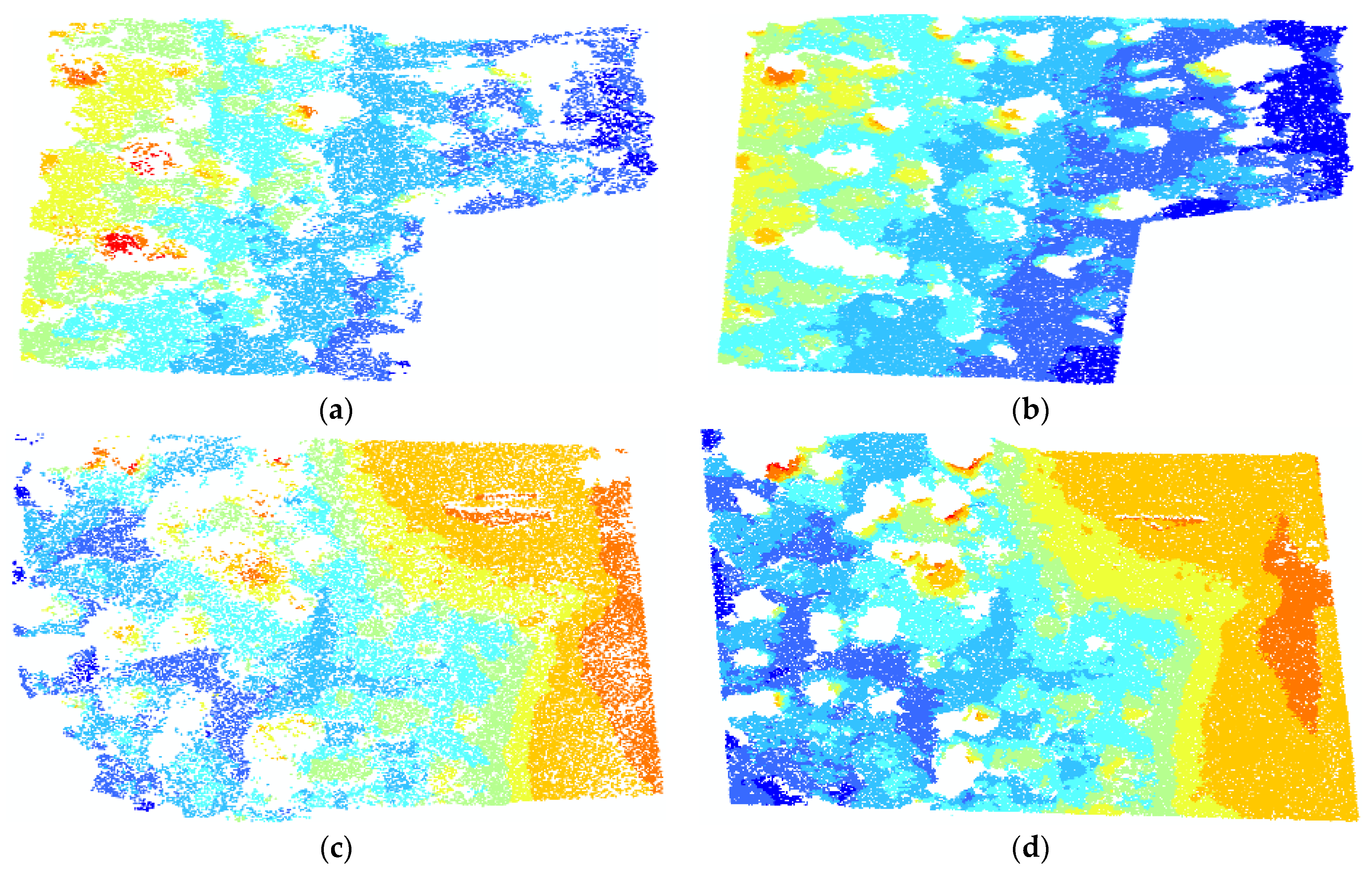
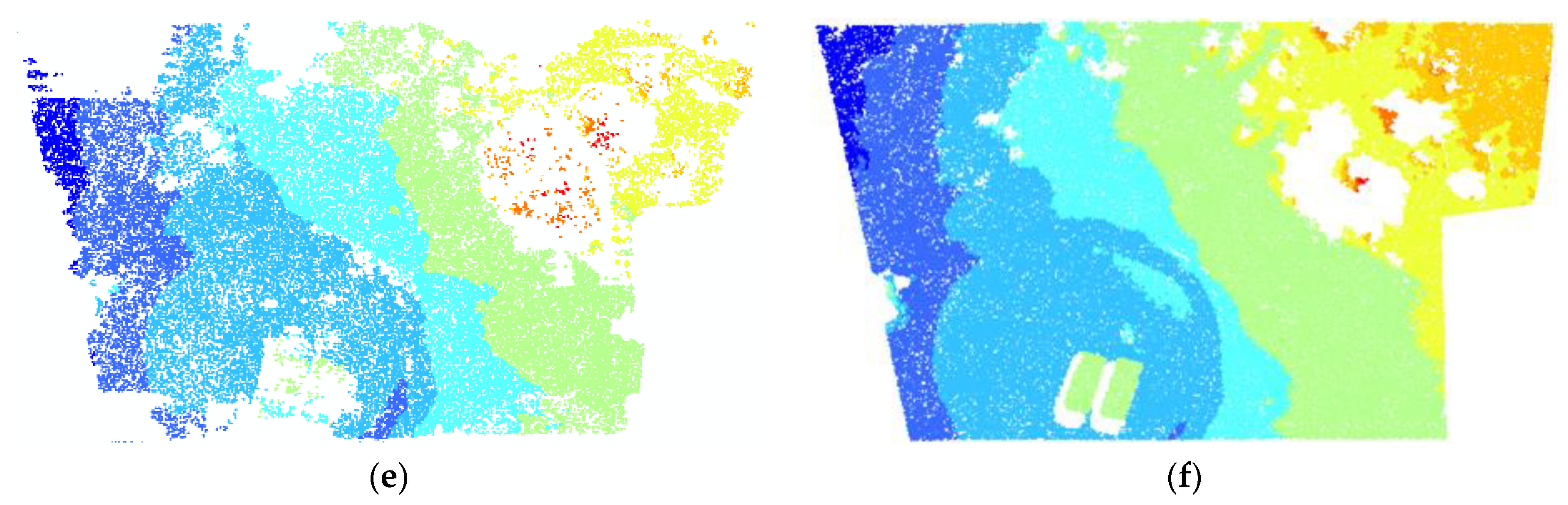
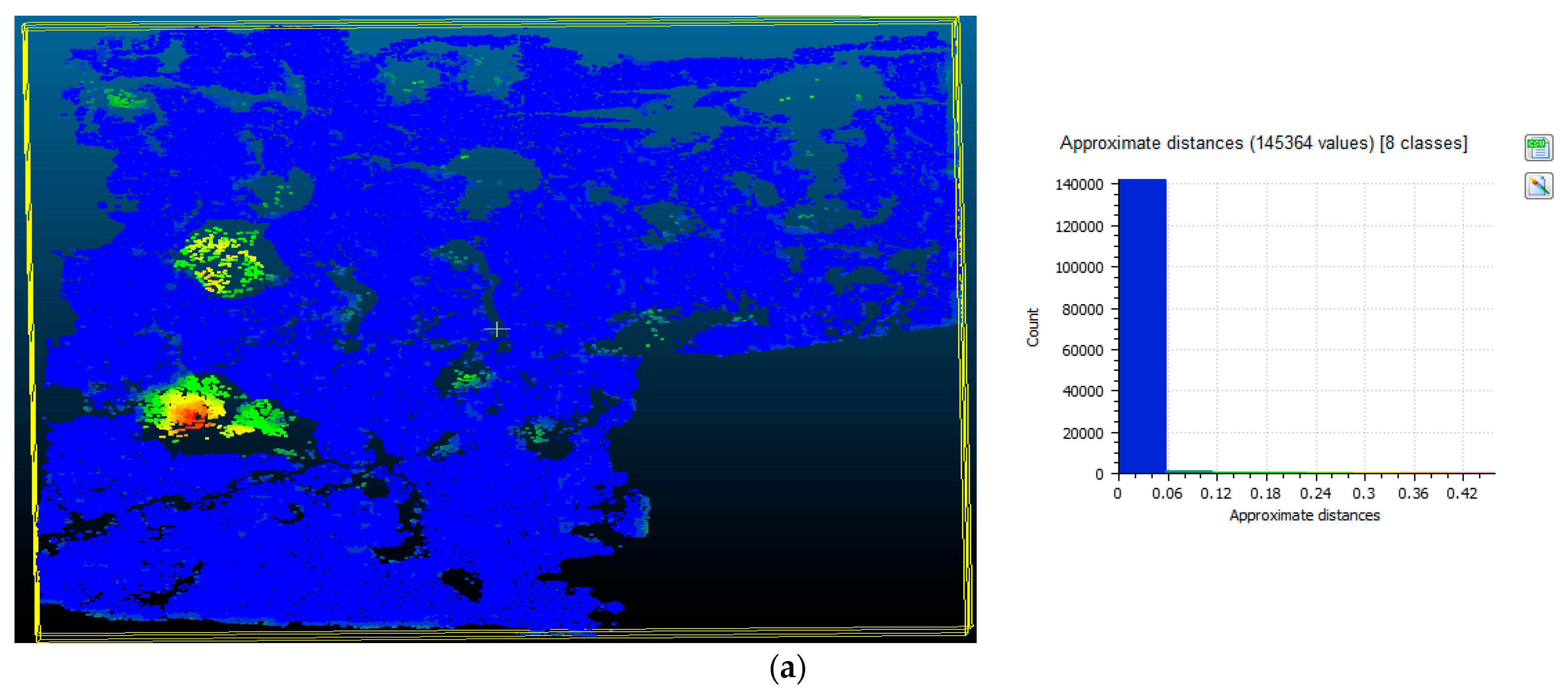
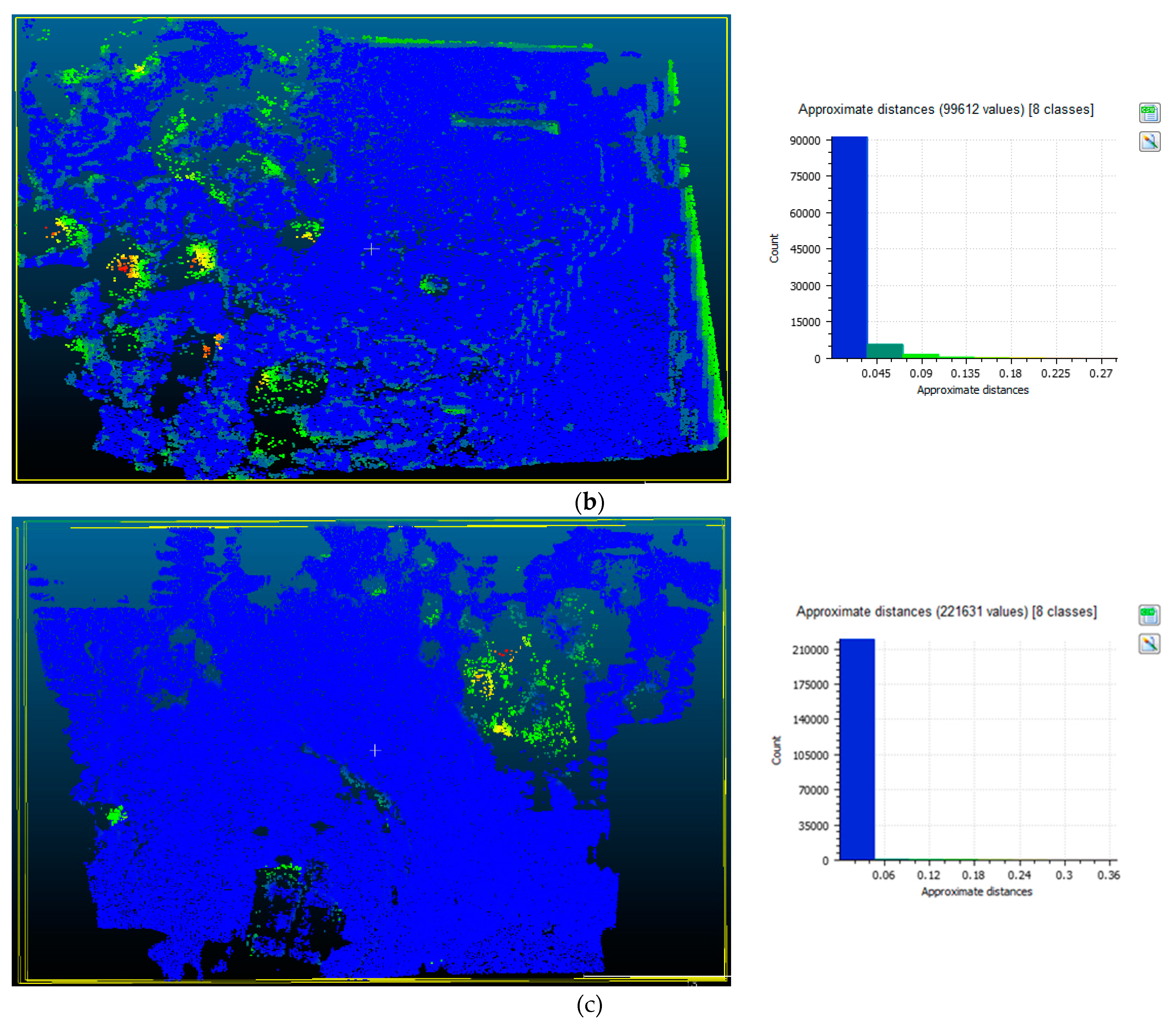
3.3. Point Cloud and DSM Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gruen, A. Development and Status of Image Matching in Photogrammetry. Photogramm. Rec. 2012, 27, 36–57. [Google Scholar] [CrossRef]
- Cramer, M. On the Use of Direct Georeferencing in Airborne Photogrammetry; Citeseer: Princeton, NJ, USA, 2001. [Google Scholar]
- Mostafa, M.M.; Hutton, J. Direct Positioning and Orientation Systems: How Do They Work? What Is the Attainable Accuracy. In Proceedings of the Proceedings, The American Society of Photogrammetry and Remote Sensing Annual Meeting, St. Louis, MO, USA, 24–27 April 2001; Citeseer: Princeton, NJ, USA, 2001; pp. 23–27. [Google Scholar]
- Mostafa, M.M.; Schwarz, K.-P. Digital Image Georeferencing from a Multiple Camera System by GPS/INS. ISPRS J. Photogramm. Remote Sens. 2001, 56, 1–12. [Google Scholar] [CrossRef]
- Poli, D. Indirect Georeferencing of Airborne Multi-Line Array Sensors: A Simulated Case Study. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 246–251. [Google Scholar]
- Ip, A.W.L. Analysis of Integrated Sensor Orientation for Aerial Mapping; Geomatics Department, University of Calgary: Calgary, AB, Canada, 2005. [Google Scholar]
- Ip, A.; El-Sheimy, N.; Mostafa, M. Performance Analysis of Integrated Sensor Orientation. Photogramm. Eng. Remote Sens. 2007, 73, 89–97. [Google Scholar] [CrossRef]
- Reshetyuk, Y. Self-Calibration and Direct Georeferencing in Terrestrial Laser Scanning. Ph.D. Thesis, KTH, Stockholm, Sweden, 2009. [Google Scholar]
- Kadhim, I.; Abed, F.M. The Potential of LiDAR and UAV-Photogrammetric Data Analysis to Interpret Archaeological Sites: A Case Study of Chun Castle in South-West England. ISPRS Int. J. Geo Inf. 2021, 10, 41. [Google Scholar] [CrossRef]
- Li, X.; Xiong, B.; Yuan, Z.; He, K.; Liu, X.; Liu, Z.; Shen, Z. Evaluating the Potentiality of Using Control-Free Images from a Mini Unmanned Aerial Vehicle (UAV) and Structure-from-Motion (SfM) Photogrammetry to Measure Paleoseismic Offsets. Int. J. Remote Sens. 2021, 42, 2417–2439. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, J.; Hao, L. Photogrammetric Processing of Low-Altitude Images Acquired by Unpiloted Aerial Vehicles. Photogramm. Rec. 2011, 26, 190–211. [Google Scholar] [CrossRef]
- Serati, G.; Sedaghat, A.; Mohammadi, N.; Li, J. Digital Surface Model Generation from High-Resolution Satellite Stereo Imagery Based on Structural Similarity. Geocarto Int. 2022, 1–30. [Google Scholar] [CrossRef]
- Mohammed, H.M.; El-Sheimy, N. A Descriptor-Less Well-Distributed Feature Matching Method Using Geometrical Constraints and Template Matching. Remote Sens. 2018, 10, 747. [Google Scholar] [CrossRef]
- Yao, G.; Yilmaz, A.; Meng, F.; Zhang, L. Review of Wide-Baseline Stereo Image Matching Based on Deep Learning. Remote Sens. 2021, 13, 3247. [Google Scholar] [CrossRef]
- Choi, S.; Kim, T.; Yu, W. Performance Evaluation of RANSAC Family. J. Comput. Vis. 1997, 24, 271–300. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Cosgriff, C.V.; Celi, L.A. Deep Learning for Risk Assessment: All about Automatic Feature Extraction. Br. J. Anaesth. 2020, 124, 131–133. [Google Scholar] [CrossRef] [PubMed]
- Maggipinto, M.; Beghi, A.; McLoone, S.; Susto, G.A. DeepVM: A Deep Learning-Based Approach with Automatic Feature Extraction for 2D Input Data Virtual Metrology. J. Process Control 2019, 84, 24–34. [Google Scholar] [CrossRef]
- Sun, Y.; Yen, G.G.; Yi, Z. Evolving Unsupervised Deep Neural Networks for Learning Meaningful Representations. IEEE Trans. Evol. Comput. 2019, 23, 89–103. [Google Scholar] [CrossRef]
- Jin, Y.; Mishkin, D.; Mishchuk, A.; Matas, J.; Fua, P.; Yi, K.M.; Trulls, E. Image Matching across Wide Baselines: From Paper to Practice. Int. J. Comput. Vis. 2021, 129, 517–547. [Google Scholar] [CrossRef]
- Ranftl, R.; Koltun, V. Deep Fundamental Matrix Estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 17–24 May 2018; pp. 284–299. [Google Scholar]
- Sun, W.; Jiang, W.; Trulls, E.; Tagliasacchi, A.; Yi, K.M. Acne: Attentive Context Normalization for Robust Permutation-Equivariant Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11286–11295. [Google Scholar]
- Zhang, J.; Sun, D.; Luo, Z.; Yao, A.; Zhou, L.; Shen, T.; Chen, Y.; Quan, L.; Liao, H. Learning Two-View Correspondences and Geometry Using Order-Aware Network. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 5845–5854. [Google Scholar]
- Zhao, C.; Cao, Z.; Li, C.; Li, X.; Yang, J. Nm-Net: Mining Reliable Neighbors for Robust Feature Correspondences. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 215–224. [Google Scholar]
- Liu, J.; Wang, S.; Hou, X.; Song, W. A Deep Residual Learning Serial Segmentation Network for Extracting Buildings from Remote Sensing Imagery. Int. J. Remote Sens. 2020, 41, 5573–5587. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou Sr, Z.; Liao Sr, G.; Yuan, K. New Loss Functions for Medical Image Registration Based on Voxelmorph. In Proceedings of the Medical Imaging 2020: Image Processing, SPIE, Houston, TX, USA, 15–20 February 2020; Volume 11313, pp. 596–603. [Google Scholar]
- Cao, Y.; Wang, Y.; Peng, J.; Zhang, L.; Xu, L.; Yan, K.; Li, L. DML-GANR: Deep Metric Learning with Generative Adversarial Network Regularization for High Spatial Resolution Remote Sensing Image Retrieval. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8888–8904. [Google Scholar] [CrossRef]
- Yang, Y.; Li, C. Quantitative Analysis of the Generalization Ability of Deep Feedforward Neural Networks. J. Intell. Fuzzy Syst. 2021, 40, 4867–4876. [Google Scholar] [CrossRef]
- Wang, L.; Qian, Y.; Kong, X. Line and Point Matching Based on the Maximum Number of Consecutive Matching Edge Segment Pairs for Large Viewpoint Changing Images. Signal Image Video Process. 2022, 16, 11–18. [Google Scholar] [CrossRef]
- Zheng, B.; Qi, S.; Luo, G.; Liu, F.; Huang, X.; Guo, S. Characterization of Discontinuity Surface Morphology Based on 3D Fractal Dimension by Integrating Laser Scanning with ArcGIS. Bull. Eng. Geol. Environ. 2021, 80, 2261–2281. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, X. Efficient and De-Shadowing Approach for Multiple Vehicle Tracking in Aerial Video via Image Segmentation and Local Region Matching. J. Appl. Remote Sens. 2020, 14, 014503. [Google Scholar] [CrossRef]
- Xiuxiao, Y.; Wei, Y.; Shu, X.U.; Yanhua, J.I. Research Developments and Prospects on Dense Image Matching in Photogrammetry. Acta Geod. Cartogr. Sin. 2019, 48, 1542. [Google Scholar]
- Bellavia, F.; Colombo, C.; Morelli, L.; Remondino, F. Challenges in Image Matching for Cultural Heritage: An Overview and Perspective. In Proceedings of the FAPER 2022, Springer LNCS, Lecce, Italy, 23–24 May 2022. [Google Scholar]
- Salehi, B.; Jarahizadeh, S. Improving the uav-derived dsm by introducing a modified ransac algorithm. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 43, 147–152. [Google Scholar] [CrossRef]
- Torr, P.H.; Zisserman, A. MLESAC: A New Robust Estimator with Application to Estimating Image Geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef]
- Chum, O.; Matas, J.; Kittler, J. Locally Optimized RANSAC. In Proceedings of the Joint Pattern Recognition Symposium, Madison, WI, USA, 16–22 June 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 236–243. [Google Scholar]
- Chum, O.; Matas, J. Matching with PROSAC-Progressive Sample Consensus. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 1, pp. 220–226. [Google Scholar]
- Frahm, J.-M.; Pollefeys, M. RANSAC for (Quasi-) Degenerate Data (QDEGSAC). In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; IEEE: Piscataway, NJ, USA, 2006; Volume 1, pp. 453–460. [Google Scholar]
- Hast, A.; Nysjö, J.; Marchetti, A. Optimal Ransac-towards a Repeatable Algorithm for Finding the Optimal Set. J. WSCG 2013, 21, 21–30. [Google Scholar]
- Raguram, R.; Chum, O.; Pollefeys, M.; Matas, J.; Frahm, J.-M. USAC: A Universal Framework for Random Sample Consensus. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 2022–2038. [Google Scholar] [CrossRef]
- Barath, D.; Matas, J.; Noskova, J. MAGSAC: Marginalizing Sample Consensus. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10197–10205. [Google Scholar]
- Korman, S.; Litman, R. Latent Ransac. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6693–6702. [Google Scholar]
- Chum, O.; Werner, T.; Matas, J. Two-View Geometry Estimation Unaffected by a Dominant Plane. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 1, pp. 772–779. [Google Scholar]
- Barath, D.; Matas, J. Graph-Cut RANSAC. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6733–6741. [Google Scholar]
- Zhang, D.; Zhu, J.; Wang, F.; Hu, X.; Ye, X. GMS-RANSAC: A Fast Algorithm for Removing Mismatches Based on ORB-SLAM2. Symmetry 2022, 14, 849. [Google Scholar] [CrossRef]
- Le, V.-H.; Vu, H.; Nguyen, T.T.; Le, T.-L.; Tran, T.-H. Acquiring Qualified Samples for RANSAC Using Geometrical Constraints. Pattern Recognit. Lett. 2018, 102, 58–66. [Google Scholar] [CrossRef]
- Raguram, R.; Frahm, J.-M.; Pollefeys, M. A Comparative Analysis of RANSAC Techniques Leading to Adaptive Real-Time Random Sample Consensus. In Proceedings of the European Conference on Computer Vision, Marseille, France, 12–18 October 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 500–513. [Google Scholar]
- AgiSoft PhotoScan Pro; Agisoft LLC: Saint Petersburg, Russia, 2021.
- Han, J.-Y.; Guo, J.; Chou, J.-Y. A Direct Determination of the Orientation Parameters in the Collinearity Equations. IEEE Geosci. Remote Sens. Lett. 2011, 8, 313–316. [Google Scholar] [CrossRef]
- Szeliski, R. Structure from Motion and SLAM. In Computer Vision; Springer: Berlin/Heidelberg, Germany, 2022; pp. 543–594. [Google Scholar]
- Elnima, E.E. A Solution for Exterior and Relative Orientation in Photogrammetry, a Genetic Evolution Approach. J. King Saud Univ. Eng. Sci. 2015, 27, 108–113. [Google Scholar] [CrossRef]
- Adjidjonu, D.; Burgett, J. Assessing the Accuracy of Unmanned Aerial Vehicles Photogrammetric Survey. Int. J. Constr. Educ. Res. 2021, 17, 85–96. [Google Scholar] [CrossRef]
- Rais, M.; Facciolo, G.; Meinhardt-Llopis, E.; Morel, J.-M.; Buades, A.; Coll, B. Accurate Motion Estimation through Random Sample Aggregated Consensus. arXiv 2017, arXiv:1701.05268. [Google Scholar]
- Lindeberg, T. Scale Invariant Feature Transform. Comput. Sci. 2012, 7, 10491. [Google Scholar] [CrossRef]
- Hartley, R.I. In Defense of the Eight-Point Algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 580–593. [Google Scholar] [CrossRef]
- Zhang, H.; Ye, C. Sampson Distance: A New Approach to Improving Visual-Inertial Odometry’s Accuracy. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 9184–9189. [Google Scholar]
- Lebeda, K.; Matas, J.; Chum, O. Fixing the Locally Optimized Ransac–Full Experimental Evaluation. In Proceedings of the British Machine Vision Conference, Surrey, UK, 3–7 September 2012; Citeseer: Princeton, NJ, USA, 2012; Volume 2. [Google Scholar]
- Chum, O.; Matas, J. Optimal Randomized RANSAC. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1472–1482. [Google Scholar] [CrossRef] [PubMed]








| Image Pairs | Books (a) | Box (b) | Kampa (c) | Kyoto (d) | Plant (e) | Valbonne (f) |
|---|---|---|---|---|---|---|
| Number of SIFT points | 167 | 418 | 227 | 730 | 157 | 97 |
| Weight (g) | 1280 | |
| Diagonal size (mm) | 350 | |
| Max speed (m/s) | 16 | |
| UAV model | DJI Phantom 3 | |
| Camera | Model | FC330 |
| Sensor | 1/2.3″ CMOS (Effective pixels: 12.4 M) | |
| Lens | FOV 94°20 mm | |
| Hover Accuracy Range | Vertical | ±0.5 m (with GPS Positioning) |
| Horizontal | ±1.5 m (with GPS Positioning) | |
| Max. flight time (minute) | 23 | |
| Image size (pixels) | 4000 × 3000 | |
| Ground resolution size of images (cm/pix) | 2 | |
| Average flight altitude (m) | 53.8 | |
| Focal length in 35 mm format (mm) | 20 | |
| ISO speed | 174 | |
| Exposure | 1/60 | |
| Aperture Value | 2.8 | |
| Image area coverage (m2) | 81 × 61 | |
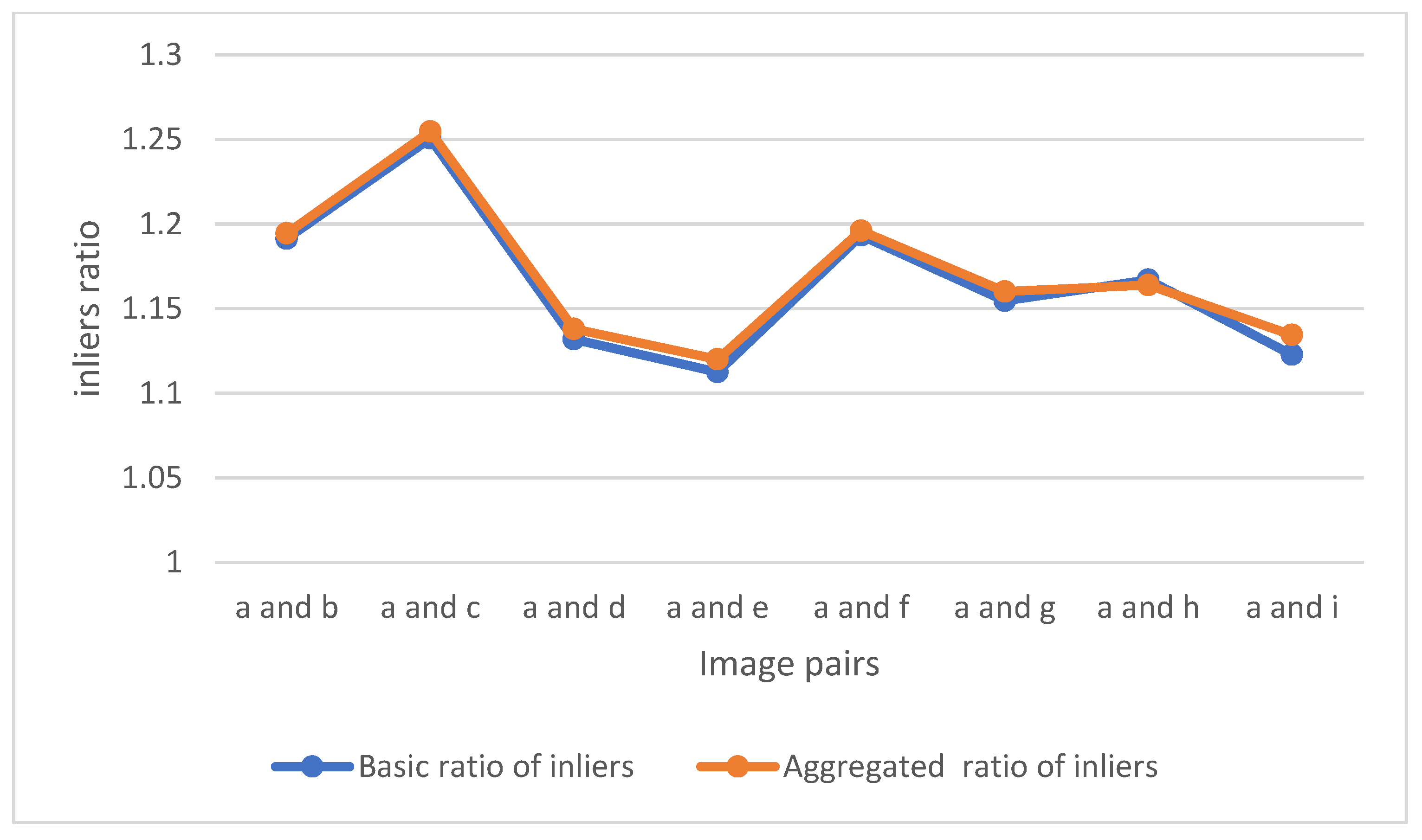
| Image Pairs | a and b | a and c | a and d | a and e | a and f | a and g | a and h | a and i |
|---|---|---|---|---|---|---|---|---|
| Number of SIFT points | 7791 | 2621 | 1083 | 420 | 4265 | 2400 | 1324 | 728 |
| Books (a) | Box (b) | Kampa (c) | Kyoto (d) | Plant (e) | Valbonne (f) | ||
|---|---|---|---|---|---|---|---|
| Inliers’ average-RMSE I(min-max) | MSAC | 80.0 ± 5.6 (67–93) | 221.7 ± 9.8 (200–247) | 70.1 ± 3.6 (61–79) | 245.7 ± 10.1 (214–266) | 52.1 ± 4.1 (41–63) | 39.1 ± 2.3 (30–44) |
| Basic LILS | 102.0 ± 6.0 (84–118) | 278.7 ± 15.2 (234–303) | 110.1 ± 8.8 (85–136) | 338.5 ± 28.6 (257–392) | 70.45 ± 5.4 (56–83) | 51.7 ± 4.1 (39–61) | |
| Aggregated LILS | 90.0 ± 6.9 (71–98) | 222.8 ± 15.6 (186–249) | 65.3 ± 4.9 (53–79) | 249.4 ± 12.7 (202–266) | 51.7 ± 4.8 (41–64) | 40.3 ± 3.5 (31–46) | |
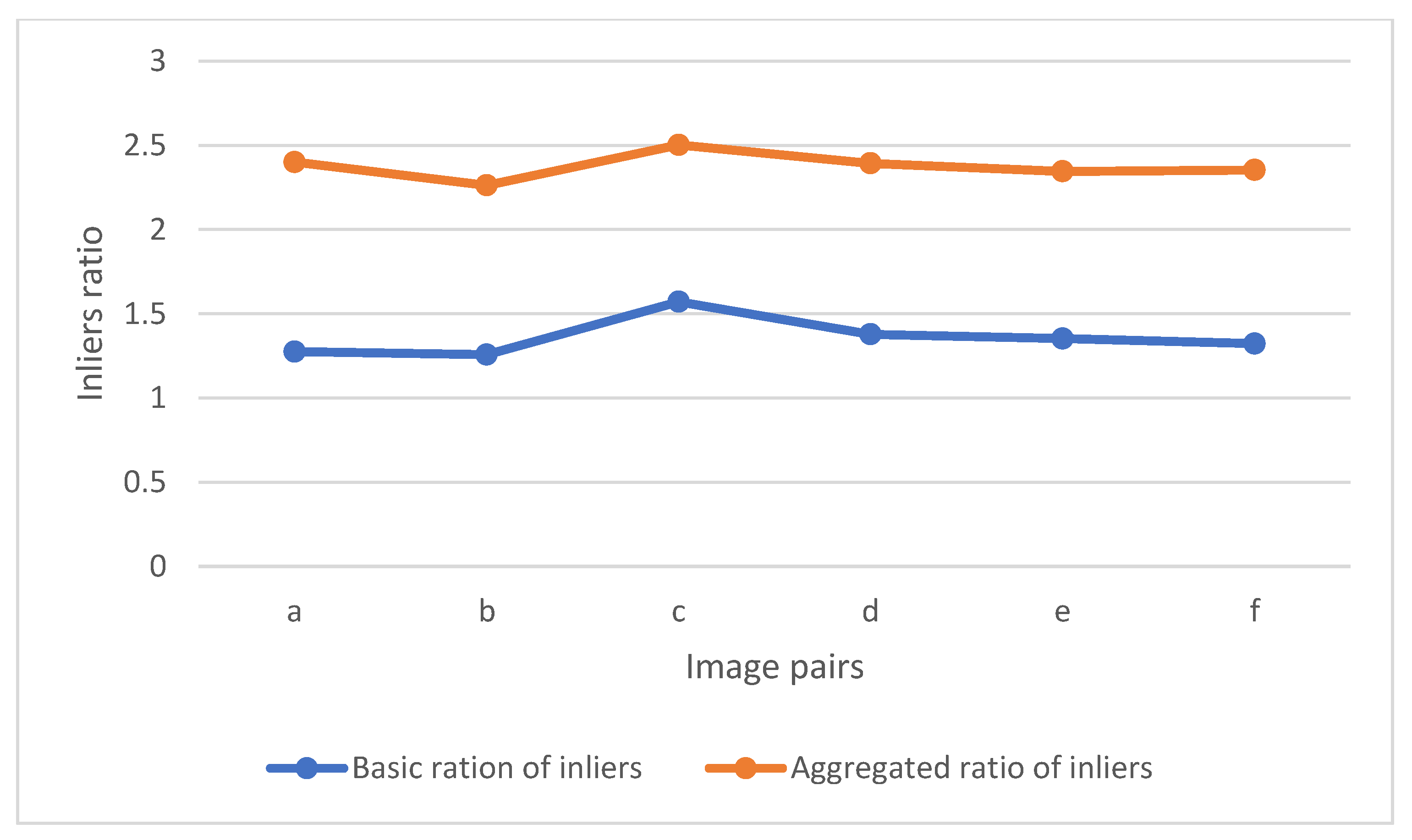
| Ratio of inliers w.r.t MSAC | Basic LILS | 1.275 | 1.2571 | 1.5706 | 1.3776 | 1.3522 | 1.3222 |
| Aggregated LILS | 1.125 | 1.0049 | 0.9315 | 1.015 | 0.9923 | 1.0306 | |
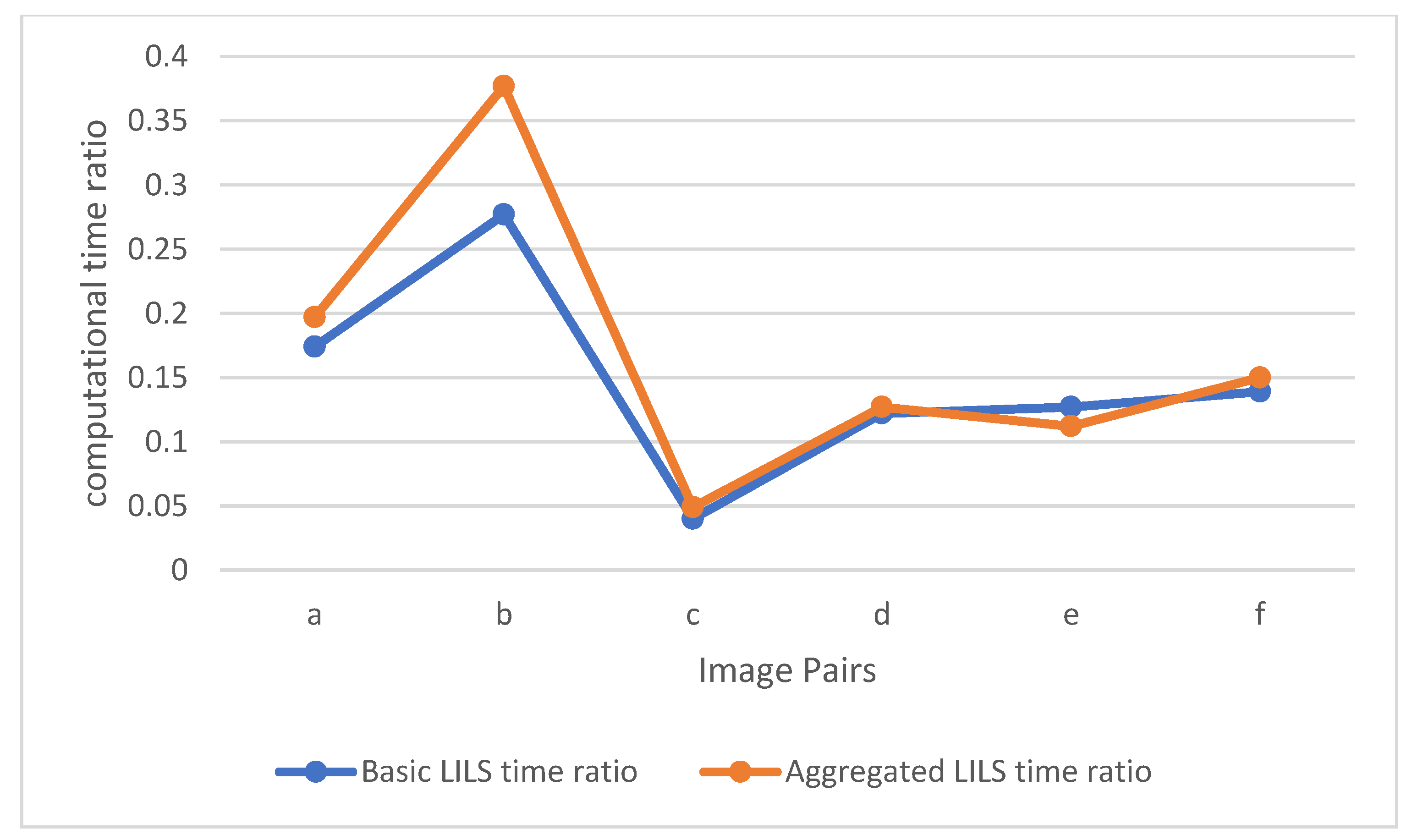
| Ratio of computational time w.r.t MSAC | Basic LILS | 0.174 | 0.277 | 0.040 | 0.122 | 0.127 | 0.139 |
| Aggregated LILS | 0.197 | 0.377 | 0.049 | 0.127 | 0.112 | 0.150 | |
| a and b | a and c | a and d | a and e | a and f | a and g | a and h | a and i | ||
| Inliers’ average-RMSE (min-max) | MSAC | 4516.5 ± 245.9 (4001–5128) | 1374.3 ± 68.2 (1228–1566) | 491.3 ± 20.1 (447–552) | 119.2 ± 4.7 (104–131) | 2416.1 ± 130.5 (2145–2699) | 1243.3 ± 66.4 (1100–1383) | 618.8 ± 30.0 (540–688) | 248.6 ± 10.5 (227–274) |
| Basic LILS | 5380.4 ± 51.4 (4935–5420) | 1593.6 ± 35.8 (1511–1644) | 556.1 ± 8.0 (531–570) | 132.6 ± 2.5 (124–137) | 2882.9 ± 14.4 (2828–2909) | 1435.5 ± 14.3 (1384–1463) | 722.1 ± 11.9 (681–743) | 279.1 ± 7.0 (243–290) | |
| Aggregated LILS | 5394.4 ± 19.8 (5301–5439) | 1598.8 ± 34.7 (1456–1644) | 559.1 ± 7.5 (538–571) | 133.5 ± 2.7 (123–139) | 2889.5 ± 13.2 (2844–2913) | 1442.3 ± 16.7 (1380–1478) | 720.2 ± 13.6 (680–746) | 282.0 ± 7.4 (260–296) | |
| Ratio of inliers w.r.t MSAC | Basic LILS | 1.1912 | 1.2505 | 1.1318 | 1.1124 | 1.1932 | 1.1545 | 1.1669 | 1.1226 |
| Aggregated LILS | 1.1943 | 1.2546 | 1.1380 | 1.1199 | 1.1959 | 1.1600 | 1.1638 | 1.1343 | |
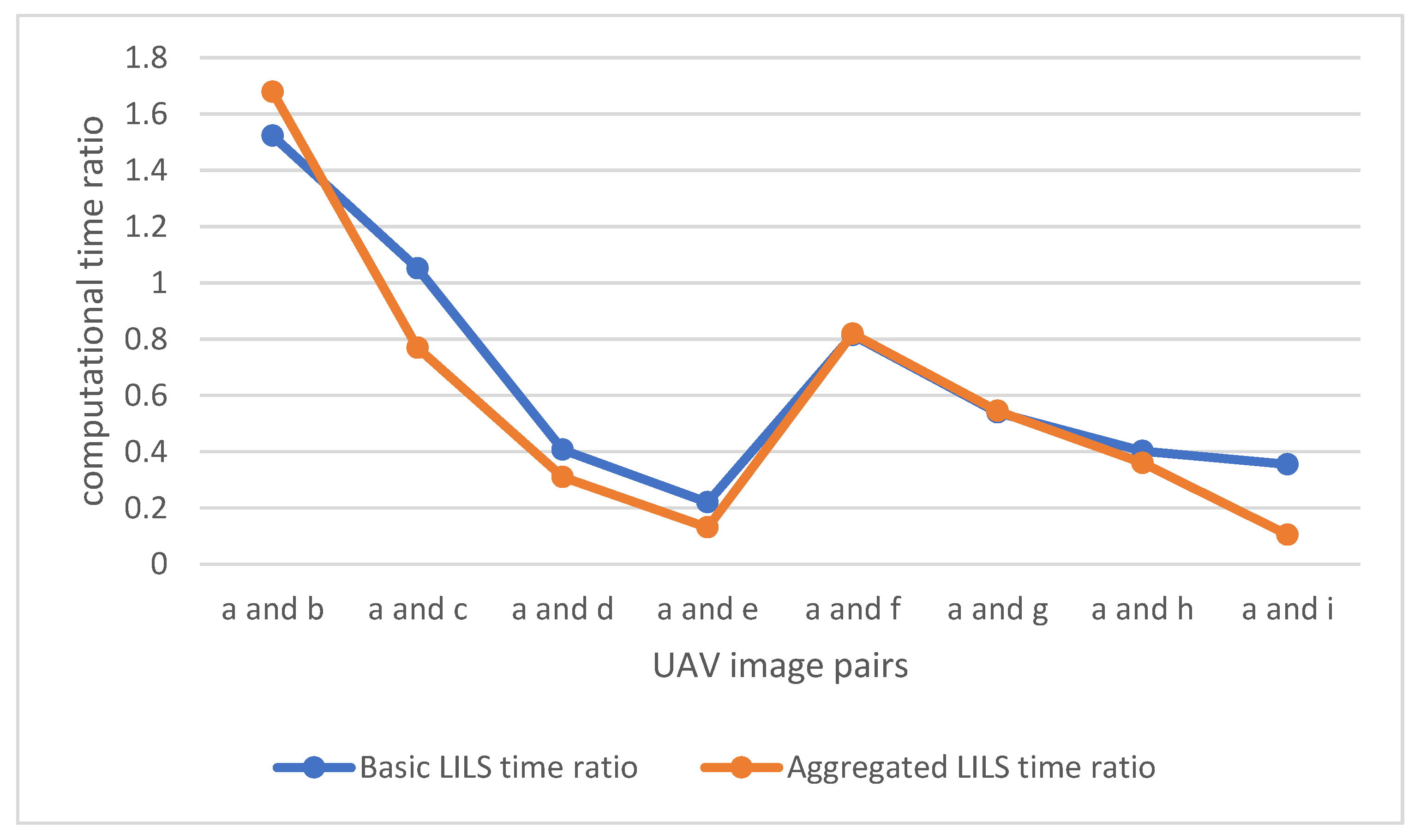
| Ratio of computational time w.r.t MSAC | Basic LILS | 1.522 | 1.051 | 0.407 | 0.220 | 0.814 | 0.539 | 0.402 | 0.355 |
| Aggregated LILS | 1.678 | 0.769 | 0.310 | 0.131 | 0.819 | 0.545 | 0.360 | 0.105 | |
| Method | Number of Points in the Generated Sparse Point Clouds | ||
|---|---|---|---|
| First Dataset (a) | Second Dataset (b) | Third Dataset (c) | |
| The proposed procedure | 4870 | 5755 | 11,292 |
| Agisoft software | 3306 | 4225 | 7418 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salehi, B.; Jarahizadeh, S.; Sarafraz, A. An Improved RANSAC Outlier Rejection Method for UAV-Derived Point Cloud. Remote Sens. 2022, 14, 4917. https://doi.org/10.3390/rs14194917
Salehi B, Jarahizadeh S, Sarafraz A. An Improved RANSAC Outlier Rejection Method for UAV-Derived Point Cloud. Remote Sensing. 2022; 14(19):4917. https://doi.org/10.3390/rs14194917
Chicago/Turabian StyleSalehi, Bahram, Sina Jarahizadeh, and Amin Sarafraz. 2022. "An Improved RANSAC Outlier Rejection Method for UAV-Derived Point Cloud" Remote Sensing 14, no. 19: 4917. https://doi.org/10.3390/rs14194917
APA StyleSalehi, B., Jarahizadeh, S., & Sarafraz, A. (2022). An Improved RANSAC Outlier Rejection Method for UAV-Derived Point Cloud. Remote Sensing, 14(19), 4917. https://doi.org/10.3390/rs14194917











