1. Introduction
Radar interferometry is a widely used technique of aerial monitoring of slow motions on the Earth’s surface. It can provide valuable information on the behavior of an underground geological structure, whether it is used as a source of water, oil, or gas, a CO
2 storage space, or, for example, as an underground gas storage facility (UGS). The periodic motions of the Earth’s surface enable, among other things, detection of unused parts of the reservoir, reactivation of faults, or failure of wells, and can be used for tuning, verification, and validation of geotechnical models of underground geological structures in which UGS facilities are built [
1,
2,
3,
4,
5]. The great advantage of this method is the aerial coverage, the detail of the description in space, high sensitivity, and the ability to monitor the development of terrain surface shifts over time. The disadvantage is the small detail in the time dimension because repeated data collection is performed in a period from days to weeks. A lack of well-reflecting surfaces that can function as permanent scatterers (PSes) can be a limitation.
The advantage of global navigation satellite system (GNSS) technology is that it is an independent, very accurate method, allowing detailed data to be collected over time [
2,
6,
7]. Its disadvantage is its ability to cover the studied area only with a sparse network of points due to the high costs associated with the installation and long-term operation of GNSS reference stations [
8,
9]. For example, [
1] used a network of 39 GPS (global positioning system) receivers for benchmarking. He compared the average time series of deformations from PS points in a radius of 100 m around the GPS receiver with the measurements from this receiver. Both measurements were evaluated relative to the selected reference point. In the case of InSAR, using a reference point is directly part of the method; in the case of GPS measurements, selecting one of the 39 receivers as a reference point was necessary. The horizontal displacement rates measured by InSAR agreed with GPS measurements within 1.8 mm a year, and the vertical displacement rates agreed within 4.8 mm a year [
1]. A worse result in the vertical direction may be explained by the general lower quality of GNSS in determining the vertical component than in the case of the horizontal components. In contrast, in the case of InSAR, higher accuracy can be expected in the vertical direction [
10].
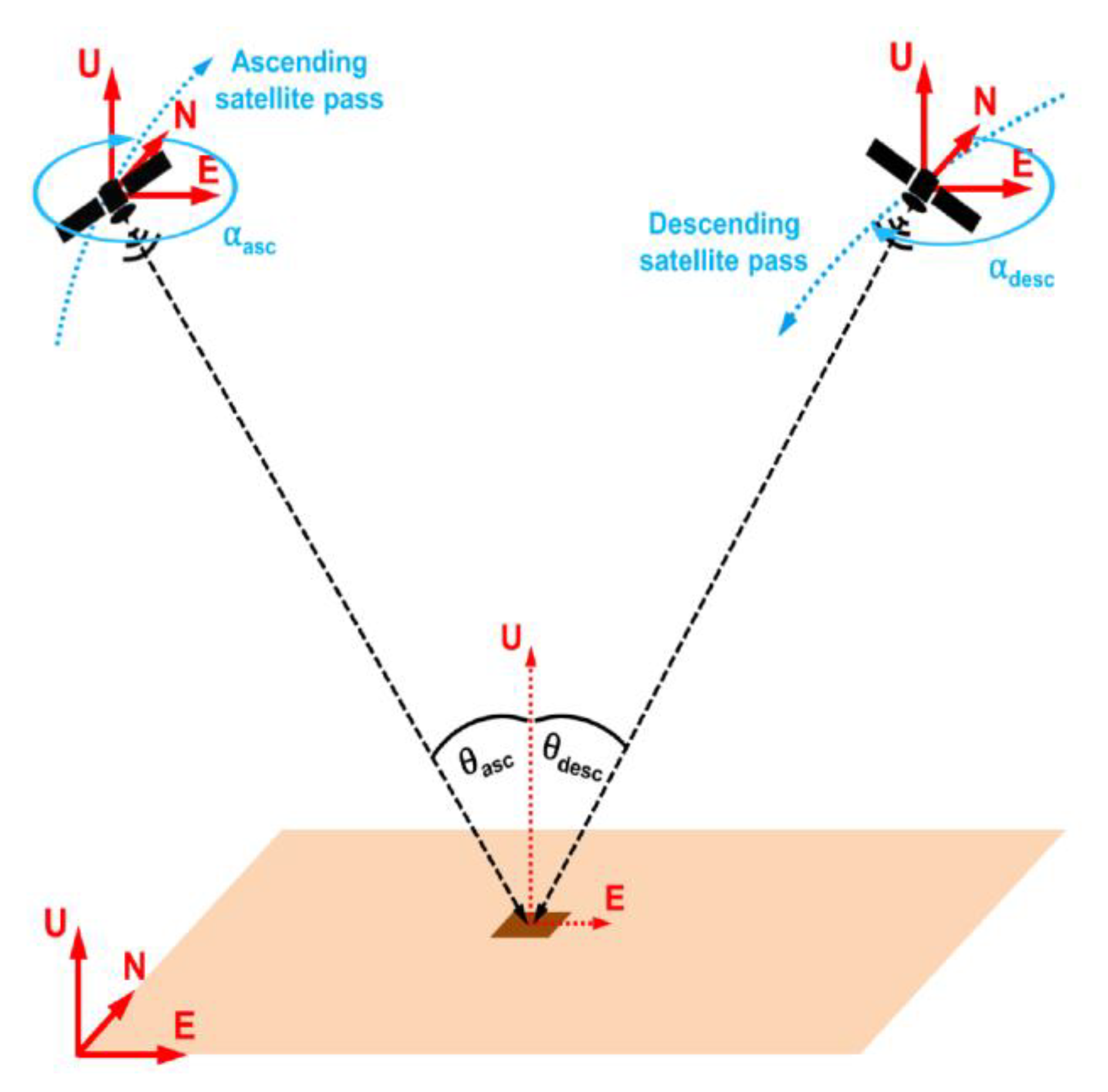
In radar interferometry, the change in distance between the satellite and the monitored point on the surface is evaluated, i.e., the change in their distance in line of sight (LOS), which is one-dimensional [
1]. However, the motion of the terrain surface, caused for example by underground processes, is three-dimensional. The one-dimensional nature of LOS implies that it is not easy to obtain a complete 3D description of terrain motion. For this reason, the direct use of LOS for vertical motion can lead to misinterpretation of the results. In addition, a simple conversion of LOS to vertical motion by cosine transformation, which completely neglects the horizontal component of motion, can lead to erroneous conclusions [
5,
11].
However, concerning measurement geometry and orbiting satellite motion, measured displacements in LOS can be broken down into three directions by combined processing of data obtained on both ascending and descending satellite tracks [
2,
11,
12]. Given the orbits of the satellites, which are usually sub-polar, the method is relatively sensitive to horizontal motions in the east–west (E–W) direction but is almost insensitive to the motions in the north–south (N–S) direction (except for polar areas). Therefore, it is not possible to evaluate the complete horizontal motion vector of the monitored point from the measurement. However, even the E–W component itself can, in some situations, provide interesting information about the behavior of the area over time. For example, this method can describe, in more detail, the deformation of the east or west-facing slopes in the E–W direction. The same applies to areas above underground gas storage. They are usually flat, and the E–W component could provide at least partial information about the behavior of the overburden of the UGS’s geological structure during the natural gas injection/withdrawal cycle. The same applies for geological faults that intersect the monitored area.
The problem of motion vector breakdown from the LOS direction into its components is not new; it was first addressed by Hoffmann and Zebker [
13] and especially by Wright et al. [
14], and then, for example, by [
1,
2,
11,
15].
Among other things, the evaluation of 3D terrain displacements is used for tuning, verifying, and validating the geomechanical model of the studied geological structure [
1,
10]. However, recently the inverse approach has emerged—the use of a deformation model based on knowledge of the change in the volume of underground fluids, based on Green’s function, which allows the use of a single-track LOS to derive a 3D vector of motion of the terrain ([
16] in [
17]). However, the necessary condition is the existence of a geomechanical model of the storage structure.
Some papers have also compared the E–W component of displacement obtained from PSInSAR with GNSS measurements. They were typically focused on monitoring motions of the area affected by subsidence, e.g., due to excessive groundwater withdrawal [
18], hydrocarbon production [
1], or underground coal mining [
2,
11]. Studies can also be found that deal with comparing landslides measurement results using GNSS and InSAR or the integration of measurement results obtained by both methods [
8,
19,
20,
21,
22]. However, only a few papers so far have dealt with long-term monitoring of the cyclical horizontal motion of the terrain above an underground gas storage and its relation to the area’s geology, e.g., [
23,
24].
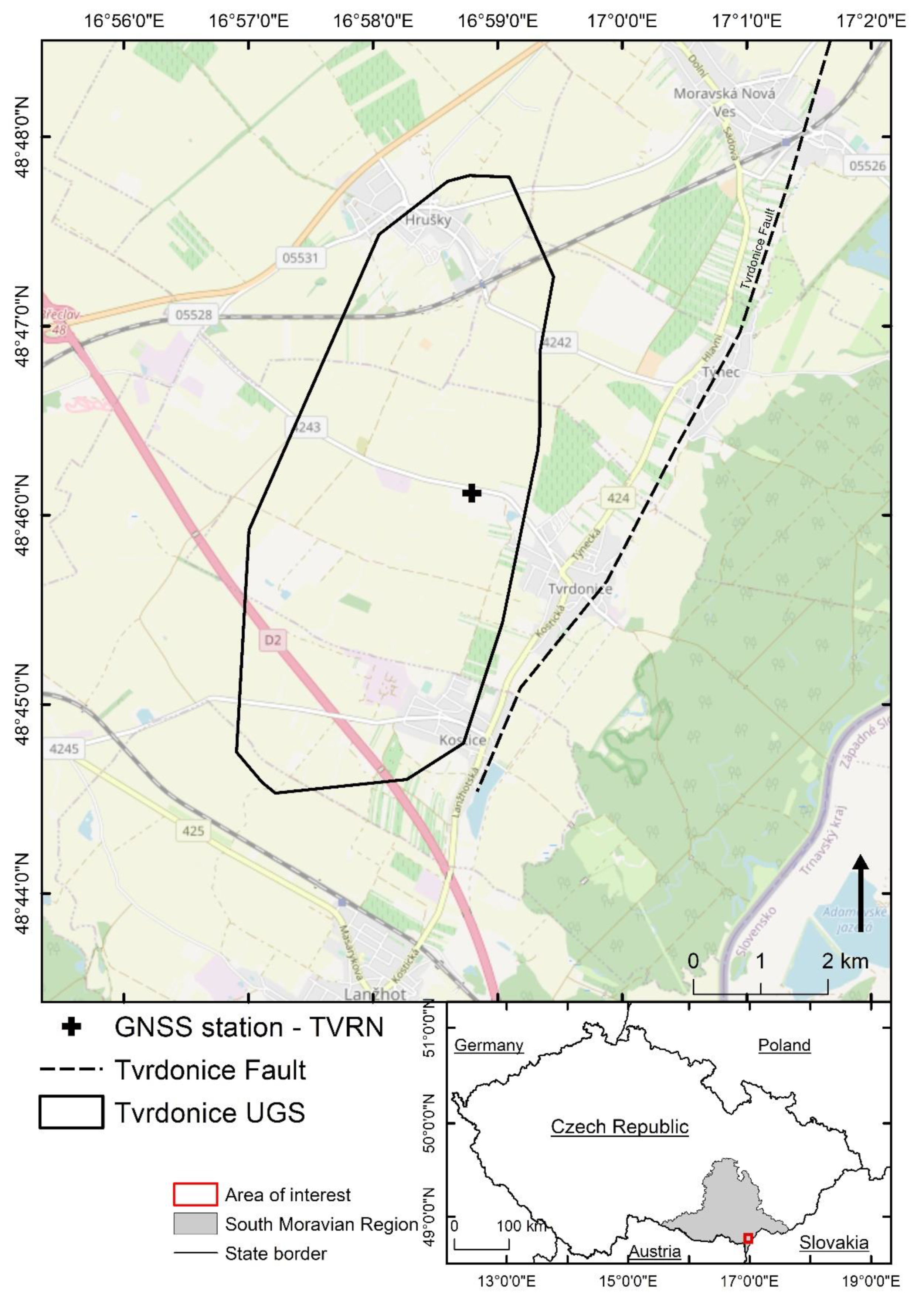
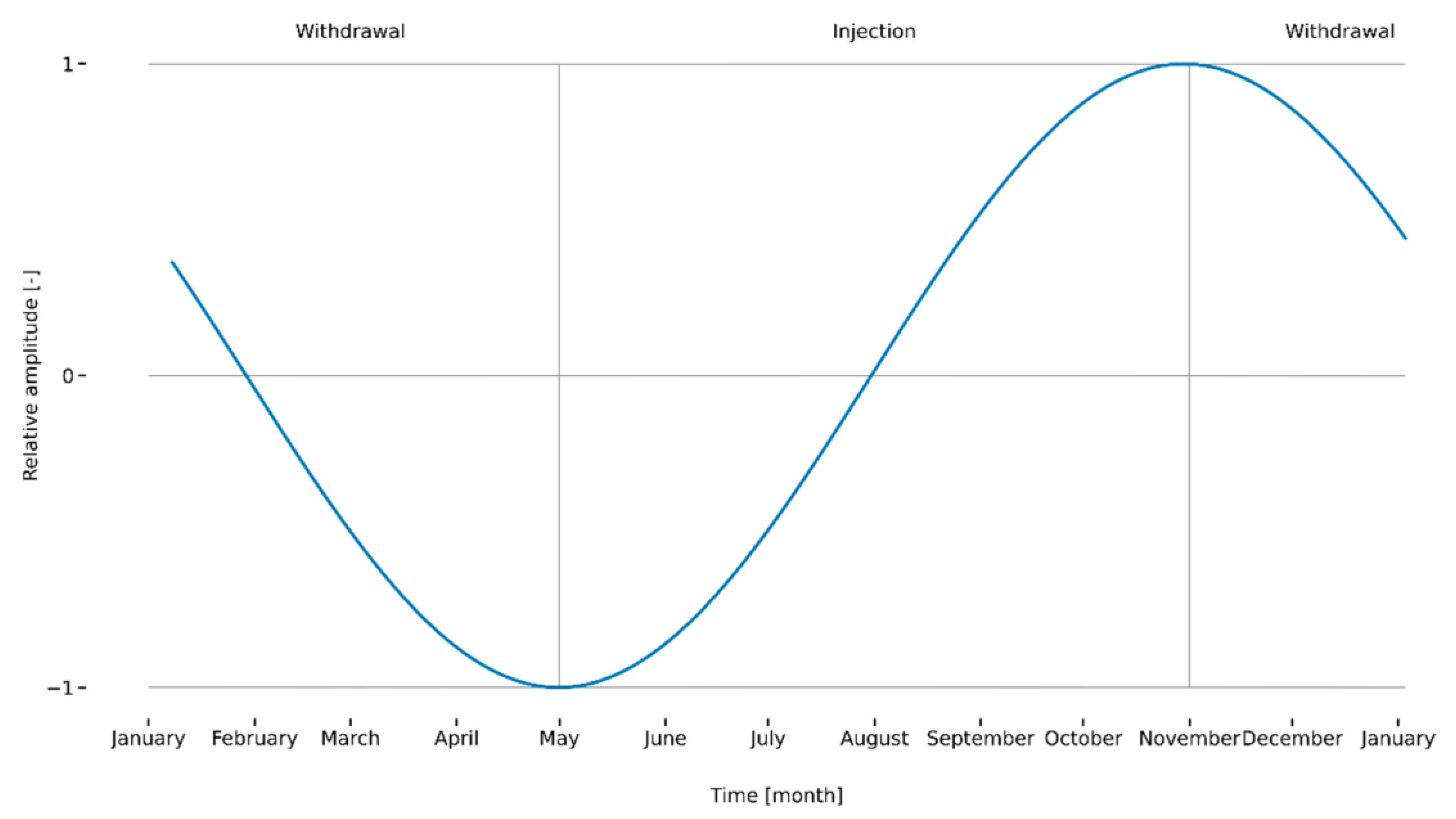
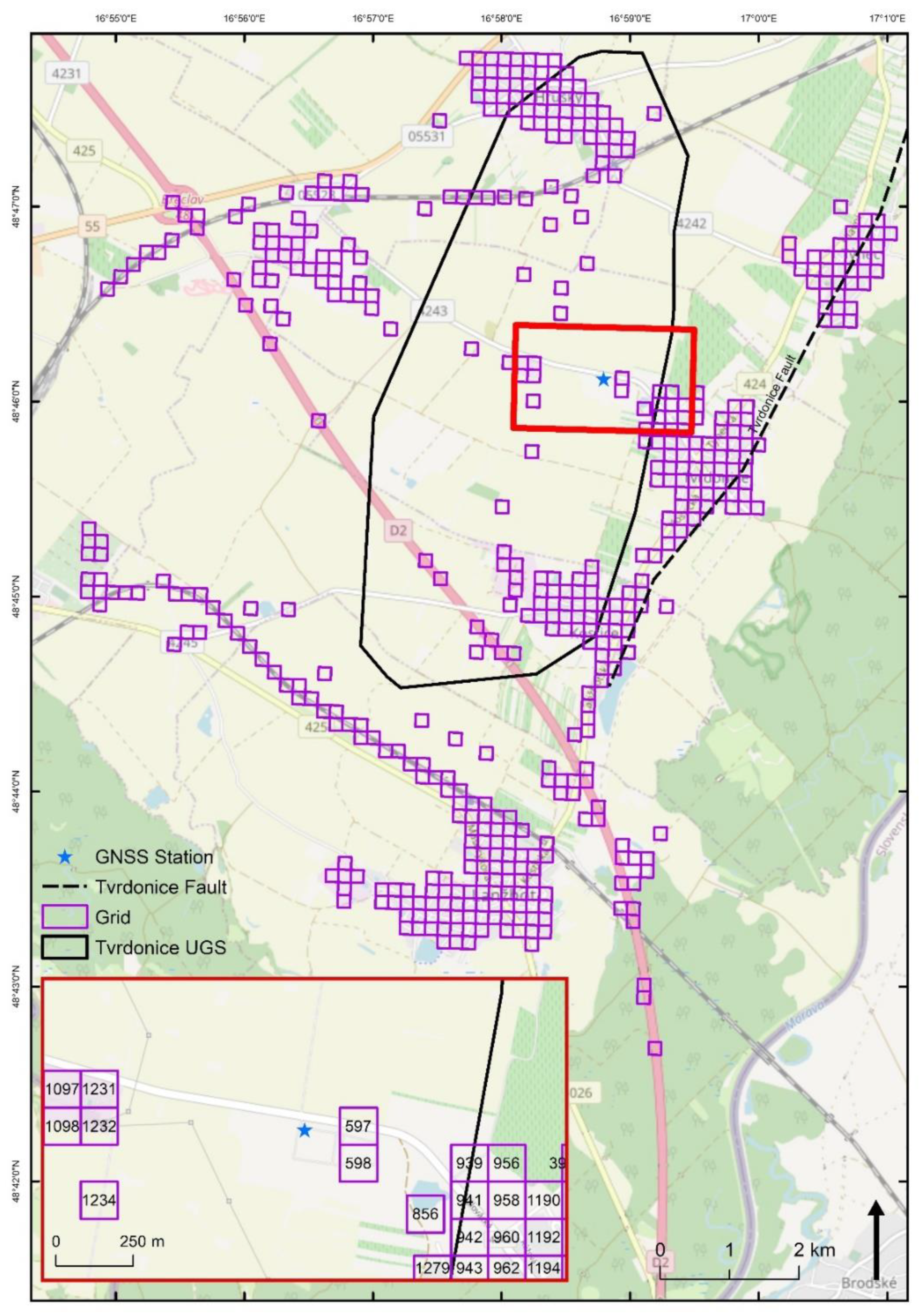
Horizontal terrain displacements induced by the injection/withdrawal of natural gas head toward the place with the most significant pressure drop, i.e., roughly to the center of the UGS (or perpendicular to the longitudinal axis of the UGS in the case of an elongated structure, as in the studied Tvrdonice UGS) during the withdrawal, and in the opposite direction from the center of the UGS at the time of injection. The magnitude of displacement and the size of the affected area are influenced by the deposition depth of the UGS storage structure and its geometry and the geomechanical properties of the storage structure and surrounding rocks, as well as changes in pore pressure in the storage structure during the injection/withdrawal cycle [
10].
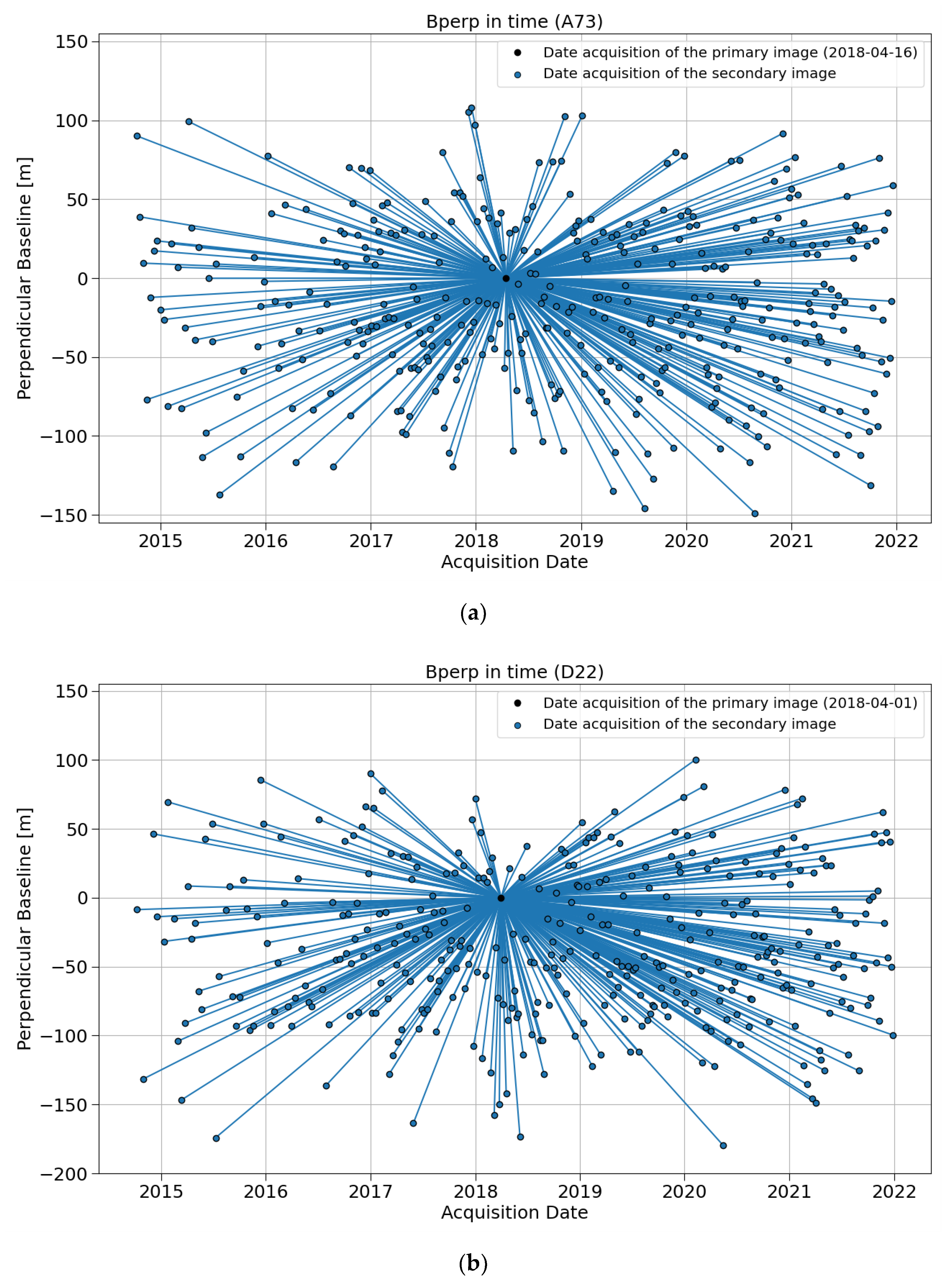
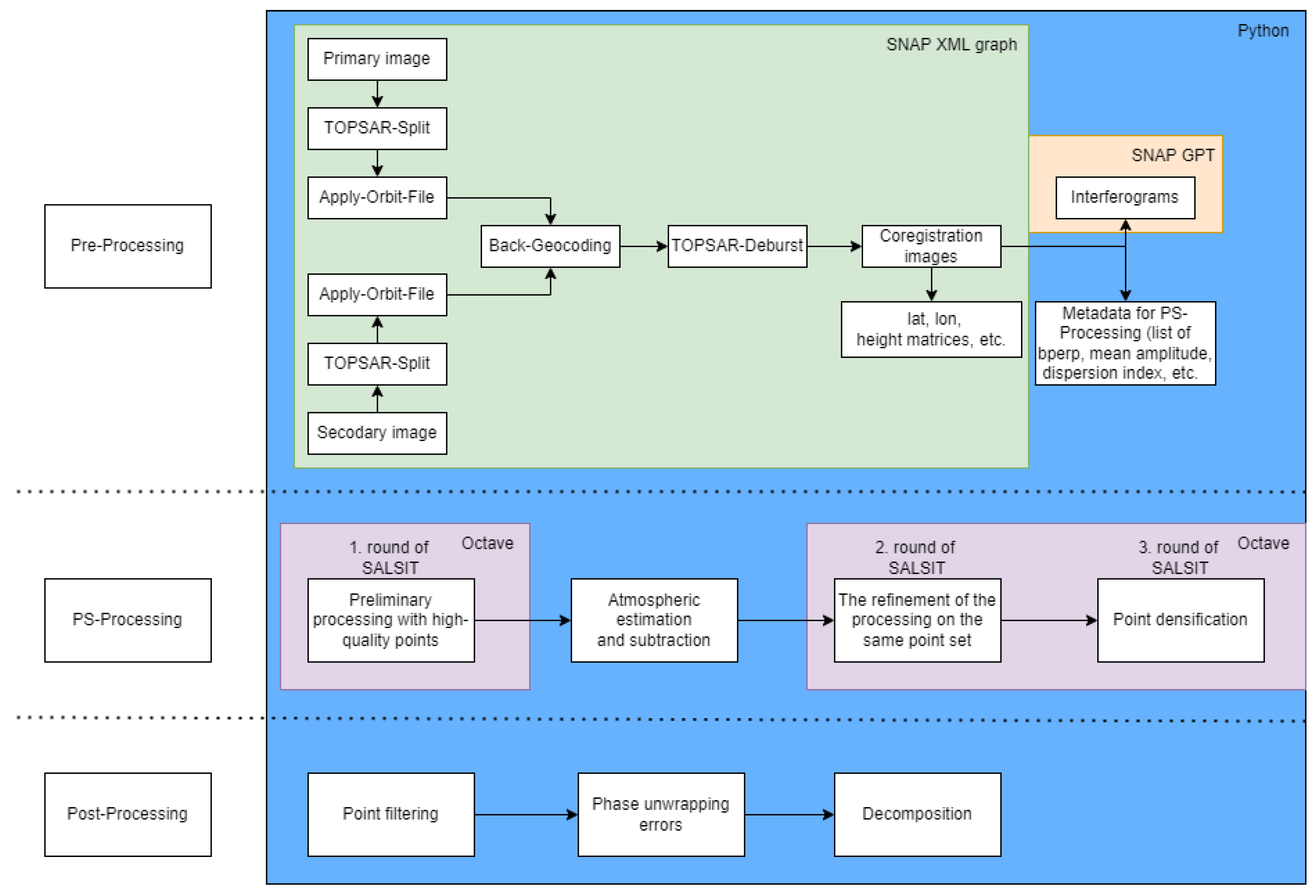
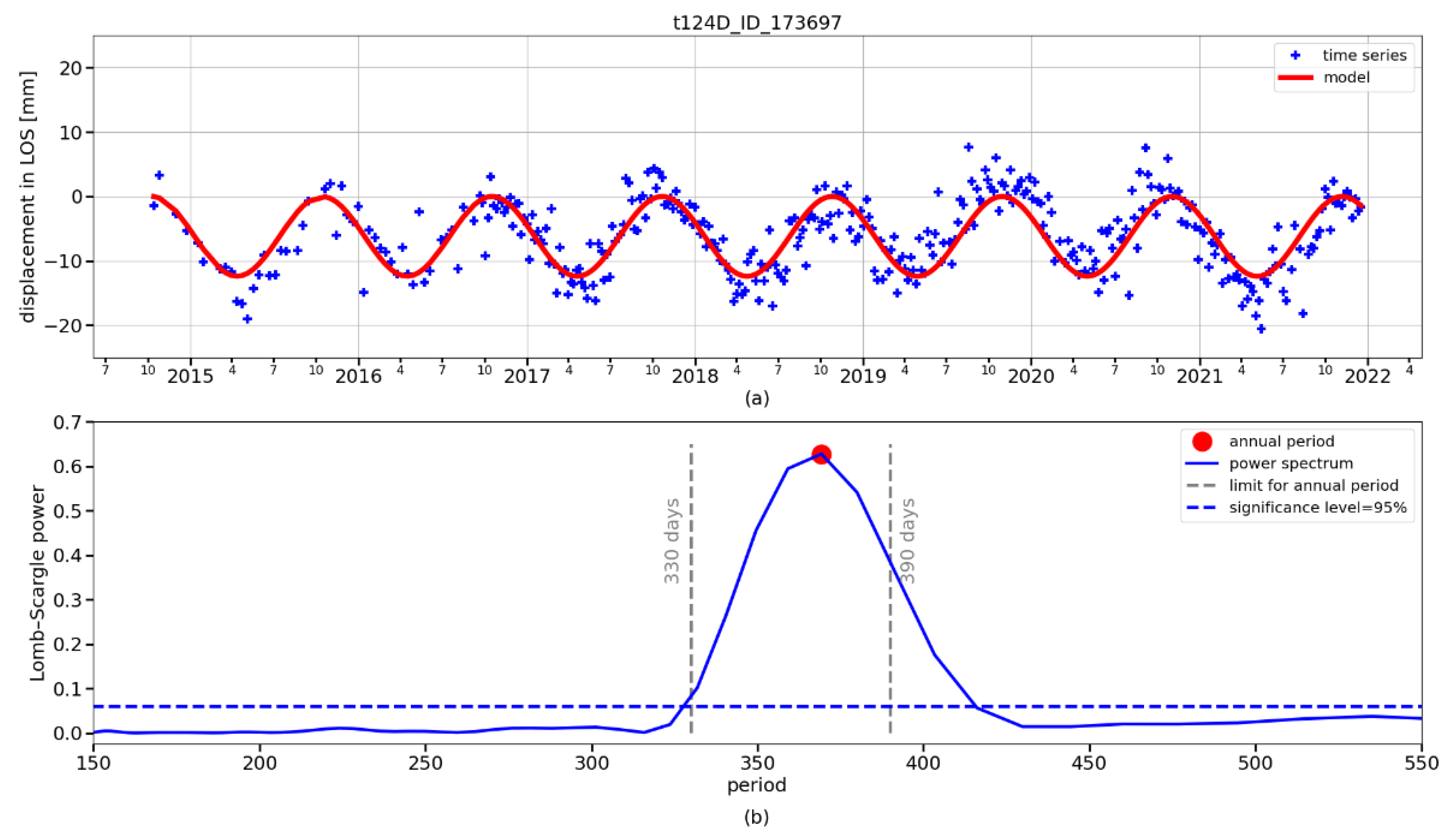
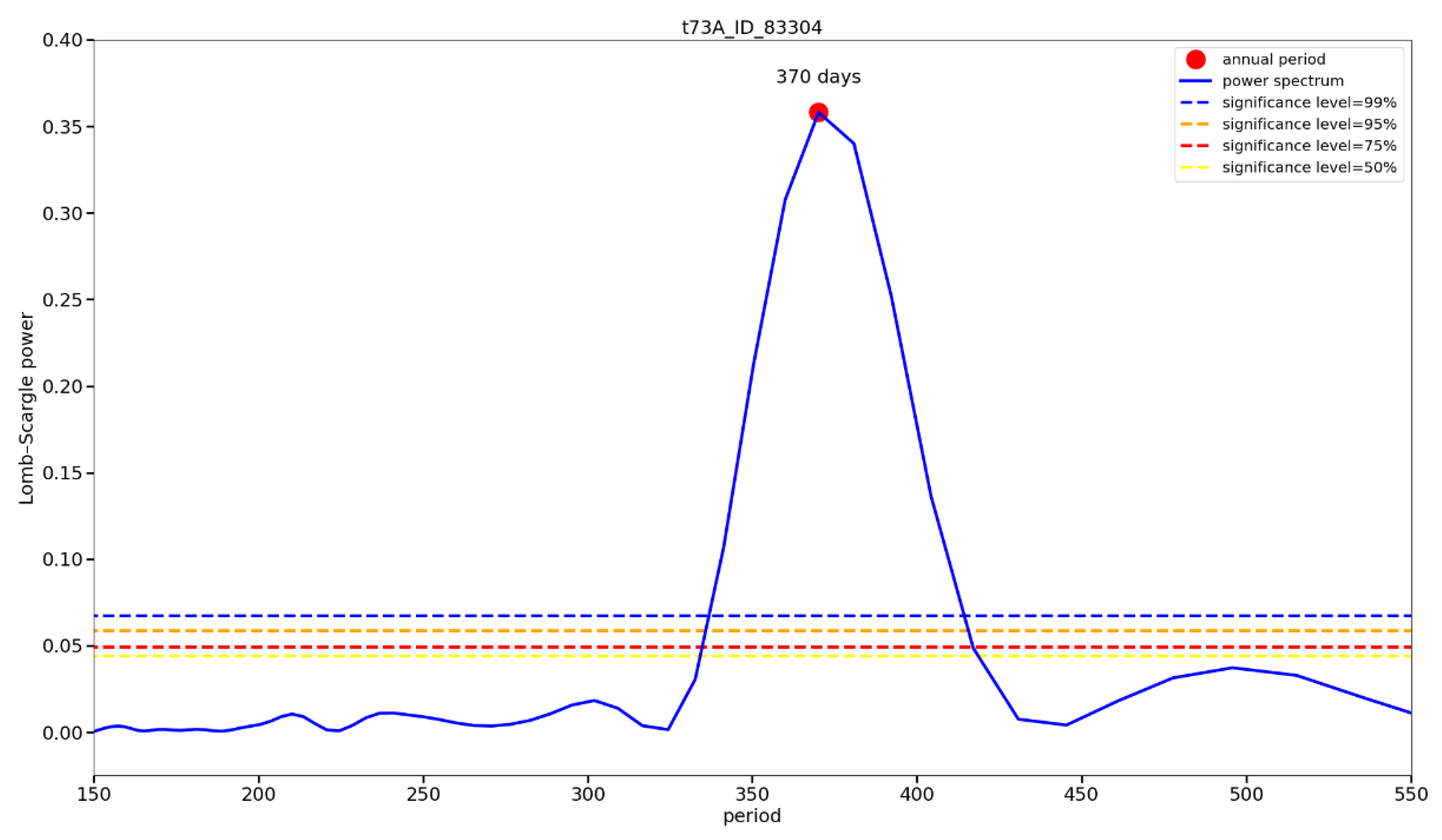
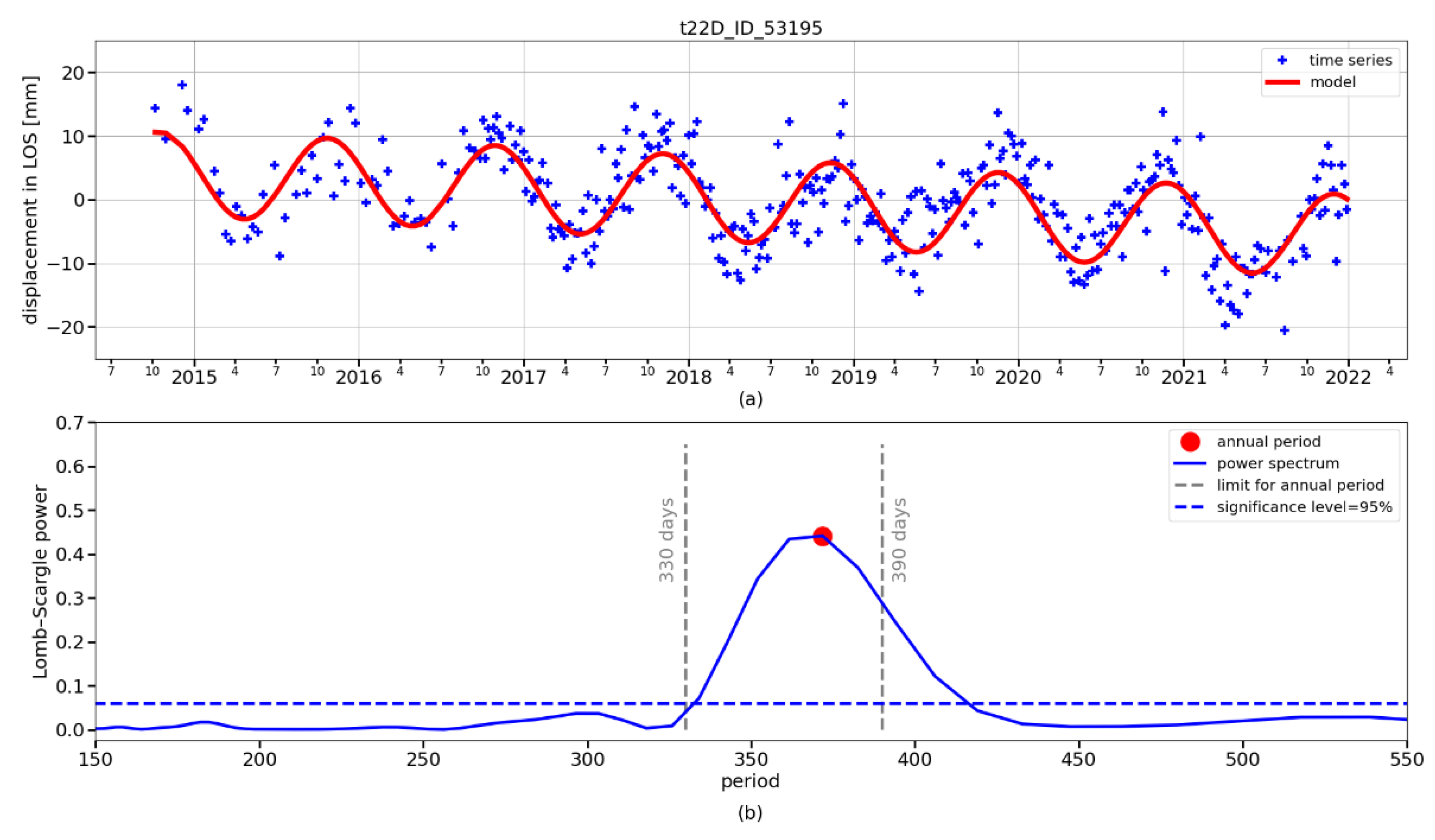
Our research was focused on a comprehensive area evaluation of periodic horizontal (E–W component) and vertical (U–D component) displacements over the selected UGS based on PSInSAR processing of freely available Sentinel-1 images. The analysis of their periodic character was based on obtaining E–W and U–D components by combined processing of time series of measurements in satellite line of sight (LOS) taken on ascending and descending tracks. For their necessary conversion to the same time frame, we used the Lomb–Scargle periodogram and models derived from it, with which we replaced the original time series. We also focused on the interpretation of the results in the context of UGS activity and the geological structure of the monitored area. The obtained results from monitoring the displacements of the Earth’s surface were validated against independent GNSS measurements.
4. Discussion and Conclusions
Our research was focused on assessing the possibility of aerial monitoring of periodic vertical and horizontal motions of the terrain above a UGS using the PSInSAR technique and on their interpretation with the UGS work cycle and considering the area’s geological structure. The first aspect concerns, in particular, the terrain above the UGS, the second also the broader surroundings of the UGS, where the motions of the terrain can induce further changes, for example, reactivating faults.
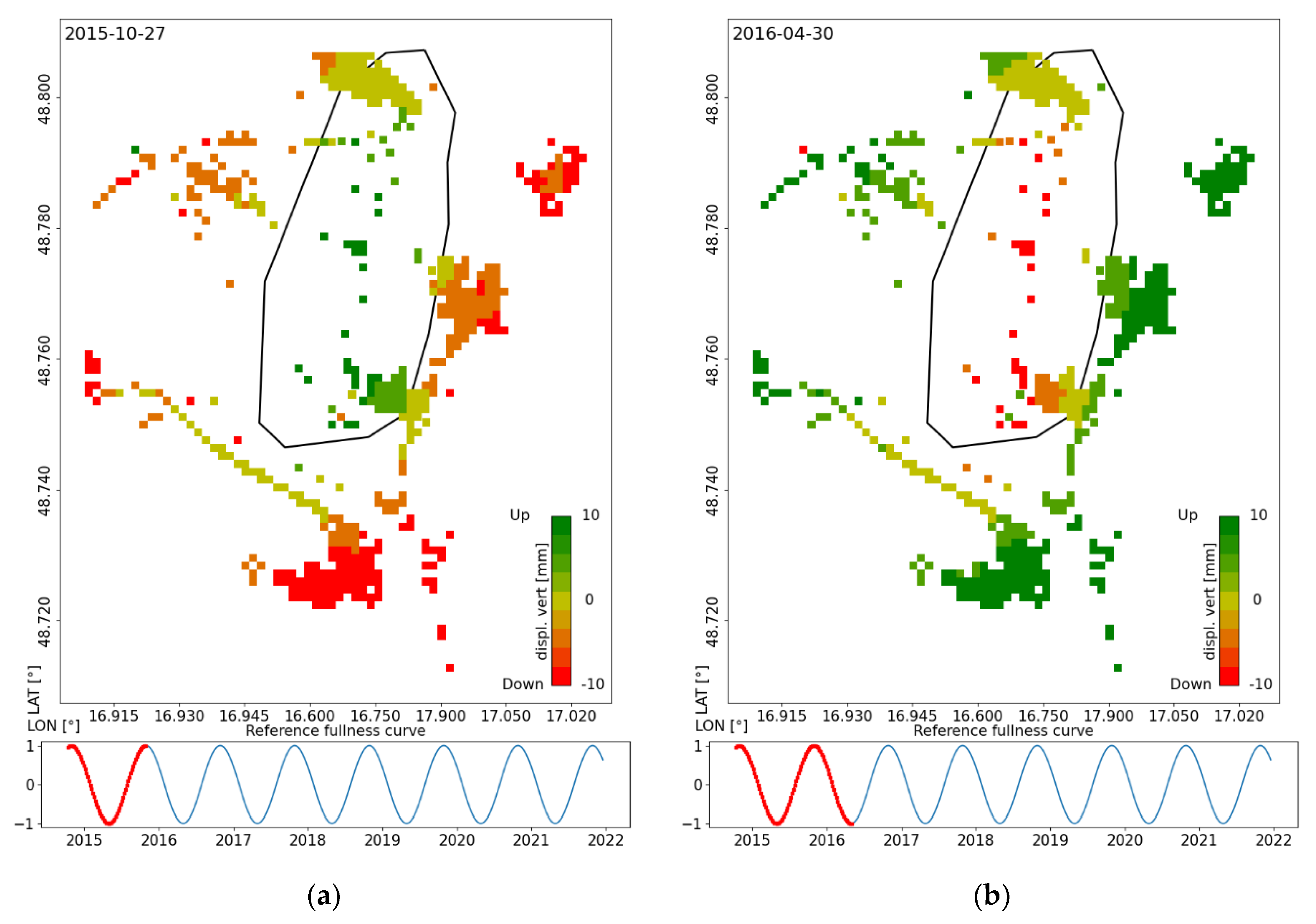
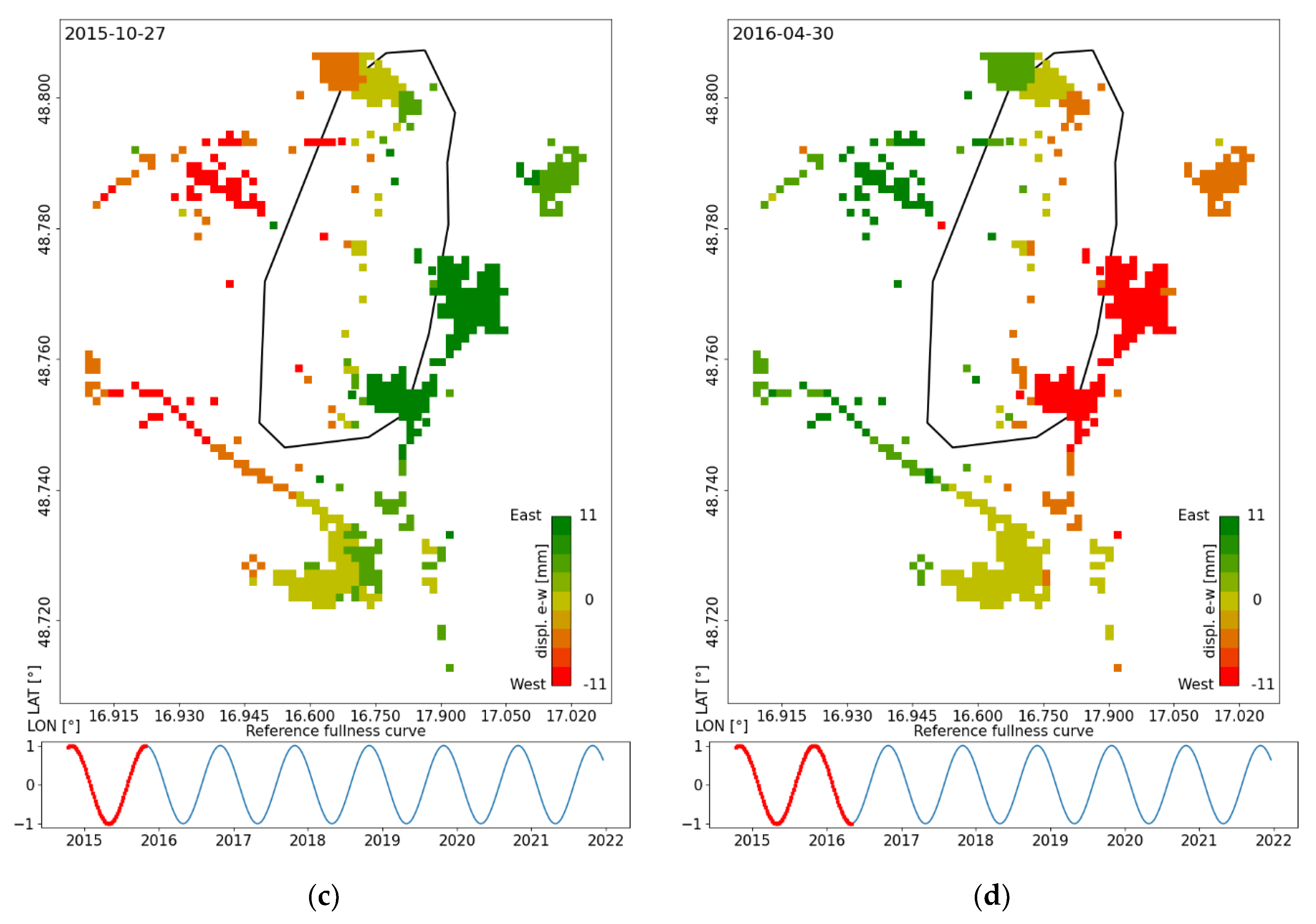
This study showed that PSInSAR is suitable for this purpose. We have found that the combined processing of PSInSAR outputs for ascending and descending tracks is suitable for the aerial monitoring of periodic terrain motions and breaking them down into E–W and U–D components (see attached animations on the web). The outputs of this processing provide a good idea of the behavior of the terrain above and in the vicinity of the UGS, and this behavior is consistent with the cyclic injection/withdrawal the UGS is subjected to.
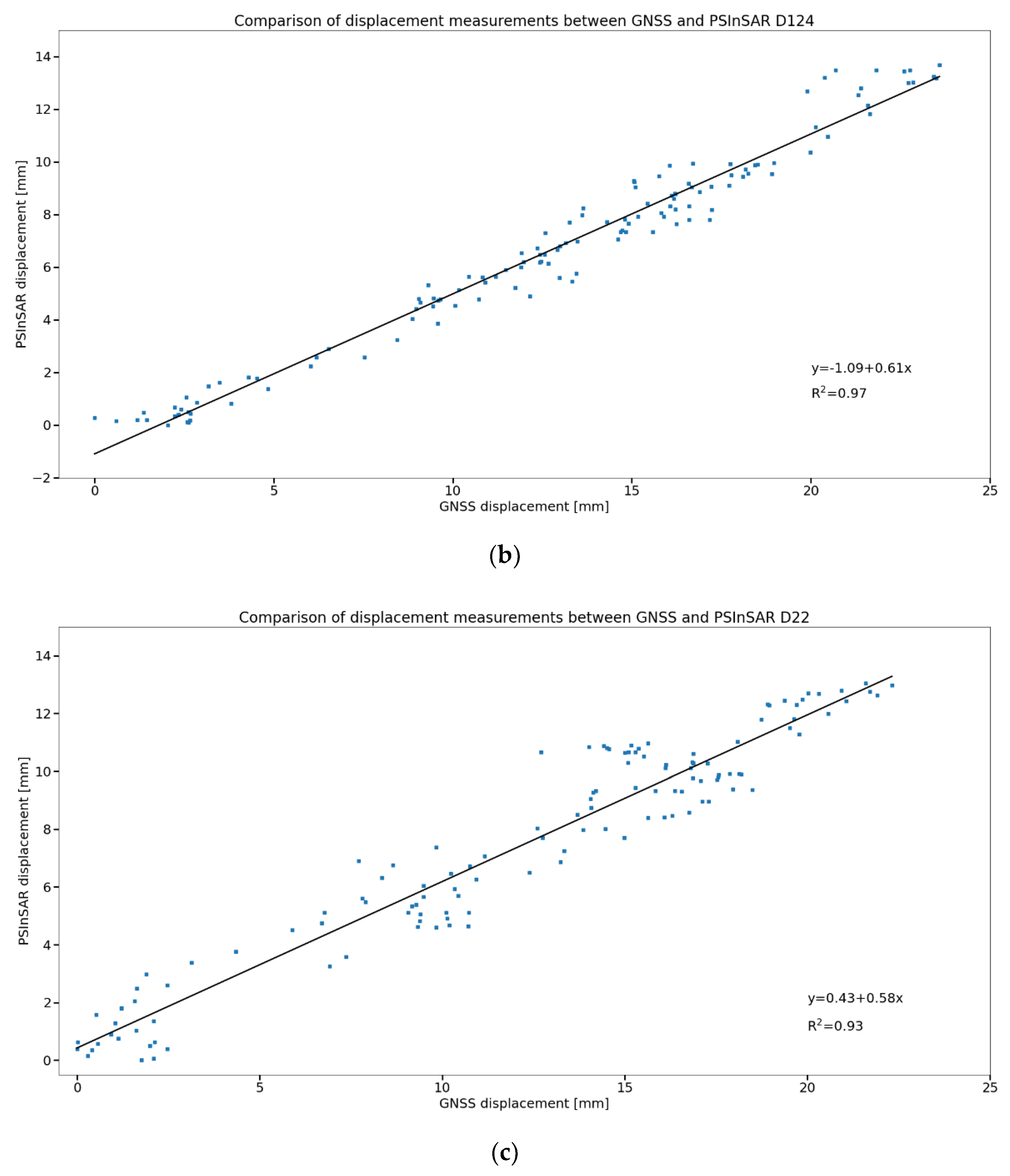
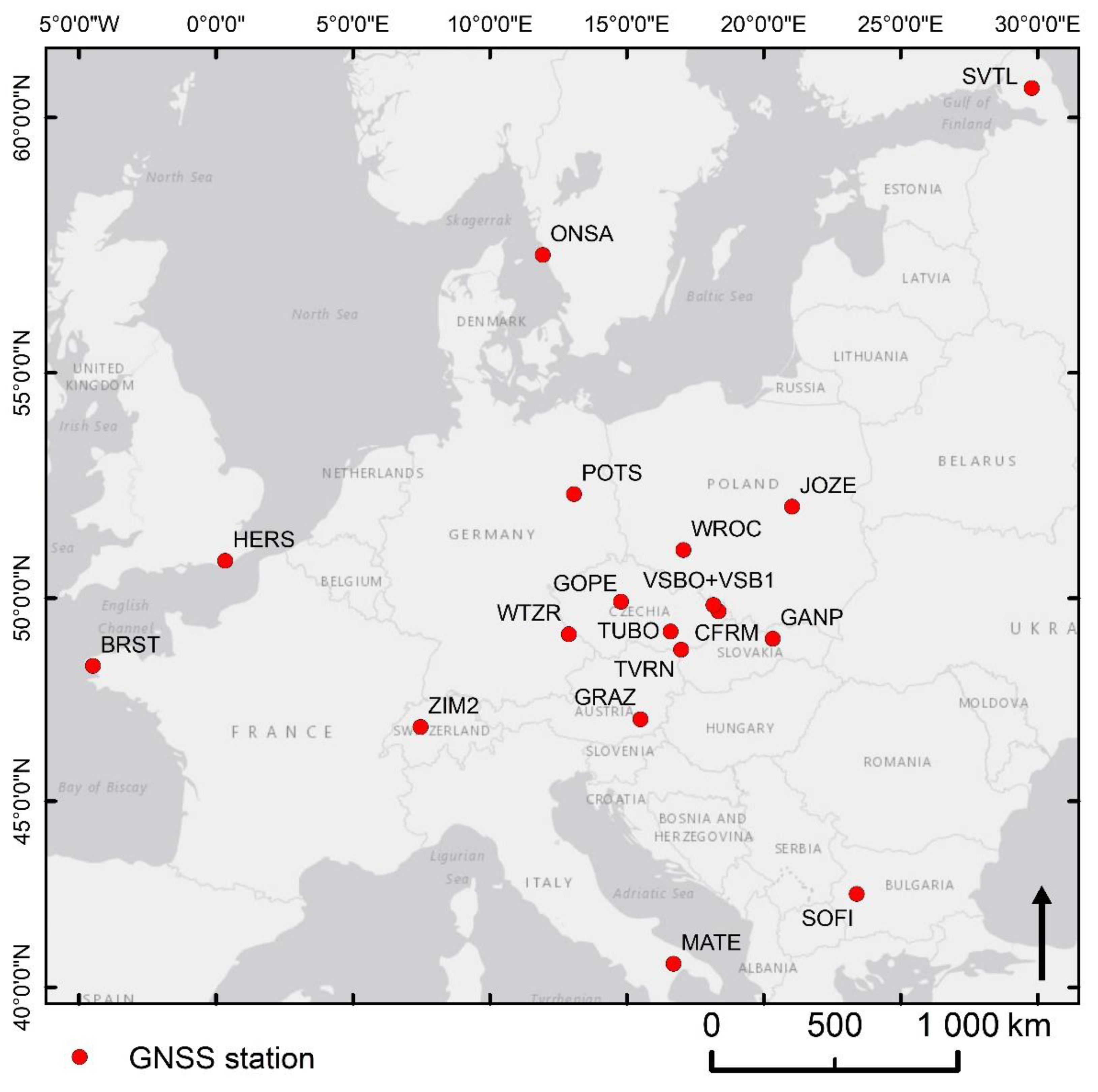
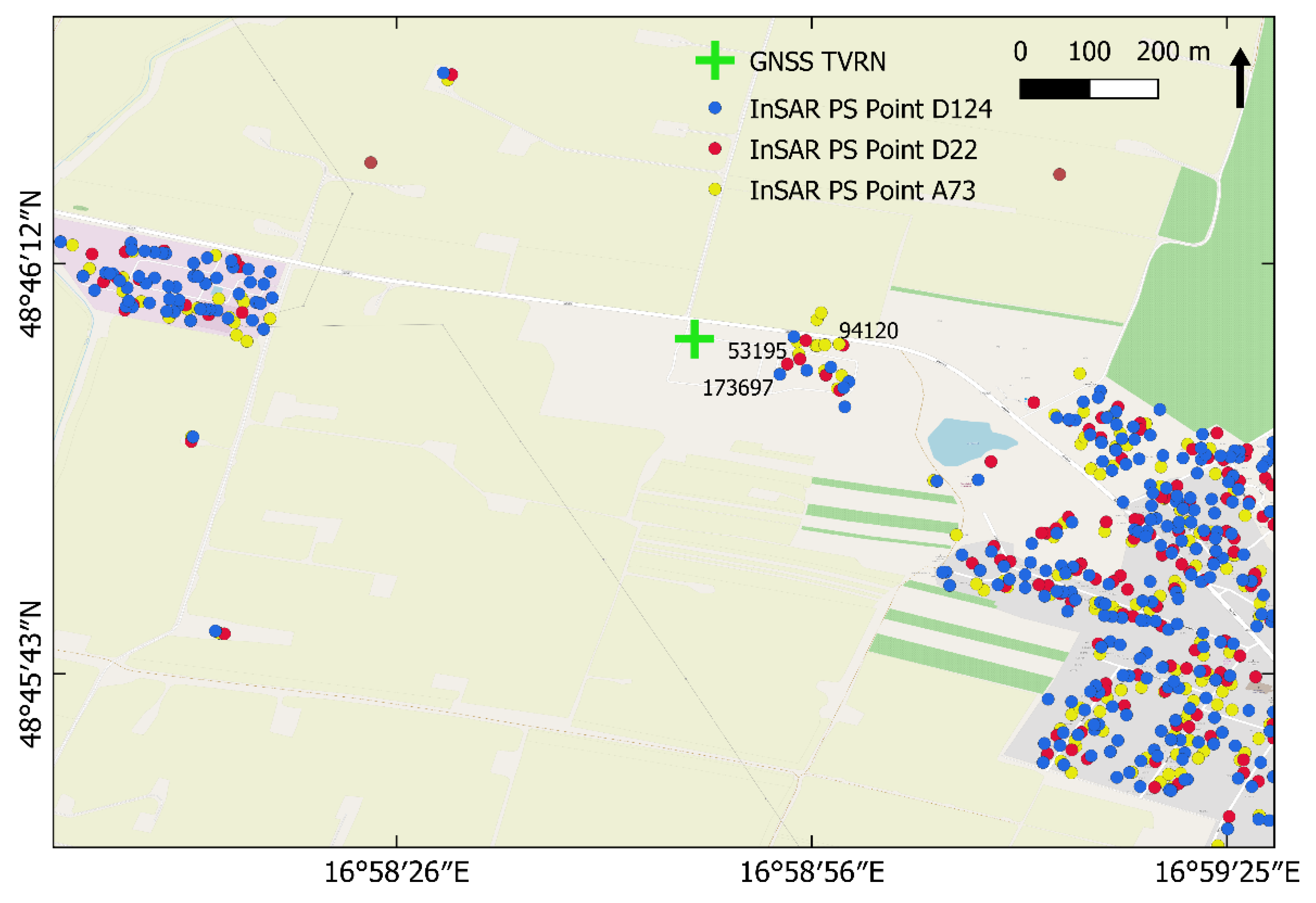
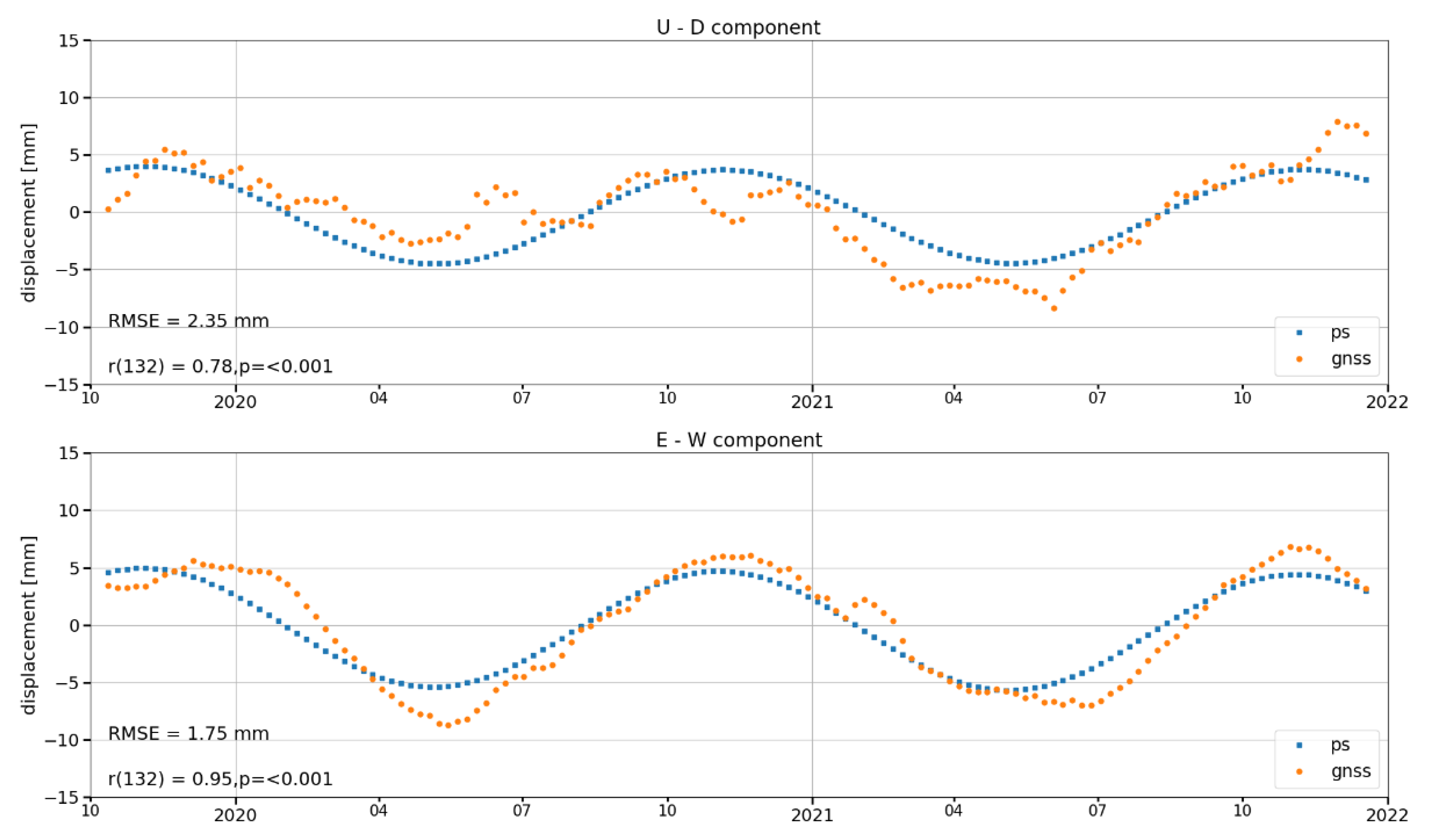
The evaluated motions in the E–W and U–D directions were also verified by independent measurements using a permanent GNSS station above the UGS. The results showed good agreement in the evaluation of motions by both methods (correlation coefficient between LOS from both methods based on descending track was on average 0.97, with an RMSE of 2.70 mm; in the case of E–W correlation the coefficient 0.95 was and the RMSE was 1.75 mm; for U–D it was 0.78 and 2.35 mm; and allow interpretation of aerial evaluation of E–W component from InSAR concerning the geology of the area and the periodic activity of UGS.
We found that the behavior of the terrain over the UGS was consistent with results published for other areas. Although these mainly related to monitoring linear shifts, they are also helpful for comparing our PSInSAR and GNSS measurements. Published works comparing the two methods were focused mainly on monitoring subsidence [
1,
2,
11,
18] or landslides [
8,
19,
20,
21]. We achieved the resulting accuracies, which are consistent with the published results. For example, in [
1], the horizontal displacement rates measured by InSAR agreed with GPS measurements within 1.8 mm a year, and the vertical displacement rates agreed within 4.8 mm a year.
Studying periodic motion of the terrain surface using PSInSAR and their verification using GNSS has so far received little attention. Such studies have only recently begun to appear. For example, [
24] dealt with cyclic motions above a UGS; its authors found the difference between the deformation rate of the GNSS reference station observations and the results of PSInSAR for Sentinel-1 tracks T114, T41, T19 to be 4.1 mm, 2.4 mm, and 3.1 mm a year, respectively. The InSAR and GNSS measurements were evaluated as consistent.
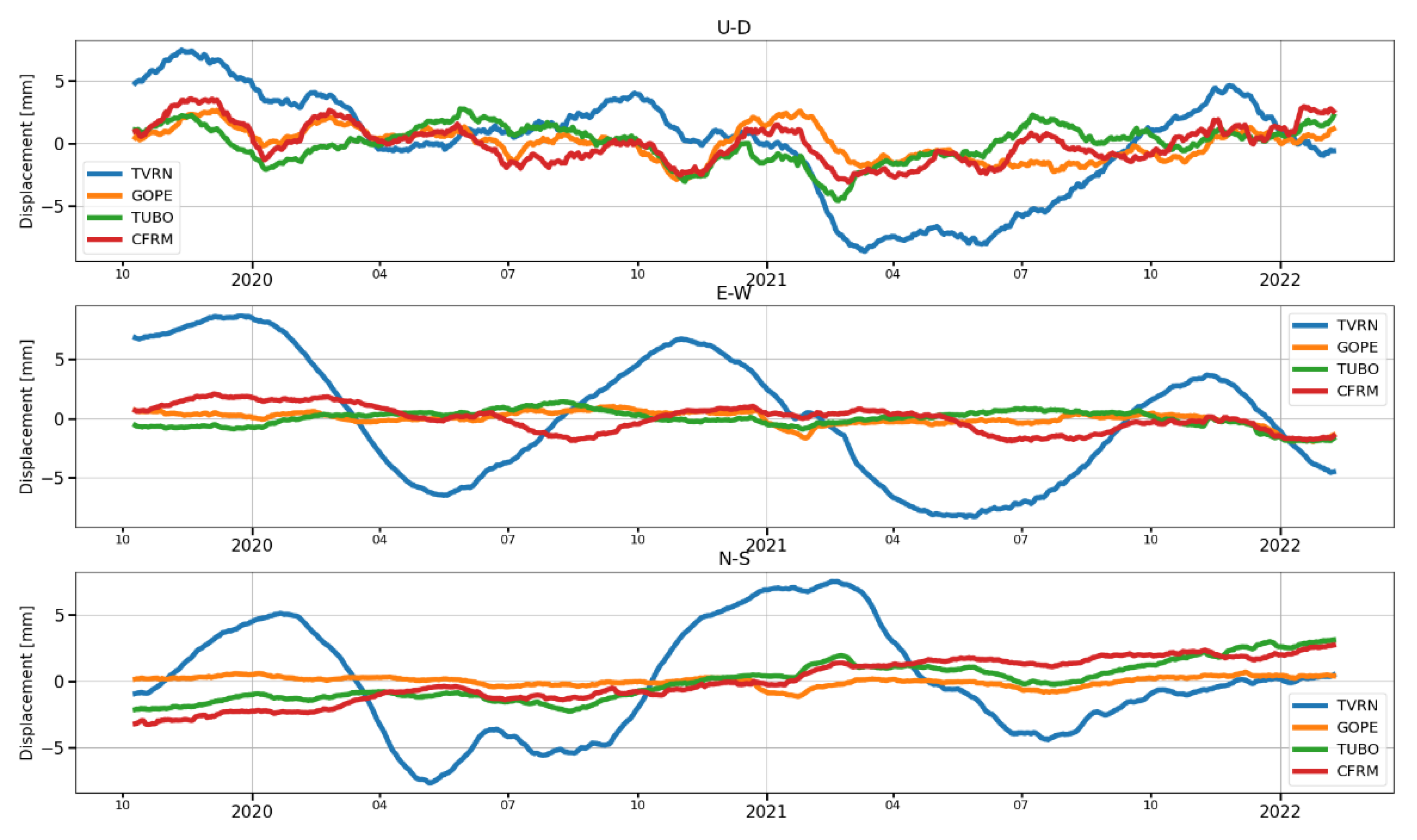
The orientation of the horizontal motions detected over the Tvrdonice UGS also followed the assumed terrain behavior described in [
10], and they were also in agreement with [
23], where the authors dealt with the 3D geomechanics of a UGS in northern Italy. During withdrawal, the terrain height decreased above the UGS, and the surface tended to move toward the center of the UGS; during injection, the direction of both motions was opposite.
The evaluated U–D motion agrees with the study presented in [
27], which was based purely on evaluating motion in the LOS direction. In this study, the authors interpreted the different behavior of the area west of the Tvrdonice fault as a consequence of motion along this fault induced by the injection and withdrawal of natural gas to and from the Tvrdonice UGS. The obtained results were interpreted as that when the UGS was filled, the terrain rose above the UGS, but the area west of the Tvrdonice fault decreased in height due to slippage down along the fault.
A detailed evaluation of the motions broken down into U–D and E–W components confirms this assumption.
Figure 16a,b shows that this region is really moving in the U–D direction in the antiphase to the injection/withdrawal cycle.
It can be assumed that systematic monitoring of UGSes could help identify degrading parts of the storage structure, non-standard well behavior, and reactivation of faults [
1,
2,
3,
4,
5].
The achieved results gave a positive answer to our research question. The PSInSAR technique allows monitoring of periodic horizontal motions in the E–W direction. To further confirm the results, it would be interesting to compare the resulting curves of periodic shifts in the terrain surface with the curve of the fullness of the monitored UGS; however, these data are unavailable due to the protection of trade secrets. Only data for the so-called virtual storage are available, which represents a sum of the fullness of all UGSes located in the Czech Republic. However, it is impossible to derive the filling curve of the Tvrdonice UGS from this total curve.
Freely available Sentinel-1 mission data were used for this study, limiting the processing results quality due to their lower spatial resolution. In further research, it would be appropriate to use data from commercial radar satellites, which have a much higher spatial resolution and often provide long-time image series, allowing one to study UGSes for a long time into the past.