GPR Image Clutter Suppression Using Gaussian Curvature Decomposition in the PCA Domain
Abstract
1. Introduction
2. Methodology
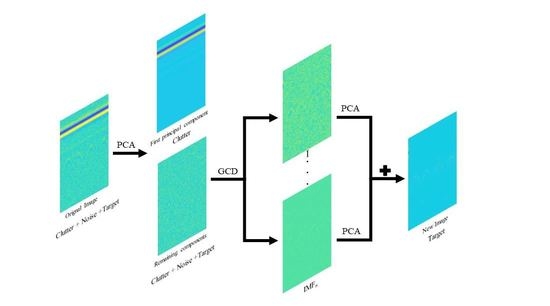
2.1. Principal Component Analysis Based Clutter Suppression
2.2. The Gaussian Curvature Filter Based Denoising
- Domain Decomposition: The original image is decomposed into four subsets: white circles , white triangles , black circles , and black triangles . This decomposition ensures that neighbors are in separate subsets and eliminates pixel dependency, as demonstrated in Figure 3a;
- Discrete representation of Tangent Plane: Triangle windows are chosen for their ease of projection to construct a hypothetical projection tangent plane, as shown in Figure 3b. After obtaining this tangent plane, we compute the distance as shown in Figure 3c, and then project the center pixel onto the triangle plane’s edge;
- Minimal Projection Operator: Computing , we employ the smallest absolute distance as the minimum projection of the current intensity. Then, we let . This operator is summarized in Algorithm 1;
- Update and filtering: All of the pixels , , , and of the minimal projection operator are iterated. The Gaussian curvature filter can be generated as:
| Algorithm 1: Minimal projection operator |
Input: Output: 1: 2: 3: 4: 5: 6: 7: 8: 9: find , such that |
3. Proposed Method
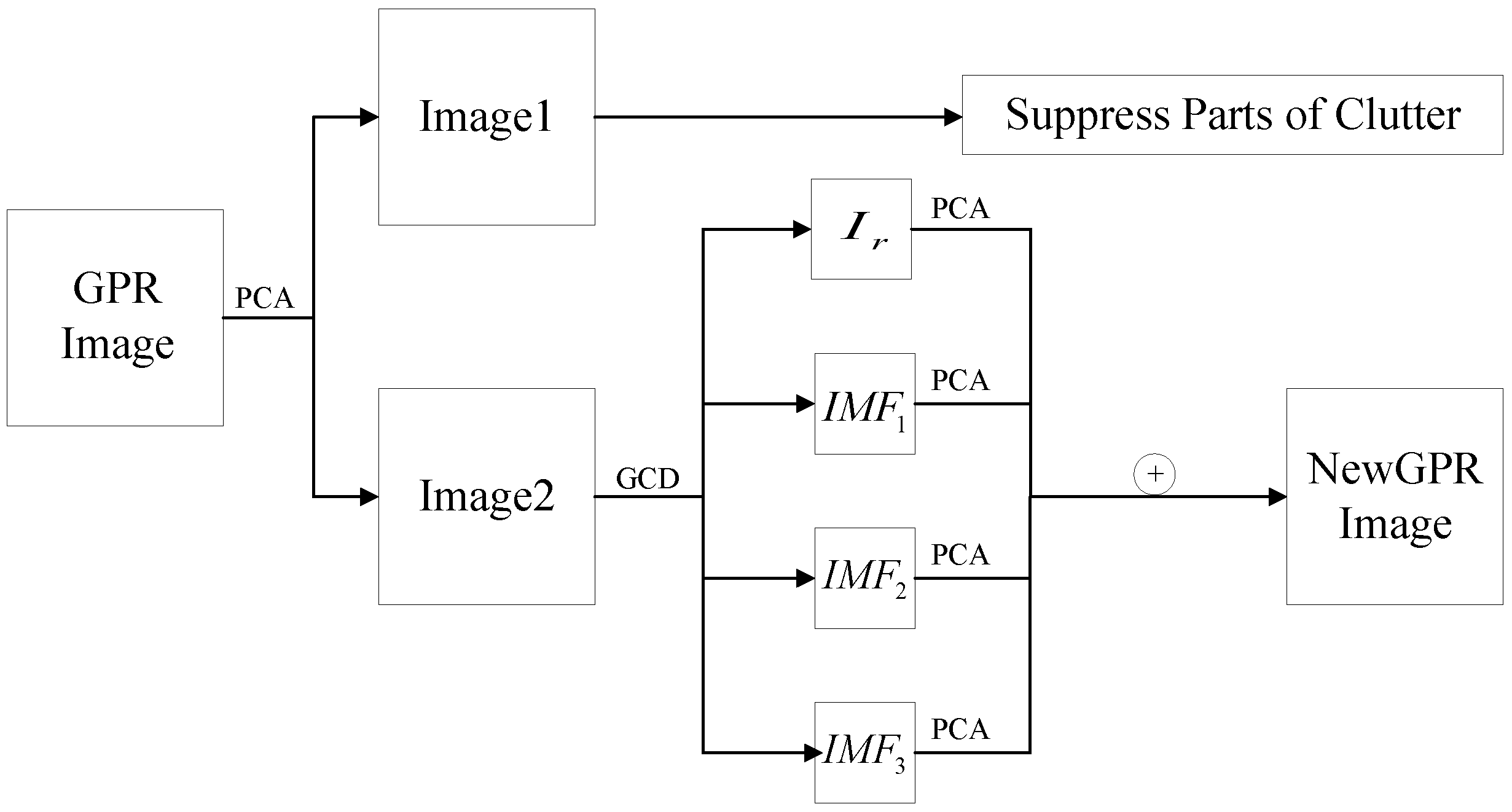
3.1. Gaussian Curvature Decomposition
| Algorithm 2: Sifting process of Gaussian Curvature Decomposition |
Input: Original image Output: , where N is the number of Initialization:. Main iteration:
|
3.2. PCGCD Based Clutter and Noise Suppression Method
4. Experiments
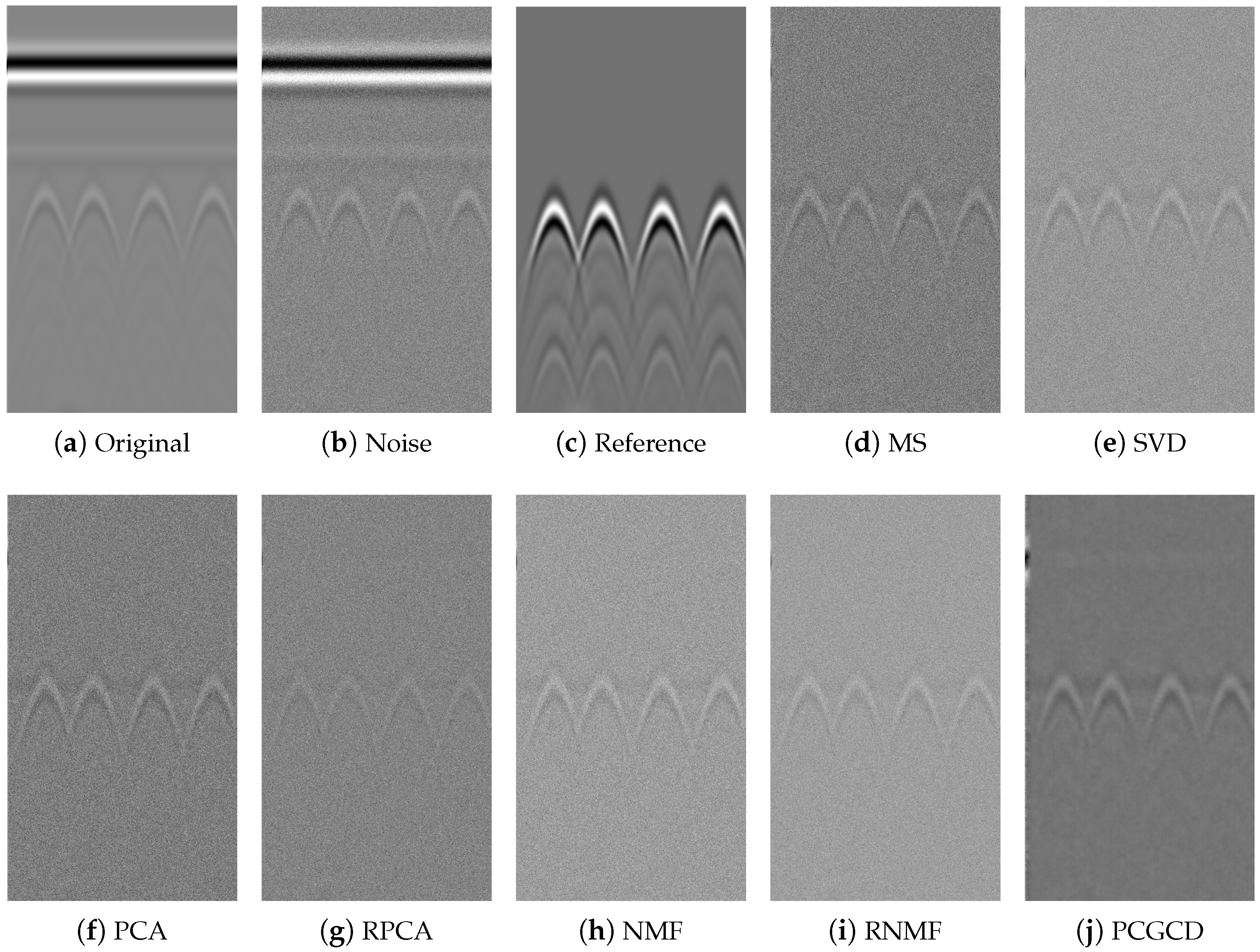
4.1. Simulation Datasets Results
4.2. Real Dataset Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, G.; Fu, L.; Chen, K.; Boateng, C.D.; Ge, S. Adaptive ground clutter reduction in ground penetrating radar data based on principal component analysis. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3271–3282. [Google Scholar] [CrossRef]
- Machado Brito-da Costa, A.; Martins, D.; Rodrigues, D.; Fernandes, L.; Moura, R.; Madureira-Carvalho, A. Ground penetrating radar for buried explosive devices detection: A case studies review. Aust. J. Forensic Sci. 2022, 54, 559–578. [Google Scholar] [CrossRef]
- Daniels, D.J. Ground Penetrating Radar; IET: London, UK, 2004; Volume 1. [Google Scholar]
- Liu, C.; Song, C.; Lu, Q. Random noise de-noising and direct wave eliminating based on SVD method for ground penetrating radar signals. J. Appl. Geophys. 2017, 144, 125–133. [Google Scholar] [CrossRef]
- Abujarad, F.; Omar, A. GPR data processing using the component-separation methods PCA and ICA. In Proceedings of the 2006 IEEE International Workshop on Imagining Systems and Techniques (IST 2006), Minori, Italy, 29 April 2006; pp. 60–64. [Google Scholar]
- Kumlu, D.; Erer, I. Clutter removal in GPR images using non-negative matrix factorization. J. Electromagn. Waves Appl. 2018, 32, 2055–2066. [Google Scholar] [CrossRef]
- Kumlu, D.; Erer, I. Improved clutter removal in GPR by robust nonnegative matrix factorization. IEEE Geosci. Remote Sens. Lett. 2019, 17, 958–962. [Google Scholar] [CrossRef]
- Song, X.; Xiang, D.; Zhou, K.; Su, Y. Improving RPCA-based clutter suppression in GPR detection of antipersonnel mines. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1338–1342. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, T. In-wall clutter suppression based on low-rank and sparse representation for through-the-wall radar. IEEE Geosci. Remote Sens. Lett. 2016, 13, 671–675. [Google Scholar] [CrossRef]
- Temlioglu, E.; Erer, I. Clutter removal in ground penetrating radar images using morphological component analysis. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1802–1806. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, Y.; Liu, Q.; Wang, Y. RNMF-guided deep network for signal separation of GPR without labeled data. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Temlioglu, E.; Erer, I. A novel convolutional autoencoder-based clutter removal method for buried threat detection in ground penetrating radar. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Ni, Z.K.; Pan, J.; Shi, C.; Ye, S.; Zhao, D.; Fang, G. DL-based clutter removal in migrated GPR data for detection of buried target. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Sun, H.H.; Cheng, W.; Fan, Z. Learning to Remove Clutter in Real-World GPR Images Using Hybrid Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Gong, Y. Spectrally Regularized Surfaces. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2015. [Google Scholar]
- Hao, Q.; Sun, B.; Li, S.; Crawford, M.M.; Kang, X. Curvature filters-based multiscale feature extraction for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
- Tang, W.; Gong, Y.; Liu, K.; Liu, J.; Pan, W.; Liu, B.; Qiu, G. Gaussian Curvature Filter on 3D Meshes. arXiv 2020, arXiv:2003.09178. [Google Scholar]
- Liu, G.; Zhou, J.; Li, T.; Wu, W.; Guo, F.; Luo, B.; Chen, S. Infrared and visible image fusion through hybrid curvature filtering image decomposition. Infrared Phys. Technol. 2022, 120, 103938. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, X.; Wu, Q.J.; Wang, Y.; He, Z.; Yang, Y. Automatic visual detection system of railway surface defects with curvature filter and improved Gaussian mixture model. IEEE Trans. Instrum. Meas. 2018, 67, 1593–1608. [Google Scholar] [CrossRef]
- Liao, J.; Wang, L. Hyperspectral image classification based on fusion of curvature filter and domain transform recursive filter. Remote Sens. 2019, 11, 833. [Google Scholar] [CrossRef]
- Verma, P.K.; Gaikwad, A.N.; Singh, D.; Nigam, M. Analysis of clutter reduction techniques for through wall imaging in UWB range. Prog. Electromagn. Res. B 2009, 17, 29–48. [Google Scholar] [CrossRef]
- Nunes, J.C.; Bouaoune, Y.; Delechelle, E.; Niang, O.; Bunel, P. Image analysis by bidimensional empirical mode decomposition. Image Vis. Comput. 2003, 21, 1019–1026. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef]

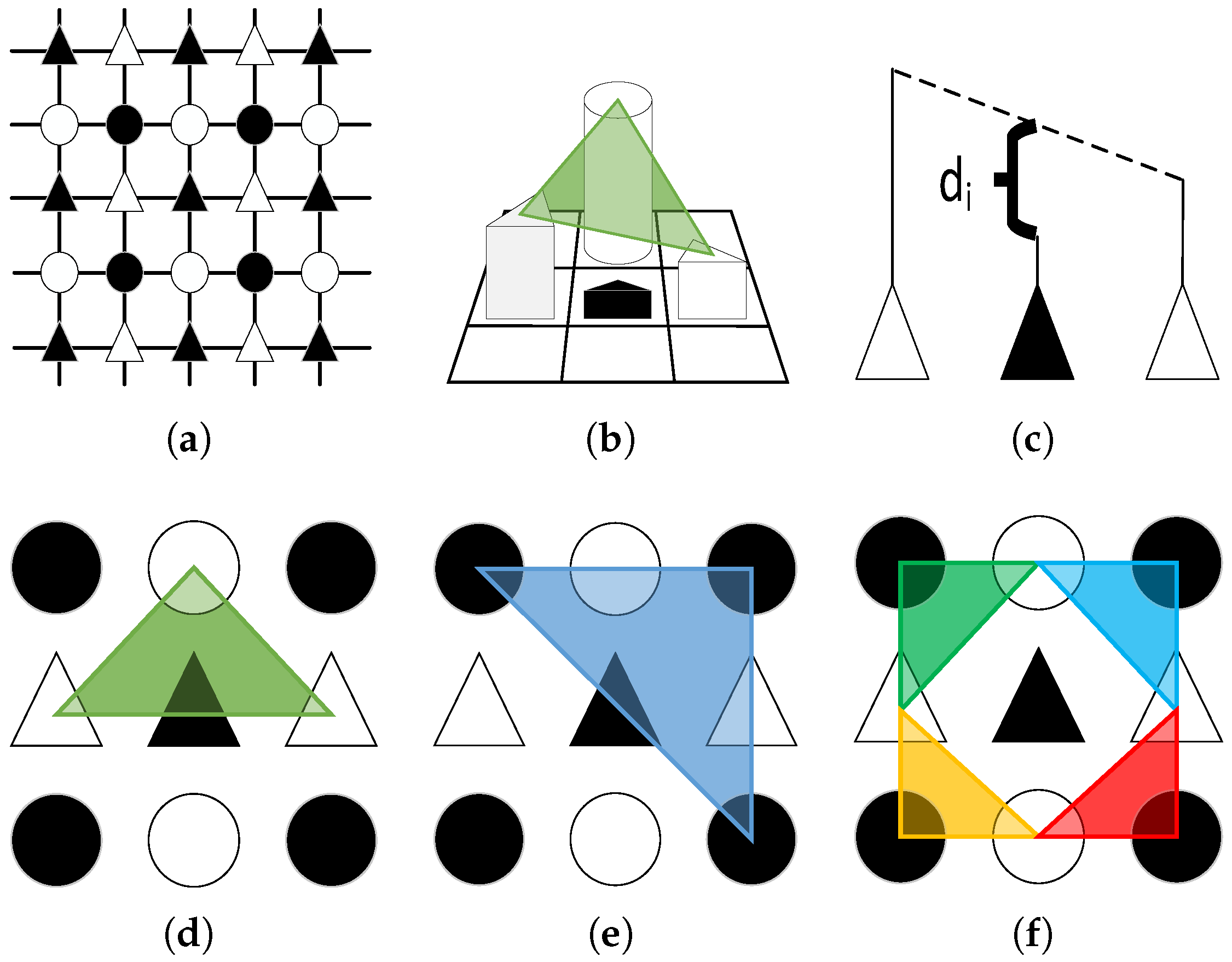
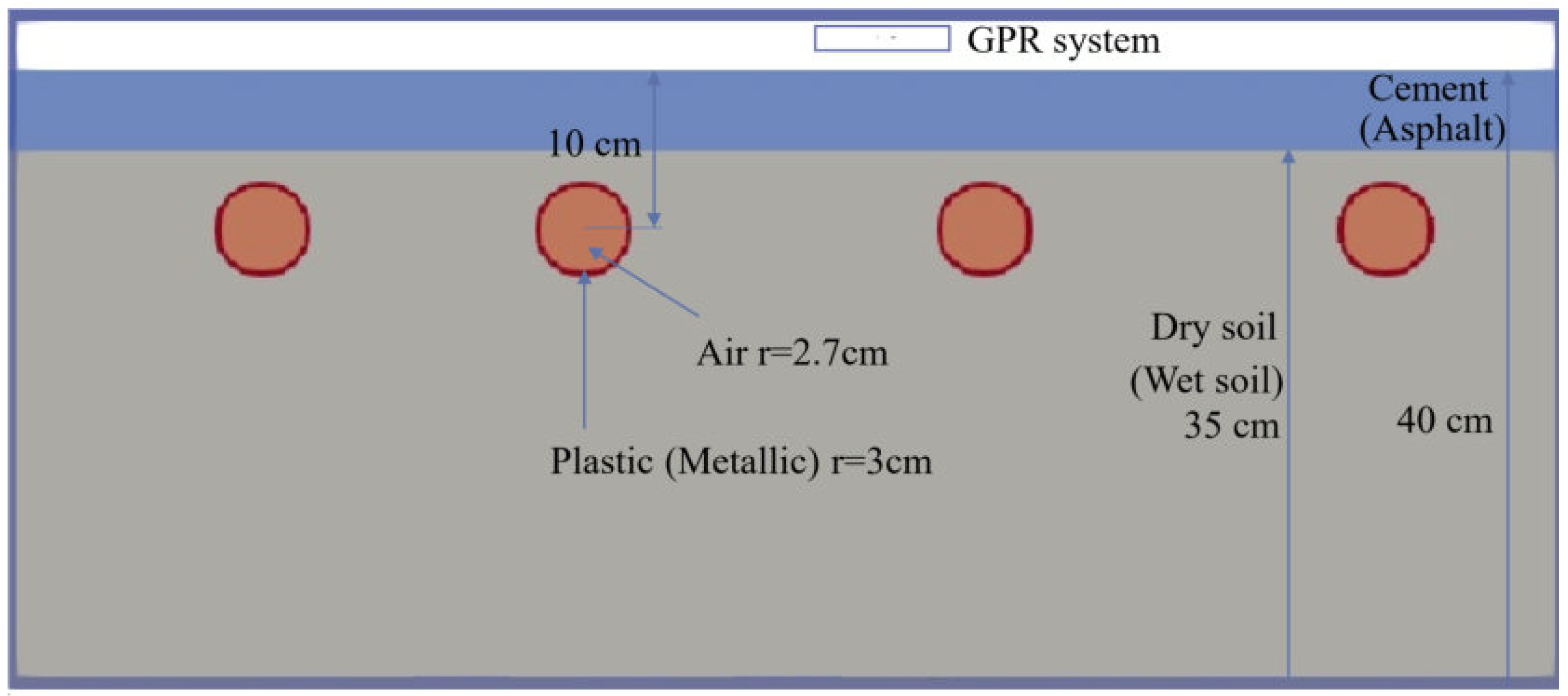


| Meterial | Relative Permittivity (F/m) | Conductivity (S/m) |
|---|---|---|
| Cement | 7 | 0.001 |
| Asphalt | 5 | 0.001 |
| Dry soil | 10 | 0.01 |
| Wet soil | 12 | 0.01 |
| Plastic | 3 | 0.01 |
| Metallic | 3.1 |
| Plastic Pipeline | Metallic Pipeline | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | MS | SVD | NMF | PCA | RNMF | RPCA | PCGCD 1 | MS | SVD | NMF | PCA | RNMF | RPCA | PCGCD |
| Cement+Dry soil | 18.39 | 17.63 | 17.29 | 18.42 | 17.23 | 19.07 | 19.63 | 20.20 | 14.67 | 14.51 | 20.13 | 14.04 | 17.40 | 23.32 |
| Cement+Wet soil | 17.82 | 17.17 | 16.82 | 17.80 | 16.76 | 18.57 | 19.27 | 19.78 | 14.67 | 14.71 | 19.64 | 14.31 | 17.65 | 22.78 |
| Asphalt+Dry soil | 17.75 | 17.79 | 17.54 | 17.74 | 17.50 | 19.04 | 19.37 | 19.91 | 14.17 | 13.83 | 19.83 | 13.385 | 17.40 | 22.45 |
| Asphalt+Wet soil | 17.86 | 16.78 | 16.79 | 17.74 | 16.74 | 18.77 | 19.34 | 19.53 | 14.25 | 14.35 | 19.53 | 13.93 | 17.08 | 22.25 |
| Plastic Pipeline | Metallic Pipeline | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | MS | SVD | NMF | PCA | RNMF | RPCA | PCGCD | MS | SVD | NMF | PCA | RNMF | RPCA | PCGCD |
| Cement+Dry soil | 0.138 | 0.193 | 0.157 | 0.137 | 0.274 | 0.147 | 0.786 | 0.164 | 0.221 | 0.178 | 0.161 | 0.323 | 0.144 | 0.831 |
| Cement+Wet soil | 0.130 | 0.182 | 0.149 | 0.128 | 0.263 | 0.145 | 0.762 | 0.148 | 0.203 | 0.162 | 0.144 | 0.296 | 0.149 | 0.819 |
| Asphalt+Dry soil | 0.130 | 0.194 | 0.156 | 0.128 | 0.274 | 0.141 | 0.777 | 0.169 | 0.229 | 0.181 | 0.169 | 0.328 | 0.146 | 0.829 |
| Asphalt+Wet soil | 0.125 | 0.179 | 0.146 | 0.124 | 0.256 | 0.144 | 0.761 | 0.156 | 0.210 | 0.174 | 0.152 | 0.317 | 0.150 | 0.817 |
| Method | MS | SVD | NMF | PCA | RNMF | RPCA | PCGCD |
|---|---|---|---|---|---|---|---|
| Time (s) | 0.0015 | 0.0024 | 0.0500 | 0.0160 | 8.1356 | 3.1347 | 0.8615 |
| Plastic Pipeline | Metallic Pipeline | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SNR (dB) | MS | SVD | NMF | PCA | RNMF | RPCA | PCGCD | MS | SVD | NMF | PCA | RNMF | RPCA | PCGCD |
| 10 | 17.38 | 17.47 | 17.42 | 17.38 | 17.90 | 18.81 | 20.77 | 17.07 | 17.08 | 16.86 | 17.08 | 17.31 | 18.29 | 20.80 |
| 15 | 17.96 | 17.79 | 17.12 | 17.92 | 17.05 | 18.86 | 21.53 | 19.86 | 14.44 | 14.35 | 19.78 | 13.91 | 17.38 | 22.63 |
| Plastic Pipeline | Metallic Pipeline | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SNR (dB) | MS | SVD | NMF | PCA | RNMF | RPCA | PCGCD | MS | SVD | NMF | PCA | RNMF | RPCA | PCGCD |
| 10 | 0.077 | 0.080 | 0.076 | 0.070 | 0.084 | 0.138 | 0.510 | 0.077 | 0.080 | 0.078 | 0.079 | 0.099 | 0.167 | 0.583 |
| 15 | 0.131 | 0.187 | 0.129 | 0.152 | 0.267 | 0.144 | 0.772 | 0.159 | 0.216 | 0.174 | 0.156 | 0.316 | 0.147 | 0.824 |
| Method | MS | SVD | NMF | PCA | RNMF | RPCA | PCGCD |
|---|---|---|---|---|---|---|---|
| PSNR | 30.88 | 31.01 | 31.01 | 29.62 | 35.36 1 | 26.90 | 29.99 |
| SSIM | 0.722 | 0.722 | 0.710 | 0.681 | 0.830 | 0.513 | 0.920 2 |
| Time (s) | 0.0051 | 0.0023 | 0.0456 | 0.0075 | 0.4181 3 | 0.1348 | 0.0350 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Q.; Bi, B.; Zhang, P.; Shen, L.; Huang, X.; Xin, Q. GPR Image Clutter Suppression Using Gaussian Curvature Decomposition in the PCA Domain. Remote Sens. 2022, 14, 4879. https://doi.org/10.3390/rs14194879
Su Q, Bi B, Zhang P, Shen L, Huang X, Xin Q. GPR Image Clutter Suppression Using Gaussian Curvature Decomposition in the PCA Domain. Remote Sensing. 2022; 14(19):4879. https://doi.org/10.3390/rs14194879
Chicago/Turabian StyleSu, Qibin, Beizhen Bi, Pengyu Zhang, Liang Shen, Xiaotao Huang, and Qin Xin. 2022. "GPR Image Clutter Suppression Using Gaussian Curvature Decomposition in the PCA Domain" Remote Sensing 14, no. 19: 4879. https://doi.org/10.3390/rs14194879
APA StyleSu, Q., Bi, B., Zhang, P., Shen, L., Huang, X., & Xin, Q. (2022). GPR Image Clutter Suppression Using Gaussian Curvature Decomposition in the PCA Domain. Remote Sensing, 14(19), 4879. https://doi.org/10.3390/rs14194879