Abstract
Point-cloud registration is a fundamental task in computer vision. However, most point clouds are partially overlapping, corrupted by noise and comprised of indistinguishable surfaces, especially for complexly distributed outdoor LiDAR point clouds, which makes registration challenging. In this paper, we propose a multi-scale features-based point cloud registration network named MSPR-Net for large-scale outdoor LiDAR point cloud registration. The main motivation of the proposed MSPR-Net is that the features of two keypoints from a true correspondence must match in different scales. From this point of view, we first utilize a multi-scale backbone to extract the multi-scale features of the keypoints. Next, we propose a bilateral outlier removal strategy to remove the potential outliers in the keypoints based on the multi-scale features. Finally, a coarse-to-fine registration way is applied to exploit the information both in feature and spatial space. Extensive experiments conducted on two large-scale outdoor LiDAR point cloud datasets demonstrate that MSPR-Net achieves state-of-the-art performance.
1. Introduction
Point cloud registration is a fundamental task in computer vision, aiming to find a transformation that can align two overlapping point clouds in a common frame. Point cloud registration plays an important role in various downstream tasks, including scene reconstruction [1,2,3,4], simultaneous localization and mapping (SLAM) [5,6], object pose estimation [7], etc. However, point cloud registration remains challenging with real-world scans due to partial overlap, noise, outliers, and so on.
In previous decades, many methods have been proposed to solve these problems. Iterative Closest Point (ICP) [8] is the best known algorithm for solving rigid registration, which alternates between finding point cloud correspondences and estimating transformation. However, ICP is affected by initialization transformation and often stalls in suboptimal local minima. ICP variants [9,10,11] attempt to alleviate this problem by searching larger parts of the transformation space or improving the correspondences. However, these algorithms do not always provide satisfactory performance and are time-consuming.
Recently, deep learning has achieved great success in point cloud registration. We can roughly categorize these methods into two categories. The first is the global feature-based methods [12,13,14,15,16], which estimate the transformation by aggregating global information without finding correspondences. Although these methods work well in the synthetic dataset [17], they usually perform poorly in real-scan point clouds, which have a low overlap region. The second is the correspondence-based methods [18,19,20,21,22], which focus on learning discriminative point features and constructing correspondences for subsequent Procrustes analysis. However, most of them rely on features extracted from local geometric structures. For repeat patterns or scale changes, they may get wrong correspondence estimation.
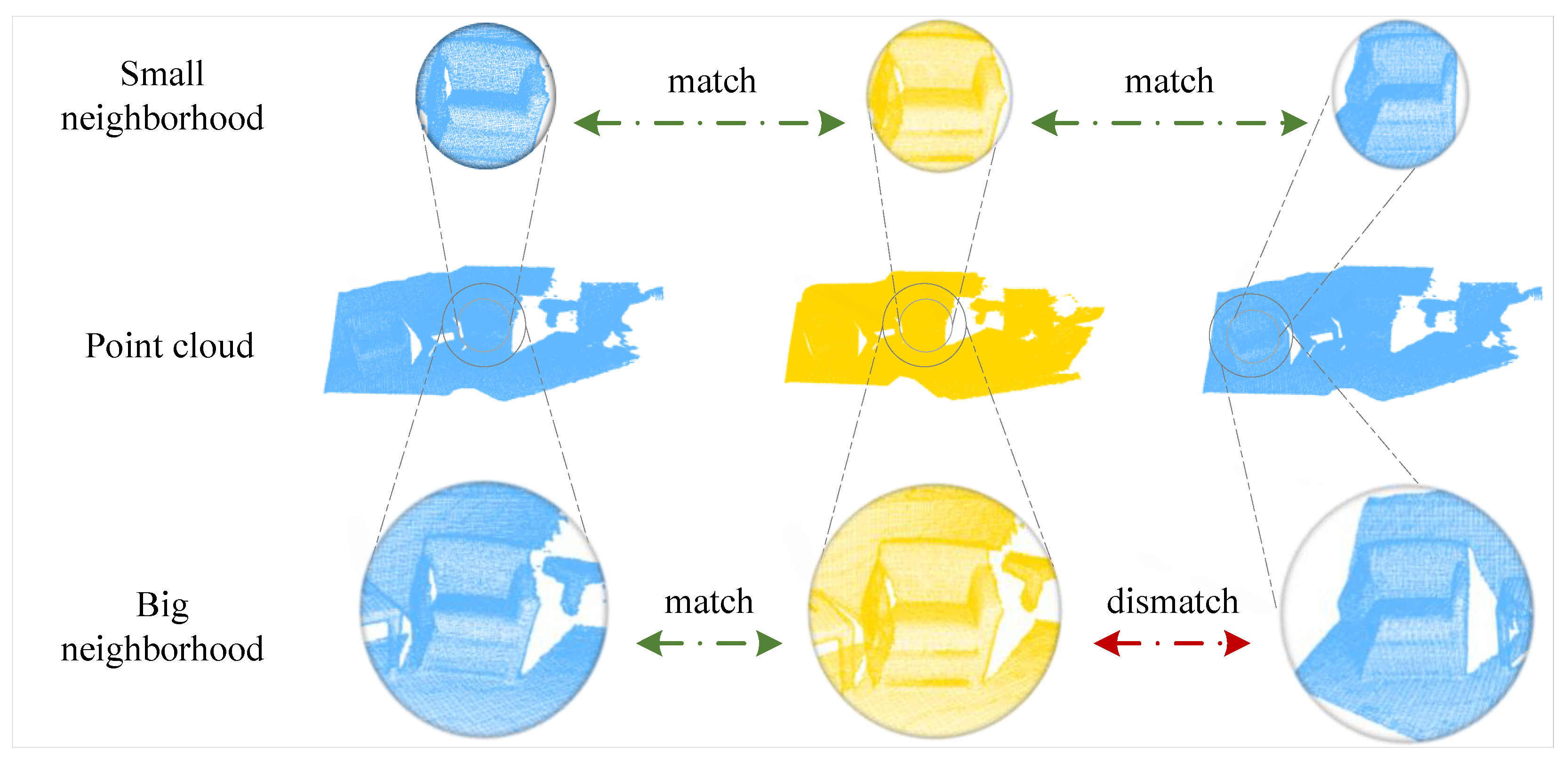
In this paper, we solve the partial-to-partial registration from a new perspective by incorporating with multi-scale keypoint features. To better understand the motivation of our method, we analyze it from the process of establishing matching correspondence in human vision. For example, when we try to match an ambiguous keypoint on a chair near a table, we may look back and forth at both scenes. We usually first pay attention to all the chairs in the scene, then compare their neighborhoods so we can sift the chairs that are near the wall or sofa. The neighborhood size is important for registration. Even if two points are matched on a low-level scale, they may have a bad correspondence (Figure 1 gives an example). However, only a few works [23,24,25] have studied the effect of neighborhood size for point cloud registration.
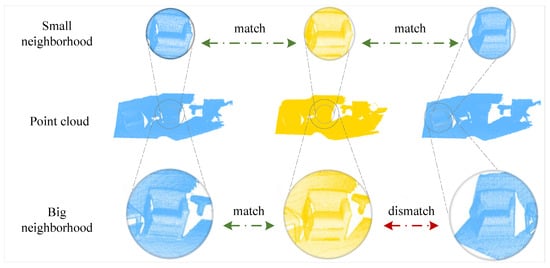
Figure 1.
A toy example for illustrating how the receptive field of a keypoint affects the correspondence selection. For a keypoint in the source point cloud, there may exist more than one corresponding point in the target in the low receptive field. As the receptive field expanding, we can exclude ambiguous correspondences gradually. The true correspondence must match at all levels.
Based on the above analysis, we propose a multi-scale features-based point cloud registration network (MSPR-Net) for outdoor LiDAR point cloud registration. Although it can be easy to get the multi-scale features of points simply by increasing the layer of the feature extraction network, there is still a problem. Generally, the multi-scale features are constructed by progressively downsampling the point cloud in the network. However, random sampling would increase the risk of a certain point losing its corresponding point in the target point cloud. The outliers of natural existence and caused by random sampling make it become more challenging to find the correct correspondence.
To solve this, we propose a Siamese multi-scale backbone to hierarchically downsample and upsample the point cloud to acquire the multi-scale features of keypoints. At the same time, a local similarity estimation module (LSEM) is employed to relocate keypoint. It generates much more stable downsampled points in the local region depending on the similarity between the features of points and the feature of the local region. In addition, to overcome the issue brought about by the low-overlapping problem, we introduce a global estimation module (GSEM) to make the downsampling more concentrated on the overlap region. Then, a bilateral outlier removal mechanism is designed to find the candidate correspondences based on the multi-scale features. Finally, a coarse-to-fine registration strategy is for robust and accuracy registration.
We evaluate the proposed MSPR-Net on two large-scale outdoor datasets: KITTI odometry dataset [26] and NuScenes dataset [27]. The results demonstrate that MSPR-Net has achieved state-of-the-art performance.
In summary, our main contributions are as follows:
- We propose a novel point cloud registration network named MSPR-Net, which achieves state-of-the-art performance in outdoor LiDAR datasets.
- We propose a local similarity estimation module and a global similarity estimation module to eliminate the instability of random samples so that the matched keypoints and their descriptors can have more consensus.
- We design a novel bilateral outlier removal strategy, which removes outliers from the source point cloud and target point cloud, respectively.
The rest of this paper is organized as follows: Related work on point cloud registration is reviewed in Section 2. A detailed description of the proposed registration framework using multi-scale features is given in Section 3. Comparative experiments and analysis are performed in Section 4. The research limitations are discussed in Section 5. Finally, conclusions are drawn in Section 6.
2. Related Works
In this section, we briefly review the approaches to 3D point-cloud registration.
2.1. Correspondence-Based Methods
Correspondence-based approaches for point cloud registration first establish correspondences between source and target point cloud and follow a robust estimation method for the rigid transformation by solving the least square problem. ICP [8] is the early correspondence matching-based method, which iteratively finds the closest point as correspondence and updates the transformation until a desired stopping criteria is met. However, ICP-style methods are sensitive to initial alignment and also easily fall into local minima. To this end, Go-ICP [28] uses a Branch-and-Bound (BnB) method to search for a globally optimal solution. Ref. [29] attempts to identify global optima using Riemannian optimization.
Recent learning-based methods use Multi-Layer Perceptron (MLP) [30] based network or GNN [31] to encode point cloud. RPM [20] develops a deep graph matching module to compute a soft correspondence matrix, which considers the local geometry and structural information on a larger scale in establishing correspondences. RIENet [32] calculates feature-to-feature correspondences with neighborhood consensus. Lepard [33] proposes a position-aware feature matching method.
2.2. Global Feature-Based Methods
PointNetLK [12] is a pioneering work of global feature-based point cloud registration, which modifies the LK algorithm [34] and combines it with PointNet [30] into a single trainable recurrent deep neural network. PCRNet [16] improves noise robustness by replacing the LK algorithm with an MLP. FMR [13] enforces registration optimization by minimizing a feature matrix projection error that is robust to noise, outliers, and density differences. OMNet [14] converts the partial-to-partial point cloud registration to the registration of the same shape by learning overlapping masks.
2.3. Multi-Scale Network
Multi-scale structures are of great importance to a number of vision tasks in both 2D and 3D, including semantic segmentation [35,36,37], object detection [38,39], face analysis [40,41], edge detection [42], feature matching [43], and boosting the model performance of those fields. As witnessed in point cloud registration, MS-SVConv [25] acquires multi-scale features by downsampling the point cloud at different voxel sizes and applying sparse convolution processing different density inputs. HRegNet [24] estimates the transformation on a multi-scale feature map to combine reliable features in the deeper layer and precise position information in the shallower layers. NgeNet [23] utilizes a KPconv-based [44] multi-scale architecture with a geometric-guided module encoding point cloud pair, then uses a voting mechanism to select proper features for transformation estimation by RANSAC [45].
3. Methods
The proposed method tackles point cloud registration in a two-stage manner. We first learn multi-scale features of down-sampled sparse points (keypoints) for matching, and afterward use a robust registration network for recovering the relative transformation.
3.1. Network Architecture
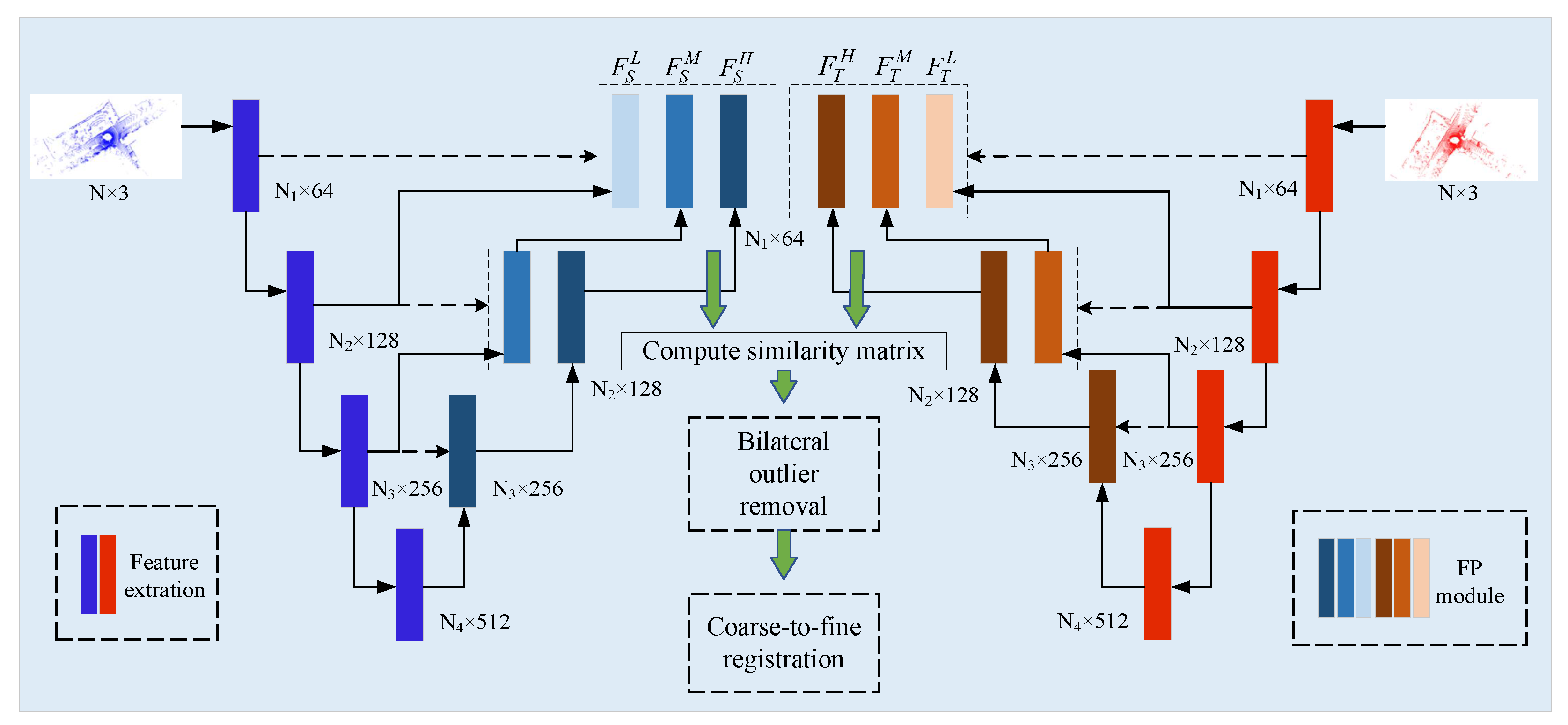
MSPR-Net is an encoder-decoder network, as shown in Figure 2. The input of MSPR-Net is a pair of point clouds , where N is the number of points. Firstly, a Siamese multi-scale backbone is utilized to process the input data, and outputs the keypoints () and their corresponding low-level, middle-level, high-level descriptors ( and ). Subsequently, a bilateral outlier removal strategy is proposed to remove the ambiguous keypoints based on the multi-scale features. Finally, a coarse-to-fine registration way is applied to exploit the information both in feature and spatial space.
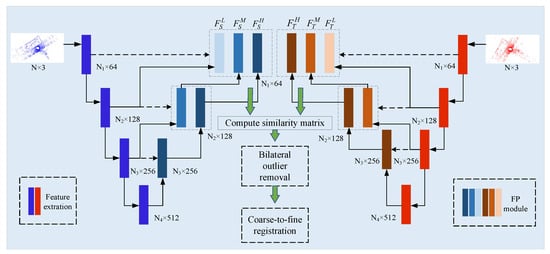
Figure 2.
The architecture of MSPR-Net. Taking the source and target point clouds as input, MSPR-Net outputs the transformations that can align them.
3.1.1. Siamese Multi-Scale Backbone
Inspired by the idea of the Siamese network [46], we detect the keypoints and extract their descriptors using the same backbone with shared weights. Without loss of generality, we utilize as an example to explain the detailed implementation of the backbone.
Shared Encoder To expand the receptive field of keypoints, we utilize the classical method [47], which processes a set of points sampled in a metric space in a hierarchical fashion. We follow the processes of downsampling keypoints, grouping, extracting features, and progressively abstracting larger and larger neighborhood sizes along the hierarchy. For the input point cloud, we totally downsample it four times. The first time is to select the keypoints for registration, and latter three are used to generate multi-scale features for the keypoint selected before. We save the feature map (denoted as , which consists of keypoints , descriptors and overlap scores ) of each layer for later decoding. The keypoint detector network and the descriptor network, which are key components of our encoder, will be described later (Section 3.1.2).
Parallel Decoder We use the point feature propagation (FP) method [47] to propagate features from subsampled points to the original points. The decoder takes as input and outputs the low-level, middle-level, high-level features of the keypoints . The FP operation is defined as
where and are the input different layer features. MLP is Multi-Layer Perceptron. is the concatenation operation and is the nearest upsampling. Then, the are calculated as follows:
3.1.2. Detector and Descriptor
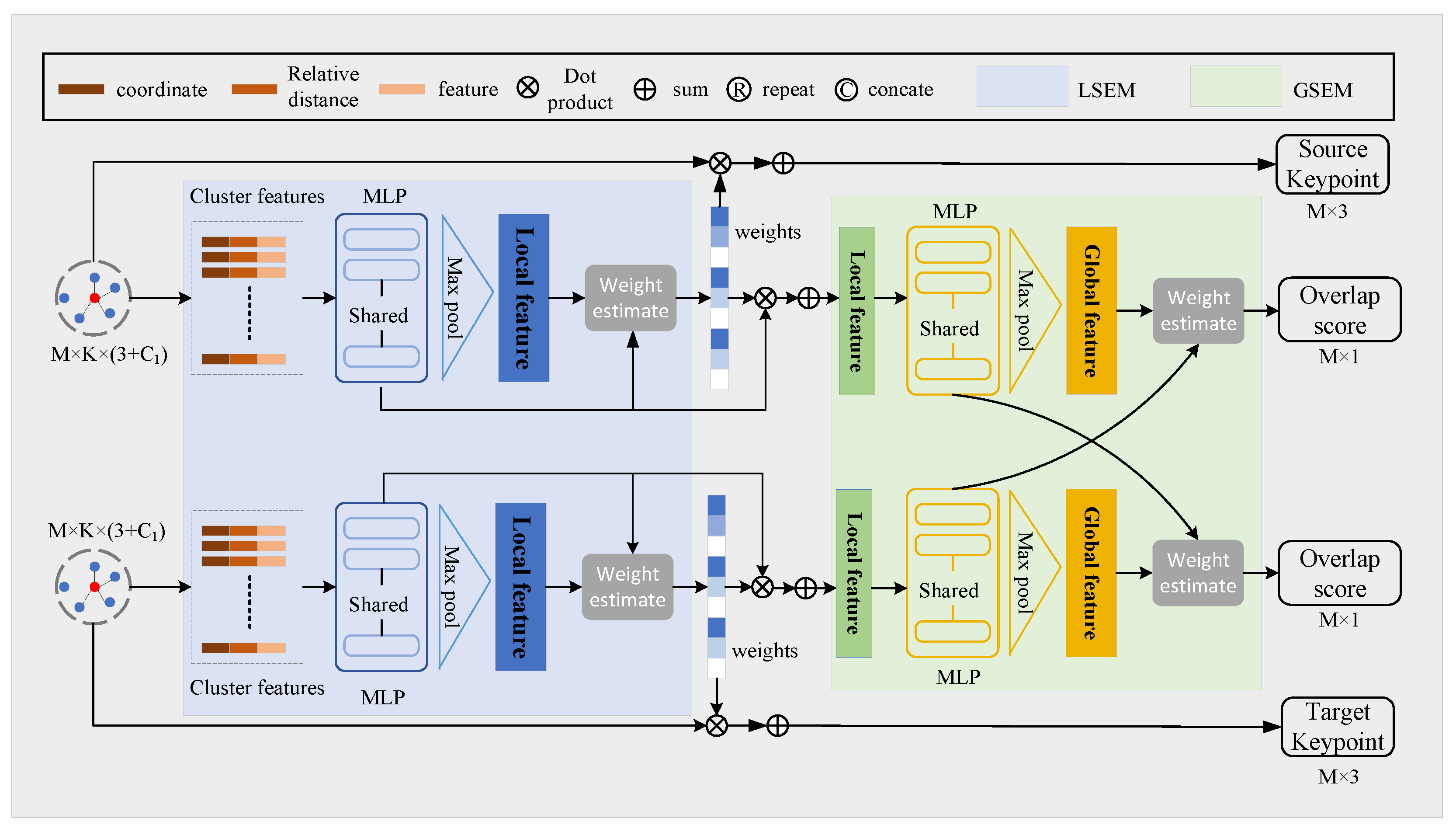
The Fast Point Sampling (FPS) is widely utilized during the feature extraction process in the PointNet-like network. However, FPS is a random sample algorithm, which means FPS may downsample the different points in the same region. This would increase the risk of a certain point losing its corresponding point in the other frame. To this end, we introduce a local similarity estimation module (LSEM) to refine the downsample results. In addition, the knowledge about potential overlap regions is important for point cloud registration. We proposed a global similarity estimation module (GSEM) to let the network be prone to downsample the overlap points.
The inputs of the detector in layer are the keypoints , descriptors , and overlap scores , where denotes the sample points in layer l, is the output dimension of descriptor. For the first layer (), the input keypoints are the original point cloud. The overlap scores are initialized to 1. For the input of each layer, we first sample candidate points using weighted FPS (WFPS [48]). Then, k nearest neighbor (kNN) algorithm is performed to group clusters center on the candidate points. The features of the cluster (denoted as ) includes the coordinates of the center, neighboring points, and their descriptors. In addition, the relative coordinates and relative distances are also calculated as a part of it.
- LSEM As shown in Figure 3, the input of LSEM is the cluster features. To simplify the formulation, the subscripts l are omitted. Firstly, is inputted into a 3-layer of Shared MLP to generate a feature map . After that, a max pooling operation is followed to get the global feature of the neighboring region. Finally, we compute the similarity of each point’s feature with the region feature, followed by a softmax function for normalization. For a local region center on , the local saliency can be calculated aswhere denotes the dot product. is the region feature and is the neighboring point’s feature. The sampled point will be relocated by the saliency weight aswhere is the coordinate of the neighborhood. We also update by the weighted sum of neighboring features to .
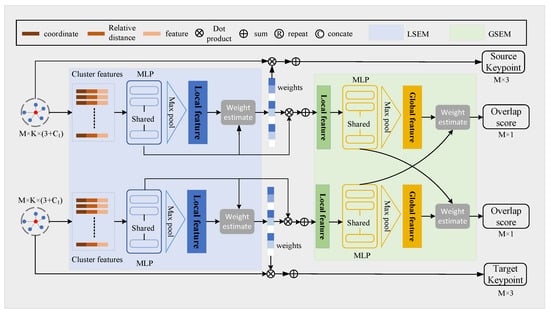 Figure 3. The network architecture of the detector. The input is the kNN clusters centered on the downsampled keypoints. The cluster features are fed into LSEM to refine the coordinates of the keypoints, then a GSEM is applied to obtain the overlap scores of the keypoints.
Figure 3. The network architecture of the detector. The input is the kNN clusters centered on the downsampled keypoints. The cluster features are fed into LSEM to refine the coordinates of the keypoints, then a GSEM is applied to obtain the overlap scores of the keypoints. - GSEM LSEM only can refine the coordinate of the downsampled keypoints in a local region, no matter whether the point is in the overlapping area or not. To enhance the overlap awareness, we propose that GSEM make the network gradually pay attention to the overlap region as hierarchically downsampled. Different from PREDATOR, [49] which predicts overlap scores by a linear function, we use a more intuitive method to express the overlap scores of the keypoints. As every keypoint has aggregated the local region information, we calculate the similarity of each keypoint’s feature in the source point cloud with the global feature of the target point cloud. Intuitively, the features of the overlap region keypoints would be more similar to the corresponding global features than other points.
The structure of GSEM is similar to LSEM. The overlap scores of the source point cloud can be calculated as
where is the feature of keypoints in the source point cloud. is the global feature of the target point cloud. represents the sigmoid operation. Moreover, we use the overlap scores as the weight for WFPS, increasing the sample probability for the overlap point. As the layer goes deeper, we can get more common information in the two-point cloud. Eventually, this information would propagate to the keypoints of the first layer by the decoder to make registration more robust.
Descriptor First, we reconstruct the clusters based on the coordinates of the relocated keypoints. Then, the cluster features are fed into another 3-layer MLP with a max pooling layer to generate descriptors.
3.2. Bilateral Outlier Removal
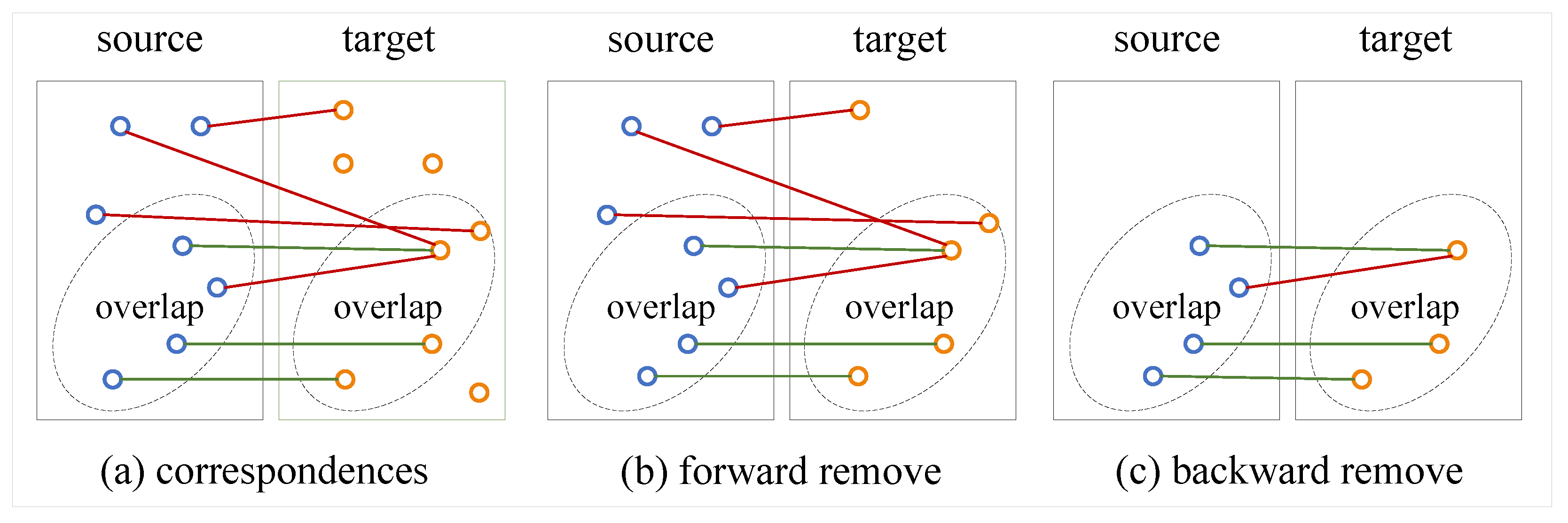
Once we get the keypoints with the multi-scale features in the source and target point cloud, the key problem then is how to find correct correspondences between them. We propose a simple but effective method to solve it. As shown in Figure 4, we apply a bilateral outlier removal strategy to remove the outliers in two directions. We first compute the similarity matrix . Here, each entry in the obtained matrix represents the matching confidence between the keypoint i and keypoint j from and respectively, and the value is less than 1. Obviously, a true correspondence would match in any level of feature matching. We simply sum the three matrices, and ideally, the right correspondences’ confidence scores would be 3. In forward, we remove the outliers in the target point cloud. We select the maximum confidence score in every row as the candidate correspondence. After this, we assign every keypoint in a corresponding point in . However, there may exist points in without a corresponding point in but still form a correspondence. To this end, we remove the outliers in whose descriptors have low similarity with the points in in backward. We classify the correspondences by confidence scores and only retain the top confidence scores in the probability proportion of .
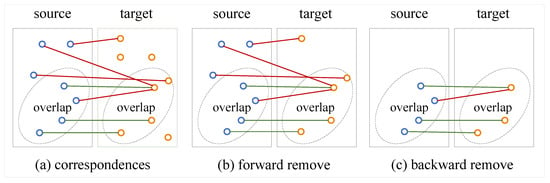
Figure 4.
Illustration of the bilateral outlier removal. (a) We select the maximum confidence scores in every row of the similarity matrix as the candidate correspondences. (b) We remove the points in the target point cloud which have no corresponding point in the source point cloud. (c) We remove the points with low confidence scores in the source point cloud.
After using the bilateral outlier removal strategy, we can filter the most outliers. However, we find that there always exist some points in that have the same corresponding point in (as shown in c in Figure 4) due to the sparse sample. So we construct a correspondence net to decouple this ambiguous situation.
3.3. Coarse-to-Fine Registration
Inspired by HRegNet [24], we construct a correspondence network based on the LSEM. It consists of an LSEM module and a 3-layer MLP with a Sigmoid function. The keypoint in and its ambiguous corresponding points in form a cluster. The feature of the cluster is obtained in the same way as before. We fed the cluster feature into LSEM to generate a new corresponding point, and the weighted sum of corresponding features is further fed into the MLP to predict a confidence score . Given the corresponding keypoints and confidence scores, the optimal transformation can be solved by using the weighted Kabsch algorithm [50].
After applying the coarse registration in the feature space, we obtain the coarse transformation , , the fine registration is applied to further reduce the registration error. We firstly transform the source keypoints using the coarse transformation , . Then, for a keypoint in , we perform a kNN search in its spatial neighborhoods to construct a cluster. Finally, a similar correspondence network is applied to get the corresponding point.
3.4. Loss Function
The training of MSPR-Net can be divided into two stages. We first train the detector network of the backbone using the probabilistic chamfer loss in USIP [51].
where . . is the nearest neighbor of in . is the corresponding overlap source.
Then, we utilize the pre-trained detector network to train MSPR-Net using the matching loss in RSKDD-Net [52], translation loss, and rotation loss.
where is a weighted sum of all target keypoints based on the descriptor distance (more details in RSKDD-Net [52]). , and R, t are ground truth transformation and estimated transformation respectively. I denotes the identity matrix. The final loss .
4. Results
MSPR-Net is evaluated on two large-scale outdoor LiDAR point cloud datasets, including the KITTI odometry dataset [26] and the NuScenes dataset [27].
4.1. Implementation Details
Following the data pre-processing method in HRegNet [24], we firstly voxelized the input point cloud and the voxel size is set to 0.3 m. After that, we randomly sample 16,384 points from the point clouds in the KITTI dataset and 8192 points in the NuScenes dataset. MSPRNet is implemented in pytorch [53] and all experiments are run on a single RTX3090GPU. Adam optimizer is used for network training. The initial learning rate is set to 0.001 and decreases by 50% every 10 epochs. The hyperparameter is set to 0.6, the and are, respectively, 0.0125 and 1.8 for the KITTI dataset, 0.025 and 2.0 for the NuScenes dataset. For batch training, we select the source keypoint and its 8 ambiguous points in the target point cloud to form a cluster in the correspondence network. For the KITTI dataset, we train 100 epochs and 50 epochs for the NuScenes dataset.
4.2. Evaluation Metrics
We evaluate the estimated transformation matrices by two metrics: relative translation error (RTE) and relative rotation error (RRE). RTE and RRE can be calculated as
where t, R are estimated values, and , are ground truth values and indicates the trace of a matrix. The registration is considered accurate if the RTE is below the thresholds m and RRE is below deg. We report the registration recall, which is defined as the ratio of successful registration. Since the RRE and RTE are primarily affected by failed registrations, we compute the average RRE and RTE only on successful registrations for better numerical reliability.
4.3. KITTI Dataset
KITTI odometry dataset comprises 11 sequences (00-10) of outdoor driving scenarios for point cloud registration. We use sequences 00 to 05 for training, 06 to 07 for validation, and 08 to 10 for testing. In addition, the current frame with the 10th frame after that was selected to form a pair point cloud. The ground truth transformations are provided by GPS. To reduce the noise in the ground truth, we use the iterative closest point (ICP) [8] method to refine the alignment.
4.3.1. Performance
We report the registration results evaluated in the test sequences of the KITTI dataset. We compare our methods with both classical methods and learning-based methods, including the current state-of-the-art methods.
- Comparison with the traditional methods. MSPR-Net is compared with point-to-point and point-to-plane ICP, RANSAC, and FGR. According to the results in Table 1, the ICP algorithm achieves the best RRE and RTE on the KITTI dataset. However, they are both in a very low recall due to the imprecise initial transformation between point cloud pairs in most cases. FGR performs slightly better than ICP, but the result is still not good. Taking advantage of the multiple iterations and outlier rejection strategy, RANSAC obtains reasonable results. Our method achieves significantly higher recall, RTE, and RRE compared to RANSAC.
 Table 1. Registration performance on the KITTI dataset.
Table 1. Registration performance on the KITTI dataset. - Comparison with the learning-based methods. We compare our approach with learning-based point cloud registration methods, including IDAM, DGR, CoFiNet, and PREDATOR. As shown in Table 1, the recall of IDAM is about 70% and the average RTE and RRE are more than 1.0, which indicates the poor applicability of the object-level point cloud registration methods to complex, large-scale LiDAR point clouds. DGR performs much better than IDAM thanks to the powerful outlier rejection mechanism based on the 6D convolutional network. However, the voxel-based representation of point clouds limits the precision of registration. CoFiNet achieves the highest recall by using a coarse-to-fine registration strategy, but it gets a relatively larger RRE and RTE due to the position error caused by the sparsity of keypoints in the deep layer. PREDATOR achieves the best registration performance among all the learning-based baseline methods. We show that our approach achieves the best RRE (0.24°). For RTE and recall, our method only has a slight margin with PREDATOR. Moreover, our method achieves almost faster speed than PREDATOR.
4.3.2. Qualitative Visualization
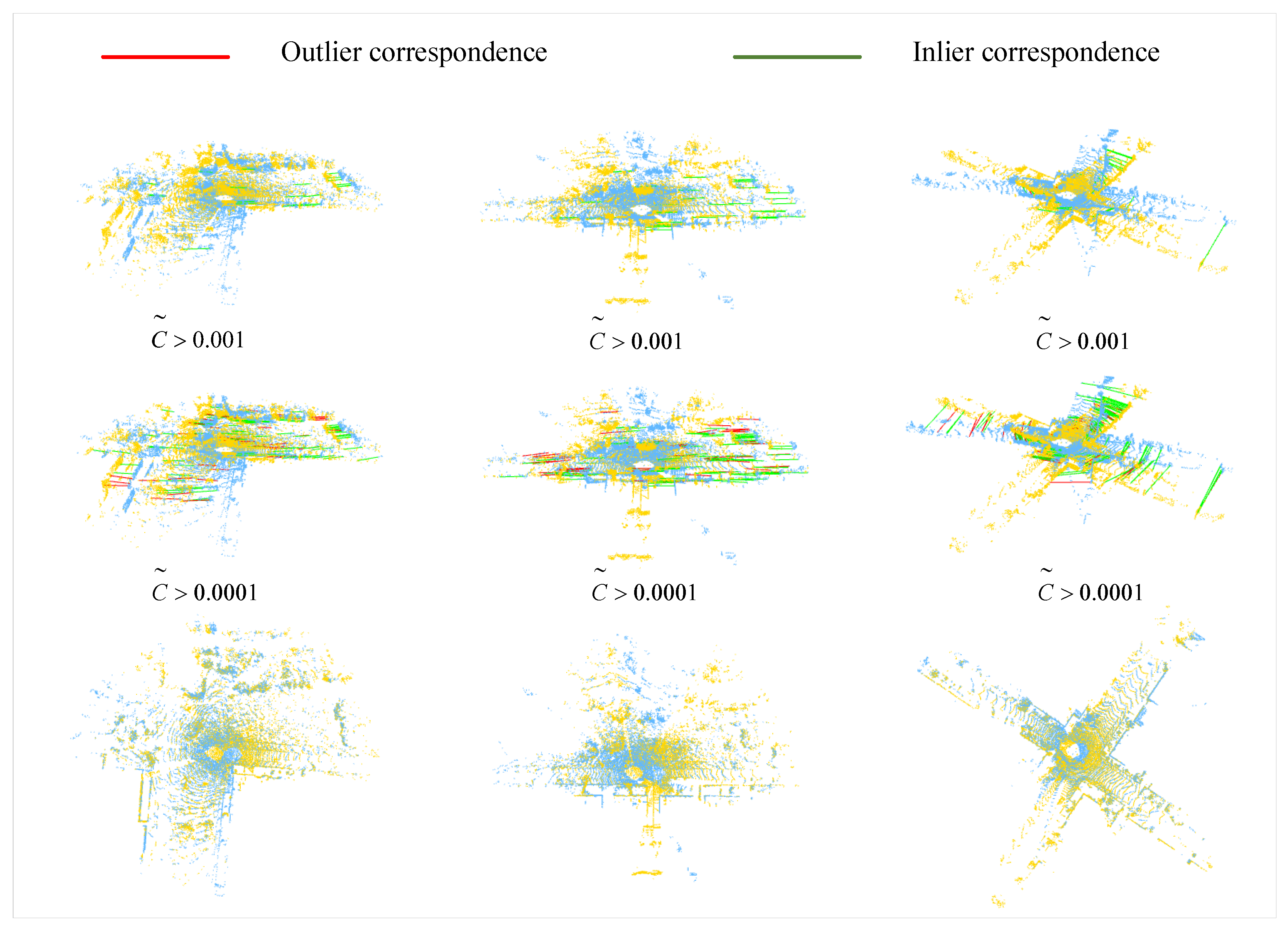
We present several qualitative samples of point cloud registration in Figure 5. Corresponding keypoints with confidence scores and are shown in the first and second row respectively. Two corresponding keypoints are considered as an inlier if the relative position error (after applying the ground truth relative transformation) is less than a distance threshold m. The green and red lines represent inlier and outlier correspondences, respectively. According to the results, the correspondences with a higher confidence score () are basically all inliers and several mismatches begin to appear when reducing the threshold of to 0.0001. The third row of Figure 5 shows the two aligned point clouds, which demonstrates that the network can precisely predict the transformation.
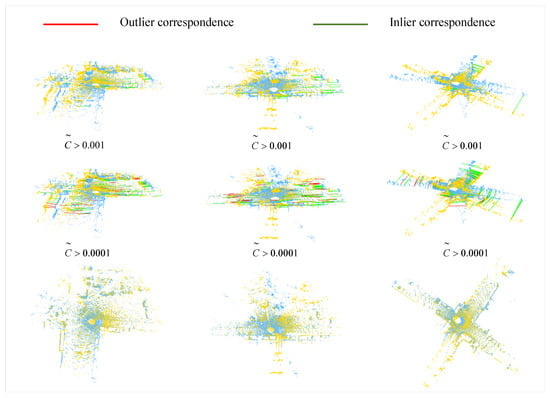
Figure 5.
Registration results of our method on the KITTI dataset. The first row shows the correspondences between source and target keypoints with confidence score and the second row shows the correspondences with confidence score , where the green lines represent inlier correspondences and red lines represent outlier correspondences. The bottom row shows the aligned two-point clouds.
4.4. NuScenes Dataset
NuScenes dataset includes 1000 scenes acquired by 3D LiDAR scanners. We split into 700 scenes for training, 150 scenes for validation, and the other 150 scenes for testing. The ground truth transformations are annotated between neighborhood frames, and the time interval is about 0.5 s. We use the current point cloud sample with the second sample after it as a pair of point clouds.
Performance
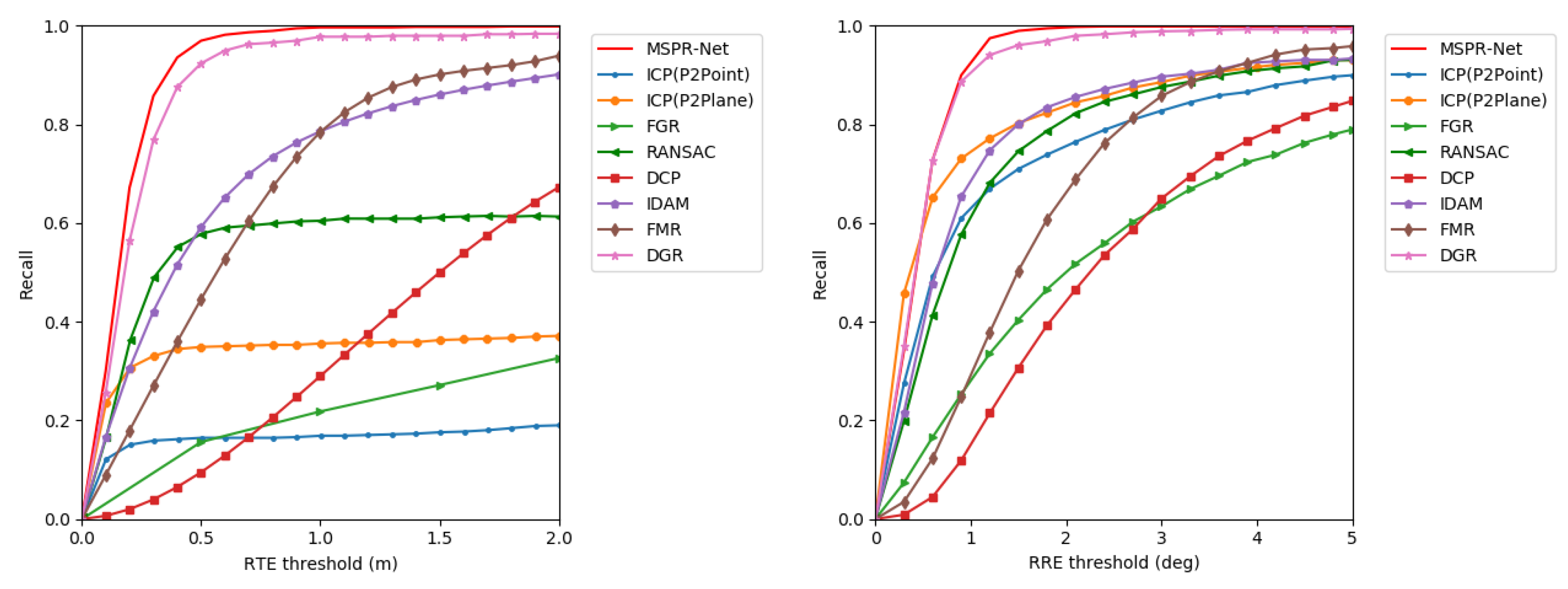
We evaluate our method on the NuScenes dataset. MSPR-Net is compared to the classical methods ICP, FGR, RANSAC, and the learning-based registration methods DCP, IDAM, FMR, and DGR. Table 2 summarizes the results. Our method outperforms all the other methods. MSPR-Net achieved 0.28° on RRE and 0.12 m on RTE, exceeding DGR (0.48° on RRE and 0.21 m on RTE) by 0.20° and 0.09 m. Moreover, our method achieves almost faster speed than DGR. Moreover, MSPR-Net performs the best recall on the NuScenes dataset. To analyze the proposed method in more detail, we present the registration recall by using different thresholds. As shown in Figure 6, our method achieves the highest registration recall among all the settings, which further demonstrates the robustness of our method.

Table 2.
Registration performance in the NuScenes dataset.
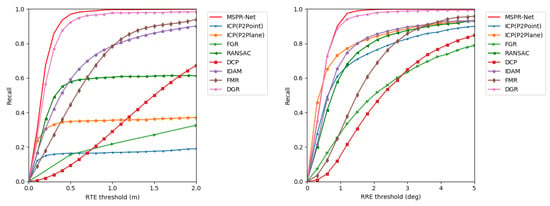
Figure 6.
Registration recall with different RTE and RRE thresholds on the NuScenes dataset.
4.5. Ablation Study
We perform abundant ablation studies on the NuScenes dataset to demonstrate the effectiveness of the components for MSPR-Net. We validate the effectiveness of the multi-scale structure (MS), bilateral outlier removal strategy (BOR), and coarse-to-fine registration pipeline. Table 3 illustrates the results of the ablation studies, where the base model (Base) is only the high-level feature with the coarse registration. According to the results, the average RTE and RRE are much reduced by the use of multi-scale structure and coarse-to-fine registration mechanism, which promotes RTE and RRE by 0.03 m and 0.11° and 0.03 m and 0.14°, respectively. In addition, the bilateral outliers removal strategy also reduces RTE and RRE by 0.01 m, 0.05°, and increases the recall by 0.01%.

Table 3.
Ablation study on NuScenes dataset.
5. Discussion
The success of our network mainly stems from the application of multi-scale features based on human vision. Although all current networks are able to extract multi-scale features, most of them only utilize fusion features with multi-scale information. Our method performs point cloud registration depending on finding correspondences in different feature scales. It makes full use of the consistency of correspondences in different scale features. Moreover, there are some limitations to our work. For example, our method would reject correspondences at the edges of overlapping regions. Usually, these correspondences only match in low neighborhood sizes. Our network would not perform well when the center of overlapping regions is comprised of indistinguishable surfaces.
6. Conclusions
In this paper, we propose MSPR-Net, an outdoor LiDAR point cloud registration network by incorporating multi-scale keypoint features. We present LSEM and GSEM modules to increase the stability of keypoints sample. To construct reliable correspondences between keypoints with different features, we propose a bilateral outlier removal strategy to reject outliers. Moreover, a coarse-to-fine registration strategy is adopted for robust and accurate registration. MSPR-Net achieves 0.24° in RRE and 0.07 m in RTE in the KITTI dataset and 0.28° in RRE and 0.12 m in RTE in the NuScenes dataset, demonstrating the high precision and effectiveness of MSPR-Net.
Author Contributions
Methodology, J.Y. and L.L.; software, J.Y. and F.Z.; validation, J.Y., F.Z. and Z.C.; writing—original draft preparation, J.Y.; writing—review and editing, Z.C. and L.L.; visualization, J.Y. and F.Z.; supervision, L.L.; funding acquisition, L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (Grant 61976227 and 62176096) and in part by the Natural Science Foundation of Hubei Province under Grant 2020CFA025.
Data Availability Statement
The KITTI odometry dataset used for this study can be accessed at http://semantic-kitti.org/ (accessed on 24 September 2022) and NuScenes dataset at https://www.nuscenes.org/ (accessed on 24 September 2022).
Acknowledgments
We would like to thank our colleagues for their helpful suggestions during the experiment and thank the editor and the anonymous reviewers for their valuable comments and suggestions that greatly improve the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Blais, G.; Levine, M.D. Registering multiview range data to create 3D computer objects. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 820–824. [Google Scholar] [CrossRef]
- Choi, S.; Zhou, Q.Y.; Koltun, V. Robust reconstruction of indoor scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5556–5565. [Google Scholar]
- Merickel, M. 3D reconstruction: The registration problem. Comput. Vision Graph. Image Process. 1988, 42, 206–219. [Google Scholar] [CrossRef]
- Sun, K.; Tao, W. A center-driven image set partition algorithm for efficient structure from motion. Inf. Sci. 2019, 479, 101–115. [Google Scholar] [CrossRef]
- Lu, W.; Zhou, Y.; Wan, G.; Hou, S.; Song, S. L3-net: Towards learning based lidar localization for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 6389–6398. [Google Scholar]
- Wan, G.; Yang, X.; Cai, R.; Li, H.; Zhou, Y.; Wang, H.; Song, S. Robust and precise vehicle localization based on multi-sensor fusion in diverse city scenes. In Proceedings of the 2018 IEEE international conference on robotics and automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 4670–4677. [Google Scholar]
- Wong, J.M.; Kee, V.; Le, T.; Wagner, S.; Mariottini, G.L.; Schneider, A.; Hamilton, L.; Chipalkatty, R.; Hebert, M.; Johnson, D.M.; et al. Segicp: Integrated deep semantic segmentation and pose estimation. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 5784–5789. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor fusion IV: Control Paradigms and Data Structures. SPIE, Boston, MA, USA, 12–15 November 1992; Volume 1611, pp. 586–606. [Google Scholar]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings Third International Conference on 3-D Digital Imaging and Modeling. Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Fitzgibbon, A.W. Robust registration of 2D and 3D point sets. Image Vis. Comput. 2003, 21, 1145–1153. [Google Scholar] [CrossRef]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-icp. In Robotics: Science and Systems; University of Washington: Seattle, WA, USA, 2009; Volume 2, p. 435. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. Pointnetlk: Robust & efficient point cloud registration using pointnet. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7163–7172. [Google Scholar]
- Huang, X.; Mei, G.; Zhang, J. Feature-metric registration: A fast semi-supervised approach for robust point cloud registration without correspondences. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11366–11374. [Google Scholar]
- Xu, H.; Liu, S.; Wang, G.; Liu, G.; Zeng, B. Omnet: Learning overlapping mask for partial-to-partial point cloud registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11 October 2021; pp. 3132–3141. [Google Scholar]
- Deng, H.; Birdal, T.; Ilic, S. Ppfnet: Global context aware local features for robust 3d point matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 195–205. [Google Scholar]
- Sarode, V.; Li, X.; Goforth, H.; Aoki, Y.; Srivatsan, R.A.; Lucey, S.; Choset, H. Pcrnet: Point cloud registration network using pointnet encoding. arXiv 2019, arXiv:1908.07906. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Wang, Y.; Solomon, J.M. Deep closest point: Learning representations for point cloud registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 3523–3532. [Google Scholar]
- Yew, Z.J.; Lee, G.H. Rpm-net: Robust point matching using learned features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11824–11833. [Google Scholar]
- Fu, K.; Liu, S.; Luo, X.; Wang, M. Robust point cloud registration framework based on deep graph matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8893–8902. [Google Scholar]
- Choy, C.; Dong, W.; Koltun, V. Deep global registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2514–2523. [Google Scholar]
- Lee, J.; Kim, S.; Cho, M.; Park, J. Deep hough voting for robust global registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11 October 2021; pp. 15994–16003. [Google Scholar]
- Zhu, L.; Guan, H.; Lin, C.; Han, R. Neighborhood-aware Geometric Encoding Network for Point Cloud Registration. arXiv 2022, arXiv:2201.12094. [Google Scholar]
- Lu, F.; Chen, G.; Liu, Y.; Zhang, L.; Qu, S.; Liu, S.; Gu, R. Hregnet: A hierarchical network for large-scale outdoor lidar point cloud registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11 October 2021; pp. 16014–16023. [Google Scholar]
- Horache, S.; Deschaud, J.E.; Goulette, F. 3d point cloud registration with multi-scale architecture and self-supervised fine-tuning. arXiv 2021, arXiv:2103.14533. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuscenes: A multimodal dataset for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11621–11631. [Google Scholar]
- Yang, J.; Li, H.; Campbell, D.; Jia, Y. Go-ICP: A globally optimal solution to 3D ICP point-set registration. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 2241–2254. [Google Scholar] [CrossRef]
- Rosen, D.M.; Carlone, L.; Bandeira, A.S.; Leonard, J.J. SE-Sync: A certifiably correct algorithm for synchronization over the special Euclidean group. Int. J. Robot. Res. 2019, 38, 95–125. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Shen, Y.; Hui, L.; Jiang, H.; Xie, J.; Yang, J. Reliable Inlier Evaluation for Unsupervised Point Cloud Registration. arXiv 2022, arXiv:2202.11292. [Google Scholar] [CrossRef]
- Li, Y.; Harada, T. Lepard: Learning partial point cloud matching in rigid and deformable scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Orleans, LA, USA, 19–20 June 2022; pp. 5554–5564. [Google Scholar]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision; Morgan Kaufmann Publishers Inc.: Vancouver, BC, Canada, 1981; Volume 81. [Google Scholar]
- Cheng, R.; Razani, R.; Taghavi, E.; Li, E.; Liu, B. 2-s3net: Attentive feature fusion with adaptive feature selection for sparse semantic segmentation network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 12547–12556. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Anwar, S.; Barnes, N. Semantic segmentation for real point cloud scenes via bilateral augmentation and adaptive fusion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1757–1767. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.; Guo, C.; Jiang, L.; Wang, Z.; Shi, J.; Wang, X.; Li, H. Pv-rcnn: Point-voxel feature set abstraction for 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10529–10538. [Google Scholar]
- Bulat, A.; Tzimiropoulos, G. How far are we from solving the 2d & 3d face alignment problem? (and a dataset of 230,000 3d facial landmarks). In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1021–1030. [Google Scholar]
- Najibi, M.; Samangouei, P.; Chellappa, R.; Davis, L.S. Ssh: Single stage headless face detector. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4875–4884. [Google Scholar]
- Liu, Y.; Cheng, M.M.; Hu, X.; Wang, K.; Bai, X. Richer convolutional features for edge detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3000–3009. [Google Scholar]
- Sun, K.; Tao, W.; Qian, Y. Guide to Match: Multi-Layer Feature Matching With a Hybrid Gaussian Mixture Model. IEEE Trans. Multimed. 2020, 22, 2246–2261. [Google Scholar] [CrossRef]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6411–6420. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Bromley, J.; Guyon, I.; LeCun, Y.; Säckinger, E.; Shah, R. Signature verification using a "siamese" time delay neural network. Adv. Neural Inf. Process. Syst. 1993, 6, 737–744. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 5105–5114. [Google Scholar]
- Zhou, Y.; Wan, G.; Hou, S.; Yu, L.; Wang, G.; Rui, X.; Song, S. Da4ad: End-to-end deep attention-based visual localization for autonomous driving. In European Conference on Computer Vision; Springer: Berlin, Germany, 2020; pp. 271–289. [Google Scholar]
- Huang, S.; Gojcic, Z.; Usvyatsov, M.; Wieser, A.; Schindler, K. Predator: Registration of 3d point clouds with low overlap. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 4267–4276. [Google Scholar]
- Kabsch, W. A solution for the best rotation to relate two sets of vectors. Acta Crystallogr. Sect. A Cryst. Physics, Diffraction, Theor. Gen. Crystallogr. 1976, 32, 922–923. [Google Scholar] [CrossRef]
- Li, J.; Lee, G.H. Usip: Unsupervised stable interest point detection from 3d point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 361–370. [Google Scholar]
- Lu, F.; Chen, G.; Liu, Y.; Qu, Z.; Knoll, A. Rskdd-net: Random sample-based keypoint detector and descriptor. Adv. Neural Inf. Process. Syst. 2020, 33, 21297–21308. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Zhou, Q.Y.; Park, J.; Koltun, V. Fast global registration. In European Conference on Computer Vision; Springer: Berlin, Germany, 2016; pp. 766–782. [Google Scholar]
- Li, J.; Zhang, C.; Xu, Z.; Zhou, H.; Zhang, C. Iterative distance-aware similarity matrix convolution with mutual-supervised point elimination for efficient point cloud registration. In European Conference on Computer Vision; Springer: Berlin, Germany, 2020; pp. 378–394. [Google Scholar]
- Yu, H.; Li, F.; Saleh, M.; Busam, B.; Ilic, S. Cofinet: Reliable coarse-to-fine correspondences for robust pointcloud registration. Adv. Neural Inf. Process. Syst. 2021, 34, 23872–23884. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).