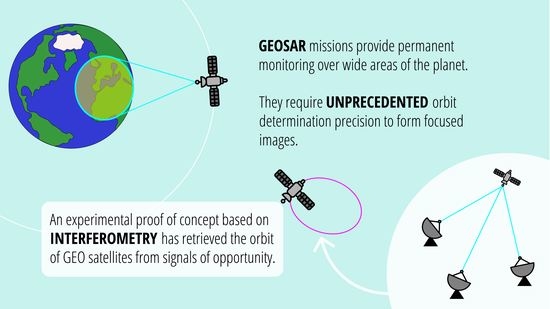
Interferometric Orbit Determination System for Geosynchronous SAR Missions: Experimental Proof of Concept

Abstract

Future Geosynchronous Synthetic Aperture Radar (GEOSAR) missions will provide permanent monitoring of continental areas of the planet with revisit times of less than 24 h. Several GEOSAR missions have been studied in the USA, Europe, and China with different applications, including water cycle monitoring and early warning of disasters. GEOSAR missions require unprecedented orbit determination precision in order to form focused Synthetic Aperture Radar (SAR) images from Geosynchronous Orbit (GEO). A precise orbit determination technique based on interferometry is proposed, including a proof of concept based on an experimental interferometer using three antennas separated 10–15 m. They provide continuous orbit observations of present communication satellites operating at GEO as illuminators of opportunity. The relative phases measured between the receivers are used to estimate the satellite position. The experimental results prove the interferometer is able to track GEOSAR satellites based on the transmitted signals. This communication demonstrates the consistency and feasibility of the technique in order to foster further research with longer interferometric baselines that provide observables delivering higher orbital precision.

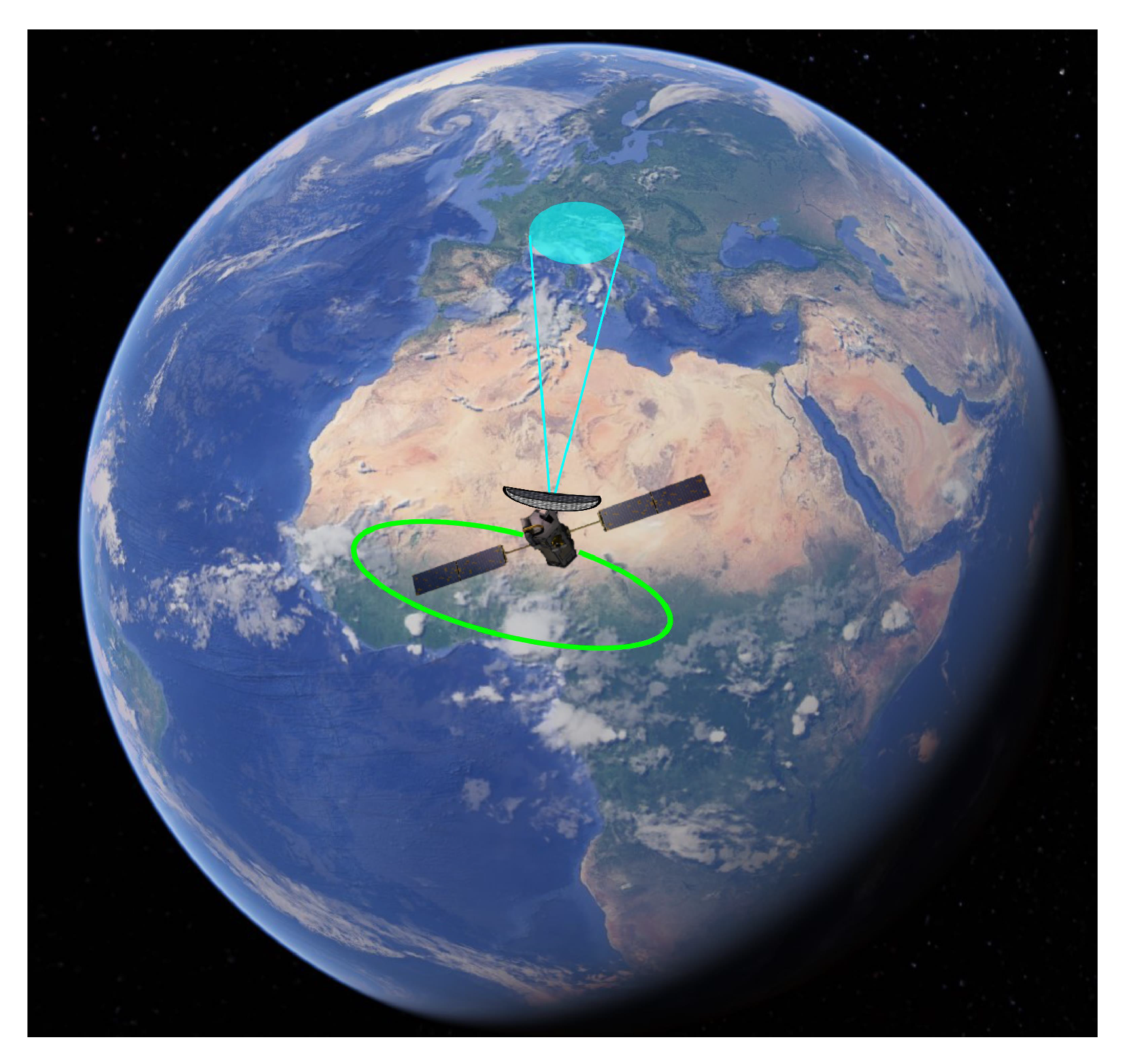
1. Introduction

Low Earth Orbit (LEO) remote sensing missions present a main limitation regarding their revisit time of several days or weeks. They cannot provide continuous monitoring over the same area of the planet. The introduction of the Geosynchronous Synthetic Aperture Radar (GEOSAR) aims to mitigate this limitation. The main strength of GEOSAR is the ability to monitor continental regions with a revisit time of less than 24 h owing to the nature of the Geosynchronous Orbit (GEO). Radar systems are sensitive to the backscatter of Earth’s surface, as well as the refractive index of the atmosphere. Therefore, GEOSAR is able to provide continuous monitoring of Earth’s surface and atmosphere. Potential applications that require continuous monitoring are, for instance: flooding monitoring and forecasting, glacier motion and snow cover monitoring, earthquakes, volcano and landslide forecasting, and subsidence and infrastructure deformation monitoring.

Several geosynchronous SAR remote sensing missions have been considered in the past or are being studied presently. The first GEOSAR proposal considered different orbital configurations including a Near-Zero Inclination (NZI) scheme [1]. The principle of operation of GEOSAR is based on the daily orbits described by the satellite over a continent. NZI GEO satellites present an inherent limited motion with respect to Earth in the order of hundreds of kilometers. This allows the spacecraft to receive the echoes from the surface in different satellite orbital positions and to coherently add them in order to form synthetic apertures of a few hours. This is sufficient to form images with a resolution of dozens of meters [2]. Otherwise, GEOSAR missions would not be feasible since they would require forming synthetic apertures artificially by means of a fuel-spending station-keeping process. As a consequence, this would reduce the lifetime of the mission. More recently, two NZI GEOSAR proposals were submitted to the Earth Explorer (EE) program of the European Space Agency (ESA), including EE-9 and EE-10 [3,4]. The latter (G-CLASS, renamed Hydroterra) was selected as one of the three candidate projects. The proposal consisted of a satellite using a C-band antenna with a diameter of 7 m. The elliptical relative motion of the spacecraft with respect to Earth, located over central Africa, allows the radar to monitor the water cycle over Europe and Africa, as qualitatively represented in Figure 1.

The single-platform GEOSAR concept considered for the Hydroterra mission can be fractionated by means of a swarm of N SAR platforms, operating in a multistatic SAR configuration in order to enhance its performance. In this way, the synthetic aperture required to obtain high-resolution images would be obtained in a fraction of the time according to the number of platforms. The coherent combinations of the echoes obtained from different tracks would improve the Signal-to-Noise Ratio (SNR) by a factor of N${}^2$, leading to metric resolution, a 20–40 min minimum observation time, and multi-polarimetric and interferometric imaging [5,6].

The NZI GEOSAR scheme implies restricted geographical coverage. Therefore, a new GEOSAR scheme with a 50${}^{\circ }$ inclination was proposed in order to provide imaging over the entire American continent [7,8]. The larger coverage is achieved by means of a nadir-point trajectory in a large “figure 8” shape, which implies shorter integration times with respect to the NZI proposal. In this case, the transmitter power and antenna diameter requirements were 15 kW and 30 m, respectively.

Studies from China propose a GEOSAR mission with an inclination of more than 50${}^{\circ }$ with a large “figure 8” shape of the nadir-point trajectory, taking into account the large latitude and longitude ranges of the country [9,10]. Such a high-inclination scheme could provide multiple observation angles for many areas, allowing the formation of three-dimensional (3D) deformation maps. A medium inclination (16${}^{\circ }$) GEOSAR scheme with a small “figure 8” nadir-point trajectory has also been studied owing to its longer coverage time over China [11].

Signals of Opportunity-Reflectometry (SoOp-R) is an emerging technology that can be used to measure the Snow Water Equivalent (SWE). The system is based on passive receivers and uses existing, strong, satellite transmissions, available across most radio bands, penetrating the Earth’s atmosphere (P to Ka band) in a bistatic radar configuration. P-band communication satellites in GEO orbits, such as the Navy’s Mobile Users Objective System (MUOS), provide higher illumination power density than Global Navigation Satellite Systems (GNSSs) and better surface penetration for snow and soil moisture sensing, thus allowing small P-band SoOp satellite receivers operating at LEO to capture the reflection with a high SNR. The use of P-band SoOp from MUOS has also been receiving increasing attention for soil moisture sensing and other land hydrology elements [12,13,14].

The previously described GEOSAR missions are currently under study. Regardless of the configuration, correct focusing of GEOSAR images depends on the compensation of the echo phase histories, which requires determining the orbit tracks with precisions in the order of 10 m or better [15]; this precision can be relaxed by one order of magnitude using SAR autofocusing techniques based on entropy minimization [15].

Therefore, GEOSAR missions present two main challenges. On the one hand, they need to compensate for the impact of distances greater than 36,000 km on the received echo power. Therefore, they require the use of high-gain antennas, significant average transmitted power, and long integration times between minutes and hours depending on the desired resolution [2,8,9,16,17]. On the other hand, they require unprecedented orbit determination precision [18]. The satellite navigation techniques used for LEOSAR missions present limitations when applied to higher orbits beyond Medium Earth Orbit (MEO). Since the GEO trajectories lie above the GNSS constellations, some studies propose to use the sidelobes GNSS signals from the other side of the Earth in order to determine the orbit of GEO satellites with precision [19]. The coverage time from a single GNSS satellite from the other side of the Earth is limited. Therefore, only dual- or multi-GNSS could provide continuous navigation solutions with a receiver threshold of 15 dB-Hz [20]. Other studies from China have improved the orbit determination precision of the BeiDou satellites in GEO orbits by combining GNSS navigation with ground tracking [21]. Hence, the advent of emerging geosynchronous remote sensing missions relies on the development of novel, precise orbit determination techniques, both spaceborne and ground-based. The technique presented in this paper aims to complement other orbit determination techniques, such as the ones based on GNSS, in order to enhance the tracking precision of future remote sensing missions from GEO.

2. Methodology

Microwave interferometry based on processing multiple observations from radio astronomy observatories over the Earth provides the highest angular resolution ever achieved [22]. It has also been successfully used for the formation of black hole images by means of the Event Horizon Telescope (EHT) collaboration [23,24]. Interferometric techniques can be used for deep-space probe tracking [25] and satellite navigation [26]. In addition, it is the most suitable technique in order to track signals of opportunity owing to other techniques, such as Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS), Satellite Laser Ranging (SLR), and GNSS navigation, require the spacecraft to be equipped with dedicated on-board instrumentation [27]. Since there are no Earth observation radars in GEO yet, current geostationary telecommunication satellites can be used as transmitters of opportunity to validate the proposed technique. The Astra $19.2^{\circ }$E constellation has been chosen due to its excellent coverage of DVB-S TV signals over Europe.

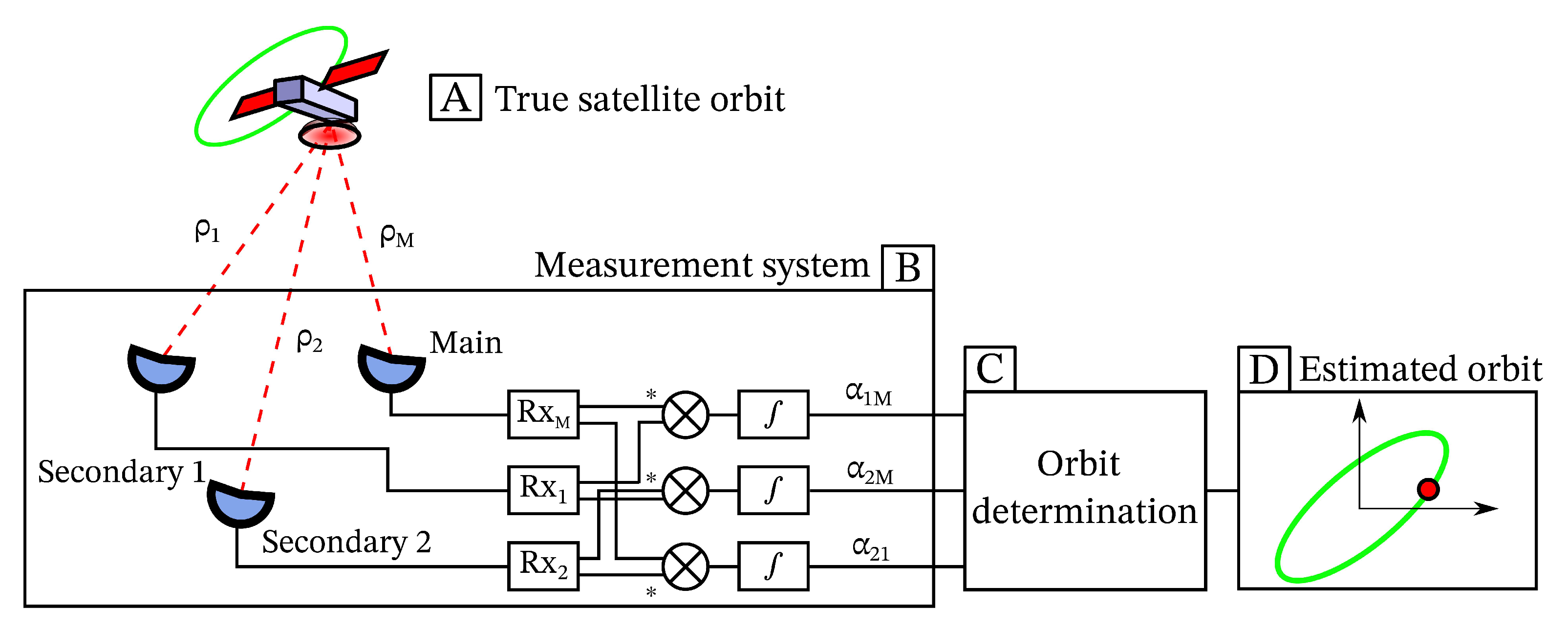
2.1. Radio Interferometer Phase Detection

The ground-based interferometer measurement system (Figure 2) retrieves information from an emitting source. It combines the signal received by different antennas at different locations. Each pair of receiving antennas forms a baseline and delivers an interferometric phase observation (${\alpha }_{ij}$). More baselines can be added in order to improve the performance of the system. For orbit determination purposes, three channels and two baselines are required in order to retrieve the azimuth and elevation angle of arrival data.

The interferometric signal is generated by means of a zero-lag correlation method, which processes the base-band of the downconverted radiofrequency signals. It compensates the coarse delay differences caused by the antenna locations and cabling. Uncorrelated receiver noise is strongly rejected in the correlation process, resulting in a high processing gain, defined as [28]:

$$G_{\mathrm{corr}}=\mathrm{BW}·\tau$$

(1)

where BW corresponds to the bandwidth of the received channel and $\tau$ is the integration time. Since Astra DVB-S TV transmissions of opportunity work with 30 MHz-bandwidth channels, using integration times in the order of one second results in a theoretical processing gain of 74.77 dB. Different GEOSAR concepts will allow working with similar values of processing gain owing to smaller bandwidths being able to be compensated by increasing the integration time.

The correlators provide complex interferometric observations where the phase provides a high-resolution observation of satellite signals’ angle of arrival. The magnitude of the correlation provides complementary information on the received signals’ SNR and alignment of different channels delays before correlation. Since the displacements on the position of the satellite produce major changes in the interferometric phases of the available baselines, the interferometric phases will be used as observables to determine the satellite orbit.

Mathematically, the interferometric phase acquisition of a single baseline is described as follows. The emitted complex signal by the target satellite along with its carrier is:

$$x\left(t\right)=s\left(t\right)e^{j(2\pi f_{c}t+{\varphi }_0)}$$

(2)

where $s\left(t\right)$ is the low-pass complex modulation signal, $f_c$ is the carrier frequency, and ${\varphi }_0$ is a constant phase. The arriving signal at the antenna, $v\left(t\right)$, is assumed to be a time-delayed transmitted signal with added noise and amplitude attenuation caused by the path loss, A.

$$v\left(t\right)=A·x(t-t_d)+\omega \left(t\right)$$

(3)

$$v\left(t\right)=A·s(t-t_d)·e^{j(2\pi f_c(t-t_d)+{\varphi }_0)}+\omega \left(t\right)$$

(4)

$$v\left(t\right)=A·s(t-t_d)·e^{j(2\pi f_{c}t-{\alpha }_d+{\varphi }_0)}+\omega \left(t\right)$$

(5)

where $t_d$ corresponds to the time delay, ${\alpha }_d$ is the phase shift due to the time delay, and $\omega \left(t\right)$ is the Additive White Gaussian Noise (AWGN) added by the receiver channel.

The downconversion process removes the carrier exponential term $2\pi f_{c}t+{\varphi }_0$ from Equation (5), yielding the following band-pass-equivalent expression:

$$v_{BB}\left(t\right)=A_{r}A·s(t-t_d)·e^{j(2\pi (f_c-f_r)t-{\alpha }_d+{\varphi }_0+{\varphi }_r\left(t\right))}+A_r{\omega }_r\left(t\right)$$

(6)

where $A_r$ is the amplitude attenuation due to the receiver gain, $f_r$ is the carrier frequency estimation, and ${\varphi }_r\left(t\right)$ is the phase introduced by each receiver downconverter whose average value is constant, thus calibrated, since the receivers local oscillators are synchronized with Phase-Locked-Loop (PLL) subsystems with the interferometer’s main clock. The fluctuations on ${\varphi }_r\left(t\right)$ are due to the phase noise of the system, which is designed to be smaller than the phase changes induced by atmospheric turbulence.

Then, the interferometric signals are obtained from the correlation of the received signal from two different receivers during a limited integration period. The cross-correlation of two power signals, $v\left(t\right)$ and $w\left(t\right)$, is defined as:

$$R_{vw}\left(\tau \right)=\langle v_{BB}\left(t\right),w_{BB}^{*}(t-\tau )\rangle$$

(7)

This is a scalar product with the second signal delayed by $\tau$ relative to the first. For each baseline, the correlator performs a sweep of the delay ($\tau$) to find the value (${\tau }_0$) that aligns the two received signals, maximizing the magnitude of the correlation and obtaining the phase differences. The magnitude of the correlation is defined as:

$$\parallel R_{vw}\left(\tau \right)\parallel =\frac{R_{vw}\left(\tau \right)}{R_{vw}\left(0\right)}$$

(8)

where $R_{vw}\left(0\right)$ corresponds to an ideal correlation where the signals are identical and perfectly aligned. It is defined by the maximum value of the integrated samples along the integration time. When normalized, $\parallel R_{vw}\left(0\right)\parallel =1$. In our case, the noise of the received signals, atmospheric turbulence and other factors limit the correlation magnitude to 0.8 under experimental conditions.

The result of developing Equation (7) yields the correlator’s output ($R_u$):

$$R_u\left({\tau }_0\right)=A_r^2{A}_v{A}_w{R}_s\left({\tau }_0\right)·e^{{\alpha }_v-{\alpha }_w-{\alpha }_{{\tau }_0}}+\eta$$

(9)

where $A_v$ and $A_w$ correspond to the amplitude of the received signals at each antenna, v and w, respectively, and ${\alpha }_v$ and ${\alpha }_w$ correspond to the phase shift of each signal along the electric path between the satellite and the receiver.

The first term contains the autocorrelation of the received baseband signal ($R_s$), and ${\alpha }_{{\tau }_0}$ is a residual phase introduced by the discrepancy between the average ${\varphi }_r$ value of each receiver. This is caused by cabling length differences and the phase differences between the local oscillators, which keep the system coherent since they are synchronized with a stable reference main system clock. The ${\alpha }_{{\tau }_0}$ term is determined by means of the interferometric system calibration. The second term ($\eta$) groups the noise terms with a zero average value resulting from the cross-products between the signals and noises of the two channels. Note that only a single-lag component of the correlation is required to retrieve the phase difference from a point source.

Both received signals are considered properly aligned if the alignment error is smaller than the correlation time of the received signal ($\Delta \tau$), which for a DVB-S signal is:

$$\Delta \tau \approx \frac{1}{\mathrm{BW}}$$

(10)

Finally, the interferometric phase, $\alpha$, is obtained as the angle of the interference signal phasor.

$$\alpha =\measuredangle R_u\left({\tau }_0\right)={\alpha }_v-{\alpha }_w-{\alpha }_{{\tau }_0}$$

(11)

This interferometric phase is used as the orbit observable in order to retrieve the satellite trajectory.

Mathematically, the interferometric phase obtained by each pair of antennas in Equation (11) can only be retrieved in the interval $(0,2\pi ]$. Therefore, in order to use the phase as the orbit observable, it is required to express it in unwrapped form: including the integer number of cumulative cycles lost along the path between the satellite and the receiving antenna.

$${\alpha }_u=mo{d}_{2\pi }\left(\alpha \right)+2\pi M$$

(12)

where M indicates the unknown integer number of the phase cycles, since the orbit determination procedure retrieves the satellite trajectory from the observation of the path differences, which are related to the unwrapped phases. The integer number of cycles of the phase (M) must be estimated, avoiding discontinuities in the interferometric phase acquisition. Otherwise, the observed phases would be satisfied by multiple possible satellite orbits.

Since the Hydroterra mission operates at the C-band and the central frequency of the signal of opportunity used to perform the experimental proof of concept is at the Ku-band, ionospheric perturbations have not been considered [29]. Should this technique be applied to missions working at lower frequencies, the ionospheric perturbations must be further studied.

2.2. Orbit Determination

The process of experimental orbit determination makes use of the orbit observables acquired by the two main baselines of the interferometer: Main-Secondary 1 and Main-Secondary 2. The third possible baseline Secondary 1-Secondary 2 is redundant, and it is used only to check the consistency of the interferometric observations.

The orbit determination module represented in Figure 2 uses two models. The first one estimates the orbit of the satellite by means of a geosynchronous dynamic model, which considers the $J_2$, $J_{22}$, $J_3$, and $J_4$ effects, Moon and Sun perturbations, and the Solar Radiation Pressure (SRP) [30]. The estimated trajectory of the spacecraft is propagated from an initial state (3D position and velocity) by means of a Runge–Kutta–Fehlberg 7(8) integrator [31].

The output of the GEO dynamical model is combined with the second model of the orbit determination module, which estimates the phase observations that the interferometric measurement system described in Figure 2 would generate. They are the result of the distance differences between the estimated position of the satellite and the position of the antenna receivers, which are well determined from geodetic measurements. Once the ${\alpha }_{\tau 0}$ phase term from Equation (9) is removed after calibration, the measured interferometric phase (${\alpha }_{ij}$) is expressed as:

$${\alpha }_{ij}\left(t\right)=\frac{2\pi }{\lambda }·n·\left({\rho }_i\left(t\right)-{\rho }_j\left(t\right)\right)$$

(13)

The measured interferometric phase (${\alpha }_{ij}$) is related to the distance between the spacecraft and the receiver ($\rho$) in terms of the range difference between the satellite and the pair of antennas (${\rho }_i-{\rho }_j$), where $\lambda$ is the wavelength of the emitted signal [26]. The atmosphere has a nonunit refractive index n, which must be considered in order to express the distance between the satellite and the receivers in terms of the electrical path length [32]. Hence, each interferometric baseline yields a set of estimated phase observations for a single estimated trajectory.

An iterative process based on the batch least-squares estimation technique [33] minimizes the Mean-Squared Error (MSE) between the measured (${\alpha }_k$) and the estimated (${\widehat{\alpha }}_k$) interferometric observations as Equation (14) details, where n is the number of samples. The sampling rate of the interferometer is 1 sample/s. The resulting estimated trajectory corresponds to the one that generates the simulated phase observations that fit best to the measured phase observations.

$$\mathrm{MSE}=\frac{1}{n}\sum _{k=1}^n{\left({\alpha }_k-{\widehat{\alpha }}_k\right)}^2$$

(14)

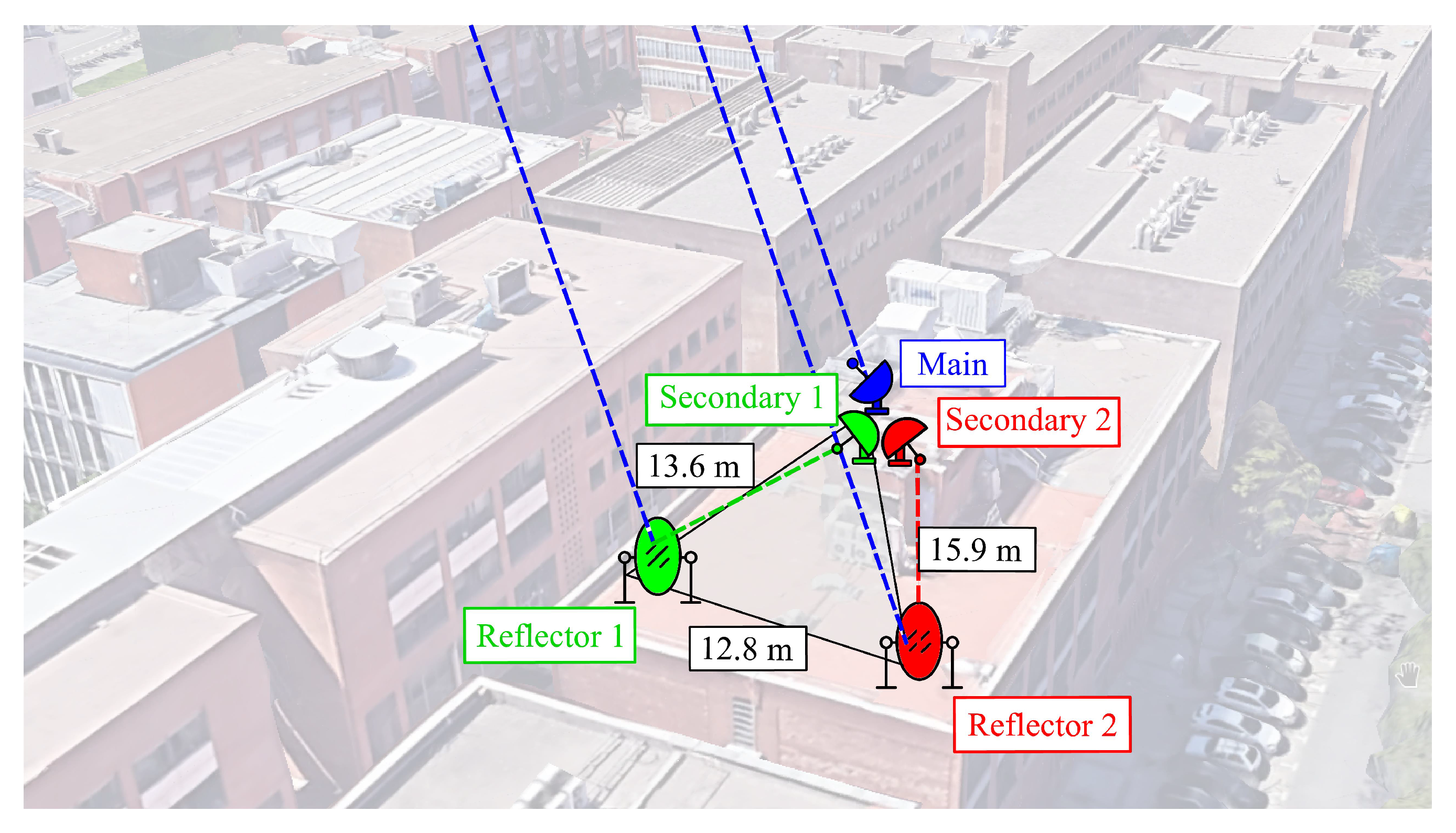
2.3. Experimental Setup

Since there are no radar satellites operating at GEO yet, the objective is to perform an experimental proof of concept by tracking illuminators of opportunity. The target constellation is Astra $19.2^{\circ }$E due to its excellent coverage of DVB-S TV signals over Europe and its high number of active channels.

The proposed interferometric orbit determination relies on the ability of coherent radio receivers to accurately preserve the phase of the downlink satellite signals [34]. The experimental system consists of three main differentiated modules: the front-end receives the channel spectrum from the satellite at the Ku-band (11.70–12.75 GHz) and performs the first downconversion to the intermediate frequency (IF) (1–2 GHz) by means of a commercial Low-Noise Block (LNB). Then, the baseband module performs the second downconversion from the IF to the baseband and digitizes the signal to be processed by the correlator. These downconversions require a set of local oscillators, which must be synchronized. The reference module provides them a clean and stable clock signal in order to preserve the phase coherence of the system.

This modular approach allows the system to be adapted to any kind of satellite transmission. Instead of receiving Ku-band signals, the front-end can be replaced by another version, which receives a radar signal (at the C-band, for instance) and downconverts it to the IF. Thus, it can track a different satellite only by changing a single module of the reception system, while leaving the rest as they are. Since a radar signal consists of pulses, the correlation method could be optimized in order to only process the useful signal sections. Other than this, pulsed radar signals pose no further problems owing to the relative motion of GEO satellites with respect to the receiver.

The three receiver antennas are clustered within 1 meter. In this way, the LNB downconverters’ local oscillators are synchronized by means of a phase-locked oscillator, which is disciplined to a common main clock. All the local oscillator connections use very short cables in order to minimize thermal phase drifts.

The measurement sensitivity of the interferometer increases with the separation between antennas (baseline). The secondary antennas are not pointing towards the satellite, but to their corresponding reflectors located about 15 m apart (Figure 3). The reflectors consist of a 1 m${}^2$ flat aluminum plate, which does not introduce any phase noise nor SNR degradation. The performance of the link is excellent since the reflected signal received in the secondary antennas is adequate to watch the satellite TV broadcast. The position of the mirrors with respect to the main antenna must be carefully determined in order to avoid errors. Therefore, the baselines of the system are extended while keeping the antenna connections very short.

This configuration has been chosen to serve as a proof of concept of the technique. It is an intermediate step before increasing baselines in order to obtain more precise orbit determinations. However, the present baseline benefits from a distance of ambiguity of about 60 km between two possible satellite positions sharing the same phase principal value [35]. Larger interferometric baselines in the order of kilometers present smaller distances of ambiguities in the order of hundreds of meters. For this reason, the short baseline configuration will be maintained throughout the duration of the project, allowing easily selecting the correct orbit from other ambiguous solutions in future large baselines.

3. Results

This section comprehends two experiments carried out to evaluate the feasibility and reliability of the interferometric system for satellite tracking. The first one (Section 3.1) compares the quality of the observations of two channels with different signal-to-noise ratio (SNR) levels. Its objective is to assess whether the system is capable of tracking weak signals well below the noise level. The latter (Section 3.2) uses the interferometric observations in order to experimentally retrieve the orbit of the observed satellite, showing the consistency and feasibility of the technique.

3.1. SNR Degradation Experiment

This experiment was carried out in order to test how the interferometric system performs under adverse conditions. It consisted of using two east–west horizontal baselines with almost an identical length of 3.5 m, sharing a common main antenna (Figure 4). On the one hand, the first baseline ($R_{1M}$) was designed to work in nominal conditions. The Secondary 1 receiver presents the same parameters as the main antenna, and it works with moderate (10 dB) SNR levels. On the other hand, the second baseline was intended to work in unfavorable conditions, i.e., a very low SNR. The parabolic reflector of the Secondary 2 receiver was removed in order to intentionally cause an important SNR degradation, resulting in a useful signal at −15 dB below noise.

The measurements acquired by the two interferometric baselines during September and October 2019 are shown in Figure 5. They correspond to the orbit observations of the geostationary Astra 1M satellite while transmitting DVB-S TV broadcasting signals from a $19.2^{\circ }$E longitude station. The left vertical axis represents the interferometric phase measurements. They match the movement of the satellite with respect to Earth. The right vertical axis shows the correlation magnitude, which is defined in Equation (8) and would be one for perfectly correlated noiseless signals.

The magnitude of the first correlation, $R_{1M}$, presents nominal values between 0.7 and 0.8, which is consistent with the channels’ limited SNR. In contrast, the magnitude of the second correlation, $R_{2M}$, drops dramatically due to the SNR degradation caused by the reflector withdrawal. However, due to the large processing gain of the correlator (Equation (1)), the quality of the phase measurements between nominal and degraded conditions is comparable. The Root-Mean-Squared Deviation (RMSD) between the measurements of both baselines presents a residual of 0.18 rad, which is small in front of the interferometric phase evolution of ≈5 rad per day.

This test demonstrates the robustness of the interferometric satellite tracking system. It is capable of working with very low (−15 dB) SNR levels. Therefore, it would be able to track satellite signals such as radar, telemetry, or pilot beacon transmissions, even in adverse SNR conditions such as radar transmission sidelobes. Hence, it only requires being in the line-of-sight of the target satellite, making a single interferometer suitable to track spacecraft in any low-inclination geosynchronous orbit. However, high-inclination geosynchronous missions, such as the ones proposed by China, with a large “figure 8” shape nadir-point trajectory, would require extra interferometric receivers in order to keep track of the spacecraft along all latitudes.

Furthermore, the results prove that the noise of the observations is not due to internal noise or a systematic uncertainty of the measurements. Even though the SNR at the Secondary 2 receiver is negative, the large processing gain of the correlator is able to recover the useful signal. Moreover, the GEO dynamical model acts as a very narrow filter since it rejects the observations, which are not compatible with the dynamics of the GEO orbit. On the other hand, the hourly pattern of phase disturbance with higher fluctuations around noon indicates an atmospheric turbulence origin, taking into account the warm air temperatures (above 22 ${}^{\circ }$C) and high relative humidity (96%) during the days of the acquisition. Figure 6 shows a comparison between the experimental phase data, obtained with the interferometric measurement system, and the simulated data, obtained from the North American Aerospace Defense Command (NORAD) Two-Line Element (TLE) set information propagated with the geosynchronous dynamical model described in Section 2.2. The right axis of the figure shows the Solar Radiation (SR) measurements obtained from an automatic weather station next to the site where the interferometric system is deployed, in Zona Universitària (Barcelona). The station is property of Servei Meteorològic de Catalunya, and the data were validated by their team. During sunny days (solar radiation higher than 600 W/m${}^2$), the troposphere is turbulent, and it generates noisy observations. Moreover, temperature effects on the experimental measurements are very significant when the solar radiation is highest, causing an important deviation from the simulated data. On the other hand, during the night and cloudy days (solar radiation lower than 600 W/m${}^2$), it remains more steady and the measurements are cleaner, showing a good fit between the experimental and simulated data. Hence, the system must be designed in order to minimize the impact of temperature drifts, in particular minimizing the length and solar exposure of radiofrequency cabling.

In summary, the most notable phase perturbations are caused by temperature and atmospheric effects. The errors caused by the limited SNR of the system are not comparable since they undergo two stringent filters, which reject most of the noise: the large processing gain of the correlator and the GEO dynamical model.

3.2. Experimental Orbit Determination from Interferometric Observables

The first approach to perform the experimental validation of the system consists of an interferometer with a separation between antennas of 10–15 m with both vertical and horizontal baseline components, as described in Section 2.3. In order to validate the feasibility of the presented technique, an evaluation of the consistency between the estimated observations and the measured ones was carried out. As described in Section 2.2, the process consisted of retrieving the estimated trajectory of the satellite by means of the measured observations and a least-squares estimation technique based on Nelder–Mead optimization, a GEO dynamical model, and a Runge–Kutta–Fehlberg 7(8) integrator. Then, the estimated observations shown in Figure 7 were obtained after computing the range differences between the estimated position of the spacecraft along time and the position of the receiver antennas. The degree of correlation between estimated observations and the measured interferometric observations during the observation window was evaluated. As depicted in Figure 7, one third of the observation window (shaded area) between station-keeping maneuvers was used to retrieve the state vector at the initial time epoch of the observation period ($t_0$). This state was propagated forward in time by means of the interferometric GEO model and the Runge–Kutta–Fehlberg 7(8) integrator. Since the model does not consider artificial perturbations, the fitting was only valid within an orbital maintenance window of about two weeks. It diverges from the actual motion of the spacecraft when orbital maneuvers are performed.

Different orbital solutions as a consequence of the 3D position ambiguity would imply an offset on the average phase value between the estimated and the measured observations in Figure 7. Since the compact baseline presents a distance of ambiguity (60 km) larger than the relative motion of the satellite with respect to the receivers (up to 50 km as shown in Figure 8), the results presented in Figure 7 and Figure 8 correspond to the correct orbital solution.

Since the interferometric system provides continuous tracking (one observation per second) of the spacecraft, the orbit determination module is able to make use of updated orbit observations in order to keep track of the spacecraft even after station-keeping maneuvers. Figure 7 shows the result of updating the orbital model with new observations every 24 h (maneuver detection), which yields a much more precise tracking of the satellite.

The short-term cycle of the phase, with a daily period, corresponds to the ellipse drawn by the spacecraft due to the inclination and eccentricity of its orbit. In addition, the interferometric observation is capable of tracking the long-term cycle of the spacecraft. With a two-week period, it corresponds to the station-keeping operations, which mitigate the effects of the irregular gravitational potential of the planet. This is a consequence of Earth’s nonsphericity and the topographical irregularities of the geoid, creating stable and unstable regions. Any orbiting satellite in a geostationary orbit will tend to deviate to a low geoid. Since the Astra 1M satellite lies above central Africa (19.2${}^{\circ }$E longitude), the stable area over the Indian Ocean causes a natural drift force towards the east [30]. This is represented from 12 to 21 April in Figure 7, where the average phase value increases, and in Figure 8, where the Earth-Centered Earth-Fixed (ECEF) coordinate system trajectory of the satellite moves along the Y axis towards the east. In order to keep the satellite in the nominal position, an orbital maneuver towards the west is periodically performed. Two station-keeping maneuvers are identified during the orbit observation period: on 5 and 21 April. Note in Figure 7 how the average phase value decreases from 5 to 13 April and from 21 to 27 April due to the movement of the satellite towards the west. Figure 8 shows the same behavior representing the retrieved trajectory in the ECEF coordinate system: the ellipse of the spacecraft moves towards the west from 9 to 12 April (Figure 8a) and from 21 to 24 April (Figure 8b). Thus, the satellite is kept within the assigned nominal station.

4. Conclusions

Geosynchronous SAR (GEOSAR) missions require unprecedented orbit determination precision in the scale of meters. A precise orbit determination technique based on interferometry is proposed, and the first experimental proof of concept is presented.

The results conclude that interferometric orbital tracking of SAR missions can be successfully performed making use of static low-gain antennas, avoiding the use of complex dynamic pointing. The interferometric system would be able to track SAR satellites making use of signals such as radar, telemetry, or pilot beacon transmissions, even in adverse SNR conditions such as radar transmission sidelobes. In comparison with other techniques, interferometry presents the advantage of tracking the radar antenna phase center, which is the information required in SAR processing, hence avoiding the need to compensate for satellite body lever arms and attitude-induced phase changes.

Solar radiation has an important effect on the interferometric phase measurements. Therefore, the system must be designed in order to minimize the impact of temperature drifts, in particular minimizing the length and solar exposure of radiofrequency cabling.

A compact interferometric baseline of 10–15 m was conceived as a validation prototype due to its convenience of operation and testing. The experimental system setup allowed acquiring continuous interferometric signals of a communications satellite along several weeks involving several cycles of orbital drift and station-keeping maneuvers. They were used to retrieve the trajectory of the satellite by means of a least-squares estimation technique, a dynamical model tailored for geosynchronous orbit, and a Runge–Kutta–Fehlberg 7(8) integrator. The estimated trajectory was used to compute the estimated observations. The good fit between the measured and the estimated data demonstrated that interferometric orbit observation is a valid technique for tracking satellites at GEO, even in the presence of station-keeping maneuvers. Furthermore, the retrieved trajectory of the satellite, represented in the ECEF coordinate system, presents the expected elliptical motion with a daily period, as well as a long-term cycle corresponding to the natural longitude drift towards the east and the subsequent station-keeping maneuver towards the west.

Since the interferometric observation system is able to work with weak satellite signals, it only requires to be in the line-of-sight of the target satellite. Therefore, a single interferometer is suitable to track spacecraft in any low-inclination geosynchronous orbit. However, high-inclination geosynchronous missions, such as the ones proposed by China, with a large “figure 8” shape nadir-point trajectory, would require extra interferometric receivers in order to keep track of the spacecraft along all latitudes.

Future work will provide observables obtained with longer interferometric baselines in order to assess the degree of precision the technique can achieve.