MS-Pansharpening Algorithm Based on Dual Constraint Guided Filtering
Abstract
1. Introduction
- (1)
- The Dual Constraint Guided Image Filtering (DCGIF) model, based on spatial region average gradient correlation and vector correlation formed by neighborhood elements. is proposed. On this basis, the DCGIF detail extraction scheme is proposed. On the one hand, the spatial detail information map extracted from the PAN is more adaptive under the guidance of MS. On the other hand, it has better integrity and accuracy under the constraints of element neighborhood correlation and average gradient correlation.
- (2)
- The MS spatial detail information injection model, based on band spectral correlation, is presented, which determines the information injection weight matrix of each band based on the spectral ratio between the original MS bands, ensuring the spectral correlation between the fused MS image bands.
- (3)
- A new scheme of MS-Pansharpening in NSST domain is proposed. First, a more effective source of spatial detail information is obtained from the NSST high frequency sub-bands of MS and PAN. Then, effective spatial detail injection information is extracted by weighted fusion, based on the region energy matrix, using the proposed DCGIF model. Finally, the spatial detail information is injected into each MS band according to the information injection model to complete the information fusion. A large number of simulation experiments show that the proposed algorithm can effectively improve the spatial resolution of the fused MS image, while maintaining its spectral characteristics, and achieve better fusion results than some conventional fusion algorithms.
2. Related Works
2.1. Guided Image Filter
2.2. NSST and Its Sub-Band Properties
3. Methodology
3.1. Construction of the Dual Constraint Guided Filtering Model
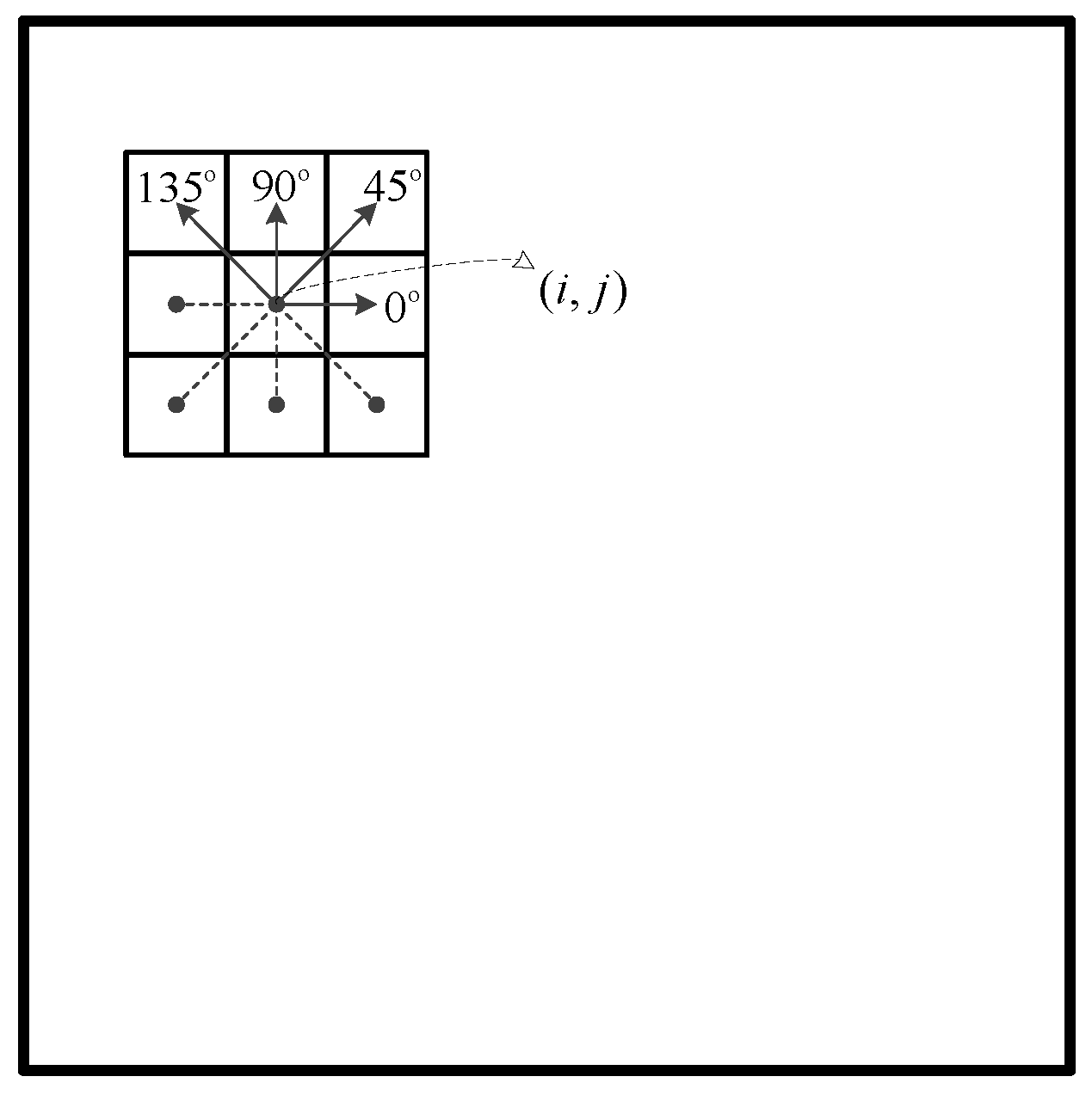
3.1.1. Neighborhood Elements Vector and Average Gradient Correlation Constraint
3.1.2. Region Edge Recognition Function Based on the Neighborhood Elements Vector Angle and the Average Gradient
3.1.3. Model Construction
3.2. MS-Pansharpening Algorithm Based on DCGIF in NSST Domain
3.2.1. Reconstruction of MS Intensity Component Guided by High Frequency Information of NSST from PAN
3.2.2. Extraction of Decision Texture Details for PAN Based on DCGIF Model
3.2.3. Detail Information Injection Model for MS Based on Spectral Correlation
3.2.4. The Process of Algorithm Implementation
| Algorithm 1 Procedures of the proposed approach. |
| Input: The registered PAN and MS RS images. |
|
|
|
|
|
|
|
|
| Output: the fused MS image. |
4. Experiment and Analysis
4.1. Data Set
4.2. Degraded Data Experiment
4.3. Real Data Experiment
4.4. Computation Complexity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chuvieco, E. Sensors and Remote Sensing Satellites; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Toth, C.; Jozkow, G. Remote sensing platforms and sensors: A survey. ISPRS J. Photogramm. Remote Sens. 2016, 115, 22–36. [Google Scholar] [CrossRef]
- Chuvieco, E. Fundamentals of Satellite Remote Sensing; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Siok, K.; Ewiak, I.; Jenerowicz, A. Multi-sensor fusion: A Simulation approach to pansharpening aerial and satellite images. Sensors 2020, 20, 7100. [Google Scholar] [CrossRef] [PubMed]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Remote Sensing Image Fusion; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Meng, X.; Xiong, Y.; Shao, F.; Shen, H.; Sun, W.; Yang, G.; Yuan, Q.; Fu, R.; Zhang, H. A large-scale benchmark data set for evaluating pansharpening performance: Overview and implementation. IEEE Geosci. Remote Sens. Mag. 2021, 9, 18–52. [Google Scholar] [CrossRef]
- Kaur, G.; Saini, K.S.; Singh, D.; Kaur, M. A comprehensive study on computational pansharpening techniques for remote sensing images. Arch. Comput. Methods Eng. 2021, 28, 4961–4978. [Google Scholar] [CrossRef]
- Carper, W.; Lillesand, T.; Kiefer, R. The use of intensity-hue-saturation transformations for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Remote Sens. 1990, 56, 459–467. [Google Scholar]
- Chavez, P.S.; Kwarteng, A.W. Extracting spectral contrast in Landsat Thematic Mapper image data using selective principal component analysis. Photogram. Eng. Remote Sess. 1989, 55, 339–348. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS + Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Tu, T.M.; Su, S.C.; Shyu, H.C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2001, 2, 177–186. [Google Scholar] [CrossRef]
- Rahmani, S.; Strait, M.; Merkurjev, D.; Moeller, M.; Wittman, T. An adaptive IHS pan-sharpening method. IEEE Geosci. Remote Sens. Lett. 2010, 7, 746–750. [Google Scholar] [CrossRef]
- Amolins, L.; Zhang, Y.; Dare, P. Wavelet based image fusion techniques-an troduction, review and comparison. ISPRS J. Photogramm. Remote Sens. 2007, 62, 249–263. [Google Scholar] [CrossRef]
- Li, H.; Manjunath, B.S.; Mitra, S.K. Multisensor image fusion using the wavelet transform. Graph. Models Image Process. 1995, 57, 235–245. [Google Scholar] [CrossRef]
- Zhou, J.; Civco, D.L.; Silander, J.A. A wavelet transform method to merge Landsat TM and SPOT panchromatic data. Int. J. Remote Sens. 1998, 19, 743–757. [Google Scholar] [CrossRef]
- Gonzalez-Audicana, M.; Otazu, X.; Fors, O.; Seco, A. Comparison between mallat’s and the “a trous” discrete wavelet transform based algorithms for the fusion of multispectral and panchromatic images. Int. J. Remote Sens. 2005, 26, 595–614. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Context-driven fusion of highspatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2300–2312. [Google Scholar] [CrossRef]
- Amro, I.; Mateos, J. Multispectral image pansharpening based on the contourlet transform. Inf. Opt. Photonics 2010, 206, 247–261. [Google Scholar]
- Amro, I.; Mateos, J. General shearlet pansharpening method using Bayesian inference. In Proceedings of the 2013 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA), Poznan, Poland, 26–28 September 2013; pp. 231–235. [Google Scholar]
- Upla, P.K.; Gajjar, P.P.; Joshi, M.V. Pan-sharpening based on non-subsampled contourlet transform detail extraction. In Proceedings of the 2013 Fourth National Conference on Computer Vision, Pattern Recognition, Image Processing and Graphics (NCVPRIPG), Jodhpur, India, 18–21 December 2013; pp. 1–4. [Google Scholar]
- Wang, X.H.; Bai, S.F.; Li, Z.; Song, R.X.; Tao, J.Z. The PAN and MS image pansharpening algorithm based on adaptive neural network and sparse representation in the NSST domain. IEEE Access 2019, 7, 52508–52521. [Google Scholar] [CrossRef]
- Zhang, L.; Shen, H.; Gong, W.; Zhang, H. Adjustable model-based fusion method for multispectral and panchromaticimages. IEEE Trans. Syst. Man Cybern. 2012, 42, 1693–1704. [Google Scholar] [CrossRef]
- Shen, H.; Meng, X.; Zhang, L. An integrated framework forthe spatio-temporal-spectral fusion of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7135–7148. [Google Scholar] [CrossRef]
- Yang, J.F.; Fu, X.Y.; Hu, Y.W.; Huang, Y.; Ding, X.H.; Paisley, J. PanNet: A deep network architecture for Pan-Sharpening. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1753–1761. [Google Scholar]
- Huang, W.; Xiao, L.; Wei, Z.; Liu, H.; Tang, S. A new pansharpeningmethod with deep neural networks. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1037–1041. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpeningby convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Liu, J.M.; Feng, Y.Q.; Zhou, C.S.; Zhang, C.X. PWNet: An adaptive weight network for the fusion of panchromatic and multispectral Images. Remote Sens. 2020, 12, 2804. [Google Scholar] [CrossRef]
- Starck, J.L.; Murtagh, F.; Fadili, J.M. Sparse Image and Signal Processing: Wavelets and Related Geometric Multiscale Analysis; Cambridge University Press: New York, NY, USA, 2015. [Google Scholar]
- Lang, M.; Guo, H.; Odegard, J.E.; Burrus, C.S.; Wells, R.O. Noise reduction using an undecimated discrete wavelet transform. IEEE Signal Process. Lett. 2016, 3, 10–12. [Google Scholar] [CrossRef]
- Cunha, D.; Arthur, L.; Zhou, J.; Do, M.N. The nonsubsampled contourlet transform: Theory, design, and applications. IEEE Trans. Image Process. 2006, 15, 3089–3101. [Google Scholar] [CrossRef] [PubMed]
- Asley, G.E.; Labate, D.; Lim, W.Q. Sparse directional image representations using the discrete shearlet transform. Appl. Comput. Harmon. Anal. 2008, 25, 25–46. [Google Scholar] [CrossRef]
- Yang, Y.; Dai, M.; Zhou, L.Y. Fusion of infrared and visible images based on NSUDCT. Infrared Laser Eng. 2012, 43, 961–966. [Google Scholar]
- Qu, Z.; Xing, Y.Q.; Song, Y.F. An image enhancement method based on non-subsampled shearlet transform and directional information measurement. Information 2018, 9, 308. [Google Scholar] [CrossRef]
- Li, J.Y.; Zhang, C.Z. Blind watermarking scheme based on schur decomposition and non-subsampled contourlet transform. Multimed. Tools Appl. 2020, 79, 30007–30021. [Google Scholar] [CrossRef]
- Kong, W.W.; Miao, Q.G.; Lei, Y. Multimodal sensor medical image fusion based on local difference in non-subsampled domain. IEEE Trans. Instrum. Meas. 2019, 68, 938–951. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Softw. Eng. 2013, 35, 1397–1409. [Google Scholar] [CrossRef]
- Guo, L.; Chen, L.; Chen, C.P.; Zhou, J. Integrating guided filter into fuzzy clustering for noisy image segmentation. Digit. Signal Process. 2018, 83, 235–248. [Google Scholar] [CrossRef]
- Liu, S.; Hu, Q.; Tong, X.; Xia, J.; Du, Q.; Samat, A.; Ma, X. A multi-scale superpixel-guided filter feature extraction and selection approach for classification of very-high-resolution remotely sensed imagery. Remote Sens. 2020, 12, 862. [Google Scholar] [CrossRef]
- Ch, M.M.I.; Riaz, M.M.; Iltaf, N.; Ghafoor, A.; Ali, S.S. A multifocus image fusion using highlevel DWT components and guided filter. Multimed. Tools Appl. 2020, 79, 12817–12828. [Google Scholar] [CrossRef]
- Li, Z.G.; Zheng, J.H.; Zhu, Z.J.; Yao, W.; Wu, S.; Wu, S. Weighted guided image filtering. IEEE Trans. Image Process. 2015, 24, 120–129. [Google Scholar] [PubMed]
- Guo, K.; Labate, D.; Lim, W.Q.; Labate, D.; Weiss, G.; Wilson, E. Wavelets with composite dilations and their MRA properties. Appl. Comput. Harmon. Anal. 2006, 20, 202–236. [Google Scholar] [CrossRef]
- Kutyniok, G.; Labate, D. Shearlets: Multiscale Analysis for Multivariate Data; Sprinter Science + Business Media, LLC.: New York, NY, USA, 2012. [Google Scholar]
- Vivone, G.; Restaino, R.; Dalla Mura, M.; Licciardi, G.; Chanussot, J. Contrast and error-based fusion schemes for multispectral image pansharpening. IEEE Geosci. Remote Sens. Lett. 2014, 11, 930–934. [Google Scholar] [CrossRef]
- Guo, K.; Kutyniok, G.; Labate, D. Sparse multidimensional representations using anisotropic dilation and shear operators. In Proceedings of the International Conference on the Interaction between Wavelets & Splines; Nashboro Press: Brentwood, TN, USA, 2006; pp. 189–201. [Google Scholar]
- Palubinskas, G. Fast, simple and good pan-sharpening method. J. Appl. Remote Sens. 2013, 7, 1–12. [Google Scholar] [CrossRef]
- Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L.M. Comparison of pansharpening algorithms: Outcome of the 2006 GRS-S data-fusion contest. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3012–3021. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Mura, M.D.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geoence Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z. Simultaneous image fusion and denoising with adaptive sparse representation. Image Process. Iet. 2019, 9, 347–357. [Google Scholar] [CrossRef]
- Li, H.; Wu, X.J.; Kittler, J. Infrared and visible image fusion using a deep learning framework. In Proceedings of the 2018 24rd International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 2705–2710. [Google Scholar]
- Wald, L. Quality of high resolution synthesised images: Is there a simple criterion? In Proceedings of the third conference Fusion of Earth data: Merging point measurements, raster maps and remotely sensed images, Nice, France, 26–28 January 2000; SEE/URISCA; pp. 99–103. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J. Remote sensing image fusion with deep convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1656–1669. [Google Scholar] [CrossRef]
- Luciano, A.; Bruno, A.; Stefano, B.; Andrea, G.; Filippo, N.; Massimo, S. Multispectral and panchromatic data fusion assessment without reference. ASPRS J. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar]
















| San Clement Area Image | Sydney Area Image | San Francisco Area Image | ||||||
|---|---|---|---|---|---|---|---|---|
| MS | PAN | MS | PAN | MS | PAN | |||
| First-scale | Sub-band 1 | 32,196 | 32,217 | 32,286 | 32,721 | 32,938 | 32,570 | |
| 7804 | 7783 | 7714 | 7279 | 7062 | 7430 | |||
| 80.49 | 80.54 | 80.72 | 81.80 | 82.35 | 81.43 | |||
| Sub-band 2 | 32,596 | 32,986 | 33,394 | 33,643 | 33,987 | 33,846 | ||
| 7404 | 7014 | 6606 | 6357 | 6013 | 6154 | |||
| 81.49 | 82.47 | 83.49 | 84.11 | 84.97 | 84.62 | |||
| Second-scale | Sub-band 1 | 34,338 | 34,551 | 34,730 | 34,790 | 35,177 | 34,627 | |
| 5662 | 5449 | 5270 | 5210 | 4823 | 5373 | |||
| 85.85 | 86.38 | 86.83 | 86.98 | 87.94 | 86.57 | |||
| Sub-band 2 | 32,509 | 32,630 | 31,260 | 30,672 | 33,262 | 31,877 | ||
| 7491 | 7370 | 8740 | 9328 | 6738 | 8123 | |||
| 81.27 | 81.58 | 78.15 | 76.68 | 83.15 | 79.69 | |||
| Sub-band 3 | 34,263 | 34,232 | 35,190 | 35,462 | 35,988 | 35,091 | ||
| 5737 | 5768 | 4810 | 4538 | 4012 | 4909 | |||
| 85.66 | 85.58 | 87.98 | 88.66 | 89.97 | 87.73 | |||
| Sub-band 4 | 31,486 | 30,936 | 30,715 | 30,660 | 31,708 | 30,171 | ||
| 8514 | 9064 | 9285 | 9340 | 8292 | 9829 | |||
| 78.72 | 77.34 | 76.79 | 76.65 | 79.27 | 75.43 | |||
| Evaluation Index | ||||
|---|---|---|---|---|
| RMSE | 23.8240 | 30.5323 | 34.8185 | 37.8988 |
| SAM | 0.3917 | 0.5453 | 0.6952 | 0.8574 |
| Correlation Coefficient | MS-Test-1 | MS-Test-2 | MS-Test-3 | MS-Test-4 | MS-Test-5 | MS-Test-6 | MS-Test-7 | MS-Test-8 |
|---|---|---|---|---|---|---|---|---|
| 0.9686 | 0.9891 | 0.9738 | 0.9853 | 0.9235 | 0.9611 | 0.9712 | 0.9792 | |
| 0.9681 | 0.9930 | 0.9850 | 0.9894 | 0.9626 | 0.9868 | 0.9673 | 0.9880 |
| Data Set | Evaluation Index | IHS | GIF | ATWT | AWLP | ASR | Deep Learning | NSST + SR + PCNN | NSST + DCGIF |
|---|---|---|---|---|---|---|---|---|---|
| Test-RS-1 | RMSE | 46.1822 | 36.9231 | 21.8892 | 22.0637 | 31.0385 | 24.1516 | 19.3740 | 16.6651 |
| ERGAS | 20.8551 | 16.6699 | 9.8857 | 9.9650 | 14.0130 | 10.9012 | 8.7466 | 7.5239 | |
| CC | 0.8357 | 0.9408 | 0.9617 | 0.9612 | 0.9408 | 0.9617 | 0.9694 | 0.9776 | |
| SSIM | 0.5867 | 0.5276 | 0.8008 | 0.8018 | 0.6706 | 0.7981 | 0.7950 | 0.8751 | |
| SAM | 4.3361 | 1.0508 | 2.7560 | 4.3361 | 1.0067 | 1.4456 | 1.3041 | 0.3463 | |
| RASE | 41.7080 | 33.3459 | 19.7685 | 19.9261 | 28.0314 | 21.8117 | 17.4970 | 15.0506 | |
| Test-RS-2 | RMSE | 42.7084 | 44.1567 | 15.7518 | 15.7411 | 28.7240 | 24.4196 | 19.5112 | 15.6839 |
| ERGAS | 32.2701 | 33.1070 | 11.9120 | 11.8041 | 21.4947 | 18.3585 | 14.7141 | 11.8500 | |
| CC | 0.8919 | 0.7885 | 0.9712 | 0.9725 | 0.9272 | 0.9522 | 0.9504 | 0.9714 | |
| SSIM | 0.7414 | 0.7176 | 0.9358 | 0.9381 | 0.8171 | 0.8834 | 0.8905 | 0.9394 | |
| SAM | 5.0471 | 3.5388 | 5.9898 | 3.5308 | 3.3412 | 3.6489 | 3.2974 | 0.3748 | |
| RASE | 64.1366 | 66.3117 | 23.6551 | 23.6389 | 43.1359 | 36.6171 | 29.3007 | 23.5530 | |
| Test-RS-3 | RMSE | 41.2275 | 44.7460 | 18.4704 | 18.6100 | 29.2235 | 21.4150 | 20.3299 | 17.5247 |
| ERGAS | 18.5383 | 20.1201 | 8.2854 | 8.3358 | 13.1382 | 9.6341 | 9.1409 | 7.8784 | |
| CC | 0.6902 | 0.8138 | 0.9431 | 0.9423 | 0.8389 | 0.9121 | 0.9267 | 0.9467 | |
| SSIM | 0.7186 | 0.5209 | 0.8623 | 0.8620 | 0.7659 | 0.8807 | 0.8285 | 0.8792 | |
| SAM | 3.2074 | 1.4370 | 2.5378 | 2.2618 | 2.0981 | 2.4695 | 2.0469 | 0.3035 | |
| RASE | 37.0416 | 40.2028 | 16.5950 | 16.7205 | 26.2563 | 19.2407 | 18.2657 | 15.7453 | |
| Test-RS-4 | RMSE | 37.2295 | 38.0868 | 18.9726 | 18.9917 | 27.3476 | 21.6457 | 19.0765 | 16.8401 |
| ERGAS | 17.6893 | 18.7514 | 9.8712 | 9.8679 | 12.7405 | 10.2940 | 9.7367 | 8.7608 | |
| CC | 0.9296 | 0.8798 | 0.9695 | 0.9695 | 0.9499 | 0.9682 | 0.9657 | 0.9745 | |
| SSIM | 0.8131 | 0.7847 | 0.9329 | 0.9332 | 0.8654 | 0.9277 | 0.9202 | 0.9515 | |
| SAM | 4.6999 | 3.5359 | 5.9898 | 4.9606 | 3.3908 | 5.3534 | 5.0577 | 0.3096 | |
| RASE | 35.2712 | 37.5283 | 19.7080 | 19.7073 | 25.5687 | 20.4844 | 19.4514 | 17.5329 |
| Evaluation Index | IHS | GIF | ATWT | AWLP | ASR | Deep Learning | NSST + SR + PCNN | NSST + DCGIF |
|---|---|---|---|---|---|---|---|---|
| 0.7561 | 0.2979 | 0.8765 | 0.8778 | 0.7765 | 0.8384 | 0.8541 | 0.8780 | |
| 0.0119 | 0.0073 | 0.0105 | 0.0092 | 0.0043 | 0.0037 | 0.0104 | 0.0109 | |
| 0.2349 | 0.6999 | 0.1142 | 0.1140 | 0.2202 | 0.1584 | 0.1370 | 0.1123 |
| Data Set | Time(s) | |||||||
|---|---|---|---|---|---|---|---|---|
| IHS | GIF | ATWT | AWLP | ASR | Deep Learning | NSST + SR + PCNN | NSST + DCGIF | |
| Test-RS-1 | 1.50 | 2.45 | 0.61 | 1.00 | 202.38 | 4.06 | 110.07 | 44.74 |
| Test-RS-2 | 1.42 | 3.04 | 0.95 | 0.96 | 207.59 | 3.69 | 122.39 | 46.13 |
| Test-RS-3 | 1.55 | 2.34 | 0.59 | 0.60 | 218.66 | 4.13 | 109.54 | 45.85 |
| Test-RS-4 | 1.60 | 2.27 | 0.58 | 0.64 | 222.32 | 3.94 | 124.96 | 51.44 |
| Test-RS-5 | 1.55 | 2.29 | 0.60 | 0.62 | 225.18 | 3.92 | 137.39 | 43.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Mu, Z.; Bai, S.; Feng, Y.; Song, R. MS-Pansharpening Algorithm Based on Dual Constraint Guided Filtering. Remote Sens. 2022, 14, 4867. https://doi.org/10.3390/rs14194867
Wang X, Mu Z, Bai S, Feng Y, Song R. MS-Pansharpening Algorithm Based on Dual Constraint Guided Filtering. Remote Sensing. 2022; 14(19):4867. https://doi.org/10.3390/rs14194867
Chicago/Turabian StyleWang, Xianghai, Zhenhua Mu, Shifu Bai, Yining Feng, and Ruoxi Song. 2022. "MS-Pansharpening Algorithm Based on Dual Constraint Guided Filtering" Remote Sensing 14, no. 19: 4867. https://doi.org/10.3390/rs14194867
APA StyleWang, X., Mu, Z., Bai, S., Feng, Y., & Song, R. (2022). MS-Pansharpening Algorithm Based on Dual Constraint Guided Filtering. Remote Sensing, 14(19), 4867. https://doi.org/10.3390/rs14194867






