A Methodology for National Scale Coastal Landcover Mapping in New Zealand
Abstract
1. Introduction
1.1. Shoreline Detection
1.2. Pixel-Based Techniques
2. Materials and Methods
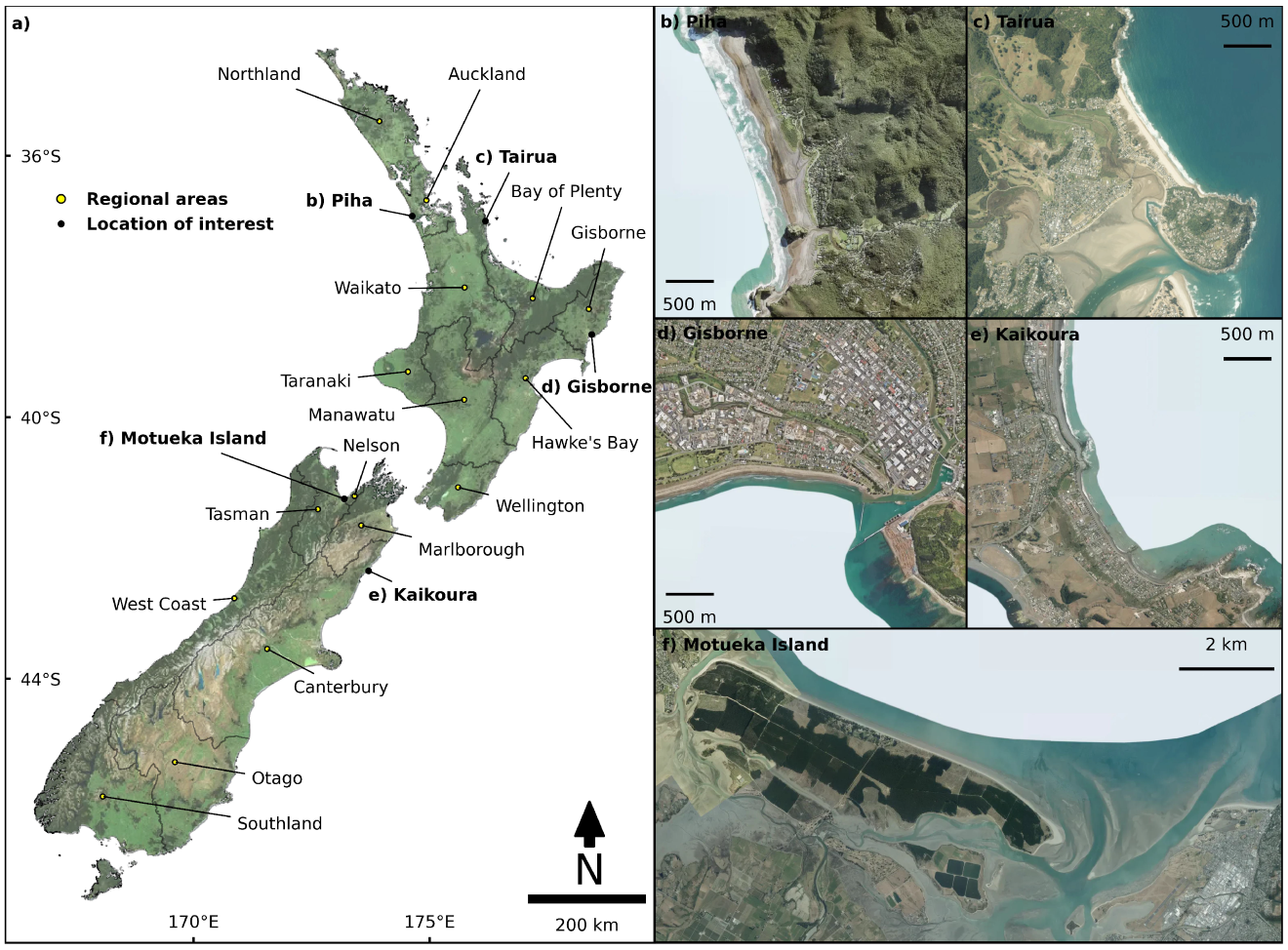
2.1. New Zealand Coastal Setting
2.1.1. Geological and Sedimentary Components
2.1.2. Climatic Processes
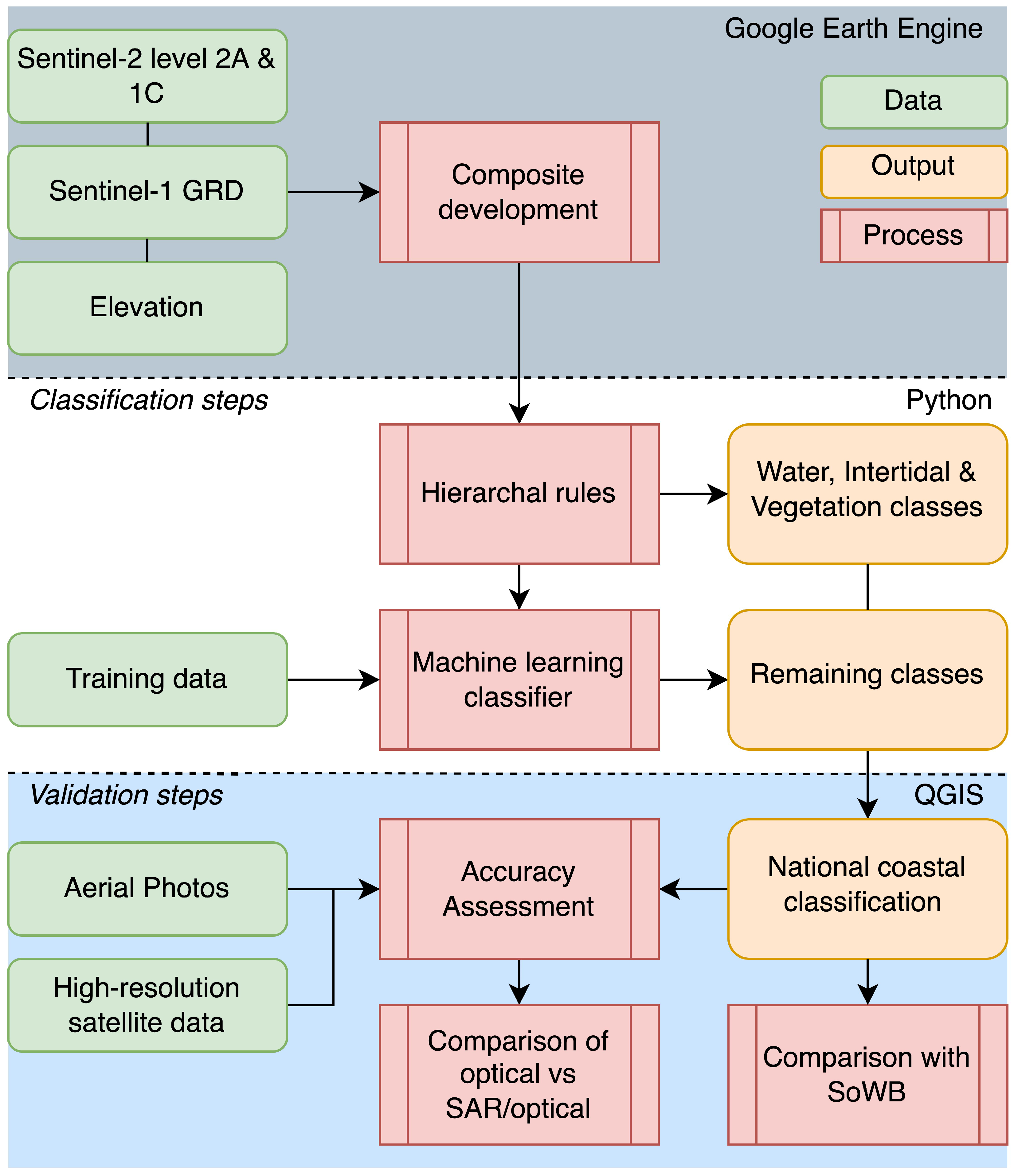
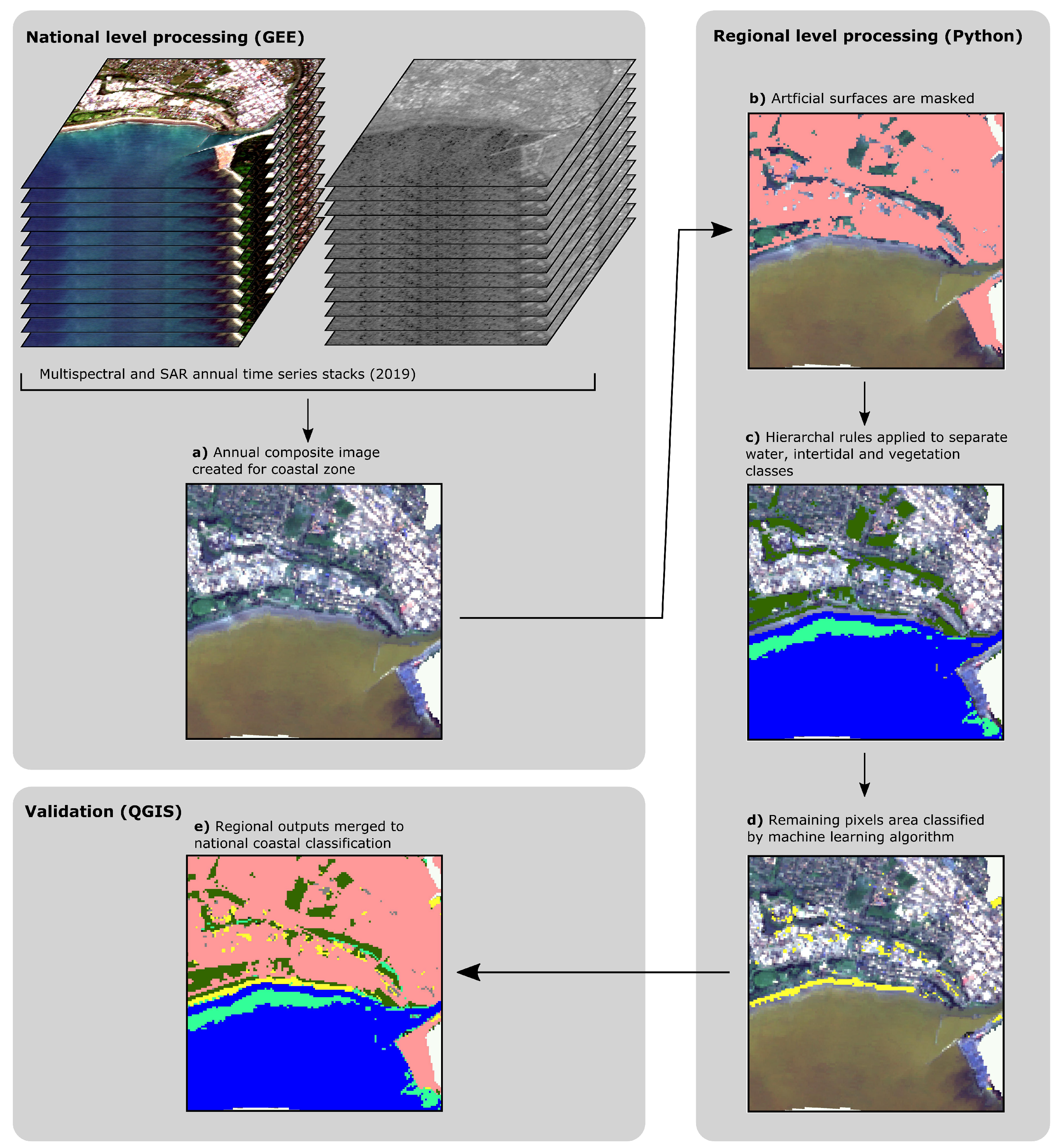
2.2. Image Composite Development
2.2.1. Multispectral Composite
2.2.2. SAR Composite
2.3. Hierarchal Rule-Based Classification
2.4. Developing Coastal Specific Training Data
2.5. Machine Learning Classification
2.6. Validation
2.6.1. Accuracy Assessment
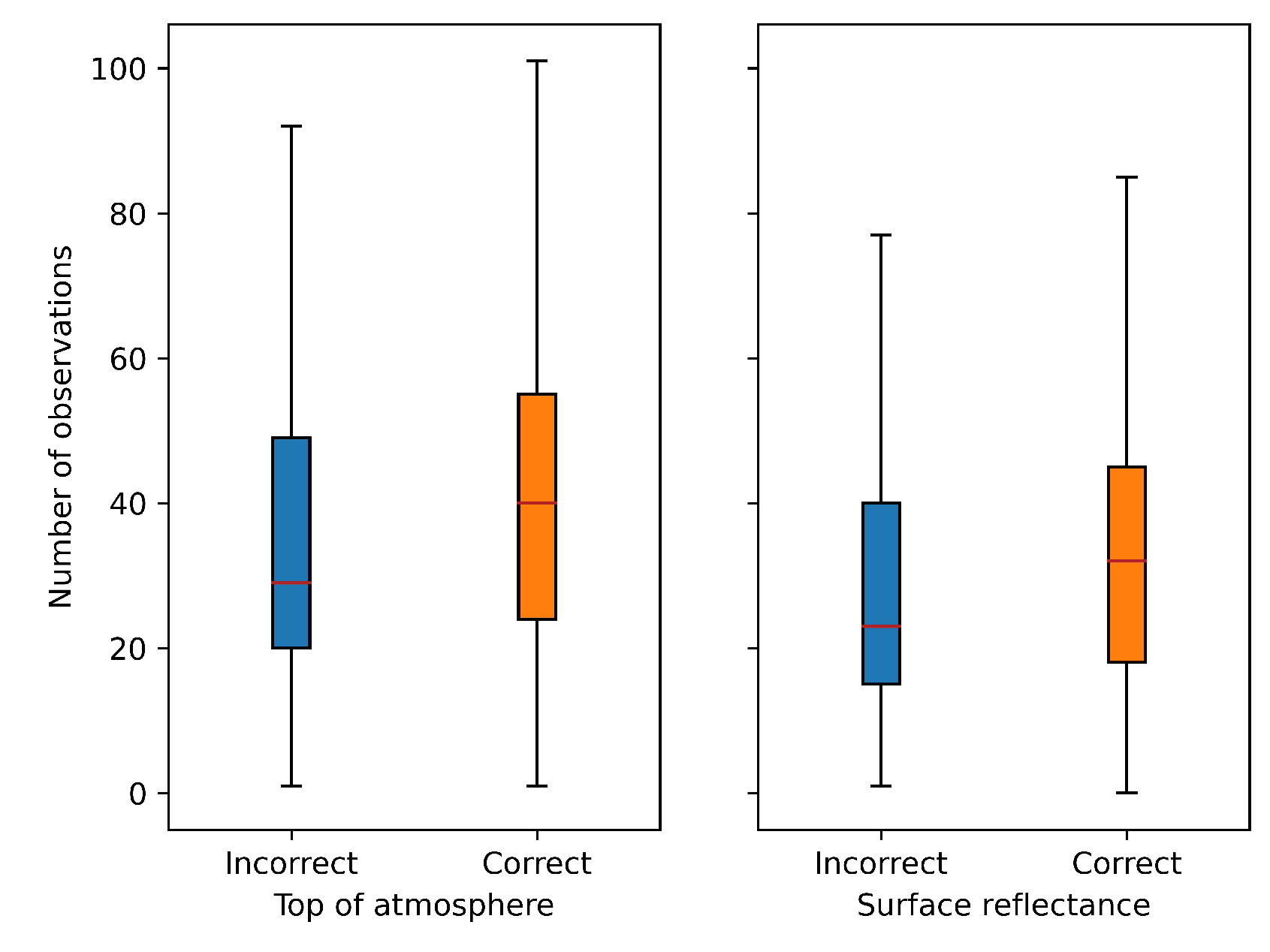
2.6.2. Impact of Observation Frequency
2.6.3. Comparison with Luijendijk et al. (2018) Classification
3. Results
3.1. 2019 SAR and Multispectral Classification
3.2. SAR Contribution
3.3. Frequency of Observations
4. Discussion
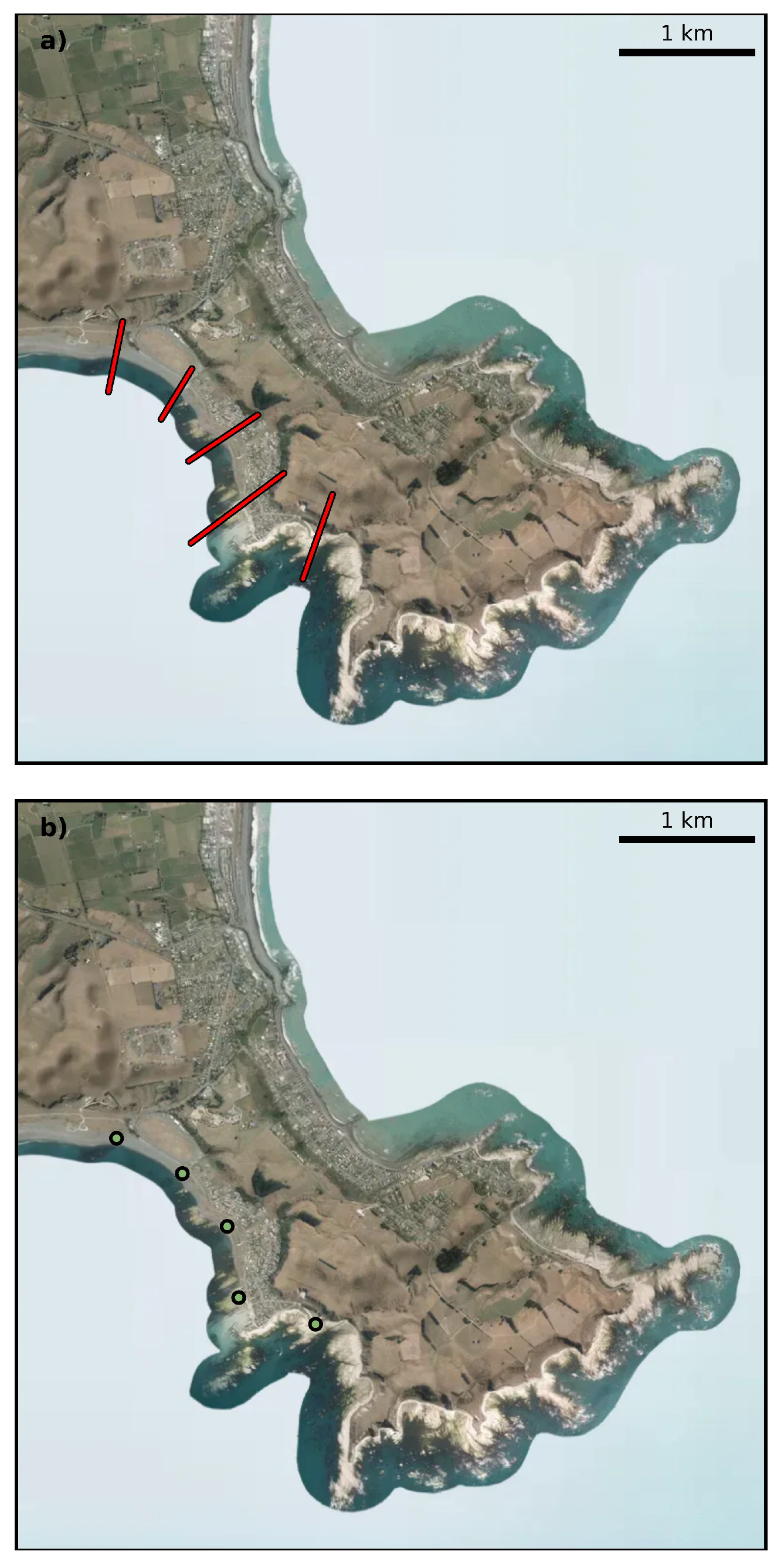
4.1. Comparison with Other Analyses of Sandy Coast in New Zealand
4.2. Impact of Observation Frequency
4.3. The Importance of SAR for Coastal Landcover Classification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AWEI | Automated Water Extraction Index |
| GEE | Google Earth Engine |
| GRD | Ground Range Detected |
| Significant wave height | |
| IW | Instantaneous waterline |
| LCDB | Landcover Database |
| LiDAR | Light detecting and ranging |
| MNDWI | Modified Normalised Difference Water Index |
| NDVI | Normalised Difference Vegetation Index |
| NDWI | Normalised Difference Water Index |
| NeCTAR | Australian National eResearch Collaboration Tools and Resources |
| RMSE | Root mean square error |
| RSGISLIB | Remote Sensing and GIS libraries |
| S1 | Sentinel-1 |
| S2 | Sentinel-2 |
| SAR | Synthetic Aperture Radar |
| SR | Surface reflectance |
| TOA | Top of Atmosphere |
References
- Revell, D.L.; Battalio, R.; Spear, B.; Ruggiero, P.; Vandever, J. A methodology for predicting future coastal hazards due to sea-level rise on the California Coast. Clim. Chang. 2011, 109, 251–276. [Google Scholar] [CrossRef]
- Lawrence, J.; Sullivan, F.; Lash, A.; Ide, G.; Cameron, C.; McGlinchey, L. Adapting to changing climate risk by local government in New Zealand: Institutional practice barriers and enablers. Local Environ. 2015, 20, 298–320. [Google Scholar] [CrossRef]
- Purkis, S.J.; Klemas, V.V. Remote Sensing and Global Environmental Change; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Boak, E.H.; Turner, I.L. Shoreline definition and detection: A review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef]
- Toure, S.; Diop, O.; Kpalma, K.; Maiga, A.S. Shoreline detection using optical remote sensing: A review. ISPRS Int. J. Geo-Inf. 2019, 8, 75. [Google Scholar] [CrossRef]
- Ford, M. Shoreline changes interpreted from multi-temporal aerial photographs and high resolution satellite images: Wotje Atoll, Marshall Islands. Remote Sens. Environ. 2013, 135, 130–140. [Google Scholar] [CrossRef]
- Blue, B.; Kench, P.S. Multi-decadal shoreline change and beach connectivity in a high-energy sand system. N. Z. J. Mar. Freshw. Res. 2017, 51, 406–426. [Google Scholar] [CrossRef]
- Splinter, K.; Harley, M.; Turner, I. Remote Sensing Is Changing Our View of the Coast: Insights from 40 Years of Monitoring at Narrabeen-Collaroy, Australia. Remote Sens. 2018, 10, 1744. [Google Scholar] [CrossRef]
- Harley, M.D.; Turner, I.L.; Kinsela, M.A.; Middleton, J.H.; Mumford, P.J.; Splinter, K.D.; Phillips, M.S.; Simmons, J.A.; Hanslow, D.J.; Short, A.D. Extreme coastal erosion enhanced by anomalous extratropical storm wave direction. Sci. Rep. 2017, 7, 6033. [Google Scholar] [CrossRef]
- Castelle, B.; Guillot, B.; Marieu, V.; Chaumillon, E.; Hanquiez, V.; Bujan, S.; Poppeschi, C. Spatial and temporal patterns of shoreline change of a 280-km high-energy disrupted sandy coast from 1950 to 2014: SW France. Estuar. Coast. Shelf Sci. 2018, 200, 212–223. [Google Scholar] [CrossRef]
- Bryan, K.R.; Kench, P.S.; Hart, D.E. Multi-decadal coastal change in New Zealand: Evidence, mechanisms and implications. N. Z. Geogr. 2008, 64, 117–128. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Vos, K.; Harley, M.D.; Splinter, K.D.; Simmons, J.A.; Turner, I.L. Sub-annual to multi-decadal shoreline variability from publicly available satellite imagery. Coast. Eng. 2019, 150, 160–174. [Google Scholar] [CrossRef]
- Pardo-Pascual, J.E.; Almonacid-Caballer, J.; Ruiz, L.A.; Palomar-Vázquez, J. Automatic extraction of shorelines from Landsat TM and ETM+ multi-temporal images with subpixel precision. Remote Sens. Environ. 2012, 123, 1–11. [Google Scholar] [CrossRef]
- Xu, N. Detecting Coastline Change with All Available Landsat Data over 1986–2015: A Case Study for the State of Texas, USA. Atmosphere 2018, 9, 107. [Google Scholar] [CrossRef]
- Liu, Q.; Trinder, J.; Turner, I.L. Automatic super-resolution shoreline change monitoring using Landsat archival data: A case study at Narrabeen–Collaroy Beach, Australia. J. Appl. Remote Sens. 2017, 11, 16036. [Google Scholar] [CrossRef]
- Mentaschi, L.; Vousdoukas, M.I.; Pekel, J.F.; Voukouvalas, E.; Feyen, L. Global long-term observations of coastal erosion and accretion. Sci. Rep. 2018, 8, 12876. [Google Scholar] [CrossRef]
- Almonacid-Caballer, J.; Sánchez-García, E.; Pardo-Pascual, J.E.; Balaguer-Beser, A.A.; Palomar-Vázquez, J. Evaluation of annual mean shoreline position deduced from Landsat imagery as a mid-term coastal evolution indicator. Mar. Geol. 2016, 372, 79–88. [Google Scholar] [CrossRef]
- Hagenaars, G.; de Vries, S.; Luijendijk, A.P.; de Boer, W.P.; Reniers, A.J.H.M. On the accuracy of automated shoreline detection derived from satellite imagery: A case study of the sand motor mega-scale nourishment. Coast. Eng. 2018, 133, 113–125. [Google Scholar] [CrossRef]
- Mcallister, E.; Payo, A.; Novellino, A.; Dolphin, T.; Medina-Lopez, E. Multispectral satellite imagery and machine learning for the extraction of shoreline indicators. Coast. Eng. 2022, 174, 104102. [Google Scholar] [CrossRef]
- U.S. Geological Survey. Landsat Collection 1 Level 1 Product Definition; Technical Report; USGS: Reston, VA, USA, 2019. Available online: https://www.usgs.gov/media/files/landsat-collection-1-level-1-product-definition (accessed on 27 April 2022).
- Liu, Y.; Huang, H.; Qiu, Z.; Fan, J. Detecting coastline change from satellite images based on beach slope estimation in a tidal flat. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 165–176. [Google Scholar] [CrossRef]
- Castelle, B.; Masselink, G.; Scott, T.; Stokes, C.; Konstantinou, A.; Marieu, V.; Bujan, S. Satellite-derived shoreline detection at a high-energy meso-macrotidal beach. Geomorphology 2021, 383, 107707. [Google Scholar] [CrossRef]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The State of the World’s Beaches. Sci. Rep. 2018, 8, 6641. [Google Scholar] [CrossRef] [PubMed]
- Bishop-Taylor, R.; Nanson, R.; Sagar, S.; Lymburner, L. Mapping Australia’s dynamic coastline at mean sea level using three decades of Landsat imagery. Remote Sens. Environ. 2021, 267, 112734. [Google Scholar] [CrossRef]
- Zhu, Z. Change detection using landsat time series: A review of frequencies, preprocessing, algorithms, and applications. ISPRS J. Photogramm. Remote Sens. 2017, 130, 370–384. [Google Scholar] [CrossRef]
- Bunting, P.; Rosenqvist, A.; Lucas, R.M.; Rebelo, L.M.; Hilarides, L.; Thomas, N.; Hardy, A.; Itoh, T.; Shimada, M.; Finlayson, C.M. The global mangrove watch—A new 2010 global baseline of mangrove extent. Remote Sens. 2018, 10, 1669. [Google Scholar] [CrossRef]
- Donchyts, G.; Baart, F.; Winsemius, H.; Gorelick, N.; Kwadijk, J.; Van De Giesen, N. Earth’s surface water change over the past 30 years. Nat. Clim. Chang. 2016, 6, 810–813. [Google Scholar] [CrossRef]
- Hansen, M.C.; Stehman, S.V.; Potapov, P.V. Quantification of global gross forest cover loss. Proc. Natl. Acad. Sci. USA 2010, 107, 8650–8655. [Google Scholar] [CrossRef]
- Fitton, J.M.; Rennie, A.F.; Hansom, J.D.; Muir, F.M. Remotely sensed mapping of the intertidal zone: A Sentinel-2 and Google Earth Engine methodology. Remote Sens. Appl. Soc. Environ. 2021, 22, 100499. [Google Scholar] [CrossRef]
- Bernier, J.C.; Miselis, J.L.; Plant, N.G.; Zambrano Bigiarini, F.; Lu, B.; Smith, K.E.L.; Manuel Álvarez-Martínez, J.; Filipponi, F.; Niculescu, S.; Xia, J.; et al. Satellite-Derived Barrier Response and Recovery Following Natural and Anthropogenic Perturbations, Northern Chandeleur Islands, Louisiana. Remote Sens. 2021, 13, 3779. [Google Scholar] [CrossRef]
- Zinnert, J.C.; Via, S.M.; Nettleton, B.P.; Tuley, P.A.; Moore, L.J.; Stallins, J.A. Connectivity in coastal systems: Barrier island vegetation influences upland migration in a changing climate. Glob. Chang. Biol. 2019, 25, 2419–2430. [Google Scholar] [CrossRef]
- Latella, M.; Luijendijk, A.; Moreno-Rodenas, A.M.; Camporeale, C. Satellite image processing for the coarse-scale investigation of sandy coastal areas. Remote Sens. 2021, 13, 4613. [Google Scholar] [CrossRef]
- Kench, P.S.; Bryan, K.R.; Hart, D.E.; Kennedy, D.M.; Hilton, M.J. A commentary on coastal research in New Zealand universities. N. Z. Geogr. 2008, 64, 93–104. [Google Scholar] [CrossRef]
- Nicol, A.; Seebeck, H.; Wallace, L. Quaternary Tectonics of New Zealand. In Landscape and Quaternary Environmental Change in New Zealand; Atlantis Press: Amsterdam, The Netherlands, 2017; pp. 1–34. [Google Scholar] [CrossRef]
- Rouse, H.; Nichol, S.; Goff, J. Introduction to the New Zealand coast. In The New Zealand Coast: Te Tai o Aoteroa, 1st ed.; Goff, J.R., Nichol, S.L., Rouse, H.L., Eds.; Dunmore Press: Palmerston North, New Zealand, 2003; pp. 9–25. [Google Scholar]
- Komar, P.D. Shoreline evolution and management of Hawke’s Bay, New Zealand: Tectonics, coastal processes, and human impacts. J. Coast. Res. 2010, 26, 143–156. [Google Scholar] [CrossRef]
- Clark, K.J.; Nissen, E.K.; Howarth, J.D.; Hamling, I.J.; Mountjoy, J.J.; Ries, W.F.; Jones, K.; Goldstien, S.; Cochran, U.A.; Villamor, P.; et al. Highly variable coastal deformation in the 2016 MW7.8 Kaikōura earthquake reflects rupture complexity along a transpressional plate boundary. Earth Planet. Sci. Lett. 2017, 474, 334–344. [Google Scholar] [CrossRef]
- Hamill, P.F.; Ballance, P.F. Heavy mineral rich beach sands of the waitakere coast, Auckland, New Zealand. N. Z. J. Geol. Geophys. 1985, 28, 503–511. [Google Scholar] [CrossRef]
- Carter, L.; Manighetti, B.; Elliot, M.; Trustrum, N.; Gomez, B. Source, sea level and circulation effects on the sediment flux to the deep ocean over the past 15 ka off eastern New Zealand. Glob. Planet. Chang. 2002, 33, 339–355. [Google Scholar] [CrossRef]
- Schofield, J.C. Coastal sands of Northland and Auckland. N. Z. J. Geol. Geophys. 1970, 13, 767–824. [Google Scholar] [CrossRef]
- Albuquerque, J.; Antolínez, J.A.A.; Gorman, R.M.; Méndez, F.J.; Coco, G. Seas and swells throughout New Zealand: A new partitioned hindcast. Ocean Model. 2021, 168, 101897. [Google Scholar] [CrossRef]
- Rueda, A.; Cagigal, L.; Antolínez, J.A.; Albuquerque, J.C.; Castanedo, S.; Coco, G.; Méndez, F.J. Marine climate variability based on weather patterns for a complicated island setting: The New Zealand case. Int. J. Climatol. 2019, 39, 1777–1786. [Google Scholar] [CrossRef]
- Coggins, J.H.; Parsons, S.; Schiel, D. An assessment of the ocean wave climate of New Zealand as represented in Kidson’s synoptic types. Int. J. Climatol. 2016, 36, 2481–2496. [Google Scholar] [CrossRef]
- Lange, W.D.; Bell, R.; Gorman, R.; Reid, S. Physical oceanography of New Zealand waters. In The New Zealand Coast: Te Tai o Aoteroa, 1st ed.; Goff, J., Nichol, S., Rouse, H., Eds.; Dunmore Press with Whitireia Publishing and Daphne Brasell Associates: Palmerston North, New Zealand, 2003; pp. 59–78. [Google Scholar]
- Brander, R.W.; Osborne, P.D.; Parnell, K. High-energy beach and nearshore processes. In The New Zealand Coast: Te Tai o Aoteroa, 1st ed.; Goff, J., Nichol, S., Rouse, H., Eds.; Dunmore Press: Palmerston North, New Zealand, 2003; pp. 119–142. [Google Scholar]
- Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Müller-Wilm, U.; Gascon, F. Sen2Cor for Sentinel-2. In Image and Signal Processing for Remote Sensing XXIII; SPIE: Warsaw, Poland, 2017; Volume 10427, pp. 37–48. [Google Scholar] [CrossRef]
- Filipponi, F. Sentinel-1 GRD Preprocessing Workflow. Proceedings 2019, 18, 11. [Google Scholar] [CrossRef]
- [dataset] Land Information New Zealand. New Zealand Coastline-Mean High Water. 2021. Available online: https://data.linz.govt.nz/layer/105085-nz-coastline-mean-high-water/ (accessed on 1 October 2021).
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Hisabayashi, M.; Rogan, J.; Elmes, A. Quantifying shoreline change in Funafuti Atoll, Tuvalu using a time series of Quickbird, Worldview and Landsat data. GIScience Remote Sens. 2017, 55, 307–330. [Google Scholar] [CrossRef]
- Holdaway, A.; Ford, M.; Owen, S. Global-scale changes in the area of atoll islands during the 21st century. Anthropocene 2021, 33. [Google Scholar] [CrossRef]
- Donchyts, G.; Schellekens, J.; Winsemius, H.; Eisemann, E.; van de Giesen, N. A 30 m resolution surfacewater mask including estimation of positional and thematic differences using landsat 8, SRTM and OPenStreetMap: A case study in the Murray-Darling basin, Australia. Remote Sens. 2016, 8, 386. [Google Scholar] [CrossRef]
- Kriegler, F.; Malila, W.; Nalepka, R.; Richardson, W. Preprocessing transformations and their effect on multispectral recognition. In Proceedings of the 6th International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 13–16 October 1969; pp. 97–131. [Google Scholar]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Vandebroek, E.; Lindenbergh, R.; van Leijen, F.; de Schipper, M.; de Vries, S.; Hanssen, R. Semi-automated monitoring of a mega-scale beach nourishment using high-resolution terraSAR-X satellite data. Remote Sens. 2017, 9, 653. [Google Scholar] [CrossRef]
- European Space Agency. Sentinel-1 SAR User Guide; Technical Report; ESA: Paris, France, 2015; Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-1-sar (accessed on 1 November 2021).
- Bunting, P.; Clewley, D.; Lucas, R.M.; Gillingham, S. The Remote Sensing and GIS Software Library (RSGISLib). Comput. Geosci. 2014, 62, 216–226. [Google Scholar] [CrossRef]
- [dataset] Land Information New Zealand. NZ Road Centrelines (Topo, 1:50k). 2022. Available online: https://data.linz.govt.nz/layer/50329-nz-road-centrelines-topo-150k/ (accessed on 8 February 2022).
- [dataset] Land Information New Zealand. NZ Building Outlines. 2021. Available online: https://data.linz.govt.nz/layer/101290-nz-building-outlines/ (accessed on 8 February 2022).
- [dataset] Landcare Research. LCDB v5.0-Land Cover Database version 5.0, Mainland, New Zealand. 2021. Available online: https://lris.scinfo.org.nz/layer/104400-lcdb-v50-land-cover-database-version-50-mainland-new-zealand/ (accessed on 1 December 2021).
- Dymond, J.R.; Shepherd, J.D.; Newsome, P.F.; Belliss, S. Estimating change in areas of indigenous vegetation cover in New Zealand from the New Zealand Land Cover Database (LCDB). N. Z. J. Ecol. 2017, 41, 56–64. [Google Scholar] [CrossRef]
- Columbus, J.; Sirguey, P.; Tenzer, R. A free, fully assessed 15-m DEM for New Zealand. Surv. Q. 2011, 66, 16–19. [Google Scholar]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Geosci. Remote Sens. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Liao, P.S.; Chen, T.S.; Chung, P.C. A fast algorithm for multilevel thresholding. J. Inf. Sci. Eng. 2001, 17, 713–727. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Colditz, R. An Evaluation of Different Training Sample Allocation Schemes for Discrete and Continuous Land Cover Classification Using Decision Tree-Based Algorithms. Remote Sens. 2015, 7, 9655–9681. [Google Scholar] [CrossRef]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Modica, G.; De Luca, G.; Messina, G.; Praticò, S. Comparison and assessment of different object-based classifications using machine learning algorithms and UAVs multispectral imagery: A case study in a citrus orchard and an onion crop. Eur. J. Remote Sens. 2021, 54, 431–460. [Google Scholar] [CrossRef]
- Tate, R.F. Correlation between a Discrete and a Continuous Variable. Point-Biserial Correlation. Ann. Math. Stat. 1954, 25, 603–607. [Google Scholar] [CrossRef]
- Wilson, E.B. Probable Inference, the Law of Succession, and Statistical Inference. J. Am. Stat. Assoc. 1927, 22, 209. [Google Scholar] [CrossRef]
- Warrens, M.J. Properties of the quantity disagreement and the allocation disagreement. Int. J. Remote Sens. 2015, 36, 1439–1446. [Google Scholar] [CrossRef]
- Wright, L.D.; Thom, B.G. Coastal depositional landforms. Prog. Phys. Geogr. Earth Environ. 1977, 1, 412–459. [Google Scholar] [CrossRef]
- Masselink, G.; Hughes, M.; Knight, J. Introduction to Coastal Process and Geomorphology, 2nd ed.; Routledge: London, UK, 2011. [Google Scholar] [CrossRef]
- Young, A.P.; Carilli, J.E. Global distribution of coastal cliffs. Earth Surf. Process. Landforms 2019, 44, 1309–1316. [Google Scholar] [CrossRef]
- Dickson, M.E.; Walkden, M.J.; Hall, J.W. Systemic impacts of climate change on an eroding coastal region over the twenty-first century. Clim. Chang. 2007, 84, 141–166. [Google Scholar] [CrossRef]
- Thomas, N.; Bunting, P.; Lucas, R.; Hardy, A.; Rosenqvist, A.; Fatoyinbo, T. Mapping mangrove extent and change: A globally applicable approach. Remote Sens. 2018, 10, 1466. [Google Scholar] [CrossRef]





| Data | Composite Bands |
|---|---|
| visible, NIR, SWIR | 15th percentile |
| NDVI | Interval mean 10–90 |
| NDWI, MNDWI, AWEI | Minimum, Maximum, Median, Standard deviation, 10th percentile, 25th percentile, 50th percentile, 75th percentile, 90th percentile |
| SAR | VV ascending orbit, VH ascending orbit, VH:VV ascending orbit, VV descending orbit, VH descending orbit, VH:VV descending orbit |
| Class | Description | Aerial Photo |
|---|---|---|
| Artificial surfaces | Any built surface or buildings associated with commercial, residential or industrial use including surrounding infrastructure, amenities and transport routes. |  |
| Bare rock | Bare surfaces dominated by unconsolidated or consolidated material that is coarser than coarse gravel. |  |
| Dark sand | Surfaces containing high concentrations of heavy minerals such as plagioclase, augite and titanomagnetite material that is finer than coarse sand (2 mm) along the coast. |  |
| Gravel | Surfaces dominated by unconsolidated material that is finer than coarse gravel and larger than coarse sand (2–60 mm). |  |
| Intertidal | Standing or flowing saline water that includes estuaries, lagoons and surfaces that are diurnally covered by water due to tidal inundation. |  |
| Light sand | Surfaces predominantly constituted by quartz, feldspar, mafic minerals and residue (lithic and shell fragments) material that is finer than coarse sand (2 mm) along the coast. |  |
| Supratidal sand | Surfaces predominantly constituted by material finer than coarse sand (2 mm), above the high water mark, that can be very sparsely vegetated and texturally different due to aeolian processes. |  |
| Vegetation | Any surface (managed or natural) that is dominated by vegetation of any species in the coastal zone. |  |
| Water | Offshore or inshore permanent saline or fresh open water in the coastal zone including artificial lakes or ponds. |  |
| Class | Training Samples | Proportion (%) |
|---|---|---|
| Bare rock | 2347 | 1.9 |
| Dark sand | 3437 | 2.78 |
| Gravel | 12,241 | 9.92 |
| Intertidal | 48,546 | 39.33 |
| Light sand | 51,573 | 41.78 |
| Supratidal sand | 5298 | 4.29 |
| Region | Proportion Correct | Allocation Disagreement | Quantity Disagreement | Overall Accuracy |
|---|---|---|---|---|
| Auckland | 0.971 | 0.021 | 0.008 | 0.935 |
| Bay of Plenty | 0.967 | 0.009 | 0.024 | 0.888 |
| Canterbury | 0.962 | 0.005 | 0.033 | 0.846 |
| Gisborne | 0.969 | 0.004 | 0.027 | 0.855 |
| Hawkes Bays | 0.958 | 0.001 | 0.041 | 0.828 |
| Manawatu | 0.828 | 0.016 | 0.157 | 0.84 |
| Marlborough | 0.987 | 0 | 0.012 | 0.911 |
| Nelson | 0.991 | 0.004 | 0.006 | 0.911 |
| Northland | 0.975 | 0.018 | 0.007 | 0.869 |
| Otago | 0.945 | 0 | 0.054 | 0.881 |
| Southland | 0.848 | 0.005 | 0.147 | 0.765 |
| Taranaki | 0.869 | 0 | 0.131 | 0.876 |
| Tasman | 0.983 | 0.004 | 0.013 | 0.895 |
| Waikato | 0.972 | 0.013 | 0.015 | 0.91 |
| Wellington | 0.841 | 0.001 | 0.158 | 0.822 |
| West Coast | 0.879 | 0.002 | 0.119 | 0.833 |
| National | 0.936 | 0.012 | 0.053 | 0.864 |
| Class | F1-Score | User Accuracy (%) | Producer Accuracy (%) | Commission | Omission | Area (Hectares) |
|---|---|---|---|---|---|---|
| Artificial surfaces | 0.92 | 99.5 | 85.44 | 0.0004 | 0.0012 | 50,710,640 |
| Bare rock | 0.9 | 93.75 | 86.61 | 0 | 0.0011 | 471,904 |
| Dark sand | 0.85 | 93.7 | 94.46 | 0 | 0.001 | 191,296 |
| Gravel | 0.83 | 74.35 | 93.29 | 0.0012 | 0.0006 | 3,401,184 |
| Intertidal | 0.69 | 54.44 | 95.11 | 0.0537 | 0.0028 | 84,433,392 |
| Light sand | 0.85 | 75.95 | 95.59 | 0.0033 | 0.002 | 9,885,152 |
| Supratidal sand | 0.94 | 86.5 | 84.27 | 0 | 0.0016 | 436,336 |
| Vegetation | 0.94 | 99.95 | 88.18 | 0.0001 | 0.0018 | 89,672,432 |
| Water | 0.81 | 99.15 | 69.06 | 0.0057 | 0.0523 | 474,867,472 |
| Data | Proportion Correct | Allocation Disagreement | Quantity Disagreement | Overall Accuracy |
|---|---|---|---|---|
| Sentinel-1 and 2 | 0.936 | 0.012 | 0.053 | 0.864 |
| Sentinel-2 | 0.899 | 0.018 | 0.083 | 0.721 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Collings, B.; Ford, M.; Dickson, M. A Methodology for National Scale Coastal Landcover Mapping in New Zealand. Remote Sens. 2022, 14, 4827. https://doi.org/10.3390/rs14194827
Collings B, Ford M, Dickson M. A Methodology for National Scale Coastal Landcover Mapping in New Zealand. Remote Sensing. 2022; 14(19):4827. https://doi.org/10.3390/rs14194827
Chicago/Turabian StyleCollings, Benedict, Murray Ford, and Mark Dickson. 2022. "A Methodology for National Scale Coastal Landcover Mapping in New Zealand" Remote Sensing 14, no. 19: 4827. https://doi.org/10.3390/rs14194827
APA StyleCollings, B., Ford, M., & Dickson, M. (2022). A Methodology for National Scale Coastal Landcover Mapping in New Zealand. Remote Sensing, 14(19), 4827. https://doi.org/10.3390/rs14194827






