Mixed Feature Prediction on Boundary Learning for Point Cloud Semantic Segmentation
Abstract
1. Introduction
- We design a mixed feature prediction task for point cloud semantic segmentation to pretrain the model to be boundary-aware.
- A dynamic feature aggregation module is proposed to perform point convolutions with adaptive receptive fields, which introduces more spatial details to the high-level feature representations.
- Experimental results validate the enhancement of our method for boundary regions in semantic segmentation predictions. In addition, the integrated feature representations learned by our method transfer well to other point cloud tasks such as classification and object detection.
2. Related Work
2.1. Point Cloud Semantic Segmentation Methods
2.2. Self-Supervised Learning
2.3. Boundary Learning in Segmentation
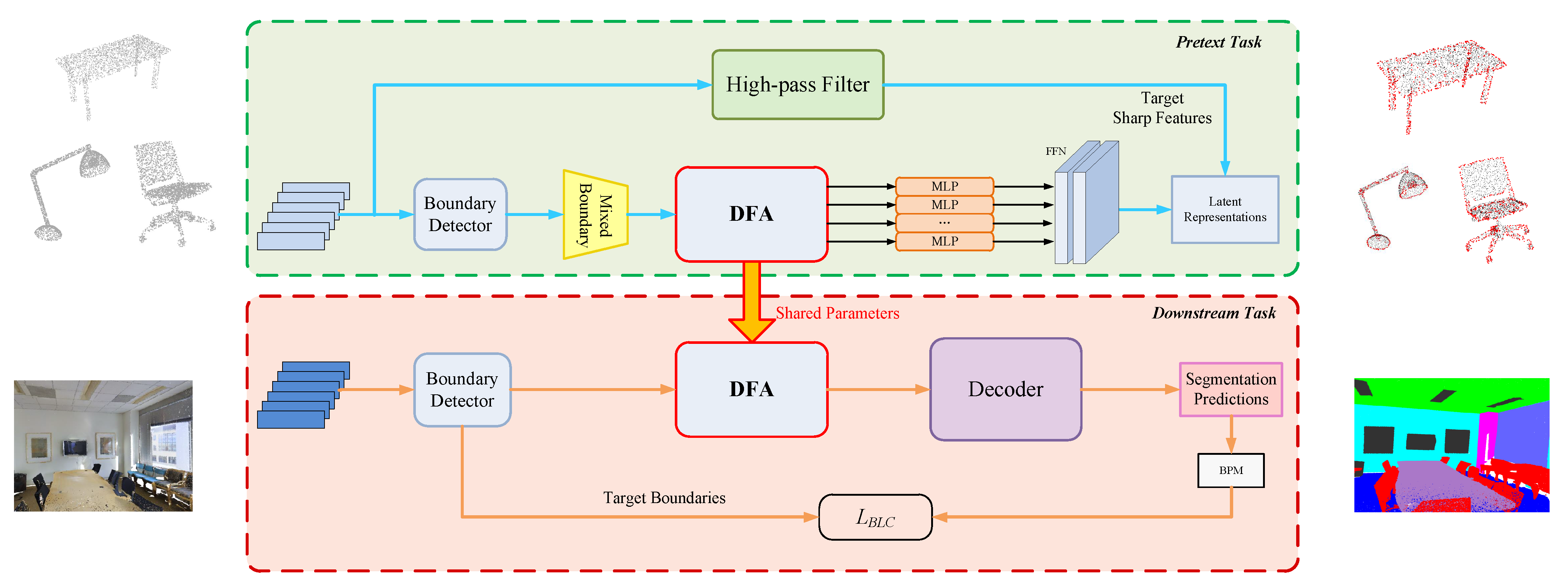
3. Methods
3.1. Overview
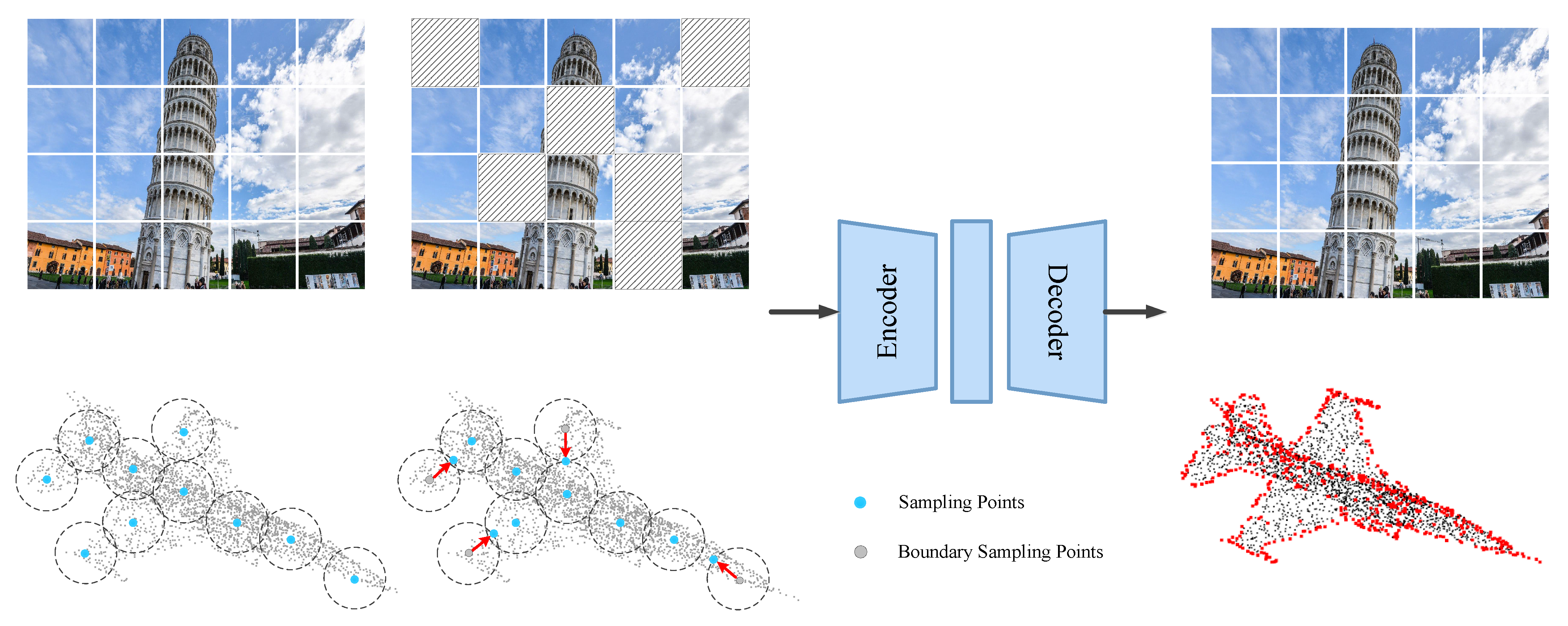
3.2. Masked Feature Pretraining
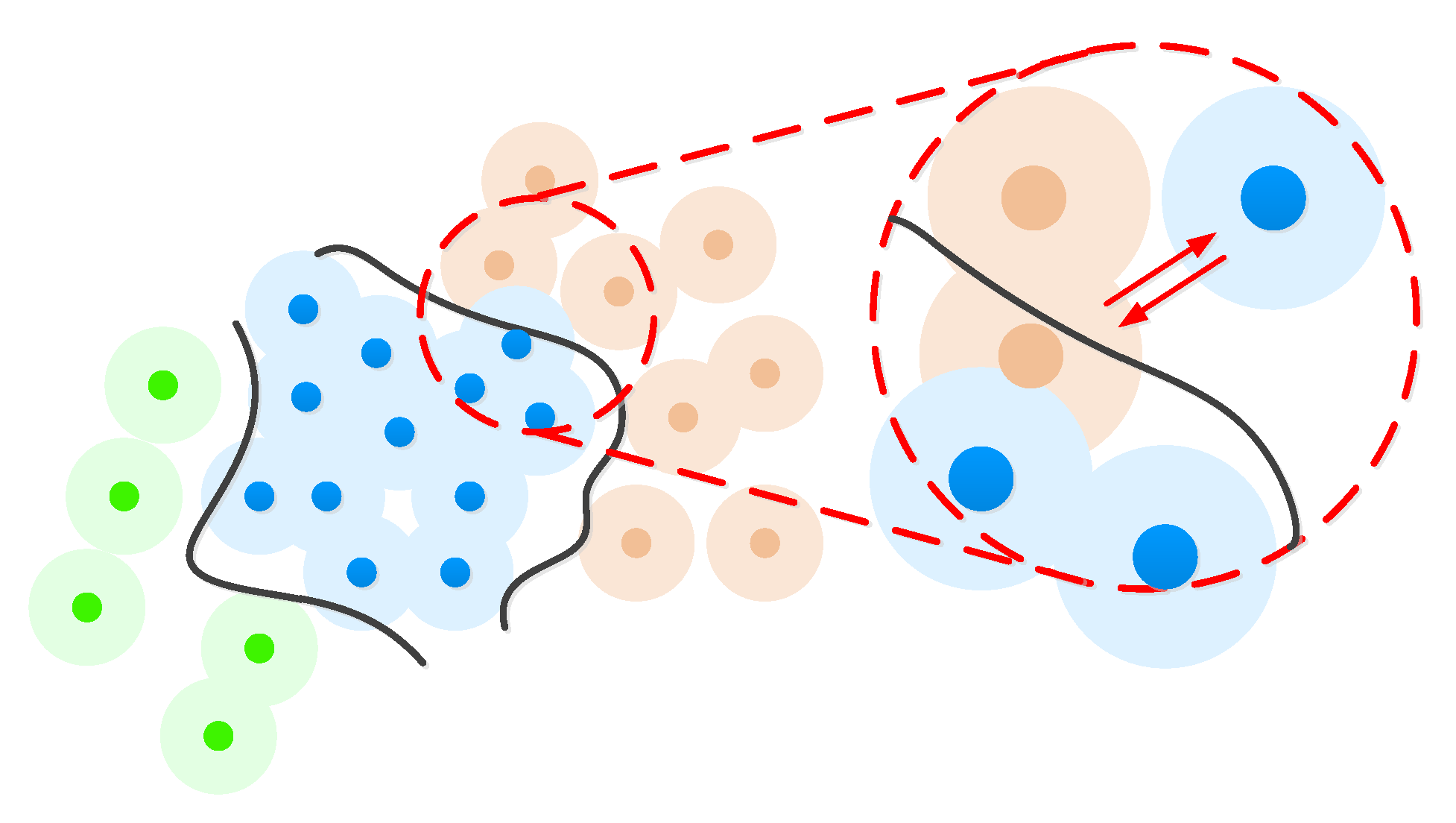
3.2.1. Boundary Detector
3.2.2. Mixed Feature Prediction Task
3.2.3. High-Pass Filter
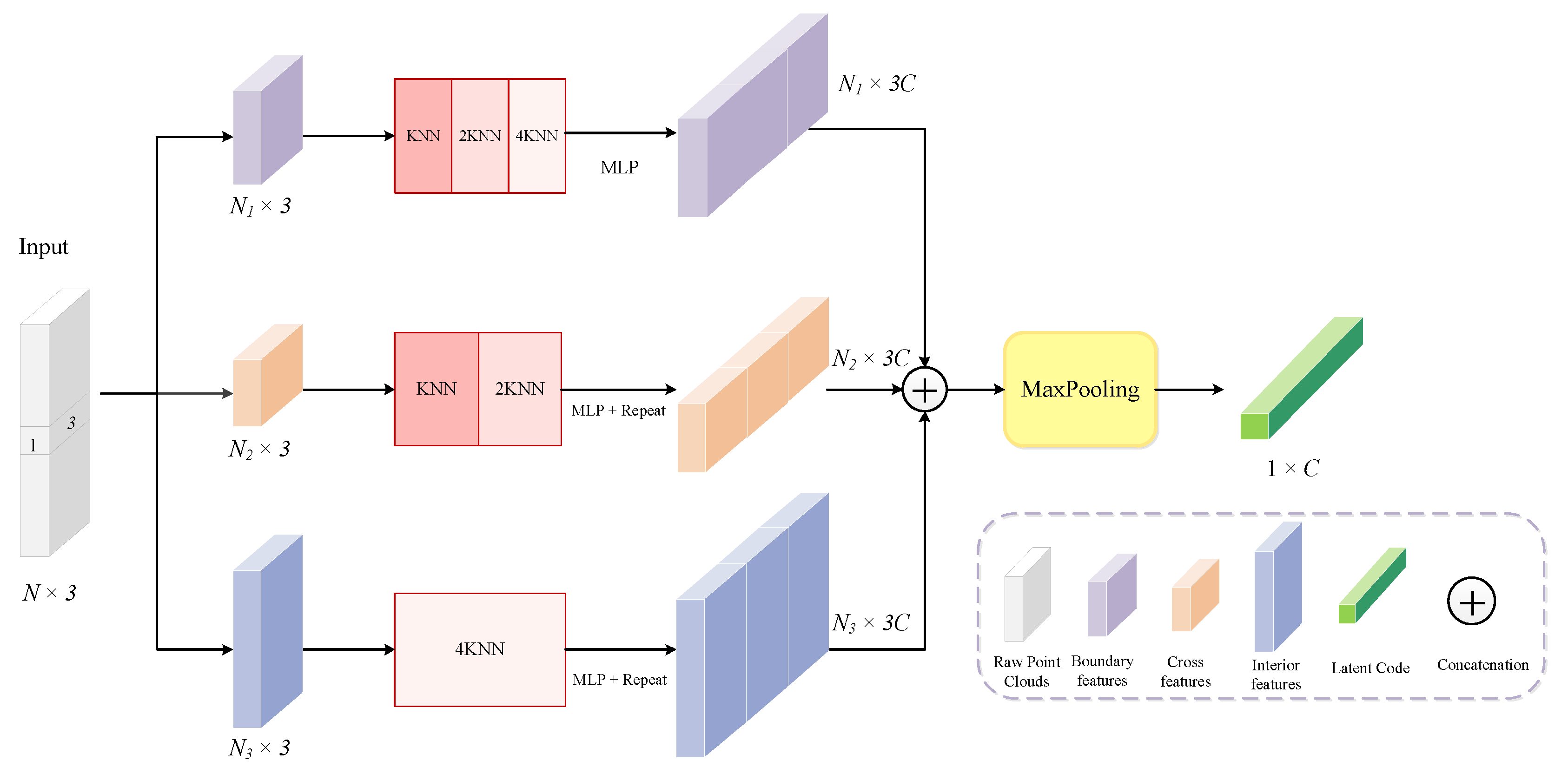
3.3. Dynamic Feature Aggregation
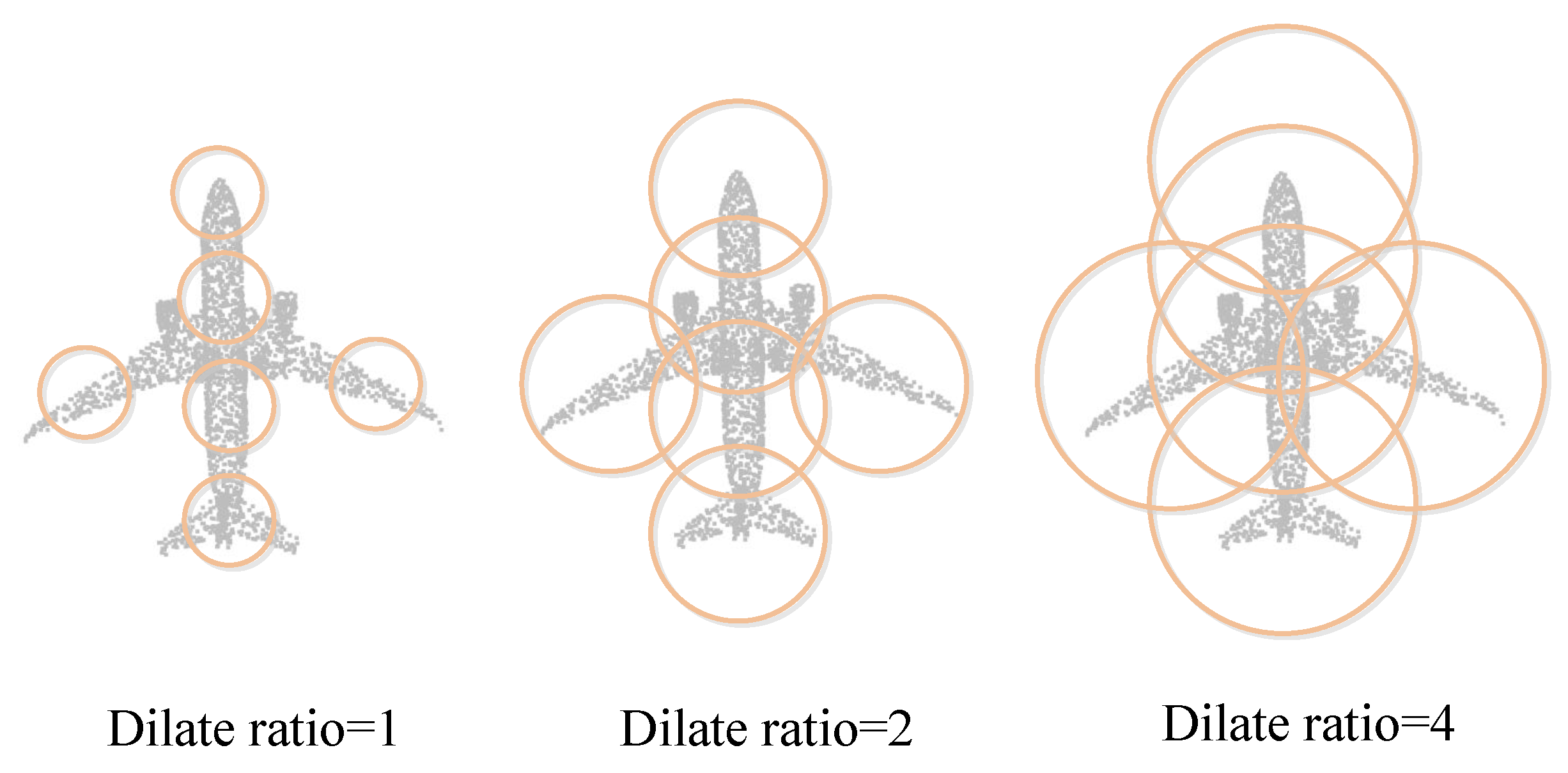
3.3.1. Spatial-Based Clustering
3.3.2. Hybrid Feature Encoder
3.4. Loss Function
4. Experiments
4.1. Experiment Setups
4.1.1. Pretraining Setups
4.1.2. Evaluation Metrics
4.2. Downstream Tasks
4.2.1. Part Segmentation on ShapeNet-Part Dataset
4.2.2. Semantic Segmentation on ScanNet v2 Dataset
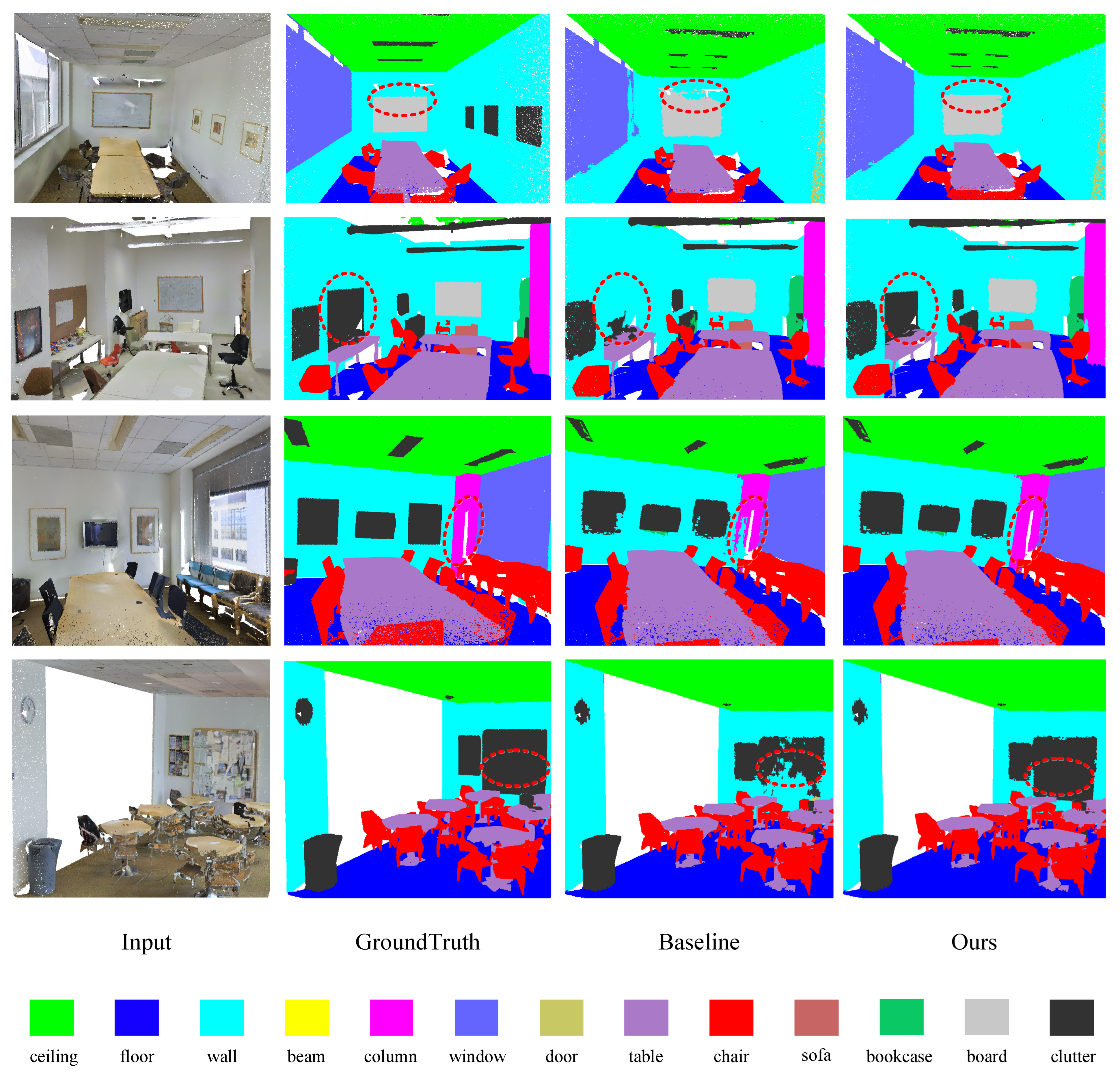
4.2.3. Semantic Segmentation on S3DIS Dataset
4.3. Transfer Learning
4.3.1. Object Classification
4.3.2. Few-Shot Classification
4.3.3. Object Detection
5. Discussion
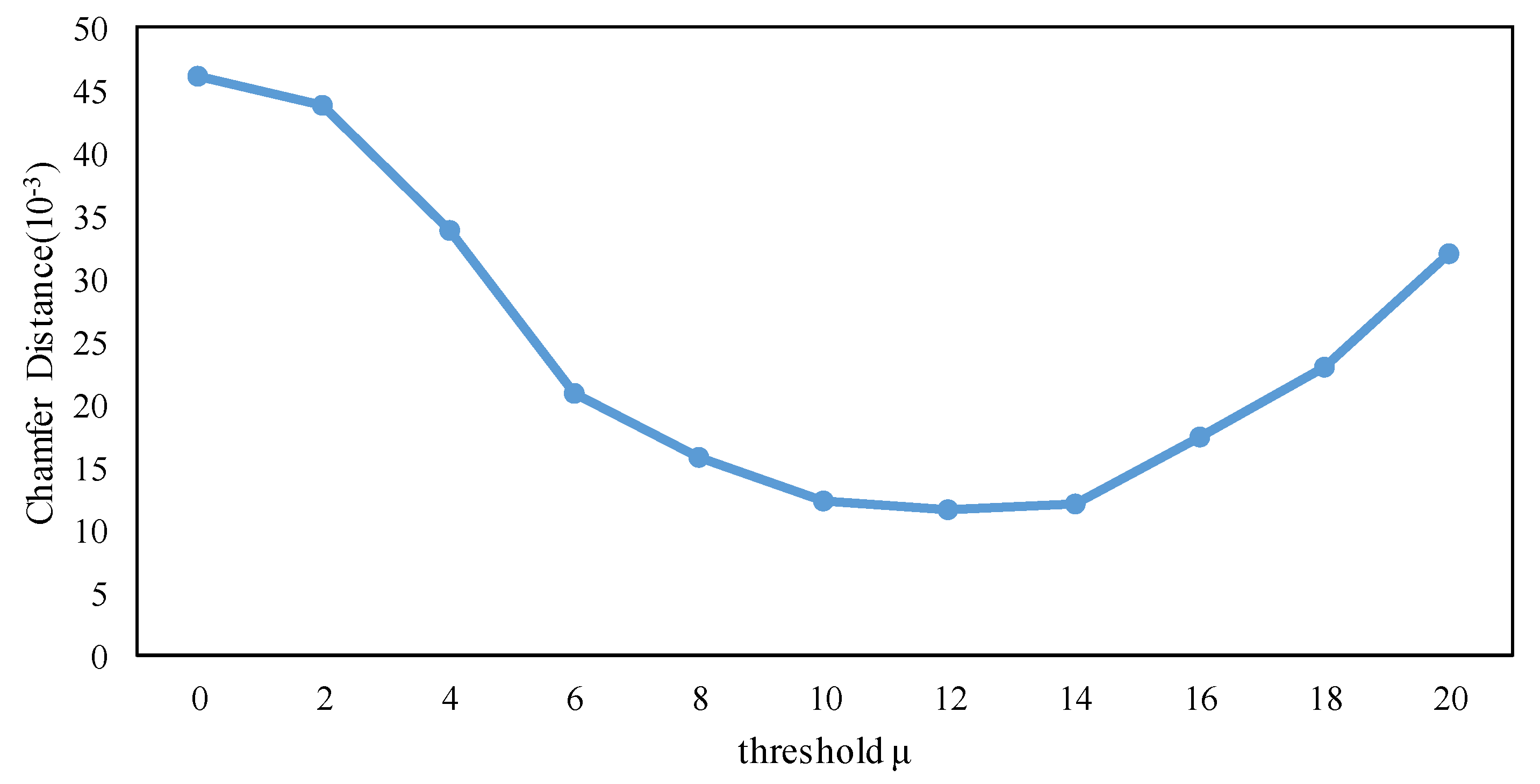
5.1. Boundary Extraction Strategies
5.2. Effectiveness of the MFP Pretraining
5.3. Effectiveness of the DFA Module
5.4. Effectiveness of the BLC Loss
5.5. Complexity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jing, W.; Zhang, W.; Li, L.; Di, D.; Chen, G.; Wang, J. AGNet: An Attention-Based Graph Network for Point Cloud Classification and Segmentation. Remote Sens. 2022, 14, 1036. [Google Scholar] [CrossRef]
- Wan, J.; Xie, Z.; Xu, Y.; Zeng, Z.; Yuan, D.; Qiu, Q. Dganet: A dilated graph attention-based network for local feature extraction on 3D point clouds. Remote Sens. 2021, 13, 3484. [Google Scholar] [CrossRef]
- Lin, X.; Wang, F.; Yang, B.; Zhang, W. Autonomous vehicle localization with prior visual point cloud map constraints in gnss-challenged environments. Remote Sens. 2021, 13, 506. [Google Scholar] [CrossRef]
- Aldibaja, M.; Suganuma, N. Graph slam-based 2.5d lidar mapping module for autonomous vehicles. Remote Sens. 2021, 13, 5066. [Google Scholar] [CrossRef]
- Huang, J.; Stoter, J.; Peters, R.; Nan, L. City3D: Large-Scale Building Reconstruction from Airborne LiDAR Point Clouds. Remote Sens. 2022, 14, 2254. [Google Scholar] [CrossRef]
- Neuville, R.; Bates, J.S.; Jonard, F. Estimating forest structure from UAV-mounted LiDAR point cloud using machine learning. Remote Sens. 2021, 13, 352. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the NAACL HLT 2019—Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 3–5 June 2019; pp. 4171–4186. [Google Scholar]
- Bansal, T.; Jha, R.; Munkhdalai, T.; McCallum, A. Self-supervised meta-learning for few-shot natural language classification tasks. In Proceedings of the EMNLP—2020 Conference on Empirical Methods in Natural Language Processing, Online, 16–20 November 2020; pp. 522–534. [Google Scholar]
- Wei, C.; Fan, H.; Xie, S.; Wu, C.Y.; Yuille, A.; Feichtenhofer, C. Masked Feature Prediction for Self-Supervised Visual Pre-Training. arXiv 2021, arXiv:2112.09133. [Google Scholar]
- Xie, Z.; Zhang, Z.; Cao, Y.; Lin, Y.; Bao, J.; Yao, Z.; Dai, Q.; Hu, H. SimMIM: A Simple Framework for Masked Image Modeling. arXiv 2021, arXiv:2111.09886. [Google Scholar]
- Yu, X.; Tang, L.; Rao, Y.; Huang, T.; Zhou, J.; Lu, J. Point-BERT: Pre-training 3D Point Cloud Transformers with Masked Point Modeling. arXiv 2021, arXiv:2111.14819. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked Autoencoders Are Scalable Vision Learners. arXiv 2021, arXiv:2111.06377. [Google Scholar]
- Zhao, Y.; Birdal, T.; Deng, H.; Tombari, F. 3D point capsule networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1009–1018. [Google Scholar]
- Yang, Y.; Feng, C.; Shen, Y.; Tian, D. FoldingNet: Point Cloud Auto-encoder via Deep Grid Deformation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 206–215. [Google Scholar]
- Gao, X.; Hu, W.; Qi, G.J. Graphter: Unsupervised learning of graph transformation equivariant representations via auto-encoding node-wise transformations. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 7161–7170. [Google Scholar]
- Generative, B.; Networks, A.; Gan, P.; Networks, G.A. Point Cloud Gan. arXiv 2018, arXiv:1810.05795. [Google Scholar]
- Vosselman, G.; Gorte, B.G.H.; Sithole, G.; Rabbani, T. Recognising structure in laser scanner point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 46, 33–38. [Google Scholar]
- Rabbani, T.; van den Heuvel, F.a.; Vosselman, G. Segmentation of point clouds using smoothness constraint. Remote Sens. Spat. Inf. Sci. 2006, 36, 248–253. [Google Scholar]
- Jagannathan, A.; Miller, E.L. Three-dimensional surface mesh segmentation using curvedness-based region growing approach. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 2195–2204. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the 31st NIPS’17 International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5100–5109. [Google Scholar]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L. KPConv: Flexible and deformable convolution for point clouds. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 6410–6419. [Google Scholar]
- Engel, N.; Belagiannis, V.; Dietmayer, K. Point Transformer. IEEE Access 2021, 9, 26–40. [Google Scholar] [CrossRef]
- Yu, X.; Rao, Y.; Wang, Z.; Liu, Z.; Lu, J.; Zhou, J. PoinTr: Diverse Point Cloud Completion with Geometry-Aware Transformers. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 12478–12487. [Google Scholar]
- Guo, M.H.; Cai, J.X.; Liu, Z.N.; Mu, T.J.; Martin, R.R.; Hu, S.M. PCT: Point cloud transformer. Comput. Vis. Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, D.; Cheng, G.; Han, J. Weakly Supervised Learning for Target Detection in Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 318–323. [Google Scholar]
- Wan, Y.; Zhao, Q.; Guo, C.; Xu, C.; Fang, L. Multi-Sensor Fusion Self-Supervised Deep Odometry and Depth Estimation. Remote Sens. 2022, 14, 1228. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Kim, K.; Mello, S.D.; Jampani, V.; Mar, C.V. Self-supervised Single-view 3D Reconstruction via Semantic Consistency. arXiv 2020, arXiv:2003.06473v1. [Google Scholar]
- Li, Y.; Li, K.; Jiang, S.; Zhang, Z.; Huang, C.; Da Xu, R.Y. Geometry-driven self-supervised method for 3D human pose estimation. In Proceedings of the AAAI 2020—34th AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 11442–11449. [Google Scholar]
- Eckart, B.; Yuan, W.; Liu, C.; Kautz, J. Self-Supervised Learning on 3D Point Clouds by Learning Discrete Generative Models. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 8244–8253. [Google Scholar]
- Tang, L.; Zhan, Y.; Chen, Z.; Yu, B.; Tao, D. Contrastive Boundary Learning for Point Cloud Segmentation. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022. [Google Scholar]
- Sauder, J.; Sievers, B. Self-supervised deep learning on point clouds by reconstructing space. arXiv 2019, arXiv:1901.08396. [Google Scholar]
- Noroozi, M.; Favaro, P. Unsupervised learning of visual representations by solving jigsaw puzzles. In Proceedings of the European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; Volume 9910, pp. 69–84. [Google Scholar]
- Li, X.; Li, X.; Zhang, L.; Cheng, G.; Shi, J.; Lin, Z.; Tan, S.; Tong, Y. Improving Semantic Segmentation via Decoupled Body and Edge Supervision. In Proceedings of the European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; Volume 12362, pp. 435–452. [Google Scholar]
- Zhen, M.; Wang, J.; Zhou, L.; Li, S.; Shen, T.; Shang, J.; Fang, T.; Quan, L. Joint semantic segmentation and boundary detection using iterative pyramid contexts. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 13663–13672. [Google Scholar]
- Yu, L.; Li, X.; Fu, C.W.; Cohen-Or, D.; Heng, P.A. EC-Net: An edge-aware point set consolidation network. In Proceedings of the European Conference on Computer Vision; Springer: Cham, Switzerland, 2018; pp. 398–414. [Google Scholar]
- Jiang, L.; Zhao, H.; Liu, S.; Shen, X.; Fu, C.W.; Jia, J. Hierarchical point-edge interaction network for point cloud semantic segmentation. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 10432–10440. [Google Scholar]
- Hu, Z.; Zhen, M.; Bai, X.; Fu, H.; lan Tai, C. JSENet: Joint Semantic Segmentation and Edge Detection Network for 3D Point Clouds. In Proceedings of the European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; Volume 12365, pp. 222–239. [Google Scholar]
- Zhang, J.; Chen, L.; Ouyang, B.; Liu, B.; Zhu, J.; Chen, Y.; Meng, Y.; Wu, D. PointCutMix: Regularization Strategy for Point Cloud Classification. arXiv 2021, arXiv:2101.01461. [Google Scholar] [CrossRef]
- Deng, Q.; Zhang, S.; DIng, Z. Point Cloud Resampling via Hypergraph Signal Processing. IEEE Signal Process. Lett. 2021, 28, 2117–2121. [Google Scholar] [CrossRef]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. ShapeNet: An Information-Rich 3D Model Repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. In Proceedings of the 7th International Conference on Learning Representations, ICLR, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Yi, L.; Kim, V.G.; Ceylan, D.; Shen, I.C.; Yan, M.; Su, H.; Lu, C.; Huang, Q.; Sheffer, A.; Guibas, L. A scalable active framework for region annotation in 3D shape collections. ACM Trans. Graph. 2016, 35, 1–12. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph Cnn for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–2. [Google Scholar] [CrossRef]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN: Convolution on X-transformed points. arXiv 2018, arXiv:1801.07791v5. [Google Scholar]
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-shape convolutional neural network for point cloud analysis. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8887–8896. [Google Scholar]
- Lei, H.; Akhtar, N.; Mian, A. Spherical Kernel for Efficient Graph Convolution on 3D Point Clouds. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3664–3680. [Google Scholar] [CrossRef]
- Dai, A.; Chang, A.X.; Savva, M.; Halber, M.; Funkhouser, T.; Nießner, M. ScanNet: Richly-annotated 3D reconstructions of indoor scenes. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2432–2443. [Google Scholar]
- Wu, W.; Qi, Z.; Fuxin, L. PointCONV: Deep convolutional networks on 3D point clouds. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9613–9622. [Google Scholar]
- Wang, P.S.; Liu, Y.; Guo, Y.X.; Sun, C.Y.; Tong, X. O-CNN: Octree-based convolutional neural networks for 3D shape analysis. ACM Trans. Graph. 2017, 36, 1–11. [Google Scholar] [CrossRef]
- Choy, C.; Gwak, J.; Savarese, S. 4D spatio-temporal convnets: Minkowski convolutional neural networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3070–3079. [Google Scholar]
- Nekrasov, A.; Schult, J.; Litany, O.; Leibe, B.; Engelmann, F. Mix3D: Out-of-Context Data Augmentation for 3D Scenes. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 116–125. [Google Scholar]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D semantic parsing of large-scale indoor spaces. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1534–1543. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Randla-Net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [CrossRef]. [Google Scholar]
- Tchapmi, L.P.; Choy, C.B.; Armeni, I.; Gwak, J.; Savarese, S. SEGCloud: Semantic Segmentation of 3D Point Clouds. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 537–547. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-Scale Point Cloud Semantic Segmentation with Superpoint Graphs. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4558–4567. [Google Scholar]
- Siqi, F.; Qiulei, D.; Fenghua, Z.; Yisheng, L.; Peijun, Y.; Fei-Yue, W. SCF-Net: Learning Spatial Contextual Features for Large-Scale Point Cloud Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14504–14513. [Google Scholar]
- Qiu, S.; Anwar, S.; Barnes, N. Semantic Segmentation for Real Point Cloud Scenes via Bilateral Augmentation and Adaptive Fusion. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20-25 June 2021. [CrossRef]. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A deep representation for volumetric shapes. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Kazhdan, M.; Funkhouser, T.; Rusinkiewicz, S. Rotation Invariant Spherical Harmonic Representation of 3D Shape Descriptors. In Proceedings of the 2003 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, Aachen, Germany, 23–25 June 2003. [Google Scholar]
- Wu, J.; Zhang, C.; Xue, T.; Freeman, W.T.; Tenenbaum, J.B. Learning a probabilistic latent space of object shapes via 3D generative-adversarial modeling. arXiv 2016, arXiv:1610.07584. [Google Scholar]
- Achlioptas, P.; Diamanti, O.; Mitliagkas, I.; Guibas, L. Learning representations and generative models for 3d point clouds. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 67–85. [Google Scholar]
- Gadelha, M.; Wang, R.; Maji, S. Multiresolution Tree Networks for 3D Point Cloud Processing; Springer: Berlin/Heidelberg, Germany, 2018; pp. 105–122. [Google Scholar]
- Liu, H.; Lee, Y.J. Masked Discrimination for Self-Supervised Learning on Point Clouds. arXiv 2022, arXiv:2203.11183. [Google Scholar]
- Xiang, T.; Zhang, C.; Song, Y.; Yu, J.; Cai, W. Walk in the Cloud: Learning Curves for Point Clouds Shape Analysis. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Ma, X.; Qin, C.; You, H.; Ran, H.; Fu, Y. Rethinking Network Design and Local Geometry in Point Cloud: A Simple Residual MLP Framework. arXiv 2022, arXiv:2202.07123. [Google Scholar]
- Uy, M.A.; Pham, Q.H.; Hua, B.S.; Nguyen, T.; Yeung, S.K. Revisiting point cloud classification: A new benchmark dataset and classification model on real-world data. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 1588–1597. [Google Scholar]
- Wang, H.; Lasenby, J.; Kusner, M.J. Unsupervised Point Cloud Pre-training via Occlusion Completion. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Zhou, B.; Lapedriza, A.; Xiao, J.; Torralba, A.; Oliva, A. Learning Deep Features for Scene Recognition using Places Database. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 487–495. [Google Scholar]
- Qi, C.R.; Litany, O.; He, K.; Guibas, L. Deep hough voting for 3D object detection in point clouds. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 9276–9285. [Google Scholar]
- Zhang, Z.; Sun, B.; Yang, H.; Huang, Q. H3DNet: 3D Object Detection Using Hybrid Geometric Primitives. In Proceedings of the European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; Volume 12357, pp. 311–329. [Google Scholar]
- Xie, S.; Gu, J.; Guo, D.; Qi, C.R.; Guibas, L.; Litany, O. PointContrast: Unsupervised Pre-training for 3D Point Cloud Understanding. In Proceedings of the European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; Volume 12348, pp. 574–591. [Google Scholar]
- Zhang, Z.; Girdhar, R.; Joulin, A.; Misra, I. Self-Supervised Pretraining of 3D Features on any Point-Cloud. arXiv 2021, arXiv:2101.02691. [Google Scholar]
- Liu, Z.; Zhang, Z.; Cao, Y.; Hu, H.; Tong, X. Group-Free 3D Object Detection via Transformers. arXiv 2022, arXiv:2104.00678. [Google Scholar]
- Qi, C.R.; Chen, X.; Litany, O.; Guibas, L.J. ImVoteNet: Boosting 3D Object Detection in Point Clouds with Image Votes. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 4403–4412. [Google Scholar]
- Bormann, R.; Hampp, J.; Hägele, M.; Vincze, M. Fast and accurate normal estimation by efficient 3d edge detection. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 3930–3937. [Google Scholar]
- Bazazian, D.; Casas, J.R.; Ruiz-Hidalgo, J. Fast and Robust Edge Extraction in Unorganized Point Clouds. In Proceedings of the 2015 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Adelaide, SA, Australia, 23–25 November 2015; pp. 1–8. [Google Scholar]


| Method | cls.mIoU (%) | int. mIoU (%) |
|---|---|---|
| PointNet [20] | 80.4 | 83.7 |
| PointNet++ [21] | 81.9 | 85.1 |
| DGCNN [44] | 82.3 | 85.1 |
| PointCNN [45] | 84.6 | 86.1 |
| KPConv [22] | 85.1 | 86.4 |
| RS-CNN [46] | 84.0 | 86.2 |
| SPH3D-GCN [47] | 84.9 | 86.8 |
| PointTransformer [23] | 83.7 | 86.6 |
| Point-BERT [11] | 84.1 | 85.6 |
| Ours | 84.5 | 86.6 |
| Method | Method | mIoU (%) |
|---|---|---|
| PointNet++ [21] | point-based | 33.9 |
| PointCNN [45] | point-based | 45.8 |
| PointConv [49] | point-based | 55.6 |
| SPH3D-GCN [47] | point-based | 61.0 |
| KPConv [22] | point-based | 68.0 |
| JSENet [38] | point-based | 69.9 |
| CBL [31] | point-based | 70.5 |
| MinkowskiNet [51] | voxel-based | 73.6 |
| O-CNN [50] | voxel-based | 76.2 |
| Mix3D [52] | voxel-based | 78.1 |
| Ours | point-based | 75.8 |
| Method | OA (%) | mAcc (%) | mIoU (%) | Ceiling | Floor | Wall | Beam | Column | Window | Door | Table | Chair | Sofa | Bookcase | Board | Clutter |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PointNet [20] | 49.0 | 41.1 | 88.8 | 97.3 | 69.8 | 0.1 | 3.9 | 46.3 | 10.8 | 59.0 | 52.6 | 5.9 | 40.3 | 26.4 | 33.2 | |
| SegCloud [55] | 57.4 | 48.9 | 90.1 | 96.1 | 69.9 | 0.0 | 18.4 | 38.4 | 23.1 | 70.4 | 75.9 | 40.9 | 58.4 | 13.0 | 41.6 | |
| PointCNN [45] | 88.1 | 75.6 | 65.4 | 92.3 | 98.2 | 79.4 | 0.0 | 17.6 | 22.8 | 62.1 | 74.4 | 80.6 | 31.7 | 66.7 | 62.1 | 56.7 |
| SPG [56] | 86.4 | 66.5 | 58.0 | 89.4 | 96.9 | 78.1 | 0.0 | 42.8 | 48.9 | 61.6 | 84.7 | 75.4 | 69.8 | 52.6 | 2.1 | 52.2 |
| KPConv [22] | 72.8 | 67.1 | 92.8 | 97.3 | 82.4 | 0.0 | 23.9 | 58.0 | 69.0 | 91.0 | 81.5 | 75.3 | 75.4 | 66.7 | 58.9 | |
| RandLA-Net [54] | 87.2 | 71.4 | 62.4 | 91.1 | 95.6 | 80.2 | 0.0 | 24.7 | 62.3 | 47.7 | 76.2 | 83.7 | 60.2 | 71.1 | 65.7 | 53.8 |
| JSENet [38] | 67.7 | 93.8 | 97.0 | 83.0 | 0.0 | 23.2 | 61.3 | 71.6 | 89.9 | 79.8 | 75.6 | 72.3 | 72.7 | 60.4 | ||
| PT [23] | 90.8 | 76.5 | 70.4 | 94.0 | 98.5 | 86.3 | 0.0 | 38.0 | 63.4 | 74.3 | 89.1 | 82.4 | 74.3 | 80.2 | 76.0 | 59.3 |
| CBL [31] | 90.6 | 75.2 | 69.4 | 93.9 | 98.4 | 84.2 | 0.0 | 37.0 | 57.7 | 71.9 | 91.7 | 81.8 | 77.8 | 75.6 | 69.1 | 62.9 |
| Ours | 90.1 | 80.3 | 69.3 | 94.2 | 98.2 | 85.3 | 0.0 | 34.0 | 64.0 | 72.8 | 88.7 | 82.5 | 74.3 | 78.0 | 67.4 | 61.5 |
| Method | OA(%) | mAcc (%) | mIoU (%) |
|---|---|---|---|
| PointNet++ [21] | 67.1 | 81.0 | 54.5 |
| DGCNN [44] | 84.1 | - | 56.1 |
| PointCNN [45] | 88.1 | 75.6 | 65.4 |
| SPG [56] | 85.5 | 73.0 | 62.1 |
| KPConv [22] | - | 79.1 | 70.6 |
| RandLA-Net [22] | 88.0 | 82.0 | 70.0 |
| SCF-Net [57] | 88.4 | 82.7 | 71.6 |
| BAAF [58] | 88.9 | 83.1 | 72.2 |
| CBL [31] | 89.6 | 79.4 | 73.1 |
| Ours | 90.2 | 80.7 | 73.5 |
| Learned Features + Linear SVM | Acc (%) |
|---|---|
| SPH [60] | 68.2 |
| 3D-GAN [61] | 83.3 |
| Latent GAN [62] | 85.7 |
| MRTNet-VAE [63] | 86.4 |
| FoldingNet [14] | 88.4 |
| PointCapsNet [13] | 88.9 |
| GraphTER [15] | 89.1 |
| Ours | 89.3 |
| Method | Input | Acc (%) |
|---|---|---|
| PointNet [20] | 1 k | 89.2 |
| PointNet++ [21] | 1 k | 90.7 |
| DGCNN [44] | 1 k | 92.9 |
| RS-CNN [46] | 1 k | 92.9 |
| PointTransformer [23] | - | 93.7 |
| Point-BERT [11] | 1 k | 93.2 |
| Point-MAE [64] | 1 k | 94.0 |
| CurveNet [65] | 1 k | 94.2 |
| PointMLP [66] | 1 k | 94.5 |
| Ours | 1k | 94.2 |
| Method | OBJ-BG | OBJ-ONLY | PB-T50_RS |
|---|---|---|---|
| PointNet [20] | 73.3 | 79.2 | 68.0 |
| PointNet++ [21] | 82.3 | 84.3 | 77.9 |
| DGCNN [44] | 82.8 | 86.2 | 78.1 |
| PointCNN [45] | 86.1 | 85.5 | 78.5 |
| Transformer [23] | 79.9 | 80.6 | 77.2 |
| Point-BERT [11] | 87.4 | 88.1 | 83.1 |
| Ours | 86.5 | 83.4 | 82.6 |
| Method | 5-Way | 10-Way | ||
|---|---|---|---|---|
| 10-Shot | 20-Shot | 10-Shot | 20-Shot | |
| DGCNN-rand [44] | 31.6 ± 2.8 | 40.8 ± 4.6 | 19.9 ± 2.1 | 16.9 ± 1.5 |
| DGCNN-OcCo [68] | 90.6 ± 2.8 | 92.5 ± 1.9 | 82.9 ± 1.3 | 86.5 ± 2.2 |
| Transformer-rand [23] | 87.8 ± 5.2 | 93.3 ± 4.3 | 84.6 ± 5.5 | 89.4 ± 6.3 |
| Transformer-OcCo [68] | 94.0 ± 3.6 | 95.9 ± 2.3 | 89.4 ± 5.1 | 92.4 ± 4.6 |
| Point-BERT [11] | 94.6 ± 3.1 | 96.3 ± 2.7 | 91.0 ± 5.4 | 92.7 ± 5.1 |
| PointMAE [64] | 96.3 ± 2.5 | 97.8 ± 1.8 | 92.6 ± 4.1 | 95.0 ± 3.0 |
| Ours-rand | 93.1 ± 3.2 | 94.2 ± 2.4 | 90.2 ± 3.9 | 92.3 ± 3.2 |
| Ours | 96.5 ± 2.1 | 97.2 ± 2.3 | 93.1 ± 3.7 | 95.2 ± 4.1 |
| Method | SUNRGB-D | |
|---|---|---|
| AP | AP | |
| Frustum PointNet [66] | 54.0 | - |
| VoteNet [70] | 57.7 | 32.9 |
| H3DNet [71] | 60.1 | 39.0 |
| PointContrast [72] | 57.5 | 34.8 |
| DepthConstrast [73] | 61.6 | 35.5 |
| GroupFree3D [74] | 63.0 | 45.2 |
| ImVoteNet [75] | 63.4 | - |
| Ours | 63.5 | 44.7 |
| Initialization | ScanNet v2 (mIoU) | S3DIS (mIoU) |
|---|---|---|
| Supervised from scratch | 70.2 | 62.7 |
| Ours-OcCo | 73.3 | 68.6 |
| Ours-discrete token | 74.6 | 69.2 |
| Ours-MFP | 75.8 | 71.4 |
| Ratio | 20% | 40% | 60% | 80% | 90% | 95% |
| OA (%) | 89.1 | 90.6 | 92.9 | 93.9 | 94.2 | 93.7 |
| Dilate Ratio d | Number of Neighbors K | ScanNet v2 (mIoU) | S3DIS (mIoU) |
|---|---|---|---|
| 1 | 20 | 74.5 | 67.6 |
| 2 | 20 | 72.3 | 67.1 |
| 4 | 20 | 61.2 | 63.3 |
| 1, 2 | 20 | 75.6 | 70.6 |
| 2, 4 | 20 | 75.3 | 69.3 |
| 1, 2, 4 | 20 | 75.8 | 71.4 |
| Dataset | ScanNet v2 (mIoU) | S3DIS (mIoU) |
|---|---|---|
| Without BLC Loss | 75.2 | 70.9 |
| With BLC Loss | 75.8 (↑ 0.6) | 71.4 (↑ 0.5) |
| Method | Input | Params | Forward Time | OA (%) |
|---|---|---|---|---|
| PointNet [20] | 1 k | 3.50 M | 13.2 ms | 89.2 |
| PointNet++ [21] | 1 k | 1.48 M | 34.8 ms | 90.7 |
| DGCNN [44] | 1 k | 1.81 M | 86.2 ms | 92.9 |
| KPConv [22] | 1 k | 14.3 M | 33.5 ms | 92.9 |
| RS-CNN [46] | 1 k | 1.41 M | 30.6 ms | 93.6 |
| Point Transformer [23] | 1 k | 2.88 M | 79.6 ms | 93.7 |
| Ours | 1 k | 0.88 M | 22.4 ms | 94.2 |
| Module | Block | Cin | Cmiddle | Cout | Nout |
|---|---|---|---|---|---|
| DFA encoder | MLP1 | 3 | (64, 64, 128) | 768 | |
| MLP2 | 3 | (64, 64, 128) | 768 | ||
| MLP3 | 3 | (64, 64, 128) | 768 | ||
| MaxPooling | N | - | 1 | - | |
| MFP decoder | MLP | 768 | (512, 256,128) | 128 | 64 |
| Linear | 128 | 64 | 2 | 64 | |
| Segmentation head | MLP | 387 | 384 × 4 | 384 | 64 |
| EdgeConv | 384 | - | 512 | 128 | |
| EdgeConv | 512 | - | 384 | 128 | |
| EdgeConv | 384 | - | 512 | 256 | |
| EdgeConv | 512 | - | 384 | 256 | |
| EdgeConv | 384 | - | 512 | 512 | |
| EdgeConv | 512 | - | 384 | 512 | |
| EdgeConv | 384 | - | 512 | 2048 | |
| EdgeConv | 512 | - | 384 | 2048 | |
| Classficiation head | MLP | 768 | (512, 256) | 40 | - |
| Target detection head | Voting layer | 256 | 256 | 259 | - |
| Proposal layer | 128 | (128, 128) | 79 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, F.; Li, J.; Song, R.; Li, Y.; Cao, K. Mixed Feature Prediction on Boundary Learning for Point Cloud Semantic Segmentation. Remote Sens. 2022, 14, 4757. https://doi.org/10.3390/rs14194757
Hao F, Li J, Song R, Li Y, Cao K. Mixed Feature Prediction on Boundary Learning for Point Cloud Semantic Segmentation. Remote Sensing. 2022; 14(19):4757. https://doi.org/10.3390/rs14194757
Chicago/Turabian StyleHao, Fengda, Jiaojiao Li, Rui Song, Yunsong Li, and Kailang Cao. 2022. "Mixed Feature Prediction on Boundary Learning for Point Cloud Semantic Segmentation" Remote Sensing 14, no. 19: 4757. https://doi.org/10.3390/rs14194757
APA StyleHao, F., Li, J., Song, R., Li, Y., & Cao, K. (2022). Mixed Feature Prediction on Boundary Learning for Point Cloud Semantic Segmentation. Remote Sensing, 14(19), 4757. https://doi.org/10.3390/rs14194757










