An Accurate Maritime Radio Propagation Loss Prediction Approach Employing Neural Networks
Abstract
1. Introduction
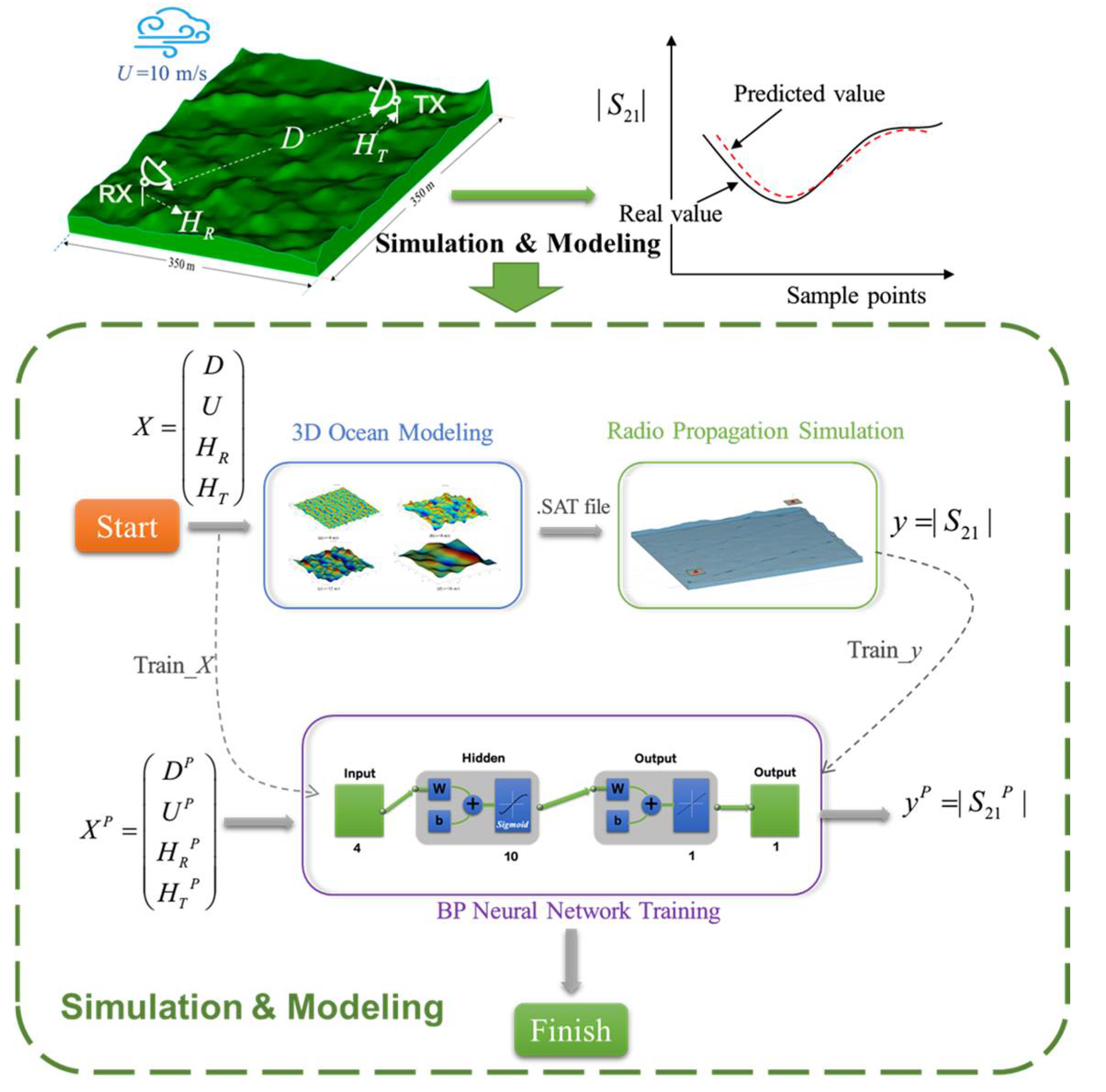
2. Methodology
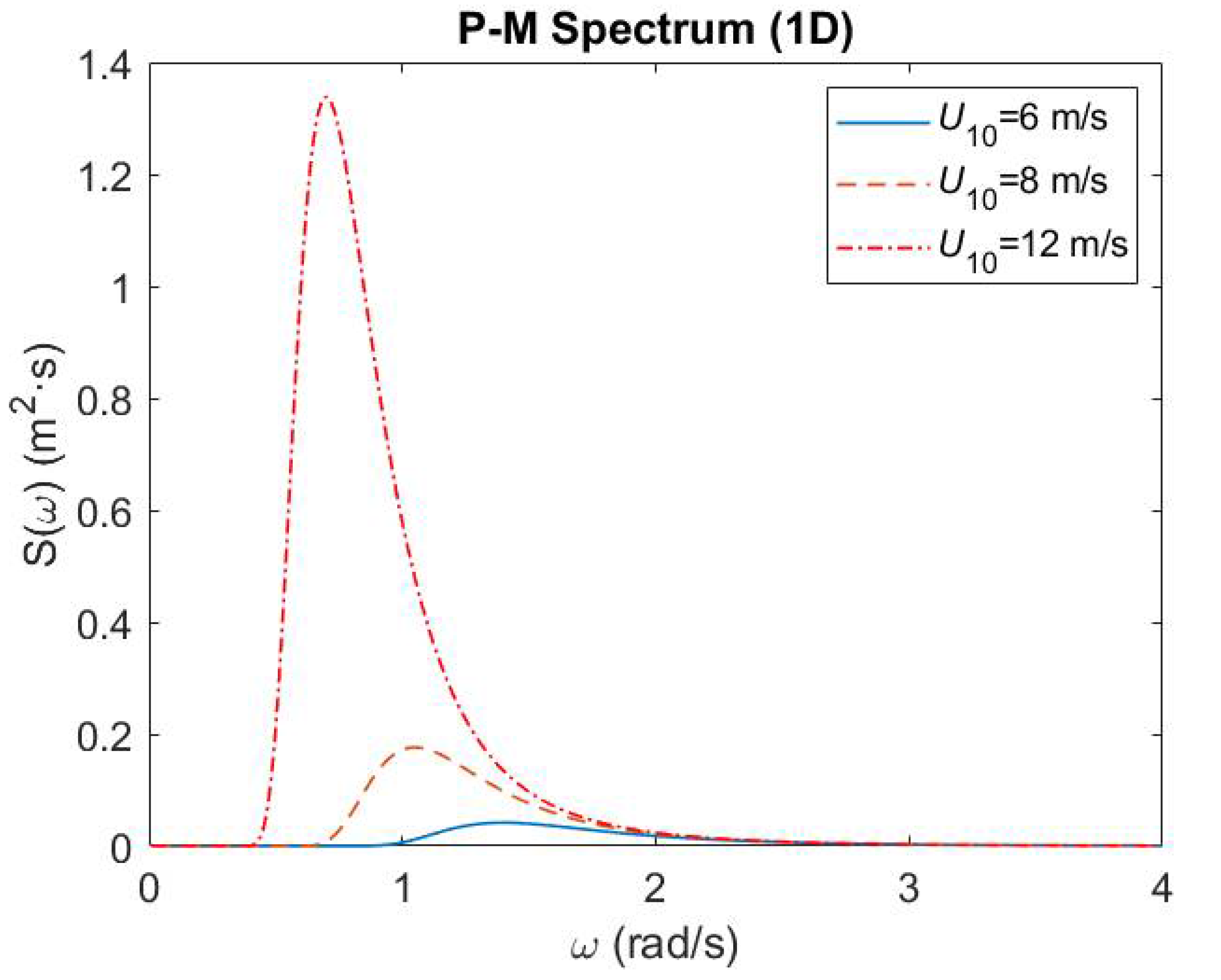
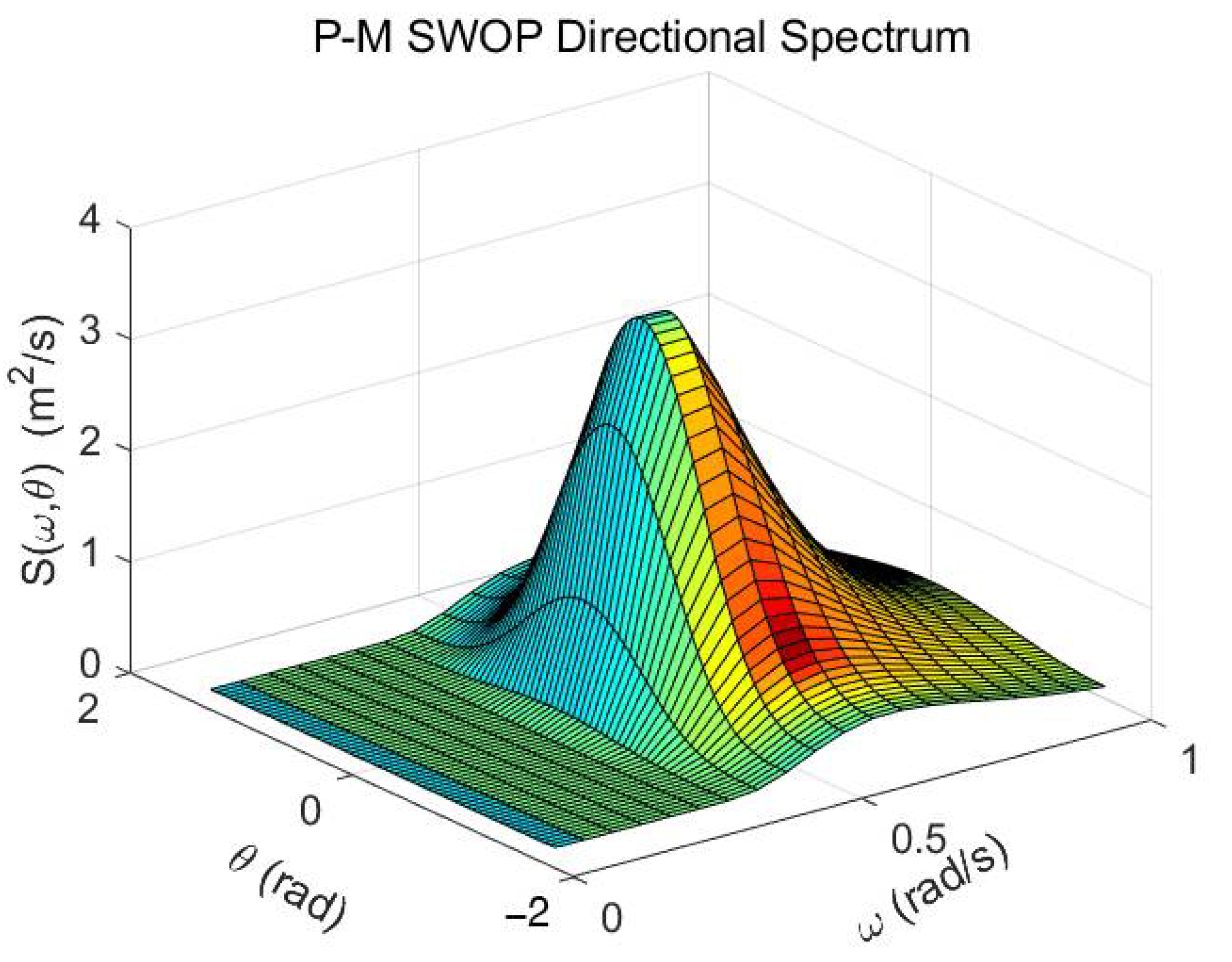
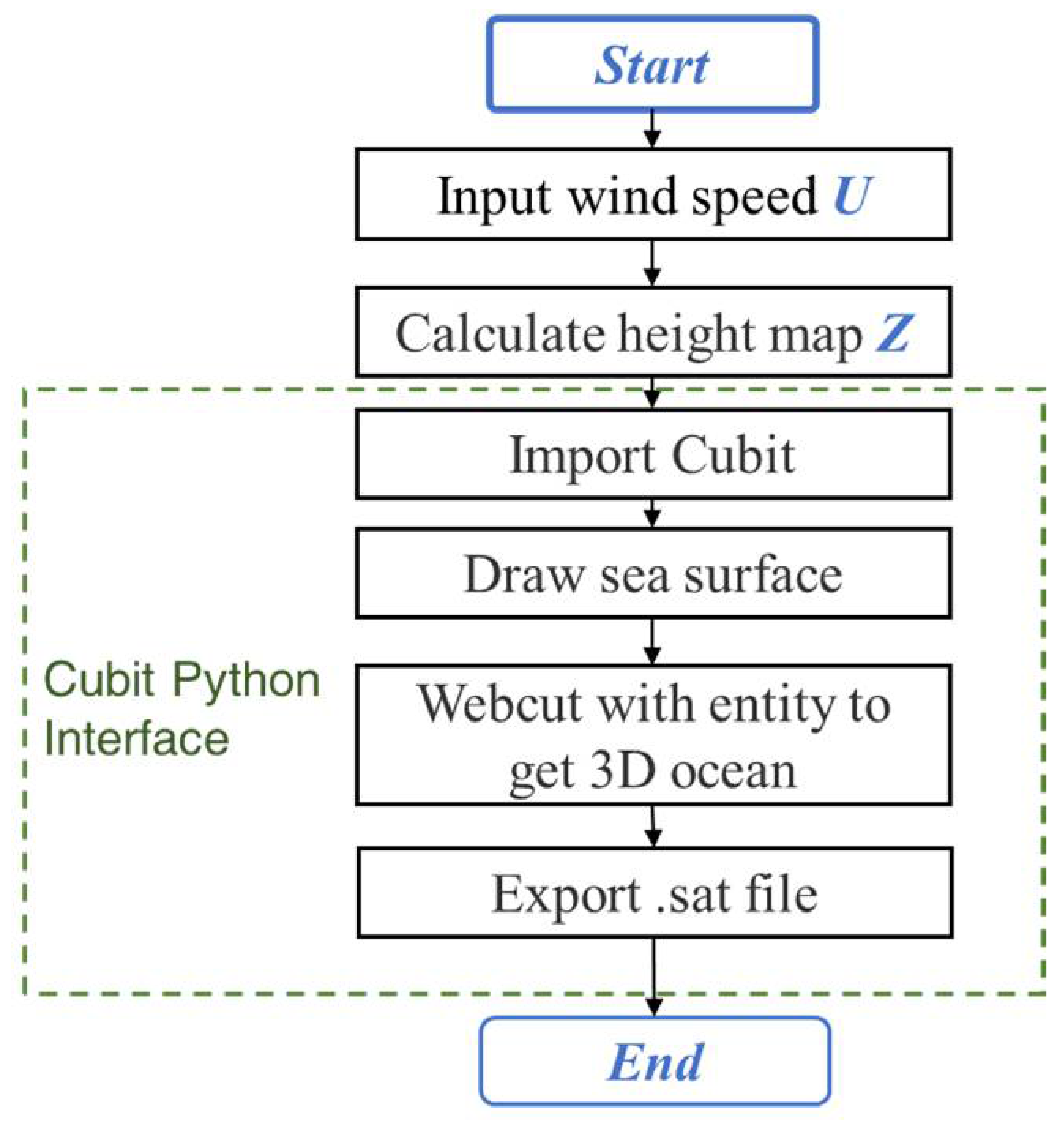
2.1. Rough Sea Surface Modeling Based on Directional Spectrum
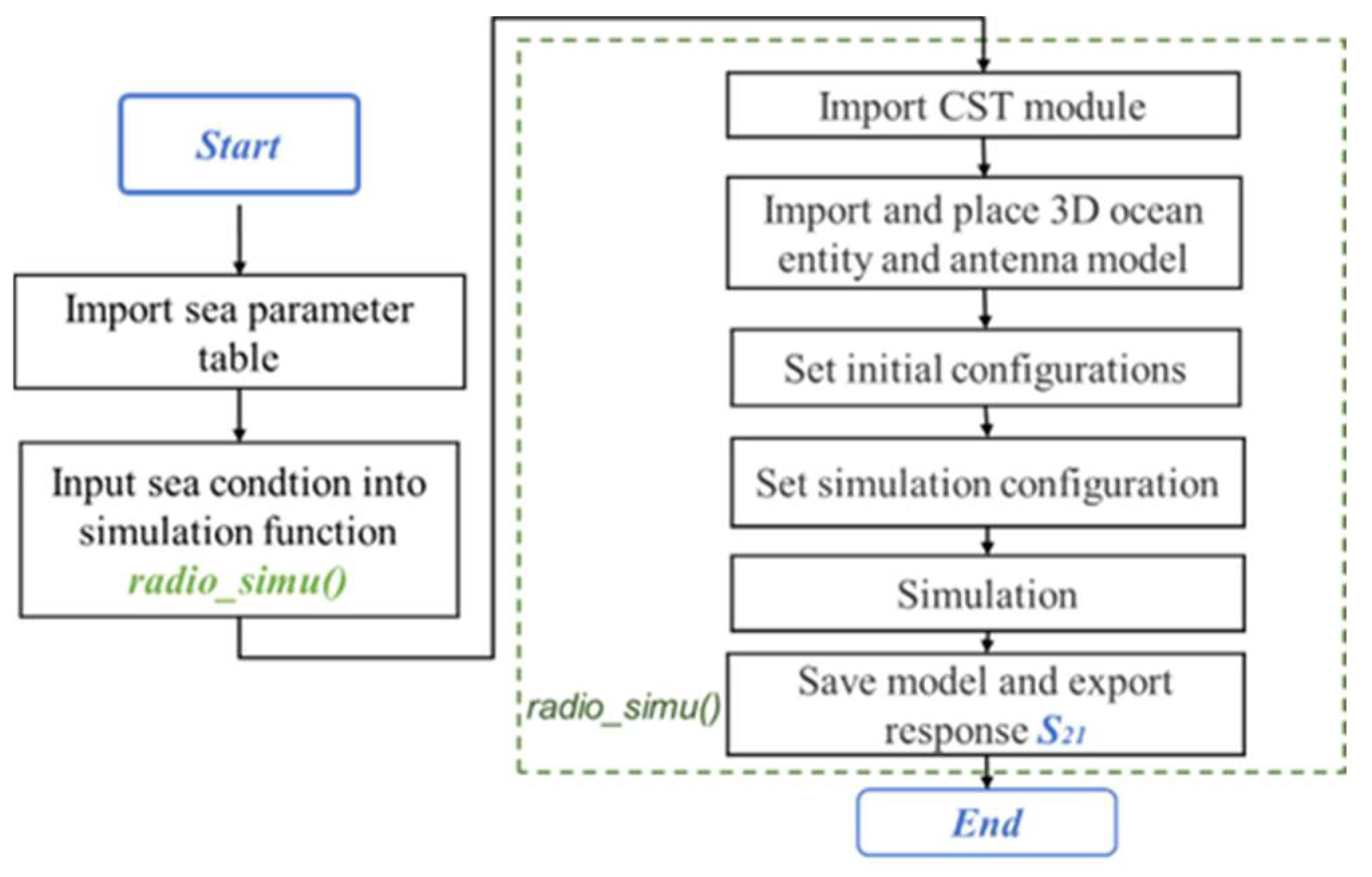
2.2. Simulation of Radio Wave Propagation over Sea
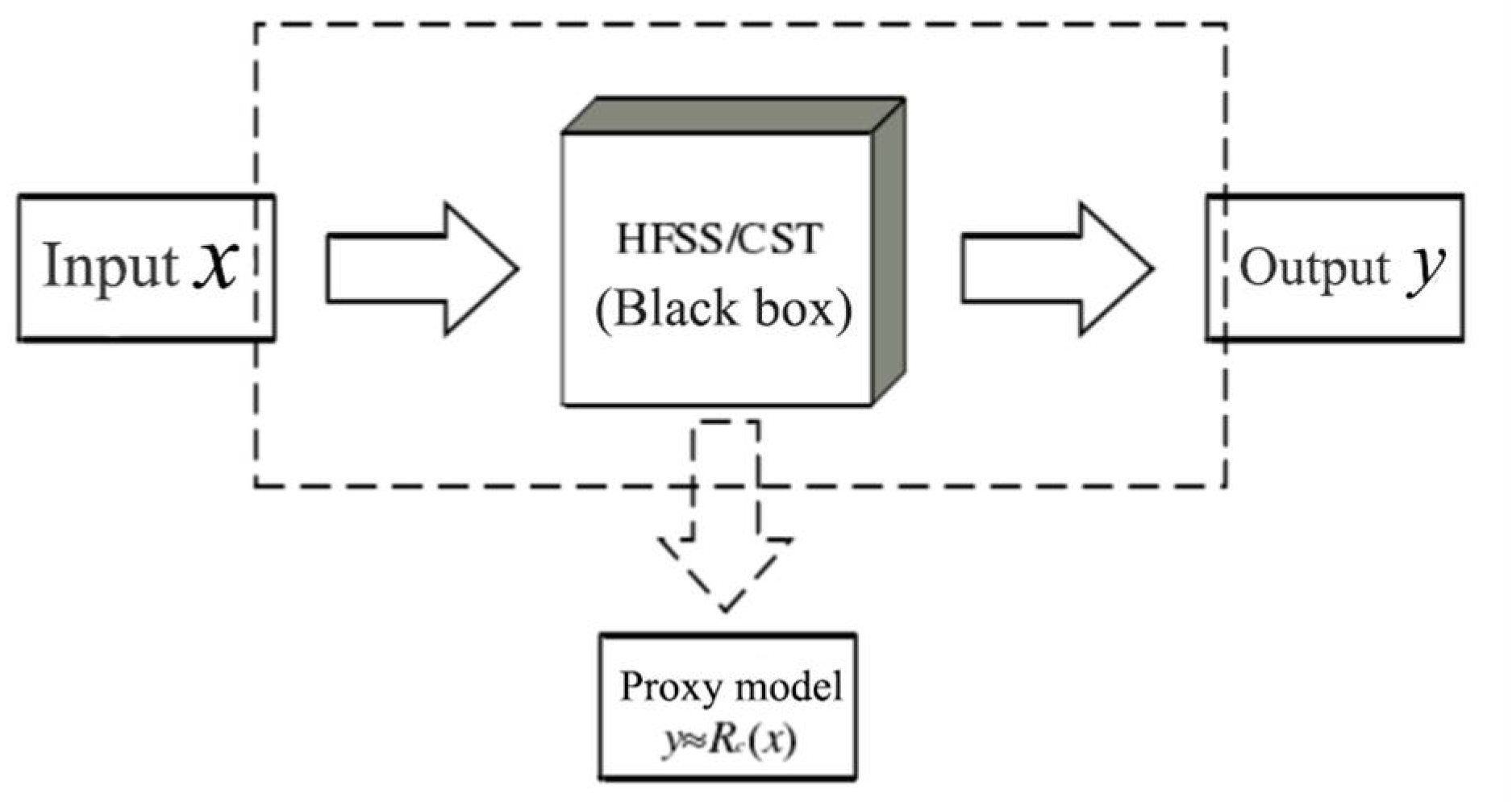
2.3. Surrogate Model Based on Machine Learning
| Algorithm 1. Back Propagation Algorithm. | |
| Input: | Train set , learning rate |
| Procedure: | |
| 1. | Randomly initialize all connection weights and thresholds in the network within the range of (0, 1) |
| 2. | Repeat |
| 3. | for all do |
| 4. | Calculate current output |
| 5. | Calculate the gradient of the output layer neuron. |
| 6. | Calculate the gradient of hidden layer neurons |
| 7. | Update connection weight and threshold |
| 8. | end for |
| 9. | until: stop requirement satisfied |
| Output: | Multi-layer feedforward neural network with connection weights and thresholds determined |
3. Results
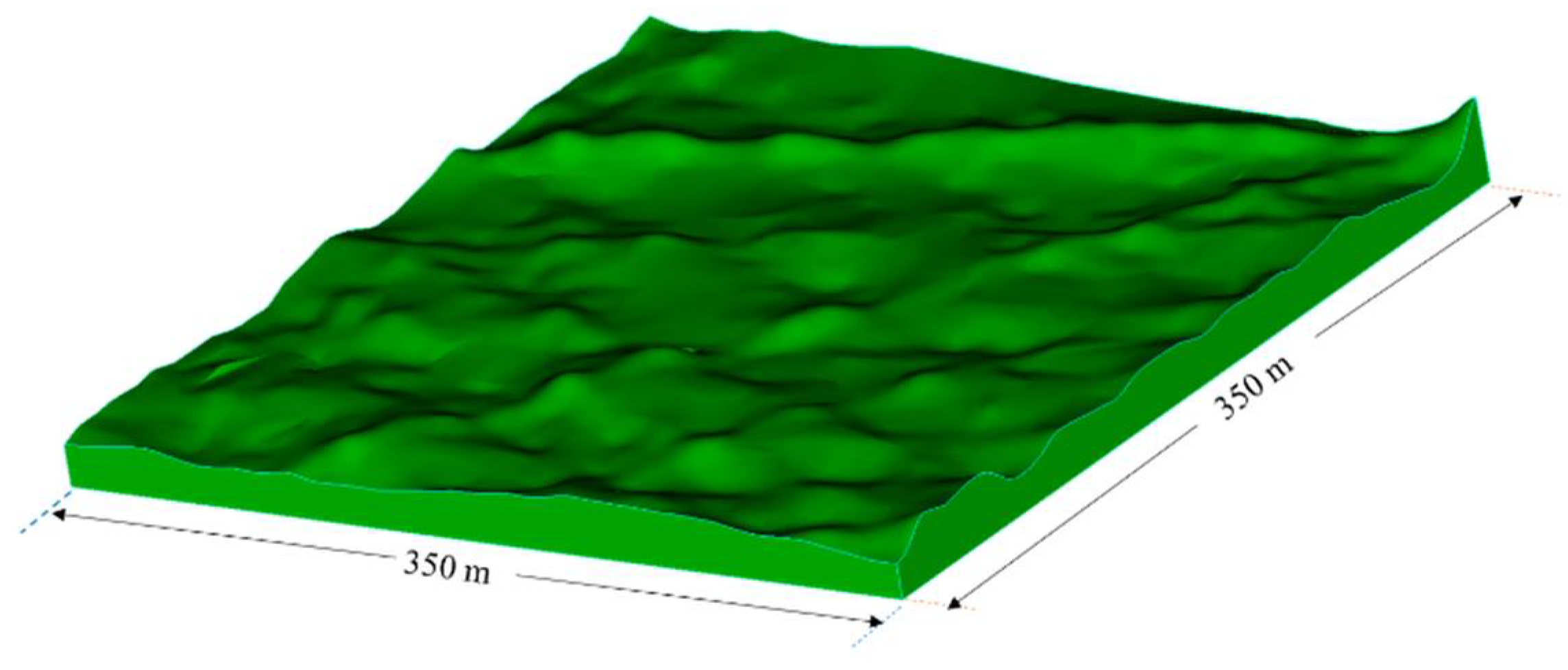
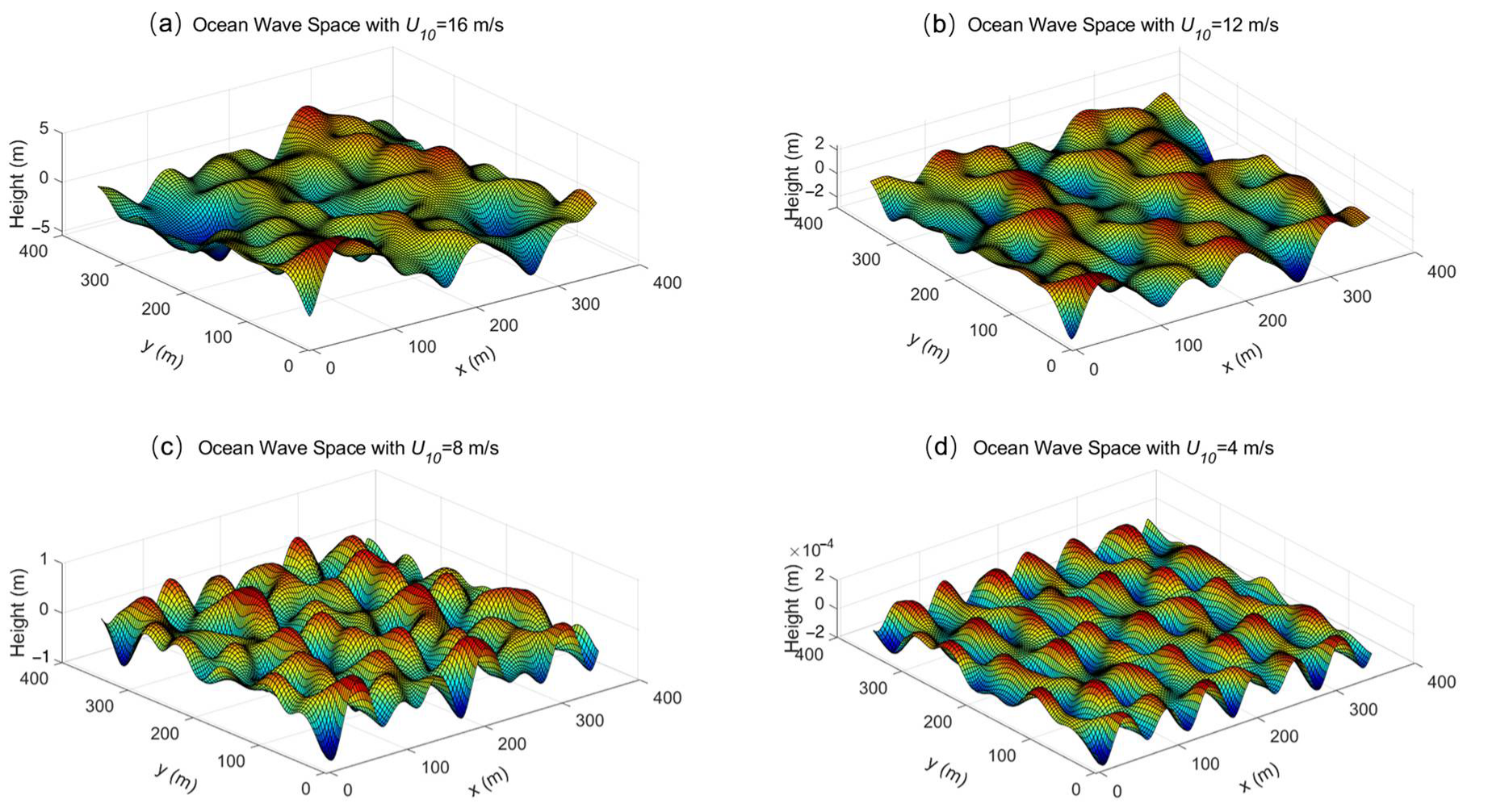
3.1. Three-Dimensional Sea Surface Establishment
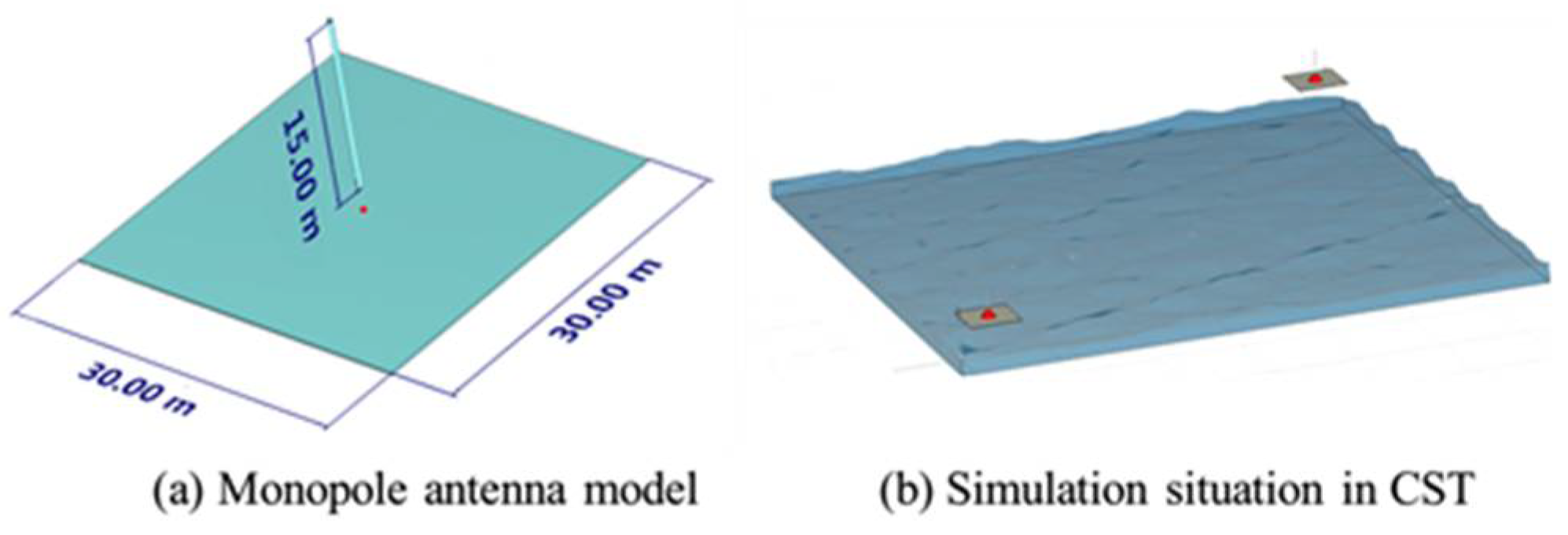
3.2. Radio Propagation Simulation over Rough Sea
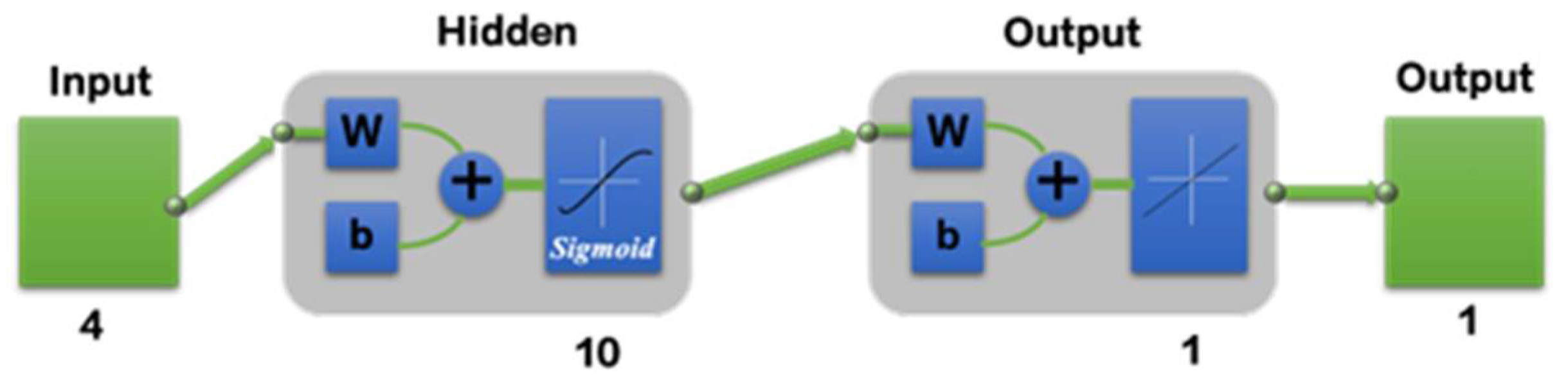
3.3. BP Neural Network Generates Prediction Model
3.3.1. Experimental Data Set
3.3.2. Evaluation Criteria for Prediction Capacity
3.3.3. Other Compared Classical Machine Learning Methods
- Support Vector Machine (SVM):
- 2.
- Decision Tree (DT) method [60]:
- 3.
- Random Forest (RF) method [61]:
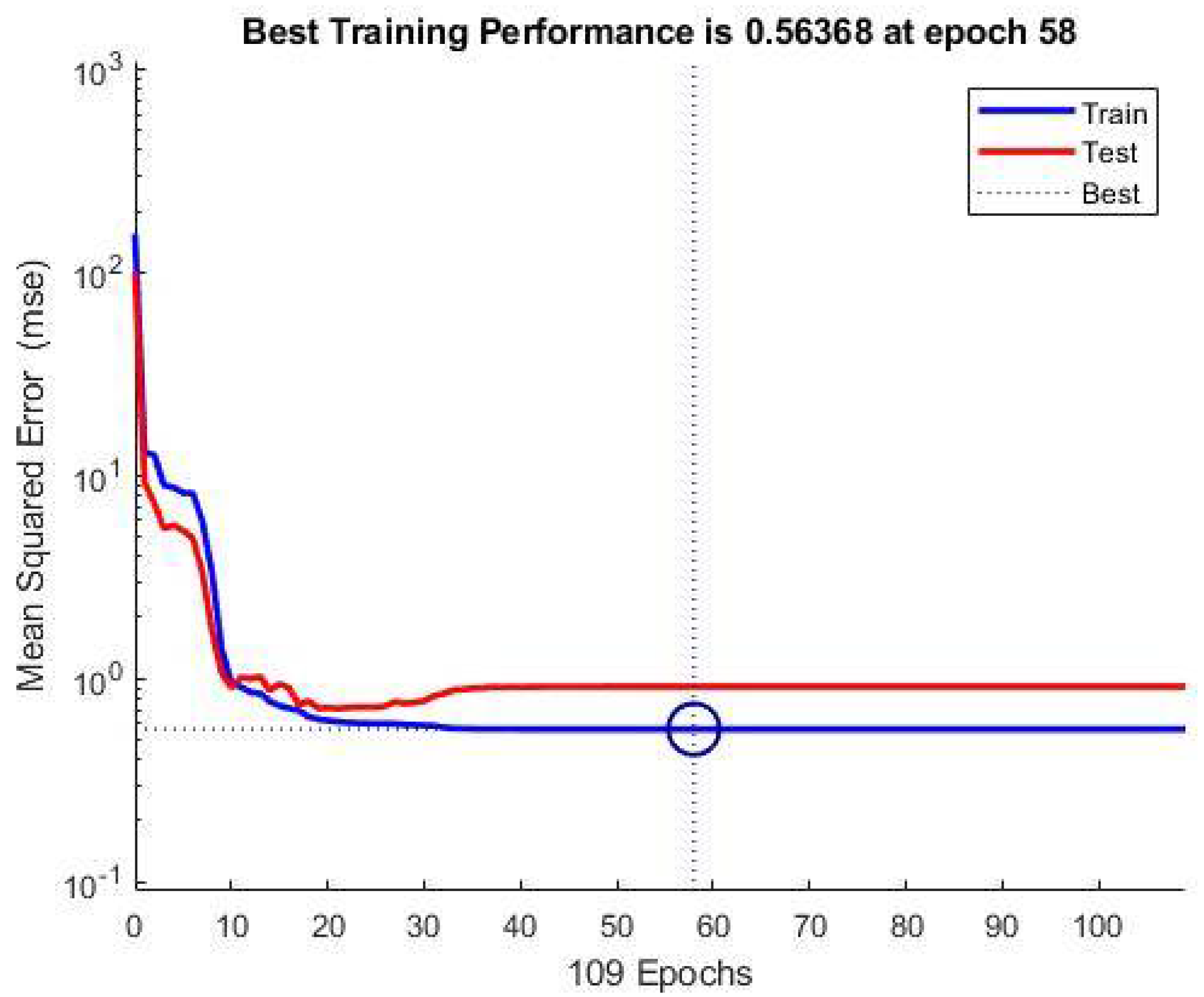
3.3.4. Optimization of the BP Neural Network
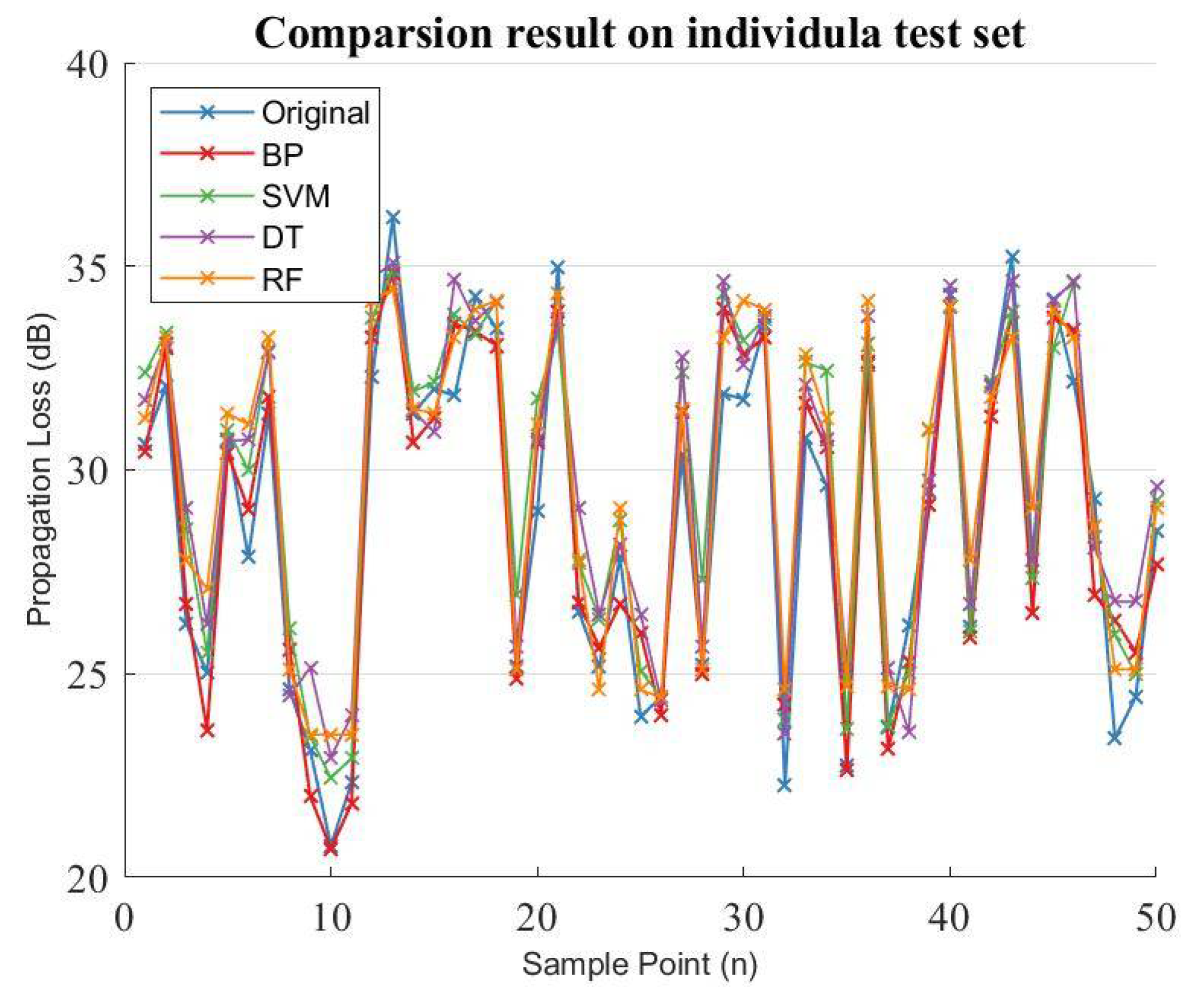
3.3.5. Propagation Loss Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Uribe, C.; Grote, W. Radio Communication Model for Underwater WSN. In Proceedings of the 2009 3rd International Conference on New Technologies, Mobility and Security, Cairo, Egypt, 23 December 2009; IEEE: Cairo, Egypt, 2009; pp. 1–5. [Google Scholar]
- Jimenez, E.; Quintana, G.; Mena, P.; Dorta, P.; Perez-Alvarez, I.; Zazo, S.; Perez, M.; Quevedo, E. Investigation on Radio Wave Propagation in Shallow Seawater: Simulations and Measurements. In Proceedings of the 2016 IEEE Third Underwater Communications and Networking Conference (UComms), Lerici, Italy, 30 August–1 September 2016; IEEE: Lerici, Italy, 2016; pp. 1–5. [Google Scholar]
- Goh, J.H.; Shaw, A.; Al-Shamma’a, A.I. Underwater Wireless Communication System. J. Phys. Conf. Ser. 2009, 178, 012029. [Google Scholar] [CrossRef]
- Shaw, A.; Al-Shamma’a, A.i.; Wylie, S.R.; Toal, D. Experimental Investigations of Electromagnetic Wave Propagation in Seawater. In Proceedings of the 2006 European Microwave Conference, Manchester, UK, 10–15 September 2006; IEEE: Manchester, UK, 2006; pp. 572–575. [Google Scholar]
- Al-Shamma’a, A.I.; Shaw, A.; Saman, S. Propagation of Electromagnetic Waves at MHz Frequencies Through Seawater. IEEE Trans. Antennas Propagat. 2004, 52, 2843–2849. [Google Scholar] [CrossRef]
- Hunt, K.P.; Niemeier, J.J.; Kruger, A. RF Communications in Underwater Wireless Sensor Networks. In Proceedings of the 2010 IEEE International Conference on Electro/Information Technology, Normal, IL, USA, 20–22 May 2010; IEEE: Normal, IL, USA, 2010; pp. 1–6. [Google Scholar]
- Button, R.; Acquisition and Technology Policy Center (Eds.) A Survey of Missions for Unmanned Undersea Vehicles; RAND Corporation monograph series; RAND: Santa Monica, CA, USA, 2009; ISBN 978-0-8330-4688-8. [Google Scholar]
- Zhang, J.P.; Wu, Z.-S.; Zhao, Z.-W.; Zhang, Y.-S.; Wang, B. Propagation modeling of ocean-scattered low-elevation GPS signals for maritime tropospheric duct inversion. Chin. Phys. B 2012, 21, 109202. [Google Scholar] [CrossRef]
- Ge, Y.; Kong, P.Y.; Tham, C.K.; Pathmasuntharam, J.S. Connectivity and Route Analysis for a Maritime Communication Network. In Proceedings of the 2007 6th International Conference on Information, Communications & Signal Processing, Singapore, 10–13 December 2007; IEEE: Singapore, 2007; pp. 1–5. [Google Scholar]
- Wang, J.; Zhou, H.; Li, Y.; Sun, Q.; Wu, Y.; Jin, S.; Quek, T.Q.S.; Xu, C. Wireless Channel Models for Maritime Communications. IEEE Access 2018, 6, 68070–68088. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications: Principles and Practice; Prentice Hall: Upper Saddle River, NJ, USA, 1996; ISBN 978-0-7803-1167-1. [Google Scholar]
- Durand, J.C.; Granier, P. Radar coverage assessment in nonstandard and ducting conditions: A geometrical optics approach. In IEE Proceedings F (Radar and Signal Processing); IET Digital Library: Wales and Scotland, UK, 1990; pp. 95–101. [Google Scholar]
- Popov, A.V.; Kopeikin, V.V. Electromagnetic Pulse Propagation over Nonuniform Earth Surface: Numerical Simulation. arXiv 2007. [Google Scholar] [CrossRef]
- Yang, K.; Molisch, A.F.; Ekman, T.; Roste, T. A Deterministic Round Earth Loss Model for Open-Sea Radio Propagation. In Proceedings of the 2013 IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; IEEE: Dresden, Germany, 2013; pp. 1–5. [Google Scholar]
- Yang, K.; Molisch, A.F.; Ekman, T.; Roste, T.; Berbineau, M. A Round Earth Loss Model and Small-Scale Channel Properties for Open-Sea Radio Propagation. IEEE Trans. Veh. Technol. 2019, 68, 8449–8460. [Google Scholar] [CrossRef]
- Doerry, A. Earth Curvature and Atmospheric Refraction Effects on Radar Signal Propagation; Sandia National Lab.: Albuquerque, NM, USA, 2013; p. 1088060. [Google Scholar]
- Gunashekar, S.D.; Siddle, D.R.; Warrington, E.M. Transhorizon Radiowave Propagation Due to Evaporation Ducting: The Effect of Tropospheric Weather Conditions on VHF and UHF Radio Paths over the Sea. Reson 2006, 11, 51–62. [Google Scholar] [CrossRef]
- Hata, M. Empirical Formula for Propagation Loss in Land Mobile Radio Services. IEEE Trans. Veh. Technol. 1980, 29, 317–325. [Google Scholar] [CrossRef]
- Medeisis, A.; Kajackas, A. On the Use of the Universal Okumura-Hata Propagation Prediction Model in Rural Areas. In Proceedings of the VTC2000-Spring. 2000 IEEE 51st Vehicular Technology Conference Proceedings (Cat. No.00CH37026), Tokyo, Japan, 15–18 May 2000; IEEE: Tokyo, Japan, 2000; Volume 3, pp. 1815–1818. [Google Scholar]
- Isabona, J.; Imoize, A.L. Terrain-Based Adaption of Propagation Model Loss Parameters Using Non-Linear Square Regression. J. Eng. Appl. Sci. 2021, 68, 33. [Google Scholar] [CrossRef]
- Kasampalis, S.; Lazaridis, P.I.; Zaharis, Z.D.; Bizopoulos, A.; Paunovska, L.; Zettas, S.; Glover, I.A.; Drogoudis, D.; Cosmas, J. Longley-Rice Model Prediction Inaccuracies in the UHF and VHF TV Bands in Mountainous Terrain. In Proceedings of the 2015 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, Ghent, Belgium, 17–19 June 2015; IEEE: Ghent, Belgium, 2015; pp. 1–5. [Google Scholar]
- Kasampalis, S.; Lazaridis, P.I.; Zaharis, Z.D.; Bizopoulos, A.; Zettas, S.; Cosmas, J. Comparison of Longley-Rice, ITU-R P.1546 and Hata-Davidson Propagation Models for DVB-T Coverage Prediction. In Proceedings of the 2014 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, Beijing, China, 25–27 June 2014; IEEE: Beijing, China, 2014; pp. 1–4. [Google Scholar]
- Ying, Q.; Zhou, Y. Research on Electromagnetic Wave Propagation Model of Sea Area. Master’s Thesis, Hainan University, Haikou, China, 2015. [Google Scholar]
- Teixeira, P.R.F.; Davyt, D.P.; Didier, E.; Ramalhais, R. Numerical Simulation of an Oscillating Water Column Device Using a Code Based on Navier–Stokes Equations. Energy 2013, 61, 513–530. [Google Scholar] [CrossRef]
- Pozzer, C.T.; Pellegrino, S.R.M. Procedural Solid-Space Techniques for Modeling and Animating Waves. Comput. Graph. 2002, 26, 877–885. [Google Scholar] [CrossRef]
- Alves, J.H.G.M.; Banner, M.L.; Young, I.R. Revisiting the Pierson–Moskowitz Asymptotic Limits for Fully Developed Wind Waves. J. Phys. Oceanogr. 2003, 33, 1301–1323. [Google Scholar] [CrossRef]
- Longuet-Higgins, H.C. A Computer Algorithm for Reconstructing a Scene from Two Projections. Nature 1981, 293, 133–135. [Google Scholar] [CrossRef]
- Joelson, M.; Ramamonjiarisoa, A. A Non-Linear Second-Order Stochastic Model of Ocean Surface Waves. Oceanol. Acta 2001, 24, 409–415. [Google Scholar] [CrossRef]
- Jensen, L.S.; Golias, R. Deep-Water Animation and Rendering. In Proceedings of the Game Developer’s Conference (Gamasutra), San Francisco, CA, USA, 10–12 October 2001. [Google Scholar]
- Tessendorf, J.; others Simulating Ocean Water. Simulating nature: Realistic and interactive techniques. Siggraph 2001, 1, 5. [Google Scholar]
- Fréchot, J. Realistic Simulation of Ocean Surface Using Wave Spectra. In Proceedings of the First International Conference on Computer Graphics Theory and Applications (GRAPP 2006), Setúbal, Portugal, 25–28 February 2006; pp. 76–83. [Google Scholar]
- Chen, L.; Shaogui, D.; Zhiqiang, L.; Yiren, F.; Jingjing, Z.; Jutao, Y. Simulation and Application of Electromagnetic Wave Propagation Logging Tool in Microwave Band Based on CST. In Proceedings of the 2021 13th International Symposium on Antennas, Propagation and EM Theory (ISAPE), Zhuhai, China, 1–4 December 2021; IEEE: Zhuhai, China, 2021; pp. 1–3. [Google Scholar]
- Cao, T.; An, C.; Tian, Y. Study on Electromagnetic Propagation Characteristics of Two-Layer Media with CST Software; AIP Publishing LLC: Chongqing, China, 2017; p. 020021. [Google Scholar]
- Seretis, A.; Sarris, C.D. An Overview of Machine Learning Techniques for Radiowave Propagation Modeling. IEEE Trans. Antennas Propagat. 2022, 70, 3970–3985. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Stocker, K.E.; Landstorfer, F.M. Empirical Prediction of Radiowave Propagation by Neural Network Simulator. Electron. Lett. 1992, 28, 724. [Google Scholar] [CrossRef]
- Popescu, I.; Nikitopoulos, D.; Constantinou, P.; Nafornita, I. ANN Prediction Models for Outdoor Environment. In Proceedings of the 2006 IEEE 17th International Symposium on Personal, Indoor and Mobile Radio Communications, Helsinki, Finland, 11–14 September 2006; IEEE: Helsinki, Finland, 2006; pp. 1–5. [Google Scholar]
- Stankovic, Z.; Milovanvic, B.; Veljkovic, M.; Dordevic, A. The Hybrid-Neural Empirical Model for the Electromagnetic Field Level Prediction in Urban Environments. In Proceedings of the 7th Seminar on Neural Network Applications in Electrical Engineering, 2004, NEUREL 2004, Belgrade, Serbia, 23–25 September 2004; IEEE: Belgrade, Serbia, 2004; pp. 189–192. [Google Scholar]
- Neskovic, A.; Neskovic, N.; Paunovic, D. Indoor Electric Field Level Prediction Model Based on the Artificial Neural Networks. IEEE Commun. Lett. 2000, 4, 190–192. [Google Scholar] [CrossRef]
- Mom, J.M.; Mgbe, C.O.; Igwue, G.A. Igwue. Application of artificial neural network for path loss prediction in urban macrocellular environment. Am. J. Eng. Res. 2014, 3, 270–275. [Google Scholar]
- Ostlin, E.; Zepernick, H.-J.; Suzuki, H. Macrocell Path-Loss Prediction Using Artificial Neural Networks. IEEE Trans. Veh. Technol. 2010, 59, 2735–2747. [Google Scholar] [CrossRef]
- Cheerla, S.; Ratnam, D.V.; Borra, H.S. Neural Network-Based Path Loss Model for Cellular Mobile Networks at 800 and 1800 MHz Bands. AEU Int. J. Electron. Commun. 2018, 94, 179–186. [Google Scholar] [CrossRef]
- Dang, M.; Wu, J.; Cui, S.; Guo, X.; Cao, Y.; Wei, H.; Wu, Z. Multiscale Decomposition Prediction of Propagation Loss in Oceanic Tropospheric Ducts. Remote Sens. 2021, 13, 1173. [Google Scholar] [CrossRef]
- Nagao, T.; Hayashi, T. Study on Radio Propagation Prediction by Machine Learning Using Urban Structure Maps. In Proceedings of the 2020 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020; IEEE: Copenhagen, Denmark, 2020; pp. 1–5. [Google Scholar]
- Wu, L.; He, D.; Ai, B.; Wang, J.; Qi, H.; Guan, K.; Zhong, Z. Artificial Neural Network Based Path Loss Prediction for Wireless Communication Network. IEEE Access 2020, 8, 199523–199538. [Google Scholar] [CrossRef]
- Imai, T.; Kitao, K.; Inomata, M. Radio Propagation Prediction Model Using Convolutional Neural Networks by Deep Learning. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–5. [Google Scholar]
- Li, Z.Y.; Hou, X.L. Ocean Wave Real-Time Simulation Based-on Ocean Wave Spectrum and FFT. AMR 2014, 926–930, 3531–3536. [Google Scholar] [CrossRef]
- Best, S.R. On the Use of Scale Brass Models in HF Shipboard Communication Antenna Design. IEEE Antennas Propag. Mag. 2002, 44, 12–23. [Google Scholar] [CrossRef]
- Baldwin, P.J.; Boswell, A.G.P.; Brewster, D.C.; Allwright, J.S. Iterative Calculation of Ship-Borne HF Antenna Performance. IEE Proc. H Microw. Antennas Propag. 1991, 138, 151. [Google Scholar] [CrossRef][Green Version]
- Baker, J.; Youn, H.-S.; Celik, N.; Iskander, M.F. Low-Profile Multifrequency HF Antenna Design for Coastal Radar Applications. Antennas Wirel. Propag. Lett. 2010, 9, 1119–1122. [Google Scholar] [CrossRef]
- Bandler, J.W.; Biernacki, R.M.; Chen, S.H.; Grobelny, P.A.; Hemmers, R.H. Space Mapping Technique for Electromagnetic Optimization. IEEE Trans. Microw. Theory Tech. 1994, 42, 2536–2544. [Google Scholar] [CrossRef]
- Zeng, F.; Duan, B. An Adaptive Metamodel and Its Application on Integrated Electromechanical Optimization of Reflector Antennas. Master’s Thesis, Xidian University, Xi’an, China, 2015. [Google Scholar]
- Li, J.; Cheng, J.; Shi, J.; Huang, F. Brief Introduction of Back Propagation (BP) Neural Network Algorithm and Its Improvement. In Advances in Computer Science and Information Engineering; Jin, D., Lin, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 553–558. [Google Scholar]
- Zhou, Z.-H. Machine Learning; Springer Nature: Berlin, Germany, 2021. [Google Scholar]
- Wang, Z.; Fan, W.; Lin, M. Study and simulation on sea-surface propagation prediction model. Chin. J. Radio Sci. 2008, 23, 1095–1099. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar]
- Abdullah, D.M.; Abdulazeez, A.M. Machine Learning Applications Based on SVM Classification A Review. Qubahan Acad. J. 2021, 1, 81–90. [Google Scholar] [CrossRef]
- Song, Y.-Y.; Ying, L. Decision Tree Methods: Applications for Classification and Prediction. Shanghai Arch. Psychiatry 2015, 27, 130. [Google Scholar] [PubMed]
- Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Hastie, T.; Rosset, S.; Zhu, J.; Zou, H. Multi-Class Adaboost. Stat. Its Interface 2009, 2, 349–360. [Google Scholar] [CrossRef]


| Author | Focus | Coverage | Limitations |
|---|---|---|---|
| Mingxia Dang (2021) [43] | Propagation loss of electromagnetic waves in the oceanic duct | Multiscale decomposition prediction method for predicting the propagation loss | Observation data based |
| Tatsuya Nagao (2020) [44] | Complex radio propagation characteristic in mobile communication | Gradient Boosting using a plurality of weak learners | Applicable only when urban Area |
| Lina Wu (2020) [45] | Wireless network loss prediction and optimization | Path loss prediction model based on MLP neural network | Applicable only when urban Area |
| T. Imai (2019) [46] | Radio propagation prediction model using convolutional neural networks (CNN) | Extract optimal parameters for propagation loss prediction from map-data using CNN | Urban macro or microcell scenario limited |
| Shankun Shen (2022) | Maritime Radio Propagation Loss Prediction | Data-inherited path loss prediction model construction in maritime environment | Large computer resources required for long distances |
| U (m/s) | 0.1 | 0.2 | 0.5 | 1 | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 18 | 20 |
| ωmax (rad/s) | 536.66 | 291.01 | 116.4 | 58.2 | 38.8 | 29.1 | 19.4 | 14.55 | 11.64 | 9.7 | 8.31 | 7.27 | 6.46 | 5.82 | 4.85 | 3.88 | 3.23 | 2.91 |
| U (m/s) | D (m) | HR (m) | HT (m) | S21 (dB) |
|---|---|---|---|---|
| 16 | 493.56053 | 18 | 9 | −34.139 |
| 12 | 171.11984 | 20 | 14 | −27.524 |
| 8 | 342.23968 | 13 | 20 | −31.445 |
| 4 | 212.13203 | 17 | 14 | −24.701 |
| 4 | 408.70772 | 17 | 8 | −33.099 |
| 8 | 476.58997 | 21 | 9 | −34.862 |
| 16 | 393.15137 | 7 | 11 | −31.071 |
| Activation Function | Learning Rate | Initial Learning Rate | Solver | Hidden Layer Size | |
|---|---|---|---|---|---|
| ReLU | 0.001 | adaptive | 0.001 | SGD | 10 |
| Prediction Approaches | MSE | |
|---|---|---|
| SVM | 0.8749 | 2.0685 |
| DT | 0.8406 | 2.6350 |
| RF | 0.8814 | 1.9605 |
| Proposed Method (BP) | 0.9250 | 1.2146 |
| Operation | Time | |
|---|---|---|
| Path Loss by Full Wave Simulation | 3D Sea Surface Generation | 30 min |
| Radio Propagation Simulation | 1.5 h | |
| OVERALL | 2 h | |
| Path Loss by Prediction Model | Input Parameter, Calculate, Output | 0.2 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, S.; Zhang, W.; Zhang, H.; Ren, Q.; Zhang, X.; Li, Y. An Accurate Maritime Radio Propagation Loss Prediction Approach Employing Neural Networks. Remote Sens. 2022, 14, 4753. https://doi.org/10.3390/rs14194753
Shen S, Zhang W, Zhang H, Ren Q, Zhang X, Li Y. An Accurate Maritime Radio Propagation Loss Prediction Approach Employing Neural Networks. Remote Sensing. 2022; 14(19):4753. https://doi.org/10.3390/rs14194753
Chicago/Turabian StyleShen, Shankun, Wei Zhang, Hangkai Zhang, Qiang Ren, Xin Zhang, and Yimin Li. 2022. "An Accurate Maritime Radio Propagation Loss Prediction Approach Employing Neural Networks" Remote Sensing 14, no. 19: 4753. https://doi.org/10.3390/rs14194753
APA StyleShen, S., Zhang, W., Zhang, H., Ren, Q., Zhang, X., & Li, Y. (2022). An Accurate Maritime Radio Propagation Loss Prediction Approach Employing Neural Networks. Remote Sensing, 14(19), 4753. https://doi.org/10.3390/rs14194753




