A Characterisation of Benthic Currents from Seabed Bathymetry: An Object-Based Image Analysis of Cold-Water Coral Mounds
Abstract
1. Introduction
Study Site
2. Materials and Methods
2.1. Multibeam Echosounder Data Acquisition and Processing
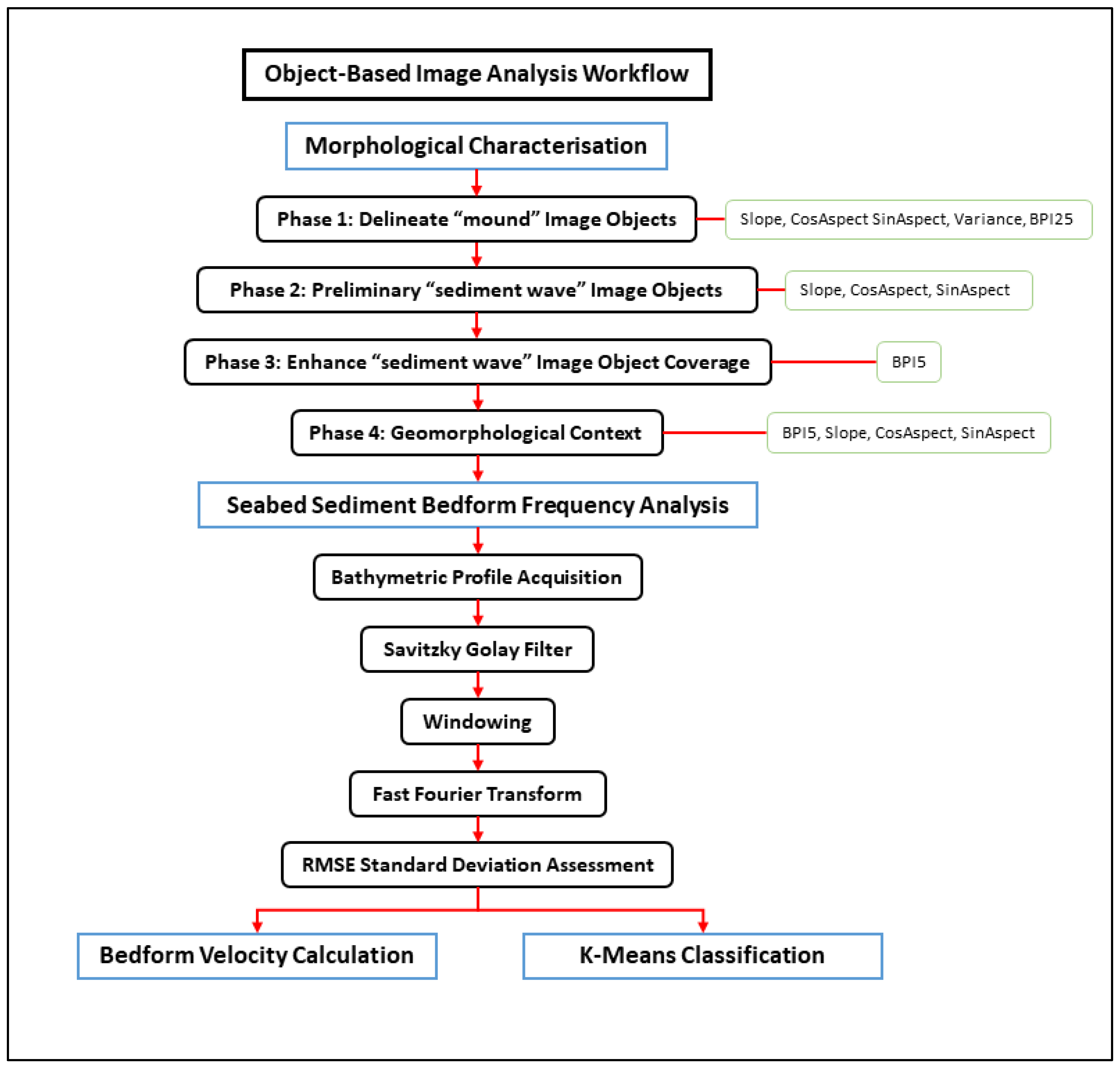
2.2. Object-Based Image Analysis
2.2.1. Morphological Characterisation
2.2.2. Seabed Sediment Bedform (SSB) Frequency Analysis
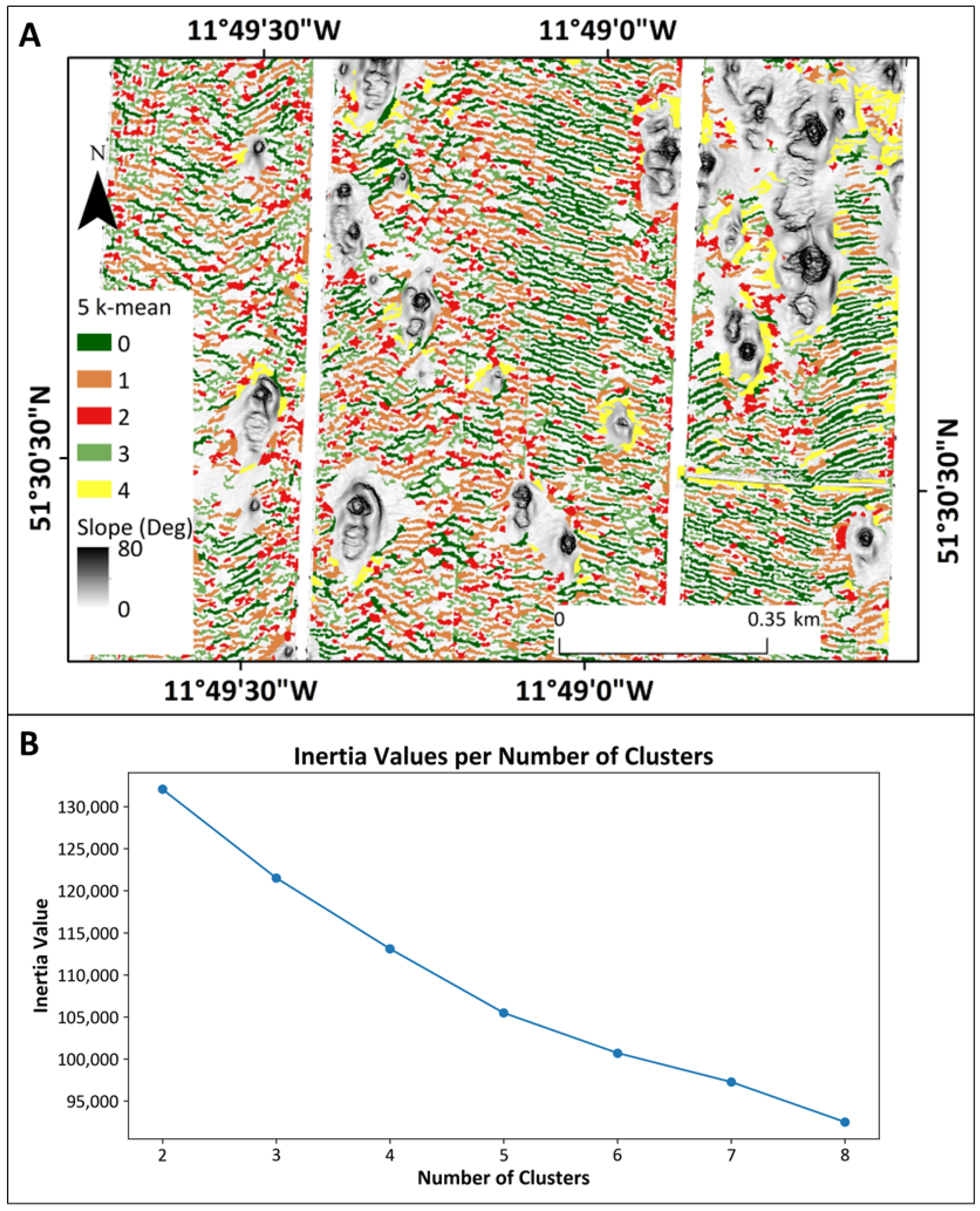
2.2.3. K-Means Classification
2.3. Bedform Velocity Calculation
3. Results
3.1. Multibeam Cross Check Analysis
3.2. Morphological Characterisation
3.3. Fast Fourier Transform and SSB Frequency Analysis
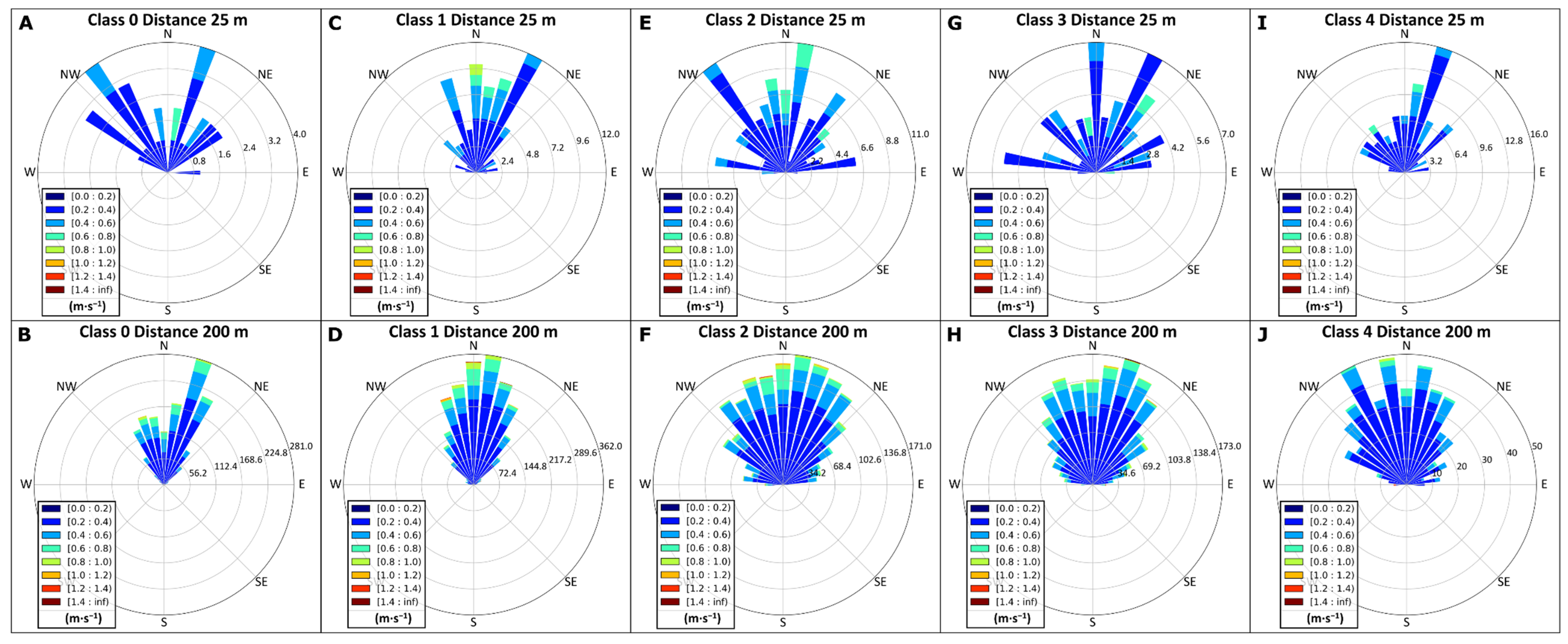
3.4. Classification
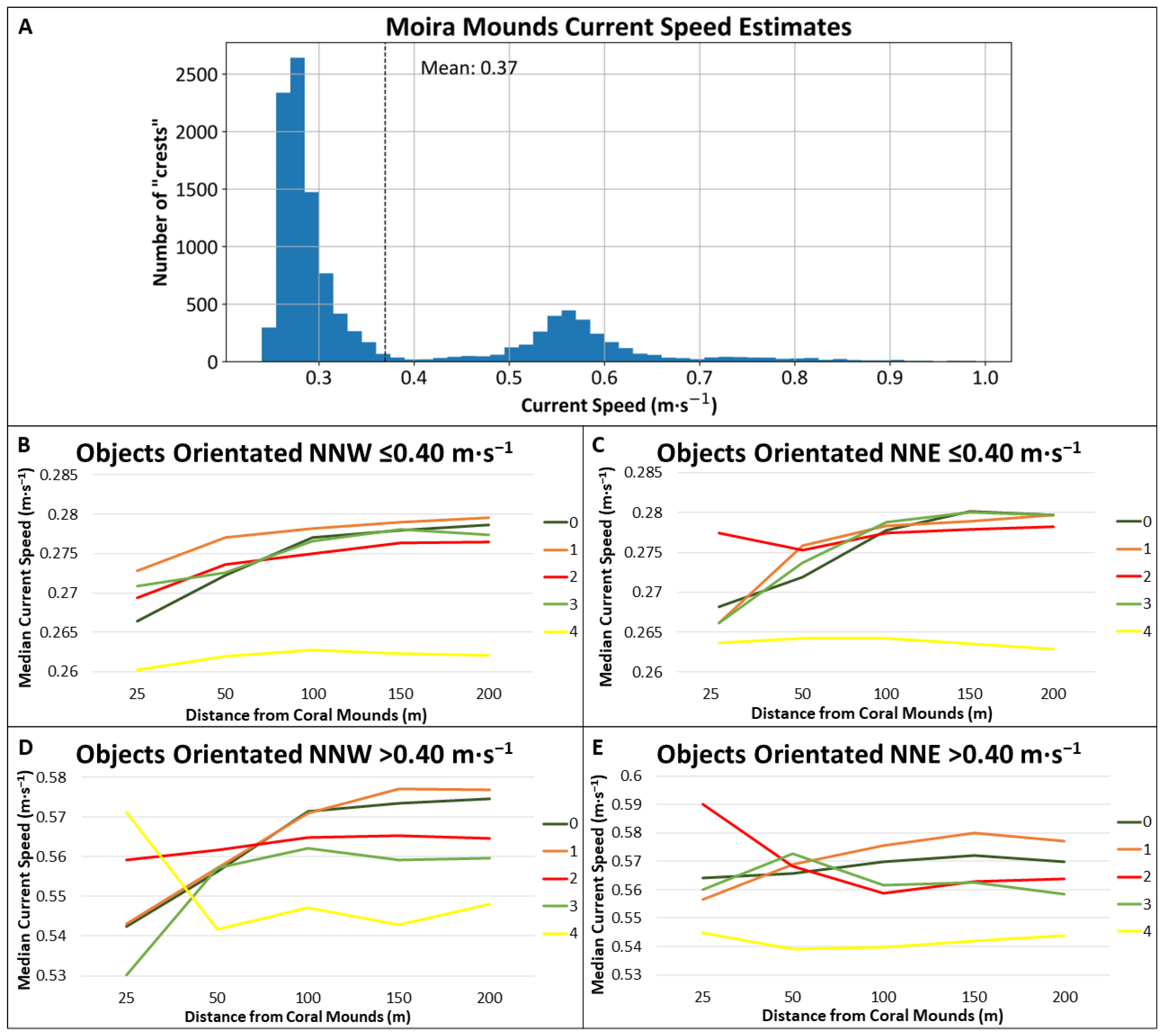
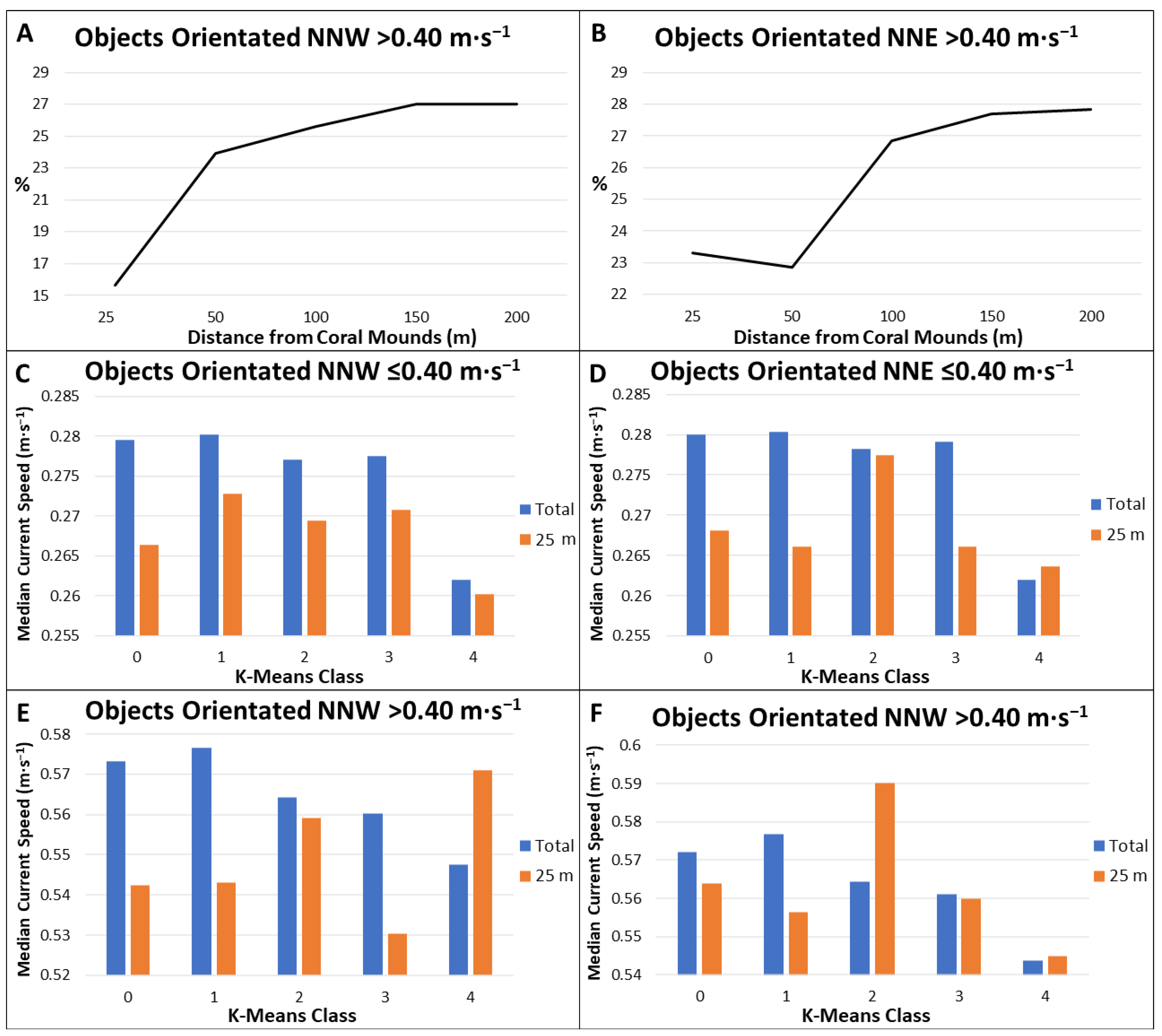
3.5. Current Velocity Analysis
4. Discussion
4.1. K-Means Classification of Sediment Bedform Type
4.2. Regional, Local and Micro Hydrodynamics
4.3. Mound Proximity and SSB Characteristics
4.4. Implications
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Carter, L.; Gavey, R.; Talling, P.J.; Liu, J.T. Insights into submarine geohazards from breaks in subsea telecommunication cables. Oceanography 2014, 27, 58–67. [Google Scholar] [CrossRef]
- Guo, Z.; Hong, Y.; Jeng, D.-S. Structure–Seabed Interactions in Marine Environments. J. Mar. Sci. Eng. 2021, 9, 972. [Google Scholar] [CrossRef]
- Prasad, D.H.; Kumar, N.D. Coastal Erosion Studies—A Review. Int. J. Geosci. 2014, 5, 341–345. [Google Scholar] [CrossRef]
- Degrendele, K.; Roche, M.; Schotte, P.; Van Lancker, V.R.M.; Bellec, V.K.; Bonne, W.M.I. Morphological Evolution of the Kwinte Bank Central Depression before and after the Cessation of Aggregate Extraction. J. Coast. Res. 2010, 77–86. [Google Scholar]
- Wheeler, A.J.; Kozachenko, M.; Masson, D.G.; Huvenne, V.A.I. Influence of benthic sediment transport on cold-water coral bank morphology and growth: The example of the Darwin Mounds, north-east Atlantic. Sedimentology 2008, 55, 1875–1887. [Google Scholar] [CrossRef]
- Roberts, J.M.; Wheeler, A.; Freiwald, A.; Cairns, S. Cold-Water Corals: The Biology and Geology of Deep-Sea Coral Habitats; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kenyon, N.H.; Akhmetzhanov, A.M.; Wheeler, A.J.; van Weering, T.C.E.; de Haas, H.; Ivanov, M.K. Giant carbonate mud mounds in the southern Rockall Trough. Mar. Geol. 2003, 195, 5–30. [Google Scholar] [CrossRef]
- Thierens, M.; Browning, E.; Pirlet, H.; Loutre, M.F.; Dorschel, B.; Huvenne, V.A.I.; Titschack, J.; Colin, C.; Foubert, A.; Wheeler, A.J. Cold-water coral carbonate mounds as unique palaeo-archives: The Plio-Pleistocene Challenger Mound record (NE Atlantic). Quat. Sci. Rev. 2013, 73, 14–30. [Google Scholar] [CrossRef]
- Baillon, S.; Hamel, J.-F.; Wareham, V.E.; Mercier, A. Deep cold-water corals as nurseries for fish larvae. Front. Ecol. Environ. 2012, 10, 351–356. [Google Scholar] [CrossRef]
- Roberts, J.M.; Cairns, S.D. Cold-water corals in a changing ocean. Curr. Opin. Environ. Sustain. 2014, 7, 118–126. [Google Scholar] [CrossRef]
- Chapron, L.; Peru, E.; Engler, A.; Ghiglione, J.F.; Meistertzheim, A.L.; Pruski, A.M.; Purser, A.; Vétion, G.; Galand, P.E.; Lartaud, F. Macro- and microplastics affect cold-water corals growth, feeding and behaviour. Sci. Rep. 2018, 8, 15299. [Google Scholar] [CrossRef]
- Boolukos, C.M.; Lim, A.; O’Riordan, R.M.; Wheeler, A.J. Cold-water corals in decline–A temporal (4 year) species abundance and biodiversity appraisal of complete photomosaiced cold-water coral reef on the Irish Margin. Deep Sea Res. Part I Oceanogr. Res. Pap. 2019, 146, 44–54. [Google Scholar] [CrossRef]
- Dorschel, B.; Wheeler, A.J.; Huvenne, V.A.I.; de Haas, H. Cold-water coral mounds in an erosive environmental setting: TOBI side-scan sonar data and ROV video footage from the northwest Porcupine Bank, NE Atlantic. Mar. Geol. 2009, 264, 218–229. [Google Scholar] [CrossRef]
- Lim, A.; Huvenne, V.A.I.; Vertino, A.; Spezzaferri, S.; Wheeler, A.J. New insights on coral mound development from groundtruthed high-resolution ROV-mounted multibeam imaging. Mar. Geol. 2018, 403, 225–237. [Google Scholar] [CrossRef]
- Lim, A.; Wheeler, A.J.; Price, D.M.; O’Reilly, L.; Harris, K.; Conti, L. Influence of benthic currents on cold-water coral habitats: A combined benthic monitoring and 3D photogrammetric investigation. Sci. Rep. 2020, 10, 19433. [Google Scholar] [CrossRef] [PubMed]
- Matos, L.; Wienberg, C.; Titschack, J.; Schmiedl, G.; Frank, N.; Abrantes, F.; Cunha, M.R.; Hebbeln, D. Coral mound development at the Campeche cold-water coral province, southern Gulf of Mexico: Implications of Antarctic Intermediate Water increased influence during interglacials. Mar. Geol. 2017, 392, 53–65. [Google Scholar] [CrossRef]
- Wienberg, C.; Titschack, J.; Frank, N.; De Pol-Holz, R.; Fietzke, J.; Eisele, M.; Kremer, A.; Hebbeln, D. Deglacial upslope shift of NE Atlantic intermediate waters controlled slope erosion and cold-water coral mound formation (Porcupine Seabight, Irish margin). Quat. Sci. Rev. 2020, 237, 106310. [Google Scholar] [CrossRef]
- De Clippele, L.H.; Gafeira, J.; Robert, K.; Hennige, S.; Lavaleye, M.S.; Duineveld, G.C.A.; Huvenne, V.A.I.; Roberts, J.M. Using novel acoustic and visual mapping tools to predict the small-scale spatial distribution of live biogenic reef framework in cold-water coral habitats. Coral Reefs 2017, 36, 255–268. [Google Scholar] [CrossRef]
- van der Kaaden, A.-S.; van Oevelen, D.; Rietkerk, M.; Soetaert, K.; van de Koppel, J. Spatial Self-Organization as a New Perspective on Cold-Water Coral Mound Development. Front. Mar. Sci. 2020, 7, 631. [Google Scholar] [CrossRef]
- Burgos, J.M.; Buhl-Mortensen, L.; Buhl-Mortensen, P.; Ólafsdóttir, S.H.; Steingrund, P.; Ragnarsson, S.Á.; Skagseth, Ø. Predicting the Distribution of Indicator Taxa of Vulnerable Marine Ecosystems in the Arctic and Sub-arctic Waters of the Nordic Seas. Front. Mar. Sci. 2020, 7, 131. [Google Scholar] [CrossRef]
- de Oliveira, L.M.C.; Lim, A.; Conti, L.A.; Wheeler, A.J. 3D Classification of Cold-Water Coral Reefs: A Comparison of Classification Techniques for 3D Reconstructions of Cold-Water Coral Reefs and Seabed. Front. Mar. Sci. 2021, 8, 640713. [Google Scholar] [CrossRef]
- Huvenne, V.A.I.; Bett, B.J.; Masson, D.G.; Le Bas, T.P.; Wheeler, A.J. Effectiveness of a deep-sea cold-water coral Marine Protected Area, following eight years of fisheries closure. Biol. Conserv. 2016, 200, 60–69. [Google Scholar] [CrossRef]
- Coiras, E.; Iacono, C.L.; Gracia, E.; Danobeitia, J.; Sanz, J.L. Automatic Segmentation of Multi-Beam Data for Predictive Mapping of Benthic Habitats on the Chella Seamount (North-Eastern Alboran Sea, Western Mediterranean). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 809–813. [Google Scholar] [CrossRef]
- Diesing, M.; Thorsnes, T. Mapping of Cold-Water Coral Carbonate Mounds Based on Geomorphometric Features: An Object-Based Approach. Geosciences 2018, 8, 34. [Google Scholar] [CrossRef]
- Savini, A.; Vertino, A.; Marchese, F.; Beuck, L.; Freiwald, A. Mapping Cold-Water Coral Habitats at Different Scales within the Northern Ionian Sea (Central Mediterranean): An Assessment of Coral Coverage and Associated Vulnerability. PLoS ONE 2014, 9, e87108. [Google Scholar] [CrossRef] [PubMed]
- Conti, L.A.; Lim, A.; Wheeler, A.J. High resolution mapping of a cold water coral mound. Sci. Rep. 2019, 9, 1016. [Google Scholar] [CrossRef]
- Calvert, J.; Strong, J.A.; Service, M.; McGonigle, C.; Quinn, R. An evaluation of supervised and unsupervised classification techniques for marine benthic habitat mapping using multibeam echosounder data. ICES J. Mar. Sci. 2014, 72, 1498–1513. [Google Scholar] [CrossRef]
- Janowski, L.; Trzcinska, K.; Tegowski, J.; Kruss, A.; Rucinska-Zjadacz, M.; Pocwiardowski, P. Nearshore Benthic Habitat Mapping Based on Multi-Frequency, Multibeam Echosounder Data Using a Combined Object-Based Approach: A Case Study from the Rowy Site in the Southern Baltic Sea. Remote Sens. 2018, 10, 1983. [Google Scholar] [CrossRef]
- Huvenne, V.A.; Tyler, P.A.; Masson, D.G.; Fisher, E.H.; Hauton, C.; Huhnerbach, V.; Le Bas, T.P.; Wolff, G.A. A picture on the wall: Innovative mapping reveals cold-water coral refuge in submarine canyon. PLoS ONE 2011, 6, e28755. [Google Scholar] [CrossRef]
- Robert, K.; Huvenne, V.A.I.; Georgiopoulou, A.; Jones, D.O.B.; Marsh, L.; Carter, G.D.O.; Chaumillon, L. New approaches to high-resolution mapping of marine vertical structures. Sci. Rep. 2017, 7, 9005. [Google Scholar] [CrossRef]
- Mayer, L.; Jakobsson, M.; Allen, G.; Dorschel, B.; Falconer, R.; Ferrini, V.; Lamarche, G.; Snaith, H.; Weatherall, P. The Nippon Foundation—GEBCO seabed 2030 project: The quest to see the world’s oceans completely mapped by 2030. Geosciences 2018, 8, 63. [Google Scholar] [CrossRef]
- Thorsnes, T. MAREANO–an introduction. Nor. J. Geol. 2009, 89, 3. [Google Scholar]
- Guinan, J.; McKeon, C.; Keeffe, E.; Monteys, X.; Sacchetti, F.; Coughlan, M.; Nic Aonghusa, C. INFOMAR data supports offshore energy development and marine spatial planning in the Irish offshore via the EMODnet Geology portal. Q. J. Eng. Geol. Hydrogeol. 2021, 54, qjegh2020-033. [Google Scholar] [CrossRef]
- Diesing, M.; Green, S.L.; Stephens, D.; Lark, R.M.; Stewart, H.A.; Dove, D. Mapping seabed sediments: Comparison of manual, geostatistical, object-based image analysis and machine learning approaches. Cont. Shelf Res. 2014, 84, 107–119. [Google Scholar] [CrossRef]
- Zelada Leon, A.; Huvenne, V.A.I.; Benoist, N.M.A.; Ferguson, M.; Bett, B.J.; Wynn, R.B. Assessing the Repeatability of Automated Seafloor Classification Algorithms, with Application in Marine Protected Area Monitoring. Remote Sens. 2020, 12, 1572. [Google Scholar] [CrossRef]
- Diesing, M.; Mitchell, P.; Stephens, D. Image-based seabed classification: What can we learn from terrestrial remote sensing? ICES J. Mar. Sci. 2016, 73, 2425–2441. [Google Scholar] [CrossRef]
- Durden, J.; Bett, B.; Schoening, T.; Morris, K.; Nattkemper, T.; Ruhl, H. Comparison of image annotation data generated by multiple investigators for benthic ecology. Mar. Ecol. Prog. Ser. 2016, 552, 61–70. [Google Scholar] [CrossRef]
- Lim, A.; Wheeler, A.J.; Conti, L. Cold-Water Coral Habitat Mapping: Trends and Developments in Acquisition and Processing Methods. Geosciences 2021, 11, 9. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Ierodiaconou, D.; Schimel, A.C.G.; Kennedy, D.; Monk, J.; Gaylard, G.; Young, M.; Diesing, M.; Rattray, A. Combining pixel and object based image analysis of ultra-high resolution multibeam bathymetry and backscatter for habitat mapping in shallow marine waters. Mar. Geophys. Res. 2018, 39, 271–288. [Google Scholar] [CrossRef]
- Trzcinska, K.; Janowski, L.; Nowak, J.; Rucinska-Zjadacz, M.; Kruss, A.; von Deimling, J.S.; Pocwiardowski, P.; Tegowski, J. Spectral features of dual-frequency multibeam echosounder data for benthic habitat mapping. Mar. Geol. 2020, 427, 106239. [Google Scholar] [CrossRef]
- Stow, D.A.; Hernández-Molina, F.J.; Llave, E.; Sayago-Gil, M.; Díaz del Río, V.; Branson, A. Bedform-velocity matrix: The estimation of bottom current velocity from bedform observations. Geology 2009, 37, 327–330. [Google Scholar] [CrossRef]
- Huvenne, V.A.I.; Blondel, P.; Henriet, J.P. Textural analyses of sidescan sonar imagery from two mound provinces in the Porcupine Seabight. Mar. Geol. 2002, 189, 323–341. [Google Scholar] [CrossRef]
- Foubert, A.; Beck, T.; Wheeler, A.J.; Opderbecke, J.; Grehan, A.; Klages, M.; Thiede, J.; Henriet, J.-P.; Polarstern, A.-X. New view of the Belgica Mounds, Porcupine Seabight, NE Atlantic: Preliminary results from the Polarstern ARK-XIX/3a ROV cruise. In Cold-Water Corals and Ecosystems; Springer: Berlin/Heidelberg, Germany, 2005; pp. 403–415. [Google Scholar]
- Wheeler, A.J.; Kozachenko, M.; Beyer, A.; Foubert, A.; Huvenne, V.A.I.; Klages, M.; Masson, D.G.; Olu-Le Roy, K.; Thiede, J. Sedimentary processes and carbonate mounds in the Belgica Mound province, Porcupine Seabight, NE Atlantic. In Cold-Water Corals and Ecosystems; Freiwald, A., Roberts, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 571–603. [Google Scholar] [CrossRef]
- Beyer, A.; Schenke, H.W.; Klenke, M.; Niederjasper, F. High resolution bathymetry of the eastern slope of the Porcupine Seabight. Mar. Geol. 2003, 198, 27–54. [Google Scholar] [CrossRef]
- Wheeler, A.J.; Kozachenko, M.; Henry, L.A.; Foubert, A.; de Haas, H.; Huvenne, V.A.I.; Masson, D.G.; Olu, K. The Moira Mounds, small cold-water coral banks in the Porcupine Seabight, NE Atlantic: Part A—An early stage growth phase for future coral carbonate mounds? Mar. Geol. 2011, 282, 53–64. [Google Scholar] [CrossRef]
- Lim, A.; Wheeler, A.J.; Arnaubec, A. High-resolution facies zonation within a cold-water coral mound: The case of the Piddington Mound, Porcupine Seabight, NE Atlantic. Mar. Geol. 2017, 390, 120–130. [Google Scholar] [CrossRef]
- White, M. Benthic dynamics at the carbonate mound regions of the Porcupine Sea Bight continental margin. Int. J. Earth Sci. 2007, 96, 1–9. [Google Scholar] [CrossRef]
- Fentimen, R.; Rüggeberg, A.; Lim, A.; Kateb, A.E.; Foubert, A.; Wheeler, A.J.; Spezzaferri, S. Benthic foraminifera in a deep-sea high-energy environment: The Moira Mounds (Porcupine Seabight, SW of Ireland). Swiss J. Geosci. 2018, 111, 561–572. [Google Scholar] [CrossRef]
- Dorschel, B.; Hebbeln, D.; Foubert, A.; White, M.; Wheeler, A.J. Hydrodynamics and cold-water coral facies distribution related to recent sedimentary processes at Galway Mound west of Ireland. Mar. Geol. 2007, 244, 184–195. [Google Scholar] [CrossRef]
- Lim, A.; Kane, A.; Arnaubec, A.; Wheeler, A.J. Seabed image acquisition and survey design for cold water coral mound characterisation. Mar. Geol. 2018, 395, 22–32. [Google Scholar] [CrossRef]
- Foubert, A.; Huvenne, V.A.I.; Wheeler, A.; Kozachenko, M.; Opderbecke, J.; Henriet, J.P. The Moira Mounds, small cold-water coral mounds in the Porcupine Seabight, NE Atlantic: Part B—Evaluating the impact of sediment dynamics through high-resolution ROV-borne bathymetric mapping. Mar. Geol. 2011, 282, 65–78. [Google Scholar] [CrossRef]
- Wheeler, A.; Capocci, R.; Crippa, L.; Connolly, N.; Hogan, R.; Lim, A.; McCarthy, E.; McGonigle, C.; O’Donnell, E.; O’Sullivan, K. Cruise Report: Quantifying Environmental Controls on Cold-Water Coral Reef Growth (QuERCi); Report No. CE15009; University College Cork: Cork, UK, 2015. [Google Scholar]
- QPS. Qimera, 1.7.6; The International Hydrographic Organization: Monaco-Ville, Monaco, 2019. [Google Scholar]
- International Hydrographic Organisation. IHO Standards for Hydrographic Surveys. In Special Publication; International Hydrographic Organisation: Monte Carlo, Monaco, 2020; p. 41. [Google Scholar]
- Walbridge, S.; Slocum, N.; Pobuda, M.; Wright, D.J. Unified Geomorphological Analysis Workflows with Benthic Terrain Modeler. Geosciences 2018, 8, 94. [Google Scholar] [CrossRef]
- Wilson, M.F.; O’Connell, B.; Brown, C.; Guinan, J.C.; Grehan, A.J. Multiscale terrain analysis of multibeam bathymetry data for habitat mapping on the continental slope. Mar. Geod. 2007, 30, 3–35. [Google Scholar] [CrossRef]
- Lang, S. Object-based image analysis for remote sensing applications: Modeling reality–dealing with complexity. In Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Blaschke, T., Lang, S., Hay, G.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–27. [Google Scholar] [CrossRef]
- Hossain, M.D.; Chen, D. Segmentation for Object-Based Image Analysis (OBIA): A review of algorithms and challenges from remote sensing perspective. ISPRS J. Photogramm. Remote Sens. 2019, 150, 115–134. [Google Scholar] [CrossRef]
- Summers, G.; Lim, A.; Wheeler, A.J. A Scalable, Supervised Classification of Seabed Sediment Waves Using an Object-Based Image Analysis Approach. Remote Sens. 2021, 13, 2317. [Google Scholar] [CrossRef]
- Trimble. eCognition Developer 9.0 User Guide; Trimble Germany GmbH: Munich, Germany, 2014. [Google Scholar]
- Lacharité, M.; Brown, C.J.; Gazzola, V. Multisource multibeam backscatter data: Developing a strategy for the production of benthic habitat maps using semi-automated seafloor classification methods. Mar. Geophys. Res. 2018, 39, 307–322. [Google Scholar] [CrossRef]
- Trimble. Ecognition Developer Reference Book 10.0.1; Trimble Germany GmbH: Munich, Germany, 2020. [Google Scholar]
- Gao, Y.; Mas, J.F.; Kerle, N.; Navarrete Pacheco, J.A. Optimal region growing segmentation and its effect on classification accuracy. Int. J. Remote Sens. 2011, 32, 3747–3763. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Marpu, P.R.; Neubert, M.; Herold, H.; Niemeyer, I. Enhanced evaluation of image segmentation results. J. Spat. Sci. 2010, 55, 55–68. [Google Scholar] [CrossRef]
- Johansen, K.; Tiede, D.; Blaschke, T.; Arroyo, L.A.; Phinn, S. Automatic Geographic Object Based Mapping of Streambed and Riparian Zone Extent from LiDAR Data in a Temperate Rural Urban Environment, Australia. Remote Sens. 2011, 3, 1139–1156. [Google Scholar] [CrossRef]
- Lebrec, U.; Riera, R.; Paumard, V.; Leary, M.J.; Lang, S.C. Automatic Mapping and Characterisation of Linear Depositional Bedforms: Theory and Application Using Bathymetry from the North West Shelf of Australia. Remote Sens. 2022, 14, 280. [Google Scholar] [CrossRef]
- Cazenave, P.W.; Dix, J.K.; Lambkin, D.O.; McNeill, L.C. A method for semi-automated objective quantification of linear bedforms from multi-scale digital elevation models. Earth Surf. Processes Landf. 2013, 38, 221–236. [Google Scholar] [CrossRef]
- Tegowski, J.; Trzcinska, K.; Kasprzak, M.; Nowak, J. Statistical and Spectral Features of Corrugated Seafloor Shaped by the Hans Glacier in Svalbard. Remote Sens. 2016, 8, 744. [Google Scholar] [CrossRef]
- Tęgowski, J.; Trzcińska, K.; Janowski, Ł.; Kruss, A.; Kusek, K.; Nowak, J. Comparison of Backscatter and Seabed Topographic Characteristics Recorded by Multibeam Echosounder at Rewal Area-Southern Baltic Sea. In Proceedings of the 2018 Joint Conference-Acoustics, Ustka, Poland, 11–14 September 2018; pp. 1–4. [Google Scholar]
- Levey, R.A.; Kjerfve, B.; Getzen, R.T. Comparison of bed form variance spectra within a meander bend during flood and average discharge. J. Sediment. Res. 1980, 50, 149–155. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Perron, J.T.; Kirchner, J.W.; Dietrich, W.E. Spectral signatures of characteristic spatial scales and nonfractal structure in landscapes. J. Geophys. Res. Earth Surf. 2008, 113, F04003. [Google Scholar] [CrossRef]
- Kuai, K.Z.; Tsai, C.W. Identification of varying time scales in sediment transport using the Hilbert–Huang Transform method. J. Hydrol. 2012, 420–421, 245–254. [Google Scholar] [CrossRef]
- Harris, R.I.D. Testing for unit roots using the augmented Dickey-Fuller test: Some issues relating to the size, power and the lag structure of the test. Econ. Lett. 1992, 38, 381–386. [Google Scholar] [CrossRef]
- Spagnolo, M.; Bartholomaus, T.C.; Clark, C.D.; Stokes, C.R.; Atkinson, N.; Dowdeswell, J.A.; Ely, J.C.; Graham, A.G.C.; Hogan, K.A.; King, E.C.; et al. The periodic topography of ice stream beds: Insights from the Fourier spectra of mega-scale glacial lineations. J. Geophys. Res. Earth Surf. 2017, 122, 1355–1373. [Google Scholar] [CrossRef]
- Wang, L.; Yu, Q.; Zhang, Y.; Flemming, B.W.; Wang, Y.; Gao, S. An automated procedure to calculate the morphological parameters of superimposed rhythmic bedforms. Earth Surf. Processes Landf. 2020, 45, 3496–3509. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Azami, H.; Mohammadi, K.; Bozorgtabar, B. An Improved Signal Segmentation Using Moving Average and Savitzky-Golay Filter. J. Signal Inf. Processing 2012, 3, 6. [Google Scholar] [CrossRef]
- Heil, J.; Häring, V.; Marschner, B.; Stumpe, B. Advantages of fuzzy k-means over k-means clustering in the classification of diffuse reflectance soil spectra: A case study with West African soils. Geoderma 2019, 337, 11–21. [Google Scholar] [CrossRef]
- Javadi, S.; Hashemy, S.M.; Mohammadi, K.; Howard, K.W.F.; Neshat, A. Classification of aquifer vulnerability using K-means cluster analysis. J. Hydrol. 2017, 549, 27–37. [Google Scholar] [CrossRef]
- Ismail, K.; Huvenne, V.A.I.; Masson, D.G. Objective automated classification technique for marine landscape mapping in submarine canyons. Mar. Geol. 2015, 362, 17–32. [Google Scholar] [CrossRef]
- Orhan, U.; Hekim, M.; Ozer, M. EEG signals classification using the K-means clustering and a multilayer perceptron neural network model. Expert Syst. Appl. 2011, 38, 13475–13481. [Google Scholar] [CrossRef]
- Wu, H.; Cheng, Z.; Shi, W.; Miao, Z.; Xu, C. An object-based image analysis for building seismic vulnerability assessment using high-resolution remote sensing imagery. Nat. Hazards 2014, 71, 151–174. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Prampolini, M.; Savini, A.; Foglini, F.; Soldati, M. Seven Good Reasons for Integrating Terrestrial and Marine Spatial Datasets in Changing Environments. Water 2020, 12, 2221. [Google Scholar] [CrossRef]
- Neakrase, L.D.V.; Klose, M.; Titus, T.N. Terrestrial subaqueous seafloor dunes: Possible analogs for Venus. Aeolian Res. 2017, 26, 47–56. [Google Scholar] [CrossRef]

| Image Layers | Scale (Pixel) |
|---|---|
| Aspect | 3 |
| Bathymetric Position Index (BPI) | 5, 25 |
| CosAspect (Northness) | 3 |
| SinAspect (Eastness) | 3 |
| Slope | 3 |
| Variance | 3 |
| Feature Category | Image Object Feature |
|---|---|
| Morphology | Length/Width |
| Shape Index | |
| Length/Area | |
| Area | |
| Roundness | |
| Elliptic Fit | |
| Asymmetry | |
| Rectangular Fit | |
| Curvature/Length | |
| Wavelength | |
| Spatial Density | Point Density |
| Bathymetric Derivative | Mean depth difference to neighbouring “troughs” |
| Mean Slope |
| Class | Area (m2) | Length/Width | Curvature/Length | Slope (Deg) | Wave Height (m) |
|---|---|---|---|---|---|
| 0 | 233 | 3.62 | 6.34 | 1.47 | 0.315 |
| 1 | 155 | 2.79 | 6.29 | 1.46 | 0.323 |
| 2 | 90 | 1.65 | 9.72 | 1.39 | 0.293 |
| 3 | 114 | 1.93 | 10.35 | 1.31 | 0.293 |
| 4 | 170 | 1.93 | 7.15 | 3.27 | 0.128 |
| K-Means Class | Category | Interpretation |
|---|---|---|
| 0 | Large straight SSBs | Elongate parallel SSBs formed due to consistent unidirectional flow. |
| 1 | Medium sinuous SSBs | Truncated parallel SSBs formed due to consistent unidirectional with an increase in bedform superimposition. |
| 2 | Small sinuous SSBs | Sinuous crests with the smallest areal extent whose profile formed due to bedform superimposition rather than increased local current speeds. |
| 3 | Medium sinuous SSBs | Sinuous crests with a moderate areal extent, this class represents the bedforms with the highest degree of interference between the two dominant current regimes. |
| 4 | Medium obstructed SSBs | Profoundly influenced by the obstruction of the current flow induced by the CWC mounds, causing a significant reduction in their wave height relative to the other classes. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Summers, G.; Lim, A.; Wheeler, A.J. A Characterisation of Benthic Currents from Seabed Bathymetry: An Object-Based Image Analysis of Cold-Water Coral Mounds. Remote Sens. 2022, 14, 4731. https://doi.org/10.3390/rs14194731
Summers G, Lim A, Wheeler AJ. A Characterisation of Benthic Currents from Seabed Bathymetry: An Object-Based Image Analysis of Cold-Water Coral Mounds. Remote Sensing. 2022; 14(19):4731. https://doi.org/10.3390/rs14194731
Chicago/Turabian StyleSummers, Gerard, Aaron Lim, and Andrew J. Wheeler. 2022. "A Characterisation of Benthic Currents from Seabed Bathymetry: An Object-Based Image Analysis of Cold-Water Coral Mounds" Remote Sensing 14, no. 19: 4731. https://doi.org/10.3390/rs14194731
APA StyleSummers, G., Lim, A., & Wheeler, A. J. (2022). A Characterisation of Benthic Currents from Seabed Bathymetry: An Object-Based Image Analysis of Cold-Water Coral Mounds. Remote Sensing, 14(19), 4731. https://doi.org/10.3390/rs14194731






