RFI Detection and Mitigation for Advanced Correlators in Interferometric Radiometers
Abstract
1. Introduction
2. Materials and Methods
- XIn, XQn, YIn, YQn: four 1-bit data streams per receiver element n (from n = 1...Nreceivers) at 57.69375 MHz, X/Y being the polarization, and I/Q the in-phase/quadrature components;
- XPn, YPn: two multi-bit Power Measurement System (PMS) streams per receiver element n (from n = 1...Nreceivers) and per polarization at ~28 kS/s.
- N is the number of samples per integration period. In this study, N = 11,538,432, corresponding to an integration time of ~200 ms at the clock sampling frequency.
- K is the number of points of the Fourier transform or the number of points in the spectrum. K is an optimization parameter that can be reduced to a smaller power-of-two number during the implementation phase, if needed for Field-Programmable Gate Array (FPGA) resource utilization optimization.
- M is the number of time segments of the Short-Time Fourier Transform (STFT) in which the signal is divided. It is defined as M = γ·N/K, where γ is the windowing factor. As will be shown in the next section, γ = 2, which is the minimum windowing factor necessary to apply a non-rectangular window function.
- Rtot is the total number of receivers of the system.
- Ravg is the number of receivers that are averaged in the RFI detection process. It will be assumed that Ravg = Rtot. In the case of a real aperture radiometer, Ravg = Rtot = 1.
- is the detection threshold for statistical and polarimetry metrics to determine whether an RFI signal is present or not, and it controls the probability of detection and the probability of false alarm. The parameter may take three different specific values: for temporal moments, for spectral moments, and for all-signal moments.
- is the maximum blanking threshold. The RFI mitigation is based on the excision of the contaminated samples out of the set of all transformed samples. The RFI mitigation operates efficiently if a reduced number of samples contain the largest fraction of the RFI power.
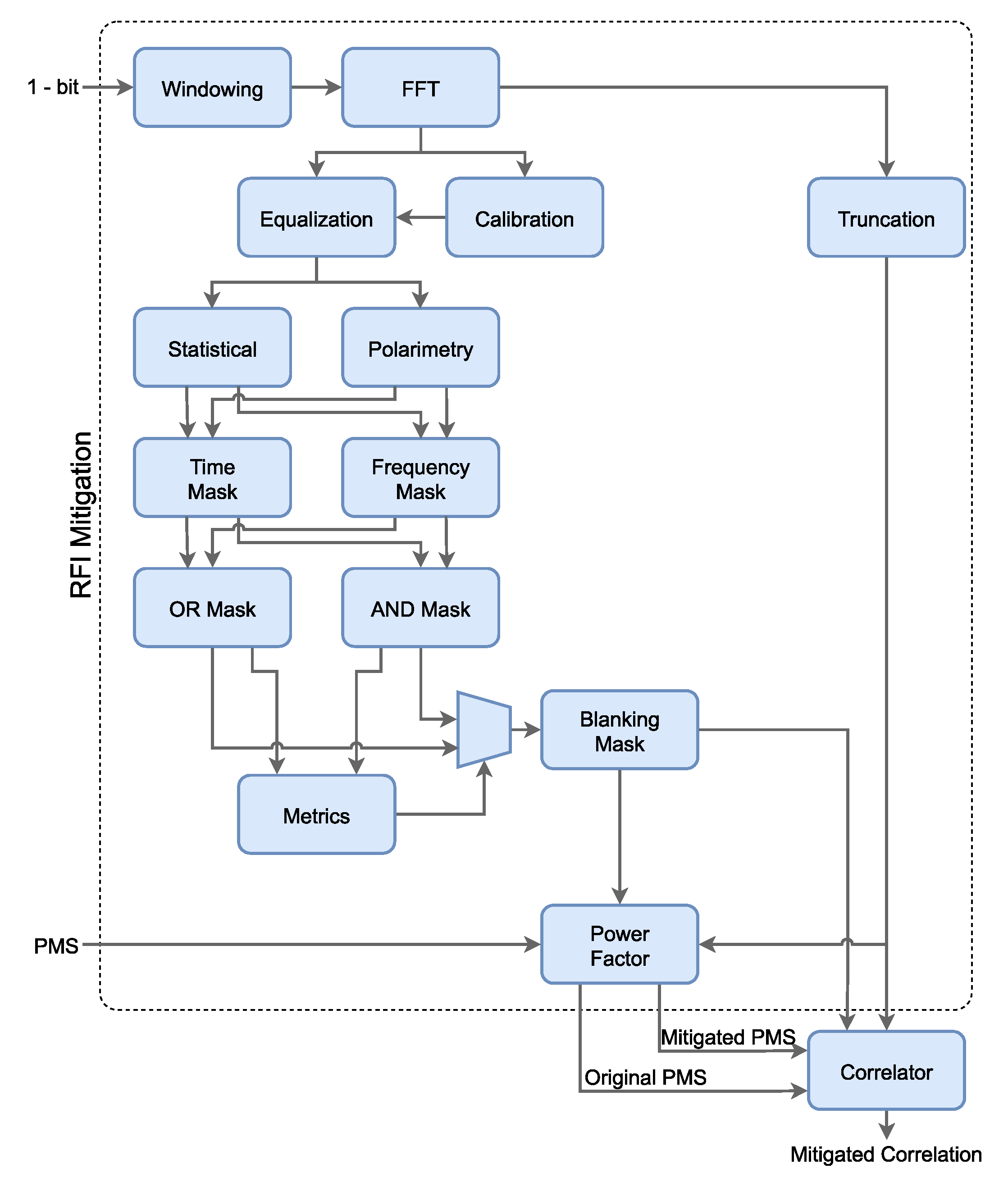
2.1. RFI Detection and Mitigation Algorithm Description
2.1.1. Windowing
2.1.2. Spectral Computation
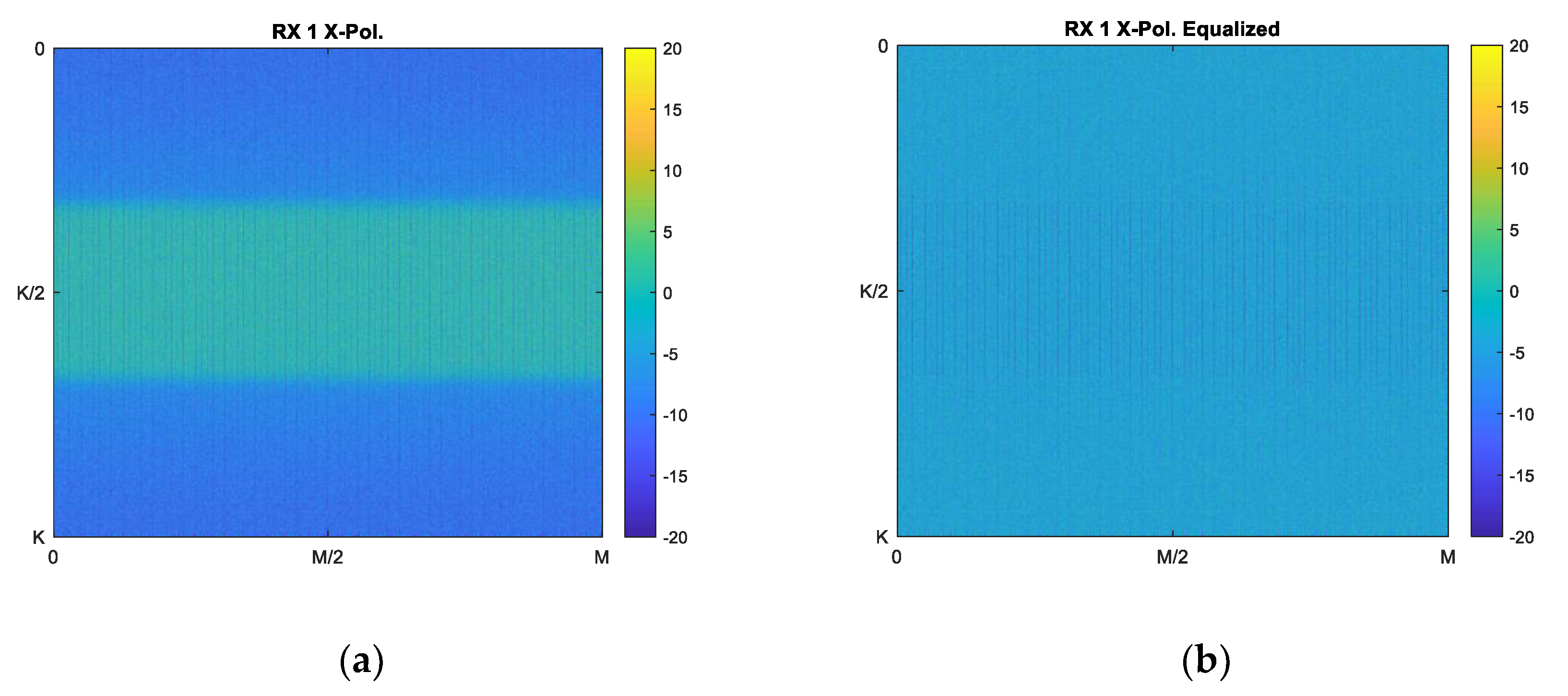
2.1.3. Calibration and Equalization
2.1.4. Statistic and Polarimetry Tests
- Stokes Parameters
- Kurtosis and Polarimetric Kurtosis
- Time-Frequency Moments
2.1.5. Computation of the OR/AND Masks
- the OR approach is computed by a tensor-logical OR operation between the vector results of the time and frequency RFI detector, denoted as ∨, whereas
- the AND approach is computed analogously using a tensor-logical AND operation, and it is denoted as ∧.
2.1.6. RFI Mitigation
- Signal Blanking
- PMS RFI Mitigation
- RFI Detection Flag
3. Results
- K is the number of points of FFT. The initial value of K was 4096, but it was proposed to run simulations with K = 16,384, 4096, 2048, 1024, and 256 and then to select the best K for the default CFAR and βth.
- αth is the RFI detection threshold for the statistical and polarimetry metrics: temporal, spectral, and all-bin moments. αth(PFA) is obtained mathematically for each value of the CFAR.
- The following CFAR values were simulated for the selected value of K: 10−8, 10−6, 10−4, 10−2, 0.1, and 0.5.
- βth is the maximum blanking threshold from 100% to 50%.
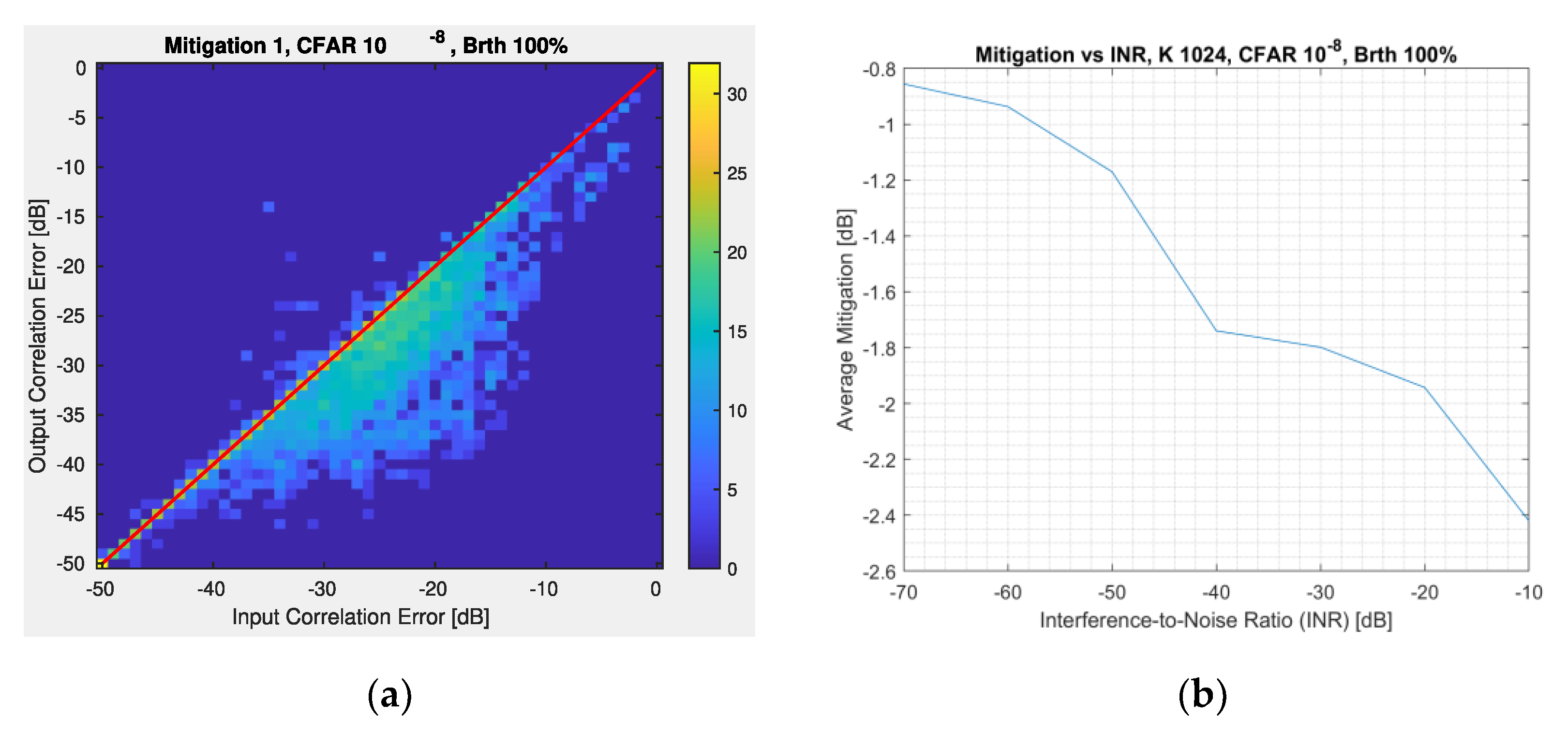
3.1. Sensitivity Performance as a Function of the Number of Averages
3.2. Algorithm Parameter Optimization
- K = 1024, no significant improvement was found for larger Ks except a better PD (from 63 to 73%), at the expense of more hardware resources to compute the FFTs.
- CFAR = 10−8, with no significant variation up to 10−6, with a moderate PD, and a negligible PFA (not detectable with the number of realizations performed). This offers less radiometric degradation and no big impact on mitigation.
- βth = 100%, no significant impact down to 95%, but 100% offers the best mitigation vs. degradation trade-off.
4. Discussion
- Quantize the signals in the frequency domain and perform the products with a reduced number of bits (1 to 5) so that multipliers can be more easily implemented using look-up tables (LUT).
- Transform the signals back to the time domain, quantize the signals in the time domain, and perform the products with a reduced number of bits (1 to 5).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Quantization Effects and Their Compensation


| FQ31 | FQ15 | FQ7 | FQ3 | FQ2 | |
|---|---|---|---|---|---|
| Correct. Fact. (m−1) | 1.0092 | 1.0321 | 1.1128 | 1.1558 | 3.3670 |
References
- Gasiewski, A.; Klein, M.; Yevgrafov, A.; Leuskiy, V. Interference mitigation in passive microwave radiometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 1682–1684. [Google Scholar]
- Querol, J.; Onrubia, R.; Alonso-Arroyo, A.; Pascual, D.; Park, H.; Camps, A. Performance Assessment of Time–Frequency RFI Mitigation Techniques in Microwave Radiometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3096–3106. [Google Scholar] [CrossRef]
- Erickson, A.; Rao, U. The Dimensions of RFI...and How ngVLA is Being Designed to Accommodate Them. Available online: https://www.ursi.org/proceedings/2019/rfi2019/24a3.pdf (accessed on 14 September 2022).
- Querol, J.; Perez, A.; Camps, A. A Review of RFI Mitigation Techniques in Microwave Radiometry. Remote Sens. 2019, 11, 3042. [Google Scholar] [CrossRef]
- Misra, S.; de Matthaeis, P. Passive Remote Sensing and Radio Frequency Interference (RFI): An Overview of Spectrum Allocations and RFI Management Algorithms [Technical Committees]. IEEE Geosci. Remote Sens. Mag. 2014, 2, 68–73. [Google Scholar] [CrossRef]
- Landry, R.J.; Boutin, P.; Constantinescu, A. New anti-jamming technique for GPS and GALILEO receivers using adaptive FADP filter. Digit. Signal Process. A Rev. J. 2006, 16, 255–274. [Google Scholar] [CrossRef]
- Tarongi, J.M.; Camps, A. Radio frequency interference detection and mitigation algorithms based on spectrogram analysis. Algorithms 2011, 4, 239–261. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterizing non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Camps, A.; Tarongi, J.M. RFI Mitigation in Microwave Radiometry Using Wavelets. Algorithms 2009, 2, 1248–1262. [Google Scholar] [CrossRef]
- Getu, T.M.; Ajib, W.; Landry, R. An Eigenvalue-Based Multi-Antenna RFI Detection Algorithm. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–5. [Google Scholar]
- Nguyen, L.H.; Tran, T.D. A comprehensive performance comparison of RFI mitigation techniques for UWB radar signals. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 3086–3090. [Google Scholar]
- Schoenwald, A.J.; Gholian, A.; Bradley, D.C.; Wong, M.; Mohammed, P.N.; Piepmeier, J.R. RFI detection and mitigation using independent component analysis as a pre-processor. In Proceedings of the 2016 Radio Frequency Interference (RFI), Socorro, NM, USA, 17–20 October 2016; pp. 100–104. [Google Scholar]
- Díez-García, R.; Camps, A. A Novel RFI Detection Method for Microwave Radiometers Using Multilag Correlators. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5300312. [Google Scholar] [CrossRef]
- Camps, A.; Vall-llossera, M.; Duffo, N.; Zapata, M.; Corbella, I.; Torres, F.; Barrena, V. Sun effects in 2-D aperture synthesis radiometry imaging and their cancelation. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1161–1167. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Gonzalez-Gambau, V. An imaging algorithm for synthetic aperture interferometric radiometers with built-in RFI mitigation. In Proceedings of the 2014 13th Specialist Meeting on Microwave Radiometry and Remote Sensing of the Environment (MicroRad), Pasadena, CA, USA, 24–27 March 2014; pp. 39–43. [Google Scholar] [CrossRef]
- Camps, A.; Swift, C.T. New Techniques in Microwave Radiometry for Earth Remote Sensing: Principles and Applications. In Review of Radio Science, 1st ed.; Chapter 22; Wiley-IEEE Press: Hoboken, NJ, USA, 2002; ISBN 0471268666. [Google Scholar]
- Emery, W.; Camps, A. Introduction to Satellite Remote Sensing; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar] [CrossRef]
- Bosch-Lluis, X.; Ramos-Perez, I.; Camps, A.; Rodriguez-Alvarez, N.; Valencia, E.; Park, H. A General Analysis of the Impact of Digitization in Microwave Correlation Radiometers. Sensors 2011, 11, 6066–6087. [Google Scholar] [CrossRef] [PubMed]
- Hagen, J.; Farley, D. Digital-correlation techniques in radio science. Radio Sci. 1973, 8, 775–784. [Google Scholar] [CrossRef]
- Camps, J.; Corbella, I.; Torres, F.; Bara, J.; Capdevila, J. RF interference analysis in aperture synthesis interferometric radiome-ters: Application to L-band MIRAS instrument. IEEE Trans. Geosci. Remote Sens. 2000, 38, 942–950. [Google Scholar] [CrossRef]
- Camps, A.; Gourrion, J.; Tarongi, J.M.; Vall Llossera, M.; Gutierrez, A.; Barbosa, J.; Castro, R. Radio-Frequency Interference Detection and Mitigation Algorithms for Synthetic Aperture Radiometers. Algorithms 2011, 4, 155–182. [Google Scholar] [CrossRef]
- González-Gambau, V.; Turiel, A.; Olmedo, E.; Martínez, J.; Corbella, I.; Camps, A. Nodal Sampling: A New Image Reconstruction Algorithm for SMOS. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2314–2328. [Google Scholar] [CrossRef]
- Van Vleck, J.H.; Middleton, D. The spectrum of clipped noise. Proc. IEEE 1966, 54, 2–19. [Google Scholar] [CrossRef]
- Hall, M. Resolution and uncertainty in spectral decomposition. First Break 2006, 24, 43–47. [Google Scholar] [CrossRef]
- Tarongi, J.M.; Camps, A. Normality Analysis for RFI Detection in Microwave Radiometry. Remote Sens. 2010, 2, 191–210. [Google Scholar] [CrossRef]







| K-FFT 4096 | βth 100% | βth 90% | βth 75% | βth 50% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | |
| CFAR 10−8 | M: −2.31dB σ: 3.73 dB | %. It. 59.3% M: −4.04 dB | %. It. 7.35% M: 1.14 dB | M: −2.58 dB σ: 5.05 dB | %. It. 56.2% M: −5.48 dB | %. It. 10.4% M: 4.80 dB | M: −2.58 dB σ: 5.05 dB | %. It. 56.2% M: −5.48 dB | %. It. 10.4% M: 4.80 dB | M: −2.58 dB σ: 5.05 dB | %. It. 56.2% M: −5.48 dB | %. It. 10.4% M: 4.80 dB |
| CFAR 10−6 | M: −2.33 dB σ: 3.75 dB | %. It. 60.8% M: −3.97 dB | %. It. 7.65% M: 1.10 dB | M: −2.56 dB σ: 5.11 dB | %. It. 57.5% M: −5.41 dB | %. It. 11.0% M: 4.98 dB | M: −2.56 dB σ: 5.12 dB | %. It. 57.5% M: −5.41 dB | %. It. 11.0% M: 4.98 dB | M: −2.56 dB σ: 5.12 dB | %. It. 57.5% M: −5.41 dB | %. It. 11.0% M: 4.98 dB |
| CFAR 10−4 | M: −2.35 dB σ: 3.82 dB | %. It. 62.2% M: −3.92 dB | %. It. 7.94% M: 1.10 dB | M: −2.52 dB σ: 5.24 dB | %. It. 58.2% M: −5.39 dB | %. It. 11.9% M: 5.24 dB | M: −2.52 dB σ: 5.24 dB | %. It. 58.2% M: −5.39 dB | %. It. 11.9% M: 5.24 dB | M: −2.52 dB σ: 5.24 dB | %. It. 58.2% M: −5.39 dB | %. It. 11.9% M: 5.24 dB |
| CFAR 10−2 | M: 5.88 dB σ: 27.8 dB | %. It. 69.0% M: −3.28 dB | %. It. 28.9% M: 28.16 dB | M: 6.24 dB σ: 29.3 dB | %. It. 63.5% M: −4.98 dB | %. It. 34.4% M: 27.3 dB | M: 6.24 dB σ: 29.3 dB | %. It. 63.5% M: −4.98 dB | %. It. 34.4% M: 27.3 dB | M: 6.24 dB σ: 29.3 dB | %. It. 63.5% M: −4.98 dB | %. It. 34.4% M: 27.3 dB |
| CFAR 10−1 | M: 6.35 dB σ: 28.3 dB | %. It. 73.6% M: −2.86 dB | %. It. 26.4% M: 32.0 dB | M: 12.0 dB σ: 33.0 dB | %. It. 41.3% M: −5.04 dB | %. It. 58.7% M: 23.9 dB | M: 12.0 dB σ: 33.0 dB | %. It. 41.3% M: −5.04 dB | %. It. 58.7% M: 23.9 dB | M: 12.0 dB σ: 33.0 dB | %. It. 41.3% M: −5.04 dB | %. It. 58.7% M: 23.9 dB |
| K-FFT 2048 | βth 100% | βth 90% | βth 75% | βth 50% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | |
| CFAR 10−8 | M: −2.21 dB σ: 3.72 dB | %. It. 57.3% M: −4.02 dB | %. It. 7.31% M: 1.26 dB | M: −2.20 dB σ: 5.20 dB | %. It. 56.2% M: −5.46 dB | %. It. 12.0% M: 5.57 dB | M: −2.20 dB σ: 5.20 dB | %. It. 56.2% M: −5.46 dB | %. It. 12.0% M: 5.57 dB | M: −2.20 dB σ: 5.20 dB | %. It. 56.2% M: −5.46 dB | %. It. 12.0% M: 5.57 dB |
| CFAR 10−6 | M: −2.24 dB σ: 3.77 dB | %. It. 58.4% M: −4.01 dB | %. It. 7.72% M: 1.26 dB | M: −2.19 dB σ: 5.30 dB | %. It. 57.5% M: −5.45 dB | %. It. 12.6% M: 5.72 dB | M: −2.19 dB σ: 5.30 dB | %. It. 57.5% M: −5.45 dB | %. It. 12.6% M: 5.72 dB | M: −2.19 dB σ: 5.30 dB | %. It. 57.5% M: −5.45 dB | %. It. 12.6% M: 5.72 dB |
| CFAR 10−4 | M: −2.20 dB σ: 4.72 dB | %. It. 60.3% M: −3.95 dB | %. It. 8.29% M: 2.09 dB | M: −2.06 dB σ: 6.08 dB | %. It. 58.2% M: −5.39 dB | %. It. 14.1% M: 6.24 dB | M: −2.06 dB σ: 6.08 dB | %. It. 58.2% M: −5.39 dB | %. It. 14.1% M: 6.24 dB | M: −2.06 dB σ: 6.08 dB | %. It. 58.2% M: −5.39 dB | %. It. 14.1% M: 6.24 dB |
| CFAR 10−2 | M: 5.79 dB σ: 26.6 dB | %. It. 66.9% M: −2.83 dB | %. It. 30.5% M: 25.2 dB | M: 6.52 dB σ: 28.8 dB | %. It. 63.5% M: −4.88 dB | %. It. 36.5% M: 26.1 dB | M: 6.52 dB σ: 28.8 dB | %. It. 63.5% M: −4.88 dB | %. It. 36.5% M: 26.1 dB | M: 6.52 dB σ: 28.8 dB | %. It. 63.5% M: −4.88 dB | %. It. 36.5% M: 26.1 dB |
| CFAR 10−1 | M: 6.50 dB σ: 28.2 dB | %. It. 72.9% M: −2.66 dB | %. It. 27.1% M: 31.2 dB | M: 12.2 dB σ: 32.9 dB | %. It. 41.3% M: −5.02 dB | %. It. 59.8% M: 23.8 dB | M: 12.2 dB σ: 32.9 dB | %. It. 41.3% M: −5.02 dB | %. It. 59.8% M: 23.8 dB | M: 12.2 dB σ: 32.9 dB | %. It. 41.3% M: −5.02 dB | %. It. 59.8% M: 23.8 dB |
| K-FFT 1024 | βth 100% | βth 90% | βth 75% | βth 50% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | |
| CFAR 10−8 | M: −1.76 dB σ: 3.30 dB | %. It. 48.8% M: −3.79 dB | %. It. 6.73% M: 1.35 dB | M: −2.08 dB σ: 4.67 dB | %. It. 46.8% M: −5.36 dB | %. It. 8.73% M: 4.92 dB | M: −2.08 dB σ: 4.67 dB | %. It. 46.8% M: −5.36 dB | %. It. 8.73% M: 4.92 dB | M: −2.08 dB σ: 4.67 dB | %. It. 46.8% M: −5.36 dB | %. It. 8.73% M: 4.92 dB |
| CFAR 10−6 | M: −1.73 dB σ: 3.30 dB | %. It. 50.1% M: −3.64 dB | %. It. 7.26% M: 1.34 dB | M: −2.06 dB σ: 4.73 dB | %. It. 47.9% M: −5.30 dB | %. It. 9.54% M: 4.96 dB | M: −2.06 dB σ: 4.73 dB | %. It. 47.9% M: −5.30 dB | %. It. 9.54% M: 4.96 dB | M: −2.06 dB σ: 4.73 dB | %. It. 47.9% M: −5.30 dB | %. It. 9.54% M: 4.96 dB |
| CFAR 10−4 | M: −1.08 dB σ: 8.32 dB | %. It. 51.2% M: −3.46 dB | %. It. 9.16% M: 7.52 dB | M: −1.43 dB σ: 9.05 dB | %. It. 49.1% M: −5.21 dB | %. It. 11.2% M: 10.1 dB | M: −1.43 dB σ: 9.05 dB | %. It. 49.1% M: −5.21 dB | %. It. 11.2% M: 10.1 dB | M: −1.43 dB σ: 9.05 dB | %. It. 49.1% M: −5.21 dB | %. It. 11.2% M: 10.1 dB |
| CFAR 10−2 | M: 8.19 dB σ: 28.5 dB | %. It. 63.9% M: −1.86 dB | %. It. 35.7% M: 26.2 dB | M: 8.57 dB σ: 31.5 dB | %. It. 60.9% M: −4.37 dB | %. It. 38.7% M: 29.1 dB | M: 8.58 dB σ: 31.5 dB | %. It. 60.9% M: −4.37 dB | %. It. 38.7% M: 29.1 dB | M: 8.58 dB σ: 31.5 dB | %. It. 60.9% M: −4.37 dB | %. It. 38.7% M: 29.1 dB |
| CFAR 10−1 | M: 8.87 dB σ: 30.7 dB | %. It. 69.7% M: −2.04 dB | %. It. 30.3% M: 33.3 dB | M: 14.7 dB σ: 35.8 dB | %. It. 37.5% M: −4.84 dB | %. It. 62.5% M: 26.4 dB | M: 14.7 dB σ: 35.8 dB | %. It. 37.5% M: −4.84 dB | %. It. 62.5% M: 26.4 dB | M: 14.7 dB σ: 35.8 dB | %. It. 37.5% M: −4.84 dB | %. It. 62.5% M: 26.4 dB |
| CFAR | K-FFT 4096 | K-FFT 2048 | K-FFT 1024 | |||
|---|---|---|---|---|---|---|
| PFA | PD | PFA | PD | PFA | PD | |
| 10−8 | <1% | 73.1% | <1% | 69.8% | <1% | 59.4% |
| 10−6 | <1% | 74.7% | <1% | 71.7% | 6% | 64.2% |
| 10−4 | <1% | 76.2% | 1% | 74.5% | 68% | 81.8% |
| 10−2 | 87% | 97.1% | 91% | 97.1% | 100% | 100% |
| 10−1 | 100% | 100% | 100% | 100% | 100% | 100% |
| K-FFT 1024 | βth 100% | βth 99% | βth 95% | βth 90% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | All #1200 | Mitigating (<0) | Degrading (>0) | |
| CFAR 10−8 | M: −2.00 dB σ: 3.69 dB | %. It. 52.0% M: −4.03 dB | %. It. 7.65% M: 1.16 dB | M: −2.04 dB σ: 5.16 dB | %. It. 48.6% M: −5.48 dB | %. It. 11.1% M: 5.62 dB | M: −1.85 dB σ: 5.19 dB | %. It. 47.7% M: −5.36 dB | %. It. 11.9% M: 5.95 dB | M: −1.85 dB σ: 5.18 dB | %. It. 47.7% M: −5.36 dB | %. It. 11.9% M: 5.95 dB |
| CFAR 10−6 | M: −2.00 dB σ: 3.68 dB | %. It. 52.4% M: −4.00 dB | %. It. 7.81% M: 1.15 dB | M: −2.05 dB σ: 5.21 dB | %. It. 48.8% M: −5.50 dB | %. It. 11.4% M: 5.57 dB | M: −1.85 dB σ: 5.21 dB | %. It. 48.0% M: −5.35 dB | %. It. 12.2% M: 5.90 dB | M: −1.85 dB σ: 5.21 dB | %. It. 48.0% M: −5.35 dB | %. It. 12.2% M: 5.90 dB |
| CFAR 10−4 | M: −1.99 dB σ: 3.68 dB | %. It. 52.4% M: −3.97 dB | %. It. 8.01% M: 1.13 dB | M: −2.04 dB σ: 5.23 dB | %. It. 48.8% M: −5.50 dB | %. It. 11.6% M: 5.61 dB | M: −1.83 dB σ: 5.23 dB | %. It. 48.0% M: −5.35 dB | %. It. 12.4% M: 5.93 dB | M: −1.83 dB σ: 5.22 dB | %. It. 48.0% M: −5.35 dB | %. It. 12.4% M: 5.93 dB |
| CFAR 10−2 | M: −1.98 dB σ: 3.67 dB | %. It. 52.7% M: −3.94 dB | %. It. 8.15% M: 1.12 dB | M: −2.03 dB σ: 5.26 dB | %. It. 49.1% M: −5.50 dB | %. It. 11.8% M: 5.65 dB | M: −1.83 dB σ: 5.25 dB | %. It. 48.2% M: −5.35 dB | %. It. 12.6% M: 5.97 dB | M: −1.82 dB σ: 5.25 dB | %. It. 48.2% M: −5.35 dB | %. It. 12.6% M: 5.97 dB |
| CFAR 10−1 | M: −1.99 dB σ: 3.69 dB | %. It. 53.3% M: −3.92 dB | %. It. 8.22% M: 1.16 dB | M: −2.03 dB σ: 5.29 dB | %. It. 49.3% M: −5.50 dB | %. It. 12.2% M: 5.60 dB | M: −1.81 dB σ: 5.29 dB | %. It. 48.5% M: −5.34 dB | %. It. 13.0% M: 5.95 dB | M: −1.81 dB σ: 5.28 dB | %. It. 48.5% M: −5.34 dB | %. It. 13.0% M: 5.95 dB |
| CFAR | K-FFT 1024 | |
|---|---|---|
| PFA | PD | |
| 10−8 | <1% | 63.5% |
| 3 · 10−8 | ~2% | 64.1% |
| 10−7 | ~2% | 64.6% |
| 3 · 10−7 | ~2% | 66,2% |
| 10−6 | 6% | 67.7% |
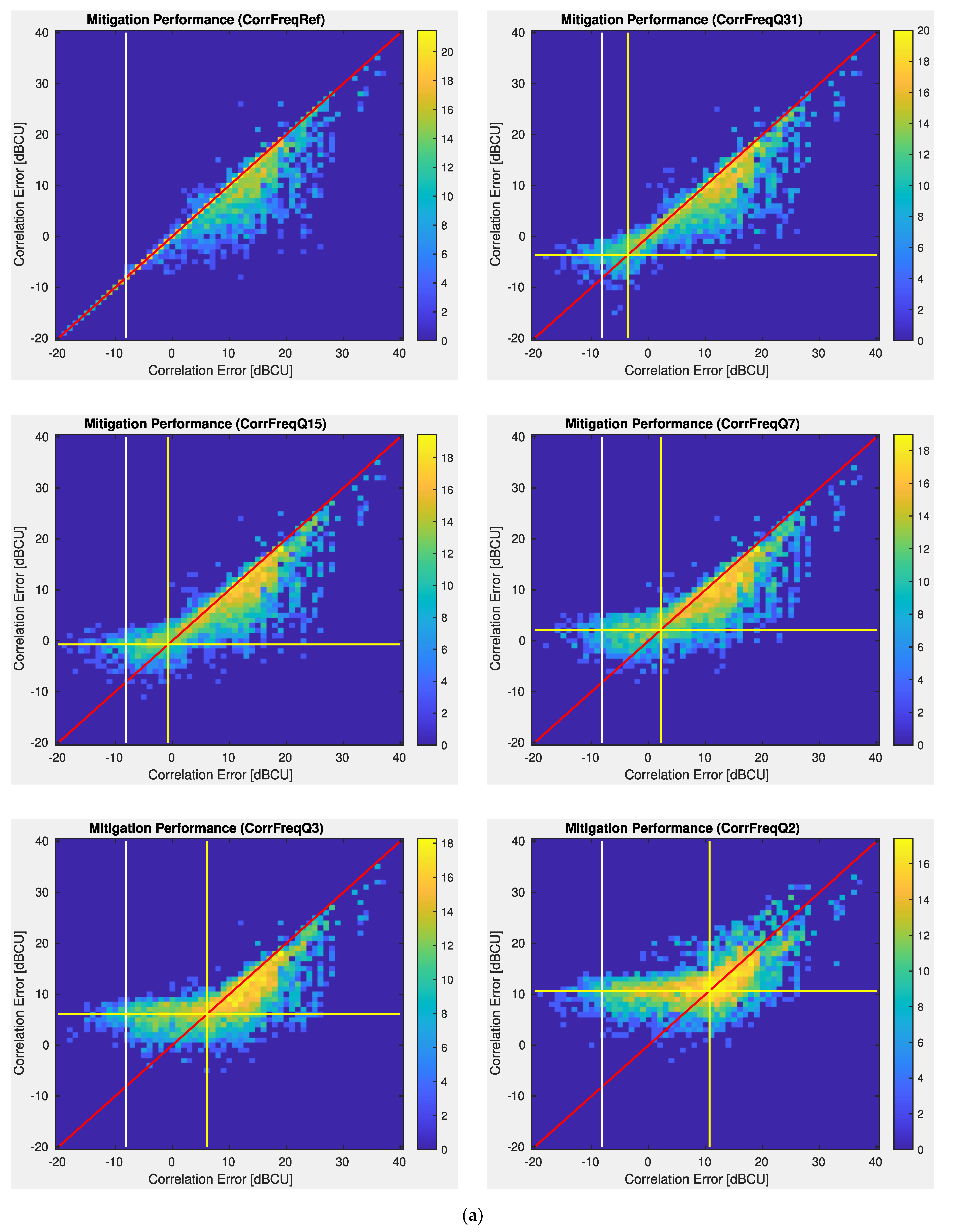
| Correlation Approach | All [1200 it.] | Mitigating (<0) | Degrading (>0) | |||
|---|---|---|---|---|---|---|
| FRef | Mean −3.00 dB | Std 4.22 dB | %. It. 57.5% | Mean −4.36 dB | %. It. 4.6% | Mean 1.82 dB |
| FQ31 | Mean −3.28 dB | Std 4.25 dB | %. It. 65.9% | Mean −4.04 dB | %. It. 10.8% | Mean 1.00 dB |
| FQ15 | Mean −3.37 dB | Std 4.28 dB | %. It. 65.6% | Mean −4.21 dB | %. It. 11.7% | Mean 1.14 dB |
| FQ7 | Mean −3.35 dB | Std 4.35 dB | %. It. 64.1% | Mean −4.39 dB | %. It. 13.5% | Mean 1.49 dB |
| FQ3 | Mean −2.73 dB | Std 4.45 dB | %. It. 59.9% | Mean −4.24 dB | %. It. 17.7% | Mean 2.33 dB |
| FQ2 | Mean 0.06 dB | Std 5.27 dB | %. It. 40.1% | Mean −3.92 dB | %. It. 37.6% | Mean 4.32 dB |
| TRefIFFT | Mean −3.10 dB | Std 4.31 dB | %. It. 64.6% | Mean −3.85 dB | %. It. 12.3% | Mean 0.67 dB |
| TQ31 | Mean −3.33 dB | Std 4.89 dB | %. It. 58.9% | Mean −4.88 dB | %. It. 18.9% | Mean 1.50 dB |
| TQ15 | Mean −1.88 dB | Std 5.00 dB | %. It. 49.9% | Mean −4.34 dB | %. It. 27.9% | Mean 2.53 dB |
| TQ7 | Mean 0.99 dB | Std 5.74 dB | %. It. 30.1% | Mean −4.34 dB | %. It. 47.8% | Mean 4.35 dB |
| TQ3 | Mean 2.03 dB | Std 5.82 dB | %. It. 24.8% | Mean −4.13 dB | %. It. 53.0% | Mean 4.91 dB |
| TQ2 | Mean 12.04 dB | Std 7.14 dB | %. It. 2.9% | Mean −3.28 dB | %. It. 74.9% | Mean 12.64 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perez-Portero, A.; Querol, J.; Camps, A.; Martin-Neira, M.; Suess, M.; Ramirez, J.I.; Zurita, A.; Closa, J.; Oliva, R.; Onrubia, R. RFI Detection and Mitigation for Advanced Correlators in Interferometric Radiometers. Remote Sens. 2022, 14, 4672. https://doi.org/10.3390/rs14184672
Perez-Portero A, Querol J, Camps A, Martin-Neira M, Suess M, Ramirez JI, Zurita A, Closa J, Oliva R, Onrubia R. RFI Detection and Mitigation for Advanced Correlators in Interferometric Radiometers. Remote Sensing. 2022; 14(18):4672. https://doi.org/10.3390/rs14184672
Chicago/Turabian StylePerez-Portero, Adrian, Jorge Querol, Adriano Camps, Manuel Martin-Neira, Martin Suess, Juan Ignacio Ramirez, Alberto Zurita, Josep Closa, Roger Oliva, and Raul Onrubia. 2022. "RFI Detection and Mitigation for Advanced Correlators in Interferometric Radiometers" Remote Sensing 14, no. 18: 4672. https://doi.org/10.3390/rs14184672
APA StylePerez-Portero, A., Querol, J., Camps, A., Martin-Neira, M., Suess, M., Ramirez, J. I., Zurita, A., Closa, J., Oliva, R., & Onrubia, R. (2022). RFI Detection and Mitigation for Advanced Correlators in Interferometric Radiometers. Remote Sensing, 14(18), 4672. https://doi.org/10.3390/rs14184672






