A Hybrid Privacy-Preserving Deep Learning Approach for Object Classification in Very High-Resolution Satellite Images

Abstract

Deep learning (DL) has shown outstanding performances in many fields, including remote sensing (RS). DL is turning into an essential tool for the RS research community. Recently, many cloud platforms have been developed to provide access to large-scale computing capacity, consequently permitting the usage of DL architectures as a service. However, this opened the door to new challenges associated with the privacy and security of data. The RS data used to train the DL algorithms have several privacy requirements. Some of them need a high level of confidentiality, such as satellite images related to public security with high spatial resolutions. Moreover, satellite images are usually protected by copyright, and the owner may strictly refuse to share them. Therefore, privacy-preserving deep learning (PPDL) techniques are a possible solution to this problem. PPDL enables training DL on encrypted data without revealing the original plaintext. This study proposes a hybrid PPDL approach for object classification for very-high-resolution satellite images. The proposed encryption scheme combines Paillier homomorphic encryption (PHE) and somewhat homomorphic encryption (SHE). This combination aims to enhance the encryption of satellite images while ensuring a good runtime and high object classification accuracy. The method proposed to encrypt images is maintained through the public keys of PHE and SHE. Experiments were conducted on real-world high-resolution satellite images acquired using the SPOT6 and SPOT7 satellites. Four different CNN architectures were considered, namely ResNet50, InceptionV3, DenseNet169, and MobileNetV2. The results showed that the loss in classification accuracy after applying the proposed encryption algorithm ranges from 2% to 3.5%, with the best validation accuracy on the encrypted dataset reaching 92%.

1. Introduction

Satellite images provide valuable and actionable insights for many remote sensing (RS) applications [1,2,3,4]. The quality of these images is highly diverse and depends on the satellite altitude, the camera sensor [5], and the RS application [6,7]. The ability of an RS sensor to detect details on the ground is referred to as spatial resolution [8]. Very-high-resolution (VHR) satellite images are a current research hotspot since they cover large areas of the Earth and capture more details about an object on the ground. Deep learning (DL) techniques have recently proven their efficiency in many tasks (e.g., speech recognition, medical imagery, and agriculture). Since their appearance in the machine learning area, they have actively demonstrated an impressive capability to learn patterns occurring in the data. They can work in a data-driven mode without hand-crafting features. Many architectures and models have been proposed for different tasks in several RS areas, such as classification of ground images [9,10], prediction of environmental characteristics, mapping of the ground envelope, recovery of natural changes, analyzing human activities on the ground, information fusion, public safety, urban life enhancement, and data building and prediction [11]. Classifying ground images remains one of the most challenging tasks. Indeed, the requirement to automatically classify ground surfaces into understandable human classes is ubiquitous.

On the other hand, running DL algorithms requires having high-performance computing resources, especially when working on large data. Most standard computers cannot run DL algorithms due to the high GPU and RAM characteristics needed. As an alternative, many cloud infrastructures have been designed in recent years to allow the training and testing of deep learning as a service (DLaaS). This offers a serverless user experience and provides flexibility, ease of use, the economics of a cloud service, and the high-computing resources required by DL. It provides a variety of popular DL frameworks, tools, and services, making it simple to train and deploy DL models using high-performance resources. However, DLaaS necessitates that the client uploads the data into the cloud for the training and testing phases. This can open the door to several matters related to privacy, confidentiality, data protection, and copyright issues [12,13].

These matters may exist to different degrees from one dataset to another. Some datasets are highly confidential and strictly forbidden to disclose, such as images related to military areas [14] or showing private information. Other datasets may not be confidential, but need high effort to collect, and the user may be reluctant to share them. In most cases, the users uploading their datasets to the cloud refuse to disclose them. This explains the necessity to adopt privacy preservation, which allows users to safeguard the privacy of their sensitive data against adversaries [15] with different capabilities. Recently, privacy-preserving deep learning (PPDL) has been in hot demand since it allows training a DL model while preserving the privacy of the training dataset [16]. An important technique consists of encrypting the data locally on the user’s machine before sending them to the server for training [17,18]. The training will be conducted on the encrypted data. Thus, the plain data will not be shared and will be stored only on the user’s machine.

In this paper, a novel hybrid PPDL approach that combines Paillier homomorphic encryption (PHE) and somewhat homomorphic encryption (SHE) is proposed. The proposed approach ensures training DL models while preserving the privacy of the training RS dataset. Combining PHE and SHE improves the encryption of satellite images while ensuring a good runtime performance for object classification.

The main contributions of the proposed study are summarized below:

• A novel hybrid PPDL approach combining Paillier homomorphic encryption and somewhat homomorphic encryption for satellite image classification is proposed. This combination will improve the security of encrypted images. Using only PHE, such as the work proposed in Alkhelaiwi et al. [19], can lead to some security issues [20]. Indeed, the capacity of the PHE schema used in [19] is constrained to addition or multiplication, but it cannot use the two operations simultaneously. As a result, this technique cannot secure data confidentiality when using it in the cloud [21]. However, integrating SHE with the encryption scheme will ensure more robustness to encrypted images while maintaining an excellent computational complexity and excellent runtime thanks to the shorter bit-length of SHE.
• To evaluate its efficiency, the proposed hybrid PPDL approach was applied to several DL-based CNN models, namely ResNet50, InceptionV3, DenseNet169, and MobileNetV2.
• Several experiments on real-world satellite image datasets were carried out to assess the overall performance of the proposed approach in terms of accuracy and security.

The remainder of the paper is organized as follows: Section 2 introduces PPDL techniques, reviews their benefits and limits, and summarizes the related works that targeted the same problem in the literature. Section 3 describes the hybrid image encryption approach introduced in the current study. Section 4 is reserved for the discussion of the experimental results. Finally, our work is concluded with a description of the possible extensions in Section 5.

2. Background and Related Works

This section introduces the most important concepts raised in this paper and the recent research studies that have been conducted in the literature related to hybrid PPDL approaches.

2.1. Privacy-Preserving Deep Learning

Machine learning (ML) is an area of study that empowers machines to understand data without explicit programming [22]. Some of its significant improvements have been underestimated in the past. Nonetheless, the current utilization of ML/DL does not consider data privacy, mainly when training or inference is performed in the cloud. To address this gap, researchers have attempted to discover privacy-preserving techniques for training and testing ML/DL models.

Privacy preservation (PP) is one of the most critical topics considered in data security. In recent years, it has become an intense preoccupation with the growing consciousness about personal data protection [23]. ML model training requires a large dataset, which may include confidential information, especially private data. Besides, the model parameters should only be accessible to the model owner. Data and model owners’ privacy is crucial to enforcing privacy-preserving deep learning protocols [24].

2.2. PPDL Methods

Several privacy-preserving techniques are used to address data privacy in deep learning models (during the training and testing phases) [22]. These techniques are categorized into three groups: (i) cryptographic approaches, (ii) perturbation approaches, and (iii) hybrid techniques [16]. They are succinctly provided in Figure 1.

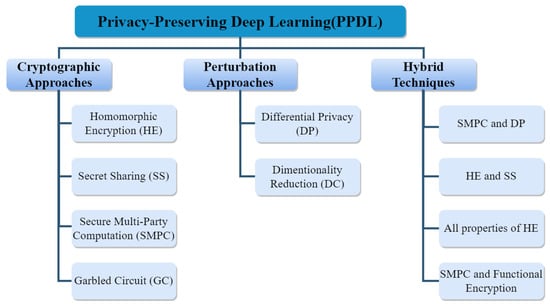
Figure 1. Different approaches to PPDL.

2.2.1. Comparison between PPDL Techniques

Table 1 presents the different privacy-preserving approaches that have been recently developed in this field with their advantages and drawbacks.

Table 1. Advantages and drawbacks of PPDL techniques.

Methodologies	Advantages	Drawbacks	References
Homomorphic encryption (HE)	Performing inference on encrypted data. The model owner has no access to the client’s private information and cannot leak or abuse it. A higher standard of sensitive data. No loss of information. FHE supports any type of operation.	Computationally pricey, which affects runtime. Bandwidth and latency concerns. PHE and SHE are limited to specific types of calculations. Increasing the total cost of ownership. FHE is still ineffective and under experimentation.	[25,26,27]
Secure multi-party computation (SMPC)	No need for a trusted third party. Sensitive information is not revealed to any party. Inference is carried out on encrypted data. The parties obtain only the resulting analysis or model. Protects against computationally powerful adversaries. Less computationally costly and complex than FHE.	Computationally intensive. Important communication overhead. Assumptions must be made about the proportions of malevolent coordinating parties in the calculation.	[27,28]
Differential privacy (DP)	Formal mathematical proof. Privacy guarantee. The user can set a suitable level of safety.	When datasets are bulky, noise and loss of information may occur.	[27]
Dimensionality reduction (DR)	Reduced storage space and execution time. The suppression of multicollinearity improves the interpretation of the ML model parameters. Reducing data to very low dimensions such as 2D or 3D makes it easier to visualize.	Partial data loss. PCA fails when the mean and covariance are insufficient to specify datasets.	[29,30]
Secret sharing (SS)	Provides the best efficiency. Individual shares can be easily modified without changing other shares. Shares can be modified while keeping the same secret. Supplying more than one share per person.	Computationally complex.	[22,31]

Homomorphic encryption ensures the confidentiality of sensitive information. However, this approach is very computationally expensive and has bandwidth and latency issues. One of its sub-methods, fully homomorphic encryption (FHE), remains inefficient in many cases. Compared to homomorphic encryption, secure multi-party computation usage is far less expensive and much less computationally complicated than FHE. However, fully homomorphic encryption induces a massive communication overhead. Furthermore, the major drawback of differential privacy is the loss of information. Finally, secret sharing is more computationally complex.

All approaches stated here are used to secure the data. However, they have some benefits and weaknesses. Our research relies on homomorphic encryption to ensure the confidentiality of helpful information, a way to better protect data security on the cloud.

2.2.2. Homomorphic Encryption

This section describes the homomorphic encryption methods used in this study. Homomorphic encryption methods are encryption techniques that allow conducting mathematical operations on encrypted data [17,32]. Due to homomorphic encryption’s performance in securely transmitting, storing, and processing encrypted data, it has been adopted in several applications, such as healthcare, medical applications, the financial sector, forensic applications, social networking advertisements, and smart vehicles, in which maintaining users’ confidentiality is of paramount importance [18,32]. Indeed, the homomorphic encryption schemes include four steps, specifically key generation, encryption, decryption, and evaluation. They are described in [33,34] and illustrated in Figure 2.

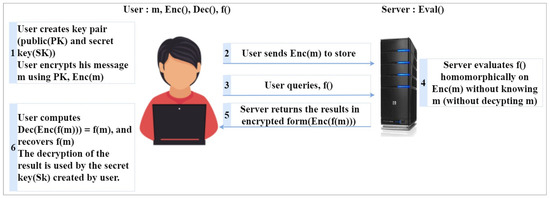
Figure 2. Homomorphic encryption steps.

• Key generation: The customer will produce the public parameter and the public and secret key (PK, SK).
• Encryption: The customer will generate the ciphertext (C) using M and PK, and C will be stored in the cloud.
• Evaluation: The server evaluates C, then the customer receives the encrypted result sent by the server.
• Decryption: The customer will obtain the original text (M) by decrypting the evaluation received from the server using SK.

In the inference phase [18]:

• The encryption and storage of the user data are carried out within the cloud.
• The consumer sends information about the training task to the cloud server.
• The data encrypted by homomorphic encryption is fed to the model in the cloud server, which transfers back the encrypted result to the consumer. Through the secret key, the user can decrypt the result. Thus, the data’s safety and privacy are preserved.

According to the allowed set of mathematical operations, homomorphic encryption is subdivided into three groups: partially homomorphic encryption (PHE), fully homomorphic encryption (FHE), and somewhat homomorphic encryption (SHE) [17,18].

2.3. Related Works

This section describes the current research works that used hybrid PPDL strategies. In 2019, Truex et al. [35] developed a technique that mixes DP and SMPC. They demonstrated that by increasing the number of parties while decreasing the data portions, the utilization of DP leads to low accuracy. They also proved that using SPMC poses vulnerability risks during the inference phase. To overcome these issues, they designed an enhanced federated learning (FL) system that combines DP and SMPC. The introduced system is scalable, secure against adversary threats, and keeps the model’s accuracy high. The authors ensured privacy without sacrificing accuracy by training the model in an FL fashion. In another study, Chase et al. [36] constructed a private collaborative framework for machine learning that combines SMPC and DP. DP is used for privacy, while the machine learning model was based on neural networks. Another hybrid approach was introduced by Chen et al. [37]. It combines homomorphic encryption and secret sharing. In fact, using homomorphic encryption only leads to potential security risks. Furthermore, using SS only reduces the efficiency, especially in the case of high-dimensional sparse features. Therefore, the authors merged homomorphic encryption and SS to construct a secure large-scale sparse logistic regression model that fulfills the requirements of both effectiveness and safeness.

El Makkaoui et al. [38] studied the hybrid approaches that use all of the homomorphic properties. They focused on partially homomorphic encryption (PHE). PHE methods are characterized by fewer operations compared to other homomorphic encryption methods. Based on PHE, the authors developed a new hybrid scheme that preserves the algebraic structure of a ring homomorphism while ensuring robustness against confidentiality attacks. In another study, Xu et al. [39] proposed a new method named HybridAlpha. It is a method for privacy-preserving federated learning based on a combination between the SMPC protocol and functional encryption. The authors disclosed the training data, the hyperparameters, and the resulting model. They tested HybridAlpha during the training of a CNN on the MNIST dataset. The training duration was minimized, as well as the volume of exchanged data.

Alkhelaiwi et al. [19] applied PHE for satellite image encryption. They developed a CNN to learn from this kind of data through the intermediate of transfer learning approaches. Data were encrypted locally before sending them to the cloud server. By comparing to the use of plain data, the encrypted data kept the high accuracy of the model. To the best of our knowledge, this is the only work that used PPDL in the context of RS. However, their work has two limitations. The first is the vulnerability of the secret key to adversarial attacks. The second is the high execution time needed to generate the key and encrypt the data.

In this paper, we designed a hybrid encryption scheme that ensures the security of the encrypted data, reduces the execution time needed for encryption, and maintains the DL models’ accuracy. We summarize in Table 2 the PPDL approaches designed in the literature. We compared them according to the application domain, the PPDL method, the dataset, and the steps.

Table 2. Comparison of hybrid PPDL techniques in the literature.

REF		[35]	[39]	[37]	[38]	[36]	[19]	The Proposed Research
Domain of application		Nursery application Classification of handwritten digits	Classification of handwritten digits	Risk control	Attack distinguishing	Classification of handwritten digits	Satellite image classification	Satellite image classification
PPDL methods	HE		√	√	√		√	√
	SS			√
	SMPC	√	√			√
	GC
	DP	√				√
	DR
ML models		Decision Trees (DT) Convolutional neural networks (CNNs) Linear support vector machines (SVMs)	CNN	Logistic regression		Small NN (3-layer) NN (4-layer)	CNN	CNN
Dataset		Nursery dataset MNIST dataset Gisette dataset	MNIST dataset	Real-world dataset	-	MNIST dataset	Satellite dataset	Satellite dataset
Goal		Combining SMPC with differential privacy to decrease the expansion of noise injection as the number of clients increases.	Use of an SMPC protocol based on a functional multi-entry encryption system.	Development of a hybrid encryption approach based on HE and SS to construct a secure large-scale sparse logistic regression model that fulfills the requirements of both effectiveness and safeness.	A hybrid HE system was created based on two different systems that back up the additive and multiplicative properties.	Development of a collaborative protocol based on an NN and the gradient descent method to add random noise to guarantee that the information will not be divulged.	Training DL models based on encrypted data with PHE to preserve the confidentiality of information.	Encryption of data using a hybrid method to enhance data encryption while ensuring good runtime and classification accuracy.

3. Materials and Methods

Using the proposed hybrid privacy-preserving deep learning (PPDL) in this study, the ML model (a CNN in our case) is encrypted locally to guarantee the privacy of the satellite image data as depicted in Figure 3. The encryption is based on partially homomorphic encryption (PHE) and somewhat homomorphic encryption (SHE). Both of them use public keys to encrypt the data on the client side. The training of the CNN is performed remotely on the cloud server without decrypting the data. The whole training process is performed only on the encrypted data. In the following paragraphs, we will give more details about the design of the hybrid technique, the Paillier algorithm used for encryption, and the SHE schemes. The CNN model works only on the encrypted data during the training and inference phases. Data privacy is then sustained during the training and testing of the model. Using the proposed hybrid approach, deep learning as a service (DLaaS) platforms will become more attractive to the users. This allows sending resources to the cloud server without compromising the privacy of the sensitive data.

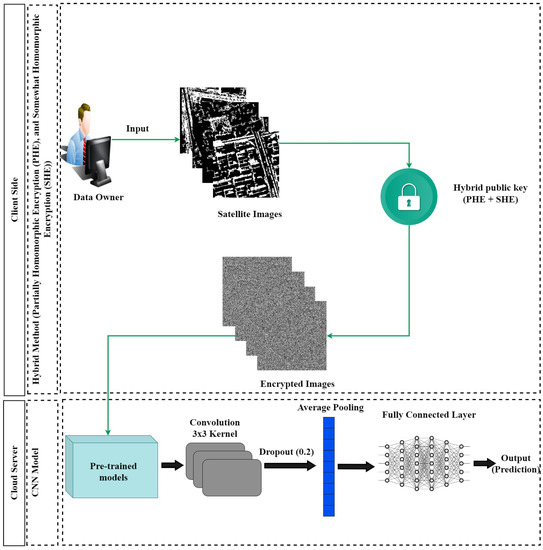
Figure 3. Proposed hybrid approach.

Hybrid Encryption Approach for Satellite Images Privacy

The basic principle of homomorphic encryption was explained in Section 2.2.2. Homomorphic encryption (HE) is subdivided into three subclasses: partially homomorphic encryption (PHE), somewhat homomorphic encryption (SHE), and fully homomorphic encryption (FHE). In this paper, we combined two of them: PHE and SHE. PHE is widely used due to its simplicity compared to the others [40]. It uses only one type of processing (addition or multiplication). Therefore, it does not require much computational cost [20]. Then, it is generally more efficient than SHE and FHE [41].

As depicted in Table 1, the FHE scheme is not efficient in practical scenarios. SHE, on the other hand, is more efficient to use. It allows only some sample operations to be executed for a limited number of times [40]. However, in general, we should bear in mind that homomorphic cryptosystems can still be attacked by some sort of malware. PHE is more prone to this risk because it uses additive homomorphic encryption [20]. Therefore, we should combine PHE with SHE to cope with these security limitations. Furthermore, SHE has an advantage over PHE. It helps to reduce the computational costs due to the shorter bit-length of SHE in the encrypted field [42].

Paillier Homomorphic Encryption Scheme

Partially homomorphic encryption (PHE) schemes use only arithmetic operations (addition or multiplication) on encoded texts. RSA is one example of multiplicative homomorphic encryption [20,43].

The Paillier scheme is an asymmetric additive PHE encryption scheme. In this scheme, $(n,g)$ is the public key. The generation of n is produced by two great prime values, p and q. Both of them have the same binary length. Besides, g represents an element of ${Z^{\ast }}_{n2}$, and its order is a multiple of n. Both p and q are used as secret keys. $\varphi \left(n\right)=(p-1)(q-1)$ has an inverse modulo n. The ${\varphi \left(n\right)}^{(-1)}$ is indicated by $\lambda$ and applied as the secret key (sk) [44]. The three steps of the PHE scheme are: key generation, encryption, and decryption, as presented in Algorithms 1–3, respectively [43,44].

Algorithm 1: Key generation (p, q).

Input: Select two great prime numbers        p, $q\in P$ randomly and independently of each other Output: two different keys are: the encryption key that is the public key $(n,g)$ and       the decryption key that is the secret key ($\lambda$,$\mu$) 1: if length (p) = length(q)      1.1: Calculate $n=p\ast q$ and $g=n+1$      1.2: Compute $\lambda$ =$\varphi \left(n\right)$ where $\varphi \left(n\right)$ is the Euler totient function and          $\varphi \left(n\right)=\left[\right(p-1)\ast (q-1\left)\right]$      1.3: Let $\mu$ be ${\varphi \left(n\right)}^{-1}$ mod n

Algorithm 2: Encryption (M, $pk$).

Input: M is a plaintext that is less than n, where M ∈ $Z_n$ Output: c is a ciphertext where c ∈ ${Z^{\ast }}_{n2}$ 1: Take r ≺ n, where $gcd$(r,n) equals 1 and r is a random value $\in {Z^{\ast }}_{n2}$ 2: c = $g^M{r}^n$ mod $n^2$

Algorithm 3: Decryption (c, $sk$).

Input: c is a ciphertext Output: M is a plaintext 1: M = $L(c^{\lambda }$ mod $n^2$).($\mu$ mod n), where c≺$n^2$

As described earlier, using only the partially homomorphic encryption (PHE) scheme has some drawbacks. Thus, we combined it with the somewhat homomorphic encryption (SHE) scheme described in the next subsection.

Somewhat Homomorphic Encryption Scheme

The SHE scheme is a subclass of homomorphic encryption, which supports both multiplicative and additive homomorphisms with a limited number of operations. The Dijk–Gentry–Halevi–Vaikuntanathan (DGHV) scheme was submitted in 2010 as the second FHE scheme, an asymmetric cryptosystem scheme [45,46]. This scheme is based on the homomorphic property, but with a limited number of operations. Therefore, it provides some properties of SHE. Various parameters are necessary for the implementation of this scheme $\lambda$. In particular, we call $\eta$ the bit-length of the secret key, $\gamma$ the bit-length of the integers in the public key, $\rho$ the bit-length of the noise, and the number of integers in the public key [47,48,49,50]. This scheme is described in the following three algorithms (Algorithm 4 (key generation), Algorithm 5 (encryption), and Algorithm 6 (decryption)).

Algorithm 4: SH.keyGenerate ($\lambda$).

Input: $\lambda$ is the secret parameter Output: public key : $pk=(x_0,x_1,...x_{\tau })$ and private key : : $sk=p$ 1: Choose randomly the private key p that is an odd number, where $p\in [2^{\eta -1},2^{\eta })$ and $\eta ={\lambda }^2$ 2: Generate an array of integers, where $q_i\in Z$, $q_i\in [0,2^{\gamma })$, $q_i\ne p$, and $\gamma ={\lambda }^5$ 3: Choose randomly $r_i\in Z$ and $r_i\in (-2^{\rho },2^{\rho })$, where $\rho =2\lambda$ and $i=0,...,\tau$ with $\tau =\gamma +\lambda$ 4: Define the function : $x_i=p{q}_i+r_i$ 5: $x_0$ is the largest pk value and must be odd. Then, the remainder of $x_0$ must be even

Algorithm 5: SH.Encryption (M, $pk$).

Input: M is the message to encode Output: c is the encrypted message 1: Take a random subset $S\in (0,1,...,\tau )$ 2: Generate a random integer $r\in (-2^{{\rho }^{\prime }},2^{{\rho }^{\prime }})$ 3: $c=(M+2r+2{\sum }_{i\in S}$$x_i)$ mod $x_0$

Algorithm 6: SH.Decryption (c, $sk$).

Input: c is the encrypted message Output: M is the original message 1: Calculate $M=$ (c mod $sk$) mod 2

Proposed hybrid encryption scheme:

In this part, we propose our new hybrid encryption scheme. The design of this proposed scheme is based on the usage of some properties of PHE and SHE, which are described above. This will ensure better encryption, which increases the privacy of satellite images. It is also an attractive scheme to be adopted in the context of sensitive data protection. The development of this new scheme requires using many authenticating functions of two classes of HE. Likewise, it employs two different public keys, one for PHE and the other for SHE, generated by their functions. The steps of our proposed hybrid encryption process are summarized in the flow chart shown in Figure 4.

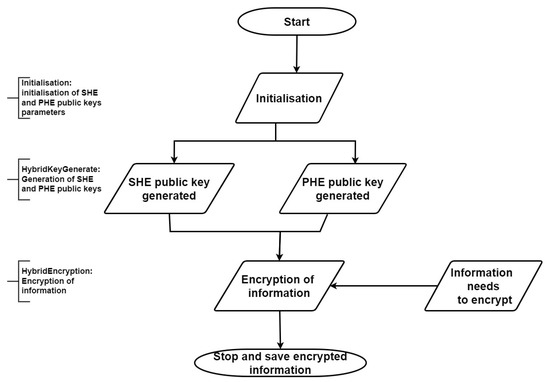
Figure 4. Hybrid encryption steps’ flow chart.

Let ($\lambda$,p, q) be the parameters used by the HybridKeyGenerate algorithm to generate the hybrid public key. $\lambda$ is the parameter used to generate the SHE public key. $(p,q)$ are the parameters used to generate the PHE public key. Let the four-tuple ($\lambda$, $k1$, M, $k2$) be considered as the input parameters for the HybridEncryption algorithm, where $\lambda$ is a secret parameter and $k2$ is the public key included in the SHE schemes. $k1$ is the public key of PHE determined by $(g,n)$, and M is the plaintext. Other parameters are also required to build this scheme, such as $\tau$ and x or $x_i$, which are defined in Algorithm 4. Hence, the generation of the ciphertext is based on these parameters and r (a random value).

The homomorphic encryption is based on a set of algorithms, as described below (Algorithms 7 and 8).

Algorithm 7: HybridKeyGenerate ($\lambda$, p, q).

Input: $\lambda$ is the secret parameter, and p and q are two huge primes having the same length in binary representation. Output: two different public keys: One is generated by the PHE scheme, and the other is developed by the SHE scheme in Algorithms 1 and 4, respectively. 1: $K1$ = keyGeneration (p,q) 2: $K2$ = SH.keyGenerate ($\lambda$)

Algorithm 8: HybridEncryption ($\lambda$, $k1$, M, $k2$).

Input: Let M be the plain message to encrypt Output: Let c be the encrypted message to decode, and $c\in Z_{n^2}$ 1: Take r less than n, where gcd(r,n) equals 1 and r is a random value ∈${Z^{\ast }}_{n^2}$ 2: Generate a random subset $S\in (0,1,...,\tau )$ 3: Compute : $c=(M+2r+2{\sum }_{i\in S}{x}_i)$ mod $n^2$

Let $c1$ and $c2$ be two ciphertexts resulting from $HybridEncryption\left(M1\right)$ and $HybridEncryption\left(M2\right)$, respectively; $r1$ and $r2$ are the two random values in ${Z^{\ast }}_{n^2}$; $pPK1$ and $pPK2$ are two different public keys. To display that the properties of homomorphic encryption are preserved in the hybrid approach:

Firstly, we considered the addition of the two ciphertexts, where $c=(M+2r+pPK)$$mod{n}^2$ and $PK={\sum }_{i\in S}{x}_i$.

We can see that:

$$\begin{array}{cc}\hfill c mod{n}^2& =(c1+c2)mod{n}^2;\hfill \\ & =\left((M1+2r1+pPK1)mod{n}^2+(M2+2r2+pPK2)mod{n}^2\right)mod{n}^2;\hfill \\ & =\left[[(M1+2r1+pPK1)+(M2+2r2+pPK2)]mod{n}^2\right]mod{n}^2\hfill \\ & =\left[[(M1+M2)+2(r1+r2)+p(PK1+PK2)]mod{n}^2\right]mod{n}^2\hfill \\ & =\left[(M+2r+pPK)mod{n}^2\right]mod{n}^2;\hfill \end{array}$$

With $M=(M1+M2)$, $r=(r1+r2)$, and $PK=(PK1+PK2)$.

Therefore,

$$\left(HybridEncryption\left(M\right)\right)mod{n}^2=(HybridEncryption\left(M1\right)+HybridEncryption\left(M2\right))mod{n}^2$$

(1)

Secondly, we considered the multiplication of the two ciphertexts:

$$\begin{array}{cc}\hfill c mod{n}^2& =(c1\times c2) mod{n}^2\hfill \\ \\ & =\left[(M1+2r1+pPK1)mod{n}^2\times (M2+2r2+pPK2)mod{n}^2\right]mod{n}^2;\hfill \\ \\ & =\left[[(M1+2r1+pPK1)\times (M2+2r2+pPK2)]mod{n}^2\right]mod{n}^2;\hfill \\ \\ & =\left[\right[M1\times M2+M1\times 2r2+M1\times pPK2+2r1\times M2+2r1\times 2r2+2r1\times pPK2;\hfill \\ & \left.+pPK1\times M2+pPK1\times 2r2+pPK1\times pPK2]mod{n}^2\right]mod{n}^2;\hfill \\ \\ & =\left[\right[(M1\times M2)+2(M1\times r2+M2\times r1+2\times r1\times r2);\hfill \\ & \left.\left.+(pPK1\times pPK2)\left(1+\frac{M1+2r1}{pPK1}+\frac{M2+2r2}{pPK2}\right)\right]mod{n}^2\right]mod{n}^2;\hfill \\ \\ & =\left[\right[(M1\times M2)+2(M1\times r2+M2\times r1+2\times r1\times r2);\hfill \\ & \left.\left.+(PK1\times PK2)\left[p^2\left(1+\frac{M1+2r1}{pPK1}+\frac{M2+2r2}{pPK2}\right)\right]\right]mod{n}^2\right]mod{n}^2;\hfill \\ \\ & =\left[(M+2r+pPK)mod{n}^2\right]mod{n}^2\hfill \end{array}$$

with $M=M1\times M2, r=(M1\times r2+M2\times r1+2\times r1\times r2), PK=PK1\times PK2, \mathrm{and} p=p^2(1+\frac{M1+2r1}{pPK1}+\frac{M2+2r2}{pPK2})mod{n}^2$.

We deduct this formula:

$$\left(HybridEncryption\left(M\right)\right)mod{n}^2=(HybridEncryption\left(M1\right)\times HybridEncryption\left(M2\right))mod{n}^2$$

(2)

The two demonstrations above prove that the designed hybrid approach conserves the properties of a homomorphism. Therefore, this hybrid approach increases the security level compared to using PHE or SHE alone. Moreover, it decreases the computation cost using a shorter bit length.

Data augmentation (DA):

Data augmentation (DA) refers to the class of techniques used for enlarging the training dataset without gathering more original data. Most DA methods either append softly changed copies of existing data or build synthetic data. When training ML models, the increased data acts as a regularizer to decrease the overfitting [51,52]. In the image domain, DA techniques include, for example, rotations, horizontal and vertical shifts, and zoom. These procedures improve the efficiency of convolutional neural networks [53].

For this study, we used the following data augmentation strategies:

• A rotation range that equals 90 degrees.
• A zoom and a shear range equal to 20%.
• A brightness scale between [0.2,…, 1.0].
• A shift range that equals 20% in height and width.
• A horizontal flip and a vertical flip.

4. Experiments and Results

This section describes the dataset used in the experiments, presents the hardware and software, and details the obtained results.

4.1. Study Regions and Dataset

Figure 5 depicts the study area representing seven cities in Saudi Arabia. The first city is Al Madinah, which is among the western cities of Saudi Arabia and is the second-holiest city in Islam after Mecca. This city has significant cultural and historical heritage. The second region is Riyadh, the capital of Saudi Arabia, and is thought to be one of the fastest-growing regions in the entire Middle East. The third city is Jeddah, the second-largest city in the western region. Jeddah is positioned in the lower Hijaz Mountains and lies on the Red Sea Coast. The fourth region is Al Qassim, which presents the country’s wealthiest city per capita and is both the seventh-most-populated area in Saudi Arabia and the fifth-most densely populated region. The fifth area is Al Qatif, one of the ancient territories in Eastern Arabia, and represents an urban area. The sixth city is Hail, an agricultural area located in northwestern Saudi Arabia. Finally, the seventh region is Dammam, the sixth-most populated city in Saudi Arabia, the capital of the eastern province of Saudi Arabia, and the center of the Saudi oil industry.

Figure 5. Study area.

Experiments were conducted on several real-world high-resolution satellite images acquired using the SPOT6 and SPOT7 satellites. These images have 2 m-resolution multispectral bands and a 0.5 m-resolution panchromatic band.

Satellite images used in this study were corrected with respect to radiometry, sensor distortions, and acquisition effects. Additionally, these images were orthorectified to eliminate the perspective effect on the ground. To prepare our dataset, satellite images representing the seven regions were split into non-overlapping blocks of 256 × 256. Four land cover types within these blocks: building, vegetation, road, and bare soil, were extracted using a semantic segmentation algorithm.

The goal of the semantic segmentation algorithm is to partition satellite images into meaningful regions. Let $I={\{b_n\in R^4\}}_{n=1}^N$ be the multi-band satellite images, where N signifies the number of pixels found in these images. The pixel values were normalized in the range of [0, 1]. Each pixel in the image was assigned a set of labels. Interested readers can refer to the detailed approach used for semantic segmentation [54]. Figure 6 illustrates samples of images in which white denotes the land cover category and black designates the values of other types. Experiments were carried out on a dataset comprising 28,776 satellite images of 224 × 224 pixels and containing each only one land cover type. The dataset was split into 90% for training and 10% for validation. Table 3 shows the number of images for each class.

Figure 6. Samples of images.

Table 3. Number of samples of each land cover type.

Land Cover Type	No. of Training Samples	No. of Validation Samples
BareSoil	6784	754
Building	7541	838
Road	5411	601
Vegetation	6162	685

4.2. Experimental Setup

Experiments were run on an AI server with a 64-bit operating system, an x64-based processor, a 2.30 GHz Intel(R) Xeon(R) Gold 5218 CPU, and 512 GB RAM. The server has eight NVIDIA Quadro RTX 8000 GPUs, each with 48 GB of memory, and runs Ubuntu 18.04. Python 3.7, Keras 2.6 library, and the TensorFlow-GPU 2.3 backend were used to design the DL networks. We trained the CNN models in parallel on the server, with each training session on a single GPU.

4.3. Metrics

We evaluated the performance of our proposed hybrid PPDL by applying several transfer learning models on the satellite dataset described above, before (plain images) and after encryption. The effectiveness of our PPDL method was validated by using several standard metrics, namely the accuracy, precision, recall, and F1-score. These metrics are defined based on the four following quantities defined for each class C:

• True positives (TPs): the number of images correctly predicted as belonging to class C.
• True negatives (TNs): the number of images of other classes correctly predicted as not belonging to class C.
• False positives (FPs): the number of images wrongly predicted as belonging to class C.
• False negatives (FNs): the number of images of class C wrongly predicted as belonging to other classes.

4.4. Results

In this section, we evaluate the performance of our hybrid PPDL. Our experiments are divided into three parts. In the first part, we present the encrypted images. The second level of our experiments examined the outcomes of the different DL models after training on the plain and encrypted data, using the metrics mentioned above. In the ultimate part, we used several security parameters to evaluate the performance of these images in terms of security.

4.4.1. Image Encryption

The proposed encryption scheme was applied to the dataset described in Section 4.1. Figure 7 illustrates a sample of the original and encrypted images. The encrypted images were obtained using the proposed hybrid encryption algorithm (Algorithm 8), which was validated to be efficient and secure. Then, the CNN model was trained and tested without visual information. The original image was encrypted by a hybrid public key (both public keys) generated by the HybridKeyGenerate algorithm (Algorithm 7).

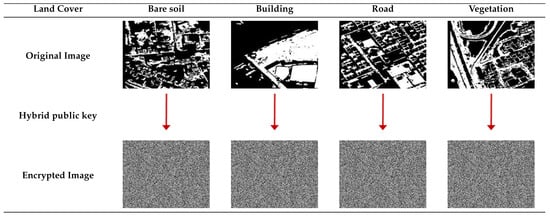
Figure 7. Land cover images belonging to the four different classes and their encrypted images.

4.4.2. Application of Transfer Learning Models

The section aims to evaluate the performance of the transfer learning models on both the plain and encrypted satellite images. Four different transfer learning models were considered, namely DenseNet169 [55], MobileNetV2 [56], InceptionV3 [57], and ResNet50 [58], all pre-trained on ImageNet [59]. Figure 8 depicts the model architecture used. Since the plain and encrypted images were in grayscale, while the transfer learning models expect three channels, we duplicated the images for each channel. Besides, we froze the first 100 layers (The term "layer" here refers to any tensor-in/tensor-out computation function, as defined in the Keras library. This includes convolutional and fully connected layers, but also paddings, pooling layers, batch normalization, and activation functions.) of each pre-trained model, removed their final dense layers, and replaced them with a convolutional layer (128 filters, 3 × 3 kernel, 1 × 1 stride, ReLU activation function), a dropout layer (0.2 rates), a global average pooling layer (output shape 128 × 1), and a fully connected layer (128 inputs and 4 output neurons, with a softmax activation function). We trained each model for 200 epochs on both the plain and encrypted datasets.

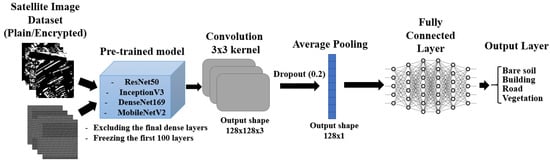
Figure 8. Model architecture used for training on the plain and encrypted datasets.

The graphical illustration of the validation accuracy progress during the training of these four models on both the plain and encrypted datasets is shown in Figure 9. The algorithms were slower to converge on the encrypted dataset, but the gap in accuracy was progressively reduced. InceptionV3 converged faster than the three other models on both datasets. This suggests that its pre-trained weights on ImageNet were incidentally closer to the optimum weight values on our dataset. We selected the weights that corresponded to the minimal loss as the validation dataset for each model. Figure 10 shows the confusion matrices among the real and predicted classes for each model on the plain and encrypted datasets. For the four models, the encryption entailed a little confusion between the road and vegetation classes (between 14% and 22% of misclassifications). In contrast, these two classes were well distinguished on the plain dataset (misclassification rate between 0.2% and 2% between these two classes). For ResNet50 and InceptionV3, the encryption also entailed a higher confusion between the bare soil and building classes (misclassification rate of 15% and 6%, respectively, compared to 7% and 3% on the plain images). This suggests that the encryption process alters the gap among class features. Nevertheless, the difference in overall accuracy for the four models between the plain and encrypted datasets remained limited (from 2.0 to 3.5 percentage points). This shows an acceptable trade-off between the usefulness and the confidentiality of the data.

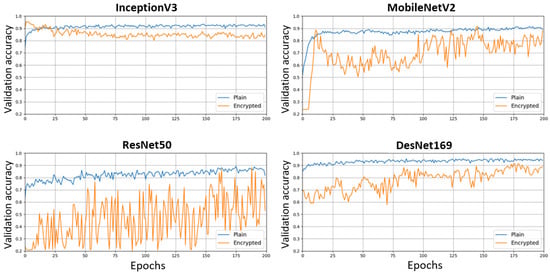
Figure 9. Evolution of the validation accuracy during training on plain and encrypted images for the 4 CNN architectures.

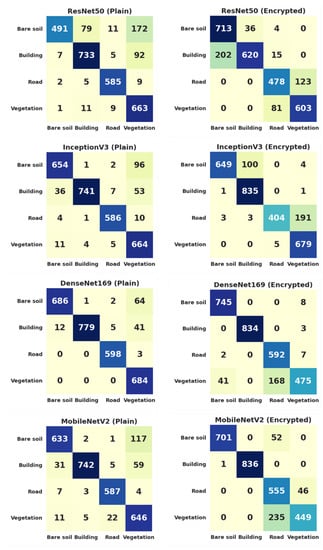
Figure 10. Confusion matrices obtained for the 4 different CNN architectures (from top to bottom: ResNet50, InceptionV3, DenseNet169, MobileNetV2), on the validation set, for both the plain (left) and encrypted (right) datasets.

Table 4 illustrates several performance metrics on the validation set for both the plain and encrypted images. The precision, recall, and F1-score were averaged, with the number of images in each class as the weights. In all three metrics, and for both the plain and encrypted datasets, DenseNet169 showed the highest performance, while ResNet50 showed the lowest performance. Nonetheless, this came at the cost of a lower inference speed for DenseNet169 (44% and 21% slower than MobileNetV2 and ResNet50, respectively). MobileNetV2 had the fastest inference speed due to its reduced architecture, designed to run on mobile devices with limited computing capabilities. The inference speed does not depend on the type of images (plain or encrypted) as long as they have the same input size (224 × 224). The inference time depends on the number of floating-point operations (FLOPs) and other factors, such as parallel operations in the GPU for each CNN architecture. This explains why DenseNet169 (with the most significant number of layers among the four networks) necessitated fewer operations (29.1 M), but a higher inference time (2.3 ms per image). On the other hand, the maximum loss in the average precision, recall, and F1-score, when shifting from the plain to the encrypted images, was 3.8 (for ResNet50), 5.2 (for MobileNetV2), and 5.2 percentage points (also for MobileNetV2), respectively, which is an acceptable range, especially when moving from the plain to the encrypted images for applications where data privacy is critical. InceptionV3 showed the least loss in the precision (1.7 percentage points), while ResNet50 showed the least loss in the recall (2) and F1-score (1.9), since its score on the plain images was already significantly lower than the three other models.

Table 4. Performance of the 4 CNN models on the validation set of the plain and encrypted data.

Weighted Average on the 4 Classes										No. of Param.	No. of Operations (FLOPS)	Inference Time per Image (ms)
CNN Models	Precision			Recall			F1-Score
	Plain	Enc	Loss	Plain	Enc	Loss	Plain	Enc	Loss
ResNet50	88.3%	84.5%	3.8%	86.0%	84.0%	2.0%	85.8%	83.9%	1.9%	25.9 M	51.8 M	1.9
InceptionV3	92.8%	91.1%	1.7%	92.0%	89.3%	2.7%	92.1%	89.0%	3.1%	24.1 M	48.3 M	1.8
DenseNet169	96.0%	93.1%	2.9%	95.5%	92.0%	3.5%	95.6%	91.8%	3.8%	14.6 M	29.1 M	2.3
MobileNetV2	94.1%	90.6%	3.5%	93.6%	88.4%	5.2%	93.7%	88.5%	5.2%	3.7 M	7.4 M	1.6

Figure 11 summarizes the performance of the four CNN models in terms of the accuracy and speed and the precision, recall, and F1-score per class. It is also clear that DenseNet169 provided the best overall performance on both the plain and encrypted images, except for the inference speed, while MobileNetV2 offered a good trade-off between the accuracy and speed, and ResNet50 showed the least accuracy on both datasets while also being the second slowest for inference. Figure 11 also shows that the encryption process did not equally affect the classes.

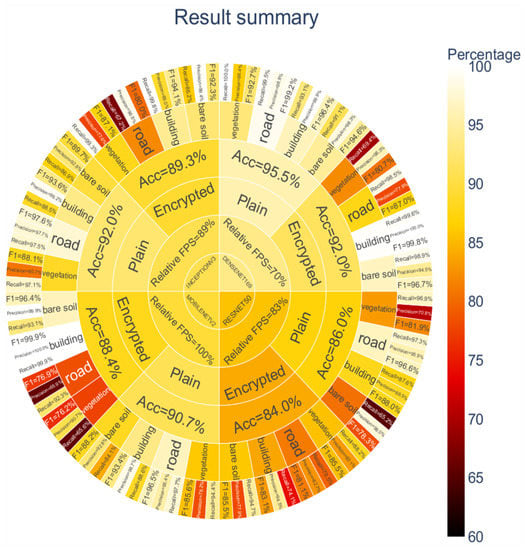
Figure 11. Summary of the results of the four CNN models in a sunburst chart. The relative FPS corresponds to the number of processed frames per second divided by the maximum obtained value (632 for MobileNetV2). The color of inner sectors (representing algorithms) corresponds to the average colors of outer sectors belonging to them: the lighter the color, the better the results are.

4.5. Evaluation

To evaluate the proposed hybrid encryption scheme, five parameters were used, namely the correlation coefficient (CC), entropy, mean-squared error (MSE), peak signal-to-noise ratio (PSNR), and structural similarity index (SSIM) [60,61,62,63,64]. The most important challenge in this work was to enhance the encryption scheme in PPDL. Table 5 shows that the proposed encryption method ensured better encryption than the work proposed by Alkhelaiwi et al. [19] concerning the five security parameters referred to earlier. The correlation coefficient value (0.0039) between the original and its corresponding encrypted image showed the efficiency of our proposed hybrid encryption (the best-encrypted images had a CC value close to 0), where the masking of the visual features in the encrypted image was guaranteed. The entropy values of both studies mentioned in Table 5 were close to 8 (which is the ideal value), but the entropy of encrypted images by the proposed approach was 7.9701, which is 0.13% higher than for [19]. In terms of the MSE, the difference between the two encryption methods attained 2.7%. This result showed that our encryption approach is more secure than [19]. Based on the low PSNR, the table below also shows that the encrypted images by the hybrid approach were more secure than the other cipher images. The lowest value of the SSIM corresponds to more secure encrypted images. This value is 33% lower for our method compared to [19].

Table 5. Comparison of the proposed approach and [19] for security parameters.

Security Parameters	Proposed Approach (Encrypted Images)	[19] (Encrypted Images)
CC	0.0039	−0.0041
Entropy	7.9701	7.9596
MSE	2.181 × ${10}^4$	2.1236 × ${10}^4$
PSNR	4.2234	4.8601
SSIM	0.0012	0.0018

5. Discussion

With the emergence of using DLaaS, if no security measures have been taken, any unauthorized user can access all the sensitive transmitted data. This opens the door to several kinds of threats, and possible misuses, which must be addressed correctly. To ensure the privacy and confidentiality of the data and restrict access to sensitive information, we can use cryptographic approaches [65], in other words, encrypting the data locally before transmitting them to the DLaaS server to train the AI model. The only constraint we must consider is conserving the accuracy recorded while training on the plain data. This paper reviewed various PPDL methods to highlight their advantages and drawbacks and proposed a new PPDL approach to address this challenge. The proposed method is based on two classes of homomorphic encryption methods, which extract many features from PHE and SHE. While preserving the data confidentiality and denying access to unencrypted data (original images), a hybrid encryption scheme can apply many operations immediately on the encrypted images (encoded images) without needing to decrypt them. Experiments were conducted using a large real-world dataset composed of 28,776 satellite images divided into four classes: bare soil, building, road, and vegetation. Moreover, the variety of datasets can enhance the performance of the CNN model. Thus, DA techniques have a very important role in increasing the diversity of satellite datasets in these models. The performance of the proposed PPDL method can be assessed from two perspectives: model accuracy and data security.

Beginning with the accuracy, the evaluation of the proposed hybrid method was assessed using four different pre-trained CNN models, which showed good accuracy when applied to an encrypted dataset. The highest accuracy was 92% and was achieved by DenseNet169, and the lowest accuracy was 84%, achieved by ResNet50. Although, the accuracy gap compared to the training on plain images is less than 3.5%, as shown by DenseNet169. We can consider it admissible for applications where security and privacy are critical. This enforces the usefulness of the proposed method in cases where we need to protect the data we used to train on DLaaS.

From the security perspective, we can note that using a combination of PHE and SHE improves the security of encrypted images. This was demonstrated using five security parameters: the correlation coefficient (CC), the entropy, the mean-squared error (MSE), the peak signal-to-noise ratio (PSNR), and the structural similarity index (SSIM). The optimal value for the CC is 0 for the most-secure encryption algorithm. The CC for the proposed algorithm is 0.0039, which reflects that we cannot correlate between the original image and its encrypted peer. Image details were almost hidden during the encryption process. Furthermore, the optimal value for the entropy is 8 for the best-possible encryption. The estimated entropy for the proposed algorithm was 7.9701, very close to the optimal. This inhibits the possibility of reconstructing the original image from the encrypted peer. Furthermore, the MSE, PSNR, and SSIM were very low. This demonstrates the low similarity rate between the original image and its associated peer. This similarity rate was estimated using three different metrics.

The main limitation of the proposed algorithm is the runtime. For one image of input size (224 × 224), we needed 21.2 s to encrypt it for a key size of 128 bits. If the user is working with a small dataset and only using a small number of images during inference, this cost is reasonable and cannot be considered a limitation. Otherwise, it will represents a drawback that should be solved.

The obtained outcomes displayed that the proposed approach provides a secure encryption method while maintaining excellent accuracy in detecting features in satellite images. This will allow us to benefit from DLaaS while keeping the privacy of the data.

6. Conclusions

DL has emerged to be used as a service in many applications due to the low usage cost and the flexibility of a wide range of DL tools and development solutions. However, DLaaS remains under several security and privacy threats. PPDL constitutes, among others, an important tool to ensure the security and privacy of sensitive data while training models on DLaaS. In this study, a hybrid approach based on Paillier homomorphic encryption and somewhat homomorphic encryption was proposed. The proposed hybrid PPDL approach was developed to preserve data privacy, which enables the adoption of DLaaS without compromising data privacy. Data will be encrypted locally on the user machine before transmitting to DLaaS. The training will be performed on the encrypted data without the need to encrypt them. The data encryption phase is based on two different steps, the public-key generation step and the encryption step. The first step generates the different public keys used to encrypt the data. The second step uses the generated public keys and plain image data to encrypt satellite images. During the study, experimental results were given based on a real-world RS dataset, and the method showed good performance in terms of accurate decisions and data security. The loss in accuracy due to encryption was less than 3.5%, which is admissible for applications where security and privacy are critical. For the security side, the proposed hybrid scheme showed robust security features as demonstrated by five security parameters: CC, entropy, MSE, PSNR, and SSIM. The main limitation was the high computational cost needed to encrypt the image. If the images are limited in size, this could be affordable. Otherwise, we need to solve this limitation.

Several possible extensions can be considered in future work. First, the proposed hybrid approach could be extended to other fields, such as medical image analysis, in order to protect critical patient data for example. In addition, the DL models can be enriched to have the possibility to be trained on plain and encrypted images, which are included in the same dataset, in order to encrypt only sensitive images while keeping others in the original form. This will lead to classifying objects in both plain and encrypted images. Finally, other encryption schemes can be implemented in the context of real-time applications. This will ensure the security of encrypted data with a faster encryption process.