A Repeater-Type SAR Deceptive Jamming Method Based on Joint Encoding of Amplitude and Phase in the Intra-Pulse and Inter-Pulse
Abstract
:1. Introduction
1.1. Background
1.2. Previous Work
1.2.1. Direct-Type Deceptive Jamming
1.2.2. Repeater-Type Deceptive Jamming
1.3. Main Contributions of This Paper
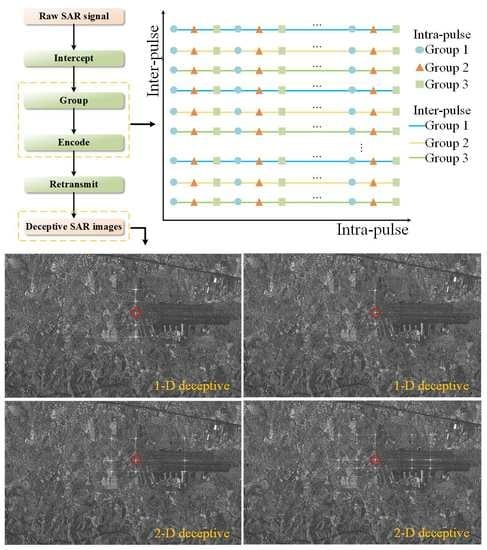
- A repeater-type deceptive jamming model is established, and a deceptive jamming method through the joint coding of amplitude and phase in intra-pulse and inter-pulse (CAPII) is proposed. The proposed method can generate false targets with different amplitudes and numbers in 2D.
- The imaging results of the proposed algorithm are analyzed and deduced in detail. Specifically, false target characteristics, including the number, position, and amplitude of the false target, are discussed separately.
- The feasibility of the proposed method is verified by simulation experiments. Using ISRJ and FDA as a comparative experiment, the superiority of the proposed method is verified.
1.4. Organization of This Paper
2. Model and Methods
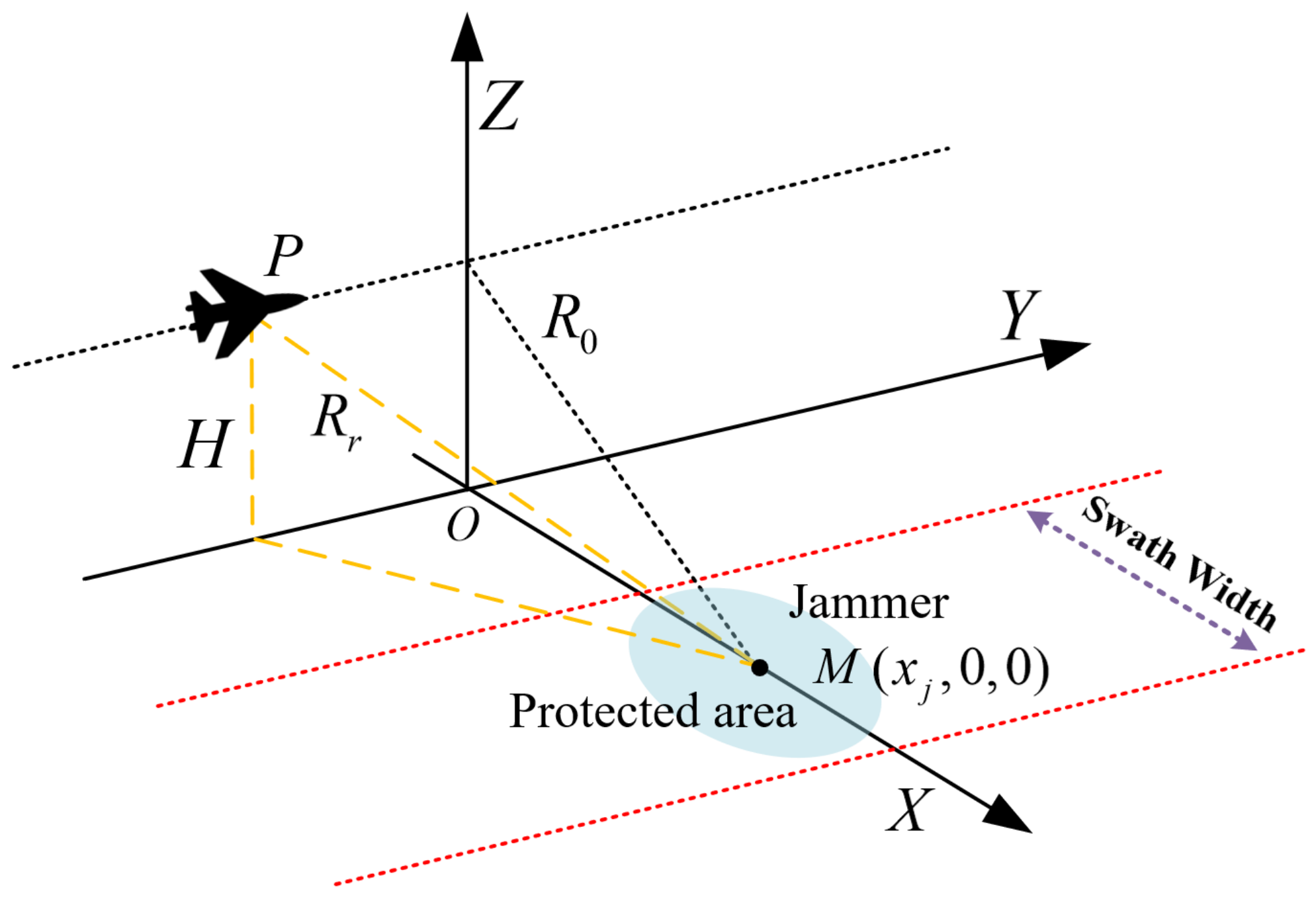
2.1. SAR Jamming Model
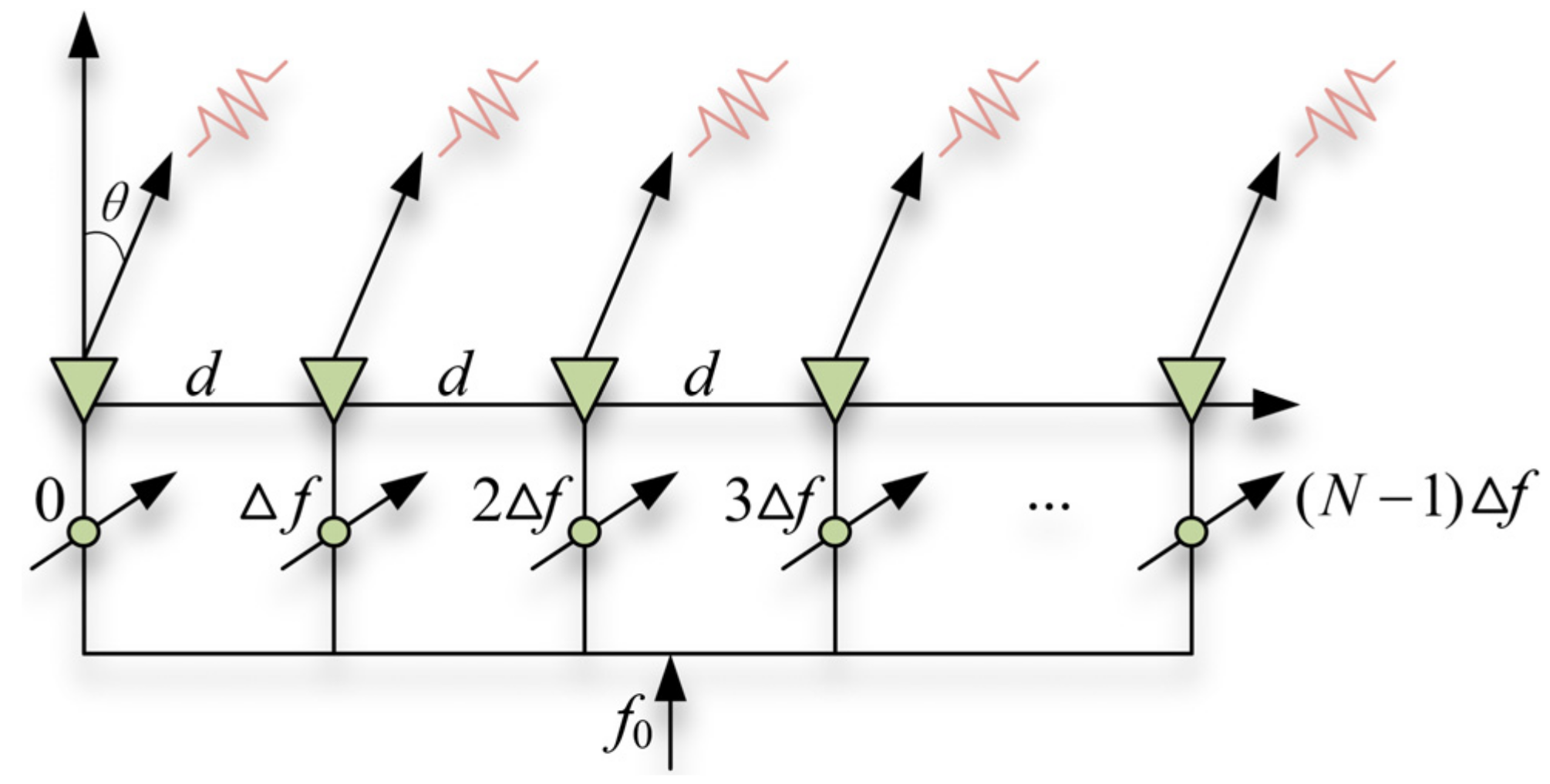
2.2. FDA-Based Deceptive Jamming Method
2.3. ISRG Method
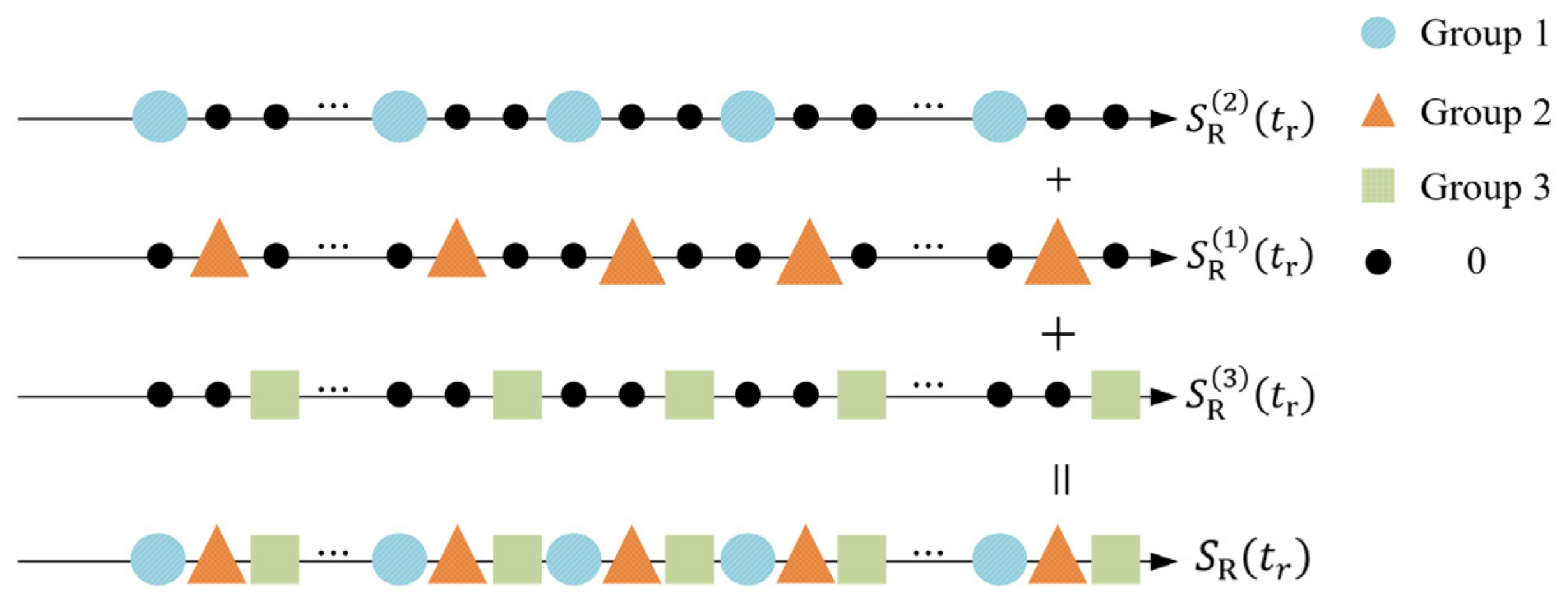
2.4. The Proposed Method
3. Signal Imaging Process and Analysis
3.1. Range Compression
3.2. Azimuth Compression
3.3. False Target Feature Analysis
3.3.1. The Number of False Targets
3.3.2. The Position of False Targets
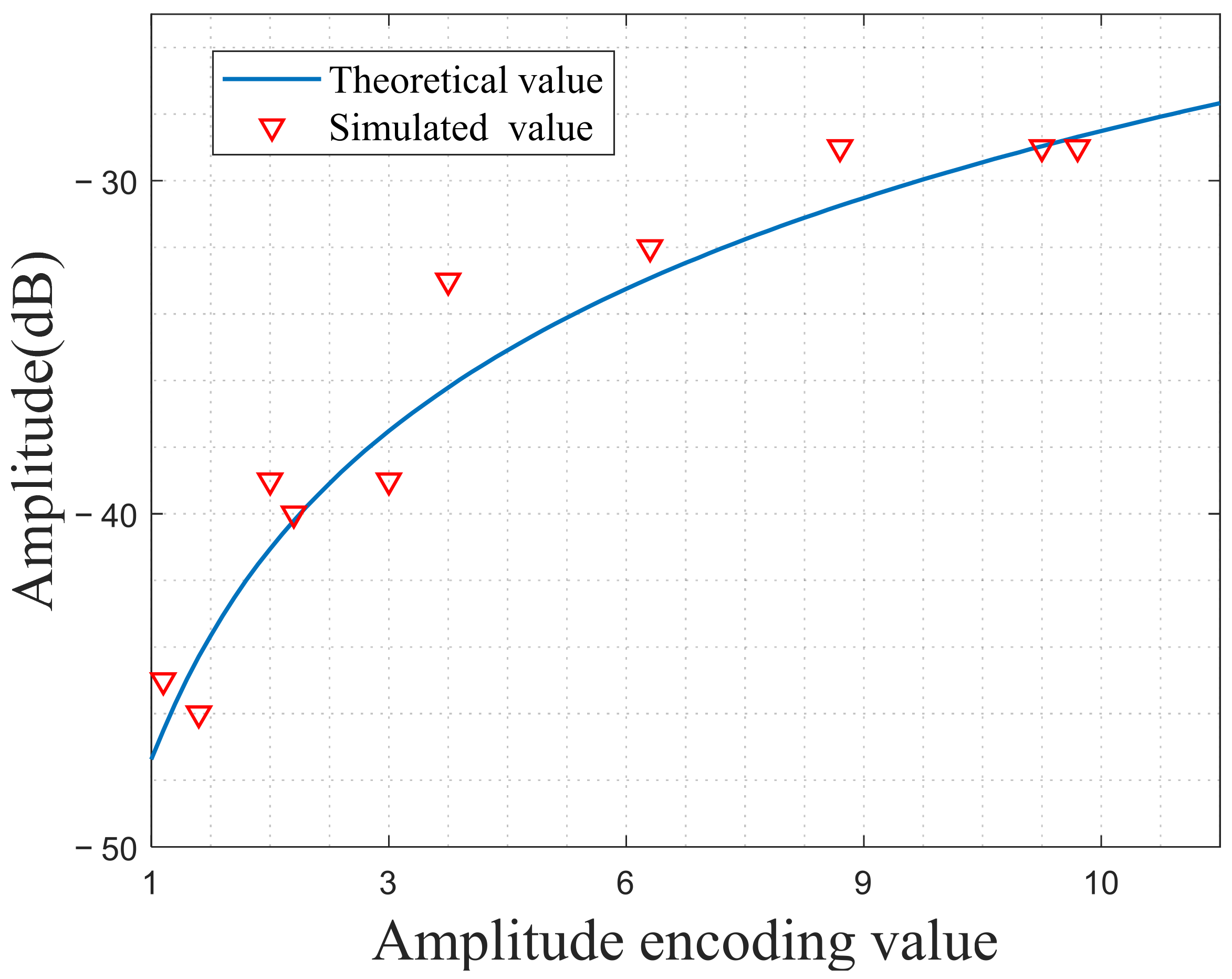
3.3.3. The Amplitude of the False Target
4. Simulation and Results
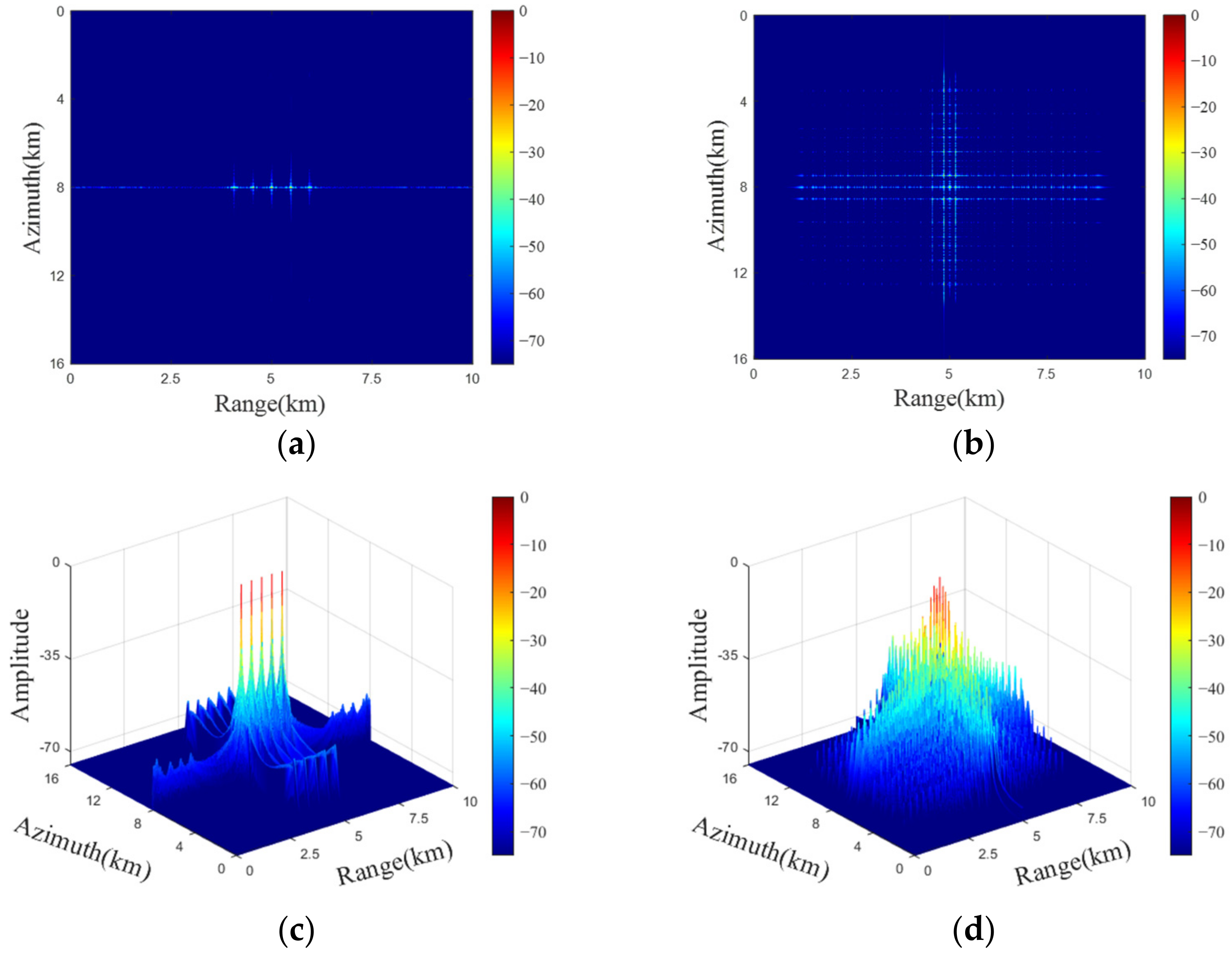
4.1. Point Target Simulation
4.2. Area Target Simulation
5. Discussion
6. Conclusions
- Realizing the control of the positions of the false targets.
- Applying the CAPII method to moving targets.
- Applying the CAPII method to a variety of modes.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reigber, A.; Scheiber, R.; Jager, M.; Prats-Iraola, P.; Hajnsek, I.; Jagdhuber, T.; Papathanassiou, K.P.; Nannini, M.; Aguilera, E.; Baumgartner, S. Very-High-Resolution Airborne Synthetic Aperture Radar Imaging: Signal Processing and Applications. Proc. IEEE 2013, 101, 759–783. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Deng, Y.; Yu, W.; Zhang, H.; Wang, W.; Liu, D.; Wang, R. Forthcoming Spaceborne SAR Development. J. Radars 2020, 9, 1–33. [Google Scholar]
- Tao, M.; Su, J.; Huang, Y.; Wang, L. Mitigation of Radio Frequency Interference in Synthetic Aperture Radar Data: Current Status and Future Trends. Remote Sens. 2019, 11, 2438. [Google Scholar] [CrossRef]
- Huber, S.; Almeida, F.; Villano, M.; Younis, M.; Krieger, G.; Moreira, A. Tandem-L: A Technical Perspective on Future Spaceborne SAR Sensors for Earth Observation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4792–4807. [Google Scholar] [CrossRef]
- Stofan, E.; Evans, D.; Schmullius, C.; Holt, B.; Plaut, J.; Zyl, J.; Wall, S.; Way, J. Overview of results of Spaceborne Imaging Radar-C, X-Band Synthetic Aperture Radar (SIR-C/X-SAR). IEEE Trans. Geosci. Remote Sens. 1995, 33, 817–828. [Google Scholar] [CrossRef]
- Li, Z.; Wang, H.; Su, T.; Bao, Z. Generation of wide-swath and high-resolution SAR images from multichannel small spaceborne SAR systems. IEEE Geosci. Remote Sens. Lett. 2005, 2, 82–86. [Google Scholar] [CrossRef]
- Ji, P.; Xing, S.; Dai, D.; Pang, B. Deceptive Targets Generation Simulation Against Multichannel SAR. Electronics 2020, 9, 597. [Google Scholar] [CrossRef]
- Ji, P.; Dai, D.; Xing, S.; Pang, B. A New Three-Dimension Deceptive Scene Generation against Single-Pass Multibaseline InSAR Based on Multiple Transponders. Sensors 2020, 20, 1053. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, B.; Tao, M.; Chen, Z.; Hong, H. A Review of Synthetic Aperture Radar Anti-Jamming Technique. J. Radars 2020, 9, 89–106. [Google Scholar]
- Zhou, F.; Sun, G.; Bai, X.; Bao, Z. A Novel Method for Adaptive SAR Barrage Jamming Suppression. IEEE Geosci. Remote Sens. Lett. 2011, 9, 292–296. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, J.; Pu, J.; Wu, Y.; Ran, D. Low Sidelobe Multi-Phase Segmented Modulation Jamming Method Based on Cosine Amplitude Weighting. J. Syst. Eng. Electron. 2021, 43, 3185–3193. [Google Scholar]
- Li, Y.; Huang, D.; Xing, S.; Wang, X. A Review of Synthetic Aperture Radar Jamming Technique. J. Radars 2020, 9, 753–764. [Google Scholar]
- Huang, L.; Dong, C.; Shen, Z.; Zhao, G. The Influence of Rebound Jamming on SAR GMTI. IEEE Geosci. Remote Sens. Lett. 2015, 12, 399–403. [Google Scholar] [CrossRef]
- Chang, X.; Li, Y.; Zhao, Y. An Improved Scattered Wave Deceptive Jamming Method Based on a Moving Jammer Beam Footprint Against a Three-Channel Short-Time SAR GMTI. IEEE Sens. Lett. 2020, 21, 4488–4499. [Google Scholar] [CrossRef]
- Zhao, B.; Huang, L.; Li, J.; Liu, M.; Wang, J. Deceptive SAR Jamming Based on 1-bit Sampling and Time-Varying Thresholds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 939–950. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, H.; Li, J.; Liu, W. Research of 3-D Deceptive Interfering Method for Single-Pass Spaceborne InSAR. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2834–2846. [Google Scholar] [CrossRef]
- Deng, Y.; Zheng, Y.; Hu, Y. Analysis of Synthetic Aperture Radar Repeater Jamming. J. Electron. Inf. Technol. 2010, 32, 69–74. [Google Scholar] [CrossRef]
- Zhang, N.; Kuang, L.; Shen, F.; Wan, Q.; Yang, W. A Jamming Technique against Airborne SAR. In Proceedings of the 2006 CIE International Conference on Radar (RADAR), Guangzhou, China, 16–19 October 2006; pp. 1–3. [Google Scholar]
- Qu, W.; Jia, X.; Wu, Y. Modeling and Simulation Analyses of SAR Signal Reconnaissance. J. Stat. Comput. Simul. 2007, 10, 2341–2345. [Google Scholar]
- Lin, X.; Liu, P.; Xue, G. Fast Generation of SAR Deceptive Jamming Signal Based on Inverse Range Doppler Algorithm. In Proceedings of the IET International Radar Conference, Xi’an, China, 14–16 April 2013; pp. 1–4. [Google Scholar]
- Sun, Q.; Shu, T.; Zhou, S.; Tang, B.; Yu, W. A Novel Jamming Signal Generation Method for Deceptive SAR Jammer. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1174–1178. [Google Scholar]
- Sun, Q.; Shu, T.; Yu, K.; Yu, W. Efficient Deceptive Jamming Method of Static and Moving Targets Against SAR. IEEE Sens. J. 2018, 18, 3601–3618. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Pan, X.; Dai, D.; Feng, D. A Frequency-Domain Three-stage Algorithm for Active Deceptive Jamming Against Synthetic Aperture Radar. IET Radar Sonar Navig. 2014, 8, 639–646. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Pan, X.; Fu, Q.; Wang, G. Inverse omega-K algorithm for the electromagnetic deceptive of synthetic aperture radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3037–3049. [Google Scholar] [CrossRef]
- Yang, K.; Ye, W.; Wu, X.; Ma, F.; Li, F. Fast Generation of Deceptive Jamming Signal Against Space-Borne SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5580–5596. [Google Scholar] [CrossRef]
- Yang, K.; Ye, W.; Ma, F.; Li, G.; Tong, Q. A Large-Scene Deceptive Jamming Method for Space-Borne SAR Based on Time-Delay and Frequency-Shift with Template Segmentation. Remote Sens. 2020, 12, 53. [Google Scholar] [CrossRef]
- Wang, S.; Yu, L.; Ni, J.; Zhang, G. A Study on the Active Deceptive Jamming to SAR. Acta Electron. Sin. 2003, 12, 1900–1902. [Google Scholar]
- Zhou, F.; Zhao, B.; Tao, M.; Bai, X.; Chen, B.; Sun, G. A Large Scene Deceptive Jamming Method for Space-Borne SAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4486–4495. [Google Scholar] [CrossRef]
- Zhang, B.; Zhou, F.; Shi, X.; Wu, Q.; Zheng, B. Multiple Targets Deceptive Jamming Against ISAR Using Electromagnetic Properties. IEEE Sens. J. 2015, 15, 2031–2038. [Google Scholar]
- Tai, N.; Wang, Y.; Han, H.; Xu, X.; Wang, C.; Zeng, Y.; Wang, L. Deceptive Jamming Against ISAR Based on Convolution and Sub-Nyquist Sampling. IEEE Sens. J. 2020, 20, 1807–1820. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, H.; Zhang, S.; Zheng, Z.; Wang, W. Deceptive Jamming on Space-Borne Sar Using Frequency Diverse Array. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 605–608. [Google Scholar]
- Bang, H.; Wang, W.; Zhang, S.; Liao, Y. FDA-Based Space–Time–Frequency Deceptive Jamming Against SAR Imaging. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2127–2140. [Google Scholar] [CrossRef]
- Huang, B.; Wang, W.; Zhang, S.; Wang, H.; Gui, R.; Lu, Z. A Novel Approach for Spaceborne SAR Scattered-Wave Deceptive Jamming Using Frequency Diverse Array. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1568–1572. [Google Scholar] [CrossRef]
- Huang, L.; Zong, Z.; Zhang, S.; Wang, W. 2-D Moving Target Deceptive Against Multichannel SAR-GMTI Using Frequency Diverse Array. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar]
- Wang, X.; Liu, J.; Zhang, W.; Fu, Q.; Liu, Z.; Xie, X. Mathematical Principle of Intermittent Sampling Repeater Jamming. Sci. Sin. (Technol.) 2006, 8, 891–901. [Google Scholar]
- Wu, X.; Bo, Z.; Dai, D.; Wang, X. Azimuth intermittent Sampling Repeater to SAR. J. Signal Process. 2010, 26, 1–6. [Google Scholar]
- Li, C.; Su, W.; Gu, H.; Ma, C.; Chen, J. Improved Interrupted Sampling Repeater Jamming based on DRFM. In Proceedings of the 2014 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Guilin, China, 5–8 August 2014; pp. 254–257. [Google Scholar]
- Feng, D.; Xu, L.; Pan, X.; Wang, X. Jamming Wideband Radar Using Interrupted-Sampling Repeater. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1341–1354. [Google Scholar] [CrossRef]
- Sun, J.; Wang, C.; Shi, Q.; Ren, W.; Yao, Z.; Yuan, N. Interrupted Sampling Repeater Signal Based on Phase Modulation. In Proceedings of the International Conference on Microwave and Millimeter Wave Technology (ICMMT), Nanjing, China, 23–26 May 2021; pp. 1–3. [Google Scholar]
- Hang, D.; Xing, S.; Li, Y.; Liu, Y.; Xiao, S. Smart Jamming Method Against SAR Based on Multiplication Modulation. Syst. Eng. Electron. 2021, 43, 3160–3168. [Google Scholar]
- Sun, G.; Xing, S.; Huang, D.; Li, Y.; Wang, X. Jamming method of intermittent sampling against SAR-GMTI Based on Noise Multiplication Modulation. Syst. Eng. Electron. 2022, 43, 1–14. [Google Scholar]
- Jin, G.; Deng, Y.; Wang, W.; Zhang, H.; Long, Y.; Zhang, Y.; Wang, R. On the SAR Imaging Performance Analysis of Alternate Transmitting Mode Based on Waveform Diversity: Theory and Simulation. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1553–1557. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| Carrier frequency | 5.4 GHz |
| Pulse width | 25 us |
| Bandwidth | 60 MHz |
| Pulse repetition frequency | 1410 Hz |
| Platform velocity | 7568.94 m/s |
| Closest slant range | 815.9 km |
| Antenna length | 15 m |
| ) | 1.2 |
| Range Position (km) | Azimuth Position (km) | Amplitude Peak Value (dB) | ||||
|---|---|---|---|---|---|---|
| Point | Theoretical | Simulated | Theoretical | Simulated | Theoretical | Simulated |
| 5 | 5 | 6.7921 | 6.7243 | −17.19 | −18.56 | |
| 6.499 | 6.672 | 8 | 8 | −14.34 | −13.22 | |
| 3.501 | 3.4280 | 9.2079 | 9.1023 | −36.17 | −38.34 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, D.; Liu, Z.; Guo, Z.; Shu, G.; Li, N. A Repeater-Type SAR Deceptive Jamming Method Based on Joint Encoding of Amplitude and Phase in the Intra-Pulse and Inter-Pulse. Remote Sens. 2022, 14, 4597. https://doi.org/10.3390/rs14184597
Cheng D, Liu Z, Guo Z, Shu G, Li N. A Repeater-Type SAR Deceptive Jamming Method Based on Joint Encoding of Amplitude and Phase in the Intra-Pulse and Inter-Pulse. Remote Sensing. 2022; 14(18):4597. https://doi.org/10.3390/rs14184597
Chicago/Turabian StyleCheng, Dongyang, Zhenchang Liu, Zhengwei Guo, Gaofeng Shu, and Ning Li. 2022. "A Repeater-Type SAR Deceptive Jamming Method Based on Joint Encoding of Amplitude and Phase in the Intra-Pulse and Inter-Pulse" Remote Sensing 14, no. 18: 4597. https://doi.org/10.3390/rs14184597
APA StyleCheng, D., Liu, Z., Guo, Z., Shu, G., & Li, N. (2022). A Repeater-Type SAR Deceptive Jamming Method Based on Joint Encoding of Amplitude and Phase in the Intra-Pulse and Inter-Pulse. Remote Sensing, 14(18), 4597. https://doi.org/10.3390/rs14184597