Abstract
Hyperspectral image (HSI) super-resolution aims at improving the spatial resolution of HSI by fusing a high spatial resolution multispectral image (MSI). To preserve local submanifold structures in HSI super-resolution, a novel superpixel graph-based super-resolution method is proposed. Firstly, the MSI is segmented into superpixel blocks to form two-directional feature tensors, then two graphs are created using spectral–spatial distance between the unfolded feature tensors. Secondly, two graph Laplacian terms involving underlying BTD factors of high-resolution HSI are developed, which ensures the inheritance of the spatial geometric structures. Finally, by incorporating graph Laplacian priors with the coupled BTD degradation model, a HSI super-resolution model is established. Experimental results demonstrate that the proposed method achieves better fused results compared with other advanced super-resolution methods, especially on the improvement of the spatial structure.
1. Introduction
Hyperspectral remote sensing has been widely used in the fields of geological exploration, agricultural production, urban planning, environmental monitoring and so on. Due to the limitation of the optical imaging mechanism of airborne spectrometers, hyperspectral image (HSI) with high spectral resolution is often accompanied by lower spatial resolution, which brings inconvenience to the applications, such as classification, anomaly detection, and object recognition [1,2]. Therefore, improving the spatial resolution of HSI has become an urgent issue. Fortunately, multispectral image (MSI) has high spatial resolution but with low spectral resolution. Therefore, the fusion of HSI and MSI (HSI–MSI), also called HSI super-resolution, provides an effective and efficient way to improve the spatial resolution of HSI and results in a high-resolution hyperspectral image (HR-HSI). Furthermore, by fusing HSI–MSI, the shortcoming of a single imaging device in spatial-spectral resolution has been overcome, and a more comprehensive and accurate understanding of the observed environment can be obtained [3,4].
1.1. Relates Works
In general, the HSI–MSI fusion methods can be categorized as four classes [5,6,7], pansharpening-based methods [8,9], matrix-based methods [10,11,12], tensor-based methods [13,14,15,16,17], and deep CNN-based methods [18,19]. Among them, matrix and tensor methods depend on the degradation model of high-resolution HSI combined with priors of the decomposition matrix or tensor factors. Regularization priors, such as low-rank [20,21,22,23,24], sparsity [25,26,27], or graph Laplacian [28,29], are widely used in HSI–MSI fusion models. However, in matrix-based methods, the HSI is unfolded into matrices, which ignores the inherent three-dimensional features. Tensor, as a multi-dimension array, provides a flexible representation of HSI and has made tensor-based HSI super-resolution methods popular recently.
In tensor-based HSI super-resolution, the HSI is modeled as a third-order tensor with two spatial dimensions and one spectral dimension, which can fully exploit the dependence across different dimensions or modes. Moreover, tensor has more flexible decomposition forms, such as canonical polyadic decomposition (CPD) [30], Tucker decomposition (TD) [23], singular value decomposition (t-SVD) [31,32], tensor ring decomposition (TRD) [33,34], tensor block term decomposition (BTD) [35,36], etc. Each decomposition leads to a different perspective in understanding the correlation between the different modes of the tensor. Canonical polyadic decomposition (CPD) represents a tensor with a sum of R tensors, in which each tensor is rank-1. Kanatsoulis et al. [37] first formulated a coupled tensor CPD-based HSI–MSI fusion model by establishing the relations between tensor mode-product and the HSI degradation model. Furthermore, the blind and semi-blind HSI–MSI fusion models were solved by the alternative optimization algorithm, which is a well-known STEREO algorithm. Xu et al. [38] proposed a HSI super-resolution model based on non-local coupled tensor patches, in which the constructed fourth-order low-rank tensor is guided by MSI, and the HR-HSI and MSI share the same nonlocal tensor CPD factor matrices. Although CPD can represent the three-dimensional data structure, it has a high computational complexity and the CP rank R is hard to compute. Tucker decomposition (TD) provides a flexible decomposition with a core tensor and three matrix factors. Each factor of TD is easy to compute. Assuming the HR-HSI has a low Tucker multilinear rank, a coupled TD-based HSI–MSI fusion model with blind and semi-blind SCOTT algorithms is proposed in [16]. Furthermore, the decomposed core tensor was estimated by solving the generalized Sylvester equation, and three factor matrices were computed by truncated singular value decomposition. In addition, TD factors can be viewed from spatial and spectral dimensions, so a dictionary learning strategy was introduced to train spatial and spectral dictionaries from MSI and low-resolution HSI, respectively [13]. Furthermore, by considering the spectral smoothness and spatial consistency as priors, a graph regularized low-rank tensor fusion method was developed in [17]. Borsoi et al. [39] assumed that there is spectral variability in HSI–MSI fusion and introduced the variability into the TD fusion model with an additive term. In general, tensor CPD and TD can be unified as tensor BTD. Specifically, tensor BTD provides a clear physical explanation for the factor matrices from the perspective of unmixing, and makes the prior of the abundance and endmember easy to model [40,41,42]. Therefore, a coupled BTD-based HSI–MSI fusion technique has become popular for the linear unmixing model involved [43,44]. The endmember and low-rank abundance map are represented by potential factor matrices under BTD. However, due to the lack of constraints on the factor matrix, the quality of the fused HSI is reduced. Therefore, other regularization terms have the potential to be combined with BTD in fusion models to improve the recovery performance.
1.2. Motivations and Contributions
In terms of regularization, factors such as total variation [45], low-rank, sparse, graph Laplacian [46], etc. have been widely exploited combined with tensor decomposition as mentioned. Among them, manifold Laplacian is an effective strategy to improve the spatial structure of images. In [46], a graph Laplacian is integrated with BTD for HSI–MSI fusion, resulting in an impressive performance. However, the local weight matrix of the graph is calculated in a pixel-wise manner, which can easily be affected by noise and cannot describe the local geometry of the image well. Therefore, to exploit the spatial neighborhood structure by generating homogeneous segmented regions and reduce the sensitivity to noise and outliers, a superpixel-guided graph Laplacian regularization is constructed in this paper. Furthermore, considering the merits of the BTD, the graph Laplacian is introduced to the BTD-based HSI–MSI fusion framework, resulting in the regularization of the proposed superpixel-based graph Laplacian with the BTD fusion method, named as SGLCBTD for short. The main contributions are as follows.
- (1)
- The MSI is segmented by regional clustering according to spectral–spatial distance measurements;
- (2)
- Two-directional tensor graphs are designed via the features of the segmented MSI superpixel blocks, whose local geometric structure is consistent with HSI;
- (3)
- The similarity weights of the superpixel blocks are calculated and graph Laplacian matrices are constructed, which is used to convey the spatial manifold structures from MSI to the factor matrices of HSI;
- (4)
- The proposed superpixel graph Laplacian BTD model is solved by the block coordinate descent algorithm, and the experimental results are displayed.
2. Background
For convenience, some necessary definitions and preliminaries of tensor are introduced first. A scalar, a vector, a matrix, and a tensor are denoted as and , respectively. and denote the -th, -th and -th element of and , respectively. The n-mode unfolding of tensor is represented by . The one-mode product of tensor with a matrix is denoted by , thus, for the n-mode products, n = 1, 2, 3. stands for the outer product of a matrix and a vector , resulting in an tensor. For two matrices and , the Khatri–Rao product is , and stands for the column-wise Khatri–Rao product along the column.
2.1. Block Term Decomposition
The block term decomposition (BTD) in rank-. terms is defined that a third-order tensor . can be decomposed as the sum of rank- terms [35]
where are full-column matrices with rank-Lr, and R is the rank of the tensor .
Let and replace it into formula (1), so
Furthermore, unfolding the tensor along the third mode results in the following expression from the matrix point of view:
where is the three-mode unfolding of tensor , matrices and have rank-R, each element of constitutes the matrix with size of , the error term is the Gaussian noise.
The Formula (3) can be easily connected with the linear unmixing model (LMM) of HSI. Specifically, matrix is the endmember matrix containing the spectral signatures of endmembers matrix represents the abundance coefficient matrix, each is the abundance corresponding to endmember . Therefore, decomposition factors and of matrix also represent the spatial abundance information.
2.2. Problem Formulation
Let represent the low spatial resolution hyperspectral image (LR-HSI) and MSI, respectively. Let be the super-resolution hyperspectral image (SRI) to be estimated. and represent the dimensions of the spatial width and height, respectively, represent the spectral dimension, and ,. It is often assumed that LR-HSI is obtained by spatial degradation of SRI, and MSI is the spectral degradation of SRI, namely,
where and are the spatial blurring and downsampling matrices, is a spectral response matrix.
Then, the HSI–MSI fusion can be formulated as
By assuming follows the rank- model as shown in (1), the HSI–MSI fusion model (6) can be rewritten as follows:
Formula (7) tells us that estimating SRI with BTD is equal to estimating the high-resolution abundance map and endmember matrix . The theorem in [44,45] gives the recoverability of a hyperspectral super-resolution problem under the BTD of rank-.
3. Proposed Methods
Generally, the HSI–MSI fusion model (7) is often added with more constraints to achieve a stable and accurate solution, such as total variation, sparsity, low-rank, graph Laplacian, etc. Among them, graph Laplacian can preserve the local manifold structure of high-dimensional image data. Moreover, considering that the superpixel provides local homogeneous regions with geometric structure involved, a superpixel-based graph Laplacian combined with a coupled BTD HSI–MSI fusion model (SGLCBTD) is proposed.
The flowchart is given in Figure 1. As it shows, the core idea of the proposed method is the construction of two graph Laplacian. To achieve this goal, four steps are performed: (1) segmenting the MSI to generate superpixel blocks; (2) extracting the features of the superpixel blocks to form two feature tensors; (3) constructing two graphs based on feature tensors, including compute the weights; and (4) establishing two graph Laplacian terms. Finally, the regularized graph Laplacian terms are introduced to the HSI–MSI fusion framework with the BTD formula.
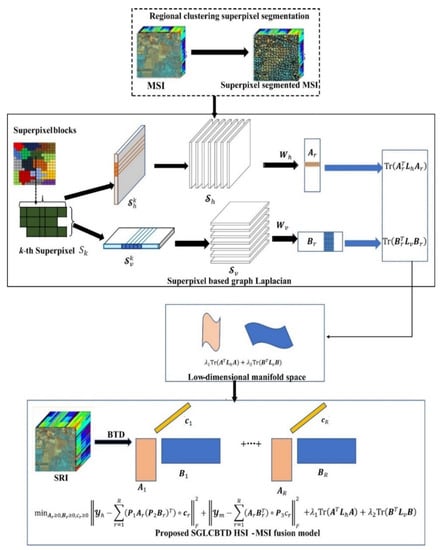
Figure 1.
Flowchart of the proposed SGLCBTD method.
3.1. Superpixel-Based Graph Laplician Construction
3.1.1. Regional Clustering-Based Superpixel Segmentation
Compared with the pixel-wise segmentation method, the superpixel segmentation method shows faster speed and more accurate segmentation results. One of the most popular superpixel segmentation methods is the simple linear iterative clustering (SLIC) algorithm. Inspired by the SLIC method, a regional clustering superpixel segmentation method is designed for HSI unmixing by integrating spatial correlation and spectral similarity at clustering procedure [47]. Specifically, the combination of spectral information divergence (SID) and spectral angler mapper (SAM) is employed as a spectral distance measurement, and Euclidean distance is used as a spatial distance. Taking this merit of the superpixel segmentation method into account, in this paper, the regional clustering superpixel segmentation method is employed to generate superpixel blocks.
3.1.2. Two-Directional Feature Tensors Extraction
Similarly to the MSI, the resultant superpixel block shows geometric spatial structure as well as spectral information. Along horizontal and vertical spatial directions, the superpixel has different features. Therefore, it is necessary to design two-directional feature tensors to represent the geometric structure.
For each irregular superpixel block , along the horizontal direction, feature tensor is constructed by its horizontal feature vectors (such as average, maximum, median or difference, etc.). Then, all horizontal feature tensors are arranged according to the second dimension, resulting in a feature tensor with a size of where N is the number of the superpixel block. Meanwhile, the vertical feature tensor is generated in the same manner.
3.1.3. Two Graph Generation
A horizontal graph with vertex and edge is defined by horizontal feature tensor derived from superpixel blocks. To be specific, taking the one-mode factorization of tensor as elements of the vertex , the weigh of the edge can be calculated as follows
where and represents the -th row and -th row of , respectively, and is the bandwidth of Gaussian kernel.
Meanwhile, a vertical graph with vertex and edge can be defined according to the vertical feature tensor in the same way.
3.1.4. Two Graph Laplacian Construction
The graph shows the spatial correlation between superpixels, which is the same as that of SRI, for the fused SRI and MSI have the same spatial structure. The manifold structure in MSI is incorporated into SRI as illustrated in Figure 2, where and are the decomposition factor of BTD. With the BTD factorization, the factor matrix represents the spatial information along the horizontal direction (first mode of the tensor), so the row relationship of HR-HSI and MSI is the same as that of . Similarly, factor matrix represents the vertical (second mode of tensor) information, so the relationship between columns in HR-HSI and MSI is the same of that of the columns of
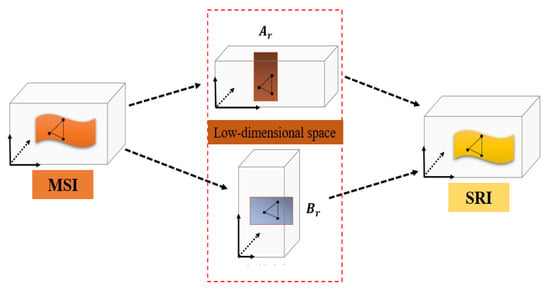
Figure 2.
The manifold structure preservation between MSI and HR-MSI.
Therefore, the similarity between rows in can be formulated as:
where and represents the -th row and -th row of respectively, is the weight of the horizontal graph.
Let , which stands for the horizontal weighted adjacency matrix. Then, the horizontal graph Laplacian matrix can be defined as where is a diagonal matrix with diagonal elements .
Therefore, Formula (9) can be rewritten as follows:
Extending this constraint to , the horizontal graph Laplacian can be written as
In the same way, the vertical graph Laplacian related to is defined as
where is the vertical graph Laplacian matrix, .
3.2. Proposed SGLCBTD Model and Algorithm
Incorporating the two mentioned graph Laplacian terms (11–12) with the coupled BTD super-resolution model (7), a superpixel graph Laplacian regularization with coupled BTD fusion model is proposed (SGLCBTD):
where and are regularization parameters.
Let us define the objective function in Equation (13) as , the above super-resolution model is solved alternately by block coordinate descent (BCD) algorithm [48], i.e., the matrices are iteratively updated via solving subproblems w.r.t. while fixing other variables as follows
where is the number of current iteration steps.
Each subproblem is a quadratic optimization problem, which leads to the generalized Sylvester equation and can be transformed into a large-scale sparse linear system of equations by Kronecker product.
Consider the subproblem (14a), fix and , the subproblem of can be rewritten as
The optimization problem is quadratic, and its solution is equivalent to compute the following general Sylvester equation [49]:
where .
For the solution of subproblem of matrices B and C, the algorithms are the same as that of matrix A.
4. Experimental Results
4.1. Experiment Setup
In this section, to demonstrate the effectiveness of the proposed HSI super-resolution method, numerical experiments are carried out on two popular datasets: Indian Pines and Pavia University datasets (https://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes, accessed on 20 March 2022). Both qualitative and quantitative analysis are used in our experiments.
4.1.1. Quality Assessment Indices
For quantitative performance, seven indices are employed to evaluate the performance [7].
- (1)
- Normalized mean square error (NMSE) is defined aswhere is the ideal HSI and is the resulted SRI.
- (2)
- Reconstruction signal-to-noise ratio (R-SNR) is inversely proportional to NMSE with the formulation as follows:
- (3)
- Spectral angle mapper (SAM) evaluates the spectral distortion and is defined aswhere is the spectral vector, is inner product of two vectors.
- (4)
- Relative global dimensional synthesis error (ERGAS) reflects the global quality of the fused results and is defined aswhere is spatial upsampling factor, is the mean of .
- (5)
- Correlation coefficient (CC) is computed as followswhere is the Pearson correlation coefficient.
- (6)
- Peak signal-to-noise rate (PSNR) for each band of HSI is defined as
- (7)
- Structural similarity index measurement (SSIM) for each band of HSI is defined as follows:where and are the mean and variance of the k-th band image and , respectively, is the covariance between and , and are constant.
4.1.2. Methods for Comparison
The proposed SGLCBTD method is compared with the state-of-the-art HSI–MSI fusion methods, including: coupled nonnegative matrix factorization (CNMF) [3], super-resolution tensor-reconstruction (STEREO) [37], STEREO with non-negative CP decomposition (CNN-CPD) [37], coupled non-negative tensor block term decomposition (CNN-BTD) [43], and graph Laplacian regularization with coupled block term decomposition (GLCBTD) [46].
In the experiment, the optimal parameters involved in different methods are set according to the author’s suggestion. Specially, in tensor-based method, considering that the Pavia University dataset has rich spatial structures, the rank of tensor R is set to 15, but for the Indian Pines dataset, the rank is 10. Meanwhile, in the related BTD rank- methods, including CNN-BTD, GLCBTD and SGLCBTD, the rank of the factor matrices is . In addition, regularization parameters and in SGLCBTD are set to . More details about the parameters are shown in Section 4.3.
4.2. Performance Comparison of Different Methods
4.2.1. Indian Pines Dataset
The Indian Pines dataset was captured by the NASA AVIRIS instrument. The size of the underlying SRI is 145 × 145 × 220 and the wavelength covers 400–2500 nm. The HSI and MSI are obtained according to the Wald protocol [50]. The degradation from SRI to HSI is that blurring with 9 × 9 Gaussian and downsampling with factor 5, resulting in with size of 29 × 29 × 220. The size of the MSI is 145 × 145 × 4. Finally, zero-mean iid. Gaussian noise is added to HSI and MSI, and the signal-to-noise ratio (SNR) is set to 30 dB.
Table 1 lists the values of R-SNR, NMSE, SAM, ERGAS and CC of the compared methods on the Indian Pines dataset, and the best values are marked in bold. It can be shown that the tensor-based methods outplay matrix-based methods. The indexes of BTD fusion methods are much better than that of CPD. Moreover, the regularized models, CNN-CPD, GLCBTD and SGLCBTD are more advantageous than STEREO and CNN-BTD methods, for the latter two have rather low indices. Most of indices of the proposed SGLCBTD achieve first place, which shows that the method performs well in spatial detail and spectral preservation. In addition, compared with the GLCBTD, the R-SNR is significantly improved by about 1.76 dB.

Table 1.
Quantitative indices comparison on the Indian Pines dataset.
The PSNR and SSIM values for each spectral band of various fusion methods are compared in Figure 3. As it can be seen, most of CNMF’s curves achieve the lowest values in each band, which means the performance of the matrix-based method is significantly lower than that of tensor-based methods. The curves of SREREO and CNN-CPD are very similar except for a higher SSIM index of CNN-CPD. Three BTD-based methods, CNN-BTD, GLCBTD and SGLCBTD perform better than other methods. The overall performances of GLCBTD and SGLCBTD are excellent, especially in SSIM curves, which shows that the graph-based method can preserve the geometric structure well. It should be mentioned, in the PSNR curve, from the 100-th band, the curve of SGLCBTD has unsatisfactory results, which is likely due to the water absorption, noise and parameters’ setting in our view. Even so, the curve is the most stable in each band of all compared methods. In general, the PSNR and SSIM curves show that the proposed SGLCBTD method has the superiority of preserving geometric structures.
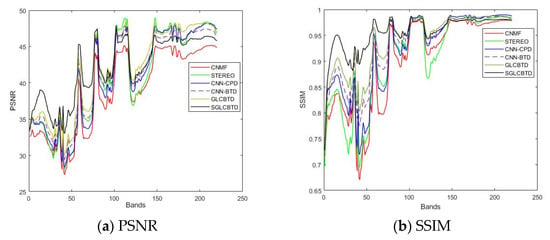
Figure 3.
PSNR and SSIM in function of each band for different methods on the Indian Pines dataset.
Figure 4 and Figure 5 show the fusion results on the Indian Pines dataset in 10-th and 100-th bands, respectively. From the visual effect, it can be seen that SGLCBTD is closer to the original image with reduced red areas and increased blue areas, moreover, the edge details are clearer than those of other methods.
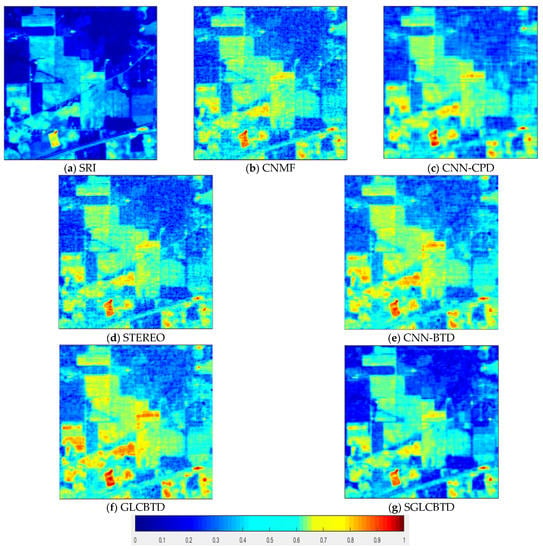
Figure 4.
Comparisons of fusion results of the 10-th band on the Indian Pines dataset.
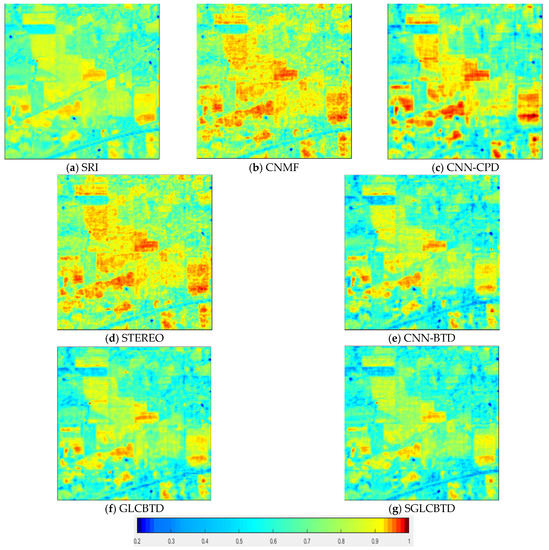
Figure 5.
Comparisons of fusion results of the 100-th band on the Indian Pines dataset.
4.2.2. Pavia University Dataset
The Pavia University dataset was captured by the ROSIS instrument. The size of the original HSI is 610 × 340 × 115, where the spectral band is from 430 nm to 860 nm. The spatial size of 200 × 200 is cropped due to hardware limitations, and the spectral band is 103 after removing the vapor absorption bands. Therefore, the underlying SRI is 200 × 200 × 103. A 9 × 9 Gaussian blurring and downsampling factor 4 are performed as degradation to obtain a HSI with size of 50 × 50 × 103. The size of MSI is 200 × 200 × 4. Finally, zero mean iid. Gaussian noise is added to HSI and MSI, the signal-to-noise ratio (SNR) is set to 25 dB.
Table 2 shows the numerical results of several comparison methods on the Pavia University dataset. It can be seen that for the Pavia University dataset with tensor rank-10, the fusion performance fusion of CNN-BTD and GLCBTD have been improved. GLCBTD is still better than CNN-BTD due to the regularization term, while SGLCBTD improves the R-SNR value of GLCBTD by 0.3 dB, and other indices have also been improved, which shows that the proposed SGLCBTD method can improve the spatial–spectral assessment values effectively.

Table 2.
Quantitative indices comparison on the Pavia University dataset.
Figure 6 shows the comparison of PSNR and SSIM curves on the Pavia University dataset of different fusion methods, in which the red solid line represents the proposed SGLCBTD method. It can be seen that the PSNR and SSIM curves of GLCBTD and SGLCBTD are roughly similar, and both of them have higher values than that of other methods. Furthermore, it should be noticed that the overall curves of SGLCBTD are the highest and most stable, which means the proposed SGLCBTD performs best among the compared methods.
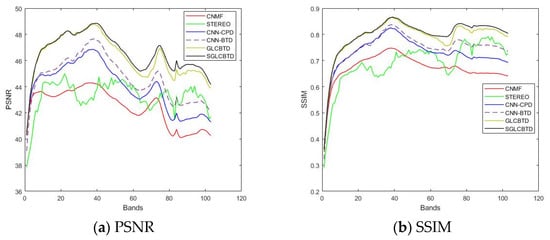
Figure 6.
PSNR and SSIM in function of each band for different methods on the Indian Pines dataset.
As shown in Figure 7 and Figure 8, the 10-th band and the 80-th band of the fusion results on the Pavia University dataset image are displayed, respectively. CNMF, CNN-CPD and STEREO have more noise unremoved as well as more blur. Relatively, BTD-based methods achieve better fusion results, among them, regularized GLCBTD and SGLCBTD methods achieve better visual effects than that of CNN-BTD. In addition, the spatial edge and texture structures of the fused image of SGLCBTD is clearer with less noise, which shows the effectiveness of SGLCBTD fusion method.
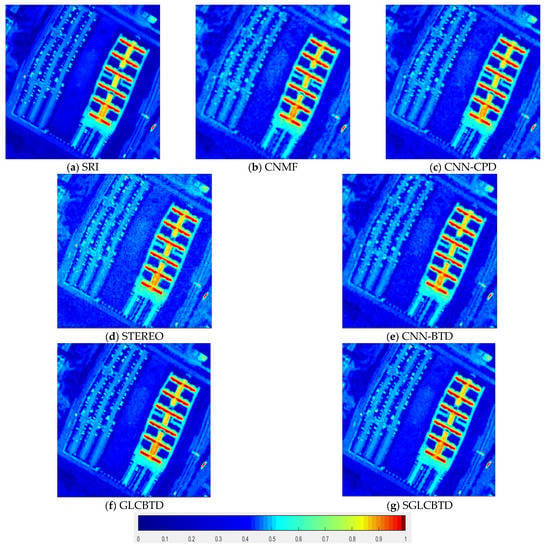
Figure 7.
Comparisons of fusion results of the 10-th band on the Pavia University dataset.

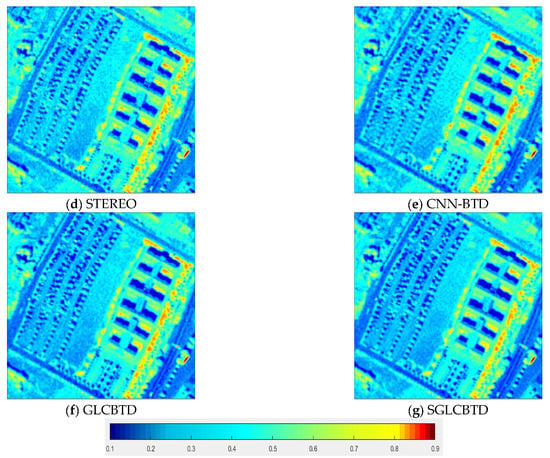
Figure 8.
Comparisons of the fusion results of the 80-th band on the Pavia University dataset.
4.3. Discussions
4.3.1. Parameter Analysis
The parameters involved in the SGLCBTD including the number of superpixel , the tensor rank the rank of factor matrices , and . The main contribution of this paper is the tensor BTD with a superpixel-based graph. Therefore, the parameter analysis is performed on R, L and N.
- (1)
- Analysis of R and L
Taking the Indian Pines dataset as an example, R-SNR is used to evaluate the performance of parameters R and L as shown in Figure 9. Given the range of R and L form 7–13 with increment 1. It can be seen that both of two curves reach the highest peak values around 10. In addition, with R or L decrease, the performance becomes worse. Considering the high computational complexity with high rank increase, for the Indian Pines, R = L = 10, while for the Pavia University dataset, R = 15, L = 10 on account of the complex geometric structures in the image.
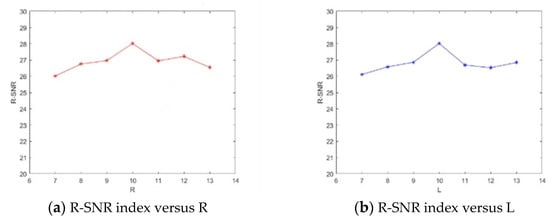
Figure 9.
R-SNR varies with different R and L on the Pavia University dataset.
- (2)
- Analysis of N
The proposed SGLCBTD method is a superpixel-based method, the number of superpixel N is crucial to the efficient as well as effectiveness. For two datasets, the parameter N is selected from the set {225, 324, 400, 625, 841, 900} and {225, 324, 400, 484, 625,784}, respectively, by experience. Figure 10 shows R-SNR curves as parameter N changes. From the Figure, for the Indian Pines dataset, R-SNR reaches the highest value when N = 400. When N > 400, the curve drops down then rises at the point N = 625. For the Pavia University dataset, R-SNR is relatively stable in the data range. In addition, when , the highest value is reached at N = 625. Compared to the Indian Pines dataset, the Pavia University dataset has a richer geometry, and the segmentation results should be finer, resulting in a larger number of superpixel blocks. It is also noted that large superpixel numbers increase the time computation and do not lead to better performance. Therefore, 400 and 625 are set as superpixel numbers for the Indian Pines and Pavia University datasets, respectively. More adaptive and accurate estimation of the parameter is still an open issue to be researched further.
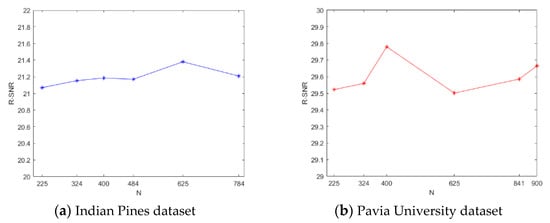
Figure 10.
R-SNR varies with different N on two datasets.
4.3.2. Time Complexity Analysis
The computational time of the compared methods on the two datasets is listed in Table 3. The running time results are recorded in MATLAB R2018b, using a GPU server with NVIDIA RTX 2080Ti/11GB. Owing to the advantages of the block coordinate descent (BCD) algorithm or the alternating direction method of multipliers (ADMM), all the compared methods converge quickly after 10 to 25 iterations. In addition, for each dataset, the time given in Table 3 is obtained by averaging the five times. As can be seen, the STEREO is the fastest method. GLCBTD and the proposed SGLCBTD methods cost more time than those of other methods due to the massive calculation of superpixel segmentation and adjacency matrix of the graph, which is a progressive work to be considered for us in the future.

Table 3.
Computational time of the compared methods (seconds).
5. Conclusions
In this paper, a HSI super-resolution method is proposed based on tenor block term decomposition, known as SGLCBTD. To preserve the spatial manifold structure of the fused HSI, two-directional spectral–spatial graphs are constructed according to feature tensors induced by the MSI segmented superpixel. Then, the manifold graph Laplacian is utilized to regularize the super-resolution HSI, resulting in the proposed HSI–MSI fusion method. In addition, the model is solved alternately by block coordinate descent algorithm. Stimulation experiments are conducted on different datasets. Compared with the state-of-the-art methods, the proposed SGLCBTD obtains better fusion performance with more spatial details retained.
For future work, two aspects should be taken into consideration. On one hand, the feature of superpixel blocks is limited, more powerful features can be exploited to further improve the preservation of the manifold structures of the HSI. On the other hand, as mentioned in Section 4.3.2, more efficient optimization algorithms need to be developed to reduce time complexity.
Author Contributions
Methodology, writing-review and editing, H.L.; Conceptualization, writing—original draft preparation, software, W.J.; Validation, data curation, Y.Z.; Supervision, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China under Grant 61971223 and Grant 61871226, in part by the Fundamental Research Funds for the Central Universities under Grant 30917015104, and in part by the Fundamental Research Funds for the Central Universities under Grant JSGP202204.
Data Availability Statement
The dataset use in this paper can be found form the link: https://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes accessed on 20 March 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, S.; Chang, C.I.; Li, X. Component Decomposition Analysis for Hyperspectral Anomaly Detection. IEEE Geosci. Remote Sens. 2022, 60, 5516222. [Google Scholar] [CrossRef]
- He, C.; Sun, L.; Huang, W.; Zhang, J.; Zheng, Y.; Jeon, B. TSLRLN: Tensor subspace low-rank learning with non-local prior for hyperspectral image mixed denoising. Signal Process. 2021, 184, 108060. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled Non-negative Matrix Factorization Unmixing for Hyperspectral and Multispectral Data Fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Wei, Q.; Bioucas-Dias, J.M.; Dobigeon, N.; Tourneret, J. Hyperspectral and Multispectral Image Fusion based on a Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3658–3668. [Google Scholar] [CrossRef]
- Dian, R.; Li, T.; Sun, B.; Guo, A.J. Recent Advances and New Guidelines on Hyperspectral and Multispectral Image Fusion. Inf. Fusion 2021, 69, 40–51. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A Critical Comparison Among Pansharpening Algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and Multispectral Data Fusion: A Comparative Review of the Recent Literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Zhang, Y.; He, M. Multi-Spectral and Hyperspectral Image Fusion Using 3-D Wavelet Transform. J. Electron. 2007, 24, 218–224. [Google Scholar] [CrossRef]
- Selva, M.; Aiazzi, B.; Butera, F.; Chiarantini, L.; Baronti, S. Hyper-sharpening: A First Approach on SIM-GA Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3008–3024. [Google Scholar] [CrossRef]
- Zou, C.; Xia, Y. Hyperspectral Image Super-Resolution Based on Double Regularization Unmixing. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1022–1026. [Google Scholar] [CrossRef]
- Huang, B.; Song, H.; Cui, H.; Peng, J.; Xu, Z. Spatial and Spectral Image Fusion Using Sparse Matrix Factorization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1693–1704. [Google Scholar] [CrossRef]
- Dong, W.; Fu, F.; Shi, G.; Cao, X.; Wu, J.; Li, G.; Li, X. Hyperspectral Image Super-Resolution via Non-Negative Structured Sparse Representation. IEEE Trans. Image Process. 2016, 25, 2337–2352. [Google Scholar] [CrossRef] [PubMed]
- Dian, R.; Fang, L.; Li, S. Hyperspectral Image Super-Resolution via Non-Local Sparse Tensor Factorization. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Hawaii, HI, USA, 21–26 July 2017; pp. 3862–3871. [Google Scholar]
- Li, S.; Dian, R.; Fang, L.; Bioucas-Dias, J.M. Fusing Hyperspectral and Multispectral Images via Coupled Sparse Tensor Factorization. IEEE Trans. Image Process. 2018, 27, 4118–4130. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Yan, L.; Zhao, X.; Fang, H.; Zhang, Z.; Zhong, S. Weighted Low-Rank Tensor Recovery for Hyperspectral Image Restoration. IEEE Trans. Cybern. 2020, 50, 4558–4572. [Google Scholar] [CrossRef] [PubMed]
- Prvost, C.; Usevich, K.; Comon, P.; Brie, D. Hyperspectral Super-Resolution with Coupled Tucker Approximation: Recoverability and SVD-Based Algorithms. IEEE Trans. Signal Process. 2020, 68, 931–946. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, M.; Yang, S.; Jiao, L. Spatial–Spectral-Graph-Regularized Low-Rank Tensor Decomposition for Multispectral and Hyperspectral Image Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1030–1040. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. Multispectral and Hyperspectral Image Fusion using a 3D-Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 639–643. [Google Scholar] [CrossRef]
- Mei, S.; Yuan, X.; Ji, J.; Wan, S.; Hou, J.; Du, Q. Hyperspectral Image Super-Resolution via Convolutional Neural Network. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 4297–4301. [Google Scholar]
- Xu, Y.; Wu, Z.; Chanussot, J.; Zhi, H. Nonlocal Patch Tensor Sparse Representation for Hyperspectral Image Super-Resolution. IEEE Trans. Image Process. 2019, 28, 3034–3047. [Google Scholar] [CrossRef]
- Dian, R.W.; Li, S.T.; Fang, L.Y.; Lu, T.; Bioucas-Dias, J.M. Nonlocal Sparse Tensor Factorization for Semiblind Hyperspectral and Multispectral Images Fusion. IEEE Trans. Cybern. 2020, 50, 4469–4480. [Google Scholar] [CrossRef]
- Long, J.; Peng, Y.; Li, J.; Zhang, L.; Xu, Y. Hyperspectral Image Super-Resolution via Subspace-based Fast Low Tensor Multi-Rank Regularization. Infrared Phys. Technol. 2021, 116, 103631. [Google Scholar] [CrossRef]
- Liu, N.; Li, L.; Li, W.; Tao, R.; Flower, J.; Chanussot, J. Hyperspectral Restoration and Fusion with Multispectral Imagery via Low-Rank Tensor-Approximation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7817–7830. [Google Scholar] [CrossRef]
- Liu, H.; Sun, P.; Du, Q.; Wu, Z.; Wei, Z. Hyperspectral Image Restoration Based on Low-Rank Recovery with a Local Neighborhood Weighted Spectral-Spatial Total Variation Model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1409–1422. [Google Scholar] [CrossRef]
- Fang, L.; Zhuo, H.; Li, S. Super-Resolution of Hyperspectral Image via Superpixel-based Sparse Representation. Neurocomputing 2017, 273, 171–177. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Ge, Z.; Cao, G.; Shi, H.; Fu, P. Adaptive Nonnegative Sparse Representation for Hyperspectral Image Super-Resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4267–4283. [Google Scholar] [CrossRef]
- Peng, J.T.; Sun, W.W.; Li, H.C.; Li, W.; Meng, X.; Ge, C.; Du, Q. Low-Rank and Sparse Representation for Hyperspectral Image Processing: A review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 10–43. [Google Scholar] [CrossRef]
- Bu, Y.; Zhao, Y. Hyperspectral and Multispectral Image Fusion via Graph Laplacian-Guided Coupled Tensor Decomposition. IEEE Trans. Geosci. Remote Sens. 2021, 59, 648–662. [Google Scholar] [CrossRef]
- Li, C.; Jiang, Y.; Chen, X. Hyperspectral Unmixing via Noise-Free Model. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3277–3291. [Google Scholar] [CrossRef]
- Fang, L.Y.; He, N.J.; Lin, H. CP Tensor-Based Compression of Hyperspectral Images. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2017, 34, 252–258. [Google Scholar] [CrossRef]
- Liu, H.Y.; Li, H.Y.; Wu, Z.B.; Wei, Z.H. Hyperspectral Image Recovery using Non-Convex Low-Rank Tensor Approximation. Remote Sens. 2020, 12, 2264. [Google Scholar] [CrossRef]
- Sun, L.; Cheng, Q.; Chen, Z. Hyperspectral Image Super-Resolution Method based on Spectral Smoothing Prior and Tensor Tubal Row-Sparse Representation. Remote Sens. 2022, 14, 2142. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Chanussot, J.; Wei, Z.H. Hyperspectral Images Super-Resolution via Learning High-Order Coupled Tensor Ring Representation. IEEE Trans Neural Netw. Learn. Syst. 2020, 31, 4747–4760. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zeng, J.; He, W.; Zhao, X.; Huang, T. Hyperspectral and Multispectral Image Fusion Using Factor Smoothed Tenson Ring Decomposition. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar]
- Lathauwer, L.D. Decompositions of a Higher-Order Tensor in Block Terms—Part II: Definitions and Uniqueness. SIAM J. Matrix Anal. Appl. 2008, 30, 1033–1066. [Google Scholar] [CrossRef]
- Lathauwer, L.D.; Nion, D. Decompositions of a Higher-Order Tensor in Block Terms—Part III: Alternating Least Squares Algorithms. SIAM J. Matrix Anal. Appl. 2008, 30, 1067–1083. [Google Scholar] [CrossRef]
- Kanatsoulis, C.I.; Fu, X.; Sidiropoulos, N.D.; Ma, W. Hyperspectral Super-Resolution: A Coupled Tensor Factorization Approach. IEEE Trans. Signal Process. 2018, 66, 6503–6517. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.B.; Chanussot, J.; Comon, P.; Wei, Z.H. Nonlocal Coupled Tensor CP Decomposition for Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2020, 58, 348–362. [Google Scholar] [CrossRef]
- Borsoi, R.A.; Pr’evost, C.; Usevich, K.; Brie, D.; Bermudez, J.M.; Richard, C. Coupled Tensor Decomposition for Hyperspectral and Multispectral Image Fusion with Inter-Image Variability. IEEE J. Sel. Top. Signal Process. 2021, 15, 702–717. [Google Scholar] [CrossRef]
- Zheng, P.; Su, H.J.; Du, Q. Sparse and Low-Rank Constrained Tensor Factorization for Hyperspectral Image Unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1754–1767. [Google Scholar] [CrossRef]
- Xiong, F.; Chen, J.Z.; Zhou, J.; Qian, Y. Superpixel-Based Nonnegative Tensor Factorization for Hyperspectral Unmixing. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 6392–6395. [Google Scholar]
- Qian, Y.; Xiong, F.; Zeng, S.; Zhou, J.; Tang, Y. Matrix-Vector Nonnegative Tensor Factorization for Blind Unmixing of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1776–1792. [Google Scholar] [CrossRef]
- Zhang, G.; Fu, X.; Huang, K.; Wang, J. Hyperspectral Super-Resolution: A Coupled Nonnegative Block-Term Tensor Decomposition Approach. In Proceedings of the 2019 IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Le Gosier, France, 15–18 December 2019; pp. 470–474. [Google Scholar]
- Prevost, C.; Borsoi, R.A.; Usevich, K.; Brie, D.; Bermudez, J.C.M.; Richard, C. Hyperspectral Super-Resolution Accounting for Spectral Variability: LL1-Based Recovery and Blind Unmixing of the Unknown Super-Resolution. SIAM J. Imag. Sci. 2022, 15, 110–138. [Google Scholar] [CrossRef]
- Ding, M.; Fu, X.; Huang, T.; Wang, J.; Zhao, X. Hyperspectral Super-Resolution via Interpretable Block-Term Tensor Modeling. IEEE J. Sel. Top. Signal Process. 2021, 15, 641–656. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, H.; Zhang, J. Hyperspectral and Mutispectral Image Fusion via Coupled Block Term Decomposition with Graph Laplacian Regularization. In Proceedings of the 2021 SPIE International Conference on Signal Image Processing and Communication (ICSIPC 2021), Chengdu, China, 16–18 April 2021; p. 11848. [Google Scholar]
- Xu, X.; Li, J.; Wu, C.S.; Plazad, A. Regional Clustering-Based Spatial Preprocessing for Hyperspectral Unmixing. Remote Sens. Environ. 2018, 204, 333–346. [Google Scholar] [CrossRef]
- Xu, Y.Y. Alternating Proximal Gradient Method for Sparse Nonnegative Tucker Decomposition. Math. Prog. Comp. 2015, 7, 39–70. [Google Scholar] [CrossRef]
- Gardiner, J.D.; Laub, A.J.; Amato, J.J.; Moler, C.B. Solution of the Sylvester Matrix Equation AXBT + CXDT = E. ACM Trans. Math. Softw. 1992, 18, 223–231. [Google Scholar] [CrossRef]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of Satellite Images of Different Spatial Resolutions: Assessing the Quality of Resulting Images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).