Radar Emitter Recognition Based on Parameter Set Clustering and Classification
Abstract
:1. Introduction
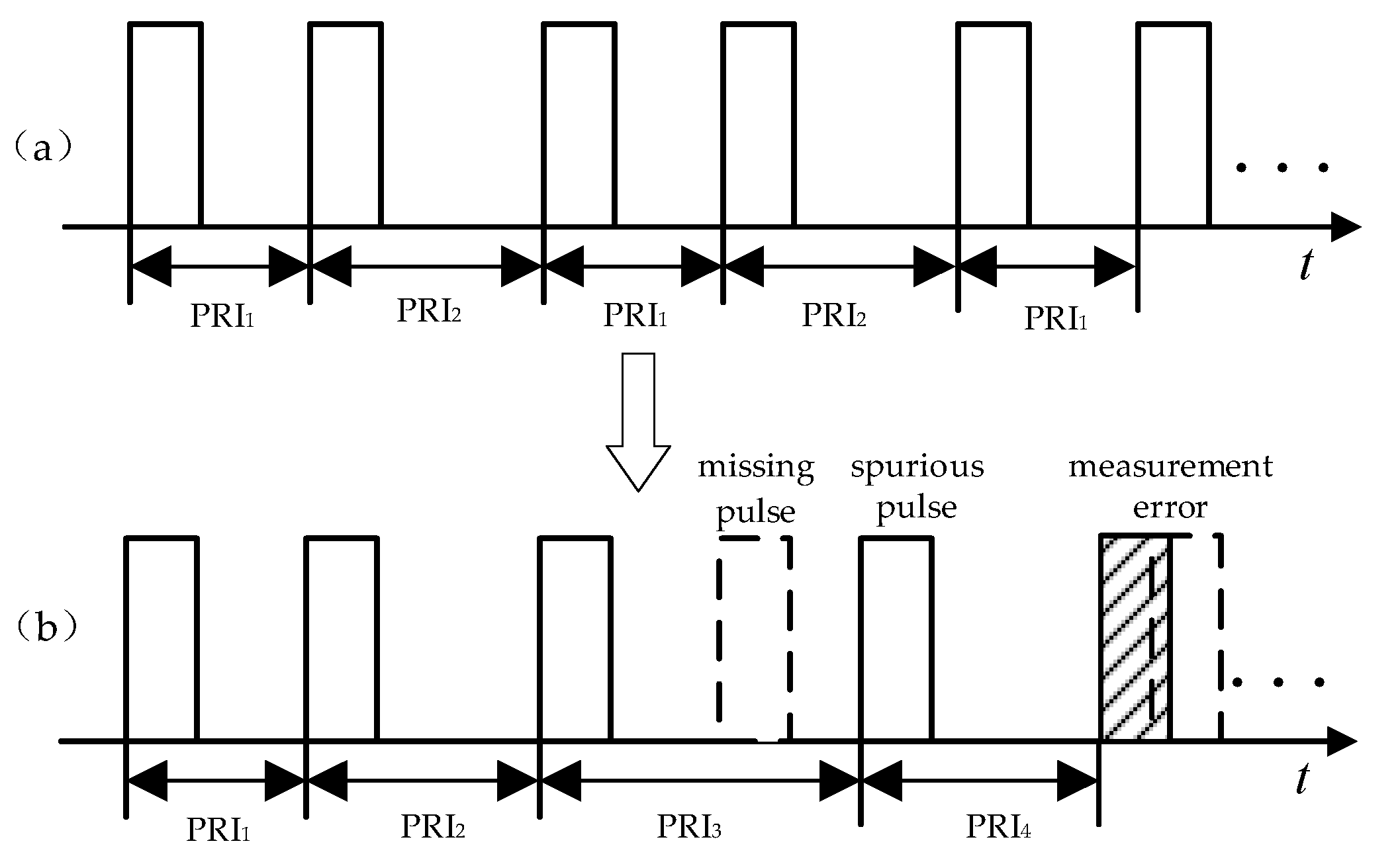
2. Radar Emitter Recognition Problem Description
3. Methods
3.1. Radar Repeat Frequency Feature Extraction
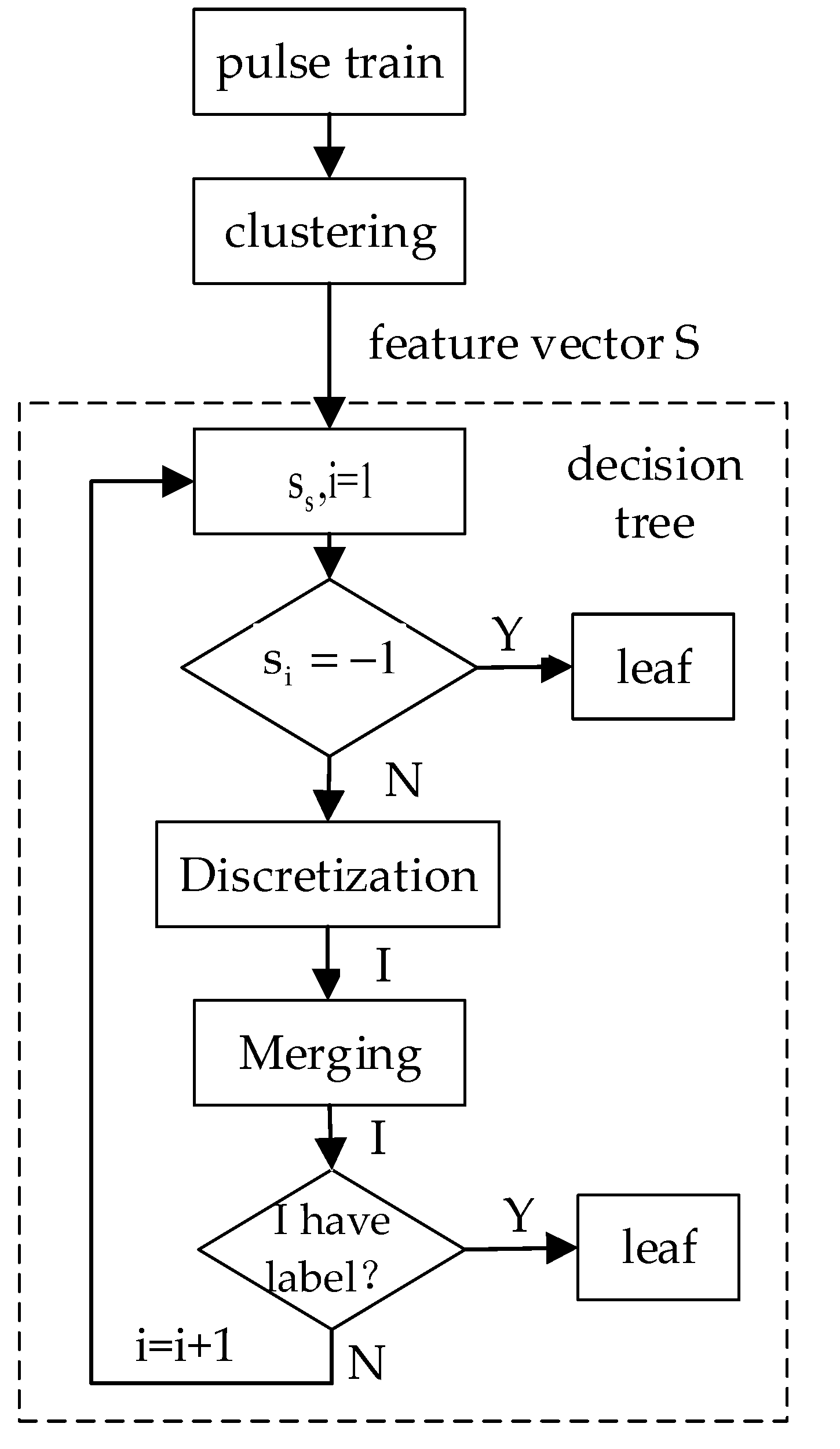
3.2. Improved Decision Tree Classification
3.2.1. Discretization
- Hypothesis H1 is true. The interval is considered closed. It corresponds to a cotyledon that is assigned a class label. The interval is reconstructed from the end of the interval that was just closed, such as {5} (leaf node) in the third layer in Figure 1.
- Hypothesis H2 is true. The interval is also considered closed because no class dominates the interval. It corresponds to a node that needs to be further split, such as {5,7} (middle node) in the second layer in Figure 1.
- Neither H1 nor H2 is true. The interval needs to be extended by adding the next sample in the current attribute value order and reanalysis needs to take place. If the node has no more samples, the interval is also closed, which corresponds to the node that needs to be further split, such as {3,4} (intermediate node) in the second layer in Figure 1.
3.2.2. Merging
4. Experiment
4.1. Parameter Settings
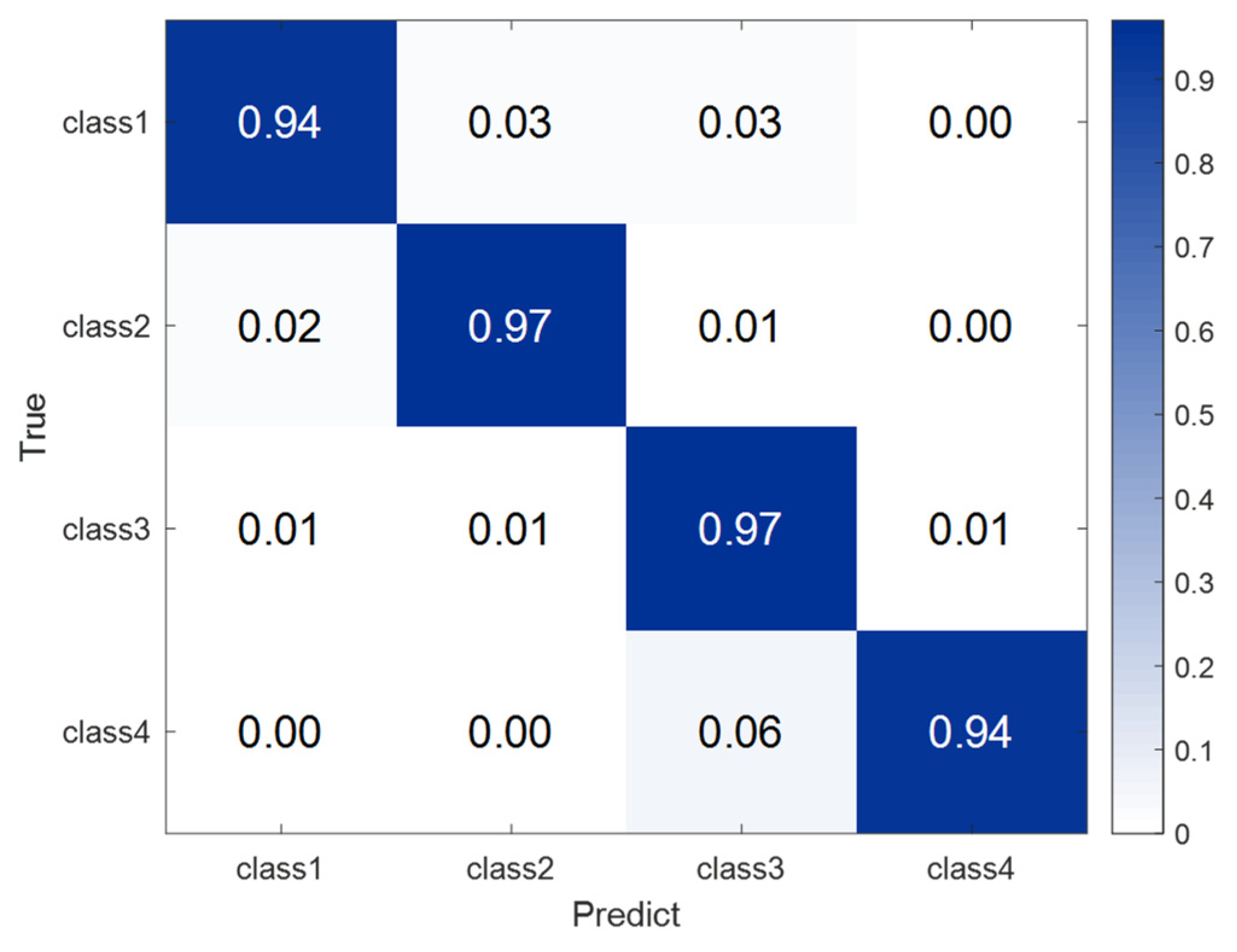
4.2. Result
5. Discussion
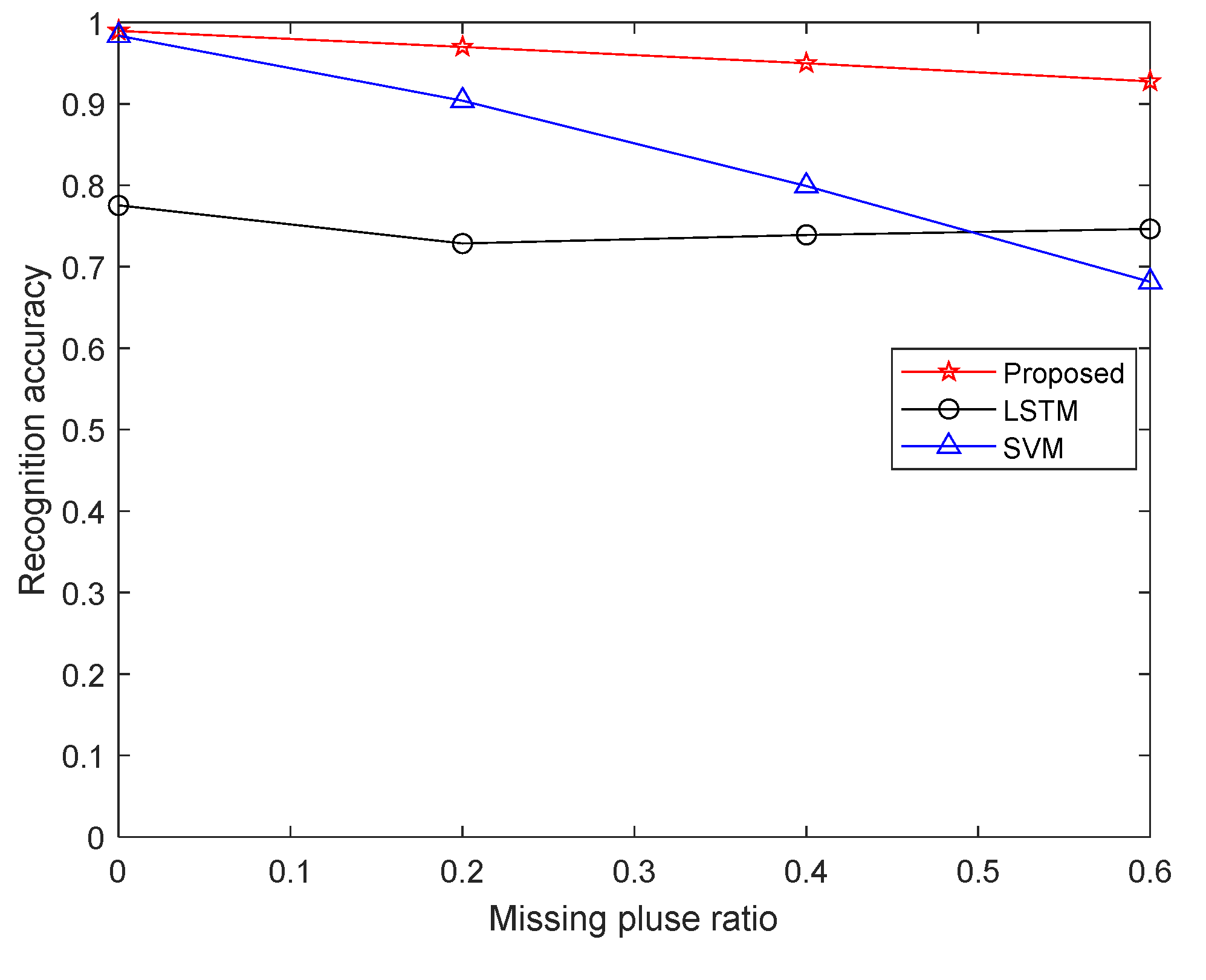
5.1. Influence of Missing Pulse Rate on Recognition Accuracy
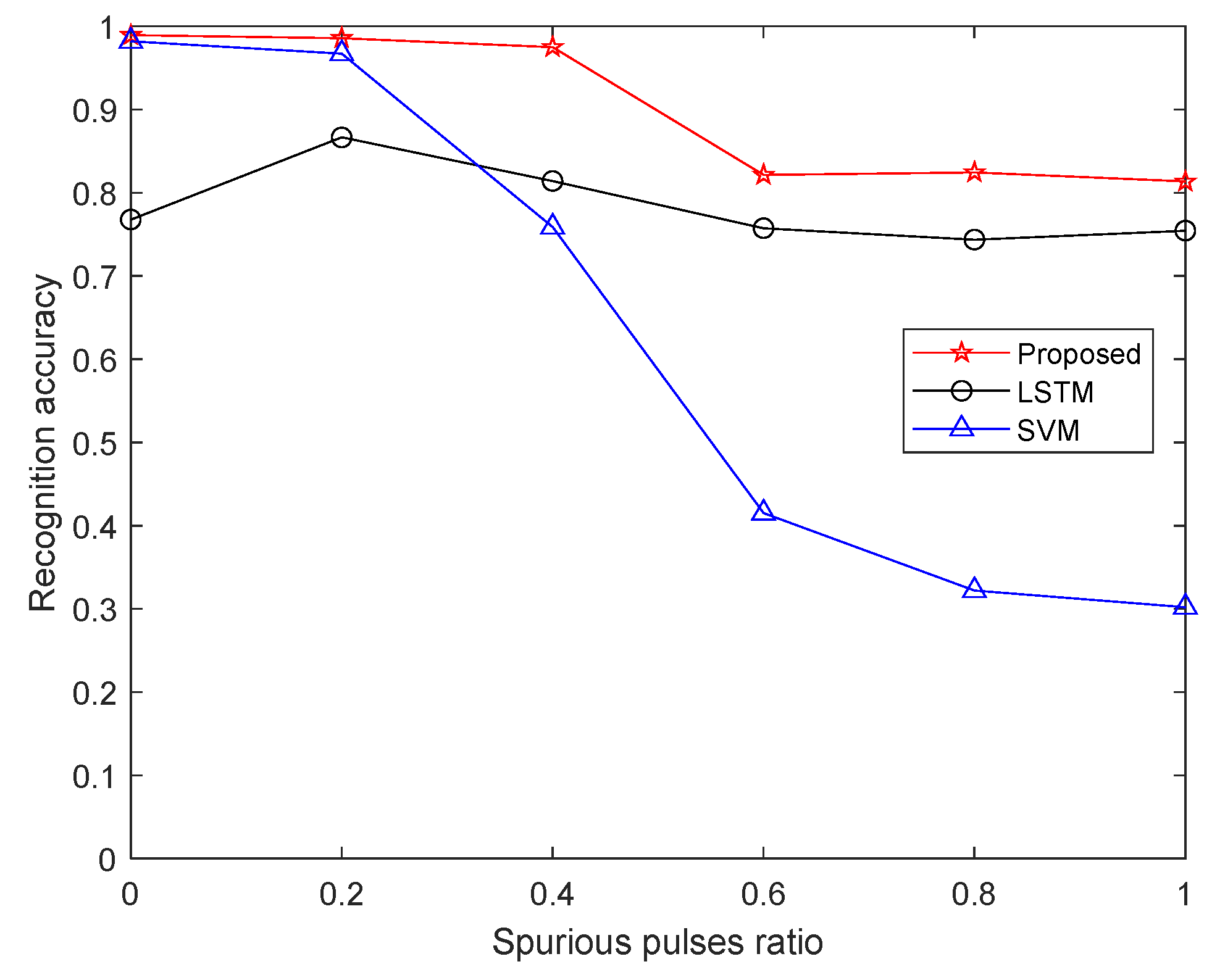
5.2. Influence of Spurious Pulse Rate on Recognition Accuracy
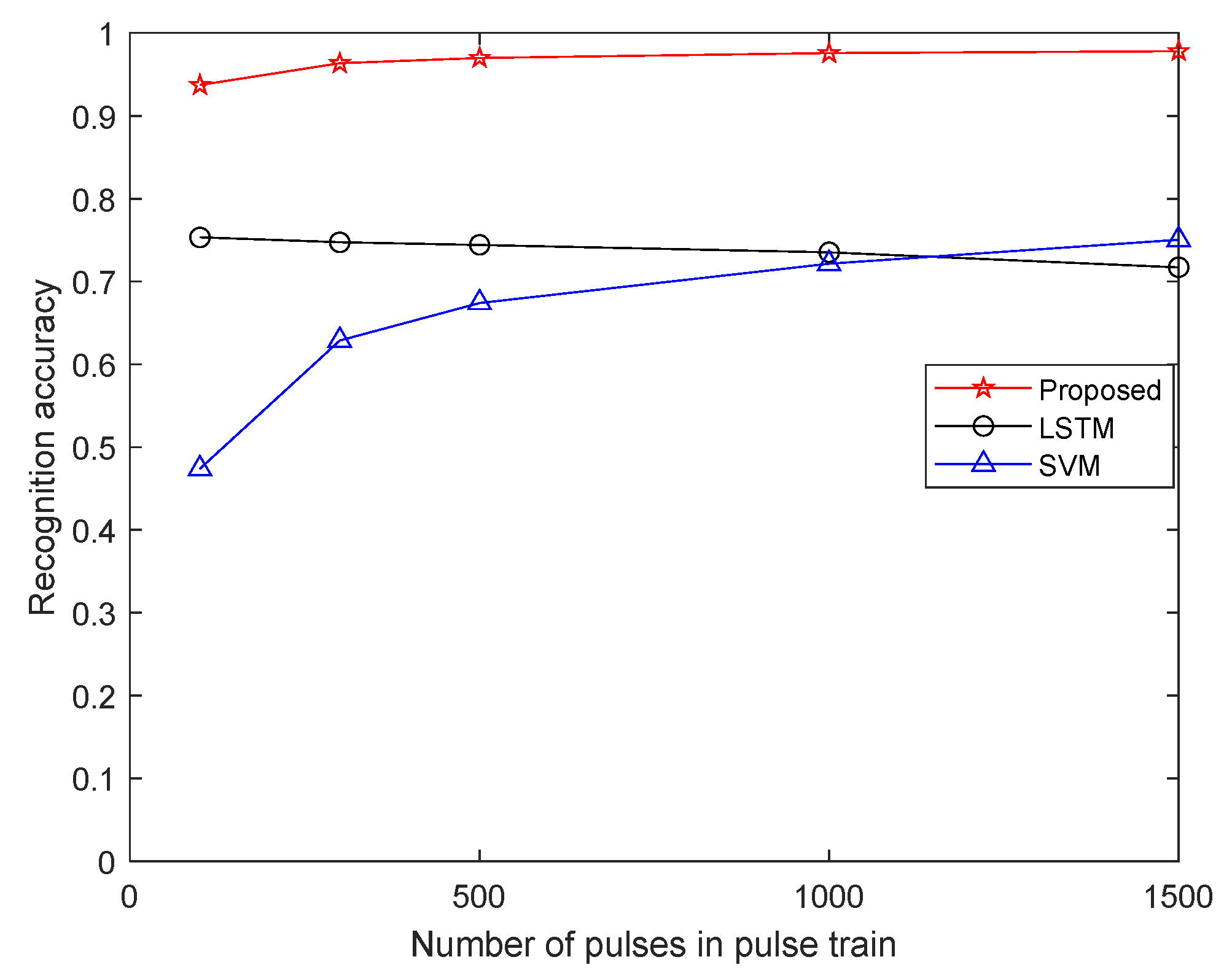
5.3. Influence of Number of Pulses in Pulse Train on Recognition Accuracy
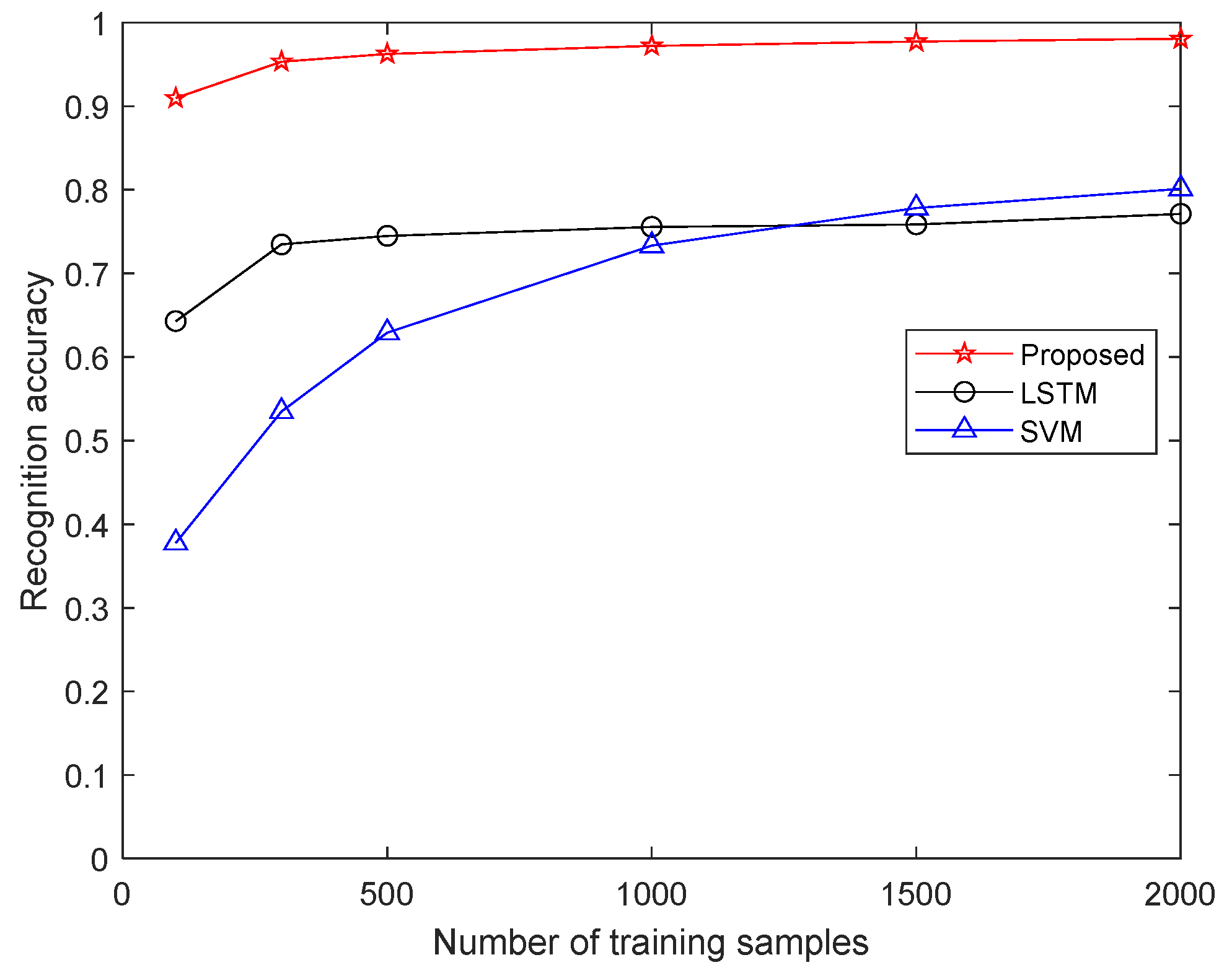
5.4. Influence of Training Samples Number on Recognition Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AOA | Angle of Arrival |
| CNN | Convolutional Neural Network |
| ESM | Electronic Support Measures |
| LSTM | Long Short-term Memory |
| PA | Pulse Amplitude |
| PDW | Pulse Descriptor Word |
| PRI | Pulse Repetition Interval |
| PW | Pulse Width |
| RER | Radar Emitter Recognition |
| RNN | Recurrent Neural Network |
| SVM | Support Vector Machine |
| TDOA | Time Difference of Arrival |
| TOA | Time of Arrival |
References
- Liu, J.; Lee, J.; Li, L.; Luo, Z.-Q.; Wong, K. Online clustering algorithms for radar emitter classification. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1185–1196. [Google Scholar] [PubMed]
- Spezio, A.E. Electronic warfare systems. IEEE Trans. Microw. Theory Techn. 2002, 50, 633–644. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; An, W.; Guo, F.C.; Liu, Z.; Jiang, W. Principles and Technologies of Electronic Warfare System; Publishing House of Electronics Industry: Beijing, China, 2014; pp. 101–103. [Google Scholar]
- Wiley, R.G. ELINT: The Interception Analysis Radar Signals; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Wu, B.; Yuan, S.; Li, P.; Jing, Z.; Huang, S.; Zhao, Y. Radar Emitter Signal Recognition Based on One-Dimensional Convolutional Neural Network with Attention Mechanism. Sensors 2020, 20, 6350. [Google Scholar] [CrossRef]
- Revillon, G. Radar emitters classification and clustering with a scale mixture of normal distributions. IET Radar Sonar Navig. 2019, 13, 128–138. [Google Scholar]
- Willson, G.B. Radar Classification Using a Neural Network. Appl. Artif. Neural Netw. 1990, 1294, 200–210. [Google Scholar]
- Zhang, W.J.; Fan, F.H.; Tan, Y. Application of cluster method to radar signal sorting. Radar Sci. Technol. 2004, 2, 219–223. [Google Scholar]
- Ye, F.; Luo, J.Q. A multi-parameter synthetic signal sorting algorithm based on BFSN clustering. Radar ECM 2005, 2, 43–45. [Google Scholar]
- Wang, S.-Q.; Zhang, D.-F.; Bi, D.-Y.; Yong, X.-J. Multi-parameter radar signal sorting method based on fast support vector clustering and similitude entropy. J. Electron. Inf. Technol. 2011, 33, 2735–2741. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, M.; Chen, C. A Deep-Learning Intelligent System Incorporating Data Augmentation for Short-Term Voltage Stability Assessment of Power Systems. Appl. Energy 2022, 308, 118347. [Google Scholar] [CrossRef]
- Lee, S.K.; Han, B.B.; Rhee, M.K.; Churl, H.J. Classification of the trained and untrained emitter types based on class probability output networks. Neurocomputing 2017, 248, 67–75. [Google Scholar]
- Feng, Y.; Cheng, Y.; Wang, G.; Xu, X.; Han, H.; Wu, R. Radar Emitter Identification under Transfer Learning and Online Learning. Information 2020, 11, 15. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.; Liu, Z.; Feng, R.; Chen, X.; Tai, N. An Unknown Radar Emitter Identification Method Based on Semi-Supervised and Transfer Learning. Algorithms 2019, 12, 271. [Google Scholar] [CrossRef]
- Meng, X.P.; Shang, C.X.; Dong, J.; Fu, X.J.; Lang, P. Automatic modulation classification of noise-like radar intrapulse signals using cascade classifier. ETRI J. 2021, 43, 991–1003. [Google Scholar]
- Xue, J.; Tang, L.; Zhang, X.G.; Jin, L. A Novel Method of Radar Emitter Identification Based on the Coherent Feature. Appl. Sci. 2020, 10, 5256. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.B.; Jin, S.S.; Zhang, Z.Y.; Wang, H.; Qi, L.; Zhou, R.L. Modulation Signal Recognition Based on Information Entropy and Ensemble Learning. Entropy 2018, 20, 198. [Google Scholar]
- Zhang, G.X.; Jin, W.D.; Hu, L.Z. Radar emitter signal recognition based on support vector machines. In Proceedings of the ICARCV 2004 8th Control, Automation, Robotics and Vision Conference, Kunming, China, 6–9 December 2004. [Google Scholar]
- Liu, Z.M. Multi-feature fusion for specific emitter identification via deep ensemble learning. Digit. Signal Processing 2020, 110, 102939. [Google Scholar] [CrossRef]
- Jordanov, I.N.; Petrov, N.; Roe, J. Radar Emitter Signals Recognition and Classification with Feedforward Networks. Procedia Comput. Sci. 2013, 22, 1192–1200. [Google Scholar]
- Shieh, C.; Lin, C. A vector neural network for emitter identification. IEEE Trans. Antennas Propag. 2002, 50, 1120–1127. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.C.; Guan, X.; He, Y. Study on radar emitter recognition signal based on rough sets and RBF neural network. In Proceedings of the 2009 International Conference on Machine Learning and Cybernetics, Baoding, China, 12–15 July 2009. [Google Scholar]
- Yin, Z.; Yang, W.; Yang, Z.; Zuo, L.; Gao, H. A study on radar emitter recognition based on SPDS neural network. Inf. Technol. J. 2011, 10, 883–888. [Google Scholar] [CrossRef]
- Liu, Z.M.; Yu, P.S. Classification, Denoising, and Deinterleaving of Pulse Streams with Recurrent Neural Networks. IEEE Trans. Aerosp. Electron. Systems 2019, 55, 1624–1639. [Google Scholar] [CrossRef]
- Li, X.Q.; Liu, Z.M.; Huang, Z.T.; Liu, W.S. Radar Emitter Classification with Attention-Based Multi-RNNs. IEEE Commun. Lett. 2020, 24, 2000–2004. [Google Scholar] [CrossRef]
- Liao, X.; Li, B.; Yang, B. A Novel Classification and Identification Scheme of Emitter Signals Based on Ward’s Clustering and Probabilistic Neural Networks with Correlation Analysis. Comput. Intell. Neurosci. 2018, 2018, 1458962. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; White, R.E.; Low, M. A comparison study of radar emitter identification based on signal transients. In Proceedings of the 2018 IEEE Radar Conference, Oklahoma City, OK, USA, 23–27 April 2018. [Google Scholar]
- Ford, B.P.; Middlebrook, V.S. Using a knowledge-based system for emitter classification and ambiguity resolution. In Proceedings of the IEEE National Aerospace and Electronics Conference, Dayton, OH, USA, 22–26 May 1989. [Google Scholar]
- Anderson, J.A.; Gately, M.T.; Penz, P.A.; Collins, D.R. Radar Signal Categorization Using A Neural Network. Proc. IEEE 1990, 78, 1646–1657. [Google Scholar] [CrossRef]
- Cheng, Y. Mean Shift, Mode Seeking, and Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 790–799. [Google Scholar] [CrossRef]
- Kuang, W.; Chan, Y.; Tsang, S.; Siu, W. Machine Learning-Based Fast Intra Mode Decision for HEVC Screen Content Coding via Decision Trees. IEEE Trans. Circuits Syst. Video 2020, 30, 1481–1496. [Google Scholar] [CrossRef]
- Müller, W.; Wysotzki, F. Automatic construction of decision trees for classification. Ann. Oper. Res. 1994, 52, 231–247. [Google Scholar] [CrossRef]
- Chikkamath, S.; SR Nirmala, S.R. Melody generation using LSTM and BI-LSTM Network. In Proceedings of the 2021 International Conference on Computational Intelligence and Computing Applications, Nagpur, India, 26–27 November 2021. [Google Scholar]

| Sample | Feature Vector | Label |
|---|---|---|
| 1 | [100,−1] | a |
| 2 | [100,300,−1] | b |
| 3 | [300,100,−1] | b |
| 4 | [300,100,200,−1] | c |
| 5 | [200,100,300,−1] | c |
| 6 | [100,300,200,400,−1] | d |
| 7 | [200,400,100,300,−1] | d |
| Radar Type | PRI Type | PRI Model (us) | STD (μs) |
|---|---|---|---|
| 1 | fixed | 300 | 2 |
| 2 | staggered | [100 300 500] | 2 |
| 3 | staggered | [100 300 500 700] | 2 |
| 4 | staggered | [100 320 500 700] | 2 |
| Module | Parameter | Value |
|---|---|---|
| clustering | PRI upper bound PRImax | 2000 µs |
| PRI lower bound PRImin | 50 µs | |
| Radius | 0.03 | |
| frequency threshold factor | 0.08 | |
| decision tree | Threshold | 0.95 |
| Confidence | 0.997 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, T.; Yuan, S.; Liu, Z.; Guo, F. Radar Emitter Recognition Based on Parameter Set Clustering and Classification. Remote Sens. 2022, 14, 4468. https://doi.org/10.3390/rs14184468
Xu T, Yuan S, Liu Z, Guo F. Radar Emitter Recognition Based on Parameter Set Clustering and Classification. Remote Sensing. 2022; 14(18):4468. https://doi.org/10.3390/rs14184468
Chicago/Turabian StyleXu, Tao, Shuo Yuan, Zhangmeng Liu, and Fucheng Guo. 2022. "Radar Emitter Recognition Based on Parameter Set Clustering and Classification" Remote Sensing 14, no. 18: 4468. https://doi.org/10.3390/rs14184468
APA StyleXu, T., Yuan, S., Liu, Z., & Guo, F. (2022). Radar Emitter Recognition Based on Parameter Set Clustering and Classification. Remote Sensing, 14(18), 4468. https://doi.org/10.3390/rs14184468







