Knowledge Graph Representation Learning-Based Forest Fire Prediction

Abstract

Forest fires destroy the ecological environment and cause large property loss. There is much research in the field of geographic information that revolves around forest fires. The traditional forest fire prediction methods hardly consider multi-source data fusion. Therefore, the forest fire predictions ignore the complex dependencies and correlations of the spatiotemporal kind that usually bring valuable information for the predictions. Although the knowledge graph methods have been used to model the forest fires data, they mainly rely on artificially defined inference rules to make predictions. There is currently a lack of a representation and reasoning methods for forest fire knowledge graphs. We propose a knowledge-graph- and representation-learning-based forest fire prediction method in this paper for addressing the issues. First, we designed a schema for the forest fire knowledge graph to fuse multi-source data, including time, space, and influencing factors. Then, we propose a method, RotateS2F, to learn vector-based knowledge graph representations of the forest fires. We finally leverage a link prediction algorithm to predict the forest fire burning area. We performed an experiment on the Montesinho Natural Park forest fire dataset, which contains 517 fires. The results show that our method reduces mean absolute deviation by 28.61% and root-mean-square error by 53.62% compared with the previous methods.

1. Introduction

Millions of hectares of forest are burned every year. Forest fires cause serious damage to the ecological balance. Dealing with forest fires costs a large amount of money and even causes casualties. Being able to pre-estimate the burning area of forest fires can effectively avoid many accidents. Therefore, forest fire prediction plays an important role in geographic information research. This paper proposes a method for predicting burning areas using representation learning based on a forest fires knowledge graph. The proposed method can predict forest fire data without artificially defined inference rules under the consideration of multi-source data fusion.

In the 1920s, research on forest fire prediction emerged all over the world. The first was the physical model. The Forest Fire Weather Index (FWI) [1] consists of six components that account for the effects of fuel moisture and weather conditions on fire behavior. The FWI enables comprehensive analysis of forest fires by calculating temperature, relative humidity, wind speed, and 24 h precipitation. In the physical model, it pays much attention to the acquisition of forest fire factors. Chen et al. [2] selected rainfall as a physical factor to investigate the impact of forest fires and proposed a measure of the impact of precipitation on fire.

Statistical machine learning models have made many advances in forest fire detection and prediction. Cortez et al. [3] tried to explore different Data Mining (DM) approaches to predicting the burned areas of forest fires, including Support Vector Machines (SVMs) and Random Forests (RFs). The methods help to predict the area burned by frequent small-scale fires. Giménez et al. [4] analyzed temperature, relative humidity, rainfall, and wind speed, and used SVM to predict the burned area of more frequent small fires. Woolford et al. [5] used a Random Forest (RF) model by considering the occurrence of lightning to improve the accuracy of forest fire predictions. Rodrigues et al. [6] explored the effectiveness of machine learning in assessing human-induced wildfires, using RF, Boosted Regression Trees (BRT), and SVM and compared them with traditional logistic regression methods. The results show that using these machine learning algorithms can improve the accuracy of forest fire predictions. Kalantar et al. [7] used multivariate adaptive regression splines (MARS), SVM, and BRT to predict forest fire susceptibility in the Chaloos Rood watershed in Iran. This study further demonstrates the superiority of BRT in forest fire prediction. Blouin et al. [8] proposed a method based on penalized-spline-based logistic additive models and the E-M algorithm to define the fire risk as the probability of a fire, which can be reported every day. Jaafari et al. [9] utilized a Weights-of-Evidence (WOE) Bayesian model to investigate the spatial relationship between historical fire events in the Chaharmahal-Bakhtiari Province of Iran. For building better forest fire prediction models, Pham et al. [10] evaluated the abilities of the machine learning methods, including a Bayesian network (BN), Naïve Bayes (NB), decision tree (DT), and multivariate logistic regression (MLR), for Pu Mat National Park. Wang et al. [11] proposed an online prediction model for the short-term forest fire risk grade. It can capture the influences of multiple prediction factors via MLR by learning historical data. Singh et al. [12] utilized the RF approach for identifying the roles of climatic and anthropogenic factors in influencing fires. Remote sensing technology can observe large-scale forest fire information. Many studies use satellite data to analyze forest fires. The MODIS (Moderate-resolution Imaging Spectroradiometer) Fire and Thermal Anomalies data and the VIIRS (Visible Infrared Imaging Radiometer Suite) Fire data show active fire detections and thermal anomalies [13]. Ma et al. [14] used satellite monitoring hotspot data from between 2010 and 2017 to analyze the impacts of meteorology, terrain, vegetation, and human activities on forest fires in Shanxi Province based on logistic model and RF model. Piralilou et al. [15] evaluated the effects of coarse (Landsat 8 and SRTM) and medium (Sentinel-2 and ALOS) spatial resolution data on wildfire susceptibility prediction using RF and SVM models.

Recently, quite a few studies have shown that deep-learning-based methods can discover more complex data patterns of forest fires than the traditional machine-learning-based models. Naderpour et al. [16] developed an optimized deep neural network to maximize the ability of a multilayer perceptron for forest fire susceptibility assessment. The method achieves higher accuracy than traditional machine learning algorithms. Youseef et al. [17] used the powerful fitting ability of neural networks to model the complex associations between forests and meteorological factors. Prapas et al. [18] implemented a variety of deep learning models to capture the spatiotemporal context and compare them against the RF model. Radke et al. [19] proposed FireCast, which implemented 2D convolutional neural networks (CNN) to predict the area surrounding a current fire perimeter. Bergado et al. [20] designed a fully convolutional network to produce daily maps of the wildfire burn probability over the next 7 days. Jafari et al. [21] collated Irish fire satellite data and field geographic data between 2001 to 2005 and used traditional logistic regression and an artificial neural network to identify areas at high fire risk. The results showed that neural network models were more accurate in classifying fire points.

Forest fire prediction involves data from lots of different fields, but the three methods mentioned above do not consider the fusion of multi-source data. The multi-source data fusion is beneficial for capturing the dependencies and correlations of the forest fire data. At present, there are many advances in the use of knowledge graphs for multi-source heterogeneous data fusion. Chen et al. [22] proposed using a spatiotemporal knowledge graph as an information management framework for emergency decision making and experimented with meteorological risks [23]. Abdul et al. [24] presented a dynamic hazard identification method founded on an ontology-based knowledge modeling framework coupled with probabilistic assessment. Ge et al. [25] proposed a disaster prediction knowledge graph for disaster prediction by integrating remote sensing information.

Although there has been research on the construction of knowledge graphs for forest fires, these knowledge graphs are basically based on manual rules for reasoning and are difficult to predict effectively on incomplete knowledge graphs.

Table 1. Summary of commonly used forest fire prediction methods.

Method Name	Interpretation	Advantages	Shortcomings
Physical model method	The method obtains more complex feature representation by constructing relationships between underlying data	The method has solid theoretical foundation and the results can be used as auxiliary features	The method has large error and is unstable effect for prediction; The method does not consider multi-source data fusion
Traditional machine learning method	The method learns forest fire features from expert-selected data through algorithms	The prediction process is clever and explicable	Manually extracted features in the method may not be the best choice for the model; The method does not consider multi-source data fusion
Deep learning method	The method constructs neural network for fitting historical forest fire data	The method can identify important feature and achieves higher accuracy	This method cannot manually adjust the intermediate training process and add expert prior knowledge; The method does not consider multi-source data fusion
Traditional knowledge graph method	The method organizes the data into a graph structure for analysis and calculation with rules or probabilistic models	The method can fuse multi-source data for in-depth search	The artificially defined inference rules are expensive, and the constructed graph structure may not be complete

shows a summary of the commonly used forest fire prediction methods. At present, there is no method for automatic semantic feature acquisition and effective calculation for the forest fire knowledge graph prediction. Knowledge graph representation learning and the graph neural network (GNN) method provide ideas for learning the feature representation of forest fire knowledge and achieve predictions with better accuracy.

In this paper, we propose a knowledge-graph- and representation-learning-based forest fire prediction method. From the perspective of multi-source data fusion, our method improves rule-based disaster prediction through the representation learning-based link prediction algorithm. The proposed forest fire prediction method consists of a deep-learning-based prediction method and a forest fire prediction knowledge graph. 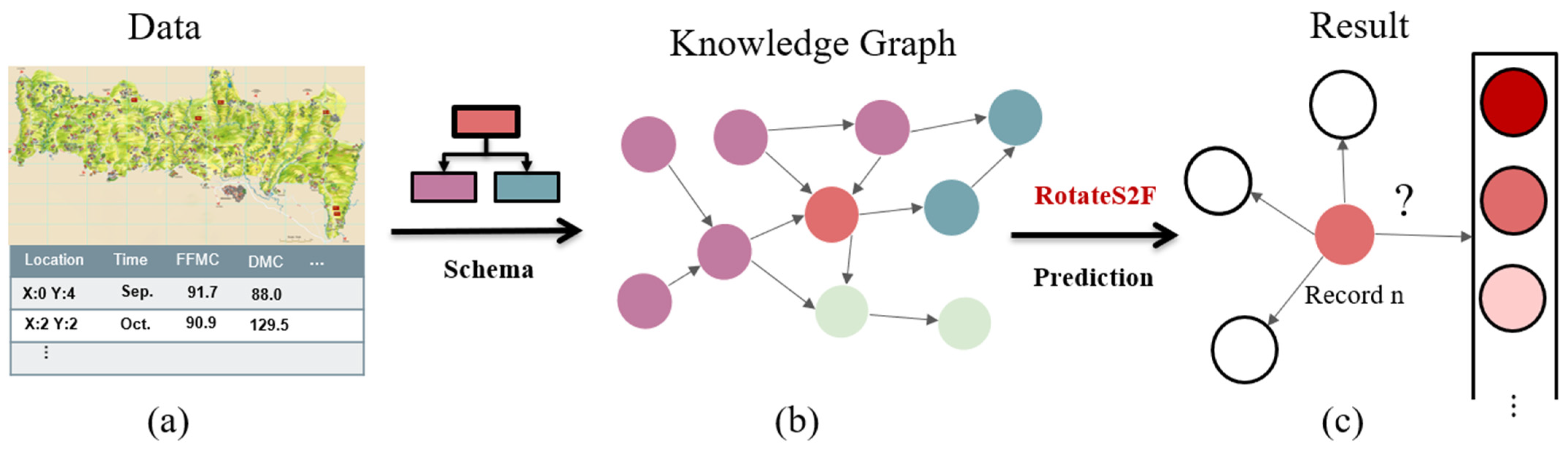Figure 1 shows the overview of our method. First, we propose a forest-fire-oriented, spatiotemporal-knowledge-graph construction method including a concept layer and a data layer. Then, we propose the Rotate Embedding and Sample to Forest Fire (RotateS2F) method. RotateS2F represents the elements in the forest fire knowledge graph as continuous vectors and predicts the burning areas of forest fires via link prediction algorithm on the graph. We experimented on the Montesinho Natural Park forest fire dataset. The results show that our method outperforms the previous methods in the prediction errors of the burning areas, i.e., the metrics of MAD and RMSE.

The contributions are summarized as follows: (1) We propose a new schema for building a forest fire knowledge graph, including time, space, and influencing factors. Compared with the physical model method, the traditional machine learning method, and the deep learning method, a knowledge graph can fuse common multi-source data involved in forest fires and capture the dependencies and correlations of the forest fire data. (2) We propose RotateS2F to learn the semantic features and structural features from the forest fire knowledge graph. Compared with the traditional knowledge graph method, we use a knowledge-graph- and representation-learning-based method to solve the problem of using the artificially defined inference rules is expensive for inference and prediction. (3) We experimented with burning area prediction. The results show that the proposed method can reduce the prediction error compared with the original method.

The rest of this article is organized as follows. Section 2 describes technical background and our approach in detail. Section 3 proposes our experimental process and results. Section 4 discusses the advantages and limitations of this method. Section 5 shows the conclusions and future work.

Table 2. Notation and descriptions.

Notation	Description
$\mathcal{G}$	A knowledge graph
$\left(h,r,t\right)$	A triple of head entity, relation and tail entity
$\left(\mathit{h},\mathit{r},\mathit{t}\right)$	Embedding of head entity, relation and tail entity
$r\in ℛ,e\in ℰ$	Relation set and entity set
$\upsilon \in \mathcal{V}$	Vertex in graph
$\xi \in {ℰ}_{\mathcal{G}}$	Edge in graph
${ℝ}^d$	d dimensional real-valued space
${ℂ}^d$	d dimensional complex space
$\mathcal{N}\left(v\right)$	$\mathrm{The}\mathrm{set}\mathrm{of}\mathrm{nodes}\mathrm{directly}\mathrm{links}\mathrm{to}\mathrm{node}\upsilon$
${\mathcal{S}}_v$	$\mathrm{Signal}\mathrm{of}\mathrm{node}\upsilon$

shows the specific symbols and their descriptions in this paper.

2. Methods

We propose a forest fire prediction method which mainly consists of two parts, including forest fire knowledge graph construction and knowledge-graph- and representation-learning-based forest fire prediction. First, we construct a schema by discretizing data, including time, space, and influencing factors. The purpose is to build unified representations of multi-domain knowledge in the same semantic space. We store the forest fire knowledge graph in the form of triples. Next, we compute the representation vector of each entity by RotatE. Then, we relate the entities in the triples to the nodes in the graph. We input the vectors of entities as initial features into the GNN. GNN computes the updated representation vectors. Finally, we predict the burning area via link prediction algorithm. Figure 2 shows the detailed process of our method. In general, we transform multi-source forest fire data into a knowledge graph according to our schema, and predict the burning area of a forest fire through a graph representation learning algorithm and a link prediction algorithm. Specifically, in part (a), we discretize continuous values by observing the data and selecting appropriate scales. We designed a schema to carry spatiotemporal data for forest fires. The discrete forest fire data can be rearranged into a forest fire knowledge graph according to the schema. In part (b), we encode the forest fire knowledge graph using the RotatE model, representing nodes and relations as continuous vectors. In part (c), we use the node vector obtained from the representation learning as the initial feature of each node. We use a combination of knowledge graph embedding (KGE) and GNN to learn the forest fire knowledge graph and predict burning areas. KGE mainly extracts the semantic features of the forest fire knowledge graph, and GNN mainly extracts the structural features of the forest fire knowledge graph. After updating the node representation by the GNN, we use the link prediction algorithm to predict the forest fire burning area of the recorded node. The predicted result is a queue in which the burning area is arranged in descending order of likelihood.

From the perspective of multi-source data fusion, we predict the burning area of forest fires on the knowledge graph. Algorithm 1 describes our prediction process. B represents a burning area. D represents a record of determining time and place, corresponding to a node n in the graph structure by function NodeIndex (line 1). Function RotateSpace is used to get the corresponding vector from complex vector space (line 2, line 6, and line 10). The first for loop randomly samples n’s neighbors and stores their vectors in the list nd (line 4 to 6). Function aggregate can aggregate the collected nodes vectors and obtain the updated vector of node n (line 7). In the second for loop, all possible burning area vectors are matched with the updated record vector a (line 9 to 11), where function match represents the vectors similarity calculation function (line 10). The burning area with the highest matching result B is output.

Algorithm 1: Knowledge-graph and representation-learning-based forest fire prediction.

Input: Entity D $\in ℰ ℰ$is the entity set of forest fire knowledge graph Output: Burning area B $\in ℝ$   1. n = NodeIndex(D);   2. e = RotateSpace(n);   3. nd = []   4. for v in n.neighbors():   5.  if random(v) is True:   6.    nd.append(RotateSpace(v));   7. a = aggregate(nd)   8. R = []   9. for f in fireNodes:   10.  R.append(match(a, RotateSpace(f)))   11. NR = sorted(R)   12. B = NR[0]   13. return B

2.1. Spatiotemporal Knowledge Graph

The knowledge graph is a concept proposed by Google in 2012 [26]. It was first used for search engines to improve information retrieval. In recent years, the knowledge graph has been widely focused on by academia and industry and applied in many fields. In a narrow sense, the knowledge graph refers to a knowledge representation method, which essentially represents knowledge as a large-scale semantic network. The generalized knowledge graph is a general term for a series of technologies related to knowledge engineering, including ontology construction, knowledge extraction, knowledge fusion, and knowledge reasoning [27]. A knowledge graph is a structure that represents facts as triples, consisting of entities, relations, and semantic descriptions. A knowledge graph is defined as [27]:

$$\mathcal{G}=\left(ℰ,ℛ,ℰ\right),$$

(1)

where $r\in ℛ,e\in ℰ$. Entity $e$ is a real-world object, and Relation $r$ represents the relations between entities.

The construction of the concept layer of a knowledge graph includes concept classifying, definitions of concept attributes, and relationships between concepts. It can be expressed in Resource Description Framework (RDF) [28] and Web Ontology Language (OWL) [29], which conform to W3C specifications. The construction of the data layer mainly focuses on organizing data into the form of triplet collection according to the principles of the concept layer.

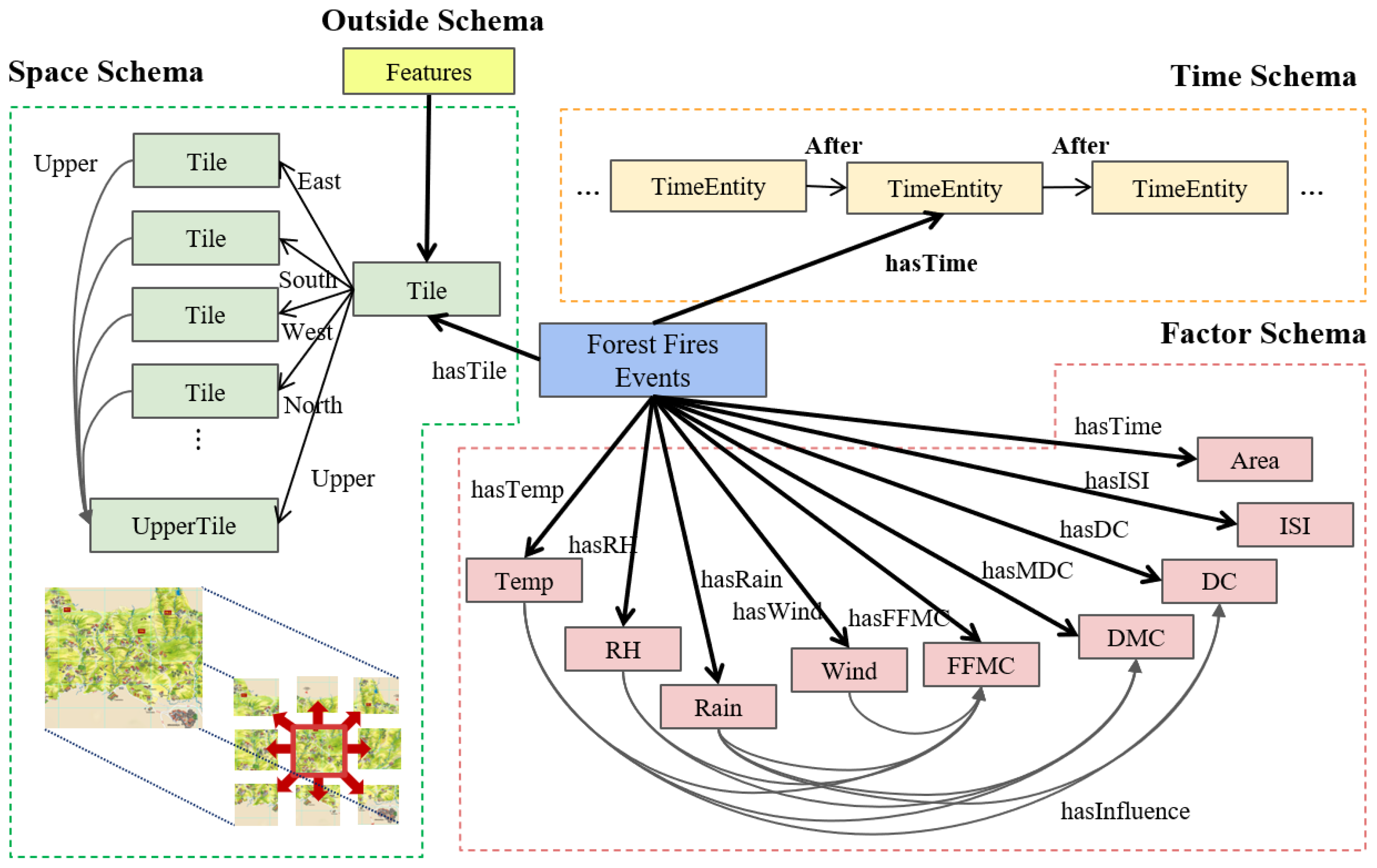
The historical forest fire events can provide empirical knowledge for predicting combustion areas. Meanwhile, the data on historical forest fires are interdependent. In this paper, we use a spatiotemporal knowledge graph to model the characteristics of forest fire events and discover the hidden relations between historical forest fire data. For this purpose, we construct a schema based on forest fire events, and the schema consists of three parts, namely, Space Schema, Time Schema, and Factor Schema, as shown in Figure 3, because forest fire events are usually related to time, space, and influencing factors. In addition, there is also an Outside Schema. We provide an outside schema interface for semantic information.

In the Space Schema, we divide the target area into M × N grid areas. In other words, we model geographical areas (tiles) as entities (nodes in graph). To describe the different areas, we uniformly define the grid in the northwest direction as the origin, with the x-axis to the east, and the y-axis to the south. The location information of each record is described by a rectangular region determined by two-dimensional coordinates. We organize each multi-level rectangular tile area in the form of a tile pyramid. The upper tile covers the 3 × 3 areas of the lower tile. We define that each tile has a cardinal direction with eight same-size surrounding tiles (north, east, south, west, northeast, southeast, southwest, and northwest). It means that one of the lowest tile regions will have nine relations with other tile regions precisely, i.e., eight directional tiles and one upper tile.

The Space Schema design is in line with Tobler’s first law of geography; that is, close things are more closely related. For the attributes of each tile, we record the contour coordinates of each tile, the center point coordinates, and the feature types contained in each tile.

In the Time Schema, each time entity represents a moment. When a fire occurs in July, we associate the fire with the entity “July” (a node in the graph structure). There are two types of relations between time points: an inclusion relation and a sequential relation. For example, (January contains, January 1) and (January 2022, after February 2022). The design allows mining of the time patterns of forest fires.

In the Factor Schema, we list the commonly used indicators for forest fire monitoring. There are lots of relations between the monitoring values because the attributes of the data are not independent, such as humidity affecting fuel moisture. We not only consider the simple relations between factors and events, but also transform the prior expert knowledge into additional relations in the knowledge graph. The FWI is one of the most commonly used fire weather hazard rating systems in the world. The calculation of many modern forest fire detection indices is defined in the FWI, including using temperature and rainfall for the drought code. We define these relations as hasInfulence in the schema. In this way, we can construct a relatively dense forest fire knowledge graph structure. This will also help to predict the burning areas of forest fires.

After constructing the concept layer, we build the data layer according to the schema. We define the graph structure corresponding to Figure 3 by constructing the rectangular contents as entities (nodes in the graph) and the arrows as relations (edges in the graph). Next, we create triples according to real forest fire data and define the triples as (forest fire attributes, relationship between forest fire attributes, and forest fire attributes). The obtained triplet set presents the spatiotemporal knowledge graph of forest fires.

There are two levels of understanding of the constructed forest fire knowledge graph. In terms of data structure, a forest fire knowledge graph consists of nodes and edges. In terms of semantic representation, a forest fire knowledge graph consists of entities and relations. For a triple (h, r, t), h is a head node in the graph structure, corresponding to the head entity at the semantic level. r is an edge in the graph structure, corresponding to the relation from h to t at the semantic level. t is a tail node in the graph structure, corresponding to the tail entity at the semantic level.

2.2. Knowledge Graph Embedding

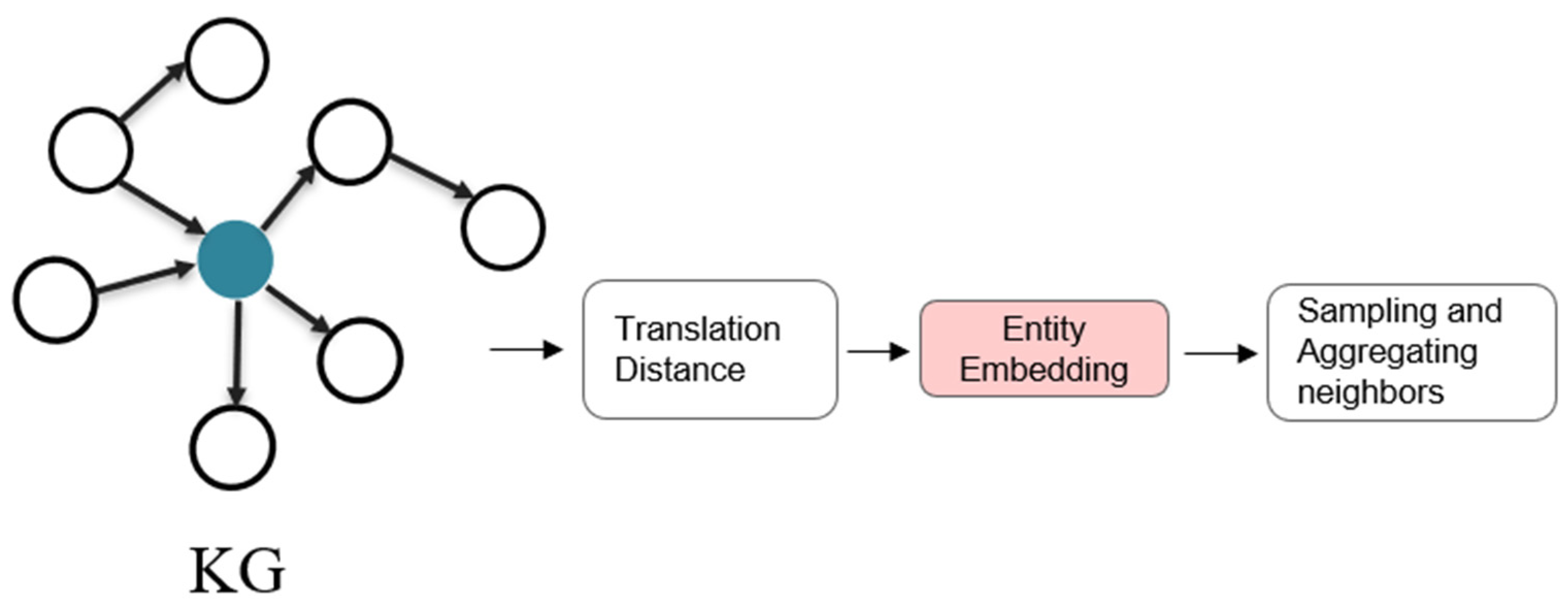
We propose the RotateS2F method to represent a forest fire knowledge graph as embeddings. Figure 4 shows an overview of RotateS2F, which mainly consists of two stages. For all forest fire triples, the first stage is to define each relation as a rotation from the head entity to the tail entity in complex vector space and minimize the translation distance. The vectors of the entities have semantic information. Then, we use the embeddings as the initial features of the GNN to further learn the structural features of entities according to the graph structure. Finally, we predict forest fire burning areas by matching nodes’ vectors on the knowledge graph, which is called the link prediction algorithm.

In recent years, knowledge representation learning (KRL, or knowledge graph embedding, KGE) plays an important role in the field of knowledge graphs. It represents entities and relations of knowledge graphs using vectors. KRL represents the semantic information of entities and relations as low-dimensional dense vectors for the distance metrics [30]. In one article [31], the knowledge graph representation models are classified in detail from the perspectives of representation space, scoring function, encoding model, and auxiliary information. TransE [32] is a classic KGE method with which to model entities and relations by translation distance. Its purpose is to embed the semantic information of entities and relations into the identical vector space through translations between vectors with the rule $h+r\approx t. h$is the representation vector of the head entity, $r$ is the representation vector of the relation, and $t$ is the representation vector of the tail entity. Based on TransE, many KGE models were proposed: TransH [33], TransR [34], TransD [35], ComplEx [36], and RotatE [37].

For the representation learning-based forest fire prediction methods, we need to consider the following situations: (1) This method can model the relations of 1-to-N, N-to-1, and N-to-N. In the field of forest fire prediction, there are often many fires in one area or period. Multiple regions may have the same climatic features. There may be multiple burning areas in a certain region, and a certain burning area may also exist in multiple regions. (2) This method needs to model a variety of feature relations. As shown in Figure 3, a forest fire knowledge graph is a standard directed graph. There are many relations with symmetry: (Region $\mathrm{A}$ is adjacent to region B, and region B is adjacent to region A), anti-symmetric (the feature of each area is anti-symmetric), inversion (the east of region A is region B, west of region B is region A), and composition (in FWI, temperature and rainfall composition affect the drought code (DC)). By comparing the current KGE methods, we found that RotatE is good at modeling one-to-many (1-N) relations and is able to infer various relation patterns, including symmetry/antisymmetry, inversion, and composition [37]. We demonstrate the effectiveness of the RotatE method on the forest fire knowledge graph compared with other KGE methods in Section 3.4.1. We ultimately embed triples in the same way as RotatE. Given a training triple ($h, r, t$) of a graph, the distance function of RotatE is defined as:

$$d_r\left(\mathit{h},\mathit{t}\right)=\left|\left| \mathit{h} \circ \mathit{r}-\mathit{t} \right|\right|,$$

(2)

where $\circ$ is the Hadmard product.

With the learning strategy, we still need to determine the negative sample generation strategy. Under the open-world assumption, we assume that the forest fire knowledge graph consists only of correct facts and that those facts that do not appear in it are either wrong or missing. According to the schema in Section 2.1, when we randomly generate negative sample sets, we can restrict the generation of relation classes by effectively generating head and tail entities instead of completely random negative sample sets without class constraints—i.e., (h, r, ?) or (?, r, t). Therefore, we don not want to generate a negative sample with wrong common sense, such as (Event001 has temperature 5 m/s). We limit the relation categories and generate logical negative samples, such as (Event001 has temperature 86 ℉), or (Event001 has temperature 77 ℉), whose corresponding correct sample is (Event001 has temperature 68 ℉). It makes the negative sample generation much more meaningful and valuable.

In addition, due to the rise in GNN, studies can better study graph structure. We use a GNN as the feature learning tool for the second stage. In recent years, many advances have been made in the research of GNNs. GNNs are a breakthrough for neural networks, enabling them to learn features of non-Euclidean structured data. There are spectral-based GCNs and spatial-based GCNs. The spectral method uses graph signal theory by taking the Fourier transform as a bridge to transfer a CNN to the graph structure, such as ChebyNet [38] or the graph wavelet neural network [39]. The spatial-based methods appear in the later stage. Based on the graph nodes, the spatial-based methods have the aggregation function to gather the neighbor node features and adopt the message transmission mechanism. They focus on the accuracy of design and efficiently use the neighbor node features of the central node to update the representations of the central node features. GraphSAGE [40] generates the node embeddings by sampling and gathering the neighboring nodes. Since there are no parameterized convolution operations, the learned aggregation function can be applied for the dynamic updating of graphs. GAT [41] proposed a GNN by adding an attention layer to the traditional GNN framework to obtain the weighted nodes’ embedding according to their neighborhoods’ features.

The structural features of a forest fire knowledge graph can be extracted by using a GNN. In the previous section, we represent all entities with the same dimension. We use the knowledge graph representation vectors as the initial features of the nodes in the GNN. For training the GNN, the forward propagation updating process of forest fire node embeddings consists of two steps. Suppose we train a K-layer network. In each layer, firstly, we randomly select the adjacent nodes of the target node according to a certain proportion. A definite aggregate function aggregates the nodes’ information, shown as Formula (3). Then, the aggregated values are consolidated and updated with the information of the node itself, shown as Formula (4).

$$a_v^{\left(k\right)}=AGGREGAT{E}^{\left(k\right)}\left(\left\{{\mathcal{S}}_u^{\left(k-1\right)}:u\in \mathcal{N}\left(v\right)\right\}\right),$$

(3)

$${\mathcal{S}}_v^{\left(k\right)}=COMBIN{E}^{\left(k\right)}\left({\mathcal{S}}_v^{\left(k-1\right)}, a_v^{\left(k\right)}\right),$$

(4)

where $u$ is the set of nodes directly linked to node $v$ in the forest fire knowledge graph, and ${\mathcal{S}}_v^{\left(k-1\right)}$ is the information from level k − 1. ${\mathcal{S}}_v^{\left(k\right)}$ is the combination of the information from the upper layer and the aggregation result of this layer. $AGGREGATE$ and $COMBINE$ are mean aggregators.

We obtain a prediction score of the relation between each two nodes by the dot product of their representations. We consider the relation with the highest prediction scores as the most likely edge. Specifically, for the link prediction-based forest fire prediction algorithm, node u represents an event node that we want to predict, and v represents the burning area node of event u. By dot product u with all candidate burning area nodes, we can get the probability of u corresponding to different burning areas. The burning area with the highest probability is v′.

2.3. Scenario and Data Environment

In our study, we used the forest fire data from Montesinho Natural Park [3], which is located in northeastern Portugal, as shown in Figure 5. They were data for three years from 2000 to 2003, including many attributes, as shown in

Table 3. The attributes of Montesinho Natural Park forest fire data [3].

Attributes	Description
X-Y location	grid-based regional location 9 × 9
Month	Months record
FFMC	Fine Fuel Moisture Code
DMC	Duff Moisture Code
DC	Drought Code
ISI	Initial Spread Index
Temp	Temperature (in°C)
RH	relative humidity (in%)
Wind	Wind speed (in km/h)
Rain	Rain (in mm/m2)
Area	Total burned area (in ha)

.

Montesinho Natural Park [3] is divided into 9 × 9 areas in the dataset. We can think of each area as a tile and generate a tile pyramid. The bottom of the pyramid contains the smallest scale of 9 × 9 tiles. We defined one upper tile to cover 3 by 3 lower tiles, so we got 81 primary tiles, 9 secondary tiles, and 1 tertiary tile. The forest fire occurrence time has a monthly scale.

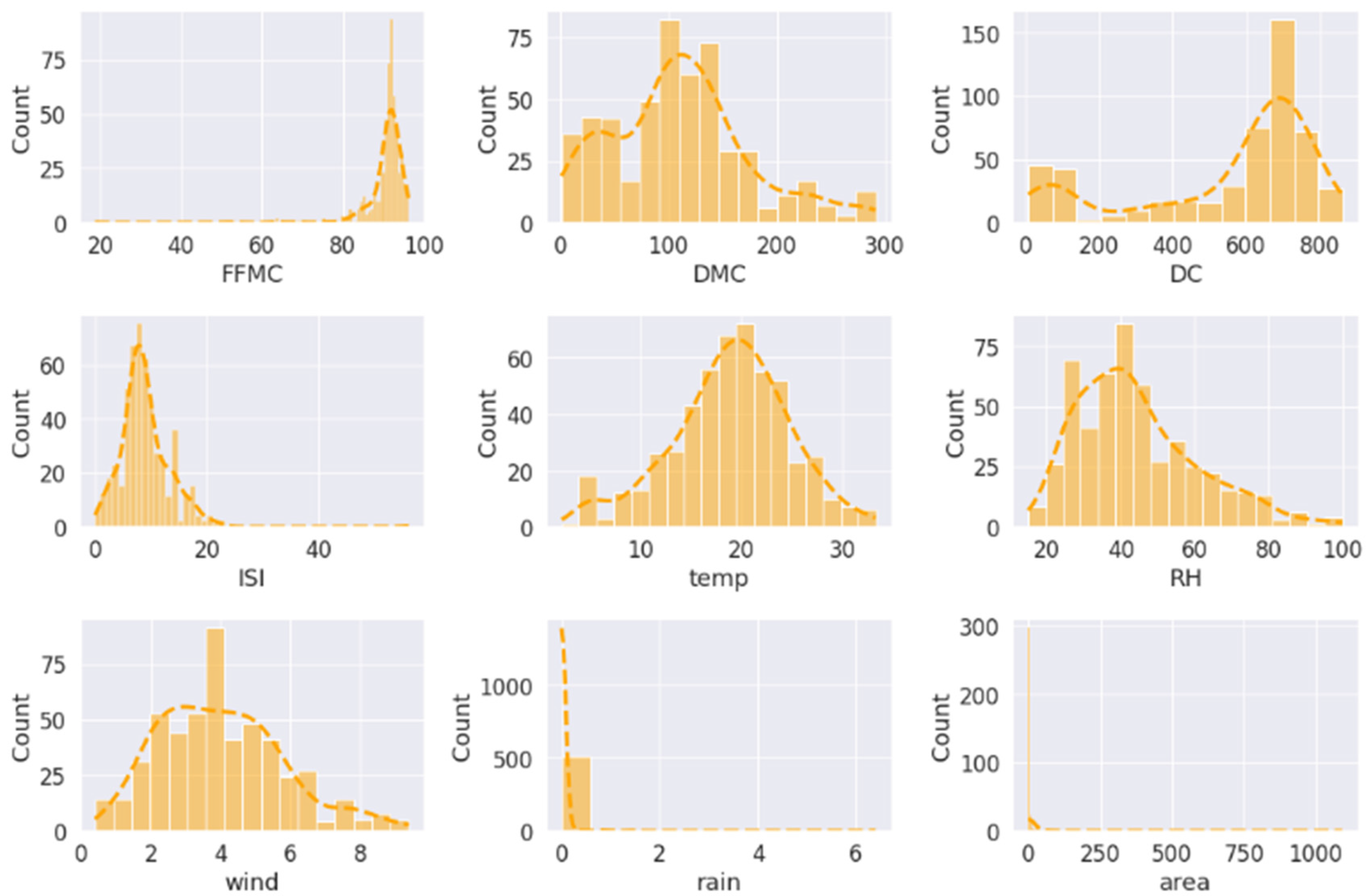
Discretization can effectively simplify data and improve the accuracy and speed of representation learning of a forest fire knowledge graph. Figure 6 shows the nine categories of continuous real-valued features for influencing factors. We first discretized the features by dividing real-valued intervals. We discretized the features by the equal-width method for each factor.

For the continuous real-valued feature, we built nodes according to the discretization of the feature. In our experiment, we set different discretization widths and observed the influence on the representation learning of the forest fire knowledge graph. With the feature discretization from class 1 to class N (the largest N represents all the values of a feature), the effect of the prediction task increases first and then decreases. If the features are classified into too few categories (at least one category), nodes cannot well represent the actual scenes of the forest fires and are too general. If each data value is defined as a single category, the graph will be very sparse. The structure features and semantic features cannot be learned well.

Table 4. Discrete intervals for each type of feature.

Feature	Discretization Width
FFMC	2.0
DMC	20.0
DC	70.0
ISI	2.0
temperature	2.0
relative humidity	5.0
wind speed	0.5
rainfall	0.1
burning area	5.0

shows the classification criteria we finally adopted. A knowledge graph $\mathcal{G}$ is generated based on the proposed data in the form of triples according to the schema structure in Section 2.1.

After feature discretization according to the width in Table 4, nodes can be used to represent forest fire objects. The data layer is obtained according to the schema shown in Figure 3. The Montesinho Natural Park forest fire data were ultimately represented as a set of triples. Thus, the forest fire knowledge graph construction was completed.

There were 757 entities, 21 relations, and 12,008 triples in the forest fire knowledge graph. We divided the triples into a training set (60%, 7025 records), validation set (20%, 2402 records), and test set (20%, 2401 records) according to fixed random seeds.

We represented nodes and edges in the forest fire knowledge graph with embedding vectors by using RotateS2F. We implemented RotateS2F with PyTorch-1.7.1. RotateS2F was trained with the batch size of 512, the fixed margin of 6.0, and the sampling temperature of 0.5 for achieving the best results in this work [37]. We used the optimizer Adam [42] for training, which is a method for stochastic optimization. It has independent adaptive learning rates for different parameters according to the changes in gradients at different moments. The epoch count was set to 1000.

Table 5. Descriptions of the parameters and the selection strategy.

Parameter	Parameter Meaning	Selection Strategy
embedding dimension	The length of a node embedding vector or a relation embedding vector	Choose dimension from {512, 1024, 2048}. Generally, the longer the length, the stronger the fitting ability, and the higher the overfitting risk. We select the dimension of 1024 after the experiment.
batch size	The amount of data in each batch computing of the neural network model.	Batch size is related to hardware; We choose batch size of 512 according to the convergence effect and hardware cost.
temperature of sampling	It is a hyper-parameter for determining the percentage of negative samples in RotatE.	Temperature of sampling is usually 0.5 or 1; The final selection is 0.5 based on experimental results.
fixed margin	It is a hyper-parameter used in the loss function to effectively optimize the distance model.	Choose the value from {3,6,9,12,18,24,30}. The finally selected value is 6.

shows the specific parameter setting meanings and strategies.

We finally represented nodes in the forest fire knowledge graph with 1024-dimensional vectors because this achieved the best results on the Montesinho Natural Park dataset in our experiment. For GNN training, we used the usual settings for the graph neural network training. We initialized the node features of the graph neural network with 1024-dimensional vectors. We set the hidden layer to have 16 neurons. The learning rate was set to 0.5, and the epoch count was set to 200. We used Adam as the optimizer of the training.

3. Results

3.1. Baselines

We selected the state-of-the-art methods of forest fire predictions for the Montesinho Natural Park data and two graph representation learning methods as baselines.

Naive average predictor (Naïve). This method strongly relies on the feature of past data. For example, given the forest fires burning area in August, the average predictor is used to predict the area burned in August next year.

Multiple regression (MR). This method uses a multivariate linear model to model forest fire data and prediction. The parameters are optimized using the least-squares algorithm. This method predicts burning area by a linear calculation using forest fire attributes as independent variables.

Decision tree (DT). In a decision tree for forest fire prediction, leaf nodes represent different burning areas and internal nodes represent the forest fire attributes. This method uses information gain as a decision factor for selecting root nodes. The forest fire features with the maximum information gain are determined as the optimal features. During the test, the DT performs layer-by-layer classification on the attribute value of a forest fire record to complete the prediction.

Random Forest (RF). This method adopts the idea of ensemble learning. In this experiment, we independently built 500 decision trees for forest fire burning area prediction by randomly sampling from the dataset. Finally, the forest fire areas were predicted according to the results of the decision trees by the majority principle. The default parameters were adopted for the method (e.g., T = 500) [3].

Multi-layer perceptron (MLP). This method uses forest fire features as input features after real value and standardization. The feature is transferred to the hidden layer for linear computation with the weights and then for nonlinear mapping by the activation function. Finally, the model is used to fit the results of the burning area. In the experiment, the model had three hidden layers. It was trained for 100 epochs [7], which were optimized by the stochastic gradient descent (SGD) algorithm.

Support Vector Machine (SVM). This method uses support vector machines to fit forest fire data. The SVM uses nonlinear mapping to transform the original training data into a higher dimension. Within this new dimension, it searches for the linear optimal separating hyperplane. This method uses a linear hyperplane to segment forest fire attributes in high-dimensional space to determine the burning area. The kernel function used in the experiment is defined as follows:

$$K\left(x,x^{\prime }\right)=\exp \left(-\gamma \frac{{\left|\left|x-x^{\prime }\right|\right|}^2}{2}\right), \gamma >0.$$

(5)

The SVM model finds the best $\gamma \in \left\{2^{-9},2^{-7},2^{-5},2^{-3},2^{-1}\right\}$and finally uses $2^{-3}$ with the best effect as the margin [3].

RotatE. The RotatE model is a well-known knowledge-graph- and representation-learning-based method [37]. We utilized the model that defines each forest fire relation as a rotation from the source forest fire entity to the target forest fire entity in the complex vector space. Considering the similarity of the datasets, we used the best hyperparameter settings on the FB15K dataset in the original paper [37]. The embedding dimensions was 1000, the batch size was 2048, the temperature of sampling was 1.0, and the fixed margin was 24. We used the record vectors learned on the forest fire knowledge graph to calculate the triple translation distances of different burning area vectors. The burning area with the smallest translation distance represents the predicted burning area.

GraphSAGE. The GraphSAGE model is a GNN model. We used the best hyperparameters from the paper [40]. The layers were 2, the learning rate was 0.001, the smoothing parameter was 0.75, and the batch size was 64. By constructing the graph structure and learning the node representation, this method determines the burning area by calculating the correlation between the record node and the burning area node.

3.2. Metrics

We use the metrics mean absolute deviation (MAD) (Formula (6)) and root-mean-square error (RMSE) (Formula (7)) to evaluate the forest fire predictions:

$$MAD=\frac{1}{N}\times {{\displaystyle \sum }}_{i=1}^N\left|y_i-{\widehat{y}}_i\right|,$$

(6)

$$RMSE=\sqrt{{{\displaystyle \sum }}_{i=1}^N{\left(y_i-{\widehat{y}}_i\right)}^2/N}$$

(7)

where $y_i$ represents the i-th predicted burning area, ${\widehat{y}}_i$ the ground truth, and $N$ the size of the test set.

3.3. Experimental Results

Table 6. The results of the MAD and RMSE (bold: the best values). Method followed by “*” indicates that the knowledge graph has removed the FWI indicator attribute relation (hasInfluence).

Method	MAD	RMSE
Naive	18.61	63.7
MR	13.07	64.5
DT	13.46	64.4
RF	13.31	64.3
MLP	13.09	64.5
SVM	13.07	64.7
RotatE	11.49	32.54
RotatE *	23.65	117.4
GNN(GraphSAGE)	33.40	39.028
RotateS2F	9.330	29.823

shows the results for all the compared methods. As expected, our RotateS2F outperformed baselines with MAD and RMSE. The results show that our method reduced MAD by 3.74 (28.61%) and RMSE by 34.377 (53.62%) compared with the previous methods.

The forest fire data in the experiment had strong dependencies and correlations. We define forest fire data as graph structures. We used RotateS2F to extract the semantic information and structure information of the graph data. The representation learning-based multi-source data fusion supports capturing better graph structure and semantic features of forest fires. Our method achieved less error than the baselines. RotatE* resulted in higher error due to removing the FWI index attribute relation (hasInfluence) from RotatE. The results of RotatE* also show the significance of expert knowledge in the graph. In addition, the results also show that our model can learn more valuable semantic information than either by knowledge graph embedding or by a graph neural network alone. We compared RotatE and GNN with our method. The results show that our method achieves better performance.

3.4. Ablation Study

3.4.1. Influence of the Knowledge Graph Embedding Model on Forest Fire Prediction

We discussed the characteristics of forest fire knowledge graphs in Section 2.2. We further verify the judgment of the model by the experiment in this section. We discuss what kind of representation model is most suitable for forest fire predictions. We used the forest fire knowledge graph data constructed in Section 2.3 in the experiment. The training set had 7025 triples, the validation set had 2402 triples, and the test set had 2401 triples. We compared RotatE to several state-of-the-art KGE modes, including TransE [32], TransH [33], TransR [34], TransD [35], DistMult [43], ANALOGY [44], and ComplEx [36] for link prediction tasks. We applied the hyperparameters which were the best settings on the FB15K dataset in the original paper.

We used five evaluation metrics: mean reciprocal rank (MMR), mean rank (MR), and correct entities ranked in the top 10/3/1 (Hits@10, Hits@3, Hits@1). Filter (Filt.) represents the possible influence of filtering out negative examples from the knowledge graph.

Table 7. The learning results of different representation learning models on our graph (bold: the best values). In parameters, ${\mathrm{N}}_{\mathrm{e}}$ and ${\mathrm{N}}_{\mathrm{r}}$ are the numbers of unique entities and relations; $m$ and $n$ are the dimensions of embedding vectors of entities and relations.

Method		MMR(r)	MR(r)	HIT @10(r)	HIT @3(r)	HIT @1(r)	Parameters
TransE	Raw	0.408	7.611	0.761	0.485	0.243	$O\left(N_{e}m+2N_{r}n\right)\left(m=n\right)$
	Filt.	0.741	2.714	0.952	0.813	0.634
TransH	Raw	0.406	6.962	0.783	0.490	0.230	$O\left(N_{e}m+2N_{r}n\right)\left(m=n\right)$
	Filt.	0.729	2.800	0.953	0.800	0.620
TransR	Raw	0.351	8.572	0.717	0.385	0.200	$O\left(N_{e}m+N_r\left(M+1\right)n\right)$
	Filt.	0.682	4.045	0.894	0.717	0.590
TransD	Raw	0.396	7.035	0.771	0.458	0.227	$O\left(2N_{e}m+2N_{r}n\right)$
	Filt.	0.725	2.854	0.948	0.787	0.618
DistMult	Raw	0.389	6.890	0.784	0.444	0.220	$O\left(N_{e}m+N_{r}n\right)\left(m=n\right)$
	Filt.	0.703	2.955	0.943	0.767	0.588
ANALOGY	Raw	0.392	6.686	0.793	0.476	0.213	$O\left(N_{e}m+\left(M/2\right)N_{r}n\right)$
	Filt.	0.718	2.971	0.945	0.891	0.608
ComplEx	Raw	0.407	6.314	0.813	0.466	0.239	$O\left(2N_{e}m+2N_{r}n\right)$
	Filt.	0.726	2.925	0.942	0.768	0.632
RotatE	Raw	0.439	7.376	0.762	0.484	0.296	$O\left(2N_{e}m+2N_{r}n\right)$
	Filt.	0.778	2.438	0.959	0.825	0.693

shows the results. RotatE works best on most of the metrics because RotatE provides more exact semantic features.

3.4.2. The Relations between Factors

Table 6 shows that RotatE is better than RotatE*. RotatE* indicates that the learned dataset does not describe the hasInfluence relation between factors. In this section, more representation learning models are used to compare the learning effect for the forest fire knowledge graph with the hasInfluence relation. In the Factor Schema, we refer to the calculation process of the FWI system value and use hasInfluence to enhance the connections between attributes. We carried out the experiment to show the benefits of considering relations between factors. Figure 7 shows the results. MeanRank represents the consideration of relation logic between factors, i.e., design hasInfluence. MeanRank★ represents the simple consideration of the relations between forest fire events and attributes, i.e., removing hasInfluence.

We compared the eight basic knowledge-graph- and representation-learning-based models with the metric of Raw, Filt. The relation between factors obviously provides better results. We conclude that the structure of the graph is more irregular when considering the relations between attributes rather than tending to the form of a bipartite graph. This was also the reason for the better results.

4. Discussion

In the main experiments, we utilized the physical model method (considering a naive average predictor of FWI), traditional machine learning methods (MR, DT, RF, SVM), and a deep learning forest fire prediction method (MLP) as baseline methods to compare with the methods based on knowledge graph data fusion. Table 6 shows that the RotateS2F model and RotatE model effectively reduce the error of fire prediction, and it also shows that the multi-source data fusion method is an effective way to reduce forest fire prediction errors. The multi-source data fusion method has the following two advantages: (1) From the perspective of heterogeneous data fusion, we designed a schema as the conceptual model, and unified the heterogeneous data involved in forest fire from the abstract semantic level. The traditional methods mostly focus on data-oriented fusion methods while rarely considering semantic concepts. Therefore, they hardly fuse the heterogeneous data by abstract semantic modeling. (2) From the perspective of multi-source data fusion, theoretically, multi-source data can provide more valuable information and allow the analysis method to consider more forest fire attributes for the sake of improving the completeness of analysis. Besides data fusion, the prediction method based on graph structure considers the dependencies and correlations of attributes of forest fires in different fields, which makes full utilization of the relations of data. It is well suitable for the actual situations of forest fires.

The traditional knowledge graph-based prediction methods need artificially defined inference rules that are hard to pre-define well. To show that our forest fire prediction method has advantages in multi-source data fusion scenarios, we compared it with RotatE and GraphSAGE. Table 6 shows that our method can learn the spatiotemporal information representation of the forest fire knowledge graphs and effectively predict forest fire burning areas. In the experimental results, our method outperformed the single knowledge-graph- and representation-learning-based method RotatE and the GNN method GraphSAGE. We speculate that both semantic features (mainly extracted by a knowledge graph and representation learning) and structural features (mainly extracted by the GNN) are important for forest fire prediction in the application scenarios of multi-source data fusion.

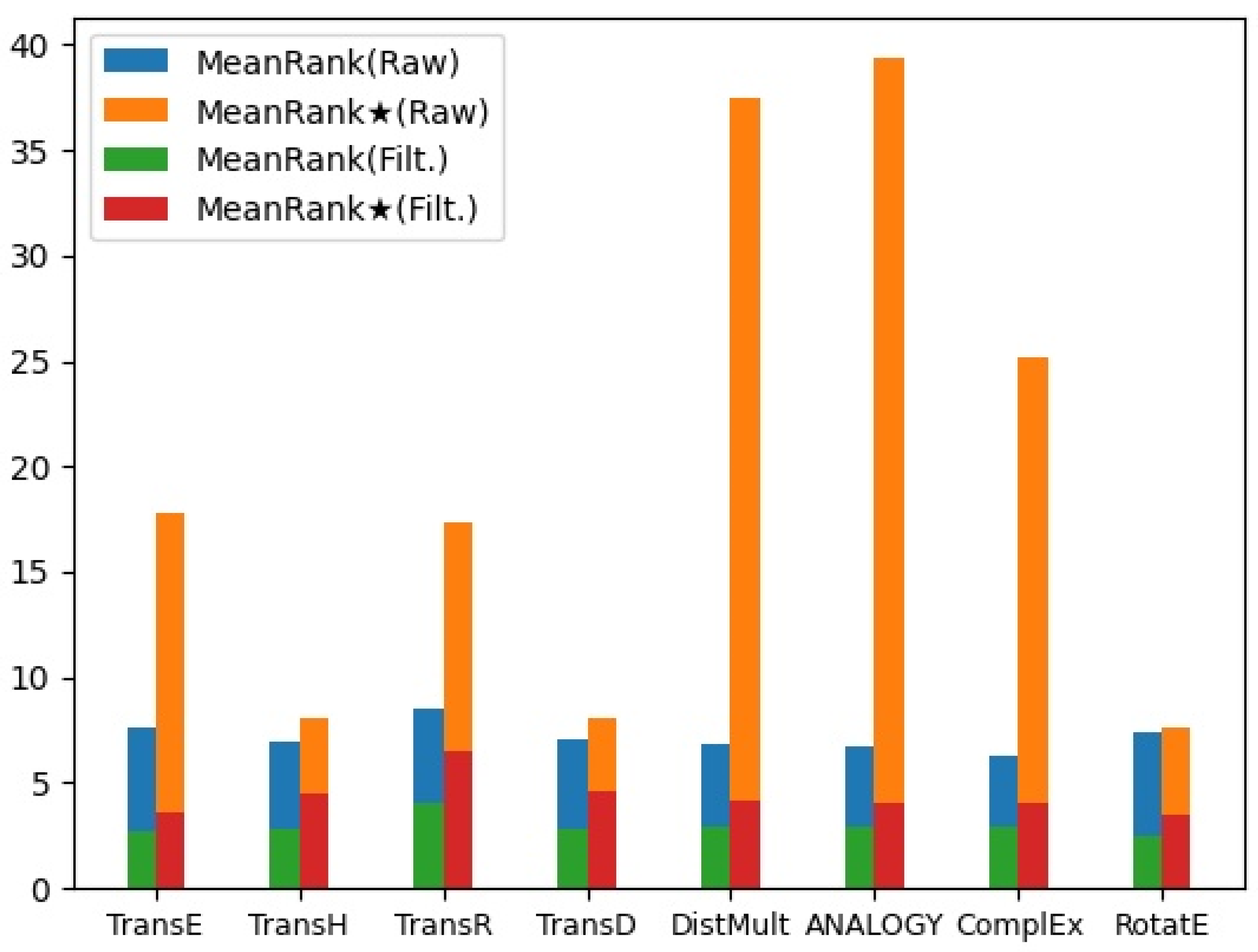
The method proposed in this paper has a certain novelty in forest-fire-oriented spatiotemporal data prediction. We combine multi-source heterogeneous data with a knowledge graph and deep learning for predicting. For the task of forest fire prediction, our method provides a novel perspective for data organization and predictive analysis. Based on the experimental results, we summarize the characteristics of our method as follows: (1) The effect of our forest fire prediction method based on a knowledge graph and representation learning on the Montesinho Natural Park dataset outperforms the baseline methods that do not consider multi-source data fusion. (2) The effect of RotatE is better than that of RotatE* in Table 6. Additionally, it is shown in Figure 7 that adding relations as prior knowledge to the forest fire knowledge graph can improve the predictions. From another perspective, when using our method to obtain the semantic information of the forest fire knowledge graph, it is necessary to construct a dense graph structure using forest fire data sources as often as possible. (3) The forest fire knowledge graph is suitable to use in our graph representation learning method, as shown in Table 7, which can model multiple relational patterns, such as symmetric, antisymmetric, one-to-many, and many-to-many relations. The ability of a knowledge graph and representation learning to model and infer various relational patterns can improve forest fire prediction.

There are limitations to our method. (1) We performed experiments on only one forest fire dataset, which cannot show that our method has good generalization performance. (2) When the datasets are too small, the results of our method may not be superior to those of the traditional machine learning methods. If the forest fire knowledge graph is sparse, our method will not work well in prediction. To avoid that situation, there are usually three methods: reducing the scale of discretization in the forest fire knowledge graph to obtain more nodes, adding additional relations, and adding additional existing data.

It is possible to expand our method for future requirements. From the perspective of model construction, if we obtain more in-depth relations between different data classes and make the graph denser, it may have better forest fire predictions. In addition, we can perform experiments on other forest fire datasets to verify the generalization of the method.

5. Conclusions

In this paper, we focused on multi-source data fusion and representational feature computation for forest fires. To address the problem of automatic calculation of semantic features in data fusion scenarios, we proposed a representation-learning-based forest fire prediction method. First, we proposed a general schema for building graphs for forest fires. Based on the schema, we organize forest fire data into a unified representation space. We then proposed the RotateS2F model to represent the elements in the forest fire knowledge graph as continuous vectors. The RotateS2F model combines the characteristics of a knowledge graph and a deep learning method and learns semantic information and graph structural information from a forest fire knowledge graph. Finally, the experiment demonstrated the superiority of our method by a reduction in MAD by 28.61% and a reduction in RMSE by 53.62% compared with the best previous methods.

In this paper, to describe the proposed method clearly, we took forest fires as an example to introduce the idea of the method. In the future, our method can be applied to other spatiotemporal event predictions with appropriate extensions. The key to the application is to construct a suitable schema to clarify the task boundary and define the representation of spatiotemporal data.